Как найти величину проекции координат

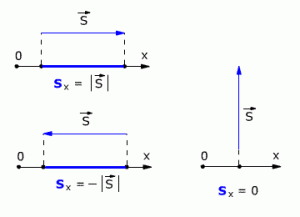
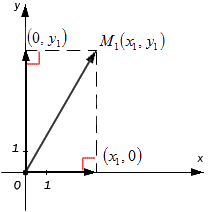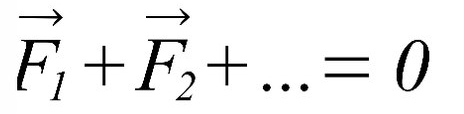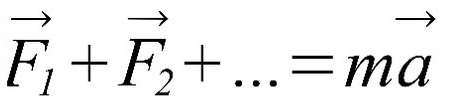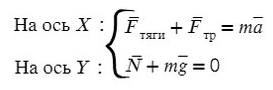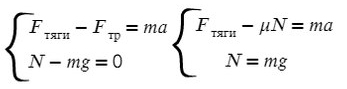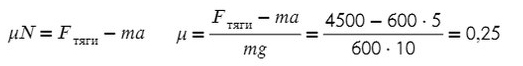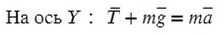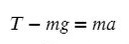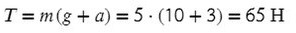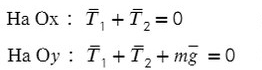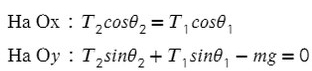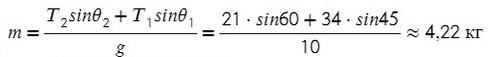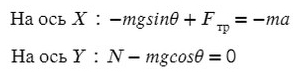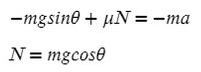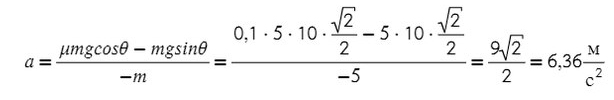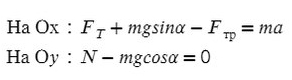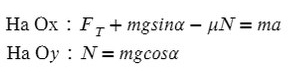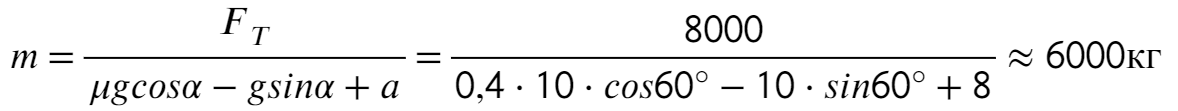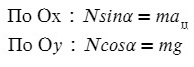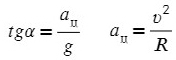Ось – это направление. Значит, проекция на ось или на направленную прямую считается одним и тем же. Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.

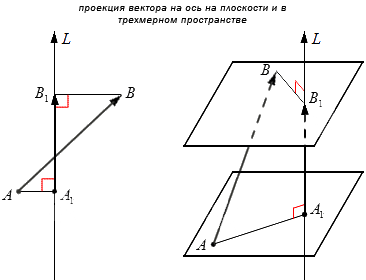
Если имеем ось L и ненулевой вектор AB→, то можем построить вектор A1B1⇀, обозначив проекции его точек A1 и B1. 

A1B→1 будет являться проекцией вектора AB→ на L.

Если идет речь о проекции a→ на ненулевой b→ или проекции a→ на направление b→, то имеется в виду проекция a→на ось, с которой совпадает направление b→. Проекция a→ на прямую, определяемая b→, имеет обозначение npb→a→→. Известно, что когда угол междуa→ и b→, можно считать npb→a→→ и b→ сонаправленными. В случае, когда угол тупой, npb→a→→ и b→противоположно направлены. В ситуации перпендикулярностиa→ и b→, причем a→ – нулевой, проекция a→ по направлению b→ является нулевым вектором.

Числовая проекция вектора на ось

Числовая характеристика проекции вектора на ось – числовая проекция вектора на заданную ось.

Числовой проекцией вектора на ось называют число, которое равно произведению длины данного вектора на косинус угла между данным вектором и вектором, который определяет направление оси.

Числовая проекция AB→ на L имеет обозначениеnp LAB→, а a→ на b→ – npb→a→.

Исходя из формулы, получим npb→a→=a→·cosa→, b→^, откуда a→ является длиной вектора a→, a⇀, b→^ – угол между векторами a→ и b→.

Получим формулу вычисления числовой проекции: npb→a→=a→·cosa→, b→^. Она применима при известных длинах a→ и b→ и угле между ними. Формула применима при известных координатах a→ и b→, но имеется ее упрощенный вид.

При известном cos(a→, b→^)=a⇀, b→a→·b→, имеем a→, b→ как скалярное произведение a→ и b→. Следуя из формулы npb→a→=a→·cosa⇀, b→^, мы можем найти числовую проекцию a→ направленную по вектору b→ и получим npb→a→=a→, b→b→. Формула эквивалента определению, указанному в начале пункта.

Числовой проекцией вектора a→ на ось , совпадающей по направлению с b→, называют отношение скалярного произведения векторовa→ иb→ к длине b→. Формула npb→a→=a→,b→b→ применима для нахождения числовой проекции a→ на прямую, совпадающую по направлению с b→, при известных a→ и b→ координатах.

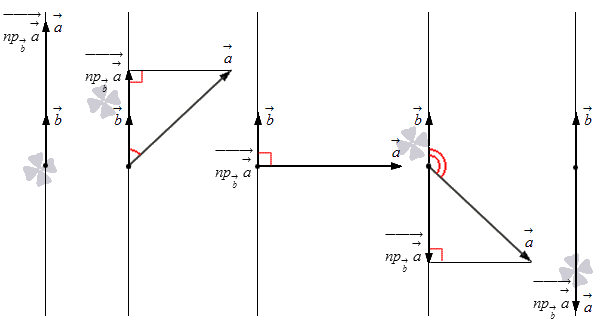
Просмотрим связь междуa→ на L и длиной проекции a→ на L. Начертим ось L, добавив a→ и b→ из точки на L, после чего проведем перпендикулярную прямую с конца a→ на L и проведем проекцию на L. Существуют 5 вариаций изображения:

Первый случай при a→=npb→a→→ означает a→=npb→a→→, отсюда следует npb→a→=a→·cos(a,→b→^)=a→·cos0°=a→=npb→a→→.

Второй случай подразумевает применение npb→a→⇀=a→·cosa→,b→, значит, npb→a→=a→·cos(a→,b→)^=npb→a→→.

Третий случай объясняет, что при npb→a→→=0→ получаем npb⇀a→=a→·cos(a→,b→^)=a→·cos90°=0, тогда npb→a→→=0 и npb→a→=0=npb→a→→.

Четвертый случай показывает npb→a→→=a→·cos(180°-a→,b→^) = -a→·cos(a →, b→^), следует npb→a→=a→·cos(a→,b→^)=-npb→a→→.

Пятый случай показывает a→=npb→a→→, что означаетa→=npb→a→→, отсюда имеем npb→a→=a→·cosa→,b→^=a→·cos180°=-a→=-npb→a→.

Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.

Уравнения проекций на оси координат

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых. Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

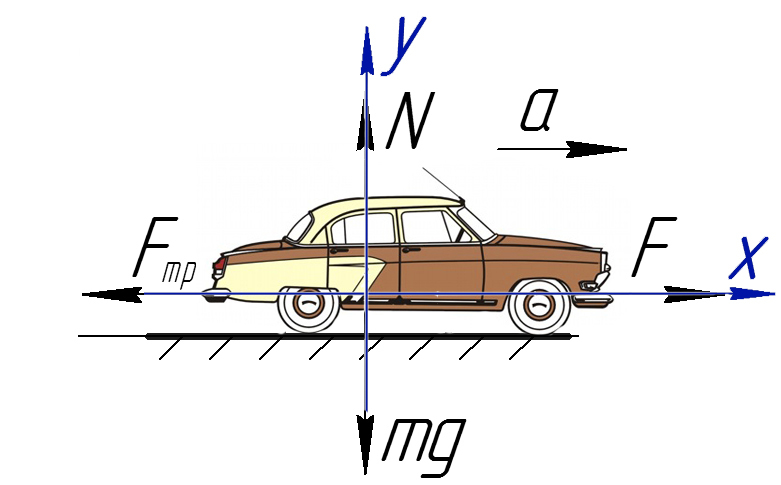
Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y: N = mg, тогда в данной задаче Fтр = μmg.

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

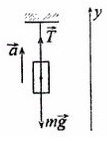
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

T – сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

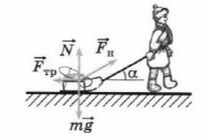
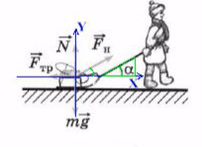
Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей.

Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

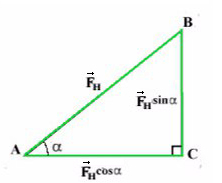
Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле , ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

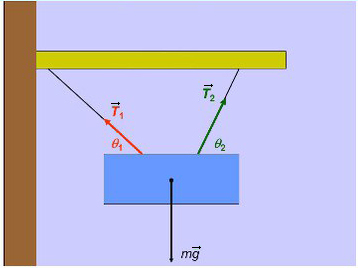
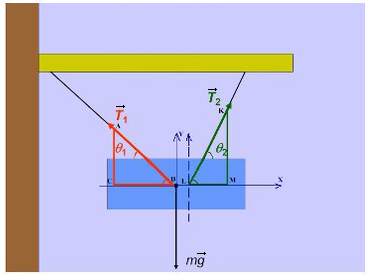
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

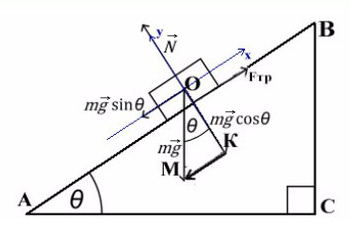
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска?

Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
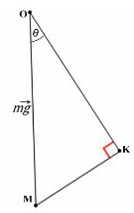
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

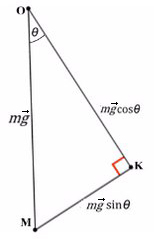
Рассмотрим поподробнее ΔKOM:

Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

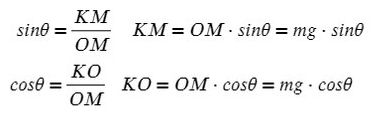
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время.

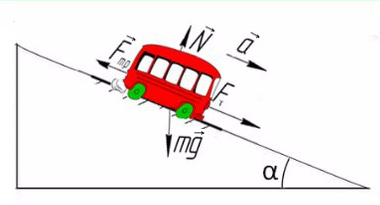
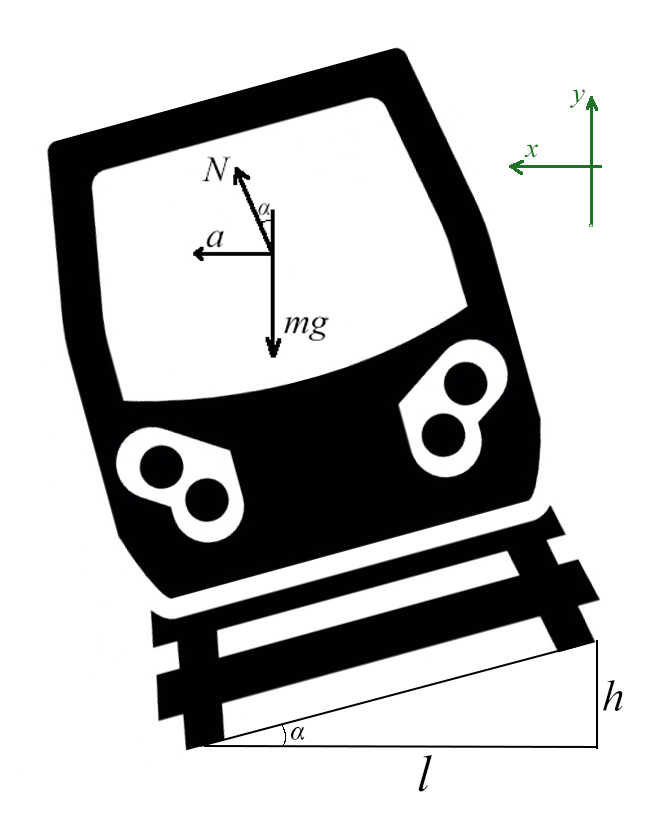
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с² и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

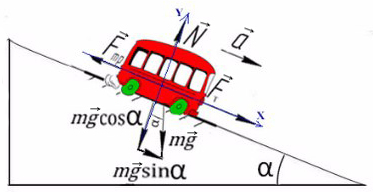
Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное – понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс – это отношение противолежащего катета к прилежащему:

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами.

Как составить уравнение проекций ?

Автор: Константин Вавилов · Опубликовано 23.09.2016 · Обновлено 28.11.2017

При решении задачек по статике, в теоретической механике или при решении задач по сопромату, часто, требуется определять сумму проекций сил на какую-то ось. Например, в термехе это используется при приведении какой-то системы сил к простейшему виду. В сопромате для определения реакций возникающих в опорах.

Уравнения проекций на примере

Рассмотрим, как составить уравнение проекций всех сил на какую-либо ось на примере. Возьмем прямоугольную декартову систему координат x-y и произвольную систему сил:

Проецируем все силы на координатные оси.Сила F1 дает положительную проекцию на ось X, так как ее направление совпадает с направлением этой оси. На ось Y эта сила не дает проекции, так как она перпендикулярная этой оси. Рассуждая, таким образом, можно записать следующие уравнения сумм проекций:

В выше описанном примере все силы были параллельны или перпендикулярны осям, но на практике же в задачах обычно силы расположены под некоторым углом к координатным осям. В таком случае силы раскладываются на две проекции параллельные осевым линиям:

Для нахождения этих сил удобнее вынести отдельно силовой треугольник и найти их следующим образом:

После этого можно записать уравнение проекций сил на горизонтальную и вертикальную ось:

Координатный способ определения движения точки в теоретической механике

Содержание:

Координатный способ определения движения точки:

При координатном способе определения движения точки должны быть даны уравнения движения, т. е. заданы координаты точки как функции времени:

Задание движения точки в прямоугольных координатах

Как известно из курса аналитической геометрии, положение точки M в пространстве может быть определено положением ее проекций P, Q и R на три взаимно перпендикулярные оси (рис. 84), называемые осями координат.

Рис. 84

Положение точки P на оси Ox вполне определяют абсциссой х. Совершенно так же положение точек Q и R определяют ординатой у и аппликатой z.

Если точка M движется относительно осей xOyz, то проекции Р, Q и R перемещаются по осям и координаты точки M изменяются.

Для определения движения точки M нужно знать ее координаты для каждого мгновения, выразить их в функциях времени.

Эти функции непрерывны, так как точка не может из одного положения перейти в другое, минуя промежуточные. Они должны быть однозначны, так как точка занимает в пространстве в каждое мгновение только одно положение.

Соотношения (58) называют кинематическими уравнениями движения точки в прямоугольных координатах, а способ определения движения точки посредством соотношений (58) называют координатным способом определения движения точки. Это название неточно, потому что, кроме прямолинейных прямоугольных координат, существует множество других координатных систем.

Если траектория точки лежит в одной плоскости, то движение точки определяют двумя уравнениями в системе координат xОy: x=x(t), y=y(t).

Следовательно, при координатном способе задания движения точки в пространстве нужно задать ее три координаты, а на плоскости—две координаты как функции времени. Если точка движется прямолинейно, то, приняв прямую, по которой она движется, за ось абсцисс, мы определим движение точки одним уравнением

Если движение точки задано в координатной форме, то для определения ее траектории надо из уравнений движения исключить время

Уравнение траектории

Можно определить траекторию точки, если в уравнениях движения (58) давать аргументу t различные значения и, вычислив соответствующие значения функций, отмечать положения точки по ее координатам. Следовательно. кинематические уравнения движения точки (58) можно
рассматривать как уравнения ее траектории в параметрической форме, а время — как независимый переменный параметр.

Однако более удобно получить уравнение траектории, исключив время из уравнений (58). В самом деле, траекторией называют геометрическое место всех положений движущейся точки, но в геометрии нет понятия времени, а поэтому для получения уравнения траектории нужно из кинематических уравнений движения (58) исключить время t. Если точка движется в плоскости, то, исключив время из уравнений (58′) и (58″), мы получим соотношение, связывающее х и у:

Это уравнение плоской кривой—траектории точки. Если же движение задано тремя уравнениями (58), то, исключив время, получим два уравнения между тремя координатами:
(59 / )

выражающие, как известно из аналитической геометрии, кривую (траекторию) в пространстве. Точнее говоря, уравнения (59) или (59′) выражают кривую, которая полностью или в некоторой своей части является геометрическим местом всех положений движущейся точки.

Иногда бывает нужно выразить в естественной форме движение точки, заданное в прямоугольных координатах уравнениями (58), и, кроме уравнения траектории, дать также уравнение (51) движения точки по траектории. Чтобы его получить, надо продифференцировать уравнения (58) и полученные дифференциалы координат точки подставить в известную из курса высшей математики формулу, выражающую абсолютную величину элемента дуги:

(60)

Проинтегрировав (60), мы получим уравнение (51), выражающее длину дуги s как функцию времени, или, что то же, закон движения точки по траектории.

Задача №1

По заданным уравнениям движения точки в координатной форме найти уравнение траектории и уравнение движения по траектории:

1) х = 5 cos 2t, y = 3+5sin 2t;
2) x=21,2 sin 2 t, у = 21,2 cos 2t.

В обоих примерах за единицу длины принят сантиметр, за единицу времени — секунда.

Решение. Чтобы определить уравнение траектории по уравнениям движения, перенесем во втором из заданных уравнений 3 влево, возведем оба уравнения в квадрат и, сложив, получим

Это уравнение окружности с центром в точке: x = 0, y = +3.

Чтобы получить закон движения, продифференцируем заданные уравнения: dx=—10 sin 2t dt, dy = 10 cos 2t dt.

Возводя в квадрат, складывая, извлекая квадратный корень и интегрируя, находим закон движения по траектории:
s=10t + C, где C = s₀.

2) Исключим время из уравнений движения во втором примере:

Это уравнение первого порядка относительно х и у, следовательно, траектория-прямая линия. Прямая отсекает на положительных направлениях осей координат отрезки по 21,2 см. Однако не вся прямая служит траекторией точки: из заданных уравнений видно, что х и у должны быть всегда положительны и не могут быть больше 21,2 см каждый, поэтому траекторией точки является лишь отрезок прямой x+y = 21,2, лежащей в первом квадранте (рис. 85).

Рис. 85

На этом примере мы видим, что траекторией точки иногда является лишь часть линии, выражаемой уравнением траектории.

Продифференцируем уравнения движения:

dx = 21,2 ∙ 2 sin t cos t dt,
dy = 21,2 ∙ 2 sin t cos t dt.

Теперь no формуле (60) нетрудно найти элемент дуги траектории:

ля получения уравнения (51) движения точки по траектории остается лишь проинтегрировать найденное выражение. Интегрируем и подставляем начальные условия (при t= 0, s₀ = 0):

Ответ. Уравнения траекторий x 2 +(y-3) 2 = 25 и x+y=21,2; уравнения движения по траектории s=10t+s₀ и s = 30 sin 2 t.

Задача №2

Движение точки задано уравнениями:
х = x’ cos φ (t)—y’ sin φ (t),
y = x’ sin φ (t) + y’ cos φ (t),

где х’ и у’ — некоторые постоянные величины, a φ(t)— любая функция времени. Определить траекторию точки.

Решение. Возведем каждое из уравнений в квадрат, а затем сложим их:

x 2 + y 2 = χ ‘2 + y ‘2 .

По условию, х’ и у’ — постоянные. Обозначая сумму их квадратов через r 2 , получим

Ответ. Окружность с центром в начале координат радиуса .

Задача №3

Поезд длиной l м сначала идет по горизонтальному пути (рис. 86, а), а потом поднимается в гору под углом 2α к горизонту. Считая поезд однородной лентой, найти траекторию его центра тяжести.

Рис. 86

Решение. Для решения задачи нужно определить координаты центра тяжести поезда, найти уравнения движения центра тяжести и исключить из них время.

Направим оси координат по внутренней и внешней равиоделяшнм угла 2α (рис. 86, б). Траектория центра тяжести поезда не зависит от скорости поезда. Для простоты подсчетов предположим, что он идет равномерно со скоростью υ м/сек и в начальное мгновение t=0 подошел к горе.

Тогда за время t сек на гору поднимется υt м состава поезда и останется на горизонтальном пути l — υt м. Будем считать, что единица длины поезда весит γ.

Применяя формулы (48), найдем координаты центра тяжести поезда:

Координаты центра тяжести представлены здесь как функции времени, следовательно, полученные соотношения являются уравнениями движения центра тяжести поезда. Определяя t (или υt) из первого уравнения и подставляя во второе, найдем уравнение траектории:

Задача №4

Мостовой кран движется вдоль цеха согласно уравнению х = t; по крану катится в поперечном направлении тележка согласно уравнению у = 1,5t (х и у—в м, t — в сек). Цепь укорачивается со скоростью t>=0,5. Определить траекторию центра тяжести груза (в начальном положении центр тяжести груза находился в горизонтальной плоскости хОу, ось Oz направлена вертикально вверх).

Решение. В условии задачи даны лишь два уравнения движения и вертикальная скорость груза:

откуда dz = 0,5dt, и легко получаем третье уравнение:

z = 0,5t

Определив t из первого уравнения, подставим во второе и в третье:

y= 1,5x, z = 0,5x

Координаты груза должны удовлетворять одновременно обоим уравнениям, т. е. траектория лежит одновременно в обеих плоскостях и является линией их пересечения.
Ответ. Прямая.

Алгебраическая величина скорости проекции точки на координатную ось равна первой производной от текущей координаты по времени:

Алгебраическая величина скорости проекции точки на ось

Пусть движение точки M определяется тремя уравнениями:
x =x(t), (58′)
y = y(t), (58″)
z = z(t). (58″‘)

По мере движения точки M в пространстве ее проекции P, Q и R движутся по своим прямолинейным траекториям, т. е. по осям координат, и их движения вполне соответствуют движению точки М.

Так, координата (абсцисса) точки P всегда равна абсциссе точки М, а координаты точек QnR всегда равны ординате и аппликате точки М. Следовательно, при движении точки M в пространстве согласно уравнениям (58) точка P движется по оси Ox согласно уравнению (58′), а точки Q и R— соответственно по осям Oy и Oz согласно уравнениям (58″) и (58″‘).

Таким образом, движение точки M в пространстве можно разложить на три прямолинейных движения ее проекций P, Q и R.

Определим скорость υ_p точки P при движении этой точки по ее прямолинейной траектории Ох, иными словами, определим скорость проекции точки M на ось Ох.

Алгебраическая величина скорости выражается по формуле (53), причем дифференциалом расстояния точки P является дифференциал абсциссы х, а поэтому

(61)

Следовательно, алгебраическая величина скорости проекции P точки M на координатную ось равна первой производной от текущей координаты х по времени t. Она положительна, если точка P движется в положительном направлении оси Ох, и отрицательна, если точка P движется в отрицательном направлении.
Аналогично получаем алгебраические скорости проекций Q и R на ось Oy и на ось Oz:

(61″)

(61″‘)

Чтобы получить векторы скоростей проекций, надо умножить величины (61) на единичные векторы:
(61)

Алгебраическая величина скорости проекции точки на ось равна проекции скорости той же точки на туже ось:

Скорость проекции и проекция скорости

Пусть точка М за бесконечно малый отрезок времени dt передвинулась по своей траектории на элемент дуги ds, абсолютную величину которого выразим формулой (60):

где dx, dy и dz — проекции элемента дуги на оси координат, или, Что то же, элементарные приращения координат точки М.

На рис. 87 эти элементы условно изображены конечными отрезками. Как видно из чертежа, косинусы углов, составляемых элементарным перемещением (а следовательно, и скоростью точки), с осями х, у и z соответственно равны

(62)

Величина скорости точки M может быть определена по (53):

Чтобы определить проекцию скорости на какую-либо ось, надо умножить абсолютную величину скорости на косинус угла между направлением скорости и направлением этой оси. Таким образом, для проекций скорости точки M на оси координат имеем:

(63′)

(63″)

(63″‘)

Рис. 87

Равенства (63) словами нужно читать так: проекция скорости точки на ось равна алгебраической скорости проекции точки на ту же ось.

Задача №5

Доказать, что проекция скорости точки M (х, у, z) иа плоскость хОу равняется скорости , с которой движется по плоскости проекция M₁ (х, у, О) точки M на ту же плоскость.

Решение. Скорость точки M составляет с осью Oz угол γ_υ, следовательно, угол, составляемый ею с плоскостью хОу, равен 90° — yυ п косинус этого угла равен sinγ_υ. Поэтому модуль проекции скорости точки M на плоскость хОу

Подводя под радикал и выражая cosγ_υ, по формуле (62), мы убедимся, что проекция скорости на плоскость равна по величине скорости проекции:

Направления векторов и тоже совпадают, так как направляющие косинусы их одинаковы. Теорема доказана.

Модуль скорости точки равен квадратному корню из суммы квадратов проекций скорости на оси координат:

Модуль скорости. Возведем в квадрат каждое из равенств:
(63)

Сумма квадратов направляющих косинусов равна единице и

(64)

Перед радикалом взят положительный знак, так как величина скорости (ее модуль) всегда положительна. В этом ее существенное отличие от алгебраической величины скорости (53), характеризующей скорость точки при движении по заданной траектории и имеющей знак « + » или «—» в зависимости от направления движения. Величину (64) иногда называют полной скоростью.

Направление скорости можно определить по направляющим косинусам скорости:

Направляющие косинусы скорости

Равенство (64) позволяет определить модуль скорости точки, движение которой задано уравнениями (58). Направление скорости определяется по косинусам углов, составляемых положительными направлениями осей координат с направлением скорости. Значения этих косинусов, называемых направляющими косинусами скорости, мы получим из уравнений (63):

(62′)

где , и — производные от х, у и z по t.

Если точка движется в плоскости хОу, то γ_υ = 90 o , cosγ_υ = 0 и cos α_υ = sin β_υ.

Задача №6

Уравнения движения суть

Определить траекторию и скорость.

Решение. Из уравнений движения следует, что х и у всегда больше нуля.
Для определения уравнения траектории возведем каждое из уравнений движения в квадрат и составим разность

x 2 – у 2 = a 2

Для определения скорости найдем сначала ее проекции:

а затем уже и полную скорость.

Ответ. Траектория — ветвь гиперболы x 2 – у 2 = a 2 — расположена в области положительных значений х; скорость .

Задача №7

Движение точки задано уравнениями

причем ось Ox горизонтальна, ось Oy направлена по вертикали вверх, υ₀, g и —величины постоянные. Найти траекторию точки, координаты наивысшего ее положения, проекции скорости на координатные оси в тот момент, когда точка находится на оси Ох.

Решение. Уравнения описывают движение тела, брошенного со скоростью υ₀ под углом α₀ к горизонту (к оси Ох).
Чтобы найти уравнение траектории, определим время из первого уравнения и подставим найденное значение во второе; получим

уравнение параболы, проходящей через начало координат (рис. 88).

Рис. 88

Чтобы определить координаты наивысшего положения, мы можем применить известные из дифференциального исчисления правила нахождения максимума функции, т. е. взять производную , приравняв ее нулю, определить значение х и, подставив его в уравнение траектории, определить соответствующее значение у, убедившись при этом, что вторая производная . Однако мы найдем координаты наивысшего положения точки другим методом, для чего, продифференцировав по времени уравнения движения точки, найдем проекции ее скорости:

Первое из этих уравнений показывает, что проекция скорости на горизонтальную ось постоянна и равна проекции начальной скорости.

Исследование второго уравнения убеждает, что проекция скорости на вертикальную ось в начальное мгновение положительна и равна υ₀ sin α₀; затем, по мере увеличения t, проекция υ_y уменьшается, оставаясь положительной до мгновения , когда υ_y обращается в нуль, после чего υ_y становится отрицательной, возрастая по абсолютной величине с течением времени t.

Таким образом, точка движется вправо, сначала поднимаясь, затем опускаясь. Мгновение , при котором точка кончила подниматься, но еще не начала опускаться, соответствует максимальному подъему точки. В это мгновение скорость горизонтальна и . Подставляя найденное значение t в уравнения движения, найдем координаты наивысшей точки траектории:

Определим проекции скорости в мгновение, когда точка находится на оси Ох. В это мгновение ордината точки равна нулю. Приравняем пулю второе из уравнений движения:

Точка находится на оси Ox два раза: при t=0 при

Первое значение t соответствует началу движения, второе —падению точки на ось Ох. Второе значение равно времени всего полета, и оно вдвое больше полученного нами ранее времени наивысшего подъема: время падения равно времени подъема.

Подставляя значение t=0 в уравнения, определяющие проекции скорости, найдем проекции скорости в начальное мгновение:

Подставляя второе из найденных значений t, найдем скорости в момент падения:

Ответ: 1) Парабола

2)

3) υ_x = υ₀ cos α₀, υ_y = υ₀ sin α₀.

причем верхний знак соответствует началу движения, а нижний—концу.

Задача №8

По осям координат (рис. 89) скользят две муфты A и B, соединенные стержнем AB длиной l. Скорость В равна υ_B.

При каком положении муфт скорость муфты А вдвое больше υ_B?

Решение. Координата точки А связана с координатой точки В соотношением

Считая х и у функциями времени и продифференцировав это равенство по времени, найдем зависимость между скоростями обеих точек:

Но и по условию надо, чтобы величина была равна 2υ_B, т. е.

откуда после алгебраических преобразований получаем ответ.

Ответ: (см. задачи № 57 и 89, где даны другие решения).

Проекция ускорения точки на координатную ось равна первой производной по времени от проекции скорости на ту же ось или второй производной от текущей координаты по времени:

Ускорение проекции и проекция ускорения

Ускорение характеризует изменение скорости точки в данное мгновение. Оно выражается пределом отношения изменения вектора скорости к соответствующему промежутку времени при стремлении этого промежутка времени к нулю.

Для того чтобы определить ускорение точки M при ее движении в пространстве, рассмотрим сначала движение по оси Ox точки Р, являющейся проекцией точки M на эту ось.

Пусть в некоторое мгновение t алгебраическая величина скорости точки P была υ_х, а в мгновение t_l = t + Δt стала υ_x+∆υ_x. Тогда ускорение точки P по величине и по знаку выразится пределом

Если знаки υ_x и a_p одинаковы, то движение точки P ускоренное, а если различны, то замедленное.

Аналогично выразятся ускорения проекций Q и R точки M на другие координатные оси:

Проекции υ_x, υ_y и υ_z сами являются производными по времени от координат точки, поэтому ускорения проекций можно выразить вторыми производными по времени от координат точки. Эти равенства характеризуют не только величины, но и знаки ускорений проекций. Иными словами, они выражают изменение алгебраических скоростей проекций P, Q и R в мгновение t.

Только что доказанная теорема о равенстве алгебраической скорости проекции точки на ось и проекции скорости той же точки на ту же ось справедлива для любого момента времени. Следовательно, эта теорема относится не только к скорости, но и к ее изменению в любое мгновение, т. е. к ускорению. Это значит, что написанные выше равенства выражают также проекции a_x, а_у и а_z ускорения а точки M на оси координат O_x, O_y и O_z:

(65)

где cosα_a, cosβ_a и cosγ_a—направляющие косинусы ускорения.

Можно рассматривать эти величины (65) как векторы, направленные по осям координат:

(65′)

Модуль ускорения точки равен квадратному корню из суммы квадратов проекций ускорения на оси координат:

Величина ускорения при координатном способе задания движения точки

Возведем в квадрат каждое из равенств:

и затем сложим их:

(66)

Перед радикалом взят знак плюс, так как модуль вектора—величина положительная. Ускорение точки в отличие от проекций ускорения на оси координат или на другие направления обычно называют полным ускорением. Поэтому равенство (66) можно прочитать так: величина полного ускорения точки равна квадратному корню из суммы квадратов его проекций на оси координат.

Направление ускорения можно определить по направляющим косинусам ускорения:
,

Направляющие косинусы ускорения

Направление ускорения определяют по косинусам углов, составляемых положительными направлениями осей координат с вектором ускорения. Формулы направляющих косинусов получаем из уравнений (65):
(67′)

(67”)

(67”’)

Для определения направления ускорения в каждом конкретном случае надо сначала найти ускорение проекций по (65), для чего необходимо дважды продифференцировать уравнения движения (58), затем найти величину ускорения по (66), а потом определить направляющие косинусы ускорения по (67).

Направление ускорения обычно не совпадает с направлением скорости, и направляющие косинусы (67) ускорения только при прямолинейном ускоренном движении точки постоянно равны направляющим косинусам (62) скорости.

Если точка движется в плоскости хОу, то γ_a = 90 o , cosγ_a = 0, cosα₀ = sin βa.

Задача №9

Точка M движется в системе координат хОу согласно уравнениям х= r cos πt, y=r sinπt, где х и у—в см, a t — в сек. Найти уравнение траектории точки М, ее скорость, направляющие косинусы скорости, ускорение, направляющие косинусы ускорения. Для значений времени t=0; 0,25; 0,5; 0,75, . 2 сек дать чертежи положений точки M, вектора скорости и вектора ускорения.

Решение. Из уравнения движения видно, что координаты точки M являются проекциями на соответствующие оси радиуса-вектора r, составляющего с осью абсцисс угол πt:

Для определения траектории точки исключаем время из уравнений движения. Получаем уравнение окружности

x 2 + y 2 = r 2

Найдем теперь проекции скорости на оси координат, для чего продифференцируем по времени уравнения движения:

откуда по (64) получаем модуль скорости

Величина скорости точки M постоянна.

Направляющие косинусы скорости определим по формуле (62′):

Эти соотношения показывают, что направление скорости непрерывно меняется и что скорость перпендикулярна радиусу-вектору, проведенному из центра О в точку М.

Ускорение точки M найдем по его проекциям, для чего продифференцируем выражения, полученные для проекций скорости:

откуда по (66) получаем величину ускорения

Ускорение характеризует быстроту изменения вектора скорости не только по величине, но и по направлению, поэтому, несмотря на постоянство модуля скорости точки М, ускорение этой точки не равно нулю. Как видно из полученного

Рис. 90

равенства, величина полного ускорения постоянна. Направление ускорения определим по направляющим косинусам согласно (67):

Направление ускорения точки M противоположно направлению радиуса-вектора.
Положения точки M в различные мгновения показаны на рис. 90, а, векторы скорости — на рис. 90,6 и векторы ускорения — на рис. 90, в.

Ответ. Точка M движется по окружности радиуса r против часовой стрелки с постоянной по величине скоростью υ = rπ и с постоянным по величине ускорением a = rπ 2 .

Задача №10

Снаряд выбрасывается из орудия с начальной скоростью υ=1600 м/сек под утлом α₀ = 55 o к горизонту. Определить теоретическую дальность и высоту обстрела, учитывая, что ускорение свободно падающих тел g = 9,81 м/сек 2 .

Решение. Сначала составим уравнения движения снаряда в координатной форме, направив оси, как показано на чертеже (см. рис. 88), для этого определим проекции ускорения:

Разделив переменные, интегрируем:
υ_х= С₁, υ_y = – gt + С2

Подставляя вместо переменных величин их начальные значения, увидим, что C₁ и C₂ равны проекциям начальной скорости:

1600 cos 55 o = C_1, 1600 sin 55 o = – gt + C_2.

Подставим их в уравнения, полученные для проекций скорости:

Разделяя переменные и интегрируя, найдем

При t = 0 координаты снаряда были: х =0, у = 0. Подставляя эти данные, найдем, что C₃ = O и C₄ = O. Значения cos 55° и sin 55° найдем в тригонометрических таблицах. Уравнения движения снаряда примут вид:

Далее поступим, как при решении задачи № 42: приравняв вертикальную скорость нулю, найдем время подъема снаряда (t= 133,7 сек); подставляя это значение t в уравнение движения по оси Оу, найдем теоретическую высоту обстрела (h = 87 636 м); удваивая время /, найдем время полета снаряда (t = 267,4 сек); подставляя это значение- в уравнение движения по оси Ох, найдем теоретическую дальность обстрела (l = 245 393 м).
Ответ. l = 245 км; h = 87,5κм.

Рекомендую подробно изучить предмет:

Теоретическая механика

Ещё лекции с примерами решения и объяснением:

• Касательное и нормальное ускорения точки
• Основные законы динамики
• Колебания материальной точки
• Количество движения
• Пара сил в теоретической механике
• Приведение системы сил к данной точке
• Система сил на плоскости
• Естественный и векторный способы определения движения точки

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

[spoiler title=”источники:”]

http://ssopromat.ru/statika/kak-sostavit-uravnenie-proektsiy/

http://www.evkova.org/koordinatnyij-sposob-opredeleniya-dvizheniya-tochki-v-teoreticheskoj-mehanike

[/spoiler]

Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

Путь

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

На рис. 1.1:

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Проекции вектора перемещения

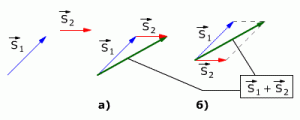
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения  (см.рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

Sx = AxBx

ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор с проекцией вектора на какую-либо ось (например, S_x). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.

Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

Sx = x – x0

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Sy = y – y0
Sz = z – z0

Здесь x₀, y₀, z₀ — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

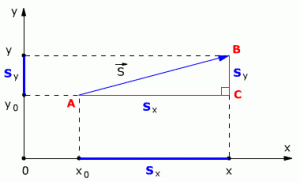
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х₀ и у₀, то есть А(х₀, у₀). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

Sx = x – x0
Sy = y – y0

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

АС = sx
CB = sy

По теореме Пифагора

S2 = Sx2 + Sy2

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Как найти проекции на оси

Чтобы найти проекцию вектора или отрезка на координатные оси, нужно опустить перпендикуляры с крайних точек на каждую из осей. Если же известны координаты вектора или отрезка, его проекцию на оси можно вычислить. То же можно сделать, если известна длина вектора и угол между ним и осью.

Вам понадобится

• – понятие о декартовой системе координат;
• – тригонометрические функции;
• – действия с векторами.

Инструкция

Изобразите вектор или отрезок в системе координат. Затем, из одного из концов отрезка или вектора опустите перпендикуляры на каждую из осей. На пересечении перпендикуляра и каждой оси отметьте точку. Повторите эту процедуру для второго конца отрезка или вектора.

Измерьте расстояние от начала координат, до каждой из точек пересечения перпендикуляров с системой координат. На каждой оси от большего расстояния вычтите меньшее – это и будет проекция отрезка или вектора на каждую из осей.

Если известны координаты окончаний вектора или отрезка, чтобы найти его проекции на оси, от координат конца вычтите соответствующие координаты начала. Если значение получается отрицательным, берите его модуль. Знак минус означает, что проекция находится в отрицательной части координатной оси. Например, если координаты начала вектора (-2;4;0), а координаты конца (2;6;4), то проекция на ось ОХ равна 2-(-2)=4, на ось OY: 6-4=2, на ось OZ: 4-0=4.

Если даны координаты вектора, то они и являются проекциями на соответствующие оси. Например, если вектор имеет координаты (4;-2;5), то это значит, что проекция на ось ОХ равна 4, на ось OY: 2, на ось OZ: 5. Если координата вектора равна 0, то и его проекция на эту ось тоже равна 0.

В том случае, если известна длина вектора и угол между ним и осью (как в полярных координатах), то для того, чтобы найти его проекцию на эту ось, нужно умножить длину этого вектора на косинус угла между осью и вектором. Например, если известно, что длина вектора составляет 4 см, а угол между ним и осью OX в системе координат XOY равен 60º.

Чтобы найти его проекцию на ось OX, умножьте 4 на cos(60º). Расчет 4•cos(60º)=4•1/2=2 см. Найдите проекцию на ось OY, найдя угол между ней и вектором 90º-60º=30º. Тогда его проекция на эту ось составит 4•cos(30º)=4•0,866=3,46 см.

Источники:

• найти проекцию вектора

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

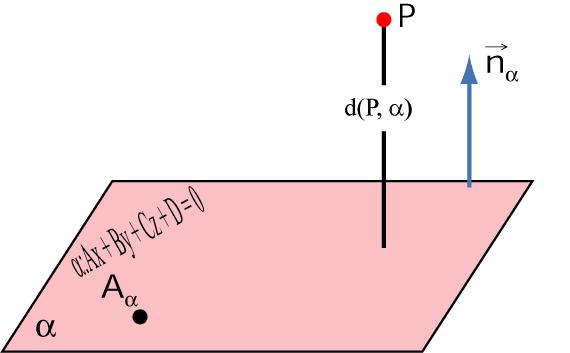
При решении геометрических задач в пространстве часто возникает проблема определения расстояния между плоскостью и точкой. В некоторых случаях это необходимо для комплексного решения. Эту величину можно вычислить, если найти проекцию на плоскость точки. Рассмотрим этот вопрос подробнее в статье.

Уравнение для описания плоскости

Перед тем как перейти к рассмотрению вопроса касательно того, как найти проекцию точки на плоскость, следует познакомиться с видами уравнений, которые задают последнюю в трехмерном пространстве. Подробнее – ниже.

Уравнением общего вида, определяющим все точки, которые принадлежат данной плоскости, является следующее:

A*x + B*y + C*z + D = 0.

Первые три коэффициента – это координаты вектора, который называется направляющим для плоскости. Он совпадает с нормалью для нее, то есть является перпендикулярным. Этот вектор обозначают n¯(A; B; C). Свободный коэффициент D однозначно определяется из знания координат любой точки, принадлежащей плоскости.

Далее в статье будем использовать записанное уравнение. Оно требуется, чтобы найти проекцию точки на плоскость.

Понятие о проекции точки и ее вычисление

Предположим, что задана некоторая точка P(x₁; y₁; z₁) и плоскость. Она определена уравнением в общем виде. Если провести перпендикулярную прямую из P к заданной плоскости, то очевидно, что она пересечет последнюю в одной определенной точке Q (x₂; y₂; z₂). Q называется проекцией P на рассматриваемую плоскость. Длина отрезка PQ называется расстоянием от точки P до плоскости. Таким образом, сам PQ является перпендикулярным плоскости.

Как можно найти координаты проекции точки на плоскость? Сделать это не сложно. Для начала следует составить уравнение прямой, которая будет перпендикулярна плоскости. Ей будет принадлежать точка P. Поскольку вектор нормали n¯(A; B; C) этой прямой должен быть параллелен, то уравнение для нее в соответствующей форме запишется так:

(x; y; z) = (x₁; y₁; z₁) + λ*(A; B; C).

Где λ – действительное число, которое принято называть параметром уравнения. Изменяя его, можно получить любую точку прямой.

После того как записано векторное уравнение для перпендикулярной плоскости линии, необходимо найти общую точку пересечения для рассматриваемых геометрических объектов. Ее координаты и будут проекцией P. Поскольку они должны удовлетворять обоим равенствам (для прямой и для плоскости), то задача сводится к решению соответствующей системы линейных уравнений.

Понятие проекции часто используется при изучении чертежей. На них изображаются боковые и горизонтальные проекции детали на плоскости zy, zx, и xy.

Вычисление расстояния от плоскости до точки

Как выше было отмечено, знание координат проекции на плоскость точки позволяет определить дистанцию между ними. Используя обозначения, введенные в предыдущем пункте, получаем, что искомое расстояние равно длине отрезка PQ. Для его вычисления достаточно найти координаты вектора PQ¯, а затем рассчитать его модуль по известной формуле. Конечное выражение для d расстояния между P точкой и плоскостью принимает вид:

d = |PQ¯| = √((x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)²).

Полученное значение d представлено в единицах, в которых задается текущая декартова координатная система xyz.

Пример задачи

Допустим, имеется точка N(0; -2; 3) и плоскость, которая описывается следующим уравнением:

2*x – y + z + 4 = 0.

Следует найти точки проекцию на плоскость и вычислить между ними расстояние.

В первую очередь составим уравнение прямой, которая пересекает плоскость под углом 90^o. Имеем:

(x; y; z) = (0; -2; 3) + λ*(2; -1; 1).

Записывая это равенство в явном виде, приходим к следующей системе уравнений:

x = 2*λ;

y = -2 – λ;

z = λ + 3;

2*x – y + z + 4 = 0.

Подставляя значения координат из первых трех равенств в четвертое, получим значение λ, определяющее координаты общей точки прямой и плоскости:

2*(2*λ) – (-2 – λ) + λ + 3 + 4 = 0 =>

6*λ + 9 = 0 =>

λ = 9/6 = 3/2 = 1,5.

Подставим найденный параметр в уравнение прямой и найдем координаты проекции исходной точки на плоскость:

(x; y; z) = (0; -2; 3) + 1,5*(2; -1; 1) = (3; -3,5; 4,5).

Для вычисления дистанции между заданными в условии задачи геометрическими объектами применим формулу для d:

d = √((3 – 0 )² + (-3,5 + 2 )² + (4,5 – 3 )²) = 3,674.

В данной задаче мы показали, как находить проекцию точки на произвольную плоскость и как вычислять между ними расстояние.