1243, 1150, 1110, 1250, 1300, 1200, 1400, 1340
ТОМА
14.12.22
Учеба и наука
1 ответ
Интервал группы
– значение варьирующего признака,
лежащее в определенных границах.
Каждый интервал
большие и меньшей границы, или один из
них.
Наименьшая граница – минимальное
значение признака в данном интервале.
Наибольшая граница – максимальное
значение признака в данном интервале.
Величина интервала- i.i– разность большего и меньшего интервалов.
Середина интервала: xi=
Равный интервал используется примерно
к однородной совокупности, обладающей
небольшой вариацией признака.
Iравных интерваловрассчитывается следующим образом:
h=
h- величина равных интервалов
xmax–
максимальное значение признака в
изучаемой совокупности.
xmin–
минимальное значение признака в изучаемой
совокупности.
n- число групп.
При использовании непрерывных признаков
одно и то же значение признака может
одновременно выступать большей и меньшей
границей у двух смежных интервалов.
Могут возникнуть проблемы отнесения
единиц в ту или иную группу, которую
можно решить заранее, определив канал.
Граница формируется по принципу
включительно/исключительно.
Дискретный признак в основе группировки
(число детей в семье, возраст в годах),
то нижняя граница интервала равна
большей границе интервала, следовательно,
один интервал увеличился на один.
Неравные интервалы. Величина может
возрастать и убывать, может быть
произвольной и специализированной.
4.Определение признаков, которые характеризуют каждую выделенную группу.
4.Значение и виды абсолютных величин. Виды относительных величин и способы их расчета.
Абсолютная величина – первая исходная
форма выражения статистических
показателей.
Абсолютная величина характеризует
масштабы, размеры изучаемых процессов,
явлений; отражает временные характеристики,
а также может характеризовать объемы
совокупности, т.е. численность.
Разновидности:
Индивидуальные(при статистическом
наблюдении)
Сводные/суммарные абсолютные
показатели(характеризуют общую величину
признака)
Абсолютная величина обязательно имеют
единицы измерения, которые являются
характеристикой сущности изучаемого
явления.
Единицы измерения:
1.Натуральные(г, кг, м, км):
А)простые
Б)сложные( при характеристике транспортной
работы (т/км)
К натуральным единицам измерения
относятся условно-натуральные измерители,
используемые, когда продукт имеет
разновидности.
2.Трудовые (человеко-час, человеко-день)
3.Универсальные (стоимостные, денежные)
Относительная величина позволяет
выявить количественное соотношение
путем деления двух абсолютных величин.
Разновидности относительных величин::
1.ОВ динамики – отражает изменения
показателя в отчетном периоде по
сравнению с простым периодом.
ОВ=i
iдин=
(цепной способ)
iдин=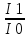
(базисный способ)
2.ОВ планового задания
iдиин=
iплан.зад.=
3.ОВ выполнения плана
iдин=iпл.зад*iвып.зад
4.ОВ структуры(показывает
долю части целого)
iстр=>α=
5.ОВ координации
iкоорд=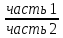
6.ОВ сравнения(показывает
во сколько раз больше или сколько
процентов составляет значение одного
и того же показателя у одного и того же
объекта по сравнению с другим за один
и тот же период времени)
iср=
7.ОВ интенсивности
( показывает насколько распространено
изучаемое явление)
iинт=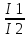
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Статистическая сводка и группировка
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Статистическая сводка
Процесс
упорядочения, систематизации и обобщения данных называется статистической
сводкой. В результате определенным образом выполненной обработки статистических
данных представляется возможным выявить сущность социально-экономических
явлений, характерные черты и существенные особенности отдельных объектов или их
групп, обнаружить закономерности и тенденции их развития.
Сводка
статистических данных осуществляется по заранее разработанным программе и
плану. При разработке программы определяются статистические подлежащее и
сказуемое. Подлежащее – это объект исследования, расчлененный на группы и
подгруппы; сказуемое – статистические показатели, которые характеризуют
подлежащее сводки.
Программа
сводки определяется задачами статистического исследования, которые можно свести
к следующим положениям:
-
выделение групп, на которые может быть расчленена изучаемая совокупность
явлений; -
определение перечня группировочных признаков, позволяющих произвести
разграничение единиц совокупности; -
обозначение границ интервалов групп при классификации по количественным
признакам; -
разработка системы статистических показателей для характеристики выделенных
групп.
В плане
сводки решаются вопросы о способах ее осуществления (вручную или с
использованием средств вычислительной техники), последовательности отдельных
операций сводки, выделении этапов сводки, выполняемых в децентрализованном и
централизованном порядке, сроках выполнения каждого этапа сводки, способах
представления результатов сводки (ряды распределения, статистические таблицы,
статистические графики и т. д.).
Статистическая группировка
Группировка
– это разделение изучаемой совокупности по значениям одного или нескольких
признаков на качественно однородные группы и характеристика этих групп с помощью
определенной системы показателей.
В
зависимости от поставленной цели и конкретного содержания исследуемого
материала посредством группировок решают три основные задачи:
- выделение социально-экономических типов явлений (процессов);
- выявление состава (структуры) изучаемой совокупности;
- установление причинно-следственных связей между признаками явлений (процессов).
Соответственно
перечисленным выше задачам используются три вида группировок: типологические,
структурные и аналитические (факторные).
Построение
группировки предполагает определение группировочного признака или основания
группировки, т. е. признака, по которому совокупность будет расчленена на
группы. Группировочные признаки могут быть количественными (возраст, уровень
производительности труда, рентабельность и т. д.) и атрибутивными (пол,
профессия, регионы и т. д.).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Величина интервалов и формула Стерджесса
При
построении группировки по количественному признаку устанавливаются границы
выделяемых групп. В этом случае, решая вопрос о величине интервала группировки
(или о числе групп), следует выбирать такое число групп, чтобы сводную
информацию можно было достаточно легко интерпретировать.
Величина
интервала при выборе равных интервалов группировки и известном числе групп
определяется по формуле:
где
и
– максимальное и минимальное значения
группировочного признака;
– число выделяемых групп.
Хороший
способ приближенного определения интервала группировки при неизвестном
изначально числе групп может быть получен на основании формулы Стерджесса:
где
– число единиц совокупности
Величина
равного интервала при построении используется обычно в тех случаях, когда
соотношение максимального и минимального значений группировочного признака в
вариационном ряду распределения не превышает десятикратного значения. При
значительной вариации группировочного признака целесообразно применять кратные
интервалы. В практике статистических исследований обычно используют удвоенные
кратные интервалы, т. е. величина каждого последующего интервала по сравнению с
предыдущим удваивается.
В
отдельных случаях статистика использует также неравные интервалы (например, при
большом объеме изучаемой совокупности, сильной колеблемости группировочного
признака и т. д.) и стандартные шкалы интервалов.
Интервалы
группировки считаются обоснованными, если коэффициенты вариации анализируемых
признаков по группам не превышают 33 %.
Вторичная группировка
Специфическим
видом группировок является так называемая вторичная группировка — операция
образования новых групп на основании уже имеющейся группировки.
Вторичная
группировка может строиться путем непосредственного укрупнения групп и по
способу пропорционального дробления групп.
Смежные темы решебника:
- Полигон, гистограмма, кумулята, огива
- Показатели вариации
- Эмпирическое корреляционное отношение
Примеры решения задач
Пример 1
По данным
таблицы произвести группировку заводов по производству продукции за отчетный
период, образовав пять групп заводов. Каждую группу охарактеризуйте числом
заводов, числом работающих, среднегодовой стоимостью ОПФ. Наряду с абсолютными
показателями по группам, вычислить их процентное соотношение. Сделать выводы.
Показатели 24-х заводов отрасли
| Номер п/п |
Среднегодовая стоимость ОПФ, млн. руб. |
Среднесписочное число работающих за отчетный период, чел. |
Производство продукции за отчетный период, млн.р. |
| 1 | 4,3 | 142,0 | 1,8 |
| 2 | 3,5 | 143,0 | 4,0 |
| 3 | 4,3 | 134,0 | 12,7 |
| 4 | 2,1 | 159,0 | 9,2 |
| 5 | 7,2 | 137,0 | 5,7 |
| 6 | 3,2 | 88,0 | 16,7 |
| 7 | 7,5 | 91,0 | 6,1 |
| 8 | 5,2 | 57,0 | 19,5 |
| 9 | 5,7 | 157,0 | 7,9 |
| 10 | 9,1 | 79,0 | 15,8 |
| 11 | 2,6 | 97,0 | 16,1 |
| 12 | 1,1 | 85,0 | 12,2 |
| 13 | 6,0 | 100,0 | 7,1 |
| 14 | 2,4 | 149,0 | 11,7 |
| 15 | 3,7 | 151,0 | 13,2 |
| 16 | 5,4 | 138,0 | 11,7 |
| 17 | 5,7 | 74,0 | 1,2 |
| 18 | 2,7 | 91,0 | 16,8 |
| 19 | 4,3 | 77,0 | 1,2 |
| 20 | 4,5 | 160,0 | 3,0 |
| 21 | 2,1 | 90,0 | 6,3 |
| 22 | 3,9 | 88,0 | 8,7 |
| 23 | 1,0 | 83,0 | 8,5 |
| 24 | 3,4 | 109,0 | 17,1 |
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
При построении группировки с равными
интервалами величина интервала h определяется по формуле
где
– наибольшее
и наименьшее значения признака в исследуемой совокупности
k- число групп
При
. границы интервалов имеют следующий вид:
| Номер группы | Нижняя граница, млн. руб. | Верхняя граница, млн. руб. |
| 1 | 1,2 | 4,9 |
| 2 | 4,9 | 8,6 |
| 3 | 8,6 | 12,3 |
| 4 | 12,3 | 16 |
| 5 | 16 | 19,7 |
Расположим предприятия по
возрастанию группировочного признака:
Расчетная вспомогательная таблица
| Группы предприятий, млн.р. | Номер п/п |
Среднегодовая стоимость ОПФ, млн. руб. |
Среднесписочное число работающих за отчетный период, чел. |
Производство продукции за отчетный период, млн.р. |
| 1,2 – 4,9 | 17 | 5,7 | 74 | 1,2 |
| 19 | 4,3 | 77 | 1,2 | |
| 1 | 4,3 | 142 | 1,8 | |
| 20 | 4,5 | 160 | 3 | |
| 2 | 3,5 | 143 | 4 | |
| Всего | 5 | 22,3 | 596 | 11,2 |
| 4,9 – 8,6 | 5 | 7,2 | 137 | 5,7 |
| 7 | 7,5 | 91 | 6,1 | |
| 21 | 2,1 | 90 | 6,3 | |
| 13 | 6 | 100 | 7,1 | |
| 9 | 5,7 | 157 | 7,9 | |
| 23 | 1 | 83 | 8,5 | |
| Всего | 6 | 29,5 | 658 | 41,6 |
| 8,6 – 12,3 | 22 | 3,9 | 88 | 8,7 |
| 4 | 2,1 | 159 | 9,2 | |
| 14 | 2,4 | 149 | 11,7 | |
| 16 | 5,4 | 138 | 11,7 | |
| 12 | 1,1 | 85 | 12,2 | |
| Всего | 5 | 14,9 | 619 | 53,5 |
| 12,3 – 16 | 3 | 4,3 | 134 | 12,7 |
| 15 | 3,7 | 151 | 13,2 | |
| 10 | 9,1 | 79 | 15,8 | |
| Всего | 3 | 17,1 | 364 | 41,7 |
| 16 – 19,7 | 11 | 2,6 | 97 | 16,1 |
| 6 | 3,2 | 88 | 16,7 | |
| 18 | 2,7 | 91 | 16,8 | |
| 24 | 3,4 | 109 | 17,1 | |
| 8 | 5,2 | 57 | 19,5 | |
| Всего | 5 | 17,1 | 442 | 86,2 |
Получаем следующую группировку:
Группировка предприятий по признаку “Производство продукции”
|
Производство продукции за отчетный период, млн. р. |
Число предприятий | Число работающих |
Среднегодовая стоимость ОПФ |
|||
| ед. | в % к итогу | чел. | в % к итогу | млн.р. | в % к итогу | |
| 1,2 – 4,9 | 5 | 20,8 | 596 | 22,2 | 22,3 | 22,1 |
| 4,9 – 8,6 | 6 | 25,0 | 658 | 24,6 | 29,5 | 29,2 |
| 8,6 – 12,3 | 5 | 20,8 | 619 | 23,1 | 14,9 | 14,8 |
| 12,3 – 16 | 3 | 12,5 | 364 | 13,6 | 17,1 | 16,9 |
| 16 – 19,7 | 5 | 20,8 | 442 | 16,5 | 17,1 | 16,9 |
| Итого | 24 | 100,0 | 2679 | 100,0 | 100,9 | 100,0 |
Вывод к задаче
Таким образом наиболее у наиболее
многочисленной группы предприятий производство продукции находится в пределах
от 4,9 до 8,6 млн.р. Эта группа по численности составляет 25% от исследуемой
совокупности, в ней работает 24,6% работающих, а стоимость ОПФ составляет 29,5%
от итоговой. В самой малочисленной группе производится от 12,3 до 16 млн.р., в
ней работает 13,6% работающих, а стоимость ОПФ составляет 16,9% от итоговой.
Пример 2
Для
выявления взаимосвязи между среднегодовой стоимостью основных фондов и стоимостью
произведенной продукции произведите аналитическую группировку предприятий,
выделив четыре группы предприятий по стоимости основных фондов с равными
интервалами.
Стоимость основных фондов и
произведенной продукции по 20 предприятиям отрасли, млн. ден.ед.
| № п/п |
Среднегодовая стоимость основных фондов |
Стоимость произведенной продукции |
| 1 | 62 | 71 |
| 2 | 72 | 79 |
| 3 | 74 | 85 |
| 4 | 24 | 30 |
| 5 | 41 | 52 |
| 6 | 46 | 56 |
| 7 | 54 | 54 |
| 8 | 144 | 166 |
| 9 | 140 | 160 |
| 10 | 118 | 139 |
| 11 | 122 | 143 |
| 12 | 78 | 84 |
| 13 | 82 | 95 |
| 14 | 82 | 92 |
| 15 | 88 | 99 |
| 16 | 86 | 104 |
| 17 | 90 | 101 |
| 18 | 94 | 112 |
| 19 | 100 | 115 |
| 20 | 112 | 123 |
| Итого | 1709 | 1960 |
Определите
по каждой группе и в целом по отрасли:
- количество предприятий;
- стоимость основных фондов: всего и в среднем на одно предприятие;
- стоимость произведенной продукции: всего и в среднем на одно предприятие;
- стоимость произведенной продукции на рубль основных фондов (фондоотдачу);
Результаты
расчетов представьте в таблице. Сделайте выводы.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
При построении группировки с равными
интервалами величина интервала h определяется по формуле
где
– наибольшее
и наименьшее значения признака в исследуемой совокупности
k- число групп
При
границы интервалов
имеют следующий вид:
| Номер группы | Нижняя граница, млн. д.е. | Верхняя граница, млн. д.е. |
| 1 | 24 | 54 |
| 2 | 54 | 84 |
| 3 | 84 | 114 |
| 4 | 114 | 144 |
Расположим
предприятия по возрастанию группировочного признака:
Расчетная вспомогательная таблица
|
Группы предприятий, млн.д.е. |
№ п/п |
Среднегодовая стоимость основных фондов, млн.д.е. |
Стоимость произведенной продукции, млн.д.е. |
| 4 | 24 | 30 | |
| 24-54 | 5 | 41 | 52 |
| 6 | 46 | 56 | |
| Итого | 3 | 111 | 138 |
| 7 | 54 | 54 | |
| 54-84 | 1 | 62 | 71 |
| 2 | 72 | 79 | |
| 3 | 74 | 85 | |
| 12 | 78 | 84 | |
| 13 | 82 | 95 | |
| 14 | 82 | 92 | |
| Итого | 7 | 504 | 560 |
| 16 | 86 | 104 | |
| 84-114 | 15 | 88 | 99 |
| 17 | 90 | 101 | |
| 18 | 94 | 112 | |
| 19 | 100 | 115 | |
| 20 | 112 | 123 | |
| Итого | 6 | 570 | 654 |
| 10 | 118 | 139 | |
| 114-144 | 11 | 122 | 143 |
| 9 | 140 | 160 | |
| 8 | 144 | 166 | |
| Итого | 4 | 524 | 608 |
Получаем следующую группировку:
Группировка предприятий отрасли
| Группы предприятий, млн.д.е. | Число предприятий | Среднегодовая стоимость основных фондов, млн.д.е. | Стоимость произведенной продукции, млн.д.е. | Фондоотдача, ден.ед. | ||
| всего | на одно предприятие | всего | на одно предприятие | |||
| 24-54 | 3 | 111 | 37,0 | 138 | 46 | 1,243 |
| 54-84 | 7 | 504 | 72,0 | 560 | 80 | 1,111 |
| 84-114 | 6 | 570 | 95,0 | 654 | 109 | 1,147 |
| 114-144 | 4 | 524 | 131,0 | 608 | 152 | 1,160 |
| Итого | 20 | 1709 | 85,5 | 1960 | 98 | 1,147 |
Вывод к задаче
Таким
образом с увеличением среднегодовой стоимости основных фондов увеличивается
стоимость произведенной продукции. Фондоотдача также имеет тенденцию к
увеличению. Средняя фондоотдача по всей совокупности предприятий составила
1,147 ден.ед.
Пример 3
Имеются
данные об уровне выполнения норм выработки рабочими двух цехов
машиностроительного предприятия:
| Цех №1 | Цех №2 | ||
| Уровень выполнения норм выработки | Число рабочих | Уровень выполнения норм выработки | Число рабочих |
| до 90 | 4 | до 93,9 | 6 |
| 90 – 90,9 | 16 | 94 – 98,9 | 15 |
| 94 – 99,9 | 24 | 99 – 100,9 | 14 |
| 100-105,9 | 66 | 101 – 104,9 | 28 |
| 106-109,9 | 40 | 105 – 108,9 | 36 |
| 110 и выше | 25 | 109 – 114,9 | 18 |
| 115 и выше | 13 | ||
| Итого | 175 | Итого | 130 |
Приведите
данные к сопоставимости. Определите, какова доля не выполняющих норму рабочих в
каждом цехе. Сделайте вывод, в каком из цехов уровень выполнения норм выработки
лучше.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Осуществим
вторичную группировку по обеим цехам по способу пропорционального дробления.
Данные
разобьем на 4 группы по выработке:
до 100
100 –
104,9
105-
109,9
110 и
выше
Цех №1:
Число рабочих в 1-й
группе (<100):
Число рабочих во 2-й
группе (100-104,9):
Число рабочих во 3-й
группе (105-109,9):
Число рабочих во 3-й
группе (110 и выше):
Цех №2:
Число рабочих в 1-й группе
(<100)
Число рабочих во 2-й
группе (100-104,9)
Число рабочих во 3-й
группе (105-109,9)
Число рабочих во 3-й
группе (110 и выше)
Получаем:
Вторичная группировка
| Цех №1 | Цех №2 | ||
| Уровень выполнения норм выработки | Число рабочих | Уровень выполнения норм выработки | Число рабочих |
| до 100 | 44 | до 100 | 28 |
| 100 – 104,9 | 55 | 100 – 104,9 | 35 |
| 105 – 109,9 | 51 | 105 – 109,9 | 39 |
| 110 и выше | 25 | 110 и выше | 28 |
| Итого | 175 | 130 |
Доля
рабочих, не выполняющих норму в 1-м цехе:
Доля
рабочих, не выполняющих норму во 2-м цехе:
Вывод к задаче
Таким
образом, выполнение норм выработки во 2-м цехе лучше, чем в первом.
Пример 4
Имеются
следующие данные о распределении сельскохозяйственных предприятий региона по
величине валовой продукции:
|
Группы сельскохозяйственных предприятий по величине валовой продукции, млн.руб. |
Число предприятий, в % к итогу | Валовая продукция, в % к итогу |
| до 100 | 10 | 17,9 |
| 100-300 | 60 | 42,4 |
| свыше 300 | 30 | 39,7 |
| Итого | 100,0 | 100,0 |
Применяя
метод вторичной группировки, образуйте группы сельскохозяйственных предприятий
по величине валовой продукции, млн.р.
до 10,
10-50, 50-100, 100-200, 200-250, свыше 250.
По каждой
группе рассчитайте оба показателя.
Решение
Осуществим
вторичную группировку по способу пропорционального дробления групп:
В первую группу
войдет 1/10 часть 1-го интервала
Во вторую группу
войдет 2/5 части 1-го интервала
В третью группу
войдет половина 1-го интервала
В четвертую группу
войдет 4/5 части 2-го интервала
В пятую группу войдет
1/5 часть 2-го интервала и 3-й интервал
Вторичная группировка
|
Группы сельскохозяйственных предприятий по величине валовой продукции, млн.руб. |
Число предприятий, % к итогу |
Стоимость реализованной продукции, % к итогу |
| до 10 | 1 | 1,79 |
| 10-50 | 4 | 7,16 |
| 50-100 | 5 | 8,95 |
| 100-250 | 48 | 33,92 |
| свыше 250 | 42 | 48,18 |
| Итого | 100,0 | 100,0 |
Задачи контрольных и самостоятельных работ
Задача 1
1.
Произведите группировку магазинов №№5…27 по признаку относительного уровня
издержек обращения (в% к розничным продажам), образовав при этом 4 группы с
равными интервалами.
2.
Охарактеризуйте каждую группу и всю совокупность магазинов числом магазинов,
размером розничных продаж, издержек обращения и торговой площади.
3.
Определите средние размеры розничных продаж, издержек обращения и торговой
площади, приходящиеся на один магазин.
4.
Определите средний относительный уровень издержек обращения по каждой группе и
в целом.
Полученные
результаты оформите в виде статистической таблицы. Сделайте выводы.
| Номер магазина |
Розничные продажи (млрд. руб.) |
Издержки обращения (млрд. руб.) | Стоимость основных средств (среднегодовая) (млрд. руб.) | Численность продавцов (чел.) | Торговая площадь (м2) |
| 5 | 235 | 24,8 | 7,8 | 132 | 1335 |
| 6 | 80 | 9,2 | 2,2 | 41 | 946 |
| 7 | 113 | 10,9 | 3,2 | 40 | 1435 |
| 8 | 300 | 30,1 | 6,8 | 184 | 1820 |
| 9 | 142 | 16,7 | 5,7 | 50 | 1256 |
| 10 | 280 | 46,8 | 6,3 | 105 | 1353 |
| 11 | 156 | 30,4 | 5,7 | 57 | 1138 |
| 12 | 213 | 28,1 | 5,0 | 100 | 1216 |
| 13 | 298 | 38,53 | 6,7 | 112 | 1352 |
| 14 | 242 | 34,2 | 6,5 | 106 | 1445 |
| 15 | 130 | 20,1 | 4,8 | 62 | 1246 |
| 16 | 184 | 22,3 | 6,8 | 60 | 1332 |
| 17 | 96 | 9,8 | 3,0 | 34 | 680 |
| 18 | 304 | 38,7 | 6,9 | 109 | 1435 |
| 19 | 95 | 11,7 | 2,8 | 38 | 582 |
| 20 | 352 | 40,1 | 8,3 | 115 | 1677 |
| 21 | 101 | 13,6 | 3,0 | 40 | 990 |
| 22 | 148 | 21,6 | 4,1 | 50 | 1354 |
| 23 | 74 | 9,2 | 2,2 | 30 | 678 |
| 24 | 135 | 20,2 | 4,6 | 52 | 1380 |
| 25 | 320 | 40,0 | 7,1 | 140 | 1840 |
| 26 | 155 | 22,4 | 5,6 | 50 | 1442 |
| 27 | 262 | 29,1 | 6,0 | 102 | 1720 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Имеются
следующие данные об урожайности картофеля и количеством внесенных минеральных
удобрений по 10 сельскохозяйственным предприятиям:
| Номер колхоза | Урожайность, ц/га |
Внесено минеральных удобрений на 1 га, кг |
Номер колхоза | Урожайность, ц/га |
Внесено минеральных удобрений на 1 га, кг |
| 1 | 128 | 140 | 6 | 183 | 197 |
| 2 | 179 | 262 | 7 | 201 | 246 |
| 3 | 221 | 289 | 8 | 195 | 276 |
| 4 | 136 | 191 | 9 | 141 | 187 |
| 5 | 164 | 202 | 10 | 192 | 253 |
Для
изучения зависимости между урожайностью картофеля и внесенными минеральными
удобрениями произведите группировку сельскохозяйственных предприятий, образовав
3 группы предприятий с равными интервалами. По каждой группе и по совокупности
в целом подсчитайте:
1) число
предприятий;
2)
среднюю урожайность картофеля;
3)
средний объем внесенных минеральных удобрений на 1 га, кг.
Результаты
представьте в таблице и сделайте выводы.
Задача 3
Имеются
следующие данные о распределении сельскохозяйственных предприятий региона по
величине валовой продукции:
|
Группы сельскохозяйственных предприятий по величине валовой продукции, млн.руб. |
Число предприятий, в % к итогу | Валовая продукция, в % к итогу |
| до 100 | 10 | 17,9 |
| 100-300 | 60 | 42,4 |
| свыше 300 | 30 | 39,7 |
| Итого | 100,0 | 100,0 |
Применяя
метод вторичной группировки, образуйте группы сельскохозяйственных предприятий
по величине валовой продукции, млн.р.
до 10,
10-50, 50-100, 100-200, 200-250, свыше 250.
По каждой
группе рассчитайте оба показателя.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Используя
данные по варианту задания, выполнить следующие расчеты:
1.
Сгруппировать показатели.
2.
Согласно полученной группировки рассчитать моду и медиану.
3.
Рассчитать средние величины, дисперсию и коэффициент вариации.
4. Найти
уровень взаимосвязи между показателями при помощи корреляционно-регрессионного
анализа.
Имеются
данные о деятельности банков одного из регионов.
| № п/п |
Срок функционирования, лет |
Объем привлеченных средств, млн. ден.ед. |
| 1 | 7 | 46 |
| 2 | 4 | 40 |
| 3 | 3 | 38 |
| 4 | 7 | 49 |
| 5 | 2 | 41 |
| 6 | 9 | 55 |
| 7 | 6 | 60 |
| 8 | 12 | 58 |
| 9 | 3 | 38 |
| 10 | 9 | 56 |
| 11 | 5 | 48 |
| 12 | 2 | 40 |
| 13 | 10 | 62 |
| 14 | 4 | 54 |
| 15 | 7 | 57 |
| 16 | 2 | 43 |
| 17 | 3 | 46 |
| 18 | 10 | 58 |
| 19 | 5 | 53 |
| 20 | 8 | 51 |
| 21 | 3 | 42 |
| 22 | 6 | 58 |
| 23 | 8 | 56 |
| 24 | 9 | 49 |
| 25 | 10 | 47 |
| 26 | 4 | 43 |
| 27 | 9 | 46 |
| 28 | 11 | 48 |
| 29 | 5 | 57 |
| 30 | 8 | 59 |
| Итого |
На основе соответствующих вашему
варианту данных построить интервальный вариационный ряд банков по объему
привлеченных средств (4 интервала) и изобразить графически.
По данным подсчитайте:
1) Средний размер привлекаемых
средств (способ моментов и квадратов);
2) Моду, медиану привлекаемых
средств;
3) Показатели вариации;
4) Показатели корреляции и
регрессии.
Сделать вывод. Начертить 4 вида
графиков.
Задача 5
По
имеющимся данным о сбыте продукции (в тыс. руб.) в различных фирмах города
произвести группировку данных, образовав 4 равных интервалов. Оформить в
таблице.
По
полученному интервальному ряду определить (аналитически и графически): средний
объем сбыта, моду, медиану.
87, 75,
66, 60, 87, 67, 66, 69, 89, 74, 90, 78, 99, 86, 76, 95, 69, 68, 87, 63
Задача 6
Произвести
анализ 20 банков, применив метод группировок, используя данные, приведенные в
таблице ниже:
Основные
показатели деятельности банков (млн.руб.)
|
Номер банка |
Капитал |
Чистые активы |
Прибыль |
| 1 | 5170 | 74104 | 1222 |
| 2 | 6412 | 22311 | 502 |
| 3 | 6424 | 30978 | 1372 |
| 4 | 4467 | 46331 | 1845 |
| 5 | 9454 | 7741 | 214 |
| 6 | 4357 | 19422 | 215 |
| 7 | 4033 | 9203 | 336 |
| 8 | 2755 | 12082 | 504 |
| 9 | 6868 | 57821 | 2635 |
| 10 | 3896 | 23787 | 794 |
| 11 | 3660 | 37528 | 694 |
| 12 | 7301 | 43129 | 934 |
| 13 | 3564 | 40927 | 1405 |
| 14 | 3327 | 17881 | 220 |
| 15 | 3280 | 21955 | 654 |
| 16 | 5153 | 31627 | 2173 |
| 17 | 5400 | 16068 | 1463 |
| 18 | 2613 | 13851 | 229 |
| 19 | 5196 | 6588 | 570 |
| 20 | 2609 | 22781 | 445 |
Задача 7
Используя
данные таблицы по 20 фирмам, сгруппируйте фирмы по следующим признакам:
низкорентабельные, рентабельные, высокорентабельные. В качестве основы
группировки возьмите прибыль на одного работающего. Для каждого выделенного
типа рассчитайте число фирм, среднюю численность персонала, стоимость
реализованной продукции на одного работающего. Результаты представьте в виде
таблицы и изобразите графически. Предложите анализ возможных факторов повышения
рентабельности.
Итоги деятельности фирм,
расположенных на территории района
| Номер в реестре | Заявленная отпускная стоимость реализованной продукции (млн. руб.) | Среднесписочная численность персонала | Заявленная прибыль (млн. руб.) | Расходы на рекламу (млн. руб.) |
| 6 | 195,2 | 181 | 16,3 | 4,0 |
| 7 | 157,8 | 1123 | 12,5 | 1,2 |
| 8 | 98,3 | 265 | 7,8 | 0,4 |
| 9 | 541,2 | 312 | 28,1 | 3,5 |
| 10 | 325,1 | 198 | 35,3 | 7,8 |
| 11 | 398,5 | 253 | 23,4 | 4,9 |
| 12 | 38,4 | 126 | 6,7 | 2,2 |
| 13 | 137,6 | 78 | 14,3 | 5,6 |
| 14 | 56,5 | 44 | 3,4 | 2,7 |
| 15 | 41,2 | 58 | 6,5 | 2,4 |
| 16 | 168,5 | 87 | 13,9 | 3,7 |
| 17 | 174,3 | 128 | 10,2 | 5,1 |
| 18 | 184,1 | 165 | 20,5 | 5,9 |
| 19 | 241,6 | 188 | 13,3 | 1,8 |
| 20 | 58,0 | 39 | 10,2 | 3,4 |
| 21 | 302,7 | 155 | 16,7 | 2,9 |
| 22 | 87,5 | 61 | 5,3 | 0,2 |
| 23 | 611,5 | 3875 | 58,3 | 10,7 |
| 24 | 257,6 | 189 | 25,0 | 3,2 |
| 25 | 107,4 | 98 | 8,8 | 3,7 |
Задача 8
Имеются
данные о распределении коммерческих банков по объявленному уставному фонду:
| Регион 1 | Регион 2 | ||
| Группы банков по уставному фонду | Удельный вес банков в общем их числе | Группы банков по уставному фонду | Удельный вес банков в общем их числе |
| до 100 | 7 | до 100 | 2 |
| 100-500 | 9 | 100-300 | 5 |
| 500-1000 | 18 | 300-500 | 6 |
| 1000-5000 | 34 | 500-700 | 7 |
| 5000-20000 | 22 | 700-1000 | 12 |
| свыше 20000 | 10 | 1000-3000 | 28 |
| 3000-5000 | 18 | ||
| 5000-10000 | 14 | ||
| свыше 10000 | 8 | ||
| Итого | 100 | Итого | 100 |
С целью
сравнения осуществите вторичную группировку коммерческих банков, для чего
выделите следующие группы банков по объявленному уставному фонду:
до 100,
100-500, 500-1000, 1000-5000, 5000-10000, свыше 10000 тыс.у.е. Сделайте выводы.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 9
Имеются
следующие данные по предприятиям по численности рабочих в 2012 г. Данные
представлены в таблице:
Исходные
данные
|
Предприятия со среднегодовой численностью рабочих (чел.) |
Число предприятий в процентах к итогу, % |
|
до 100 |
33,9 |
| 100-200 | 20,0 |
| 200-500 | 23,7 |
| 500-1000 | 11,8 |
| 1000-3000 | 8,0 |
| 3000-5000 | 2,3 |
|
5000 и более |
0,3 |
| Итого | 100,0 |
Используя
данные таблицы, необходимо провести перегруппировку предприятий по
численности рабочих, приняв следующие интервалы:
до 50
чел.
50 – 300
чел.
300 – 800
чел.
800 -1500
чел.
1500 –
4000 чел.
4000 –
9000 чел.
более
9000 чел.
Задача 10
Имеются
следующие данные о распределении промышленных предприятий двух регионов по
численности занятого на них промышленно-производственного персонала.
| Регион 1 | Регион 2 | ||||
|
Группы предприятий по численности работающих, чел. |
Число предприятий, % |
Численность промышленно-производственного персонала, тыс.чел. |
Группы предприятий по численности работающих, чел. |
Число предприятий, % |
Численность промышленно-производственного персонала, тыс.чел. |
| до 100 | 32 | 1 | до 300 | 34 | 1 |
| 101-500 | 38 | 4 | 301-600 | 28 | 6 |
| 501-1000 | 17 | 10 | 601-1000 | 20 | 10 |
| 1001-2000 | 9 | 15 | 1001-2000 | 13 | 15 |
| 2001-5000 | 3 | 32 | 2001-4000 | 4 | 43 |
| 5001 и более | 1 | 38 | 4001 и более | 1 | 25 |
| Итого | 100 | 100 | Итого | 100 | 100 |
Постройте
вторичную группировку данных о распределении промышленных предприятий, пересчитав
данные:
а)
региона 2 в соответствии с группировкой региона 1;
б)
региона 1 в соответствии с группировкой региона 2;
в)
регионов 1 и 2, образовав следующие группы промышленных предприятий по
численности ППП: до 500, 500-1000, 1000-2000, 2000-3000, 3000-4000, 4000-5000,
5000 и более.
Задача 11
По данным
таблицы 2 произвести вторичную группировку, образовав три группы предприятий по
среднегодовой стоимости ОПФ.
|
Группы предприятий по среднегодовой стоимости ОПФ, тыс.руб. |
Число предприятий, % |
Объем продукции, % |
Среднегодовая численность работающих |
Среднегодовая стоимость ОПФ |
| до 75 | 6.4 | 0.1 | 0.8 | 0.0 |
| 75-200 | 5.5 | 0.2 | 0.5 | 0.1 |
| 200-300 | 15.4 | 1.8 | 2.4 | 0.4 |
| 300-2500 | 36.6 | 9.7 | 12.4 | 4.4 |
| 2500-5000 | 30.4 | 17.2 | 17.3 | 9.6 |
| 5000-10000 | 1.9 | 27.7 | 29.0 | 20.8 |
| и более | 3.8 | 43.3 | 37.6 | 64.7 |
| Итого | 100.0 | 100.0 | 100.0 | 100.0 |
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
ПРАКТИЧЕСКОЕ
ЗАНЯТИЕ № 1.
Группировка статистических данных и
построение рядов распределения.
Студент должен:
знать:
– принципы построения и виды
статистических группировок и статистических рядов распределения;
уметь:
– построить группировку данных в соответствии
с поставленными целями и задачами;
– построить ряд распределения и
представить его графическое изображение;
– произвести перегруппировку
статистических данных для обеспечения их сопоставимости;
– формулировать вывод по полученным
результатам.
Методические указания
Группировка
– это разбиение совокупности на группы, однородные по какому-либо признаку. С
точки зрения отдельных единиц совокупности группировка – это объединение
отдельных единиц совокупности в группы, однородные по каким-либо признакам.
Метод группировки
основывается на следующих категориях – это группировочный
признак, число групп и интервал группировки.
Признак, по которому
осуществляется группировка, называется основанием группировки, или группировочным признаком. Группировочные
признаки могут быть атрибутивными и количественными.
Атрибутивные признаки регистрируются
в виде текстовой записи (например, профессии рабочих, социальная группа
населения). Количественные признаки имеют непосредственное числовое выражение
(стаж работы, размер дохода). Группировка может выполняться по одному признаку
(простая группировка) и по нескольким
признакам (комбинированная группировка).
После определения
основания группировки следует решить вопрос о количестве групп, на которое надо разбить исследуемую совокупность.
При группировке по атрибутивному признаку число групп определяется
количеством соответствующих наименований, т.е.
градаций, видов, состояний у признака, если число этих наименований не
очень велико. Если признак имеет большое количество разновидностей, то
разрабатывается классификация – систематизированное распределение явлений и
объектов на определённые группы, классы, разряды на основании их сходства и
различия.
При группировке по количественному признаку число групп определяется в
зависимости от характера изменения признака и задач исследования. Если
количественный признак меняется прерывно
(дискретно), т.е. может принимать только некоторые – чаще целые значения
(например, тарифный разряд рабочих), то число групп должно соответствовать
количеству значений признака. При небольшом объёме совокупности не следует
образовывать большое число групп, т.к. они будут малочисленными, а показатели, рассчитанные для таких групп не позволят
получить адекватную характеристику исследуемого явления. В каждом конкретном
случае при определении числа групп следует исходить не только из степени колеблемости признака, но ещё учитывать и особенности объекта и цель
исследования.
При непрерывном изменении признак принимает, любые значения (например, стаж работы,
возраст рабочих), поэтому группы ограничиваются значениями признака в интервале
«от и до». На практике используют три вида интервалов: равные, неравные
(постепенно увеличивающиеся) и
специализированные.
Здесь необходимо
учитывать несколько условий:
а) число групп детерминируется
уровнем колеблемости группировочного
признака. Чем значительнее вариация признака, тем больше при прочих равных
условиях должно быть групп;
б) число групп должно отражать
реальную структуру изучаемой совокупности;
в) не допускается выделение пустых
групп. Если проблема пустых групп все же возникает, при проведении структурных
группировок используют неравные интервалы.
Наличие пустых групп или малое число статистических единиц в них свидетельствуют
о неправильном определении их числа.
Группировка с равными
интервалами
строится, если вариация признака проявляется в узких границах и распределение
носит равномерный характер. Величина равного интервала определяется по формуле:
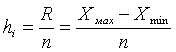 (1)
(1)
где R – размах вариации определяется как разность между
наибольшим и наименьшим значением признака в совокупности R=Xmax – Xmin;
n – число
групп.
Для расчёта величины
интервала по этой формуле необходимо заранее установить число групп п (при числе наблюдений более 200
используют 10 – 15 групп). Возможен и другой способ установления числа групп. В
этом случае используется формула Стерджесса:
n =1 + 3.322 lgN (2)
где
n – число групп;
N – число
единиц совокупности.
Применение этой формулы
целесообразно при большом числе единиц совокупности. При объёме совокупности
20-25 единиц число групп рекомендуется принимать п ≤ 4.
Формула Стерджесса позволяет определить величину интервала без
предварительного установления числа групп:
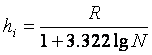 (3)
(3)
В практических расчетах можно
использовать следующие соотношения, полученные на основании формулы Стерджесса:
|
N |
15-24 |
25-44 |
45-89 |
90-179 |
180-359 |
360 и более |
|
n |
5 |
6 |
7 |
8 |
9 |
10 |
Зависимость
Стерджесса дает хорошие результаты, если совокупность
состоит из большого числа единиц, распределение близко к нормальному,
и при этом используются равные интервалы. Существует еще один способопределения
количества выделяемых групп, он связан с применением
среднеквадратичного отклонения равными и
неравными σ: если величина
(ширина) интервала равна 0,5σ , то выделяется
12 групп, если 2/3σ ,- то 9
групп, если σ – то 6 групп.
Прежде чем определять
размах вариации, из совокупности следует исключить аномальные значения
признака. Если максимальное или минимальное значение сильно отличается от
смежных с ним значений, то для определения величины интервала используют не
максимальное и минимальное значения, а значения, несколько превышающее минимум
и несколько меньше максимума. Полученную по формуле (1) величину округляют. Она является шагом интервала.
Существуют следующие правила
определения шага интервала.
Если величина интервала –
величина, имеющая один знак до запятой (например, 0,66; 1,375; 5,82), то
полученные значения следует округлить до десятых и использовать в качестве шага
интервала (соответственно 0,7; 1,4; 5,8). Когда рассчитанная величина интервала
имеет две значащие цифры до запятой и несколько знаков после запятой, то это
значение надо округлить до целого числа. Пусть величина интервала, исчисленная
по формуле (1.1), равна 12,785. Тогда это значение следует округлить до целого
числа, т.е. до 13. В случае, когда рассчитанная величина интервала представляет
собой трёхзначное, четырёхзначное и так далее число, эту величину необходимо
округлить до ближайшего числа, кратного 100 или 50. Например, 248 следует
округлить до 250. Чаще всего, полученное значение величины (ширины) интервала округляется в бóльшую сторону.
При округлении в меньшую сторону последний интервал делают открытым.
В каждой выделенной группе
рассчитываются следующие параметры:
![]() – верхняя граница интервала;
– верхняя граница интервала;
![]() – нижняя граница
– нижняя граница
интервала;
![]() – ширина
– ширина
интервала;
![]() – середина i-го интервала.
– середина i-го интервала.
Нижней
границей интервала (![]() ) называется
) называется
наименьшее
значение признака в интервале – данной группе. Верхней границей интервала (![]() ) называется
) называется
наибольшее
значение признака в интервале – данной группе.
Интервалы
группировки бывают равными
и неравными (прогрессивно
возрастающими, прогрессивно убывающими, произвольными, специализированными). Если
вариация признака проявляется в сравнительно узких границах, и распределение
статистических единиц носит достаточно равномерный характер, то строят группировку с
равными интервалами.
На основе рассчитанной ширины интервала
![]() последовательно определяются границы интервалов
последовательно определяются границы интервалов ![]() и
и ![]() . Определение
. Определение
границ начинается с первой группы. Ее нижняя граница принимается равной минимальному
значению признака в совокупности , т. е. ![]() , а верхняя
, а верхняя
граница определяется как ![]()
Для второй группы нижняя граница
принимается равной верхней границе первой группы, т. е. ![]() , верхняя
, верхняя
определяется как ![]()
и т. д. В целом границы интервалов
определяются формулами:
![]() и
и ![]()
Середина интервала
(центральная варианта) ![]() определяется как
определяется как
полусумма
верхней и нижней границ, т.е. по
формуле:
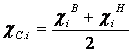
Параметр середина интервала используется при расчете обобщающих
характеристик изучаемой совокупности.
Интервалы могут быть открытыми и закрытыми. Открытые интервалы – это те интервалы, у
которых указана только одна граница: верхняя – у первого, нижняя – у последнего.
Закрытые
интервалы – это те интервалы, у которых обозначены обе границы.
Величина открытого интервала принимается равной величине смежного с ним закрытого
интервала.
Основной задачей распределения
единиц совокупности по группам является
подсчет числа единиц, попавших в каждую из выделенных групп ![]() . При распределении
. При распределении
единиц наблюдения по выделенным группам, особенно если группировочный
признак является непрерывным, имеет место неопределенность: к какой группе
относить единицы со значениями признака, совпадающими с границами интервалов?
Для устранения неопределенности используют принцип единообразия – такие единицы включаются в группу, в
которой нижняя граница совпадает со значением признака. Например, имеются группы
предприятий по объему производства, млн. руб.: 400
– 450; 450 – 500; 500 – 550; 550 – 600.
К какой группе следует отнести
предприятия с объемом производства 500млн. руб.? В соответствии с принципом
единообразия – ко второй группе. (Т.е нижняя граница – включительно, а верхняя
– исключительно)
Группировка с неравными
интервалами применяются
в статистике, когда значения признака варьируют неравномерно и в значительных
размерах. Неравные интервалы часто применяются в аналитических группировках. В
этом случае интервалы выбираются так, чтобы число единиц в образовавшихся
группах было достаточно велико, т.е. группы были одинаково заполнены.
В типологических
группировках используются специализированные интервалы.
Границы в них устанавливаются там, где начинается переход от одного качества к
другому. Наметить точки перехода можно только на основе теоретического анализа,
используя для выделения типов совокупность признаков, характеризующих различные
стороны изучаемого явления.
Иногда имеющуюся
группировку необходимо несколько изменить: объединить ранее выделенные
относительно мелкие группы в небольшое число более крупных, типичных групп или
изменить границы прежних групп с тем, чтобы сделать группировку сопоставимой с
другими. Такая переработка результатов первичной группировки называется перегруппировкой,
или
вторичной группировкой.
Для
количественной характеристики каждой группы часто выполняют расчет структурных
характеристик. Расчет заключается в определении для каждой группы удельного веса (доли) ее единиц в общем объеме
статистической совокупности. Как и любая относительная величина,
этот показатель может быть определен
в виде коэффициентов, или в виде процентов:
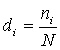 или
или ![]()
Рассчитав такие доли для всех групп, мы
получаем структуру изучаемой статистической совокупности, равную полному набору
долей:
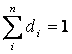 или
или 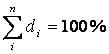
На основе анализа
показателей структуры делаются соответствующие выводы. В выводах отражаются два
положения:
Какие значения признака
встречаются в совокупности наиболее часто, какие наиболее редко.
Каков характер изменения структуры
явления в зависимости от изменения значения признака. Выводы должны быть сделаны обязательно, иначе пропадает смысл построения группировки.
Метод
группировки предусматривает построение рядов распределения. Статистический ряд
распределения – это упорядоченное распределение единиц совокупности на
группы по определённому варьирующему признаку. В зависимости от признака,
положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения,
построенные по качественным признакам. Такие ряды принято оформлять в виде
таблиц. Атрибутивные ряды распределения характеризуют состав совокупности по
тем или иным существенным признакам. Взятые за несколько периодов времени, эти
данные позволяют исследовать изменение структуры.
Вариационными называют ряды распределения,
построенные по количественному признаку. Любой вариационный ряд состоит из двух
элементов: вариантов и частот. Вариантами считаются отдельные значения признака, которые он принимает в вариационном
ряду, т.е. варианта – это конкретное значение варьирующего признака. Частоты – это численности отдельных
вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие,
как часто встречаются те или иные варианты в ряду распределения. Сумма всех
частот определяет численность всей совокупности, её объём. Частостями называются частоты, выраженные в долях единицы или в процентах к
итогу. Соответственно сумма частостей равна 1 или
100%.
На практике для анализа рядов
распределения используют их графическое
изображение, позволяющее судить и о
форме распределения, и о характере изменения частот вариационного ряда.
Полигон используется
при изображении дискретных вариационных рядов. Для его построения в
прямоугольной системе координат по оси абсцисс в одинаковом масштабе
откладываются ранжированные значения варьирующего признака, а по оси ординат
наносится шкала для выражения величины частот. Полученные на пересечении
абсцисс и ординат точки соединяют прямыми линиями и получают ломаную линию,
называемую полигоном частот. Иногда
для замыкания полигона крайние точки (слева и справа на ломаной линии)
соединяют с точками на оси абсцисс, в этом случае получается многоугольник. На
оси ординат могут наноситься не только значения частот, но и частостей вариационного ряда.
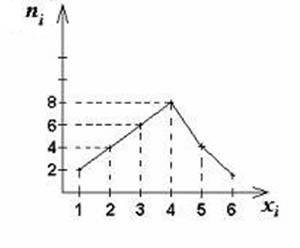
Рис. 1.
Полигон распределения
Гистограмма
применяется для изображения интервального вариационного ряда. При построении
гистограммы на оси абсцисс откладываются величины интервалов, а частоты
изображаются прямоугольниками, построенными на соответствующих интервалах.
Высота столбиков в случае равных интервалов должна быть пропорциональна
частотам. В результате получается гистограмма – график, на котором ряд
распределения изображён в виде смежных друг с другом столбиков. При построении
гистограммы распределения вариационного ряда с неравными интервалами по оси
ординат наносят не частоты, а плотность распределения признака в
соответствующих интервалах. Это необходимо сделать для устранения влияния
величины интервала на распределение и иметь возможность сравнивать частоты. Плотность распределения – это частота,
рассчитанная на единицу ширины интервала, т.е. сколько единиц в каждой группе
приходится на единицу величины интервала.
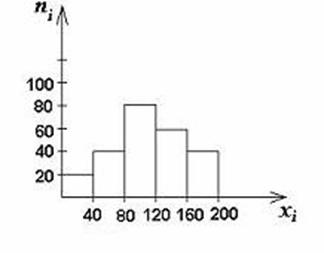
Рис.2. Гистограмма
распределения равноинтервального ряда
Для
графического изображения вариационных рядов может быть использована
кумулятивная кривая. При помощи кумуляты (кривой
сумм) изображается ряд накопленных частот. Накопленные частоты определяются
путём последовательного суммирования частот по группам и показывают, сколько
единиц совокупности имеют значения признака не больше, чем рассматриваемое
значение. При построении кумуляты интервального
вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат
накопленные частоты, которые наносят на поле в виде перпендикуляров к оси
абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и
получают ломаную линию, т.е.
кумуляту. Изображение вариационного ряда в
виде кумуляты особенно эффективно для рядов, частоты
которых выражены в процентах к сумме частот ряда, или же выражены частостями.
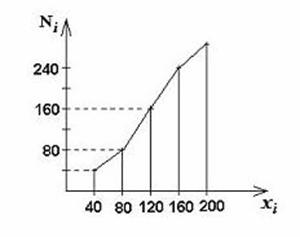
Рис. 3. Кумулята
распределения
Если
при графическом изображении вариационного ряда в виде кумуляты
оси поменять местами, то получим огиву.
С помощью кумулятивных кривых графически изображают процесс концентрации.
Ряд распределения представляет
собой простейшую группировку, в которой каждая выделяемая группа
характеризуется одним показателем – численностью единиц объекта, попавших в
каждую группу. Построение рядов распределения является составной частью сводной
обработки данных, при которой каждая группа единиц характеризуется многими
показателями. Перечень таких показателей формируется в соответствии с целями
статистического исследования и задачами группировки. Для получения обобщённой
характеристики явления следует использовать систему
показателей, которая предусматривает исчисление абсолютных, относительных и средних
величин.
Стоимость расчета интервала рыночных цен – от 4000 рублей в зависимости от количества и характера сделок.
Если Вам требуется консультация Вы можете обратится к нашим специалистам по следующим телефонам 8(843)209-05-31, 8(843)265-52-32 или на электронную почту info@law115.ru

Расчет интервала рыночных цен в контролируемых сделках
Метод сопоставимых рыночных цен используется для определения соответствия цены, примененной в контролируемой сделке, рыночной цене, при наличии на соответствующем рынке товаров (работ, услуг) хотя бы одной сопоставимой сделки, предметом которой являются идентичные (при их отсутствии – однородные) товары (работы, услуги), а также при наличии достаточной информации о такой сделке (абз. 2 п. 3 ст. 105.7 НК РФ).
Интервал рыночных цен определяется на основе имеющейся информации о ценах, примененных в течение анализируемого периода, или информации на ближайшую дату до совершения контролируемой сделки (п. 4 ст. 105.9 НК РФ).
Представляется, что в п. 4 ст. 105.9 НК РФ использована не вполне удачная формулировка, допускающая возможность выбора («или»), но при этом не уточняющая, кто и как делает этот выбор, и при каких обстоятельствах используется информация за анализируемый период, а при каких – информация на определенную дату (ближайшую к контролируемой сделке). Очевидно, что при использовании этих двух вариантов можно получить абсолютно разные данные об интервале рыночных цен, которые неизбежно станут предметом налоговых споров и судебных разбирательств.
Ситуация 1. При наличии информации только об одной сопоставимой сделке, предметом которой являются идентичные (при их отсутствии – однородные) товары (работы, услуги), цена указанной сделки может быть признана одновременно минимальным и максимальным значением интервала рыночных цен только в случае, когда коммерческие и (или) финансовые условия указанной сделки полностью сопоставимы с коммерческими и (или) финансовыми условиями анализируемой сделки (либо с помощью соответствующих корректировок обеспечена полная сопоставимость таких условий), а также при условии, что продавец товаров (работ, услуг) в сопоставимой сделке не занимает доминирующего положения на рынке этих идентичных (при их отсутствии – однородных) товаров (работ, услуг) (п. 2 ст. 105.9 НК РФ).
Ситуация 2. При наличии информации о нескольких сопоставимых сделках (в том числе совершенных налогоплательщиком, при условии, что указанные сделки совершены с лицами, не являющимися взаимозависимыми с налогоплательщиком), предметом которых являются идентичные (при их отсутствии – однородные) товары (работы, услуги), интервал рыночных цен определяется в следующем порядке.
1 шаг. Построение интервала рыночных цен.
Вся совокупность цен по сопоставимым сделкам упорядочивается по возрастанию.
В полученной выборке каждому значению цены, начиная с минимального, присваивается порядковый номер, при этом все одинаковые значения включаются в выборку с самостоятельным номером. В выборку не включается цена, примененная в анализируемой сделке.
При наличии достаточного количества сопоставимых сделок, совершенных налогоплательщиком с невзаимозависимыми лицами, другие сделки в интервал не включаются (пп. 1 п. 3 ст. 105.9 НК РФ).
Пример 1.
2 шаг. Расчет минимального значения интервала рыночных цен.
Если частное от деления на четыре числа значений в выборке является целым числом, то минимальным значением интервала признается среднее арифметическое значения цены, имеющего в выборке порядковый номер, равный этому целому числу, и значения цены, имеющего следующий по возрастанию порядковый номер в этой выборке (абз. 2 пп. 2 п. 3 ст. 105.9 НК РФ).
Допустим, в выборке есть 12 упорядоченных по возрастанию значений цен по сопоставимым сделкам (в рублях):
70, 86, 89, 90, 91, 94, 94, 100, 103, 103, 103, 116.
Частное от деления 12 (числа значений) на 4 составляет 3.
Следовательно, минимальным значением интервала будет среднее арифметическое третьего (89 руб.) и четвертого (90 руб.) чисел выборки, что составит 89,5 руб. ((89 + 90) / 2).
Таким образом, минимальное значение рыночной цены в данном примере составит 89,5 руб.
3 шаг. Расчет максимального значения интервала рыночных цен.
Если произведение 0,75 и числа значений цен в выборке является целым числом, то максимальным значением интервала рыночных цен признается среднее арифметическое значения цены, имеющего в выборке порядковый номер, равный этому целому числу, и значения цены, имеющего следующий по возрастанию порядковый номер в этой выборке (абз. 2 пп. 3 п. 3 ст. 105.9 НК РФ).
В выборке есть 12 упорядоченных по возрастанию значений цен по сопоставимым сделкам (в рублях):
70, 86, 89, 90, 91, 94, 94, 100, 103, 105, 106, 116.
Произведение числа 0,75 и 12 (числа значений) составляет 9.
Следовательно, максимальным значением интервала будет среднее арифметическое девятого (103 руб.) и десятого (105 руб.) чисел выборки, что составит 104 руб. ((103 + 105) / 2).
Таким образом, максимальное значение рыночной цены в данном примере составит 104 руб.
Вывод.
Если цена, примененная в анализируемой сделке, находится в пределах интервала рыночных цен (от 89,5 руб. до 104 руб.), для целей налогообложения признается, что такая цена соответствует рыночной цене.
Пример 2.
2 шаг. Расчет минимального значения интервала рыночных цен.
Если частное от деления на четыре числа значений в выборке не является целым числом, то минимальным значением интервала рыночных цен признается значение цены, имеющее в выборке порядковый номер, равный целой части этого дробного числа, увеличенной на единицу (абз. 3 пп. 2 п. 3 ст. 105.9 НК РФ).
Допустим, в выборке есть 11 упорядоченных по возрастанию значений цен по сопоставимым сделкам (в рублях):
70, 86, 89, 90, 91, 94, 94, 100, 103, 103, 116.
Частное от деления 11 (числа значений) на 4 составляет 2,75, и его целая часть равна 2.
Следовательно, минимальным значением интервала будет значение третьего (89 руб.) числа выборки, поскольку именно оно имеет порядковый номер, равный двойке, увеличенной на единицу.
Таким образом, минимальное значение рыночной цены в данном примере составит 89 руб.
3 шаг. Расчет максимального значения интервала рыночных цен.
Если произведение 0,75 и числа значений цен в выборке не является целым числом, то максимальным значением интервала рыночных цен признается значение цены, имеющее в выборке порядковый номер, равный сумме целой части этого дробного числа, увеличенной на единицу (абз. 2 пп. 3 п. 3 ст. 105.9 НК РФ).
В выборке есть 11 упорядоченных по возрастанию значений цен по сопоставимым сделкам (в рублях):
70, 86, 89, 90, 91, 94, 94, 100, 103, 103, 116.
Произведение числа 0,75 и 11 (числа значений) составляет 8,25, и его целая часть равна 8.
Следовательно, максимальным значением интервала будет значение девятого (103 руб.) числа выборки, поскольку именно оно имеет порядковый номер, равный восьмерке, увеличенной на единицу.
Таким образом, максимальное значение рыночной цены в данном примере составит 103 руб.
Вывод.
Если цена, примененная в анализируемой сделке, находится в пределах интервала рыночных цен (от 89 руб. до 103 руб.), для целей налогообложения признается, что такая цена соответствует рыночной цене.
Следует отметить, что применение метода сопоставимых рыночных цен к работам и услугам представляется затруднительным. Так как найти идентичную и даже однородную работу или услугу (например, стоимость пошива одинакового платья в двух разных ателье зависит от репутации ателье, срока изготовления вещи, его удаленности и других условий). Кроме того, на качество выполнения работы и услуги, как правило, оказывают немалое влияние деловые характеристики непосредственного исполнителя, т.е. его личность, что, разумеется, повторяться не может, следовательно, не может быть одинаковой и цена.
Информационные, консультационные, маркетинговые и т.п. услуги также обладают признаком индивидуальности, – не может быть предоставлена в рамках консультации, исследования рынка и т.п. абсолютно одинаковая информация. Следовательно, и признаков идентичности либо однородности быть не может. Сказанное относится и к медицинским, образовательным услугам, выполнению строительных, монтажных и т.п. работ. Видимо, в связи с объективной невозможностью установления цены на идентичные (однородные) услуги (работы) налоговые органы на сегодняшний день крайне редко прибегают к методу сопоставимых рыночных цен при контроле за ценой работ или услуг, о чем свидетельствует почти полное отсутствие арбитражной практики по рассматриваемой категории дел.
