Как найти величину силы действующей на заряд - Сайт, где вы сможете решить свои вопросы

Закон Кулона

Между электрическими зарядами действует сила. Как она зависит от величины зарядов и других факторов?
Этот вопрос исследовал в 1780-е годы французский физик Шарль Кулон (1736-1806). Он воспользовался крутильными весами, очень похожими на те, которые применял Кавендиш для определения гравитационной постоянной.
Если к шарику на конце стержня, подвешенного на нити, подности заряд, стержень слегка отклоняется, нить закручивается, и угол поворота нити будет пропорционален действующей между зарядами силе (крутильные весы). С помощью этого прибора Кулон определил зависимость силы от величины зарядов и расстояния между ними.

В те времена еще не было приборов для точного определения величины заряда, но Кулон сумел приготовить небольшие шарики с известным соотношением зарядов. Если заряженный проводящий шарик, рассуждал он, привести в соприкосновение с точно таким же незаряженным шариком, то имевшийся на первом заряд в силу симметрии распределится поровну между двумя шариками.
Это дало ему возможность получать заряды, составлявшие 1/2, 1/4 и т.д. от первоначального.
Несмотря на некоторые трудности, связанные с индуцированием зарядов, Кулону удалось доказать, что сила, с которой одно заряженное тело действует на другое малое заряженное тело, прямо пропорциональна электрическому заряду каждого из них.
Другими словами, если заряд любого из этих тел удвоить, то удвоится и сила; если же удвоить одновременно заряды обоих тел, то сила станет вчетверо больше. Это справедливо при условии, что расстояние между телами остается постоянным.
Изменяя расстояние между телами, Кулон обнаружил, что действующая между ними сила обратно пропорциональна квадрату расстояния: если расстояние, скажем, удваивается, сила становится вчетверо меньше.

Итак, заключил Кулон, сила, с которой одно малое заряженное тело (в идеальном случае -точечный заряд, т.е. тело, подобно материальной точке не имеющее пространственных размеров) действует на другое заряженное тело, пропорциональна произведению их зарядов Q₁ и Q₂ и обратно пропорциональна квадрату расстояния между ними:

Здесь k -коэффициент пропорциональности.
Это соотношение известно как закон Кулона; его справедливость подтверждена тщательными экспериментами, гораздо более точными, чем первоначальные трудно воспроизводимые опыты Кулона. Показатель степени 2 установлен в настоящее время с точностью 10 -16 , т.е. он равен 2 ± 2?10 -16 .

Коль скоро мы теперь имеем дело с новой величиной — электрическим зарядом, мы можем подобрать такую единицу измерения, чтобы постоянная к в формуле равнялась единице. И действительно, такая система единиц еще недавно широко использовалась в физике.

Речь идет о системе СГС (сантиметр-грамм-секунда), в которой используется электростатическая единица заряда СГСЭ. По определению два малых тела, каждое с зарядом 1 СГСЭ, расположенные на расстоянии 1 см друг от друга, взаимодействуют с силой 1 дина.

Теперь, однако, заряд чаще всего выражают в системе СИ, где его единицей является кулон (Кл).
Точное определение кулона через электрический ток и магнитное поле мы приведем позднее.
В системе СИ постоянная k имеет величину k = 8,988?10 9 Нм 2 /Кл 2 .

Заряды, возникающие при электризации трением обычных предметов (расчески, пластмассовой линейки и т.п.), по порядку величины составляют микрокулон и меньше (1 мкКл = 10 -6 Кл).
Заряд электрона (отрицательный) приблизительно равен 1,602?10 -19 Кл. Это наименьший известный заряд; он имеет фундаментальное значение и обозначается символом е, его часто называют элементарным зарядом.
е = (1,6021892 ± 0,0000046)?10 -19 Кл, или е ? 1,602?10 -19 Кл.

Поскольку тело не может приобрести или потерять долю электрона, суммарный заряд тела должен быть целым кратным элементарного заряда. Говорят, что заряд квантуется (т.е. может принимать лишь дискретные значения). Однако, поскольку заряд электрона е очень мал, мы обычно не замечаем дискретности макроскопических зарядов (заряду 1 мкКл соответствуют примерно 10 13 электронов) и считаем заряд непрерывным.

Формула Кулона характеризует силу, с которой один заряд действует на другой. Эта сила направлена вдоль линии, соединяющей заряды. Если знаки зарядов одинаковы, то силы, действующие на заряды, направлены в противоположные стороны. Если же знаки зарядов различны, то действующие на заряды силы направлены навстречу друг другу.
Заметим, что в соответствии с третьим законом Ньютона сила, с которой один заряд действует на другой, равна по величине и противоположна по направлению силе, с которой второй заряд действует на первый.
Закон Кулона можно записать в векторной форме подобно закону всемирного тяготения Ньютона:

где F₁₂ — вектор силы, действующей на заряд Q1 со стороны заряда Q2,
— расстояние между зарядами,
— единичный вектор, направленный от Q2 к Q1.
Следует иметь в виду, что формула применима лишь к телам, расстояние между которыми значительно больше их собственных размеров. В идеальном случае это точечные заряды. Для тел конечного размера не всегда ясно, как отсчитывать расстояние r между ними, тем более что распределение заряда может быть и неоднородным. Если оба тела — сферы с равномерным распределением заряда, то r означает расстояние между центрами сфер. Важно также понимать, что формула определяет силу, действующую на данный заряд со стороны единственного заряда. Если система включает несколько (или много) заряженных тел, то результирующая сила, действующая на данный заряд, будет равнодействующей (векторной суммой) сил, действующих со стороны остальных зарядов. Постоянная к в формуле Закона Кулона обычно выражается через другую константу, ?₀, так называемую электрическую постоянную, которая связана с k соотношением k = 1/(4??₀). С учетом этого закон Кулона можно переписать в следующем виде:

где с наивысшей на сегодня точностью

Запись большинства других уравнений электромагнитной теории упрощается при использовании ?₀, поскольку 4? в окончательном результате часто сокращается. Поэтому мы будем обычно использовать Закон Кулона, считая, что:

Закон Кулона описывает силу, действующую между двумя покоящимися зарядами. Когда заряды движутся, между ними возникают дополнительные силы, и их мы обсудим в последующих главах. Здесь же рассматриваются только покоящиеся заряды; этот раздел учения об электричестве называется электростатикой.

Продолжение следует. Коротко о следующей публикации:

Электрическое поле — один из двух компонентов электромагнитного поля, представляющий собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, либо возникающий при изменении магнитного поля.

Закон Кулона.

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.

В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов. Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.

В аналитическом виде закон Кулона имеет вид:

где |q₁| и |q₂| — модули зарядов; r — расстояние между ними; k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.

Сила взаимодействия между зарядами зависит также от среды между заряженными телами.

В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.

Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока — 1 ампер (А), которая входит в число основных единиц СИ.

За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока 1 А за 1 с.

Заряд в 1 Кл очень велик. Сила взаимодействия двух точечных зарядов по 1 Кл каждый, расположенных на расстоянии 1 км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой 1 т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в 1 А — вполне обычный ток, протекающий по проводам в наших квартирах).

Коэффициент k в законе Кулона при его записи в СИ выражается в Н · м 2 /Кл 2 . Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:

Часто его записывают в виде , где ɛ₀ =8,85 · 10 — 12 Kл 2 /H·м 2 — электрическая постоянная. В среде с диэлектрической проницаемостью ɛ закон Кулона имеет вид:

Закон Кулона простым языком

Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.

Рисунок 1. Закон Кулона

История открытия

Эксперименты с заряженными частицами проводили много физиков:

Г. В. Рихман;
профессор физики Ф. Эпинус;
Д. Бернулли;
Пристли;
Джон Робисон и многие другие.

Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.

Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).

Рис. 2. Крутильные весы

У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10 -9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1 º . Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.

Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.

Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.

Формулировка

Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.

Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F₁|=|F₂|=(k_e*q₁*q₂) / r 2

Рис. 3. Взаимодействие точечных зарядов

Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.

Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.

Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:

соблюдение точечности зарядов;
неподвижность заряженных тел;
закон выражает зависимости между зарядами в вакууме.

Границы применения

Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.

Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 – 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.

Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 10 18 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.

Кулоновские силы подпадают под действие третьего закона Ньютона: F₁ = – F₂. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m₁* m₂ ) / r 2 , где m₁ и m₂ – массы взаимодействующих тел, а r – расстояние между ними.

Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.

Коэффициент k

Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.

Коэффициент k в СИ выражается следующим образом: k = 1/4πε₀, где ε₀ – электрическая постоянная: ε₀ = 8,85 ∙10 -12 Кл 2 /Н∙м 2 . Выполнив несложные вычисления, мы находим: k = 9×10 9 H*м 2 / Кл 2 . В метрической системе СГС k =1.

На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.

Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.

Закон Кулона в диэлектриках

Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε₀.

Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.

Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.

Применение на практике

Вся современная электротехника построена на принципах взаимодействия кулоновских сил. Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.

Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.

На базе электростатики появилось много изобретений:

конденсатор;
различные диэлектрики;
антистатические материалы для защиты чувствительных электронных деталей;
защитная одежда для работников электронной промышленности и многое другое.

На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).

Рис. 4. Большой адронный коллайдер

Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.

Источник

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Зако́н Куло́на — физический закон, описывающий взаимодействие между двумя неподвижными точечными электрическими зарядами в вакууме. Сила, с которой заряд $q_{1}$ действует на заряд $q_{2}$ , согласно этому закону находится (в СИ) как

${displaystyle {vec {F}}_{12}={frac {1}{4pi varepsilon _{0}}}cdot {frac {q_{1}q_{2}({vec {r}}_{2}-{vec {r}}_{1})}{|{vec {r}}_{2}-{vec {r}}_{1}|^{3}}}}$

где ${displaystyle |{vec {r}}_{2}-{vec {r}}_{1}|=r_{12}}$ — расстояние между зарядами, ${displaystyle {vec {r}}_{1}}$ , ${displaystyle {vec {r}}_{2}}$ — их радиус-векторы, а $varepsilon _{0}$ — электрическая постоянная. По величине, ${displaystyle F_{12}=q_{1}q_{2}/(4pi varepsilon _{0}r_{12}^{2})}$ .

Также под законом Кулона понимается формула для вычисления электрического поля точечного заряда, вместе с её обобщением на произвольное распределение зарядов в пространстве:

${displaystyle {vec {E}}({vec {r}}_{0})={frac {1}{4pi varepsilon _{0}}}int _{V}{frac {({vec {r}}_{0}-{vec {r}})rho ({vec {r}}),dV}{|{vec {r}}_{0}-{vec {r}}|^{3}}}}$

Здесь ${vec {r}}_{0}$ — радиус-вектор точки, в которой определяется поле, а — радиус-вектор элемента объёма , заряд ( rho — плотность заряда) которого даёт вклад в поле.

Закон Кулона в классической электродинамике[править | править код]

Установление и формулировки закона[править | править код]

Закон открыт Шарлем Кулоном в 1785 году. Проведя большое количество опытов с металлическими шариками, Кулон дал такую формулировку закона:

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.

Современная формулировка^[1]:

Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.

В векторном виде в формулировке Ш. Кулона закон записывается как

${displaystyle {vec {F}}_{12}=kcdot {frac {q_{1}cdot q_{2}}{r_{12}^{2}}}cdot {frac {{vec {r}}_{12}}{r_{12}}}}$

где $vec{F}_{12}$ — сила, с которой заряд 1 действует на заряд 2; — величина зарядов (со знаком); $vec{r}_{12}$ — вектор, направленный от заряда 1 к заряду 2 и по модулю равный расстоянию между зарядами ( $r_{12}$ ); — коэффициент пропорциональности.

Условия применимости[править | править код]

Для того, чтобы закон был верен, необходимы:

точечность зарядов, то есть расстояние между заряженными телами должно быть много больше их размеров. Здесь две оговорки: а) существует обобщение закона Кулона на случай тел конечных размеров; б) можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;
их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;
расположение зарядов в вакууме.

В отдельных ситуациях, с корректировками, закон может быть применен также для взаимодействий зарядов в среде и для движущихся зарядов^[2]. Но в общем случае при наличии неоднородных диэлектриков он неприменим, поскольку помимо заряда $q_{1}$ на зарад $q_{2}$ действуют связанные заряды, возникшие при поляризации.

Выражения в разных системах единиц[править | править код]

В СГСЭ единица измерения заряда выбрана таким образом, что коэффициент равен единице.

В Международной системе единиц (СИ) одной из основных единиц является единица силы электрического тока — ампер, а единица заряда — кулон — производная от него. Величина ампера определена таким образом, что k = c²·10⁻⁷ Гн/м = 8,9875517873681764⋅10⁹ Н·м²/Кл² (или Ф⁻¹·м). В СИ коэффициент k записывается в виде:

$k={frac {1}{4pi varepsilon _{0}}}$

где $varepsilon _{0}$ ≈ 8,85418781762⋅10⁻¹² Ф/м — электрическая постоянная.

В случае среды, заполненной бесконечным однородным изотропным диэлектрическим веществом, в знаменатель формулы закона Кулона добавляется диэлектрическая проницаемость среды ε. Тогда

${displaystyle k={frac {1}{varepsilon }},,}$

(в СГСЭ) ${displaystyle quad k={frac {1}{4pi varepsilon _{0}varepsilon }},,}$

(в СИ).

Закон Кулона и уравнения Максвелла[править | править код]

Закон Кулона и принцип суперпозиции для электрических полей в вакууме полностью равносильны уравнениям Максвелла для электростатики ( rho — плотность заряда, — вектор электрического смещения) и ( — напряжённость электрического поля). То есть закон Кулона и принцип суперпозиции для электрических полей выполняются тогда и только тогда, когда выполняются уравнения Максвелла для электростатики, и наоборот, уравнения Максвелла для электростатики выполняются, тогда когда выполняются закон Кулона и принцип суперпозиции для электрических полей^[3].

Исторически закон Кулона был одним из эмпирических законов, служивших предпосылками для формулирования уравнения Максвелла. Однако при современном изложении учения об электромагнетизме этот закон (равно как и, скажем, закон Ампера) нередко позиционируется как следствие уравнений Максвелла, которым придаётся статус фундаментальных аксиом.

Вывод закона Кулона из уравнений Максвелла[править | править код]

Уравнение Максвелла с помощью теоремы Гаусса может быть приведено к интегральной форме

${displaystyle oint limits _{mathbf {S} }{vec {D}}cdot d{vec {s}}=Q}$

где — суммарный заряд внутри замкнутой поверхности , по которой проводится интегрирование. Если «суммарный» заряд состоит из одного точечного заряда $q_{1}$ , пространство заполнено однородным диэлектриком, то есть ${displaystyle {vec {D}}=varepsilon _{0}varepsilon {vec {E}}}$ , а поверхность представляет собой сферу с центром в месте нахождения заряда, то из-за симметрии поле заряда $q_{1}$ в любой точке на поверхности сферы будет одним и тем же по величине и направленным от центра или к центру. Тогда интеграл оказывается равным ${displaystyle Dcdot S=varepsilon _{0}varepsilon Ecdot 4pi l^{2}}$ , где через обозначен радиус сферы, отсюда ${displaystyle E=q_{1}/(4pi varepsilon _{0}varepsilon l^{2})}$ . Если на поверхность сферы поместить другой точечный заряд $q_{2}$ , на него будет действовать сила. Поскольку поле есть отношение действующей на произвольный заряд силы к величине данного заряда ( ${displaystyle E=F/q_{2}}$ ), приходим к выражению закона Кулона ${displaystyle F=q_{1}q_{2}/(4pi varepsilon _{0}varepsilon l^{2})}$ .

Обобщение на случай распределения заряда[править | править код]

Если на заряд $q_{2}$ действует не точечный заряд $q_{1}$ , а заряд, распределённый в пространстве с плотностью ${displaystyle rho _{1}({vec {r}})}$ (Кл/м³), то область, где ${displaystyle rho _{1}neq 0}$ , можно мысленно разбить на малые (в пределе — бесконечно малые) элементы объёма ${displaystyle dV_{1}}$ и каждый такой элемент рассматривать как точечный заряд ${displaystyle rho _{1}({vec {r}}_{1}),dV_{1}}$ . По принципу суперпозиции, суммарная сила, действующая на заряд $q_{2}$ со стороны таких элементов, может быть определена как интеграл по ним:

${displaystyle {vec {F}}_{12}={frac {q_{2}}{4pi varepsilon _{0}}}int _{V_{1}}{frac {({vec {r}}_{2}-{vec {r}}_{1}),rho _{1}({vec {r}}_{1})dV_{1}}{|{vec {r}}_{2}-{vec {r}}_{1}|^{3}}}}$

где радиус-вектором ${displaystyle {vec {r}}_{2}}$ задаётся положение заряда $q_{2}$ , а радиус-вектором ${displaystyle {vec {r}}_{1}}$ — положение элемента . Если в случае точечного $q_{1}$ вектор ${displaystyle {vec {r}}_{1}}$ был фиксированным, то теперь он пробегает все положения элементов.

Если же не только заряд $q_{1}$ , но и заряд $q_{2}$ являются распределёнными, то производится интегрирование и по элементам первого, и по элементам второго заряда, а именно

${displaystyle {vec {F}}_{12}={frac {1}{4pi varepsilon _{0}}}int _{V_{2}}int _{V_{1}}{frac {({vec {r}}_{2}-{vec {r}}_{1}),rho _{1}({vec {r}}_{1})dV_{1},rho _{2}({vec {r}}_{2})dV_{2}}{|{vec {r}}_{2}-{vec {r}}_{1}|^{3}}}}$

Закон Кулона и расчёт электрического поля[править | править код]

Взаимодействие двух зарядов может быть истрактовано как взаимодействие одного из зарядов с электрическим полем, создаваемым другим зарядом. Это становится виднее, если соответствующим образом перегруппировать сомножители в выражении для силы:

${displaystyle {vec {F}}_{12}={frac {1}{4pi varepsilon _{0}}}cdot {frac {q_{1}q_{2}({vec {r}}_{2}-{vec {r}}_{1})}{|{vec {r}}_{2}-{vec {r}}_{1}|^{3}}}=q_{2}cdot left[{frac {1}{4pi varepsilon _{0}}}cdot {frac {q_{1}({vec {r}}_{2}-{vec {r}}_{1})}{|{vec {r}}_{2}-{vec {r}}_{1}|^{3}}}right]=q_{2}cdot E_{1}({vec {r}}_{2})}$

Тем самым закон Кулона фактически становится основой для вычисления поля. Так же, как и при рассмотрении силы, возможно обобщение последнего равенства на случай распределения зарядов.

Для нахождения поля () и электрического потенциала varphi в точке ${vec {r}}_{0}$ , создаваемых распределённым зарядом, производится интегрирование:

${displaystyle {vec {E}}({vec {r}}_{0})={frac {1}{4pi varepsilon _{0}}}int {frac {({vec {r}}_{0}-{vec {r}}),dq({vec {r}})}{|{vec {r}}_{0}-{vec {r}}|^{3}}},qquad varphi ({vec {r}}_{0})={frac {1}{4pi varepsilon _{0}}}int {frac {dq({vec {r}})}{|{vec {r}}_{0}-{vec {r}}|}}}$

где заряд обычно записывается как (и интегрирование тогда выполняется по объёму), но в ряде задач может задаваться как (если заряд поверхностный, [ sigma ] = Кл/м², интерирование по площади) или как (заряд линейный [ lambda ] = Кл/м, интеграл по линии).

Если всё пространство заполнено однородным диэлектриком с проницаемостью , то формулы сохраняют свою актуальность, если в них $varepsilon _{0}$ заменить на $varepsilon _{0}varepsilon$ . В других случаях, за редкими исключениями, формулы неприменимы, так как необходимо учитывать вклад в том числе связанных зарядов ( ${displaystyle rho =rho _{f}+rho _{b}}$ , где ${displaystyle rho _{f}}$ — плотность стороннего, а ${displaystyle rho _{b}}$ — связанного заряда), возникающих при поляризации, — а эти заряды заранее неизвестны.

Аналогии в других областях классической физики[править | править код]

Закон Кулона совершенно аналогичен по форме закону всемирного тяготения. При этом функцию гравитационных масс выполняют электрические заряды^[4] разных знаков.

Магнитостатическими аналогами закона Кулона являются закон Ампера (в части нахождения сил взаимодействия) и закон Био — Савара — Лапласа (в части расчёта по́ля).

Об открытии и исторической значимости закона[править | править код]

Впервые исследовать экспериментально закон взаимодействия электрически заряженных тел предложил^[5] Г. В. Рихман в 1752—1753 гг. Он намеревался использовать для этого сконструированный им электрометр-«указатель». Осуществлению этого плана помешала его трагическая гибель.

В 1759 г. профессор физики Санкт-Петербургской академии наук Ф. Эпинус, занявший кафедру Рихмана после его гибели, впервые предположил^[6], что заряды должны взаимодействовать обратно пропорционально квадрату расстояния. В 1760 г. появилось краткое сообщение^[7] о том, что Д. Бернулли в Базеле установил квадратичный закон с помощью сконструированного им электрометра. В 1767 г. Пристли в своей «Истории электричества»^[8] отметил, что опыт Франклина, обнаружившего отсутствие электрического поля внутри заряженного металлического шара, может означать, что «сила электрического притяжения подчиняется тем же законам, что и сила тяжести, а следовательно, зависит от квадрата расстояния между зарядами»^[9]. Шотландский физик Джон Робисон утверждал (1822), что в 1769 г. обнаружил, что шары с одинаковым электрическим зарядом отталкиваются с силой, обратно пропорциональной квадрату расстояния между ними, и таким образом предвосхитил открытие закона Кулона (1785)^[10].

Примерно за 11 лет до Кулона, в 1771 г., закон взаимодействия зарядов был экспериментально открыт Г. Кавендишем, однако результат не был опубликован и долгое время (свыше 100 лет) оставался неизвестным. Рукописи Кавендиша были вручены Дж. Максвеллу лишь в 1874 г одним из потомков Кавендиша на торжественном открытии Кавендишской лаборатории и опубликованы в 1879 г.^[11].

Сам Кулон занимался исследованием кручения нитей и изобрел крутильные весы. Он открыл свой закон, измеряя с помощью них силы взаимодействия заряженных шариков.

Закон Кулона является первым открытым количественным и сформулированным на математическом языке фундаментальным законом для электромагнитных явлений. С открытия закона Кулона началась современная наука об электромагнетизме^[12].

Закон Кулона в квантовой механике[править | править код]

В квантовой механике закон Кулона формулируется не при помощи понятия силы, как в классической механике, а при помощи понятия потенциальной энергии кулоновского взаимодействия. В случае, когда рассматриваемая в квантовой механике система содержит электрически заряженные частицы, к оператору Гамильтона системы добавляются слагаемые, выражающие потенциальную энергию кулоновского взаимодействия, так, как она вычисляется в классической механике^[13]. Это утверждение не следует из остальных аксиом квантовой механики, а получено путём обобщения опытных данных.

Так, оператор Гамильтона атома с зарядом ядра Z имеет вид:

${displaystyle H=-{frac {hbar ^{2}}{2m}}sum _{j}nabla _{j}^{2}-Ze^{2}sum _{j}{frac {1}{r_{j}}}+sum _{i>j}{frac {e^{2}}{r_{ij}}}.}$

Здесь m — масса электрона, е — его заряд, $r_{j}$ — абсолютная величина радиус-вектора j-го электрона vec r_j , а $r_{ij}=|vec r_{i} - vec r_{j}|$ . Первое слагаемое выражает кинетическую энергию электронов, второе слагаемое — потенциальную энергию кулоновского взаимодействия электронов с ядром и третье слагаемое — потенциальную кулоновскую энергию взаимного отталкивания электронов. Суммирование в первом и втором слагаемом ведется по всем Z электронам. В третьем слагаемом суммирование идёт по всем парам электронов, причём каждая пара встречается однократно^[14].

Закон Кулона с точки зрения квантовой электродинамики[править | править код]

Согласно квантовой электродинамике, электромагнитное взаимодействие заряженных частиц осуществляется путём обмена виртуальными фотонами между частицами. Принцип неопределённости для времени и энергии допускает существование виртуальных фотонов на время между моментами их испускания и поглощения. Чем меньше расстояние между заряженными частицами, тем меньшее время нужно виртуальным фотонам для преодоления этого расстояния и следовательно, тем большая энергия виртуальных фотонов допускается принципом неопределенности. При малых расстояниях между зарядами принцип неопределённости допускает обмен как длинноволновыми, так и коротковолновыми фотонами, а при больших расстояниях в обмене участвуют только длинноволновые фотоны. Таким образом, с помощью квантовой электродинамики можно вывести закон Кулона^[15]^[16].

Степень точности закона Кулона[править | править код]

Закон Кулона — экспериментально установленный факт. Его справедливость неоднократно подтверждалась всё более точными экспериментами. Одним из направлений таких экспериментов является проверка того, отличается ли показатель степени r в законе от 2. Для поиска этого отличия используется тот факт, что^[], какова бы ни была форма полости или проводника^[17].

Такие опыты впервые провел Кавендиш и повторил Максвелл в усовершенствованном виде, получив для максимального отличия показателя в степени от двух величину ${displaystyle {frac {1}{21600}}}$ ^[18].

Эксперименты, проведённые в 1971 г. в США Э. Р. Уильямсом, Д. Е. Фоллером и Г. А. Хиллом, показали, что показатель степени в законе Кулона равен 2 с точностью до $(3,1 pm 2,7) times 10^{-16}$ ^[19].

Для проверки точности закона Кулона на внутриатомных расстояниях У. Ю. Лэмбом и Р. Резерфордом в 1947 г. были использованы измерения относительного расположения уровней энергии водорода. Было установлено, что и на расстояниях порядка атомных 10⁻⁸ см, показатель степени в законе Кулона отличается от 2 не более чем на 10⁻⁹^[20]^[21].

Коэффициент в законе Кулона остаётся постоянным с точностью до 15⋅10⁻⁶^[21].

Поправки к закону в квантовой электродинамике[править | править код]

На небольших расстояниях (порядка комптоновской длины волны электрона):

${displaystyle lambda _{e}={frac {hbar }{m_{e}c}}approx 3{,}86cdot 10^{-13}}$

м^[22],

где m_e — масса электрона, hbar — постоянная Планка, — скорость света) становятся существенными нелинейные эффекты квантовой электродинамики: на обмен виртуальными фотонами накладывается генерация виртуальных электрон-позитронных (а также мюон-антимюонных и таон-антитаонных) пар, а также уменьшается влияние экранирования (см. перенормировка). Оба эффекта ведут к появлению экспоненциально убывающих членов порядка $e^{-2r/lambda_e}$ в выражении для потенциальной энергии взаимодействия зарядов и, как результат, к увеличению силы взаимодействия по сравнению с вычисляемой по закону Кулона.

Например, выражение для потенциала точечного заряда в системе СГС, с учётом радиационных поправок первого порядка, принимает вид
^[23]:

$Phi(r) = frac{Q}{r}cdotleft(1+ frac{alpha}{4sqrt{pi}}frac{e^{-2r/lambda_e}}{(r/lambda_e)^{3/2}}right),$

где — комптоновская длина волны электрона,
${displaystyle alpha ={frac {e^{2}}{hbar c}}}$ — постоянная тонкой структуры и .

На расстояниях порядка ${displaystyle lambda _{W}={frac {hbar }{m_{w}c}}sim }$ 10⁻¹⁸ м, где m_w — масса W-бозона, в игру вступают уже электрослабые эффекты.

В сильных внешних электромагнитных полях, составляющих заметную долю от поля пробоя вакуума (порядка ${displaystyle {frac {m_{e}c^{2}}{elambda _{e}}}sim }$ 10¹⁸ В/м или ${displaystyle {frac {m_{e}c}{elambda _{e}}}sim }$ 10⁹ Тл, такие поля наблюдаются, например, вблизи некоторых типов нейтронных звёзд, а именно магнитаров) закон Кулона также нарушается в силу дельбрюковского рассеяния обменных фотонов на фотонах внешнего поля и других, более сложных нелинейных эффектов. Это явление уменьшает кулоновскую силу не только в микро-, но и в макромасштабах, в частности, в сильном магнитном поле кулоновский потенциал падает не обратно пропорционально расстоянию, а экспоненциально^[24].

Закон Кулона и поляризация вакуума[править | править код]

Явление поляризации вакуума в квантовой электродинамике заключается в образовании виртуальных электронно-позитронных пар. Облако электронно-позитронных пар экранирует электрический заряд электрона. Экранировка растет с ростом расстояния от электрона, в результате эффективный электрический заряд электрона e_e является убывающей функцией расстояния ^[25]. Эффективный потенциал, создаваемый электроном с электрическим зарядом , можно описать зависимостью вида . Эффективный заряд e_e(r) зависит от расстояния по логарифмическому закону:

$frac{e_e(r)}{e}=1+frac{2alpha}{3pi}lnfrac{r_e}{r}+dots,$

где

${displaystyle alpha ={frac {e^{2}}{4pi varepsilon _{0}hbar c}}approx 7.3cdot 10^{-3}}$

— постоянная тонкой структуры;

${displaystyle r_{e}={frac {e^{2}}{4pi varepsilon _{0}c^{2}m_{e}}}approx 2.8cdot 10^{-13}}$

см — классический радиус электрона^[26]^[27].

Эффект Юлинга[править | править код]

Явление отклонения электростатического потенциала точечных зарядов в вакууме от значения закона Кулона известно как эффект Юлинга, который впервые вычислил отклонения от закона Кулона для атома водорода. Эффект Юлинга даёт поправку к лэмбовскому сдвигу 27 МГц^[28]^[29].

Закон Кулона и сверхтяжёлые ядра[править | править код]

В сильном электромагнитном поле вблизи сверхтяжёлых ядер с зарядом Z > 170 осуществляется перестройка вакуума, аналогичная обычному фазовому переходу. Это приводит к поправкам к закону Кулона^[30].

См. также[править | править код]

Электростатика
Электрическое поле
Дальнодействие
Закон Био — Савара — Лапласа
Закон притяжения
Шарль Огюстен де Кулон
Кулон (единица измерения)
Принцип суперпозиции
Уравнения Максвелла

Примечания[править | править код]

↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — С. 17. — 656 с. — ISBN 5-9221-0227-3.
↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 8-е, стереотипное. — М.: Физматлит, 2001. — С. 132. — («Теоретическая физика», том II). — ISBN 5-9221-0056-4.
↑ Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 4 «Электростатика», п. 1 «Статика», с. 70-71;
↑ Ландсберг Г. С. Элементарный учебник физики. Том II. Электричество и магнетизм. — М.: Наука, 1964. — Тираж 100 000 экз. — С. 33.
↑ Novi Comm. Acad. Sc. Imp. Petropolitanae, v. IV, 1758, p. 301.
↑ Эпинус Ф. Т. У. Теория электричества и магнетизма. — Л.: АН СССР, 1951. — 564 с. — (Классики науки). — 3000 экз. Архивировано 17 ноября 2012 года.
↑ Abel Socin (1760) Acta Helvetica, vol. 4, pages 224-225.
↑ J. Priestley. The History and present state of Electricity with original experiments. London, 1767, p. 732.
↑ Уиттекер Э. История теории эфира и электричества. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 76. — 512 с. — ISBN 5-93972-070-6.
↑ John Robison, A System of Mechanical Philosophy (London, England: John Murray, 1822), vol. 4. На стр. 68 Робисон заявляет, что в 1769 он обнародовал свои измерения силы, действующей между сферами с одинаковым зарядом, и описывает также историю исследований в этой области, отмечая имена Эпинуса, Кавендиша и Кулона. На стр. 73 Архивная копия от 1 декабря 2016 на Wayback Machine автор пишет, что сила изменяется как x^−2,06.
↑ ‘Филонович С. Р. Кавендиш, Кулон и электростатика. — М.: Знание, 1988. — С. 48.
↑ Спиридонов О. П. Универсальные физические постоянные.— М.: Просвещение.— 1984.— с. 52-53;
↑ Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — М., 2002. — С. 74. — («Теоретическая физика», том III).
↑ Бете Х. Квантовая механика. — Пер. с англ., под ред. В. Л. Бонч-Бруевича. — М.: Мир, 1965. — С. 11.
↑ Пайерлс Р. Е. Законы природы. пер. с англ. под ред. проф. Халатникова И. М. , Государственное издательство физико-математической литературы, М., 1959, тир. 20000 экз., 339 с., Гл. 9 «Электроны при высоких скоростях», п. «Силы при больших скоростях. Другие трудности», c. 263
↑ Окунь Л. Б. … z Элементарное введение в физику элементарных частиц Архивная копия от 25 ноября 2010 на Wayback Machine, М., Наука, 1985, Библиотечка «Квант», вып. 45, п. «Виртуальные частицы», с. 57.
↑ Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 10 «Поле внутри полости проводника», с. 106—108;
↑ Калашников С. Г.,
Электричество, М., ГИТТЛ, 1956, гл. III «Разность потенциалов», п. 34 «Точная проверка закона Кулона», с. 68—69; «Добавления», 1. «Теория опытов Кавендиша и Максвелла», с. 642—645;
↑ E. R. Williams, J. E. Faller, H. A. Hill «New Experimental Test of Coulomb’s Law: A Laboratory Upper Limit on the Photon Rest Mass», Phys. Rev. Lett. 26, 721—724 (1971);
↑ W. E. Lamb, R. C. Retherford. Fine Structure of the Hydrogen Atom by a Microwave Method (англ.) // Physical Review. — 1947. — Vol. 72, no. 3. — P. 241—243.
↑ ¹ ² Р. Фейнман, Р. Лейтон, М. Сэндс, Фейнмановские лекции по физике, вып. 5, «Электричество и магнетизм», пер. с англ., под ред. Я. А. Смородинского, изд. 3, М., Едиториал УРСС, 2004, ISBN 5-354-00703-8 (Электричество и магнетизм), ISBN 5-354-00698-8 (Полное произведение), гл. 5 «Применения закона Гаусса», п. 8 «Точен ли закон Кулона?», с. 103;
↑ CODATA Архивная копия от 11 февраля 2012 на Wayback Machine (the Committee on Data for Science and Technology)
↑ Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Квантовая электродинамика. — Издание 3-е, исправленное. — М.: Наука, 1989. — С. 565—567. — 720 с. — («Теоретическая физика», том IV). — ISBN 5-02-014422-3.
↑ Neda Sadooghi. Modified Coulomb potential of QED in a strong magnetic field (англ.). Архивировано 18 января 2015 года.
↑ Окунь Л. Б. Физика элементарных частиц. Изд. 3-е, М.: «Едиториал УРСС», 2005, ISBN 5-354-01085-3, ББК 22.382 22.315 22.3о, гл. 2 «Гравитация. Электродинамика», «Поляризация вакуума», с. 26-27;
↑ «Физика микромира», гл. ред. Д. В. Ширков, М., «Советская энциклопедия», 1980, 528 с., илл., 530.1(03), Ф50, ст. «Эффективный заряд», авт. ст. Д. В. Ширков, стр. 496;
↑ Яворский Б. М. «Справочник по физике для инженеров и студентов вузов» / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев, 8-e изд., перераб. и испр., М.: ООО «Издательство Оникс», ООО «Издательство Мир и образование», 2006, 1056 стр.: илл., ISBN 5-488-00330-4 (ООО «Издательство Оникс»), ISBN 5-94666-260-0 (ООО «Издательство Мир и образование»), ISBN 985-13-5975-0 (ООО «Харвест»), УДК 530(035) ББК 22.3, Я22, «Приложения», «Фундаментальные физические постоянные», с. 1008;
↑ Uehling E. A ., Phys. Rev., 48, 55, (1935)
↑ Швебер С., Бете Г., Гофман Ф. Мезоны и поля. Том 1 Поля гл. 5 Свойства уравнения Дирака п. 2. Состояния с отрицательной энергией c. 56, гл. 21 Перенормировка, п. 5 Поляризация вакуума с 336
↑ Мигдал А. Б. Поляризация вакуума в сильных полях и пионная конденсация// Успехи физических наук Т. 123— в. 3.— 1977 г., ноябрь.— с. 369—403;

Литература[править | править код]

Филонович С. Р. Судьба классического закона. — М.: Наука, 1990. — 240 с., ISBN 5-02-014087-2 (Библиотечка «Квант», вып. 79), тир. 70500 экз.

Ссылки[править | править код]

Закон Кулона (видеурок, программа 10 класса)

Источник

Пусть
на заряд Q
действуют несколько сил со стороны
других зарядов. Для того чтобы определить
результирующую силу
,
действующую на этот заряд, нужно узнать
еёнаправление
и модуль.

Направление
результирующей силы
определяетсяпо
принципу суперпозиции
сил (векторной суммы), а модуль – из
геометрических построений.

Рекомендуемая
последовательность решения задач:

сделать
рисунок, на котором, в соответствии с
условием задачи, указать расположение
всех зарядов;
построить
силы, действующие со стороны каждого
заряда на заряд Q
с учётом знаков всех зарядов (см. рис.
2). Все силы должны быть приложены к
точке, в которой расположен заряд Q
(то есть начинаться в этой точке) и
направлены по линии, соединяющей заряды;
построить
векторную сумму всех сил (по правилу
треугольника или параллелограмма, если
силы по результатам построений не
лежат на одной прямой). Таким образом,
мы определим направление
вектора результирующей силы;
модуль
равнодействующей силы вычисляется в
зависимости от расположения и величины
составляющих её сил, каждая из которых
рассчитывается по закону Кулона.

Например,
для системы, состоящей из трех зарядов,

П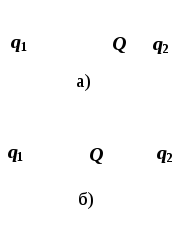ри
расчете модуля результирующей силы по
результатам построения возможны четыре
варианта (рис. 2, а, б, в, г):

векторы
составляющих сил направлены в одну
сторону. Модуль определяется как
алгебраическая сумма сил:

;

векторы
составляющих сил направлены в разные
стороны. Модуль определяется как
алгебраическая разность сил:

;

векторы
составляющих сил образуют между собой
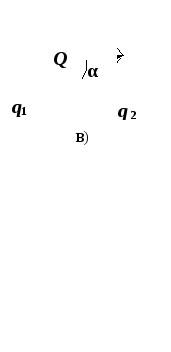
угол α.
Модуль определяется по теореме косинусов:

;

векторы
составляющих сил перпендикулярны друг
другу. Модуль определяется по теореме
Пифагора (частный случай теоремы
косинусов):

1. Как ведет себя
положительный заряд + q₁,
помещенный в поле неподвижного
отрицательного заряда– q₂:

а) движется с
постоянной скоростью к q₂;

б) движется
равноускоренно к заряду q₂;

в) движется
равнозамедленно к заряду q₂;

г) остается в покое.

2. Если отрицательный
точечный заряд, находящийся посередине
между точечными зарядами qи2q, заменить
на противоположный по знаку заряд, как
изменится модуль и направление
результирующей силы?

а) модуль силы не
меняется, направление меняется на
противоположное;

б) модуль силы
уменьшается в 2 раза, направление меняется
на противоположное;

в) модуль силы
равен нулю;

г) модуль силы
увеличится в 2 раза, направление не
меняется;

д) модуль силы
увеличится в 3 раза, направление не
меняется.

3.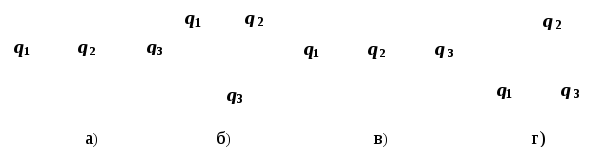
Как направлена равнодействующая сила
на зарядq₃со стороны зарядовq₁иq₂(|q₁|=|q₂|расстояния между зарядами одинаковые):

4. Как направлена
сила, действующая на положительный
точечный заряд, расположенный в центре
квадрата?

Задача
1.1. В
вершинах равностороннего треугольника
со стороной а
расположены два положительных и один
отрицательный заряды, одинаковых по
величине и равных q.
Найти силу, действующую на заряд Q₀ < 0,
расположенный на пересечении медиан.

Р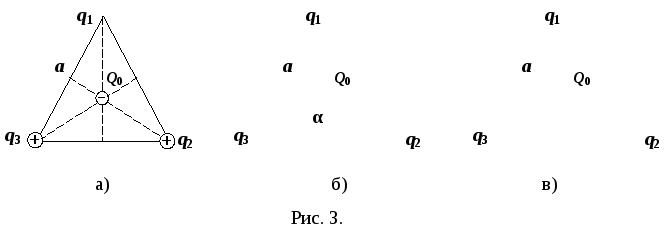ешение.Сделаем
рисунок, произвольно расположив заряды
в вершинах треугольника. Расставим
силы, действующие на заряд Q₀
со стороны зарядов q₁,
q₂,
и
q_3,
и обозначим их соответственно
(рис. 3, а).

Направление
результирующей силы по определяем по
принципу суперпозиции:

Для
этого необходимо сложить три вектора.
Так как величина зарядов q₁,
q₂
и
q₃
одинакова и они равноудалены от заряда
Q₀,
то силы
будут одинаковы по модулю.

Из
рисунка видно, что сначала удобно сложить
векторы
по правилу параллелограмма (рис. 3 б).

Модуль
вектора
определим по теореме косинусов

где
α
– угол между векторами
.

С
учётом того, что
,α
= 120º; cos
α
= – 0,5, получим:
.

Теперь
нужно сложить векторы
.
(рис. 3 в). Из рисунка видно, что эти векторы
направлены в одну сторону, значит, их
векторная сумма равна их алгебраической
сумме. С учётом того, что,
модуль результирующей силы

По закону Кулона


Обратите
внимание,
что в законе Кулона все заряды пишутся
со знаком «+», так как знак заряда
учитывался при геометрических построениях.

Расстояние
r
выразим из рисунка через сторону
треугольника а:

Окончательно
получим:

Задача
1.2. В
вершинах правильного шестиугольника
со стороной а
расположены точечные заряды q,
2q,
3q,
4q,
5q,
6q.
Найти силу, действующую на заряд Q₀
> 0, расположенный на пересечении
диагоналей.

Решение.
Сделаем
рисунок, произвольным образом расположив
заряды в вершинах шестиугольника. Если
все заряды одноимённые, то между зарядом
Q₀
и остальными зарядами действует сила
отталкивания. Расставим силы, действующие
на заряд Q₀
со стороны каждого заряда, и обозначим
их соответствующими индексами (рис. 4,
а).

По
закону Кулона

; ;;;;.

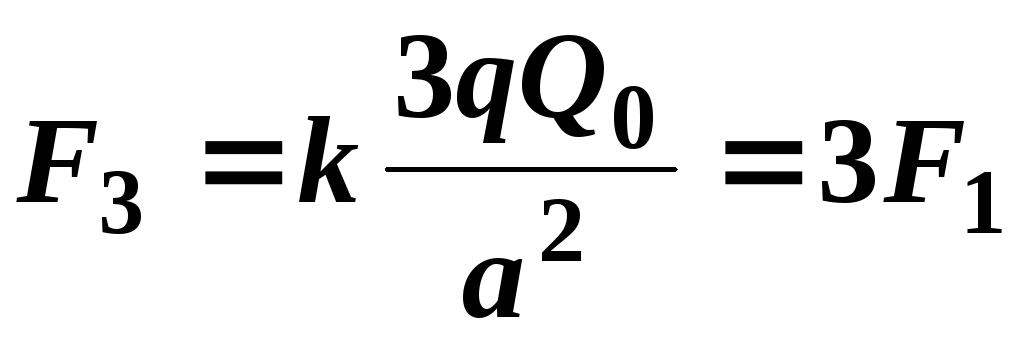
По принципу
суперпозиции

Сначала
сложим попарно силы, лежащие на одной
прямой (рис. 4 б). Так как эти силы направлены
в разные стороны, то модули равнодействующих
сил равны алгебраической разности этих
сил.

Равнодействующая
сил
равнаи направлена в сторону большей силы, то
есть в сторону.
Равнодействующая силравнаи направлена в сторону.
Наконец, равнодействующая силравнаи направлена в сторону.

Мы видим, что
векторы равнодействующих сил одинаковы.

Теперь
сложим векторы
(см. задачу 1.1):

По
теореме косинусов

С
учётом того, что
,α
= 120º; cos
α
= – 0,5, получим:

Теперь
осталось сложить векторы
(рис. 4 в). Так как векторы сонаправлены
и одинаковы по модулю, то окончательно
получим:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Сила Лоренца

4.7

Средняя оценка: 4.7

Всего получено оценок: 348.

4.7

Средняя оценка: 4.7

Всего получено оценок: 348.

На проводник с током в магнитном поле действует сила Ампера. Однако магнитное поле способно взаимодействовать и с отдельными электрическими зарядами. Рассмотрим кратко эту тему, узнаем, как определить направление и величину силы, действующей на заряд в магнитном поле.

Взаимодействие магнитного поля с зарядами

Опыты показывают, что магнитное поле никак не влияет на покоящийся электрический заряд. Почему же магнитное поле взаимодействует с проводником с электрическим током, который представляет собой движущиеся электрические заряды ?

Причина в движении зарядов. Магнитное поле не взаимодействует с зарядом, пока его скорость в этом поле равна нулю. Однако, как только заряд начинает двигаться, сразу же возникает сила, направленная перпендикулярно вектору скорости заряда.

Это приводит к интересному результату. Из механики известно, что если материальная точка движется под действием силы, направленной перпендикулярно вектору скорости, то ее траектория представляет собой окружность. Именно это и происходит с движущимися заряженными частицами в однородном магнитном поле. Заряженные частицы под действием магнитного поля движутся по окружностям.

Рис. 1. Движение заряженной частицы в магнитном поле.

Сила Лоренца

Сила, которая возникает при движении заряда в магнитном поле, называется силой Лоренца. Именно силы Лоренца, действующие на отдельные заряды в проводнике, приводят к появлению общей силы Ампера. Поэтому формулу силы Лоренца можно получить из закона Ампера.

Сила Ампера равна:

$$F_A= IB Δl sin alpha$$

Величина тока, идущая в проводнике, прямо пропорциональна величине заряда носителей $q$, их концентрации $n$, скорости их движения $v$ и площади поперечного сечения проводника $S$:

$$I = qnvS$$

Подставляя это выражение в предыдущую формулу, получим:

$$ F_A = qnvSBΔl sin alpha$$

Сила Ампера действует на проводник в результате сложения сил Лоренца, действующих на каждый из зарядов в проводнике. То есть для получения силы Лоренца, действующей на отдельный носитель, надо величину силы Ампера поделить на число носителей. Число носителей $N$ равно произведению концентрации носителей на объем проводника:

$$N=nSΔl$$

Следовательно, сила Лоренца равна:

$$F_L = {F_A over N}= qvB sin alpha$$

Как и в случае силы Ампера, угол $alpha $ — это угол между направлением движения носителя заряда (вектором скорости) и вектором магнитной индукции.

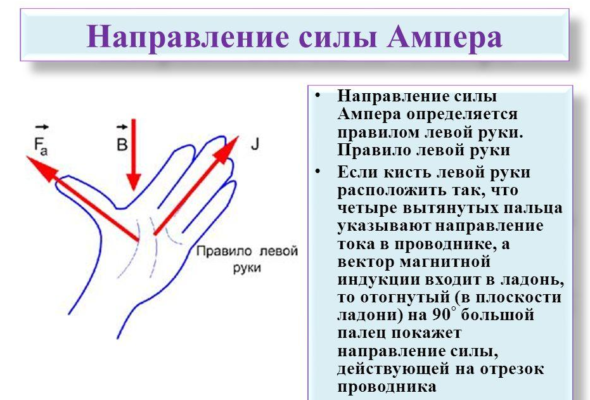
Направление силы Лоренца определяется точно так же, как и направление силы Ампера: с помощью мнемонического правила левой руки. Если расположить левую руку так, чтобы четыре пальца были направлены по направлению движения положительного заряда (против направления для отрицательного), а перпендикулярная составляющая индукции $B_{perp}$ входила в ладонь, то большой палец покажет направление силы Лоренца.

Рис. 2. Правило левой руки.

Получается, что сила Лоренца всегда направлена перпендикулярно движению заряженной частицы. А это значит, что сила Лоренца не совершает работу и, следовательно, не меняет кинетическую энергию частицы. Она меняет лишь направление ее движения.

Примером использования силы Лоренца является отклоняющая система кинескопов. Отклоняющие системы в телевизорах с кинескопами представляют собой электрические катушки, создающие меняющееся магнитное поле. Под действием этого поля на электроны, вылетающие из электронной пушки, начинает действовать сила Лоренца, они отклоняются и направляются в нужную в данный момент точку экрана.

Рис. 3. Отклоняющая система кинескопа.

Что мы узнали?

Сила Лоренца — это сила, действующая со стороны магнитного поля на движущийся электрический заряд. Сила Лоренца направлена перпендикулярно скорости движения частицы, и для определения этого направления используется правило левой руки. В однородном магнитном поле траектории заряженных частиц, движущихся под действием силы Лоренца, представляют собой окружности.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 348.

А какая ваша оценка?

Источник

Между заряженными телами существует сила взаимодействия, благодаря которой они могут притягиваться или отталкиваться друг от друга. Закон Кулона описывает данную силу, показывает степень её действия в зависимости от размеров и формы самого тела. Об этом физическом законе пойдёт речь в данной статье.

Содержание

1 Неподвижные точечные заряды
2 Крутильные весы Шарля Кулона
3 Коэффициент пропорциональности k и электрическая постоянная
4 Направление силы Кулона и векторный вид формулы
5 Где закон Кулона применяется на практике
6 Направление сил в законе Кулона
7 История открытия закона

Неподвижные точечные заряды

Закон Кулона применим к неподвижным телам, размер которых намного меньше их расстояния до других объектов. На таких телах сосредоточен точечный электрический заряд. При решении физических задач размерами рассматриваемых тел пренебрегают, т.к. они не имеют особого значения.

На практике покоящиеся точечные заряды изображаются следующим образом:

В данном случае q₁ и q₂ — это положительные электрические заряды, и на них действует сила Кулона (на рисунке не показана). Размеры точечных объектов не имеют значения.

Обратите внимание! Покоящиеся заряды располагаются друг от друга на заданном расстоянии, которое в задачах обычно обозначается буквой r. Далее в статье данные заряды будем рассматривать в вакууме.

Крутильные весы Шарля Кулона

Это прибор, разработанный Кулоном в 1777 году, помог вывести зависимость силы, названной в последствии в его честь. С его помощью изучается взаимодействие точечных зарядов, а также магнитных полюсов.

Крутильные весы имеют небольшую шёлковую нить, расположенную в вертикальной плоскости, на которой висит уравновешенный рычаг. На концах рычага расположены точечные заряды.

Под действием внешних сил рычаг начинает совершать движения по горизонтали. Рычаг будет перемещаться в плоскости до тех пор, пока его не уравновесит сила упругости нити.

В процессе перемещений рычаг отклоняется от вертикальной оси на определённый угол. Его принимают за d и называют углом поворота. Зная величину данного параметра, можно найти крутящий момент возникающих сил.

Крутильные весы Шарля Кулона выглядят следующим образом:

Коэффициент пропорциональности k и электрическая постоянная

В формуле закона Кулона есть параметры k — коэффициент пропорциональности или — электрическая постоянная. Электрическая постоянная представлена во многих справочниках, учебниках, интернете, и её не нужно считать! Коэффициент пропорциональности в вакууме на основе можно найти по известной формуле:

$k = frac {1}{4cdot picdot varepsilon_0}$

Здесь $varepsilon_0=8.85cdot 10^{-12} frac {C^2}{Hcdot m^2}$ — электрическая постоянная,

— число пи,

$k=9cdot 10^{9} frac {Hcdot m^2}{C^2}$ — коэффициент пропорциональности в вакууме.

Дополнительная информация! Не зная представленные выше параметры, найти силу взаимодействия между двумя точечными электрическими зарядами не получится.
Формулировка и формула закона Кулона

Чтобы подытожить вышесказанное, необходимо привести официальную формулировку главного закона электростатики. Она принимает вид:

Сила взаимодействия двух покоящихся точечных зарядов в вакууме прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними. Причём произведение зарядов необходимо брать по модулю!

$F=kcdot frac {|q_1|cdot |q_2|}{r^2}$

В данной формуле q₁ и q₂— это точечные заряды, рассматриваемые тела; r² — расстояние на плоскости между этими телами, взятое в квадрате; k — коэффициент пропорциональности ( $9cdot 10^{9} frac {Hcdot m^2}{C^2}$ для вакуума).

Направление силы Кулона и векторный вид формулы

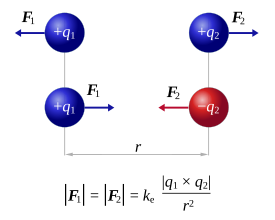
Для полного понимания формулы закон Кулона можно изобразить наглядно:

F_1,2— сила взаимодействия первого заряда по отношению ко второму.

F_2,1— сила взаимодействия второго заряда по отношению к первому.

Также при решении задач электростатики необходимо учитывать важное правило: одноимённые электрические заряды отталкиваются, а разноимённые притягиваются. От этого зависит расположение сил взаимодействия на рисунке.

Если рассматриваются разноимённые заряды, то силы их взаимодействия будут направлены навстречу друг другу, изображая их притягивание.

Формула основного закона электростатики в векторном виде можно представить следующим образом:

$vec F_1_2=frac {1}{4cdot picdot varepsilon_0}cdot frac {q_1cdot q_2}{r_1_2^3}cdot vec r_1_2$

— сила, действующая на точечный заряд q1, со стороны заряда q2,

— радиус-вектор, соединяющий заряд q2 с зарядом q1,

Важно! Записав формулу в векторном виде, взаимодействующие силы двух точечных электрических зарядов надо будет спроецировать на ось, чтобы правильно поставить знаки. Данное действие является формальностью и часто выполняется мысленно без каких-либо записей.

Где закон Кулона применяется на практике

Основной закон электростатики — это важнейшее открытие Шарля Кулона, которое нашло своё применение во многих областях.

Работы известного физика использовались в процессе изобретения различных устройств, приборов, аппаратов. К примеру, молниеотвод.

При помощи молниеотвода жилые дома, здания защищают от попадания молнии во время грозы. Таким образом, повышается степень защиты электрического оборудования.

Молниеотвод работает по следующему принципу: во время грозы на земле постепенно начинают скапливаться сильные индукционные заряды, которые поднимаются вверх и притягиваются к облакам. При этом на земле образуется немаленькое электрическое поле. Вблизи молниеотвода электрическое поле становится сильнее, благодаря чему от острия устройства зажигается коронный электрический заряд.

Далее образованный на земле заряд начинает притягиваться к заряду облака с противоположным знаком, как и должно быть согласно закону Шарля Кулона. После этого воздух проходит процесс ионизации, а напряжённость электрического поля становится меньше возле конца молниеотвода. Таким образом, риск попадания молнии в здание минимален.

Обратите внимание! Если в здание, на котором установлен молниеотвод, попадёт удар, то пожара не произойдёт, а вся энергия уйдёт в землю.

На основе закона Кулона было разработано устройство под названием “Ускоритель частиц”, которое пользуется большим спросом сегодня.

В данном приборе создано сильное электрическое поле, которое увеличивает энергию попадающих в него частиц.

Направление сил в законе Кулона

Как и говорилось выше, направление взаимодействующих сил двух точечных электрических зарядов зависит от их полярности. Т.е. одноимённые заряды будут отталкиваться, а разноимённые притягиваться.

Кулоновские силы также можно назвать радиус-вектором, т.к. они направлены вдоль линии, проведённой между ними.

В некоторых физических задачах даются тела сложной формы, которые не получается принять за точечный электрический заряд, т.е. пренебречь его размерами. В сложившейся ситуации рассматриваемое тело необходимо разбить на несколько мелких частей и рассчитывать каждую часть по отдельности, применяя закон Кулона.

Полученные при разбиении вектора сил суммируются по правилам алгебры и геометрии. В результате получается результирующая сила, которая и будет являться ответом для данной задачи. Данный способ решения часто называют методом треугольника.

История открытия закона

Взаимодействия двух точечных зарядов рассмотренным выше законом в первый раз были доказаны в 1785 Шарлем Кулоном. Доказать правдивость сформулированного закона физику удалось с использованием крутильных весов, принцип действия которых также был представлен в статье.

Кулон также доказал, что внутри сферического конденсатора нет электрического заряда. Так он пришёл к утверждению, что величину электростатических сил можно менять путём изменения расстояния между рассматриваемыми телами.

Таким образом, закон Кулона по-прежнему является главнейшим законом электростатики, на основе которого было сделано немало величайших открытий. В рамках данной статьи была представлена официальная формулировка закона, а также подробно описаны его составляющие части.

Источник

Закон Кулона

Закон Кулона.

Закон Кулона простым языком

История открытия

Формулировка

Границы применения

Коэффициент k

Закон Кулона в диэлектриках

Применение на практике

Закон Кулона в классической электродинамике[править | править код]

Установление и формулировки закона[править | править код]

Условия применимости[править | править код]

Выражения в разных системах единиц[править | править код]

Закон Кулона и уравнения Максвелла[править | править код]

Вывод закона Кулона из уравнений Максвелла[править | править код]

Обобщение на случай распределения заряда[править | править код]

Закон Кулона и расчёт электрического поля[править | править код]

Аналогии в других областях классической физики[править | править код]

Об открытии и исторической значимости закона[править | править код]

Закон Кулона в квантовой механике[править | править код]

Закон Кулона с точки зрения квантовой электродинамики[править | править код]

Степень точности закона Кулона[править | править код]

Поправки к закону в квантовой электродинамике[править | править код]

Закон Кулона и поляризация вакуума[править | править код]

Эффект Юлинга[править | править код]

Закон Кулона и сверхтяжёлые ядра[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Сила Лоренца

Взаимодействие магнитного поля с зарядами

Сила Лоренца

Что мы узнали?

Тест по теме

Оценка доклада

Неподвижные точечные заряды

Крутильные весы Шарля Кулона

Направление силы Кулона и векторный вид формулы

Где закон Кулона применяется на практике

Направление сил в законе Кулона

История открытия закона

Вам также может понравиться

Как найти заметки на компе

Как найти северную надбавку

Как найти погоду в волгограде

Добавить комментарий Отменить ответ