Как найти величину ставки процента

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Как найти процентную ставку

В наше время человеку весьма далекому от бухгалтерии и финансов постоянно приходится сталкиваться с процентами. При оформлении кредита и вкладов в банке, при получении зарплаты и всевозможных скидок. В таких случаях просто указывается процентная ставка. Рассчитывать же конкретные суммы, как правило, приходится самому человеку.

Вам понадобится

• Калькулятор.

Инструкция

Чтобы найти простую процентную ставку от некоторой суммы, умножьте количество процентов на известную сумму и разделите на сто. В виде формулы это правило можно записать следующим образом:Пс = С * К% / 100,где:Пс – процентная ставка,
С – сумма,
К% – количество процентов.

Пример.
Сотруднику при устройстве на работу обещали оклад: 30000 рублей в месяц. Какую сумму получит работник по окончании месяца?Решение.
Предприятие обязано удержать с зарплаты своего сотрудника подоходный налог, процентная ставка которого составляет 13%. То есть в данном случае:
30000 * 13 / 100 = 3900 (рублей). Соответственно, в кассе работник получит:
30000 – 3900 = 26100 рублей. (На практике данная сумма может оказаться немногим больше, так как обычно применяются налоговые вычеты, т.е. подоходный налог взимается не со всей суммы).

Чтобы определить обратную процентную ставку, вычтите из суммы (с процентами) эту же сумму, разделенную на сто плюс количество процентов и умноженную на сто. Чтобы не ошибиться при расчете обратных процентов, воспользуйтесь калькулятором и следующей формулой:Опс = С – С / (100+К%) * 100,где:Опс – обратная процентная ставка,
С – сумма (с процентами),
К% – количество процентов (уже начисленных).

При расчете процентной ставки, обязательно учтите: какие данные (суммы, количества, массы) вам предоставлены – «чистые» или уже с начисленными процентами. Пример.
На упаковке майонеза написано: «+50% бесплатно». Майонез стоит 60 рублей.
Вопрос: на какую сумму бесплатного майонеза добавлено в упаковку.Решение.
На первый взгляд решение очевидно: 50% от 60 рублей – 30 рублей. Обычно на такое «решение» и рассчитывают производители. Однако на самом деле:Опс = 60 – 60/(100+50)*100 = 20 (рублей).Как видно, ошибка составляет 10 рублей, или 50%. Причем, производитель указал все правильно: он упаковал майонеза на 40 рублей, а потом решил добавить (+) майонеза на сумму (20 руб.), составляющую 50% от этой суммы (40 руб.).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Нередко
возникает вопрос, под какую ставку
нужно дать кредит в сумме PV,
чтобы через определенный срок получить
обратно сумму FV?

По формуле простых
процентов

.
(1.16)

По формуле сложных
процентов

.
(1.17)

Пример
1.8 Фирма
дала в кредит дочерней фирме 50 000 руб.
сроком на 3 года с ежегодным начислением
процентов. Под какой процент нужно дать
кредит, чтобы вернуть 60 000 руб.?

Решение.

PV=50
000 руб.

FV=60
000 руб

k=3

m=1

r=?

r=m·((FV/PV)^(1/(m·k))-1)

r=(6/5)^(1/3)-1=0,06266

r6,27%

1.3.6 Номинальная и эффективная ставки

Величину
годовой процентной ставки r
часто называют номинальной
ставкой в отличие от процентной ставки
за период r
t/T
или 1/m.

Для
сравнения эффективности предложений
различных банков по кредитным операциям
их пересчитывают к эффективной
процентной ставке
,
обеспечивающей ту же доходность, но при
начислении процентов один раз в году.
Сравнивая (1.6) с

,

получим

,

откуда

=(1.7)

Пример
1.9 Определим
эффективную годовую ставку в первых
трех случаях примера 1.4.

Решение.
Очевидно, что в четвертом случае, при
ежегодных начислениях процентов, она
составляет 12%. Для

m
= 12

=(1+0,12/12)^12-1=0,1268;

m
= 4

=(1+0,12/4)^4-1=0,1255;

m
= 2

=(1+0,12/2)^2-1=0,1236.

Как и следовало
ожидать, ежемесячное начисление
обеспечивает самую большую эффективную
ставку.

Замена
в договоре номинальной ставки r
при m
– разовом начислении процентов на
эффективную

не изменяет финансовых обязательств
участвующих сторон. Обе ставки эквивалентны
в финансовом отношении. Вообщеразные
по величине номинальные ставки являются
эквивалентными, если соответствующие
им эффективные ставки имеют одну и ту
же величину.

При
подготовке контрактов может возникнуть
необходимость в определении r
по заданным значениям
иm.
Из (1.7) находим

(1.8)

1.4 Начисление налогов и проценты

Во многих странах
проценты облагаются налогом. Очевидно,
что налог на проценты уменьшает наращенную
сумму и реальную процентную ставку
банка.

Пусть
процентная ставка банка r,
ставка налога на проценты
н, начальная
сумма банковского вклада PV,
задан срок размещения вклада.

1. Простые
   проценты

Наращенная
сумма вклада: FV=
PV
(1+
r),
где FV
и PV взяты по абсолютной величине.

Проценты:
I=
FV-PV=
PVr

Проценты
после уплаты налога: I_н=I.·(1-
н)= PV··r·(1-
н)

Наращенная
сумма после уплаты налога:

FV=PV+I_н=
PV·[1+·r·(1-
н)].
(1.18)

1. Сложные
   проценты

Наращенная
сумма вклада:
.

Проценты:
I=
FV-PV=.

Проценты
после уплаты налога: I_н=I·(1-
н)=
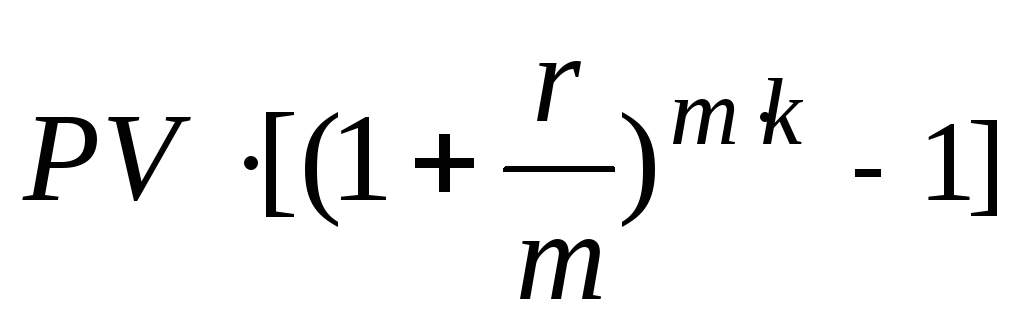·(1-
н).

Наращенная
сумма после уплаты налога

FV=PV+I_н=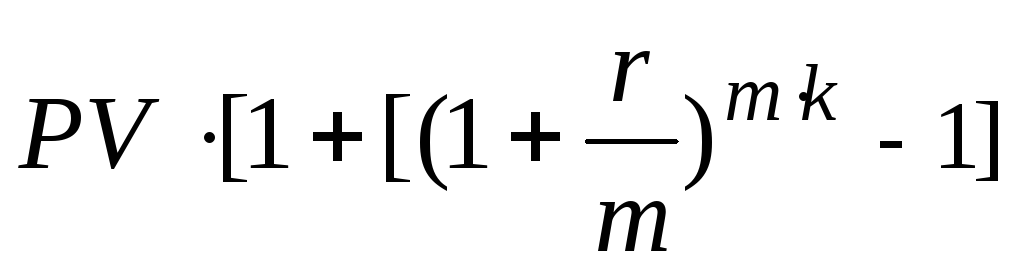·(1-
н)], откуда

F

V=·(1-н)+н]
(1.19)

Пример
1.10 Клиент
внес в банк 1000 $ на год. Процентная ставка
банка 16%. Налог на проценты 8%. Требуется
определить сумму налога N,
процент и наращенную сумму в двух
случаях: 1) простых процентов; 2) сложных
процентов при ежемесячном начислении
процентов.

Решение.

PV=1000
$

r=0,16

н=0,08

t=T

k=1

m=12

I_н=?,
FV=?

1. Простые проценты

1. Без налога

I=
PVr=1000·0,16=160
$,

FV=PV+I=1160$.

б) С налогом

N=
PV··r·н=1000·0,16·0,08=12,8
$

I_н
= PV··r·(1-
н)= 1000·0,16·
(1-0,08)=147,2 $

Можно записать

I_н
= I-
N=160-12,8=147,2
$

FV=PV+
I_н
=1147,2 $

FV=PV+I=1172,27 $

1. Сложные проценты

а) Без налога

I==1000*[(1+0,16/12)^12-1]=172,27
$

б) С налогом

I_н
=.
(1-
н)=
172,27*(1-0,08)=158,49 $

FV=PV+
I_н
=1158,49
$; N=I- I_н=172,27-158,49=13,78
$

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Наверняка каждый, кто когда-то брал кредит или становился вкладчиком банка, вначале сталкивался с понятием «банковская процентная ставка»:

Процентная ставка – это сумма, выраженная в процентном измерении, которая устанавливается банком за пользование кредитом и выплачивается за определенный период – год, квартал или месяц.

• Если деньги кладутся на текущий банковский счет или депозит, вкладчик является кредитором банка, а сам банк – заемщиком.
• Если клиент занимает деньги у банка (берет кредит), то кредитором теперь является банк, а клиент – заемщиков.

Знание этих простых истин избавит от комплексов, которые населению внушают банки, разъясняя им многокилометровые формулы расчетов процентов с биномами Ньютона, факториалами, сложными корнями, степенями и прочей математической лабудой сложностью.

Процентная ставка определяет цену денег

В любом из этих двух случаев процентная ставка имеет оценивающее денежное измерение: какими будут сбережения вкладчика или банка через месяц, год или несколько лет.

Процентная ставка по депозитам вкладчиков обычно ниже ставки по банковским кредитам. В этом заключен основной заработок банковских и финансовых учреждений – взять деньги по меньшей цене и распорядиться ими, переодолжив по более высокой.

Для вкладчиков же депозит – это в основном способ сохранения денежных средств, а не заработка, так депозитные ставки сейчас низки, а в некоторых банках Европы они даже отрицательные.

Базовая процентная ставка – это наименьший кредитный процент, предоставляемый крупным надежным кампаниям и клиентам. БПС обычно устанавливается центральными банками.

Историческая справка о ставках

Исторические размахи ставок впечатляют:

• В Германии, например, базовая процентная ставка колебалась в диапазоне от 90% до 2% в периоды 1920 – 2000 гг.
• В Великобритании – 0,5 – 15% в 1989 – 2009 гг.
• В США ставка ФРС США в 1954 – 2008 гг варьировала между 19 % и 0.25 %.
• В Зимбабве в период гиперинфляции 2007 г. кредитная ставка доходила до 800 %.

Виды ставок

Фиксированные и плавающие ставки

Процентные ставки бывают:

• Фиксированными – неизменными в течение определенного срока.
• Плавающими – изменяемыми и периодически пересматриваемыми банком, в зависимости от некоторых показателей.

Так, классическим показателем является LIBOR – средняя ставка лондонской межбанковской кредитной биржи.

Многие банки определяют плавающую ставку по формуле: LIBOR + n, где n – фиксированная ставка конкретного банка.

Банки России могут ориентироваться на независимую индикативную ставку, например, MosPrime Rate.

Кредитополучателю на растущем рынке кредитных ставок выгодней брать кредит по фиксированной процентной ставке.

Декурсивные и антисипативные ставки

По времени выплаты ставки бывают:

• декурсивными – выплачиваемыми в конце вместе с возвратом кредита;
• антисипативными – выплачиваемыми авансом при предоставлении кредита.

Декурсивные ставки выгодны для заемщиков, а антисипативные – для кредиторов, но банки обычно действуют в своих интересах:

• проценты на депозитах рассчитываются декурсивным способом,
• кредитные – антисипативным: при выдаче кредита сразу определяется суммарный процент, который затем делится на количество периодов (обычно месяцев).

Декурсивный и антисипативный способы используются при подсчете простых и сложных процентов, когда первоначальная сумма капитала в каждом отчетном периоде меняется.

• Декурсивный способ удобно использовать при плавающих ставках.
• Антисипативный способ удобен в периоды нестабильности в качестве гаранта выплаты сложных процентов.

Декурсивную ставку еще называют ссудным процентом, так как она определяет отношение полученного дохода (процентов) к начальной денежной сумме.

Как рассчитать ссудный процент и сумму наращивания

Формула определения ссудного процента:

i = I/P   (1), где:

• i (income) – ссудный процент;
• I – сумма всех начисленных за отчетный период процентов;
• P – первоначальная денежная сумма (present value).

Сумма наращивания F (future value) определяется по формуле:

F = P + i*n*P = P*(1 + i*n).    (2)

Здесь n – количество расчетных периодов.

Отношение F/P  – это коэффициент наращивания k_n.

k_n = 1 + i*n.  (3)

Подсчет суммы наращивания F называется компаундингом.

Компаундинг на примере расчета

1. Произведем компаундинг банковского кредита размером в 1 млн. руб., выданного под 12 % годовых (простой ставке), сроком на 10 лет по формуле (2)

F = 1000000 *(1 + 0,12 *10) = 2200000 руб.

Первоначальная денежная сумма, выданная банком в долгосрочный десятилетний кредит, часто применяемый в ипотеке, наросла на 1200000 руб., то есть более, чем в два раза.

1. Рассчитать сумму наращивания можно и за небольшой период (меньше года). В этом случае формула определения F (2) преобразуется:

F = P * (1 + i * d/K) .    (4)

• d – количество календарных дней, на которые взят кредит;
• K – количество дней в году, т.е. 365 или 366.

Рассчитаем наращенную сумму кредита в размере 50000 руб, выданного МФО под указанный в договоре годовую простую ставку в 15 % сроком на 91 день.

Вставив значения в формулу (4), получим:

F = 50000 * (1 + 0,15 *91/365 ) = 51870 руб.

Часто банки и МФО требуют вернуть суммы больше расчетных – это означает, что были насчитаны дополнительно скрытые проценты в виде всевозможных комиссий. Перед заключением договора следует внимательно прочитывать все его пункты в поисках незаконных способов наращивания капитала.

Аналогично можно рассчитать, сколько денег заработает вкладчик, положив деньги на депозит.

Дисконтирование

Обратная операция – расчет первоначальной суммы P по наращенной F – называется дисконтированием.

Дисконтирование считается по формуле:

P = F/ (1 + i*n).    (5)

К примеру, необходимо посчитать, сколько денег P нужно положить на трехгодичный депозит с простой ставкой 10 %, чтобы накопить сумму F в размере 100000 руб.

Произведем расчет по формуле (5):

P = 100000/(1 + 0,1*3)  = 76923 руб.

Расчеты при плавающей ставке

Если ставка плавающая, то наращенная сумма рассчитывается путем суммирования ставок за каждый период их изменения, и формула преобразовывается в некую абстрактную:

F = P *(1 + ∑(1…N) n*i)    (6), где:

• n – период от одного до N;
• i– переменная величина ставки;
• ∑(1…N) – сумма произведений  n*i за все расчетные периоды.

Выглядит страшно на первый взгляд, а как это происходит, очень легко понять по примеру:

Необходимо рассчитать наращенную сумму кредита в размере 500000, выданного на три года, с процентной ставкой за первый год – 11% годовых, если каждые полгода ставка с учетом инфляции возрастает на 1,5 %.

Используем для расчета формулу (6):

F = 500000 *(1 + 0,11 + 0.5 (0,125 + 0,14 + 0,155 + 0,17)) = 500000 * 1.405 = 702500 руб.

Обратите внимание на то, что коэффициент наращивания k, рассчитываемый при фиксированном проценте по формуле (3), при плавающем проценте определяется выражением в скобках формулы (6):

K = 1 + ∑(1…N) n*i.    (7)

В данном примере его величина – 1.405.

Расчеты сложных процентов

Этот метод расчета в банковской сфере используется при начислении процентов на долгосрочных депозитах, когда процент начисляется на наращенную предшествующими процентами сумму.

Формула расчета сложных процентов приведена на рисунке ниже.

Размер ставки и инфляция

Процентная ставка может быть номинальной и реальной:

• Номинальная – установленная банком.
• Реальная – с поправкой на инфляцию.

Реальная ставка i _real меньше номинальной i _nom на уровень инфляции π.

i _real = i _nom – π.

Эту формулу обычно используют при маленьком уровне инфляции. При большом инфляционном уровне расчеты производят по более сложной формуле Фишера:

i _real = (i _{nom – π)/(1 + π).}

Реальная цена денег

Чтобы определить реальную стоимость денег с учетом инфляции через какое-то время, используют формулу:

R= N/(1+i)ª.

R – реальная стоимость денег;

N – номинальная стоимость;

i– инфляционная ставка;

a – количество периодов (лет, месяцев и т.д.).

Банки обычно повышают процентную кредитную ставку в периоды повышенной инфляции, закладывая ее рост в номинальную ставку. Такой шаг, помимо борьбы с понижением цены денег, дает им возможность поднять процентную ставку по депозитам, чтобы не лишиться вкладчиков.

Финансовая безграмотность населения выгодна банкирам

Иногда проценты кредитования, особенно быстрого, противоречат здравому смыслу и являются завуалированной аферой. Поэтому понимание, что такое банковский процент и как рассчитать сумму наращивания должно быть у каждого, кто хочет взять кредит.

Пользуясь финансовой безграмотностью населения, банки сегодня предлагают столь мудреные и сложные формулы расчета, которые требует калькулятора инженера или программиста. Между тем, рассчитать общую сумму кредитных выплат (она же сумма наращивания), как видно по примерам, довольно просто на обычном калькуляторе и даже на листочке. Можно считать по разным формулам выплаты по телу кредита и по процентам, но отклонения между вашими итоговыми расчетами и банковскими все равно не должны быть слишком большими. Тем более здесь приведены формулы расчета по простым, а не сложным процентам, что не противоречит принципам аннуитетных платежей, используемых сегодня при кредитовании.

Банки сегодня практически не используют дифференцированный способ погашения кредита, при котором при начислении процентов учитывается оставшаяся сумма долга, а не первоначальная. Мотивируется это якобы «заботой о клиентах»: зачем, дескать, им напрягать мозги и каждый месяц производить сложные расчеты? Таким образом и получается, что наше кредитование – одно из самых невыгодных в мире.

Давайте посмотрим, во что обходится такая трогательная опека самим заемщикам, и без того оказывающимся в долговых ямах из-за грабительского процента по ипотеке.

На калькуляторе Сбербанка посчитайте переплату по кредиту 2000000 млн. руб. сроком на 10 лет под 16 % годовых при аннуитетных и дифференцированных платежах.

Разница между первым и вторым способами составляет почти 350000руб. Согласны ли вы сэкономить эти деньги, но зато считать проценты каждый месяц? А если даже и не устраивать проверочные расчеты, а просто поверить ипотечному калькулятору? 🙂

Видео: Бешеные процентные ставки.