Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
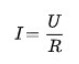
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
Общие схемы типов соединений представлены на рисунке 1.
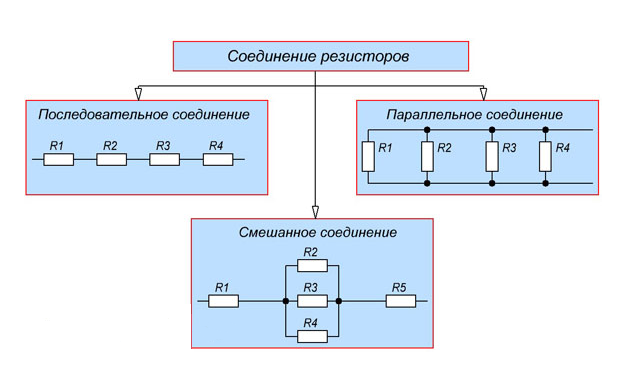
Рисунок 1. Типы соединений резисторов
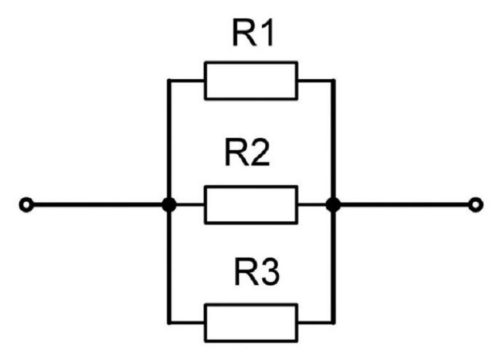
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
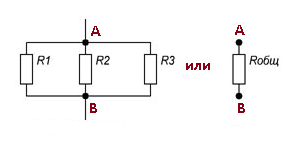
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
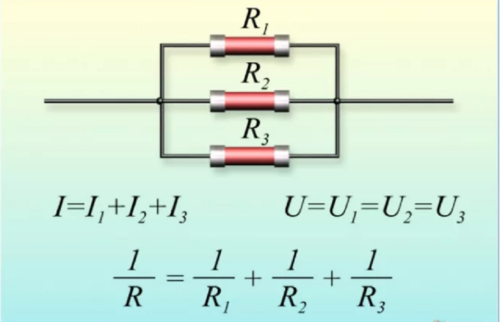
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
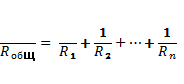
и рассчитывается по формуле:
![]()
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
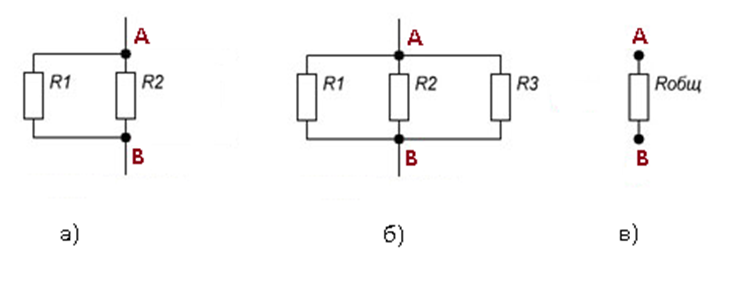
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
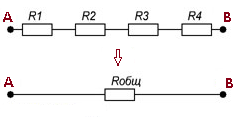
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
![]()
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
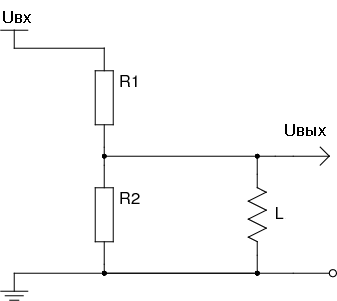
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
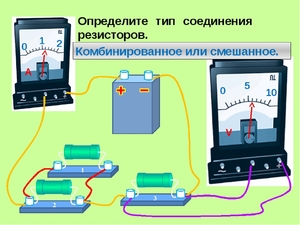
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
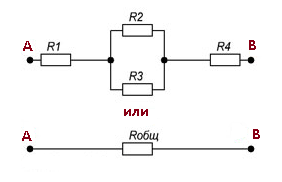
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
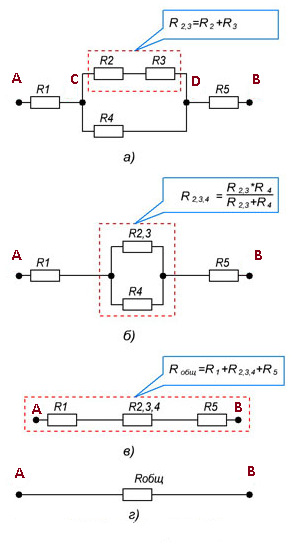
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.
Содержание
- Как найти силу тока на каждом резисторе
- Пример 1
- Пример 2
- Пример 3
- R1 – 20 Ом (0.5 Вт)
- R2 – 80 Ом (1 Вт)
- Определение силы тока на резисторе при разных типах соединения
- Последовательное соединение резисторов
- Параллельное соединение резисторов
- Смешанное соединение резисторов в цепи
- Параллельное соединение резисторов, а также последовательное
- Что такое резистор и для чего он нужен
- Понятие параллельного подключения резисторов
- Последовательное подключение
- Смешанное подключение
- Что ещё нужно учитывать при подключении резисторов
- Какая мощность тока при последовательном и параллельном соединении
- Мощность при параллельном соединении
- Мощность при последовательном соединении
- Как правильно рассчитать сопротивление
- При последовательном соединении
- При параллельном соединении
- Как рассчитать сложные схемы соединения резисторов
- Преобразование «звезда-треугольник»
- Чему равна сила тока в цепи при параллельном соединении резисторов
- Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
- Сила тока в резисторе
- Определение силы тока на резисторе при разных типах соединения
- Последовательное соединение резисторов
- Параллельное соединение резисторов
- Смешанное соединение резисторов в цепи
- Резисторы, ток и напряжение
- Как рассчитать общее сопротивление, общую силу тока и напряжение на каждом из резисторов?
- Поделиться в социальных сетях
- Комментарии и отзывы (2)
- Виктор
- Макаров Дмитрий (Эксперт)
Как найти силу тока на каждом резисторе
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
 Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
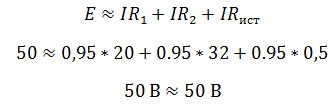
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
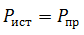
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
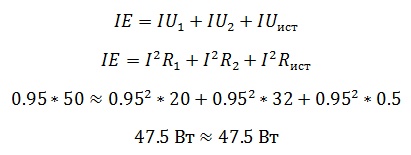
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах 
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
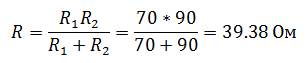
А затем напряжение

Зная напряжения, найдем токи, протекающие через резисторы
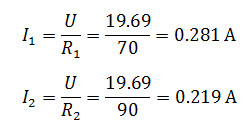
Как видите, токи получились теми же.
Пример 3
В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.
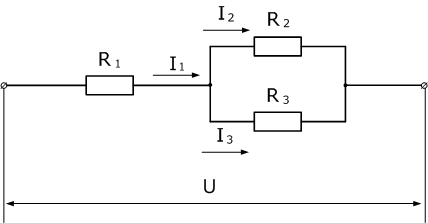
Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи
 Отсюда мощность, выделяемая на R 1
Отсюда мощность, выделяемая на R 1
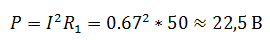 Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
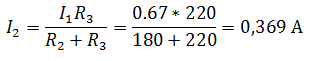
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2

Таким образом производится расчет простых цепей постоянного тока.
Резистор тока выполняет сразу несколько очень важных задач: служит ограничителем электрического тока в цепи, создает падение напряжения на отдельных ее участках и разделяет пульсирующий ток.
Помимо номинального сопротивления, одним из наиболее важных параметров резистора является рассеиваемая мощность. Она зависима от напряжения и тока. Мощность – это то тепло, которое выделяется на резисторе, когда под воздействием протекающего тока он нагревается. При пропуске тока, превышающего заданное значение мощности, резистор может сгореть.

Мощность постоянного тока может быть рассчитана по простой формуле P(Вт) = U(В) * I(А),
Чтобы избежать сгорания резистора тока, необходимо учитывать его мощность. Соответственно, если схема указывает на замену резистора с мощностью 0,5 Ватт – 0,5 Ватт в данном случае – минимум.

Мощность резистора может зависеть от его размеров. Как правило, чем меньше резистор – тем меньше мощность его рассеивания. Стандартный ряд мощностей резисторов тока состоит из значений:
Рассмотрим на примере: номинальное сопротивление нашего резистора тока – 100 Ом. Через него течет ток 0,1 Ампер. Чтобы узнать мощность, на которую рассчитан наш резистор тока, необходимо воспользоваться следующей формулой: P(Вт) = I2(А) * R(Ом),
- P(Вт) – мощность,
- R(Ом) – сопротивление цепи (в данном случае резистора),
- I(А) – ток, протекающий через резистор.
Внимание! При расчётах следует соблюдать размерность. Например, 1 кА= 1000 А . Это же касается и других величин.
Итак, рассчитаем мощность для нашего резистора тока: P(Вт) = 0,12(А) *100 (Ом)= 1(Вт)
Получилось, что минимальная мощность нашего резистора составляет 1 Ватт. Однако в схему следует установить резистор с мощностью в 1,5 – 2 раза выше рассчитанной. Соответственно идеальным для нас будет резистор тока мощностью 2 Вт.
Бывает, что ток, протекающий через резистор неизвестен. Для расчёта мощности в таком случае предусмотрена специальная формула:

Соединение цепи может быть последовательным и параллельным. Однако никакого труда не составляет рассчитать мощность резистора тока как в параллельной, так и в последовательной цепи. Следует учитывать лишь то, что в последовательно цепи через резисторы течет один ток.
Например, нам необходимо произвести замену резистора тока сопротивлением 100 Ом. Ток, протекающий через него – 0,1 Ампер. Соответственно, его мощность – 1 Ватт. Следует рассчитать мощность двух соединенных последовательно резисторов для его замены. Согласно формуле расчёта мощности, мощность рассеивания резистора на 20 Ом – 0,2 Вт, мощность резистора на 80 Ом – 0,8 Вт. Стандартный ряд мощностей поможет выбрать резисторы тока:
R1 – 20 Ом (0.5 Вт)
R2 – 80 Ом (1 Вт)
Из всего вышесказанного можно сделать вывод, что разное сопротивление резисторов гарантирует их разную выделяемую мощность, так как она распределяется между резисторами разных номиналов. Если не учитывать это обстоятельство, то можно столкнуться с большим количеством трудностей. Если один из резисторов выбран неправильно – второй работает в тяжелом температурном режиме. Также присутствует угроза возгорания резистора из-за несоблюдения правил мощности.
Для того, чтобы сэкономить время и не рассчитывать мощность каждого отдельного резистора тока нужно запомнить одно простое правило: мощность заменяемого резистора должна быть равна мощности каждого резистора, составляющего параллельную или последовательную цепь. То есть при замене резистора мощностью 0,5 Вт надо следить за тем, чтобы каждый из резисторов для замены имел мощность не менее 0,5 Вт.
При параллельном соединение резисторов важно помнить, что чем меньше сопротивление резистора, тем больший ток через него протекает, а значит на нем будет рассеяна большая мощность.
В упрощенном понимании электрическая цепь представляет собой совокупность элементов, реализующих определенные задачи при взаимодействии с электрическим током. При этом каждая из деталей выполняет свои функции при строго определенных параметрах. Они могут значительно отличаться от входящих значений. Одним из самых распространенных элементов электрической схемы является резистор.

Резистор выступает своеобразным ограничителем силы тока. По своей сути этот элемент является дополнительным сопротивлением, которое измеряется в омах. Собственно, зная это значение можно определить силу тока в резисторе, а также напряжение в цепи после него.
Определение силы тока на резисторе при разных типах соединения
Самым простым способом определить силу тока в резисторе можно воспользовавшись мультиметром. Измерение проводятся в разрыве цепи после резистора. На тестере выставляется максимальный диапазон величин, а щупы прибора подсоединяются к месту разъединения проводника. На дисплее мультиметра будут отображены результаты измерения силы тока в резисторе.

Но данный вариант не всегда возможен. Под рукой может не оказаться тестера или технически невозможно разорвать цепь чтобы измерить силу тока на резисторе. В такой ситуации на помощь придет известный из школьной физики закон Ома, который выглядит следующим образом:
I = U/R, где у нас I – сила тока, U – напряжение, R – сопротивление.
В системе СИ эти величины измеряются в амперах (А), вольтах (В), омах (Ом) соответственно.
Подставляя необходимые значения в формулу можно определить сопротивление, напряжение и силу тока на резисторе или любом участке, или элементе электрической цепи.

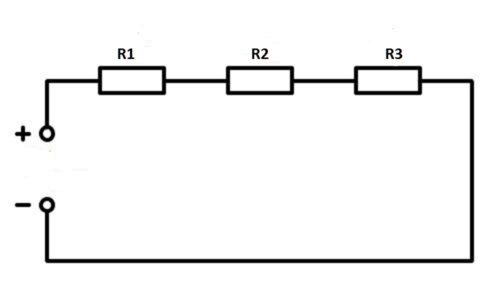
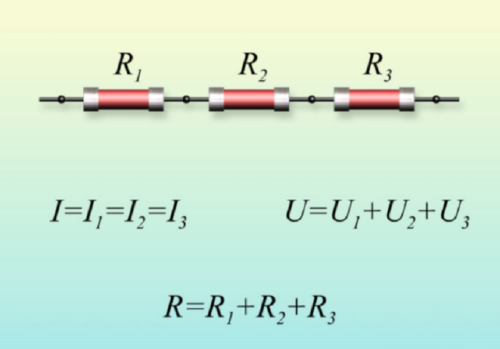
Последовательное соединение резисторов
Рассмотрим электрическую цепь, в которой три резистора расположены последовательно, т.е. друг за другом. Общее их сопротивление (R) будет рано сумме сопротивлений отдельного резистора (r).
Для наглядности примера, в качестве резисторов рассмотрим обычные 40 Вт лампы накаливании. В данном случае вольфрамовая нить обладает своим сопротивлением и ее вполне можно считать резистором. Также введем понятие мощности нагрузки или резистора (P), которая измеряется в ватах (Вт).

Она имеет прямолинейную зависимость от силы тока и напряжения и вычисляется по формуле: P=I х U. С помощью несложных вычислений мы можем найти силу тока на резисторе, в качестве которого выступает лампочка.
Сила тока (I) = Мощность лампы (Р) / Напряжение (U) = 40 Вт / 220 В = 0,1818 А.
Для последовательного соединения элементов в электрической цепи справедливо правило, что силы тока протекающие через все проводники одинакова. Таким образом сила тока в резисторе r2 или r3 также будет 0,1818 А. Но в нашем варианте с лампочками будет отмечена одна особенность – яркость свечения уменьшится. Это происходит из-за того, что резистор выступает в качестве делителя напряжения. Этот нюанс часто используют для продления срока службы не ответственных устройств. Например, впаяв сопротивление перед лампочкой можно продлить срок ее службы, но при этом придется смерится с недостатком освещенности.
Параллельное соединение резисторов
При параллельном расположении резисторов в сети, они имеют общую точку контакта на входе и на выходе. В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.
Несмотря на то, что общий ток в цепочке резисторов, соединенных параллельно на выходе равен сумме токов в самостоятельной ветке, для конкретного участка он может отличаться. Это обусловлено тем же законом Ома, при условии разности сопротивлений. Чтобы узнать силу тока на каждом резисторе в соответствующей ветке, необходимо знать их сопротивление. При параллельном соединении, напряжение на обособленном участке, является постоянной величиной. Соответственно сила тока отельного резистора легко вычисляется по закону Ома для участка цепи.

Смешанное соединение резисторов в цепи
В чистом виде параллельные и последовательные цепи в электротехнике встречаются крайне редко. Как правило, присутствует их совместная комбинация. Для того чтобы найти силу тока в каждом резисторе при смешанном соединении, необходимо цепь разбить на участки. Таким образом при расположении элементов друг после друга, т.н. «каскадом», применяются правила и формулы для последовательного соединения.

Результаты измерения силы тока в резисторе. Различные типы резисторов.
Необходимо отметить, что для упрощения расчетов параллельно расположенные резисторы можно группировать. При вычислении силы тока на определенном участке, они принимаются за самостоятельный элемент. Соответственно в этом случае формулы используются как для расчета параметров при параллельном соединении.
Источник
Параллельное соединение резисторов, а также последовательное
Ни одна электрическая схема не обходится без резисторов. Что это такое, для чего он нужен и какими способами их подключают в электрическую цепь рассмотрим подробно.
Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
Как правильно рассчитать сопротивление
Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где
- U – падение напряжение на конкретном резистивном элементе;
- I – ток, протекающий через него.
При последовательном соединении
Для двух элементов считаем Rобщ = R1+R2.
Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.
При параллельном соединении
Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).
Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле
Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.
Как рассчитать сложные схемы соединения резисторов
Сложные схемы рассчитываются путем группировки по параллельному и последовательному способу соединения.

Перед нами сложная схема – задача рассчитать общее сопротивление:
- R2, R3, R4 объединим в последовательную группу – применим формулу R2,3,4 = R2+R3+R4.
- R5 и R2,3,4 – параллельно соединенные резисторы, рассчитаем R5,2,3,4 = 1/ (1/R5+1/R2,3,4).
- R5,2,3,4, R1, R6 опять объединяем в последовательную группу – суммируя величины, получаем Rобщ = R5,2,3,4+R1+R6.
Для больших схем существуют специальные методы, облегчающие расчет. Один из таких методов – эквивалентное преобразование «треугольника» в «звезду». Такая система расчета применяется в том случае, когда невозможно по схеме определить последовательное или параллельное подключение резисторов.
Преобразование «звезда-треугольник»
Для соединения резистивных элементов, кроме вышеописанных способов, существует несколько других видов соединения:
- «звезда» – соединение трех ветвей с одним общим узлом;
- «треугольник» – соединение ветвей схемы в виде треугольника, сторонами которого служат ветви, вершины представляют узлы.
Справка: Узел – точка, в которой соединяются три и более проводника электрической цепи.
Эквивалентность замены предполагает стабильность токов, входящих в каждый узел, при одинаковых напряжения между одноименными узлами «треугольника» и «звезды».

Сопротивление резистора луча «звезды» равно произведению сопротивлений резисторов прилегающих сторон «треугольника», деленному на сумму сопротивлений резисторов трех сторон «треугольника».
Сопротивление резисторов сторон «треугольника» равно сумме произведения сопротивлений резисторов двух прилегающих лучей «звезды», деленного на сопротивление третьего луча.

О разнице подключения звезда и треугольник читайте здесь.
Чему равна сила тока в цепи при параллельном соединении резисторов
Согласно правилу Кирхгофа ток, поступающий в узел, равен току, выходящему из узла, – величина тока до группы параллельных резисторов и после нее должна быть неизменной.
Ток в группе параллельных резисторов распределяется по цепи в зависимости от их номинала, после прохождения через сопротивления суммируется в узле и выходит из него неизменным I = I1+I2+I3+…+In.
Как определить величину эквивалентного сопротивления при последовательном соединении резисторов
Справка: Эквивалентом сопротивления называется замена части схемы, состоящей из нескольких резистивных элементов, одним элементом.
Для последовательного соединения эквивалентное сопротивление равно сумме сопротивлений резисторов, включенных в группу, для расчета применяется формула Rэкв = R1+R2+…+Rn.
Например: Нужно посчитать эквивалентное сопротивление данной схемы.

Решение задачи производится путем разделения резистивных элементов на системные группы.
Выделяем первую группу из последовательно соединенных элементов – R2, R3, R4.

Выделяем вторую группу из последовательных элементов R1, R5, R6.

Получаем величину двух эквивалентных сопротивлений Rобщ1 и Rобщ2, соединенных параллельно.
Делаем расчет всей схемы Rэкв= Rобщ1× Rобш2/ (Rобщ1+ Rобщ2).
Зная способы соединения и формулы расчета можно рассчитать любую сложную схему соединения резистивных элементов, однако существует множество онлайн калькуляторов, которые сделают это быстрей человека, достаточно только ввести нужные параметры компонентов схемы.
Источник
Сила тока в резисторе
В упрощенном понимании электрическая цепь представляет собой совокупность элементов, реализующих определенные задачи при взаимодействии с электрическим током. При этом каждая из деталей выполняет свои функции при строго определенных параметрах. Они могут значительно отличаться от входящих значений. Одним из самых распространенных элементов электрической схемы является резистор.

Резистор выступает своеобразным ограничителем силы тока. По своей сути этот элемент является дополнительным сопротивлением, которое измеряется в омах. Собственно, зная это значение можно определить силу тока в резисторе, а также напряжение в цепи после него.
Определение силы тока на резисторе при разных типах соединения
Самым простым способом определить силу тока в резисторе можно воспользовавшись мультиметром. Измерение проводятся в разрыве цепи после резистора. На тестере выставляется максимальный диапазон величин, а щупы прибора подсоединяются к месту разъединения проводника. На дисплее мультиметра будут отображены результаты измерения силы тока в резисторе.

Но данный вариант не всегда возможен. Под рукой может не оказаться тестера или технически невозможно разорвать цепь чтобы измерить силу тока на резисторе. В такой ситуации на помощь придет известный из школьной физики закон Ома, который выглядит следующим образом:
I = U/R, где у нас I – сила тока, U – напряжение, R – сопротивление.
В системе СИ эти величины измеряются в амперах (А), вольтах (В), омах (Ом) соответственно.
Подставляя необходимые значения в формулу можно определить сопротивление, напряжение и силу тока на резисторе или любом участке, или элементе электрической цепи.

Последовательное соединение резисторов
Рассмотрим электрическую цепь, в которой три резистора расположены последовательно, т.е. друг за другом. Общее их сопротивление (R) будет рано сумме сопротивлений отдельного резистора (r).
R=r1+r2+r3
Для наглядности примера, в качестве резисторов рассмотрим обычные 40 Вт лампы накаливании. В данном случае вольфрамовая нить обладает своим сопротивлением и ее вполне можно считать резистором. Также введем понятие мощности нагрузки или резистора (P), которая измеряется в ватах (Вт).

Она имеет прямолинейную зависимость от силы тока и напряжения и вычисляется по формуле: P=I х U. С помощью несложных вычислений мы можем найти силу тока на резисторе, в качестве которого выступает лампочка.
Сила тока (I) = Мощность лампы (Р) / Напряжение (U) = 40 Вт / 220 В = 0,1818 А.
Для последовательного соединения элементов в электрической цепи справедливо правило, что силы тока протекающие через все проводники одинакова. Таким образом сила тока в резисторе r2 или r3 также будет 0,1818 А. Но в нашем варианте с лампочками будет отмечена одна особенность – яркость свечения уменьшится. Это происходит из-за того, что резистор выступает в качестве делителя напряжения. Этот нюанс часто используют для продления срока службы не ответственных устройств. Например, впаяв сопротивление перед лампочкой можно продлить срок ее службы, но при этом придется смерится с недостатком освещенности.
Параллельное соединение резисторов

При параллельном расположении резисторов в сети, они имеют общую точку контакта на входе и на выходе. В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.
Несмотря на то, что общий ток в цепочке резисторов, соединенных параллельно на выходе равен сумме токов в самостоятельной ветке, для конкретного участка он может отличаться. Это обусловлено тем же законом Ома, при условии разности сопротивлений. Чтобы узнать силу тока на каждом резисторе в соответствующей ветке, необходимо знать их сопротивление. При параллельном соединении, напряжение на обособленном участке, является постоянной величиной. Соответственно сила тока отельного резистора легко вычисляется по закону Ома для участка цепи.

Смешанное соединение резисторов в цепи
В чистом виде параллельные и последовательные цепи в электротехнике встречаются крайне редко. Как правило, присутствует их совместная комбинация. Для того чтобы найти силу тока в каждом резисторе при смешанном соединении, необходимо цепь разбить на участки. Таким образом при расположении элементов друг после друга, т.н. «каскадом», применяются правила и формулы для последовательного соединения.

Результаты измерения силы тока в резисторе. Различные типы резисторов.
Необходимо отметить, что для упрощения расчетов параллельно расположенные резисторы можно группировать. При вычислении силы тока на определенном участке, они принимаются за самостоятельный элемент. Соответственно в этом случае формулы используются как для расчета параметров при параллельном соединении.
Источник
Резисторы, ток и напряжение
В этой статье мы рассмотрим резистор и его взаимодействие с напряжением и током, проходящим через него. Вы узнаете, как рассчитать резистор с помощью специальных формул. В статье также показано, как специальные резисторы могут быть использованы в качестве датчика света и температуры.
Представление об электричестве
Новичок должен быть в состоянии представить себе электрический ток. Даже если вы поняли, что электричество состоит из электронов, движущихся по проводнику, это все еще очень трудно четко представить себе. Вот почему я предлагаю эту простую аналогию с водной системой, которую любой желающий может легко представить себе и понять, не вникая в законы.
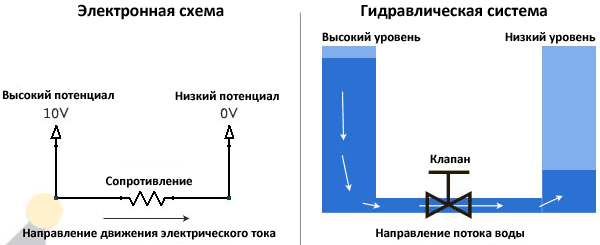
Обратите внимание, как электрический ток похож на поток воды из полного резервуара (высокого напряжения) в пустой(низкое напряжение). В этой простой аналогии воды с электрическим током, клапан аналогичен токоограничительному резистору.
Из этой аналогии можно вывести некоторые правила, которые вы должны запомнить навсегда:
— Сколько тока втекает в узел, столько из него и вытекает
— Для того чтобы протекал ток, на концах проводника должны быть разные потенциалы.
— Количество воды в двух сосудах можно сравнить с зарядом батареи. Когда уровень воды в разных сосудах станет одинаковым, она перестанет течь, и при разряде аккумулятора, разницы между электродами не будет и ток перестанет течь.
— Электрический ток будет увеличиваться при уменьшении сопротивления, как и скорость потока воды будет увеличиваться с уменьшением сопротивления клапана.
Я мог бы написать гораздо больше умозаключений на основе этой простой аналогии, но они описаны в законе Ома ниже.
Резистор

Резисторы могут быть использованы для контроля и ограничения тока, следовательно, основным параметром резистора является его сопротивление, которое измеряется в Омах. Не следует забывать о мощности резистора, которая измеряется в ваттах (Вт), и показывает, какое количество энергии резистор может рассеять без перегрева и выгорания. Важно также отметить, что резисторы используются не только для ограничения тока, они также могут быть использованы в качестве делителя напряжения для получения низкого напряжения из большего. Некоторые датчики основаны на том, что сопротивление варьируется в зависимости от освещённости, температуры или механического воздействия, об этом подробно написано в конце статьи.
Закон Ома
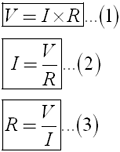
Понятно, что эти 3 формулы выведены из основной формулы закона Ома, но их надо выучить для понимания более сложных формул и схем. Вы должны быть в состоянии понять и представить себе смысл любой из этих формул. Например, во второй формуле показано, что увеличение напряжения без изменения сопротивления приведет к росту тока. Тем не менее, увеличение тока не увеличит напряжение (хотя это математически верно), потому что напряжение — это разность потенциалов, которая будет создавать электрический ток, а не наоборот (см. аналогию с 2 емкостями для воды). Формула 3 может использоваться для вычисления сопротивления токоограничивающего резистора при известном напряжении и токе. Это лишь примеры, показывающие важность этого правила. Вы сами узнаете, как использовать их после прочтения статьи.
Последовательное и параллельное соединение резисторов
Понимание последствий параллельного или последовательного подключения резисторов очень важно и поможет вам понять и упростить схемы с помощью этих простых формул для последовательного и параллельного сопротивления:
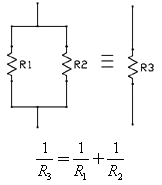
В этом примере схемы, R1 и R2 соединены параллельно, и могут быть заменены одним резистором R3 в соответствии с формулой:
В случае с 2-мя параллельно соединёнными резисторами, формулу можно записать так:
Кроме того, что эту формулу можно использовать для упрощения схем, она может быть использована для создания номиналов резисторов, которых у вас нет.
Отметим также, что значение R3 будет всегда меньше, чем у 2 других эквивалентных резисторов, так как добавление параллельных резисторов обеспечивает дополнительные пути
электрическому току, снижая общее сопротивление цепи.
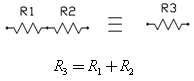
Последовательно соединённые резисторы могут быть заменены одним резистором, значение которого будет равно сумме этих двух, в связи с тем, что это соединение обеспечивает дополнительное сопротивление тока. Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R3=R1+R2
В интернете есть удобные он-лайн калькуляторы для расчета последовательного и параллельного соединения резисторов.
Токоограничивающий резистор
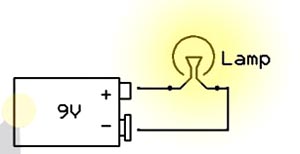
Самая основная роль токоограничивающих резисторов — это контроль тока, который будет протекать через устройство или проводник. Для понимания их работы, давайте сначала разберём простую схему, где лампа непосредственно подключена к 9В батареи. Лампа, как и любое другое устройство, которое потребляет электроэнергию для выполнения определенной задачи (например, светоизлучение) имеет внутреннее сопротивление, которое определяет его текущее потребление. Таким образом, отныне, любое устройство может быть заменено на эквивалентное сопротивление.

Теперь, когда лампа будет рассматриваться как резистор, мы можем использовать закон Ома для расчета тока, проходящего через него. Закон Ома гласит, что ток, проходящий через резистор равен разности напряжений на нем, поделенное на сопротивление резистора: I=V/R или точнее так:
I=(V1-V2)/R
где (V1-V2) является разностью напряжений до и после резистора.

Теперь обратите внимание на рисунок выше, где добавлен токоограничительный резистор. Он будет ограничивать ток идущий к лампе, как это следует из названия. Вы можете контролировать, количество тока протекающего через лампу, просто выбрав правильное значение R1. Большой резистор будет сильно снижать ток, а небольшой резистор менее сильно (так же, как в нашей аналогии с водой).
Математически это запишется так:
Из формулы следует, что ток уменьшится, если значение R1 увеличится. Таким образом, дополнительное сопротивление может быть использовано для ограничения тока. Однако важно отметить, что это приводит к нагреву резистора, и вы должны правильно рассчитать его мощность, о чем будет написано дальше.
Вы можете воспользоваться он-лайн калькулятором для расчета токоограничительного резистора светодиода.
Резисторы как делитель напряжения
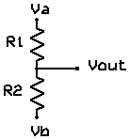
Как следует из названия, резисторы могут быть использованы в качестве делителя напряжения, другими словами, они могут быть использованы для уменьшения напряжения путем деления его. Формула:
Если оба резистора имеют одинаковое значение (R1=R2=R), то формулу можно записать так:
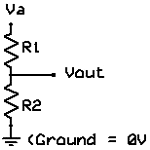
Другой распространенный тип делителя, когда один резистор подключен к земле (0В), как показано на рисунке 6B.
Заменив Vb на 0 в формуле 6А, получаем:
Узловой анализ
Теперь, когда вы начинаете работать с электронными схемами, важно уметь их анализировать и рассчитывать все необходимые напряжения, токи и сопротивления. Есть много способов для изучения электронных схем, и одним из наиболее распространенных методов является узловой, где вы просто применяете набор правил, и рассчитываете шаг за шагом все необходимые переменные.
Упрощенные правила узлового анализа
Определение узла
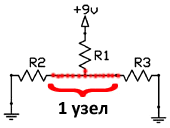
Узел – это любая точка соединения в цепи. Точки, которые связаны друг с другом, без других компонентов между ними рассматриваются как единый узел. Таким образом, бесконечное число проводников в одну точку считаются одним узлом. Все точки, которые сгруппированы в один узел, имеют одинаковые напряжения.
Определение ветви
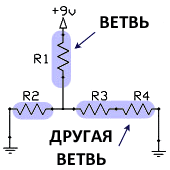
Ветвь представляет собой набор из 1 и более компонентов, соединенных последовательно, и все компоненты, которые подсоединены последовательно к этой цепи, рассматриваются как одна ветвь.
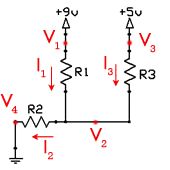
Все напряжения обычно измеряются относительно земли напряжение на которой всегда равно 0 вольт.
Ток всегда течет от узла с более высоким напряжением на узел с более низким.
Напряжение на узле может быть высчитано из напряжения около узла, с помощью формулы:
V1-V2=I1*(R1)
Перенесем:
V2=V1-(I1*R1)
Где V2 является искомым напряжением, V1 является опорным напряжением, которое известно, I1 ток, протекающий от узла 1 к узлу 2 и R1 представляет собой сопротивление между 2 узлами.
Точно так же, как и в законе Ома, ток ответвления можно определить, если напряжение 2х соседних узлах и сопротивление известно:
I 1=(V1-V2)/R1
Текущий входящий ток узла равен текущему выходящему току, таким образом, это можно записать так: I 1+ I3=I2
Важно, чтобы вы были в состоянии понимать смысл этих простых формул. Например, на рисунке выше, ток протекает от V1 до V2, и, следовательно, напряжение V2 должно быть меньше, чем V1.
Используя соответствующие правила в нужный момент, вы сможете быстро и легко проанализировать схему и понять её. Это умение достигается практикой и опытом.
Расчет необходимой мощности резистора
При покупке резистора вам могут задать вопрос: «Резисторы какой мощности вы хотите?» или могут просто дать 0.25Вт резисторы, поскольку они являются наиболее популярными.
Пока вы работаете с сопротивлением больше 220 Ом, и ваш блок питания обеспечивает 9В или меньше, можно работать с 0.125Вт или 0.25Вт резисторами. Но если напряжение более 10В или значение сопротивления менее 220 Ом, вы должны рассчитать мощность резистора, или он может сгореть и испортить прибор. Чтобы вычислить необходимую мощность резистора, вы должны знать напряжение через резистор (V) и ток, протекающий через него (I):
P=I*V
где ток измеряется в амперах (А), напряжение в вольтах (В) и Р — рассеиваемая мощность в ваттах (Вт)
На фото предоставлены резисторы различной мощности, в основном они отличаются размером.
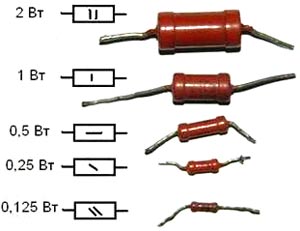
Разновидности резисторов
Резисторы могут быть разными, начиная от простых переменных резисторов (потенциометров) до реагирующих на температуру, свет и давление. Некоторые из них будут обсуждаться в этом разделе.
Переменный резистор (потенциометр)
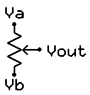
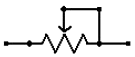
На рисунке выше показано схематическое изображение переменного резистора. Он часто упоминается как потенциометр, потому что он может быть использован в качестве делителя напряжения.

Они различаются по размеру и форме, но все работают одинаково. Выводы справа и слева эквивалентны фиксированной точке (например, Va и Vb на рисунке выше слева), а средний вывод является подвижной частью потенциометра, а также используется для изменения соотношения сопротивления на левом и правом выводах. Следовательно, потенциометр относится к делителям напряжения, которым можно выставить любое напряжение от Va к Vb.
Кроме того, переменный резистор может быть использован как тока ограничивающий путем соединения выводов Vout и Vb, как на рисунке выше (справа). Представьте себе, как ток будет течь через сопротивление от левого вывода к правому, пока не достигнет подвижной части, и пойдет по ней, при этом, на вторую часть пойдет очень мало тока. Таким образом, вы можете использовать потенциометр для регулировки тока любых электронных компонентов, например лампы.
LDR (светочувствительные резисторы) и термисторы
Есть много датчиков основанных на резисторах, которые реагируют на свет, температуру или давление. Большинство из них включаются как часть делителя напряжения, которое изменяется в зависимости от сопротивления резисторов, изменяющегося под воздействием внешних факторов.

Терморезисторы

Фоторезистор (LDR)
Как вы можете видеть на рисунке 11A, фоторезисторы различаются по размеру, но все они являются резисторами, сопротивление которых уменьшается под воздействием света и увеличивается в темноте. К сожалению, фоторезисторы достаточно медленно реагируют на изменение уровня освещённости, имеют достаточно низкую точность, но очень просты в использовании и популярны. Как правило, сопротивление фоторезисторов может варьироваться от 50 Ом при солнце, до более чем 10МОм в абсолютной темноте.
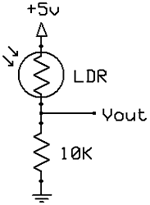
Как мы уже говорили, изменение сопротивления изменяет напряжение с делителя. Выходное напряжение можно рассчитать по формуле:
Если предположить, что сопротивление LDR изменяется от 10 МОм до 50 Ом, то Vout будет соответственно от 0.005В до 4.975В.
Термистор похож на фоторезистор, тем не менее, термисторы имею гораздо больше типов, чем фоторезисторы, например, термистор может быть либо с отрицательным температурным коэффициентом (NTC), сопротивление которого уменьшается с повышением температуры, или положительным температурным коэффициентом (PTC), сопротивление которого будет увеличиваться с повышением температуры. Сейчас термисторы реагируют на изменение параметров среды очень быстро и точно.
Схемотехническое обозначение резисторов
Про определение номинала резистора используя цветовую маркировку можно почитать здесь.
 Шпакунов А.
Шпакунов А.  Опубликована: 2012 г.
Опубликована: 2012 г.  0
0  2
2
Источник
Как рассчитать общее сопротивление, общую силу тока и напряжение на каждом из резисторов?
Добрый день. Вопрос смешной, но мне необходимо понять, или я не прав, или сайт на котором я прохожу тренинг работает некорректно. Имеется элементарная задачка на расчет значений в параллельном соединении. Условие: В цепи имеются параллельно соединённые два резистора 2 и 4 Ом с источником питания 12В. Предлагается рассчитать общее сопротивление, общую силу тока и напряжение на каждом из резисторов. Согласно формулам 1/Rоб=1/R1+1/R2; 1/Rоб=1/2+1/4=2/4+1/4=3/4=0.75; Rоб=1/0.75=1,33 Ом. Общая сила тока Iоб=I1+I2; I1=U/R1=12/2=6; I2=U/R2=12/4=3; Iоб=6+3=9 А, ну и напряжение на каждом из резисторов неизменно и составляет по 12 В. При данном решении, сайт мне выдает,что напряжение рассчитано правильно, а вот расчет общего сопротивления и общей силы тока показывает как не верное. Спасибо.
Поделиться в социальных сетях
Комментарии и отзывы (2)
Виктор
Это арифметические ошибки программы. Ток общий 12/1,33333…=9.02. 12*0.75=9.00.
Макаров Дмитрий (Эксперт)
Приведенные вами расчеты полностью справедливы для цепи с двумя последовательно соединенными резисторами. Вы правильно рассчитали величину общего сопротивления. Единственное, что меня смущает – зачем вам сложности при расчете результирующего тока, ведь у вас уже есть общее сопротивление. Имея значение приведенного к общему сопротивления, вам достаточно разделить напряжение на резисторах ( 12В ) на их общее сопротивление, у меня получилось 9,02 А, если округлить величину до сотых, но это скорее личное предпочтение – обязательного требования рассчитывать так ни у кого нет, тем более, что результат и моих, и ваших расчетов совпадает.
В остальных расчетах ошибок не выявил, поэтому делаю вывод, что ошибается программа на сервисе. Для выявления сбоя в алгоритме нужно увидеть тело программы, скорее всего, сбился какой-то логический алгоритм.
Источник
Содержание
- Сила тока в резисторе
- Определение силы тока на резисторе при разных типах соединения
- Последовательное соединение резисторов
- Параллельное соединение резисторов
- Смешанное соединение резисторов в цепи
- Как определить силу тока в резисторе при разных типах соединения
- Типы соединений резисторов
- Как найти сопротивление параллельно соединенных резисторов?
- Резистор и сопротивление
- Каталог
- Показать каталог
- Резистор и сопротивление
- Теория
- Последовательное соединение резисторов
- Мощность при последовательном соединении
- Параллельное соединение резисторов
- Мощность при параллельном соединении
- Последовательное и параллельное соединение резисторов
- Что такое резистор и для чего он нужен
- Понятие параллельного подключения резисторов
- Типы проводников
- Последовательное подключение
- Теоретическая часть
- Примеры расчета
- Общее сопротивление Rобщ
- Смешанное подключение
- Что ещё нужно учитывать при подключении резисторов
- Общее сопротивление Rобщ
- Схема параллельного соединения
- Как высчитывать сопротивление составных резисторов
- Какая мощность тока при последовательном и параллельном соединении
- Мощность при параллельном соединении
- Мощность при последовательном соединении
- Параллельное соединение проводников
- Сопротивление при параллельном соединении проводников
- Напряжение при параллельном соединении проводников
- Сила тока при параллельном соединении проводников
- Зависимость сопротивления
- Электрические величины
- Тип и геометрические параметры
- Температурные показатели
- Формула для вычисления напряжения
- Отличия между двумя видами подключений
- Как рассчитать сложные схемы соединения резисторов
Сила тока в резисторе
В упрощенном понимании электрическая цепь представляет собой совокупность элементов, реализующих определенные задачи при взаимодействии с электрическим током. При этом каждая из деталей выполняет свои функции при строго определенных параметрах. Они могут значительно отличаться от входящих значений. Одним из самых распространенных элементов электрической схемы является резистор.

Резистор выступает своеобразным ограничителем силы тока. По своей сути этот элемент является дополнительным сопротивлением, которое измеряется в омах. Собственно, зная это значение можно определить силу тока в резисторе, а также напряжение в цепи после него.
Определение силы тока на резисторе при разных типах соединения
Самым простым способом определить силу тока в резисторе можно воспользовавшись мультиметром. Измерение проводятся в разрыве цепи после резистора. На тестере выставляется максимальный диапазон величин, а щупы прибора подсоединяются к месту разъединения проводника. На дисплее мультиметра будут отображены результаты измерения силы тока в резисторе.

Но данный вариант не всегда возможен. Под рукой может не оказаться тестера или технически невозможно разорвать цепь чтобы измерить силу тока на резисторе. В такой ситуации на помощь придет известный из школьной физики закон Ома, который выглядит следующим образом:
I = U/R, где у нас I – сила тока, U – напряжение, R – сопротивление.
В системе СИ эти величины измеряются в амперах (А), вольтах (В), омах (Ом) соответственно.
Подставляя необходимые значения в формулу можно определить сопротивление, напряжение и силу тока на резисторе или любом участке, или элементе электрической цепи.

Последовательное соединение резисторов
Рассмотрим электрическую цепь, в которой три резистора расположены последовательно, т.е. друг за другом. Общее их сопротивление (R) будет рано сумме сопротивлений отдельного резистора (r).
Для наглядности примера, в качестве резисторов рассмотрим обычные 40 Вт лампы накаливании. В данном случае вольфрамовая нить обладает своим сопротивлением и ее вполне можно считать резистором. Также введем понятие мощности нагрузки или резистора (P), которая измеряется в ватах (Вт).

Она имеет прямолинейную зависимость от силы тока и напряжения и вычисляется по формуле: P=I х U. С помощью несложных вычислений мы можем найти силу тока на резисторе, в качестве которого выступает лампочка.
Сила тока (I) = Мощность лампы (Р) / Напряжение (U) = 40 Вт / 220 В = 0,1818 А.
Для последовательного соединения элементов в электрической цепи справедливо правило, что силы тока протекающие через все проводники одинакова. Таким образом сила тока в резисторе r2 или r3 также будет 0,1818 А. Но в нашем варианте с лампочками будет отмечена одна особенность – яркость свечения уменьшится. Это происходит из-за того, что резистор выступает в качестве делителя напряжения. Этот нюанс часто используют для продления срока службы не ответственных устройств. Например, впаяв сопротивление перед лампочкой можно продлить срок ее службы, но при этом придется смерится с недостатком освещенности.
Параллельное соединение резисторов
При параллельном расположении резисторов в сети, они имеют общую точку контакта на входе и на выходе. В этом случае общее напряжение будет соответствовать значению напряжения на каждом отрезке, а вот ток будет суммироваться (I об= I1 + I2 +I3). Это соотношение имеет большое значение для практического применения и получило название – закон разветвленной цепи.
Несмотря на то, что общий ток в цепочке резисторов, соединенных параллельно на выходе равен сумме токов в самостоятельной ветке, для конкретного участка он может отличаться. Это обусловлено тем же законом Ома, при условии разности сопротивлений. Чтобы узнать силу тока на каждом резисторе в соответствующей ветке, необходимо знать их сопротивление. При параллельном соединении, напряжение на обособленном участке, является постоянной величиной. Соответственно сила тока отельного резистора легко вычисляется по закону Ома для участка цепи.

Смешанное соединение резисторов в цепи
В чистом виде параллельные и последовательные цепи в электротехнике встречаются крайне редко. Как правило, присутствует их совместная комбинация. Для того чтобы найти силу тока в каждом резисторе при смешанном соединении, необходимо цепь разбить на участки. Таким образом при расположении элементов друг после друга, т.н. «каскадом», применяются правила и формулы для последовательного соединения.

Результаты измерения силы тока в резисторе. Различные типы резисторов.
Необходимо отметить, что для упрощения расчетов параллельно расположенные резисторы можно группировать. При вычислении силы тока на определенном участке, они принимаются за самостоятельный элемент. Соответственно в этом случае формулы используются как для расчета параметров при параллельном соединении.
Урок №2. Сопротивление. Закон Ома. Резистор.
Источник
Как определить силу тока в резисторе при разных типах соединения
Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
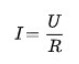
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
Общие схемы типов соединений представлены на рисунке 1.

Рисунок 1. Типы соединений резисторов
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)

Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
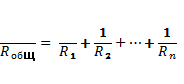
и рассчитывается по формуле:
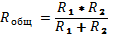
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
Сопротивление на участке АВ (1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Источник
Резистор и сопротивление
Каталог
Показать каталог
Резистор и сопротивление
Теория
КОМПОНЕНТЫ
ARDUINO
RASPBERRY
ИНТЕРФЕЙСЫ ПЕРЕДАЧИ ДАННЫХ
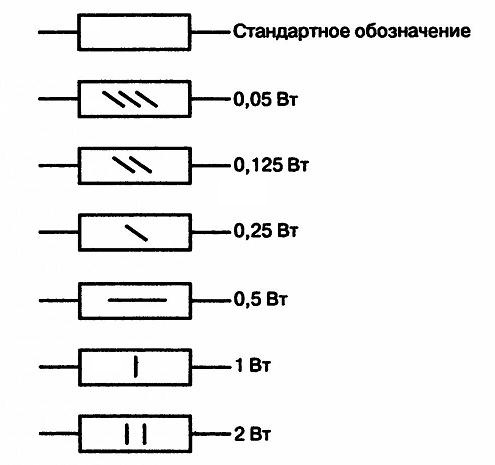
1 кОм = 1000 Ом,
1 МОм = 1000 кОм,
1 ГОм = 1000 МОм
Последовательное соединение резисторов
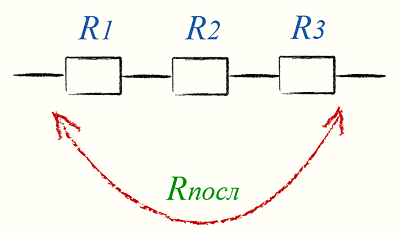
Это справедливо и для большего количества соединённых последовательно резисторов:
Цепь из последовательно соединённых резисторов будет всегда иметь сопротивление большее, чем у любого резистора из этой цепи.
При последовательном соединении резисторов изменение сопротивления любого резистора из этой цепи влечёт за собой как изменение сопротивления всей цепи так и изменение силы тока в этой цепи.
Мощность при последовательном соединении
R = 200 + 100 + 51 + 39 = 390 Ом
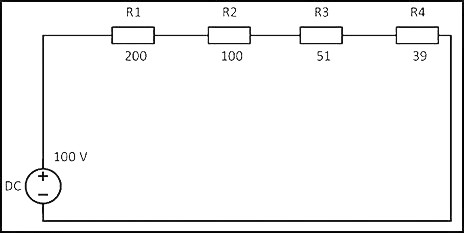
Учитывая напряжение в цепи, равное 100 В, по закону Ома сила тока будет составлять
I = U/R = 100 В/390 Ом = 0,256 A
На основании полученных данных можно рассчитать мощность резисторов при последовательном соединении по следующей формуле:
P = I 2 x R = 0,256 2 x 390 = 25,55 Вт
Таким же образом можно рассчитать мощность каждого отдельно взятого резистора:
P1 = I 2 x R1 = 0,256 2 x 200 = 13,11 Вт;
P2 = I 2 x R2 = 0,256 2 x 100 = 6,55 Вт;
P3 = I 2 x R3 = 0,256 2 x 51 = 3,34 Вт;
P4 = I 2 x R4 = 0,256 2 x 39 = 2,55 Вт.
Если сложить полученные мощности, то общая Р составит:
Робщ = 13,11 + 6,55 + 3,34 + 2,55 = 25,55 Вт
Параллельное соединение резисторов
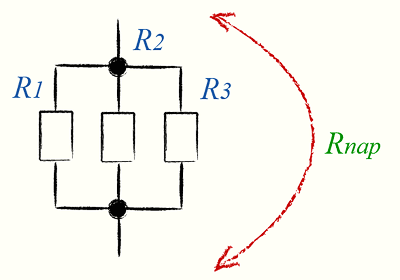
Расчет параллельного сопротивления двух параллельно соединённых резисторов R1 и R2 производится по следующей формуле:
Параллельное соединение трёх и более резисторов требует более сложной формулы для вычисления общего сопротивления:
Сопротивление параллельно соединённых резисторов будет всегда меньше, чем у любого из этих резисторов.
Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением. Общая мощность, в таком случае, вычисляется умножением мощности одного резистора на количество параллельно соединённых резисторов.
Мощность при параллельном соединении
1/R = 1/200 + 1/100 + 1/51 + 1/39 ≈ 0,06024 Ом
R = 1 / 0,06024 ≈ 16,6 Ом
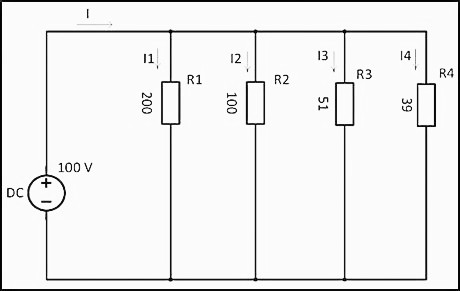
Используя значение напряжения 100 В, по закону Ома рассчитывается сила тока
I = U/R = 100 В x 0,06024 Ом = 6,024 A
Зная силу тока, мощность резисторов, соединенных параллельно, определяется следующим образом
P = I 2 x R = 6,024 2 x 16,6 = 602,3 Вт
Расчет силы тока для каждого резистора выполняется по формулам:
На примере этих сопротивлений прослеживается закономерность, что с уменьшением сопротивления, сила тока увеличивается.
Существует еще одна формула, позволяющая рассчитать мощность при параллельном подключении резисторов:
P1 = U 2 /R1 = 100 2 /200 = 50 Вт;
P2 = U 2 /R2 = 100 2 /100 = 100 Вт;
P3 = U 2 2/R3 = 100 2 /51 = 195,9 Вт;
P4 = U 2 2/R4 = 100 2 /39 = 256,4 Вт
Если сложить полученные мощности, то общая Р составит:
Робщ = 50 + 100 + 195,9 + 256,4 = 602,3 Вт
Источник
Последовательное и параллельное соединение резисторов

Что такое резистор и для чего он нужен
Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.
Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.
Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.
Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).
Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.
Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:
- С правого края – правый.
- С левого края – левый.
Понятие параллельного подключения резисторов
При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.
При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.
Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Последовательное и параллельное соединение резисторов
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Последовательное подключение
При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.
При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.
Теоретическая часть
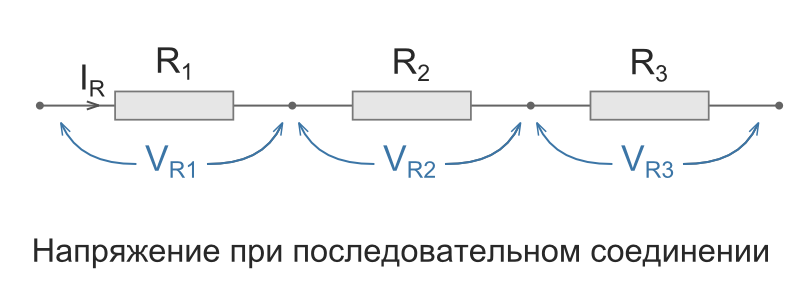
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Будет интересно➡ SMD резисторы: что это такое и для чего используются?
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.
Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Смешанное подключение
При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени. О параллельном соединении резистора и конденсатора читайте тут.
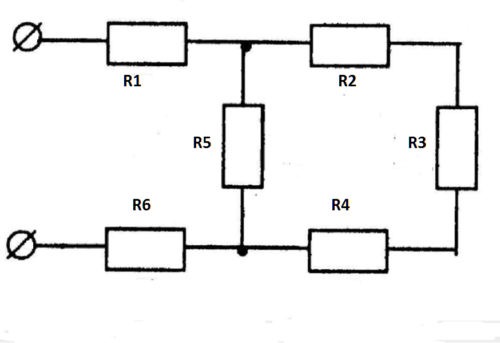
Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.
Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.
Что ещё нужно учитывать при подключении резисторов
Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.
При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.
То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.
Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.
Схема параллельного соединения
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Урок 11. ВСЕ Способы соединения резисторов
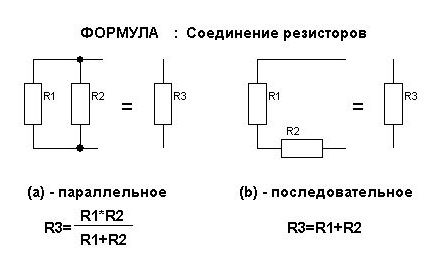
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.
Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Какая мощность тока при последовательном и параллельном соединении
Определение мощности отдельного резистивного элемента производится по формуле
P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.
Мощность при параллельном соединении
Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где
- R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
- I – сила тока в цепи.
При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.
Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.
Мощность при последовательном соединении
Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где
- R – рассчитанное нами сопротивление для определенной схемы;
- U – падение напряжения на данном резистивном элементе.
Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.
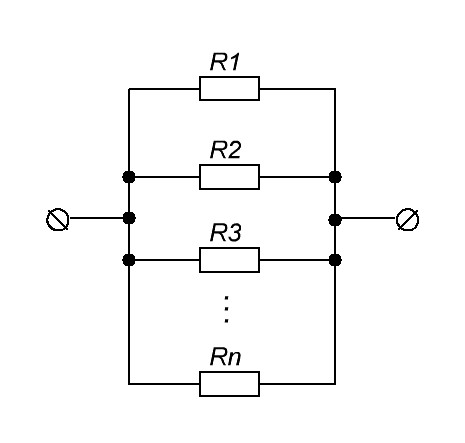
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.
параллельное соединение резисторов
Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле
Если же мы имеем только два параллельно соединенных проводника
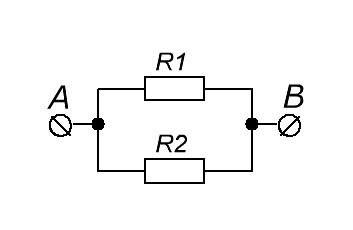
То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.
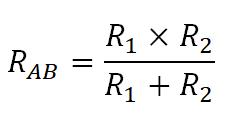
Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn
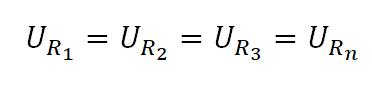
Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.
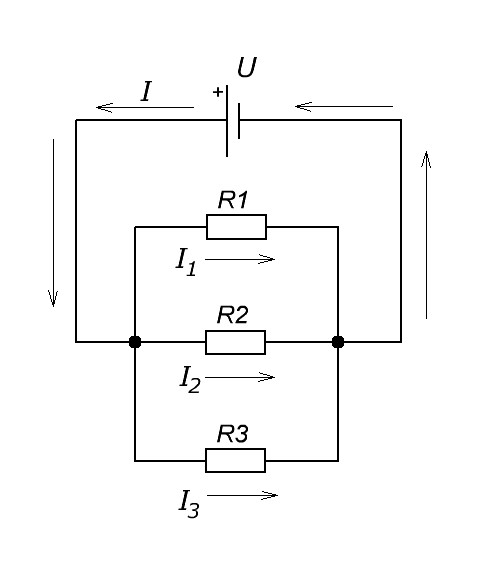
Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
Если бы у нас еще были резисторы, соединенные параллельно, то для них
В этом случае, сила тока в цепи будет равна:
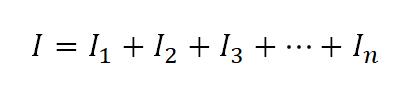
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.
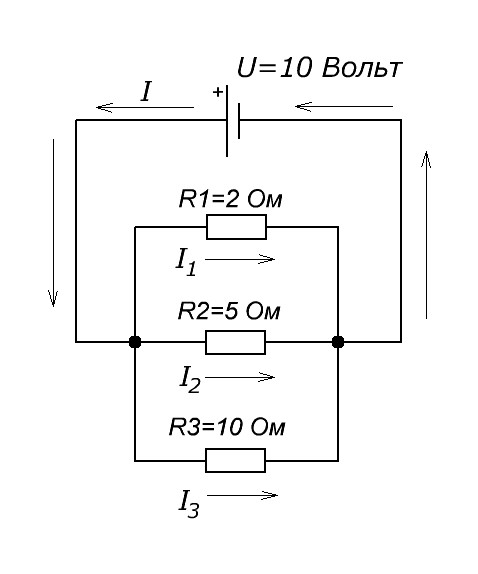
Воспользуемся формулами, которые приводили выше.
Если бы у нас еще были резисторы, соединенные параллельно, то для них
I1 = U/R1 = 10/2=5 Ампер
I2 = U/R2 = 10/5=2 Ампера
I3 = U/R3 = 10/10=1 Ампер
Далее, воспользуемся формулой
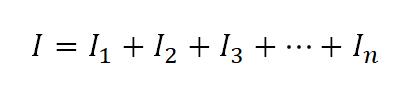
чтобы найти силу тока, которая течет в цепи
I=I1 + I2 + I3 = 5+2+1=8 Ампер
2-ой способ найти I
Чтобы найти Rобщее мы должны воспользоваться формулой
Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
последовательное и параллельное соединение резисторов
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Урок 11. ВСЕ Способы соединения резисторов
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a 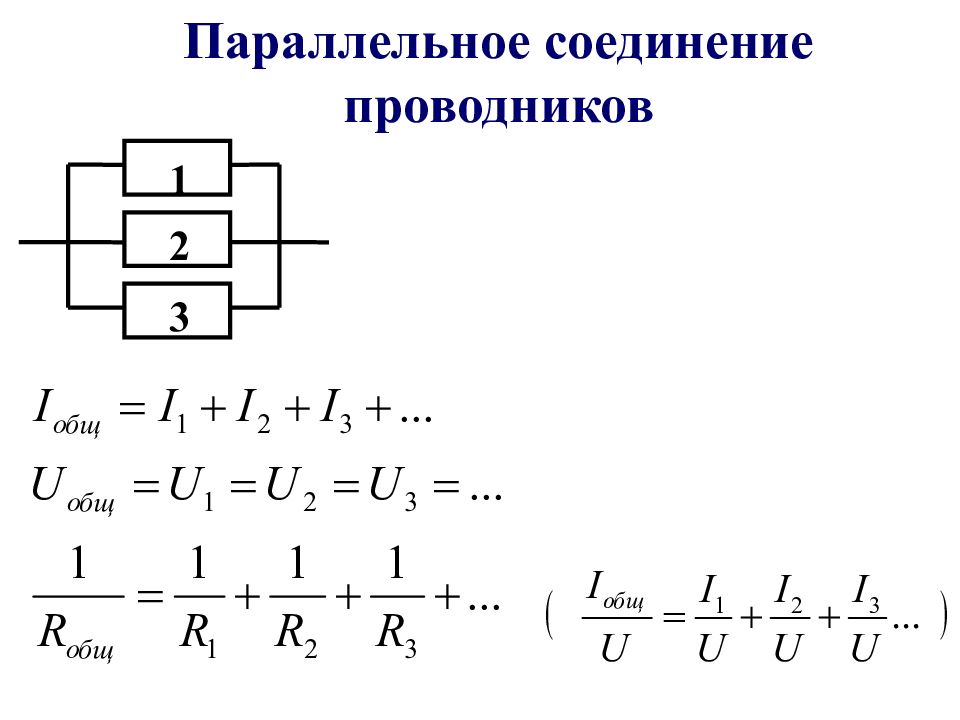
Стандартная формула напряжения
Формула для вычисления напряжения
При данном виде соединения все линии будут находиться в двух точках. Потому напряжение для всех резисторов будет равным.
При подсоединении двух и более приборов друг с другом, напряжение на выводах такой схемы — это показатель на каждом резисторе.
Напряжения условно обозначаются как U. По закону Ома, зная, что I = U/R, можно рассчитать по формуле:
U = U1 = U2 = … = Uобщ.
Обратите внимание! Помимо вычисления напряжения, рекомендуется знать мощность проводников. Они не должны сильно отличаться друг от друга. Параллельное соединение также можно встретить в лампочках, кабелях сигнализации автомобиля, фарах и прочем.
Также иногда можно встретить смешанный вид подключения. Это когда в цепи применяется два типа подключения, и параллельное, и последовательное. Оно чаще всего используется в контурных обогревателях.
Желательно изучить каждый вид подключения и схемы к ним. Профессиональные электрики рекомендует не выполнять подключений самостоятельно, если у человека совсем нет опыта в этой сфере. Так как в цепи может случиться короткое замыкание или возгорание, в лучшем случае выход из строя прибора.

Определение мощности на примере ламп
В заключении необходимо отметить, каждому человеку желательно знать свойства последовательного и параллельного соединения проводников. Чтобы в будущем не путаться при выполнении простых работ в электрике своего дома.
ЧТО ТАКОЕ ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ
Отличия между двумя видами подключений
Схема последовательного подключения говорит о том, что проводники установлены в особом расположении друг за другом. Поэтому сила тока у них одинаковая. Эти элементы создают в цепи Uобщее.
Пример подключения с предохранителем
Заряды не собираются в узлах электрической цепи, иначе было бы видно, как напряжение меняется. Минусом этой схемы будет то, что если любой элемент сломается, то вся цепь разорвется и перестанет работать. Например, если взять новогоднюю гирлянду. Если одна лампочка перестала работать, то другие тоже не загораются. Это и будет главным различием между последовательным и параллельным соединением. Ниже описана характеристика резисторов при параллельном объединении.
Как рассчитать сложные схемы соединения резисторов
Если соединять большее количество элементов, надо в рассмотренные формулы добавить необходимое количество слагаемых.
- источник постоянного тока 12V;
- сопротивление параллельных резисторов, Ом: 10, 40, 60, 80.
- основная формула: 1/Rэкв = 1/R1 + 1/R2 + 1/R3 + 1/R4;
- подставив исходные данные, вычисляют проводимость: G = 1/Rэкв =1/10 + 1/40 + 1/60 +1/80 = 0,1 + 0,025 + 0,0166 +0,0125 = 0,1541;
- эквивалентное сопротивление: Rэкв = 1/0,1541 ≈ 6,5 Ом;
- ток в цепи: Iобщ = Uип/ Rэкв = 12/ 6,5 ≈ 1,85 А.
По аналогичной технологии делают расчеты более сложных цепей. На рисунке обозначены номиналы сопротивлений. В обоих случаях применяется одинаковый источник питания с Uип = 12V.
Расчет 1 (последовательное и параллельное соединение):
- для каждого параллельного участка можно использовать формулу: Rобщ = 1/ (1/R1 + 1/R2) = R1*R2/R1 + R2;
- эквивалентное сопротивление первой части: Rэкв1 = (2*4)/ (2+4) = 1,3 Ом;
- второй: Rэкв2 = (15*5)/ (15+5) = 3,75 Ом;
- общее: Rэкв = 1,3 + 10 + 3,75 = 15,05 Ом;
- Iобщ = Uип/ Rэкв = 12/ 15,05 ≈ 0,8 А.
Расчет 2 (сложное параллельное соединение):
- в этом варианте сначала вычисляют проводимость части (R3, R4, R5) по формуле: G345 = 1/5 + 1/10 + 1/ 20 =7/20 = 0,35 сим;
- Rэкв (345) = 1/0,35 ≈ 2,857 Ом;
- суммарное значение для цепи: R1 + R2 = 20 Ом;
- по аналогии с предыдущим способом определяют: G12345 = 0,4 сим и Rэкв(12345) = (20*2,857)/ 20 + 2,857) ≈ 2,5 Ом;
- после добавления последнего элемента (R6=7,5 Ом) получают итоговый результат: Rэкв = 2,5 + 7,5 = 10 Ом;
- делением определяют силу тока в нагрузке, подключенной к источнику тока 12 V: I = 12/10 = 1,2 А.
В последнем примере применен дополнительный компонент цепи (R6). Соответственно, для этой схемы не будет выполняться рассмотренная выше пропорция равенства напряжений (источника и на подключенной нагрузке).
В этом случае разница потенциалов на шестом резисторе составит:
U6 = I *R6 = 1,2 * 7,5 = 9 В.
Соответственно, изменится напряжение между контрольными точками:
Uав = I * Rэкв(12345) = 1,2*2,5 = 12-9 =3V.
Вторая часть формулы демонстрирует проверку вычитанием напряжений (Uип — U6).
Источник
Загрузить PDF
Загрузить PDF
В параллельной цепи резисторы соединены таким образом, что электрический ток в цепи делится между резисторами и проходит через них одновременно (сравните это с автодорогой, которая разделяется на две параллельные дороги и делит поток машин на два потока, движущихся параллельно друг другу). В этой статье мы расскажет вам, как вычислить напряжение, силу тока и сопротивление в параллельной цепи.
Шпаргалка
- Формула для вычисления общего сопротивления RT в параллельной цепи: 1/RT = 1/R1 + 1/R2 + 1/R3 + …
- Напряжение в параллельной цепи одинаковое на каждом ее элементе: VT = V1 = V2 = V3 = …
- Формула для вычисления общей силы тока в параллельной цепи: IT = I1 + I2 + I3 + …
- Закон Ома: V = IR
-

1
Определение. Параллельная цепь — это цепь, в которой ток течет из точки А в точку В одновременно по нескольким элементам цепи (то есть поток электронов разбивается на несколько потоков, которые на конечном участке цепи вновь объединяются в единый поток). В большинстве задач, в которых присутствует параллельная цепь, нужно вычислить напряжение, сопротивление и силу тока.
- Элементы, подключенные параллельно, находятся на отдельных ветвях цепи.
-

2
Сила тока и сопротивление в параллельных цепях. Представьте себе автостраду с несколькими полосами, на каждой из которых установлен пункт пропуска, замедляющий движение автомобилей. Построив новую полосу, вы увеличите скорость движения (даже если и на этой полосе вы поставите пункт пропуска). Аналогично с параллельной цепью — добавив новую ветвь, вы уменьшите общее сопротивление цепи и увеличите силу тока.
-

3
Общая сила тока в параллельной цепи равна сумме силы тока на каждом элементе этой цепи. То есть, если известна сила тока на каждом резисторе, сложите эти силы тока, чтобы найти общую силу тока в параллельной цепи: IT = I1 + I2 + I3 + …
-

4
Общее сопротивление в параллельной цепи. Оно вычисляется по формуле: 1/RT = 1/R1 + 1/R2 + 1/R3 + …, где R1, R2 и так далее — это сопротивление соответствующих элементов (резисторов) этой цепи.
- Например, параллельная цепь включает два резистора и сопротивление каждого равно 4 Ом. 1/RT = 1/4 + 1/4 → 1/RT = 1/2 → RT = 2 Ом. То есть общее сопротивление параллельной цепи с двумя элементами, сопротивления которых равны, в два раза меньше сопротивления каждого резистора.
- Если какая-либо ветвь параллельной цепи не имеет сопротивления (0 Ом), то весь ток пройдет именно через эту ветвь.[1]
-

5
Напряжение. Напряжение — это разность электрических потенциалов между двумя точками электрической цепи. Так как здесь рассматриваются две точки без учета пути движения тока по цепи, напряжение в параллельной цепи одинаково на каждом элементе этой цепи, то есть: VT = V1 = V2 = V3 = …
-

6
Вычислите значения неизвестных величин по закону Ома. Закон Ома описывает взаимосвязь между напряжением V, силой током I и сопротивлением R: V = IR. Если вам известны значения двух величин из этой формулы, вы можете найти значение третьей величины.
- Вы можете применить закон Ома для всей цепи (V = ITRT) или для одной ветви этой цепи (V = I1R1).
Реклама
-

1
Нарисуйте таблицу, чтобы облегчить решение задачи, особенно если неизвестны значения сразу нескольких величин в данной параллельной цепи.[2]
Рассмотрим пример электрической цепи с тремя параллельными ветвями. Обратите внимание, что здесь под ветвями подразумеваются резисторы с сопротивлениями R1, R2, R3.R1 R2 R3 Общее Единицы измерения V В I А R Ом -

2
Внесите в таблицу данные вам значения. Например, к электрической цепи подключена батарея, напряжение которой равно 12 В. Цепь включает три параллельные ветви с сопротивлениями 2 Ом, 4 Ом, 9 Ом.
R1 R2 R3 Общее Единицы измерения V 12 В I А R 2 4 9 Ом -

3
Заполните значения напряжения для каждого элемента цепи. Помните, что общее напряжение в параллельной цепи и напряжение на каждом резисторе этой цепи равны.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I А R 2 4 9 Ом -

4
Вычислите силу тока на каждом резисторе по закону Ома. Так как теперь в каждом столбце вашей таблицы есть значения двух величин, вы с легкостью вычислите значение третей величины при помощи закона Ома: V = IR. В нашем примере нужно найти силу тока, поэтому перепишите формулу закона Ома следующим образом: I = V/R
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 12/2 = 6 12/4 = 3 12/9 = ~1,33 А R 2 4 9 Ом -

5
Вычислите общую силу тока. Помните, что общая сила тока в параллельной цепи равна сумме сил тока на каждом элементе этой цепи.
R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1,33 6 + 3 + 1,33 = 10,33 А R 2 4 9 Ом -

6
Вычислите общее сопротивление. Сделайте это одним из двух способов. Либо используйте формулу
1/RT = 1/R1 + 1/R2 + 1/R3, либо формулу закона Ома: R = V/I.R1 R2 R3 Общее Единицы измерения V 12 12 12 12 В I 6 3 1.33 10,33 А R 2 4 9 12 / 10,33 = ~1,17 Ом Реклама
-

1
Вычислите мощность тока по формуле: P = IV. Если вам дана мощность тока на каждом участке цепи, то общая мощность вычисляется по формуле: PT = P1 + P2 + P3 + ….
-

2
Вычислите общее сопротивление в параллельной цепи, состоящей из двух ветвей (двух резисторов).
- RT = R1R2 / (R1 + R2)
-

3
Найдите общее сопротивление в параллельной цепи, если сопротивление всех резисторов одинаково: RT = R1 / N, где N — количество резисторов в цепи.[3]
- Например, если в параллельной цепи два резистора с одинаковым сопротивлением, то общее сопротивление цепи будет вдвое меньше сопротивления одного резистора. Если в цепи восемь одинаковых резисторов, то общее сопротивление будет в восемь раз меньше сопротивления одного резистора.
-

4
Вычислите силу тока на каждом резисторе, если напряжение неизвестно. Это можно сделать, воспользовавшись правилом Кирхгофа.[4]
Вам необходимо вычислить сопротивление каждого резистора и общую силу тока в цепи.- Два резистора в параллельной цепи: I1 = ITR2 / (R1 + R2)
- Несколько (более двух) резисторов в параллельной цепи. В этом случае для вычисления I1 найдите общее сопротивление всех резисторов за исключением R1. Для этого воспользуйтесь формулой для вычисления общего сопротивления в параллельной цепи. Затем используйте правило Кирхгофа, заменив R2 полученным значением.
Реклама
Советы
- В параллельной цепи напряжение одинаково на всех резисторах.
- Возможно, в вашем учебнике закон Ома представлен следующей формулой: E = IR или V = AR. Здесь присутствуют другие обозначения величин, но суть закона Ома не меняется.
- Общее сопротивление часто именуется эквивалентным сопротивлением.
- Если у вас нет калькулятора, найти общее сопротивление, используя значения R1, R2 и так далее, довольно проблематично. Поэтому воспользуйтесь законом Ома.
- Если в задаче дана параллельно-последовательная цепь, сделайте вычисления для ее параллельного участка, а затем для полученной последовательной цепи.
Реклама
Об этой статье
Эту страницу просматривали 172 858 раз.
Была ли эта статья полезной?
Расчет простых цепей постоянного тока
В электротехнике принято считать, что простая цепь – это цепь, которая сводится к цепи с одним источником и одним эквивалентным сопротивлением. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений. Исключением служат цепи, содержащие более сложные соединения звездой и треугольником. Расчет цепей постоянного тока производится с помощью закона Ома и Кирхгофа.
Пример 1
Два резистора подключены к источнику постоянного напряжения 50 В, с внутренним сопротивлением r= 0,5 Ом. Сопротивления резисторов R1 = 20 и R2 = 32 Ом. Определить ток в цепи и напряжения на резисторах.

Так как резисторы подключены последовательно, эквивалентное сопротивление будет равно их сумме. Зная его, воспользуемся законом Ома для полной цепи, чтобы найти ток в цепи.
 Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.
Теперь зная ток в цепи, можно определить падения напряжений на каждом из резисторов.

Проверить правильность решения можно несколькими способами. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем.
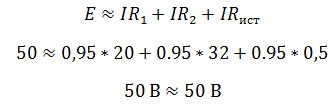
Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур. Более удобным способом проверки является баланс мощностей.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
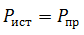
Мощность источника определяется как произведение ЭДС на ток, а мощность полученная приемником как произведение падения напряжения на ток.
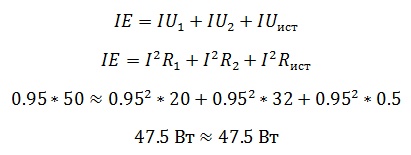
Преимущество проверки балансом мощностей в том, что не нужно составлять сложных громоздких уравнений на основании законов Кирхгофа, достаточно знать ЭДС, напряжения и токи в цепи.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора R1=70 Ом и R2=90 Ом, равен 500 мА. Определить токи в каждом из резисторов.

Два последовательно соединенных резистора ничто иное, как делитель тока. Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах 
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.

Если у вас возникли затруднения, прочтите статью законы Кирхгофа.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала рассчитать сопротивление цепи
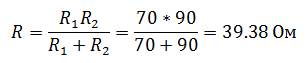
А затем напряжение

Зная напряжения, найдем токи, протекающие через резисторы
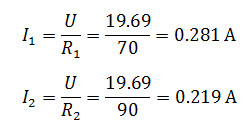
Как видите, токи получились теми же.
Пример 3
В электрической цепи, изображенной на схеме R1=50 Ом, R2=180 Ом, R3=220 Ом. Найти мощность, выделяемую на резисторе R1, ток через резистор R2, напряжение на резисторе R3, если известно, что напряжение на зажимах цепи 100 В.

Чтобы рассчитать мощность постоянного тока, выделяемую на резисторе R1, необходимо определить ток I1, который является общим для всей цепи. Зная напряжение на зажимах и эквивалентное сопротивление цепи, можно его найти.
Эквивалентное сопротивление и ток в цепи
 Отсюда мощность, выделяемая на R1
Отсюда мощность, выделяемая на R1
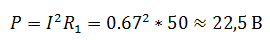 Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
Ток I2 определим с помощью формулы делителя тока, учитывая, что ток I1 для этого делителя является общим
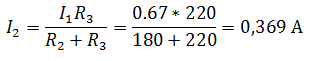
Так как, напряжение при параллельном соединении резисторов одинаковое, найдем U3, как напряжение на резисторе R2
![]()
Таким образом производится расчет простых цепей постоянного тока.
