Как найти величину вакуума

Выше рассматривался
случай, когда абсолютное давление в
точке больше атмосферного. Обратимся
теперь к случаю, когда p_A
‹ p_a.
Положим, что
таким давлением характеризуется точка
m,
показанная на
рис. 2-10. Давление в точке т
при условии
p_A
‹ p_a
можно измерить
с помощью так называемого обратного
пьезометра, или, что то же, вакуумметра,
представляющего собой изогнутую трубку
V.

Очевидно, горизонт
жидкости в такой трубке опустится ниже
точки т;
заглубление
точки т
по отношению
к горизонту жидкости в трубке V
будет
отрицательным (h_вак
на рис. 2-10).

Рис. 2-10. Вакуум h_вак– вакуумметрическая высота или высота
вакуума

Можно сказать,
что:

а) давление в точке
т
со стороны
жидкости в сосуде равно

p_A
= p₀
+ γh; (2-50)

б) давление в точке
т со
стороны жидкости в трубке V
равно

(2-51)

Соединяя знаком
равенства два приведенных выражения,
получим:

p_A
= p_a
–
γh_вак (2-52)

откуда

hизб =

где р – избыточное
давление в точке n
(2-53)

Величину h_изб
называют вакуумметрической высотой
или высотой вакуума. Как видно, h_изб
характеризует
разность двух давлений: атмосферного
и абсолютного давления в точке p_A
– p_a.
Именно эта разность, а не само давление,
называется вакуумом (от латинского
слова vacuum
«пустота»). Можно сказать, что вакуум
в данной точке жидкости есть недостаток
давления в этой точке до атмосферного.
Иногда вакуумом
называют также состояние жидкости,
когда давление в ней менее атмосферного.
Величина вакуума может выражаться тремя
способами:

1. единицами
   ,
   например, кН/м²,
   т. е. кПа (или, например, кгс/см²);

1. единицами длины
   (единицами высоты) вертикального столба
   жидкости, характеризуемой определенной
   величиной γ;

2. в долях атмосферного
   давления (в обычных условиях вакуум не
   может быть больше того давления, которое
   развивает в данном месте атмосфера).

Если в данной точке
вакуум равен, например, 4 м вод. ст., то
это значит, что абсолютное давление в
этой точке равно 6 м вод. ст.

В § 1-4, п. 6 было
рассмотрено поднятие жидкости в
капиллярной трубке К
(см. рис. 1-5).

Рис. 2-11. Высота капиллярного поднятия
/г_кпжидкости в трубке К
Заштрихованы эпюры гидростатического,
давления: положительного и отрицательного
(по отношению к атмосферному давлению)

Не учитывая вовсе
молекулярного давления, можем сказать,
что в жидкости, находящейся в капиллярной
зоне, должен иметь место вакуум. Эпюра
изменения величины h_вак
вдоль оси М
– N капиллярной
трубки К
(рис. 2-11)
выразится треугольником ABC:
эпюра же
избыточного давления

h_изб
=
=

для линии АЕ
представится
треугольником ADE.

Поскольку в данном
случае вакуум образуется за счет разности
давлений плоской и вогнутой поверхностных
пленок, то он, вообще говоря, может быть
и больше одной атмосферы.

§ 2-8, Потенциальная энергия жидкости. Потенциальный напор

1.
Удельная потенциальная энергия жидкости.
Жидкость, находящаяся в покое или
движении, обладает определенным запасом
механической энергии, т. е. способностью
производить работу. Покоящаяся жидкость
обладает только так называемой
потенциальной энергией.

Покажем на рис.
2-9 горизонтальную координатную плоскость
ОО,
которую назовем
плоскостью сравнения. На плоскости ОО
наметим начало
оси z,
причем эту ось направим вверх. Ординаты
z
различных точек жидкости будем называть
отметками; «отметка» точки есть возвышение
ее над плоскостью сравнения. Будем
рассматривать точку n
жидкости;
пьезометрическая высота h_изб
для этой точки, а также ее отметка z
показаны на чертеже.

Выделим у точки
некоторый
объем жидкости весом G
и приключим к этой точке открытую трубку
П.
Под действием
избыточного давления р
в точке n
объем жидкости
весом G
поднимается в трубке П
на высоту h_изб
над плоскостью
MN
и на высоту H
над плоскостью сравнения ОО
(см. рис. 2-9).

Из сказанного
должно быть ясно, что рассматриваемый
объем жидкости, сосредоточенный в точке
n,
может произвести работу:

во-первых, за счет
своего падения на плоскость ОО
с высоты z;
эта возможная работа будет

(ЭП)_z
= zG; (2-54)

во-вторых, за счет
своего поднятия под давлением р
на высоту h_изб;
эта возможная
работа будет

(ЭП)_р
= h_избG. (2-55)

Полная работа,
которую может произвести объем жидкости
весом G,

(ЭП)
= (ЭП)_z
+ (ЭП)_p
= zG
+ h_избG. (2-56)

Величина (ЭП)
и называется
потенциальной энергией определенного
объема жидкости (в данном случае объема
весом G).

Удельной потенциальной
энергией (УЭП)
называется энергия, отнесенная к единице
веса жидкости, находящейся в точке n:

(УЭП)
=
=z
+ h_изб
= H.
(2-57)

Как видно, внутри
удельной потенциальной энергии (полной)
в общем случае следует различать два
вида потенциальной энергии:

1) удельную
потенциальную
энергию
положения
(УЭП)_z,
равную
z;

2) удельную
потенциальную
энергию
давления
(УЭП)_р,
равную

h_изб
=

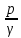
2.
Потенциальный напор.
В гидравлике
слово напор применяется в особом смысле;
напором принято
называть удельную энергию жидкости, т.
е. меру энергии, принадлежащей единице
веса жидкости.

В соответствии с
этим потенциальный напор будет
представлять собой величину H
[см. формулу (2-57)]; при этом величина z
(отметка точки) может быть названа
геометрическим напором; величина же
h_изб
(пьезометрическая высота) – напором
давления. Достаточно величины H,
z,
h_изб
умножить на единицу веса жидкости, и мы
при этом получим соответствующие энергии
этой единицы веса жидкости.

Можно сказать, что
потенциальный
напор (удельная
потенциальная энергия) слагается
из двух напоров: геометрического напора
(удельной
энергии положения) и напора
давления (удельной
энергии давления).

Все поясненные
выше напоры имеют размерность длины и
выражаются соответствующими отрезками:
H,
z,
h_изб
(рис. 2-9).

Следует запомнить,
что с геометрической
точки зрения потенциальный напор Н
в данной точке (например, в точке п)
по отношению к какой-либо горизонтальной
плоскости сравнения ОО
представляет собой сумму двух линейных
величин: отметки данной точки z
и соответствующей ей пьезометрической
высоты h_изб:

Н = z + hизб

или

H = z +

. (2-58)

Величина Н
(представляющая
собой превышение над плоскостью сравнения
ОО
уровня жидкости
в открытом пьезометре, подключенном к
рассматриваемой точке) характеризуется
следующей особенностью: для
всех точек покоящейся жидкости величина
Н
одинакова:

Н
= const
(по всему объему). (2-59)

Для доказательства
справедливости этого положения напишем:

H
= z += z += z +
=

=
T +
= const, (2-60)

где Т
– превышение
горизонта жидкости в сосуде над плоскостью
ОО
(Т= const).

Рис. 2-12. Удельная потенциальная энергия.
Потенциальный напор

Н – потенциальный напор или удельная
потенциальная энергия жидкости; H_A– абсолютный потенциальный напор или
абсолютная потенциальная удельная
энергия жидкости

Рис. 2-13. Поле сил тяжести (описываемое
потенциальной функцией z)
и поле архимедовых сил (описываемых
потенциальной функциейp/γ),
внутри которых одновременно мысленно
перемещается одна единица веса жидкости.

– H
= z
+ p/γ- суммарная потенциальная функция,
отнесенная к единице веса жидкости;p/γ
=const;z
z =const

Возьмем закрытый
сосуд (рис. 2-12). Наметим в жидкости ряд
точек: 1, 2, 3, 4,
… К каждой
такой точке приключим пьезометр П.
Основываясь
на (2-59), можем утверждать, что горизонт
жидкости во всех пьезометрах должен
установиться на одной и той же высоте.

Отсюда ясно, что
по горизонтам жидкости в пьезометрах
П
можно провести
некоторую плоскость РР,
которая должна
быть горизонтальной. Эта горизонтальная
плоскость РР
называется
пьезометрической плоскостью. Как видно,
эта плоскость РР
(или, как обычно
говорят, пьезометрическая линия Р
– Р) возвышается
над плоскостью сравнения на величину
Н.

В заключение
подчеркнем следующее: так
как Н
постоянна для всех точек покоящейся
жидкости, то, следовательно, во всех
точках такой жидкости полная удельная
потенциальная энергия (УЭП)
одинакова:

(УЭП)
= const
(по всему объему). (2-61)

3.
Потенциальный напор, отвечающий
абсолютному давлению.
Выше при
пояснении
удельной энергии и напора мы оперировали
открытым пьезометром П.
Если бы мы
вместо пьезометра П
пользовались
закрытым пьезометром П₀,
то вместо потенциального напора Н
получили бы
абсолютный потенциальный напор H_A
(см. рис. 2-9 и 2-12). Очевидно, напор H_A
должен выражать абсолютную удельную
потенциальную энергию, подсчитанную
без учета противодавления со стороны
атмосферы.

Пьезометрическая
линия P_A
– P_A,
определяемая
напором H_A,
должна возвышаться над пьезометрической
линией Р-Р
на высоту,
равную p₀/γ.

4.
Дополнительные замечания о потенциальном
напоре.
Представим на рис. 2-13 сосуд А,
причем вес
всей жидкости, наполняющей этот сосуд,
обозначим через G.
Наметим на рисунке дополнительно:
плоскость сравнения ОО
и эквипотенциали
поля сил тяжести, т. е. линии z=
const
(см. линии 0, 1,
2, 3, …, 8,
показанные
длинными штриховыми линиями).

Как известно из
механики, потенциальная энергия (ЭП)
жидкости, заполняющей сосуд и находящейся
только в поле сил тяжести, равна
(относительно плоскости сравнения ОО)
GH_c,
где H_c
– возвышение
центра тяжести рассматриваемого объема
жидкости над плоскостью сравнения. Наша
жидкость, падая на плоскость ОО,
должна произвести
работу, равную GH_c.
Именно эту
работу будем называть собственной
потенциальной энергией объема жидкости,
заполняющей сосуд и находящейся только
в поле сил тяжести; обозначая ее через
(ЭП)_соб,
имеем:

(ЭП)_соб
= GH_c. (А)

Выше мы ввели
понятие потенциального напора H
и определили эту величину как меру
энергии, принадлежащей единице веса
жидкости. Следует подчеркнуть, что
исходя из понятия потенциального напора
недопустимо подсчитывать собственную
энергию покоящейся жидкости. Действительно,
если бы мы попытались это сделать, то
для величины (ЭП)_соб
получили бы неправильное выражение:

(ЭП)_соб
= GH
(. (Б)

Вопрос о потенциальном
напоре H
(о величине удельной потенциальной
энергии) надлежит понимать (в связи с
дальнейшим рассмотрением вопросов
гидродинамики; см., например, § 3-15 и §
9-4) следующим образом.¹

Рассматриваем
жидкость, находящуюся в сосуде А,
как некоторую
(в данном случае) неподвижную среду.
Намечаем в этой среде одну единицу веса
жидкости. При этом считаем, что данная
единица веса (рис. 2-13) заключена как бы
в невесомый контейнер, образованный
«стальными» невесомыми стенками,
изолирующими эту единицу веса от
окружающей жидкости. Далее представляем
себе, что данная единица веса жидкости
перемещается внутри упомянутой
неподвижной среды (например, от точки
m
до точки n).
При этом потенциальный напор H
(удельную потенциальную энергию) следует
понимать как меру энергии, принадлежащей
указанной единице веса жидкости,
перемещающейся в окружающей ее неподвижной
жидкой среде.

Покажем, что данная
движущаяся единица веса жидкости
действительно обладает (при определенных
поставленных условиях) потенциальной
энергией, равной (H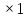
ед. веса). С этой целью прежде всего
обратим внимание на следующее существенное
обстоятельство.

Неподвижная среда
тяжелой жидкости, находящейся в сосуде
А,
обусловливает
существование скалярного поля давлений
(p/γ),
причем величина
=ƒ(x,y)
является
потенциальной функцией векторного
поля градиентов давления

J_p
=

Линии равного
потенциала
=const
показаны на рис. 2-13 пунктиром: первая
эквипотенциаль О
совпадает с
поверхностью жидкости, ее наименование
p/γ
= 0; последняя
(самая нижняя) эквипотенциаль 4′
должна совпадать
с дном сосуда, ее наименование будет
=h,
где h
– глубина воды
в сосуде.

Имея в виду
сказанное, заключаем, что намеченная
нами единица веса жидкости одновременно
перемещается в двух разных потенциальных
полях:

а) в векторном поле
сил тяжести, описываемом потенциальной
функцией z;

б) в поле векторов
J_p,
описываемом
потенциальной функцией p/γ.

Как видно, при
указанной постановке вопроса сама
тяжелая жидкость, находящаяся в сосуде
А,
интересует
нас только как «материал», создающий
неподвижное потенциальное поле,
описываемое функцией p/γ
(внутри которого перемещается выделенная
единица веса жидкости).

Легко видеть, что
работа данной единицы веса при перемещении
ее от точки т
до точки п
(см. рис. 2-13),
равняется:

1) за
счет движения ее только в потенциальном
поле сил тяжести величине

(z₇
–z₅)

ед. веса;

2) за
счет движения ее только в потенциальном
поле градиентов давления величине

(z₅
–z₇)

ед. веса,

где z₅
и z₇
– возвышение над плоскостью сравнения
соответственно точек п
и т.

Как видно, полная
работа данной единицы веса, перемещающейся
одновременно в двух потенциальных
полях,

(z₇
–z₅)
=
0,

а следовательно,
полная потенциальная энергия единицы
веса жидкости, находящейся в любой
точке, расположенной внутри сосуда,
одинакова и равна величине Н
(поскольку
этой величиной энергии, как видно из
рис. 2-13, обладают единицы веса жидкости,
расположенные, например, на свободной
поверхности жидкости).

Именно указанным
образом можно более точно разъяснить
вопрос о потенциальной энергии некоторого
объема покоящейся жидкости, который
одновременно находится в двух различных
векторных неподвижных силовых
потенциальных полях.

Данный вопрос
можно разъяснить еще и следующим образом.
Возьмем кубический метр жидкости,
заключенный в практически невесомый
прочный (например, стальной) контейнер,
имеющий кубическую форму. Далее представим
себе, что этот контейнер (заполненный
тяжелой жидкостью) перемещается в
воздухе (т. е. только в поле сил тяжести).
Очевидно, работа, выполненная этим
контейнером, определится разностью
наименований соответствующих линий
равного потенциала только поля сил
тяжести («начальной» и «конечной»
эквипотенциалей). После этого удалим
из нашего контейнера жидкость и тем
самым сделаем его невесомым. Этот пустой
невесомый контейнер будем мысленно
перемещать не в воздухе, а в окружающей
жидкости, т. е. только в векторном поле
градиентов J_p
давления.
Очевидно, за счет давления жидкости на
стенки пустого контейнера сверху и
снизу (т. е. за счет архимедовой силы,
имеющей свою потенциальную функцию в
виде p/γ)
мы получим ту
же работу, что и выше, когда мы мысленно
перемещали данный контейнер в воздухе
(в поле сил тяжести). Однако две эти
работы (работа
только в поле сил тяжести и работа только
в поле сил давления – архимедовых сил)
будут иметь разные знаки, причем сумма
этих работ будет равна нулю.

Как видно,
рассматривая вопрос о потенциальной
энергии одной единицы веса жидкости,
находящейся в сосуде А,
мы должны
представлять себе воображаемое
перемещение этой единицы веса в окружающей
ее жидкости, при этом мы должны учитывать,
что данная единица веса жидкости
одновременно перемещается в двух разных
силовых потенциальных полях:

1. в поле сил тяжести,
   описываемом приведенной потенциальной
   функцией, равной z,
   и

2. в поле архимедовой
   силы, описываемой приведенной
   потенциальной функцией, равной p/γ.

Очевидно, что
полная потенциальная энергия
рассматриваемой единицы веса, одновременно
находящейся в двух различных силовых
потенциальных полях, должна равняться
(относительно произвольно намеченной
плоскости сравнения ОО)
величине z
+=H.

Таким образом,
величина H
не есть удельная потенциальная энергия
жидкости (находящейся, например, в
некотором сосуде; см. рис. 2-13), подсчитанная
относительно принятой плоскости
сравнения ОО
в предположении,
что на жидкость действуют только силы
тяжести. Величина H
представляет собой отнесенную к единице
веса жидкости потенциальную функцию,
описывающую суммарное векторное силовое
поле, образованное силами тяжести и еще
«архимедовыми силами» (точнее говоря,
силами, выражаемыми градиентами давления
J_p;
см. выше).

Соседние файлы в папке Чугаев_1

• #
• #
• #
• #
• #
• #

Запрос «Абсолютная пустота» перенаправляется сюда; о книге Станислава Лема см. Абсолютная пустота (книга).

Ва́куум (от лат. vacuus — пустота) — пространство, свободное от вещества. В технике и прикладной физике под вакуумом понимают среду, состоящую из газа при давлении значительно ниже атмосферного^[1].

Вакуум характеризуется соотношением между длиной свободного пробега молекул газа λ и характерным размером среды d, так называемым числом Кнудсена . Под d может приниматься расстояние между стенками вакуумной камеры, диаметр вакуумного трубопровода и т. д. В зависимости от величины соотношения λ/d различают низкий (), средний () и высокий () вакуум.

Технический вакуум[править | править код]

На практике сильно разреженный газ называют техническим вакуумом. В макроскопических объёмах идеальный вакуум (среда, лишённая молекул газа) практически недостижим, поскольку при конечной температуре все материалы обладают ненулевой плотностью насыщенных паров. Кроме того, многие материалы (в частности толстые металлические, стеклянные и иные стенки сосудов) пропускают газы. В микроскопических объёмах, однако, достижение идеального вакуума в принципе возможно.

Мерой степени разрежения вакуума служит длина свободного пробега молекул газа , связанной с их взаимными столкновениями в газе, и характерного линейного размера сосуда, в котором находится газ.

Строго говоря, техническим вакуумом называют газ в сосуде или трубопроводе с давлением ниже, чем в окружающей атмосфере. Согласно другому определению, когда молекулы или атомы газа перестают сталкиваться друг с другом, и газодинамические свойства сменяются вязкостными (при давлении около 1 мм рт.ст.), говорят о достижении низкого вакуума (; 10¹⁶ молекул на 1 см³). Обычно между атмосферным воздухом и высоковакуумным насосом стоит так называемый форвакуумный насос, создавая предварительное разрежение, поэтому низкий вакуум часто называют форвакуум. При дальнейшем понижении давления в камере увеличивается средняя длина свободного пробега молекул газа. При молекулы газа гораздо чаще сталкиваются со стенками, чем друг с другом. В этом случае говорят о высоком вакууме (10⁻⁵ мм рт.ст.; 10¹¹ молекул на 1 см³). Сверхвысокий вакуум соответствует давлению 10⁻⁹ мм рт. ст. и ниже. В сверхвысоком вакууме, например, обычно проводятся эксперименты с использованием сканирующего туннельного микроскопа. Для сравнения, давление в космосе на несколько порядков ниже — 10⁹ молекул на 1 см³ (миллиард молекул в кубическом сантиметре), в дальнем же космосе и вовсе может достигать 10⁻¹⁶ мм рт.ст. и ниже (1 молекула на 1 см³)^[2].

Высокий вакуум в микроскопических порах некоторых кристаллов и в ультратонких капиллярах достигается уже при атмосферном давлении, поскольку диаметр поры/капилляра становится меньше, чем длина свободного пробега молекулы, равная в воздухе при нормальных условиях ~60 нанометрам^[3].

Аппараты, используемые для достижения и поддержания вакуума, называются вакуумными насосами. Для поглощения газов и создания необходимой степени вакуума используются геттеры. Более широкий термин вакуумная техника включает также приборы для измерения и контроля вакуума, манипулирования предметами и проведения технологических операций в вакуумной камере и т. д. Высоковакуумные насосы являются сложными техническими приборами. Основные типы высоковакуумных насосов — это диффузионные насосы, основанные на увлечении молекул остаточных газов потоком рабочего газа, геттерные, ионизационные насосы, основанные на внедрении молекул газа в геттеры (например, титан) и криосорбционные насосы (в основном, для создания форвакуума).

Даже в идеальном вакууме при конечной температуре всегда имеется некоторое тепловое излучение (газ фотонов). Таким образом, тело, помещённое в идеальный вакуум, рано или поздно придёт в тепловое равновесие со стенками вакуумной камеры за счёт обмена тепловыми фотонами.

Вакуум является хорошим термоизолятором; перенос тепловой энергии в нём происходит лишь за счёт теплового излучения, конвекция и теплопроводность исключены. Это свойство используется для теплоизоляции в термосах (сосудах Дьюара), состоящих из ёмкости с двойными стенками, пространство между которыми вакуумировано.

Вакуум широко применяется в электровакуумных приборах — радиолампах (например, магнетронах микроволновых печей), электронно-лучевых трубках и т. п.

Физический вакуум[править | править код]

Вакуум квантовой теории поля[править | править код]

Под физическим вакуумом в квантовой физике понимают низшее (основное) энергетическое состояние квантованного поля, обладающее нулевыми импульсом, моментом импульса и другими квантовыми числами. При этом такое состояние вовсе не обязательно соответствует пустоте: поле в низшем состоянии может быть, например, полем квазичастиц в твёрдом теле или даже в ядре атома, где плотность чрезвычайно высока. Физическим вакуумом называют также полностью лишённое вещества пространство, заполненное полем в таком состоянии^[4][5]. Такое состояние не является абсолютной пустотой. Квантовая теория поля утверждает, что, в согласии с принципом неопределённости, в физическом вакууме постоянно рождаются и исчезают виртуальные частицы: происходят так называемые нулевые колебания полей. В некоторых конкретных теориях поля вакуум может обладать нетривиальными топологическими свойствами. В теории могут существовать несколько различных вакуумов, различающихся плотностью энергии или другими физическими параметрами (в зависимости от применяемых гипотез и теорий). Вырождение вакуума при спонтанном нарушении симметрии приводит к существованию непрерывного спектра вакуумных состояний, отличающихся друг от друга числом голдстоуновских бозонов. Локальные минимумы энергии при разных значениях какого-либо поля, отличающиеся по энергии от глобального минимума, носят название ложных вакуумов; такие состояния метастабильны и стремятся распасться с выделением энергии, перейдя в истинный вакуум или в один из нижележащих ложных вакуумов.

Некоторые из этих предсказаний теории поля уже были успешно подтверждены экспериментом. Так, эффект Казимира^[6] и лэмбовский сдвиг атомных уровней объясняется нулевыми колебаниями электромагнитного поля в физическом вакууме. На некоторых других представлениях о вакууме базируются современные физические теории. Например, существование нескольких вакуумных состояний (упомянутых выше ложных вакуумов) является одной из главных основ инфляционной теории Большого взрыва.

Ложный вакуум[править | править код]

Ложный вакуум — состояние в квантовой теории поля, которое не является состоянием с глобально минимальной энергией, а соответствует её локальному минимуму. Такое состояние стабильно в течение определённого времени (метастабильно), но может «туннелировать» в состояние истинного вакуума.

Эйнштейновский вакуум[править | править код]

Эйнштейновский вакуум — иногда встречающееся название для решений уравнений Эйнштейна в общей теории относительности для пустого, без материи, пространства-времени. Синоним — пространство Эйнштейна.

Уравнения Эйнштейна связывают метрику пространства-времени (метрический тензор g_μν) с тензором энергии-импульса. В общем виде они записываются как

где тензор Эйнштейна G_μν является определённой функцией метрического тензора и его частных производных, R — скалярная кривизна, Λ — космологическая постоянная, T_μν — тензор энергии-импульса материи, π — число пи, c — скорость света в вакууме, G — гравитационная постоянная Ньютона.

Вакуумные решения этих уравнений получаются при отсутствии материи, то есть при тождественном равенстве нулю тензора энергии-импульса в рассматриваемой области пространства-времени: T_μν = 0. Часто лямбда-член также принимается равным нулю, особенно при исследовании локальных (некосмологических) решений. Однако при рассмотрении вакуумных решений с ненулевым лямбда-членом (лямбда-вакуум) возникают такие важные космологические модели, как модель Де Ситтера (Λ > 0) и модель анти-Де Ситтера (Λ < 0).

Тривиальным вакуумным решением уравнений Эйнштейна является плоское пространство Минковского, то есть метрика, рассматриваемая в специальной теории относительности.

Другие вакуумные решения уравнений Эйнштейна включают в себя, в частности, следующие случаи:

• Космологическая модель Милна (частный случай метрики Фридмана с нулевой плотностью энергии)
• Метрика Шварцшильда, описывающая геометрию вокруг сферически симметричной массы
• Метрика Керра, описывающая геометрию вокруг вращающейся массы
• Плоская гравитационная волна (и другие волновые решения)

Космическое пространство[править | править код]

Космическое пространство имеет очень низкую плотность и давление и является наилучшим приближением физического вакуума. Космический вакуум не является действительно совершенным, даже в межзвёздном пространстве есть несколько атомов водорода на кубический сантиметр. Плотность ионизированного атомарного водорода в межгалактическом пространстве Местной группы оценивается в 7×10⁻²⁹ г/см³^[7].

Звёзды, планеты и спутники держат свои атмосферы силой притяжения, и как таковой у атмосферы нет чётко очерченной границы: плотность атмосферного газа просто уменьшается с расстоянием от объекта. Атмосферное давление Земли падает до примерно 3,2×10⁻² Па на 100 км высоты — на так называемой линии Кармана, которая является общим определением границы с космическим пространством. За этой линией изотропное давление газа быстро становится незначительным по сравнению с давлением излучения от Солнца и динамическим давлением солнечного ветра, поэтому определение давления становится трудно интерпретировать. Термосфера в этом диапазоне имеет большие градиенты давления, температуры и состава, и сильно варьируется в связи с космической погодой.

Плотность атмосферы в течение первых нескольких сотен километров выше линии Кармана всё ещё достаточна для оказания значительного сопротивления движению искусственных спутников Земли. Большинство спутников работают в этой области, называемой низкой околоземной орбитой, и должны подрабатывать двигателями каждые несколько дней для поддержания стабильной орбиты.

Космическое пространство заполнено большим количеством фотонов, так называемым реликтовым излучением, а также большим количеством реликтовых нейтрино, пока не поддающихся обнаружению. Текущая температура этих излучений составляет около 3 К, или −270 °C^[8].

История изучения вакуума[править | править код]

Идея вакуума (пустоты) была предметом споров ещё со времён древнегреческих и древнеримских философов. Атомисты — Левкипп (ок. 500 г. до н. э.), Демокрит (около 460—370 гг. до н. э.), Эпикур (341—270 гг. до н. э.), Лукреций (ок. 99—55 гг. до н. э.) и их последователи — предполагали, что всё существующее — атомы и пустота между ними, причём без вакуума не было бы и движения, атомы не могли бы двигаться, если бы между ними не было пустого пространства. Стратон (ок. 270 г. до н. э.) и многие философы в более поздние времена полагали, что пустота может быть «сплошной» (vacuum coacervatum) и «рассеянной» (в промежутках между частицами вещества, vacuum disseminatum).

Напротив, Аристотель (384—322 гг. до н. э.) и ряд других философов считали, что «природа не терпит пустоты». Концепция «боязни пустоты» (horror vacui), зародившаяся ещё до Аристотеля, у Эмпедокла (ок. 490—430 гг. до н. э.) и других философов ионийской школы, в философской мысли Средневековой Европы стала доминирующей и приобрела религиозно-мистические черты.

Некоторые предпосылки к эмпирическому исследованию вакуума существовали ещё в античности. Древнегреческие механики создавали различные технические устройства, основанные на разрежении воздуха. Например, водяные насосы, действующие путём создания разрежения под поршнем, были известны ещё во времена Аристотеля. До нашего времени сохранился рисунок пожарного насоса, изобретённого «отцом пневматики» Ктезибием (ок. 250 г. до н. э.). Водяные насосы такого типа были фактически прообразами вакуумного поршневого насоса, появившегося спустя почти два тысячелетия. Ученик Ктезибия, Герон Александрийский, разработал поршневой шприц для вытягивания гноя, тоже являющийся по существу вакуумным устройством.

Эмпирическое изучение вакуума началось лишь в XVII веке, с концом Возрождения и началом научной революции Нового времени. К этому моменту уже давно было известно, что всасывающие насосы могут поднимать воду на высоту не более 10 метров. Например, в трактате Георгия Агриколы (1494—1555) «О горном деле» приведено изображение цепочки водяных насосов для откачки воды из шахты.

Галилей в своих «Беседах и математических доказательствах двух новых наук»^[9] (1638), книге, которая завершила разгром аристотелевской физики, указывал, ссылаясь на практику, что высота, до которой всасывающие насосы поднимают воду, всегда одна и та же — около 18 локтей. В этой книге он, в частности, описывает фактически вакуумный прибор с поршнем, необходимый для сравнения сопротивления на разрыв воды и твёрдого тела, хотя и объясняет сопротивление растяжению, характерное для твёрдых тел и жидкостей, боязнью пустоты, предполагая существование между частицами вещества мельчайших пустых пор, расширяющихся при растяжении.

Под влиянием трактата Галилея, где указывалось на ограниченность «боязни пустоты», в 1639—1643 гг. Гаспаро Берти на фасаде своего дома в Риме соорудил устройство (в более поздней терминологии, барометрическую водяную трубу), которое можно считать первой установкой для физического исследования вакуума. В верхней, стеклянной закрытой части трубы высотой более 10 м, над водяным столбом, уравновешенным атмосферным давлением, обнаруживалось пустое пространство (на самом деле оно было заполнено водяными парами под давлением, равным упругости паров воды при температуре окружающей среды, а также выделившимся из воды растворённым воздухом, то есть давление в полости составляло около 0,1 атмосферы). Эмануэль Маньяно закрепил в этой полости колокольчик и молоток. Воздействуя на молоток магнитом, он ударял молотком по колокольчику. В результате этого первого в истории эксперимента в вакууме (точнее, в разреженном газе) было обнаружено, что звук колокольчика был приглушённым^[10].

Учёный Рафаэло Маджотти^[11] (1597—1656) из Рима сообщил об опытах Берти и Маньяно ученику Галилея, флорентийцу Эванджелисте Торричелли. При этом Маджотти высказал мысль, что более плотная жидкость остановилась бы на более низком уровне^[12]. В 1644 году Торричелли (с помощью Винченцо Вивиани, другого ученика Галилея) сумел создать первую вакуумную камеру. Его работы, связанные с теориями атмосферного давления, послужили основой дополнительных экспериментальных методик. Вакуум по методу Торричелли (торричеллиева пустота) достигается путём наполнения ртутью длинной стеклянной трубки, запаянной с одного конца, а затем переворачиванием её таким образом, чтобы открытый конец трубки оказался под поверхностью ртути в более широком открытом сосуде^[13]. Ртуть будет вытекать из трубки, пока сила тяжести ртутного столба не будет скомпенсирована атмосферным давлением. В свободном от ртути пространстве в верхнем, запаянном конце трубки образуется вакуум. Этот метод лежит в основе работы ртутного барометра. При стандартном атмосферном давлении высота ртутного столба, уравновешенного атмосферным давлением, равна 760 мм.

Около 1650 года немецкий учёный Отто фон Герике изобрёл первый вакуумный насос (поршневой цилиндр с водяным уплотнением), позволивший легко откачивать воздух из герметичных ёмкостей и экспериментировать с вакуумом^[14]. Насос, названный автором antlia pneumatica, был ещё очень далек от совершенства и требовал не менее трёх человек для манипуляций с поршнем и кранами, погруженными в воду, для лучшей изоляции образующейся пустоты от наружного воздуха. Однако с его помощью Герике сумел продемонстрировать многие свойства вакуума, в частности, поставив знаменитый опыт с Магдебургскими полушариями. Герике создал также водяной барометр, по принципу действия аналогичный ртутному барометру Торричелли, хотя из-за меньшей плотности воды по сравнению с ртутью высота водяного столба, уравновешивающего атмосферное давление, в 13,6 раз больше — около 10 метров. Герике впервые выяснил, что вакуум не проводит звук и что горение в нём прекращается^[15].

Вакуумный насос Герике был значительно усовершенствован Робертом Бойлем, что позволило ему выполнить ряд экспериментов для выяснения свойств вакуума и его влияния на различные объекты. Бойль обнаружил, что в вакууме гибнут мелкие животные, огонь потухает, а дым опускается вниз (и, следовательно, так же подвержен влиянию силы тяжести, как и другие тела). Бойль выяснил также, что поднятие жидкости в капиллярах происходит и в вакууме, и тем самым опроверг господствовавшее тогда мнение, что в этом явлении участвует давление воздуха. Напротив, перетекание жидкости через сифон в вакууме прекращалось, чем было доказано, что это явление обусловлено атмосферным давлением. Он показал, что при химических реакциях (таких, как гашение извести), а также при взаимном трении тел тепло выделяется и в вакууме.

Влияние на людей и животных[править | править код]

Люди и животные, подвергшиеся воздействию вакуума, теряют сознание через несколько секунд и умирают от гипоксии в течение нескольких минут, но эти симптомы, как правило, не похожи на те, которые показывают в популярной культуре и СМИ. Снижение давления понижает температуру кипения, при которой кровь и другие биологические жидкости должны закипеть, но упругое давление кровеносных сосудов не позволяет крови достичь температуры кипения 37 °С^[16]. Хотя кровь не вскипает, эффект образования газовых пузырьков в ней и других жидкостях тела при низких давлениях, известный как эбуллизм (воздушная эмфизема), является серьёзной проблемой. Газ может раздувать тело в два раза больше его нормального размера, но ткани достаточно эластичны, чтобы предотвратить их разрыв^[17]. Отёки и эбуллизм можно предотвратить специальным лётным костюмом. Астронавты шаттлов носили специальную эластичную одежду под названием Crew Altitude Protection Suit (CAPS), которая предотвращает эбуллизм при давлении более 2 кПа (15 мм рт.ст.)^[18]. Быстрое испарение воды охлаждает кожу и слизистые оболочки до 0 °С, особенно во рту, но это не представляет большой опасности.

Эксперименты на животных показывают, что после 90 секунд нахождения организма в вакууме обычно происходит быстрое и полное восстановление организма, однако более долгое пребывание в вакууме фатально и реанимация бесполезна^[19]. Имеется лишь ограниченный объем данных о влиянии вакуума на человека (как правило, это происходило при попадании людей в аварию), но они согласуются с данными, полученными в экспериментах на животных. Конечности могут находиться в вакууме гораздо дольше, если дыхание не нарушено^[20]. Роберт Бойль в 1660 году первым показал, что вакуум смертелен для мелких животных.

Измерение[править | править код]

Степень вакуума определяется количеством вещества, оставшимся в системе. Вакуум, в первую очередь, определяется абсолютным давлением, а полная характеристика требует дополнительных параметров, таких как температура и химический состав. Одним из наиболее важных параметров является средняя длина свободного пробега (MFP) остаточных газов, которая указывает среднее расстояние, которое частица пролетает за время свободного пробега от одного столкновения до следующего. Если плотность газа уменьшается, MFP увеличивается. MFP в воздухе при атмосферном давлении очень короткий, около 70 нм, а при 100 мПа (~1×10⁻³ торр) MFP воздуха составляет примерно 100 мм. Свойства разреженного газа сильно изменяются, когда длина свободного пробега становится сравнима с размерами сосуда, в котором находится газ.

Вакуум подразделяется на диапазоны в соответствии с технологией, необходимой для его достижения или измерения. Эти диапазоны не имеют общепризнанных определений, но типичное распределение выглядит следующим образом^[21][22]:

	Давление (мм рт.ст.)	Давление (Па)
Атмосферное давление	760	1,013×10+5
Низкий вакуум	от 760 до 25	от 1×10+5 до 3,3×10+3
Средний вакуум	от 25 до 1×10−3	от 3,3×10+3 до 1,3×10−1
Высокий вакуум	от 1×10−3 до 1×10−9	от 1,3×10−1 до 1,3×10−7
Сверхвысокий вакуум	от 1×10−9 до 1×10−12	от 1,3×10−7 до 1,3×10−10
Экстремальный вакуум	<1×10−12	<1,3×10−10
Космическое пространство	от 1×10−6 до <3×10−17	от 1,3×10−4 до <1,3×10−15
Абсолютный вакуум	0	0

Применение[править | править код]

Вакуум полезен для многих процессов и применяется в разных устройствах. Впервые для массово используемых товаров он был применён в лампах накаливания с целью защиты нити от химического разложения. Химическая инертность материалов, обеспечиваемая вакуумом, также полезна для электронно-лучевой сварки, холодной сварки, вакуумной упаковки и вакуумной жарки. Сверхвысокий вакуум используется при изучении атомарно чистых субстратов, так как только очень высокий вакуум сохраняет поверхности чистыми на атомарном уровне в течение достаточно длительного времени (от минут до суток). При высоком и сверхвысоком вакуумировании устраняется противодействие воздуха, позволяя пучкам частиц осаждать или удалять материалы без загрязнения. Этот принцип лежит в основе химического осаждения из газовой фазы, вакуумного напыления и сухого травления, которые применяются в производстве полупроводников и оптических покрытий, а также в химии поверхности. Снижение конвекции обеспечивает теплоизоляцию в термосах. Глубокий вакуум понижает температуру кипения жидкости и способствует низкой температуре дегазации, которая используется в сублимационной сушке, приготовлении клея, перегонке, металлургии и вакуумной очистке. Электрические свойства вакуума делают возможными электронные микроскопы и вакуумные трубки, включая катодные лучевые трубки. Вакуумные выключатели используются в электрических распределительных устройствах. Вакуумный пробой имеет промышленное значение для производства определенных марок стали или материалов высокой чистоты. Исключение трения воздуха полезно для накопления энергии маховика и ультрацентрифуг.

Управляемые вакуумом машины[править | править код]

Вакуум обычно используется, чтобы произвести всасывание, которое имеет ещё более широкий спектр применения. Паровой двигатель Ньюкомена использовал вакуум вместо давления, чтобы управлять поршнем. В XIX веке вакуум был использован для тяги на экспериментальной пневматической железной дороге Изамбарда Брунеля. Вакуумные тормоза когда-то широко использовались на поездах в Великобритании, но, за исключением исторических железных дорог, они были заменены пневматическими тормозами.

Вакуум впускного коллектора можно использовать для того, чтобы управлять вспомогательным оборудованием на автомобилях. Наиболее известное применение – это вакуумный усилитель для увеличения мощности тормозов. Ранее вакуум применялся в вакуум-приводах стеклоочистителя и топливных насосах Autovac. Некоторые авиационные приборы (авиагоризонт и указатель курса) обычно управляются вакуумом, как страховка от выхода из строя всех (электрических) приборов, поскольку ранние самолеты часто не имели электрических систем, и поскольку есть два легкодоступных источников вакуума на движущемся самолете, двигатель и трубка Вентури. При вакуумноиндукционной плавке применяют электромагнитную индукцию в вакууме.

Поддержание вакуума в конденсаторе важно для эффективной работы паровых турбин. Для этого используется паровой инжектор или водокольцевой насос. Обычный вакуум, поддерживаемый в паровом объёме конденсатора на выхлопном патрубке турбины (еще его называют давление конденсатора турбины), находится в диапазоне от 5 до 15 кПа, в зависимости от типа конденсатора и условий окружающей среды.

Дегазация[править | править код]

Испарение и сублимация в вакууме называется дегазацией. Все материалы, твердые или жидкие, немного парят (происходит газовыделение), и их дегазация необходима, когда давление вакуума падает ниже давления их пара. Парение материалов в вакууме имеет такой же эффект, как натекание, и может ограничить достижимый вакуум. Продукты испарения могут конденсироваться на близлежащих более холодных поверхностях, что может вызвать проблемы, если они покроют оптические приборы или вступят в реакцию с другими материалами. Это вызывает большие трудности при полётах в космосе, где затемненный телескоп или элемент солнечной батареи может сорвать высокозатратную операцию.

Самым распространенным выделяющимся продуктом в вакуумных системах является вода, поглощённая материалами камер. Её количество может быть уменьшено сушкой или прогревом камеры и удалением абсорбирующих материалов. Испаряющаяся вода может конденсироваться в масле пластинчато-роторных насосов и резко уменьшить их рабочую скорость, если не используется газобалластное устройство. Высоковакуумные системы должны быть чистыми, в них не должно оставаться органических веществ, чтобы свести к минимуму газовыделение.

Сверхвысокие вакуумные системы, как правило, отжигаются, желательно под вакуумом, чтобы временно повысить испарение всех материалов и выпарить их. После того, как большая часть испаряющихся материалов выпарена и удалена, система может быть охлаждена для уменьшения парения материалов и минимизации остаточного газовыделения во время эксплуатации. Некоторые системы охлаждают существенно ниже комнатной температуры с помощью жидкого азота для полного прекращения остаточного газовыделения и одновременно создания эффекта криогенной откачки системы.

Откачка и атмосферное давление[править | править код]

Газы вообще нельзя вытолкнуть, поэтому вакуум не может быть создан всасыванием. Всасывание может распространить и разбавить вакуум, позволяя высокому давлению вводить в него газы, но, прежде чем всасывание может произойти, необходимо вакуум создать. Самый простой способ создать искусственный вакуум — расширить объём камеры. Например, мышца диафрагмы расширяет грудную полость, что приводит к увеличению объёма легких. Это расширение уменьшает давление и создает низкий вакуум, который вскоре заполняется воздухом, нагнетаемым атмосферным давлением.

Чтобы продолжать опустошение камеры бесконечно, не используя постоянно её увеличение, вакуумирующий её отсек может быть закрыт, продут, расширен снова, и так много раз. Это принцип работы насосов с принудительным вытеснением (газопереносных), например, ручной водяной насос. Внутри насоса механизм расширяет небольшую герметичную полость для создания вакуума. Из-за перепада давления часть жидкости из камеры (или колодца, в нашем примере) вталкивается в маленькую полость насоса. Затем полость насоса герметично закрывается от камеры, открывается в атмосферу и сжимается до минимального размера, выталкивая жидкость.

Приведенное выше объяснение представляет собой простое введение в вакуумирование и не является типичным для всего диапазона используемых насосов. Разработаны много вариаций насосов с принудительным вытеснением, и множество конструкций насосов основаны на радикально других принципах. Насосы передачи импульса, которые имеют некоторое сходство с динамическими насосами, используемыми при более высоких давлениях, могут обеспечить намного более высокое качество вакуума, чем насосы с принудительным вытеснением. Газосвязывающие насосы, способные захватывать газы в твердом или поглощенном состоянии, работают часто без движущихся частей, без уплотнений и без вибрации. Ни один из этих насосов не является универсальным; каждый тип имеет серьёзные ограничения применения. У всех есть трудности с откачкой газов с малой массой молекул, особенно водорода, гелия и неона.

Самое низкое давление, которое может быть достигнуто в системе, кроме устройства насосов, также зависит от многих факторов. Несколько насосов могут быть соединены последовательно в так называемые ступени для достижения более высокого вакуума. Выбор уплотнений, геометрии камеры, материалов и процедур откачки — всё будет иметь эффект. В совокупности всё это называют вакуумной техникой. И иногда, итоговое давление — не единственная существенная характеристика. Насосные системы отличаются масляным загрязнением, вибрацией, избирательной откачкой определенных газов, скоростями откачки, прерывистостью эксплуатации, надежностью или устойчивостью к высоким скоростям натекания.

В системах со сверхвысоким вакуумом необходимо учитывать некоторые очень «странные» пути натекания и источники парения. Неприемлемым источником испарений становится способность к водопоглощению алюминия и палладия, приходится учитывать даже адсорбционную способность твердых металлов, таких как нержавеющая сталь или титан. Некоторые масла и смазки будут кипеть при высоком вакууме. Возможно, придется учитывать влияние кристаллической структуры металла на проницаемость металлических стенок камер, например, параллельность направления зёрен металлических фланцев торцу фланца.

Самые низкие давления, которые в настоящее время достижимы в лабораторных условиях, составляют около 10^-13 торр (13 пПа). Однако, давления ниже, чем 5×10^-17 торр (6,7 фПа) были косвенно измеряемы криогенной вакуумной системе. Это соответствует ≈100 частиц / см³.

См. также[править | править код]

Применения

• Вакуумная формовка
• Электровакуумные приборы (электронные лампы, кинескопы, магнетроны, фотоумножители и т. д.)

Примечания[править | править код]

Литература[править | править код]

• Борисов В.П. Вакуум: от натурфилософии до диффузионного насоса. — М.: НПК «Интелвак», 2001.
• Научные основы вакуумной техники. — М., 1964.
• Грошковский Я. Техника высокого вакуума. — М., 1975.
• Основы вакуумной техники. 2-е изд. — М., 1981.
• Розанов Л. И. Вакуумная техника. 2-е изд. — М., 1990.
• L. B. Okun. On the concepts of vacuum and mass and the search for higgs (англ.) // Modern Physics Letters A. — 2012. — Vol. 27. — P. 1230041. — doi:10.1142/S0217732312300418. — arXiv:1212.1031.
• Крамер Д. и др. Точные решения уравнений Эйнштейна. М.: Мир, 1982. — 416 с.
• Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
• Паули В. Теория относительности. М.: Наука, 1991
• Гриб А. А. Проблема неинвариантности вакуума в квантовой теории поля. М.: Атомиздат, 1978

Вакуум в насадке. Для определения величины вакуума в сжатом сечении насадка запишем
уравнение Бернулли, связывающее это сечение с выходным сечением:

,

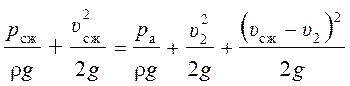где 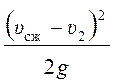 – потери напора на внезапное расширение струи.

Далее
получаем

,

.

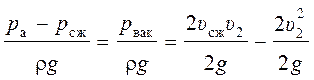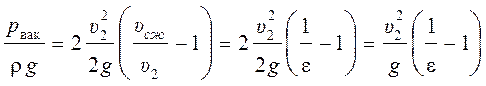Заменив скорость  ее
выражением через коэффициент скорости насадка, т. е. , получим

.

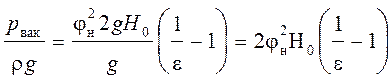Обозначив

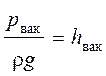
и подставив 0,82; 0,64, получим

.

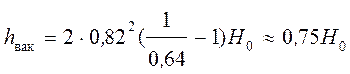При некотором критическом напоре
 абсолютное
давление внутри насадка в сжатом сечении (p_сж) становится равным нулю, и поэтому при истечении воды
в атмосферу

.

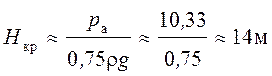При H> H_кр давление  должно бы стать отрицательным, но отрицательных
давлений в жидкости из условия отсутствия разрыва сплошности не бывает.
Поэтому, при  (рис.
7.5, б) происходит внезапное изменение режима истечения, а именно, при вакууме
более 10 м водного столба начинается засасывание воздуха в насадок через выходное
отверстие, струя отрывается от стенки насадка, вакуум исчезает. Струя после
сжатия уже не расширяется, а пролетает внутри насадка, не соприкасаясь с его
стенками. Истечение становится точно таким же, как и из отверстия в тонкой
стенке с теми же значениями коэффициентов истечения. Насадок теряет свои преимущества в пропускной способности по сравнению
с отверстием.

Относительная длина насадка. Все сказанное в отношении наружного цилиндрического
насадка справедливо лишь для случая, когда l/d / 3…4 ¸ 6…7.

При меньших значениях l/d
вихревая зона соединяется с атмосферой, вакуум не создается и струя вытекает
как из отверстия. При увеличении длины насадка начинают играть роль потери напора
на трение, в результате чего коэффициент расхода насадка уменьшается. При l/d > 60 расход через
насадок будет меньше, чем расход через отверстие.

Внутренний цилиндрический
насадок.

Цилиндрический
насадок, установленный с внутренней стороны, называется внутренним
цилиндрическим насадком (рис. 7.6). Струя на входе во внутренний цилиндрический насадок (рис.
7.6, а) испытывает большeе сжатие, чем в наружном насадке, поэтому коэффициенты
скорости и расхода здесь меньше, чем в наружном цилиндрическом насадке.
Внутренний насадок характеризуется следующими коэффициентами:

, , .

При малой длине внутреннего
насадка (l < 3d) (рис. 7.6, б) струя вытекает из него, не касаясь стенок. При
этом коэффициенты расхода, скорости, сжатия и сопротивления имеют следующие
значения: , , , . Таким образом, цилиндрический насадок обладает существенными
недостатками: на первом режиме – сопротивление и недостаточно высокий
коэффициент расхода, а на втором – очень низкий коэффициент расхода.

Цилиндрический насадок может быть
значительно улучшен путем закругления входной кромки.

Коноидальный насадок. Насадок имеет сложную форму (рис. 7.7). Выходной участок –
цилиндрической формы, а вход выполняется по профилю свободно вытекающей через
отверстие струи. Благодаря этому обеспечивается безотрывность течения внутри
насадка, сжатие струи отсутствует (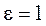). Он имеет коэффициенты
расхода и скорости, близкие к единице (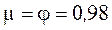), и
очень малые потери (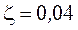), а также устойчивый режим
истечения без кавитации.

На практике коноидальные насадки
применяют сравнительно редко из-за большой трудоемкости их изготовления; вместо
них обычно используют конически сходящиеся насадки.

Конический сходящийся
насадок. Насадок, имеющий форму усеченного
конуса, сходящегося по направлению к выходному отверстию, называется
коническим сходящимся насадком (рис. 7.8).

В случае конического сходящегося насадка
сжатие струи на входе меньше, чем в наружном цилиндрическом, но зато появляется
внешнее сжатие на выходе из насадка, после чего жидкость течет параллельными
струйками. Вследствие меньшего внутреннего сжатия потери напора в этом насадке
меньше, чем во внешнем цилиндрическом, а скорость больше.

Коэффициенты μ, φ, ε и  зависят от
угла конусности .
Коэффициент расхода достигает максимального значения, равного  при .
Коэффициент скорости для этого случая равен  Сжатие струи при выходе из насадка оценивается
коэффициентом  Потери
малы, так как S_с примерно
равна площади S на выходе из насадка  Значения коэффициентов истечения отнесены к выходному
сечению насадка.

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание – внизу страницы.

По определению вакуум – это пространство свободное от вещества. В технике и прикладной физике под вакуумом понимают среду, содержащую газ при давлении значительно ниже атмосферного.

Рассмотрим для наглядности на примере, что такое вакуум и как его измеряют.

На нашей планете существует атмосферное давление, принятое за единицу (одна атмосфера). Оно меняется в зависимости от погода, от высоты над уровнем моря и так далее, но это мы не будем принимать во внимание, так как оно ни как не будет влиять на понятие вакуум в нашем случае. Итак, мы имеем давление на поверхности земли равное 1 атмосфере, все, что ниже 1 атмосферы и будет техническим вакуумом.

Возьмем какой нибудь сосуд и закроем его герметичной крышкой. Давление в сосуде будет равно 1 атмосфере. Если мы начнем откачивать из сосуда воздух, то в нем возникнет разряжение, которое и будет называться вакуумом. 

На картинке условно изображено 3 сосуда, в левом сосуде 10 кружочков, пусть это будет равно 1 атмосфере. Откачаем половину получим 0,5 атмосфер, откачаем еще – получим 0,1 атмосферу (это 3 сосуд, один кружочек).

Так как в сосуде всего одна атмосфера, то теоритически максимальный вакуум мы можем получить ноль атмосфер. Почему теоритически? Потому, что абсолютно все молекулы из сосуда выловить невозможно.

Поэтому в любом сосуде, в котором откачали воздух (газ) всегда остается какое то минимальное его количество. И это количество называется остаточным давлением, т.е. давление которое осталось в сосуде после откачки из него газов.

Существуют специальные насосы, которые могут достичь глубокого вакуума до 0,00001 Па, но все равно не до нуля.

В обычной жизни редко требуется вакуум ниже 0,5 – 10 Па (0,0005 – 0,0001 атм.).

Есть несколько вариантов измерения вакуума, которые зависят от выбора точки отсчета.

1. За единицу принимается атмосферное давление, т.е. все, что ниже атмосферного давления технический вакуум. Шкала вакууметра от 1,0 атм. до 0 атм.

2. За ноль принимается атмосферное давление. Т.е. вакуум все отрицательные число от 0 и до -1. Шкала вакууметра от 0 и до -1.

Так шкалы могут быть в других единицах измерения, к примеру кПа, mBar и так далее, но все это аналогично шкалам в атмосферах. Но мы рекомендуем приобретать вакууметры все атки со шкалой кПа (Па), так как это соответствует международнйо системе измерения СИ.

На картинке показаны вакууметры с различными шкалами, но с одинаковым вакуумом.

Из всего сказанного выше видно, что величина вакуума не может быть больше атмосферного давления.

К нам почти каждый день обращаются люди, которые хотят получить вакуум -2, -3 атм и т.д.

И они очень удивляются когда узнают, что это невозможно (кстати, каждый второй из них говорит, что “вы сами ничего не знаете”, “а у соседа так” и т.д. и.т.п.)

На самом деле, все эти люди хотят формовать детали под вакуумом, но чтобы прижим детали был более 1 кг/см2 (1 атмосферы).

Этого можно достичь, если накрыть изделие плёнкой, откачать из под неё воздух (в этом случае, в зависимости от созданного вакуума, максимальный прижим составит 1 кг/см2 (1 атм=1 кг/см2)), и после этого поместить это всё в автоклав, в котором будет создано избыточное давление. То есть для создания прижима в 2 кг/см2, достаточно создать в автоклаве избыточное давление в 1 атм.

Теперь несколько слов о том, как многие клиенты измеряют вакуум:

включают насос, прикладывают палец (ладонь) к всасывающему отверстию вакуумного насоса и сразу делают вывод о величине вакуума.

Обычно, все очень любят сравнивать советский вакуумный насос 2НВР-5ДМ и предлагаемый нами его аналог VE-2100.

После такой проверки, всегда говорят одно и тоже – вакуум у 2НВР-5ДМ выше (хотя на самом деле оба насоса выдают одинаковые параметры по вакууму).

В чем же причина такой реакции? А как всегда – в отсутствии знаний законов физики и что такое давление вообще.

Немного ликбеза: давление «P» – это сила, которая действует на некоторую площадь поверхности, направленная перпендикулярно этой поверхности (отношение силы «F» к площади поверхности «S»), то есть P=F/S.

По-простому – это сила, распределённая по площади поверхности.

Из этой формулы видно, что чем больше площадь поверхности, тем меньше будет давление. А также сила, которая потребуется для отрыва руки или пальца от входного отверстия насоса, прямо пропорциональна величине площади поверхности (F=P*S).

Диаметр всасывающего отверстия у вакуумного насоса 2НВР-5ДМ – 25 мм (площадь поверхности 78,5 мм2).

Диаметр всасывающего отверстия у вакуумного насоса VE-2100 – 6 мм (площадь поверхности 18,8 мм2).

То есть для отрыва руки от отверстия диаметром 25 мм, требуется сила в 4,2 раза большая, чем для диаметра отверстия 6 мм (при одинаковом давлении).

Именно по этому, когда вакуум измеряют пальцами, получается такой парадокс.

Давление «P», в этом случае, рассчитывается как разница между атмосферным давлением и остаточным давлением в сосуде (то есть вакуумом в насосе).

Как посчитать силу прижима какой-либо детали к поверхности?

Очень просто. Можно воспользоваться формулой приведенной выше, но попробуем объяснить попроще.

Например, пусть требуется узнать, с какой силой может быть прижата деталь размером 10х10 см при создании под ней вакуума насосом ВВН 1-0,75.

Берём остаточное давление, которое создаёт этот вакуумный насос серии ВВН.

Конкретно у этого водокольцевого насоса ВВН 1-0,75 оно составляет 0,4 атм.

1 атмосфера равна 1 кг/см2.

Площадь поверхности детали – 100 см2 (10см х10 см).

То есть, если создать максимальный вакуум (то есть давление на деталь будет 1 атм), то деталь прижмётся с силой 100 кг.

Так как у нас вакуум 0,4 атм, то прижим составит 0,4х100=40 кг.

Но это в теории, при идеальных условиях, если не будет подсоса воздуха и т.п.

Реально нужно это учитывать и прижим будет на 20…40% меньше в зависимости от типа поверхности, скорости откачки, и т.п.

Теперь пару слов о механических вакуумметрах.

Эти устройства показывают остаточное давление в пределах 0,05…1 атм.

То есть он не покажет более глубокого вакуума (будет всегда показывать «0»). Например, в любом пластинчато-роторном вакуумном насосе, по достижении его максимального вакуума, механический вакуумметр всегда будет показывать «0». Если требуется визуальное отображение значений остаточного давления, то нужно ставить электронный вакуумметр.

Часто к нам приходят клиенты, которые формуют детали под вакуумом (например, детали из композиционных материалов: углепластика, стеклопластика и т.п.), это нужно для того, чтобы во время формовки из связующего вещества (смолы) выходил газ и тем самым улучшались свойства готового продукта, а так же деталь прижималась к форме плёнкой, из-под которой откачивают воздух.

Встаёт вопрос: каким вакуумным насосом пользоваться – одноступенчатым или двухступенчатым?

Обычно думают, что раз вакуум у двухступенчатого выше, то и детали получаться лучше.

Вакуум у двухступенчатого насоса 0,2 Па, а у одноступенчатого 2 Па. Кажется, что раз разница в давлении в 10 раз, то и прижиматься деталь будет гораздо сильнее.

Но так ли это на самом деле?

1 атм = 100000 Па = 1 кг/см2.

Значит разница в прижиме плёнки при вакууме 0,2 Па и 2 Па составит 0,00018 кг/см2 (кому не лень – посчитает сам).

То есть, практически, разницы никакой не будет, т.к. выигрыш в 0,18 г в силе прижима погоды не сделает.

Информация взята с сайта:
 

ноябрь 29, 2015