После того, как трем
маленьким шарикам массой m каждый, подвешенным на
нитях длиной l, закрепленных в одной точке, сообщили равные одноименные
заряды, они расположились в вершинах равностороннего треугольника со стороной a. Определите заряд шариков.
Решение.
В качестве тела отсчета
выберем поверхность Земли и будем считать систему отсчета, связанную с ней,
инерциальной. Предположим, что точка подвеса покоится по отношению к выбранной
системе отсчета.
В качестве физической
системы рассмотрим заряженный шарик, который примем за материальную точку,
заряд шарика будем считать точечным. Выделенная физическая система является
незамкнутой, так как взаимодействует с материальными объектами, не включенными
в нее. Эти взаимодействия могут быть описаны соответствующими силами. Так как
заряженный шарик покоится по отношению к выбранной инерциальной системе
отсчета, то геометрическая сумма сил, действующих на него, равна нулю.
Если пренебречь
взаимодействием шарика с электрическим полем Земли и воздухом, то условие
равновесия может быть записано в следующем виде.
Где mg –
сила тяжести шарика, Fупр – сила упругости
нити, F21 – сила электростатического
взаимодействия с зарядом второго шарика.
Силы, действующие на
шарик, схематически показаны на рисунке выше. Из рисунка видно, что сила F21 расположена в горизонтальной
плоскости, а силы Fупр и mg –
в вертикальной.
Проецируя векторы,
изображающие соответствующие силы, на оси OX
и OY, получим систему уравнений.
Где α – угол между
высотой треугольника H и его стороной l. Выразим значение модуля силы упругости из второго уравнения и
подставим его в первое.
По условию задачи
заряды всех шариков одинаковы, т.е. q1 = q2 = q.
Где e – диэлектрическая проницаемость воздуха, a –
расстояние между центрами шариков.
Откуда находим заряд
шарика q.
Принимая во внимание,
что e = 1, получим окончательный ответ.
Полученное значение
заряда является ответом задачи, если выражение стоящее в знаменателе под
корнем, положительно, т.е. если выполнено условие a
< l/2.
Ответ: 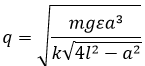
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Определить заряд шара
romazol91@mail.ru
Знаток
(289),
закрыт
10 лет назад
Потенциал. 223.Заряженный шар радиусом 2 см помещен в трансформаторное масло ( = 2,2). Определить заряд шара, если известно, что на расстоянии 5 см от поверхности шара потенциал равен 90 В.
Валентина ???
Гений
(71098)
11 лет назад
Используем формулу потенциала заряженного шара в точке, расположенной на расстоянии от его поверхности: 
r – расстояние от заряда, образующего поле, до точки, в которой нужно найти потенциал.
( в нашем случае это 7 см=0,07 м)
Электростатика – раздел электродинамики,
изучающий взаимодействие неподвижных
электрических зарядов.
Электрический заряд – физическая
величина, определяющая силу электромагнитного
взаимодействия. Заряд обозначается
буквой q, измеряется
в кулонах (Кл).
В природе существует два вида
электрических зарядов, которые условно
назвали «положительный» и «отрицательный».
Заряды одного знака отталкиваются,
разных знаков – притягиваются.
Электрический заряд всегда связан с
частицей. Существуют частицы без заряда,
но не существует заряда без частицы.
Величина электрического заряда не
зависит от скорости движения частицы.
Минимальный заряд, встречающийся в
природе, называется элементарным.
Величина элементарного заряда е =
1,610-19
Кл. Заряды электрона, протона, позитрона
(античастица для электрона) равны по
модулю элементарному. Заряд любого
макроскопического тела кратен
элементарному, т. е. электрический заряд
– дискретная величина.
Все вещества состоят из атомов или
молекул. Атом состоит из положительно
заряженного ядра и отрицательно
заряженных электронов, движущихся
вокруг ядра. Поэтому любое макроскопическое
тело содержит электрически заряженные
частицы. Если суммарный заряд тела равен
нулю, то говорят что тело электрически
нейтральное или незаряженное. Электрический
заряд любой системы равен алгебраической
сумме зарядов тел, входящих в систему.
Заряды могут перераспределятся между
телами системы. Если система тел
электрически изолирована (через границу
системы не проникают другие заряды), то
в ней выполняется закон сохранения
заряда:
алгебраическая сумма зарядов электрически
изолированной системы постоянна:
q1
+ q2
+ … + qn
= const.
Электризация – это процесс получения
электрически заряженных тел из
нейтральных.
При электризации трением одни вещества
отдают электроны, а другие их присоединяют.
Причина этого явления – в различии
энергии связи электронов с атомами в
этих веществах. Атом, потерявший электрон
называется положительным ионом,
присоединивший к себе электрон –
отрицательным ионом.
Точечный заряд – это заряженное
тело, размер которого много меньше
расстояния его возможного действия на
другие тела.
Закон Кулона (1875 г.): Сила взаимодействия
между двумя неподвижными точечными
зарядами, находящимися в вакууме, прямо
пропорциональна произведению модулей
зарядов, обратно пропорциональна
квадрату расстояния между ними и
направлена по прямой, соединяющей
заряды:
![]() .
.
Коэффициент k, входящий
в закон Кулона, зависит от выбора системы
единиц. В системе СИ
![]() .
.
Здесь
![]()
– электрическая постоянная.
Закон Кулона был получен экспериментально.
Он справедлив только для точечных
зарядов или равномерно заряженных
шаров. Электростатические взаимодействия
осуществляются посредством
электростатического поля.
Электростатическое поле это вид
материи который образуется неподвижными
электрическими зарядами и его можно
обнаружить по его действию на неподвижные
электрические заряды.
Силовой характеристикой электростатического
поля является напряженность –
векторная физическая величина, численно
равная силе с которой поле действует
на единичный пробный положительный
заряд, помещенный в заданной точке поля.
![]() .
.
Направление вектора напряженности
совпадает с направлением вектора силы,
действующей на положительный заряд,
помещенный в данной точке поля. Из закона
Кулона на основании определения
напряженности поля получаем формулу
для напряженности поля точечного заряда
на расстоянии r от него:
![]() .
.
Для наглядности электростатическое
поле представляют непрерывными линиями
напряженности – касательные к которым
в каждой точке совпадают по направлению
с направлением вектора напряженности
электростатического поля в данной
точке.
Линии напряженности не пересекаются
(в противном поле напряженность поля в
точке пересечения не имела бы определенного
значения); начинаются на положительных
зарядах (источники поля) и стекаются к
отрицательным зарядам (стоки). Модуль
вектора напряженности пропорционален
числу линий напряженности на густоте
линий напряженности можно судить о
модуле вектора напряженности на единицу
поверхности (густоте линий напряженности).
Электростатическое поле, векторы
напряженности которого одинаковы во
всех точках пространства, называется
однородным.
Принцип суперпозиции электрических
полей: напряженность поля системы
зарядов в данной точке равна векторной
сумме напряженностей полей, созданным
в этой точке каждым зарядом в отдельности:
![]() .
.
Теорема Гаусса.
Потоком вектора напряженности через
замкнутый контур площадью S
называется произведение проекции
вектора напряженности на нормаль к
контуру на площадь контура:
![]() .
.
Поток вектора напряженности через
произвольную замкнутую поверхность
равен алгебраической сумме зарядов,
расположенных внутри этой поверхности,
деленной на электрическую постоянную:
![]() .
.
Напряженность поля точечного заряда.
Д ля
ля
определения напряженности проведем
сферическую поверхность S
радиусом r с центром
совпадающим с зарядом и воспользуемся
теоремой Гаусса. Так как внутри указанной
области находится только один заряд q,
то согласно указанной теореме получим
равенство:
![]()
(1), где En
– нормальная составляющая напряженности
электрического поля. Из соображений
симметрии нормальная составляющая
должна быть равна самой напряженности
и постоянна для всех точек сферической
поверхности, поэтому E=En=const.
Поэтому ее можно вынести за знак суммы.
Тогда равенство (1) примет вид
![]() ,
,
что и было получено из закона Кулона и
определения напряженности электрического
поля.
Электрическое поле заряженной сферы
Е сли
сли
сфера проводящая, то весь заряд находится
на поверхности. Рассмотрим две области
I – внутри сферы радиуса
R с зарядом q
и вне сферы область II.
Для определения напряженности в области
I проведем сферическую
поверхность S1
радиусом r1 (0<r1<R)
и воспользуемся теоремой Гаусса. Так
как внутри указанной области зарядов
нет, то согласно указанной теореме
получим равенство:
![]()
(1), где En
– нормальная составляющая напряженности
электрического поля. Из соображений
симметрии нормальная составляющая
должна быть равна самой напряженности
и постоянна для всех точек сферической
поверхности, поэтому E1=En=const.
Поэтому ее можно вынести за знак суммы.
Тогда равенство (1) примет вид
![]() .
.
Т. к. площадь сферы не равна нулю, то Е1=0
(во всех точках области I)
– внутри проводника зарядов нет и
напряженность поля равна нулю.
В области II Rr2
проведем сферическую поверхность S2
радиусом r2 и
воспользуемся теоремой Гаусса:
![]()
(2),
![]()
– напряженность поля вне сферы
рассчитывается по той же формуле, что
и напряженность поля точечного заряда.
Электрическое поле заряженного шара
Заряд равномерно распределен по всему
объему шара, поэтому введем понятие
объемной плотности заряда:
![]() .
.
Рассмотрим две области I
– внутри сферы радиуса R
с зарядом q и вне сферы
область II.
Для определения напряженности в области
I проведем сферическую
поверхность S1
радиусом r1 (0<r1<R)
и воспользуемся теоремой Гаусса:

– напряженность поля внутри шара
увеличивается прямо пропорционально
расстоянию до центра шара.
В области II R
r2
проведем сферическую поверхность S2
радиусом r2 и
воспользуемся теоремой Гаусса:
![]()
(2),
![]()
– напряженность поля вне шара рассчитывается
по той же формуле, что и напряженность
поля точечного заряда.
Электрическое поле заряженной нити
Д ля
ля
равномерно заряженной нити введем
понятие линейной плотности заряда![]() .
.
Для определения напряженности окружим
участок проволоки длиной ℓ
цилиндрической поверхностью S
радиусом r с осью совпадающей
с проволокой и воспользуемся теоремой
Гаусса. При этом весь поток вектора
напряженности будет проходить только
через боковую поверхность цилиндра,
площадь которой
![]() ,
,
т.к. поток через оба основания цилиндра
равен нулю. Тогда
![]()
– напряженность поля нити убывает обратно
пропорционально расстоянию.
Напряженность поля заряженной плоскости
Е сли
сли
плоскость бесконечна и заряжена
равномерно, т. е. поверхностная плотность
заряда = q/S
одинакова в любом ее месте, то линии
напряженности электрического поля в
любой точке перпендикулярны этой
плоскости. Такое же направление они
сохраняют и на любом расстоянии от
плоскости, т.е. поле заряженной плоскости
однородное.
Для нахождения напряженности электрического
поля заряженной плоскости мысленно
выделим в пространстве цилиндр, ось
которого перпендикулярна заряженной
плоскости, а основания параллельны ей
и одно из оснований проходит через
интересующую нас точку поля. Цилиндр
вырезает из заряженной плоскости участок
площадью S, и такую же
площадь имеют основания цилиндра,
расположенные по разные стороны от
плоскости (рис.). Согласно теореме Гаусса
поток Ф вектора напряженности
электрического поля через поверхность
цилиндра связан с электрическим зарядом
внутри цилиндра выражением
![]() .
.
С другой стороны, так как линии
напряженности пересекают лишь основания
цилиндра, поток вектора напряженности
можно выразить через напряженность
электрического поля у обоих оснований
цилиндра:
![]() .
.
В самом деле, поток через боковую
поверхность цилиндра (см. рис.), равен
нулю, поскольку линии напряженности
параллельны боковой поверхности
цилиндра.
Из двух выражений для потока вектора
напряженности получим:
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
Силы электростатического взаимодействия зависят от формы и размеров наэлектризованных тел, а также от характера распределения заряда на этих телах. В некоторых случаях можно пренебречь формой и размерами заряженных тел и считать, что каждый заряд сосредоточен в одной точке.
Точечный заряд – это электрический заряд, когда размер тела, на котором этот заряд сосредоточен, намного меньше расстояния между заряженными телами. Приближённо точечные заряды можно получить на опыте, заряжая, например, достаточно маленькие шарики.
Взаимодействие двух покоящихся точечных зарядов определяет основной закон электростатики – закон Кулона. Этот закон экспериментально установил в 1785 году французский физик Шарль Огюстен Кулон (1736 – 1806). Формулировка закона Кулона следующая:
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональная произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Эта сила взаимодействия называется кулоновская сила, и формула закона Кулона будет следующая:
F = k · (|q1| · |q2|) / r2
где |q1|, |q2| – модули зарядов, r – расстояния между зарядами, k – коэффициент пропорциональности.
Коэффициент k в СИ принято записывать в форме:
k = 1 / (4πε0ε)
где ε0 = 8,85 * 10-12 Кл/Н*м2 – электрическая постоянная, ε – диэлектрическая проницаемость среды.
Для вакуума ε = 1, k = 9 * 109 Н*м/Кл2.
Сила взаимодействия неподвижных точечных зарядов в вакууме:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2]
Если два точечных заряда помещены в диэлектрик и расстояние от этих зарядов до границ диэлектрика значительно больше расстояния между зарядами, то сила взаимодействия между ними равна:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2] = k · (1 /π) · [(|q1| · |q2|) / r2]
Диэлектрическая проницаемость среды всегда больше единицы (π > 1), поэтому сила, с которой взаимодействуют заряды в диэлектрике, меньше силы взаимодействия их на том же расстоянии в вакууме.
Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела (рис. 1.8).

Рис. 1.8. Силы взаимодействия двух неподвижных точечных заряженных тел.
Кулоновские силы, как и гравитационные силы, подчиняются третьему закону Ньютона:
F1,2 = -F2,1
Кулоновская сила является центральной силой. Как показывает опыт, одноимённые заряженные тела отталкиваются, разноимённо заряженные тела притягиваются.
Вектор силы F2,1, действующей со стороны второго заряда на первый, направлен в сторону второго заряда, если заряды разных знаков, и в противоположную, если заряды одного знака (рис. 1.9).
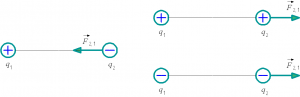
Рис. 1.9. Взаимодействие разноименных и одноименных электрических зарядов.
Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.
В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы (рис. 1.10). На тонкой серебряной нити подвешена лёгкая стеклянная палочка с, на одном конце которой закреплён металлический шарик а, а на другом противовес d. Верхний конец нити закреплён на вращающейся головке прибора е, угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарик b, неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шариками a и b при различных их положениях.
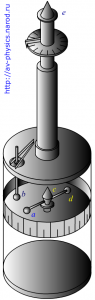
Рис. 1.10. Опыт Кулона (крутильные весы).
При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а следовательно, и определить новое значение силы взаимодействия при новом заряде.
Электризация и электрический заряд
Определения
Электростатика — раздел физики, изучающий неподвижные заряды.
Электризация — процесс, в результате которого тело приобретает электрический заряд. Если тело начиняет притягивать к себе другие тела, то говорят, что оно наэлектризовано, или приобрело электрический заряд.
Электрический заряд — физическая величина, определяющая способность тел участвовать в электромагнитных взаимодействиях.
Электрический заряд обозначается как q. Единица измерения — Кулон (Кл).
В природе существуют два вида зарядов, которые условно назвали положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные притягиваются.
Закон сохранения зарядаАлгебраическая сумма зарядов в замкнутой системе сохраняется:
∑qi=const.
Замкнутая система в электростатике — такая система, которая не обменивается зарядами с окружающей средой.
Экспериментально доказано, что заряды можно делить, но до определенного предела. Носитель наименьшего электрического заряда — электрон. Он заряжен отрицательно.
Заряд электрона:
qe=−1,6·10−19 Кл
Масса электрона:
me=9,1·10−31 кг
Модуль любого заряда кратен заряду электрона:
q=Nqe
N — избыток электронов.
В процессе электризации от одного тела к другому передаются только электроны. Если у тела избыток электронов, то оно заряжено отрицательно, а если недостаток, то — положительно.
Внимание! Заряженные тела притягивают к себе нейтральные тела и тела с противоположным зарядом. Отталкивание наблюдается только между одноименно заряженными телами.
Пример №1. На двух одинаковых металлических шарах находятся положительный заряд 7 нКл и отрицательный заряд 1 нКл. Каким станет заряд на каждом шаре при соприкосновении шаров?
После того, как шары соприкоснутся, заряд на них выровняется. Так как большим зарядом обладает положительно заряженный шар, то оба шара в итоге будут заряжены положительно:
(7 – 1)/2 нКл = 3 нКл
Каждый шар будет иметь положительный заряд, равный 3 нКл.
Закон Кулона
Закон Кулона — основной закон электростатики, который был открыт экспериментально в 1785 году.
Закон Кулона
Два неподвижных точечных заряда в вакууме взаимодействуют друг с другом с силой, прямо пропорциональной квадрату расстояния между ними:
FK=k|q1||q2|r2
FK — сила, с которой взаимодействуют два точечных заряда (кулоновская сила, или сила Кулона). |q1| (Кл) и |q2| (Кл) — модули зарядов, r (м) — расстояние между зарядами, k — коэффициент пропорциональности, который численно равен силе взаимодействия между двумя точечными зарядами по 1 Кл, находящимися на расстоянии 1 м друг от друга:
k=14πε0=9·109 Н·м2/Кл2
ε0 — электрическая постоянная равная, 8,85∙10–12 Кл2/(Н∙м2).
Закон Кулона в среде
FK=k|q1||q2|εr2
ε — диэлектрическая проницаемость. Это табличная величина, которая показывает, во сколько раз электрическое взаимодействие в среде уменьшается по сравнению с вакуумом.
Направление силы Кулона
Направление силы Кулона зависит от знаков зарядов. На рисунке ее прикладывают к центру заряженного тела.
Подсказки к задачам
Подсказка №1
При соприкосновении одинаковых проводящих шариков, один из которых заряжен, заряд между шариками делится поровну:
q′
1=q′2=q2
Подсказка №2
При соприкосновении одинаковых проводящих шаров заряды складываются с учетом знаков и делятся поровну. Модули зарядом двух шариков:
q′1=q′2=|q1±q2|2
Пример №2. Два маленьких одинаковых металлических шарика заряжены положительными зарядами q и 5q и находятся на некотором расстоянии друг от друга. Шарики привели в соприкосновении и раздвинули на прежнее расстояние. Как изменилась сила взаимодействия шариков?
Изначально сила Кулона была равна:
FK1=kq5qr2=5kq2r2
Когда шарики коснулись, заряд каждого из них стал равен:
q′=5q+q2=3q
После того, как шарики раздвинули на прежнее расстояние, сила взаимодействия между ними стала равна:
FK2=k3q3qr2=9kq2r2
Поделим вторую силы на первую и получим:
FK2FK1=9kq2r2·r25kq2=95=1,8
Следовательно, после всех манипуляций сила взаимодействия между двумя заряженными шариками увеличилась в 1,8 раз.
Задание EF17493
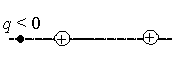 Точечный отрицательный заряд q помещён слева от неподвижных положительно заряженных шариков (см. рисунок). Куда направлена равнодействующая кулоновских сил, действующих на заряд q?
Точечный отрицательный заряд q помещён слева от неподвижных положительно заряженных шариков (см. рисунок). Куда направлена равнодействующая кулоновских сил, действующих на заряд q?
а) вверх
б) вниз
в) вправо
г) влево
Алгоритм решения
- Вспомнить, как взаимодействуют разноименные заряды.
- Установить взаимодействие заряда с каждым из шариков.
- Выяснить, куда будет направлена равнодействующая сила, действующая на заряд со стороны заряженных шариков.
Решение
Отрицательные и положительные заряды притягиваются. Следовательно, каждый из положительно заряженных шариков притягивает отрицательный заряд q к себе — каждая из сил (FK1 и FK2) будет направлена вправо. Поэтому их равнодействующая FK тоже будет направлена вправо.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17545
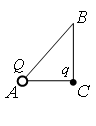 В треугольнике АВС угол С – прямой. В вершине А находится точечный заряд Q. Он действует с силой 2,5·10–8 Н на точечный заряд q, помещённый в вершину С. Если заряд q перенести в вершину В, то заряды будут взаимодействовать с силой 9,0·10–9 Н. Найдите отношение AC/BC.
В треугольнике АВС угол С – прямой. В вершине А находится точечный заряд Q. Он действует с силой 2,5·10–8 Н на точечный заряд q, помещённый в вершину С. Если заряд q перенести в вершину В, то заряды будут взаимодействовать с силой 9,0·10–9 Н. Найдите отношение AC/BC.
а) 0,36
б) 0,60
в) 0,75
г) 1,67
Алгоритм решения
1.Записать исходные данные.
3.Применить закон Кулона для данного случая.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Сила, с которой заряд Q действует на точечный заряд q, помещенный в вершину С: FKC = 2,5∙10–8 Н.
• Сила, с которой заряд Q действует на точечный заряд q, помещенный в вершину В: FKB = 9∙10–9 Н.
Запишем закон Кулона:
FK=k|q1||q2|r2
Применим закон Кулона для 1 и 2 случая:
FKC=k|q||Q|AC2
FKB=k|q||Q|AB2
По условию задачи нужно найти соотношение сторон треугольника АС к ВC. Для этого выразим известные стороны треугольника из формул выше:
AC=√k|q||Q|FKC
AB=√k|q||Q|FKB
Сторону ВС можно выразить с помощью теоремы Пифагора (АВС — прямоугольный треугольник, так как угол С является прямым):
BC=√AB2−AC2=√k|q||Q|FKB−k|q||Q|FKC=√k|q||Q|(FKC−FKB)FKBFKC
Отсюда:
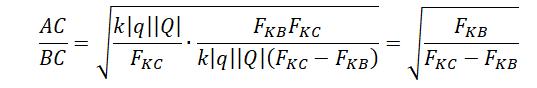
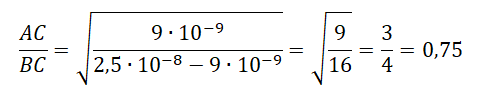
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17737
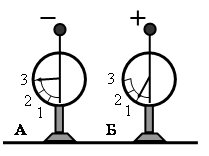 На рисунке изображены два одинаковых электрометра, шары которых имеют заряды противоположных знаков. Если их шары соединить проволокой, то показания обоих электрометров
На рисунке изображены два одинаковых электрометра, шары которых имеют заряды противоположных знаков. Если их шары соединить проволокой, то показания обоих электрометров
Ответ:
а) не изменятся
б) станут равными 1
в) станут равными 2
г) станут равными 0
Алгоритм решения
1.Записать показания электрометров.
2.Установить, что произойдет, если их соединить проволокой.
3.Вычислить показания электрометров после их соединения.
Решение
Запишем показания электрометров:
• Слева электрометр показывает отрицательный заряд q1, равный «3».
• Справа электрометр показывает положительный заряд q2, равный «1».
Когда электрометры соединятся проволокой, избыточный отрицательный заряд в виде электронов частично переместится из левого электрометра в правый электрометр так, что показания приборов выровняются. Они будут показывать:
q=|−q1+q2|2=22=1
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.5k
