Числовая ось
Прямую, на которой выбрана начальная точка, положительное направление и единичный отрезок, называют координатной или числовой осью.
Рассмотрим прямую с начальной точкой O и выбранным положительным направлением, указанным стрелкой:
За единицу длины на данной прямой возьмём произвольный отрезок. Такая прямая будет называться осью.
Если отложить по оси от точки O единицу длины (произвольно взятый отрезок) вправо и влево 1, 2, 3, 4, 5 и более раз, а концы полученных отрезков, расположенных справа, отметить положительными числами +1, +2 и так далее, а слева — отрицательными числами -1, -2 и так далее, то такую ось называют числовой осью:
Число 0 на ней будет совпадать с точкой O. Таким образом, любое число (положительное, отрицательное или нуль) может быть отображено только одной точкой оси.
Точка и число являются разными понятиями. Когда говорят, что данная точка изображает число, например, 2,5, это значит, что данная точка находится на расстоянии 2,5 единиц длины влево от начальной точки O.
Вместо того, чтобы говорить: Точка соответствует числу 2,5
— или: Точка изображает число 2,5
, — говорят просто: Точка 2,5
и т. д.
Число, которое соответствует данной точке, называется координатой этой точки.
Так как все точки на оси имеют определённые координаты, то такую ось также называют координатной осью или координатной прямой.
Ось – это направление. Значит, проекция на ось или на направленную прямую считается одним и тем же. Проекция бывает алгебраическая и геометрическая. В геометрическом понимают проекцию вектора на ось как вектор, а алгебраическом – число. То есть применяются понятия проекция вектора на ось и числовая проекция вектора на ось.
Если имеем ось L и ненулевой вектор AB→, то можем построить вектор A1B1⇀, обозначив проекции его точек A1 и B1.
A1B→1 будет являться проекцией вектора AB→ на L.
Проекцией вектора на ось называют вектор, начало и конец которого являются проекции начала и конца заданного вектора. npLAB→→ принято обозначать проекцию AB→ на L. Для построения проекции на L опускают перпендикуляры на L.
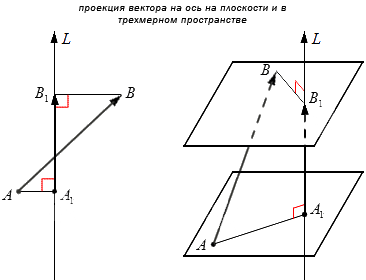
Пример проекции вектора на ось.
На координатной плоскости Оху задается точка M1 (x1, y1). Необходимо построить проекции на Ох и Оу для изображения радиус-вектора точки M1. Получим координаты векторов (x1, 0) и (0, y1).
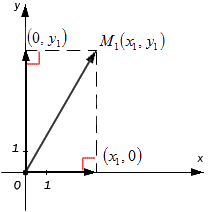
Если идет речь о проекции a→ на ненулевой b→ или проекции a→ на направление b→, то имеется в виду проекция a→на ось, с которой совпадает направление b→. Проекция a→ на прямую, определяемая b→, имеет обозначение npb→a→→. Известно, что когда угол междуa→ и b→, можно считать npb→a→→ и b→ сонаправленными. В случае, когда угол тупой, npb→a→→ и b→противоположно направлены. В ситуации перпендикулярностиa→ и b→, причем a→ – нулевой, проекция a→ по направлению b→ является нулевым вектором.
Числовая проекция вектора на ось
Числовая характеристика проекции вектора на ось – числовая проекция вектора на заданную ось.
Числовой проекцией вектора на ось называют число, которое равно произведению длины данного вектора на косинус угла между данным вектором и вектором, который определяет направление оси.
Числовая проекция AB→ на L имеет обозначениеnp LAB→, а a→ на b→ – npb→a→.
Исходя из формулы, получим npb→a→=a→·cosa→, b→^, откуда a→ является длиной вектора a→, a⇀, b→^ – угол между векторами a→ и b→.
Получим формулу вычисления числовой проекции: npb→a→=a→·cosa→, b→^. Она применима при известных длинах a→ и b→ и угле между ними. Формула применима при известных координатах a→ и b→, но имеется ее упрощенный вид.
Узнать числовую проекцию a→ на прямую по направлению b→ при длине a→ равной 8 и углом между ними в 60 градусов. По условию имеем a⇀=8, a⇀, b→^=60°. Значит, подставляем числовые значения в формулу npb⇀a→=a→·cosa→,b→^=8·cos 60°=8·12=4.
Ответ: 4.
При известном cos(a→, b→^)=a⇀, b→a→·b→, имеем a→, b→ как скалярное произведение a→ и b→. Следуя из формулы npb→a→=a→·cosa⇀, b→^, мы можем найти числовую проекцию a→ направленную по вектору b→ и получим npb→a→=a→, b→b→. Формула эквивалента определению, указанному в начале пункта.
Числовой проекцией вектора a→ на ось , совпадающей по направлению с b→, называют отношение скалярного произведения векторовa→ иb→ к длине b→. Формула npb→a→=a→,b→b→ применима для нахождения числовой проекции a→ на прямую, совпадающую по направлению с b→, при известных a→ и b→ координатах.
Задан b→=(-3, 4). Найти числовую проекцию a→=(1, 7) на L.
Решение
На координатной плоскости npb→a→=a→, b→b→ имеет вид npb→a→=a→, b→b→=ax·bx+ay·bybx2+by2, при a→=(ax, ay) и b→=bx, by. Чтобы найти числовую проекцию вектора a→ на ось L, нужно: npLa→=npb→a→=a→,b→b→=ax·bx+ay·bybx2+by2=1·(-3)+7·4(-3)2+42=5.
Ответ: 5.
Найти проекцию a→ на L, совпадающей с направлением b→, где имеются a→=-2, 3, 1 и b→=(3, -2, 6). Задано трехмерное пространство.
Решение
По заданнымa→=ax, ay, az и b→=bx, by, bz вычислим скалярное произведение: a⇀, b→=ax·bx+ay·by+az·bz. Длину b→ найдем по формуле b→=bx2+by2+bz2. Отсюда следует, что формула определения числовой проекции a→ будет: npb→a⇀=a→, b→b→=ax·bx+ay·by+az·bzbx2+by2+bz2.
Подставляем числовые значения: npLa→=npb→a→=(-2)·3+3·(-2)+1·632+(-2)2+62=-649=-67.
Ответ: -67.
Просмотрим связь междуa→ на L и длиной проекции a→ на L. Начертим ось L, добавив a→ и b→ из точки на L, после чего проведем перпендикулярную прямую с конца a→ на L и проведем проекцию на L. Существуют 5 вариаций изображения:
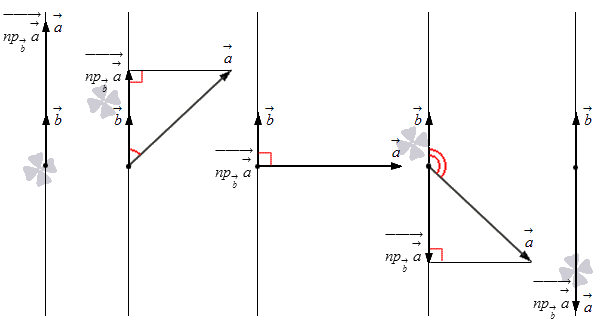
Первый случай при a→=npb→a→→ означает a→=npb→a→→, отсюда следует npb→a→=a→·cos(a,→b→^)=a→·cos0°=a→=npb→a→→.
Второй случай подразумевает применение npb→a→⇀=a→·cosa→,b→, значит, npb→a→=a→·cos(a→,b→)^=npb→a→→.
Третий случай объясняет, что при npb→a→→=0→ получаем npb⇀a→=a→·cos(a→,b→^)=a→·cos90°=0, тогда npb→a→→=0 и npb→a→=0=npb→a→→.
Четвертый случай показывает npb→a→→=a→·cos(180°-a→,b→^) = -a→·cos(a →, b→^), следует npb→a→=a→·cos(a→,b→^)=-npb→a→→.
Пятый случай показывает a→=npb→a→→, что означаетa→=npb→a→→, отсюда имеем npb→a→=a→·cosa→,b→^=a→·cos180°=-a→=-npb→a→.
Числовой проекцией вектора a→ на ось L, которая направлена как и b→, имеет значение:
- длины проекции вектора a→ на L при условии, если угол между a→ и b→ меньше 90 градусов или равен 0: npb→a→=npb→a→→ с условием 0≤(a→,b→)^<90°;
- ноля при условии перпендикулярности a→ и b→: npb→a→=0, когда (a→, b→^)=90°;
- длины проекции a→ на L, умноженной на -1, когда имеется тупой или развернутый угол векторов a→ и b→: npb→a→=-npb→a→→ с условием 90°<a→,b→^≤180°.
Дана длина проекцииa→ на L, равная 2. Найти числовую проекциюa→ при условии, что угол равен 5π6 радиан.
Решение
Из условия видно, что данный угол является тупым: π2<5π6<π. Тогда можем найти числовую проекцию a→ на L: npLa→=-npLa→→=-2.
Ответ: -2.
Дана плоскость Охyzс длиной вектора a→ равной 63,b→(-2, 1, 2) с углом в 30 градусов. Найти координаты проекции a→ на ось L.
Решение
Для начала вычисляем числовую проекцию вектораa→: npLa→=npb→a→=a→·cos(a→,b→)^=63·cos30°=63·32=9.
По условию угол острый, тогда числовая проекция a→= длине проекции вектора a→: npLa→=npLa→→=9. Данный случай показывает, что векторы npLa→→ и b→ сонаправлены, значит имеется число t, при котором верно равенство: npLa→→=t·b→. Отсюда видим, что npLa→→=t·b→, значит можем найти значение параметра t: t=npLa→→b→=9(-2)2+12+22=99=3.
Тогда npLa→→=3·b→ с координатами проекции вектора a→ на ось L равны b→=(-2,1, 2), где необходимо умножить значения на 3. Имеем npLa→→=(-6, 3, 6). Ответ: (-6, 3, 6).
Необходимо повторить ранее изученную информацию об условии коллинеарности векторов.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
Координаты на прямой
Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление — положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).
Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О.
Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.
Определение:
Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.
Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором—букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.
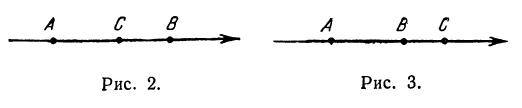
Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным; если же его направление противоположно направлению оси, то — отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:
Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.
Сложение направленных отрезков производится по следующему правилу:
Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.
Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:
(рис. 2 и 3).
Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.
Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать
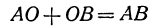
(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или
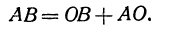
Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, поскольку его начало не является началом координат. Но в силу равенства (1)
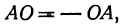
поэтому можно написать
Получен следующий результат:
Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.
Это верно для любого отрезка, лежащего на координатной оси.
Теперь дадим одно из самых важных определений: Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.
Точку А, имеющую координатной число х, будем обозначать А (х).
Указанные на рис. 4 точки имеют следующие координаты:
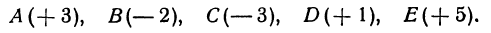
Будем также писать
Если даны точки А(х1) и В(х2), то на основании формул (3) и (4) получим
т. е. направленный отрезок равен разности координат его конца и начала.
Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.
Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:
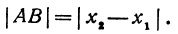
Пример:
Если даны точки А (+4), В (+8), то отрезок АВ = (+8) — (+4), а его длина |АВ|= |+ 4 | = 4.
Если даны точки М (+5) и Р (+3), то отрезок МР = (+3)—(+5) = —2, а его длина |МР| = | —2| = 2. Даны две точки: Q (+ 3) и S (—4). Длина отрезка
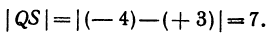
Даны две точки R (— 6) и Т (—2); отрезок RТ = ( — 2) — (—6) = +4, а его длина | RТ | = 4.
Пример:
Начало отрезка АВ находится в точке А (—950), а конец—в точке В ( —1200); найти его направление и длину.
Отрезок АВ = ( — 1200)—( — 950) = —250. Так как он
получился отрицательным, то его направление противоположно направлению оси. Его длина равна | АВ | = | —250 | = 250.
Задача:
На координатной оси даны две точки: A (x1) и В (x2) Найти точку С, лежащую между ними и делящую отрезок АВ в отношении т : п.
Чтобы найти точку, надо найти ее координату. По условию задачи должно быть
Обозначая координату искомой точки С через х и выражая отрезки через координаты, т. е. применяя формулу (5), получим, что АС = х—х1, СВ = х2 — х. Подставляя эти выражения в равенство (6), будем иметь
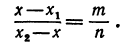
Решая последнее уравнение относительно х, найдем:
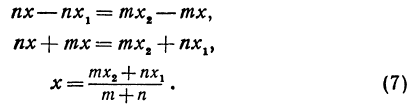
Это и есть координата искомой точки.
Пример:
Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка А (+ 3) и конец В ( + 5) (рис. 5).
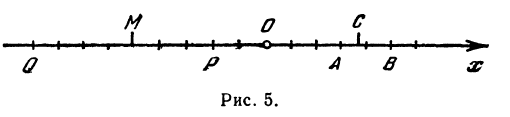
Здесь т = 1, п = 2, х1=-3, х2 = 5. Применяя формулу (7), получим
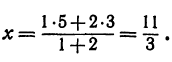
Пример:
Найти точку М, делящую расстояние между точками Р ( — 2) и Q (—9) в отношении 3:4 (рис. 5). Здесь т = 3, п = 4, х1 = —2, х2 = —9. По формуле (7) находим
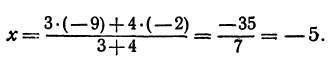
Если т = n т. е. точка С делит отрезок АВ пополам, тогда формула (7) перепишется так:
Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.
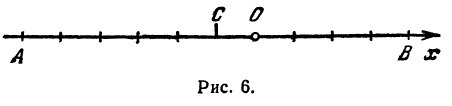
Пример:
Найдем середину отрезка, заключенного между точками А (—6) и B (4) (рис. 6).
Применяя формулу (8), получим, что
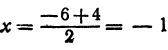
Координаты на плоскости
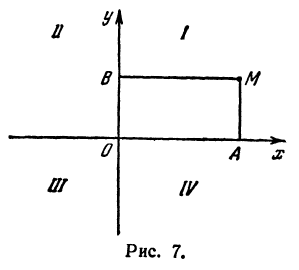
Возьмем на плоскости две взаимно перпендикулярные прямые, пересекающиеся в точке О. На каждой из этих прямых зададим направление, указав его стрелкой (рис. 7).
Установим масштаб, общий для обеих прямых, а за начало отсчета выберем точку О.
Определение:
Координатными осями на плоскости называются две взаимно перпендикулярные прямые, на которых установлены: 1) на-правления, 2) масштаб и 3) общая точка отсчета.
Назовем одну из осей осью Ох или осью абсцисс, другую — осью Оу или осью ординат. Точку их пересечения назовем началом координат.
Возьмем произвольную точку M, лежащую на плоскости, и опустим из нее перпендикуляры на оси координат, т. е. найдем ее проекции на оси. Обозначим проекцию на ось Ох через А, а проекцию на ось Оу через В. Обозначим координату точки А (по оси Ох) через х, а координату точки В (по оси Оу) через у. Введем определение:
Определение:
Абсциссой точки называется координата ее проекции на ось Ох. Ординатой точки называется координата ее проекции на ось Оу.
Абсциссу точки обычно обозначают буквой х, ординату— буквой у. Точку М, имеющую абсциссу х и ординату у, обозначают следующим образом: пишут скобку и в ней на первом месте ставят абсциссу, на втором ординату и разделяют эти два числа запятой или точкой с запятой. Таким образом, запись точки выглядит так: М(х, у).
Координатные оси разделяют плоскость на четыре части, которые называют четвертями.
Первой четвертью называется та часть плоскости, в которой абсцисса и ордината положительны.
Второй четвертью — та часть, в которой абсцисса отрицательна, а ордината положительна.
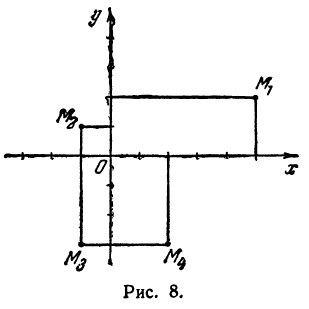
Третьей четвертью — та часть, в которой абсцисса и ордината отрицательны, и, наконец, четвертой, — та часть, в которой абсцисса положительна, а ордината отрицательна (рис. 7), На рис. 8 указаны точки M1 (5, 2), М2 ( — 1, 1), М3 (-1, -3), М4 (2, -3). Заметим, что абсцисса х = ОА по абсолютной величине равна расстоянию точки от оси ординат, так как ОА = ВМ (см. рис. 7), а ордината — расстоянию точки М от оси абсцисс, так как ОВ = АМ.
Пример:
Найти точку Р( — 4, 2) (рис. 9), Возьмем на оси Ох точку А с координатой —4, ее координатный отрезок ОА = —4. На оси Оу возьмем точку В с координатным отрезком ОВ= 2. Восставим перпендикуляры к осям из точек А и В, точка их пересечения и даст искомую точку Р.
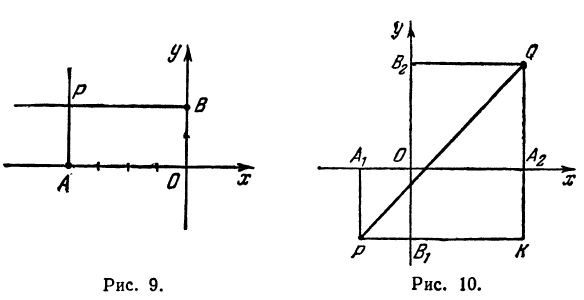
Задача:
Найти расстояние между точками Р (х1, у1) и Q( х1, у1 ). Иначе говоря, нужно найти длину отрезка РQ(рис. 10).
Обозначим проекцию точки Р на ось Ох через А1, а ее проекцию на ось Оу — через В1. Проекцию точки Q на ось Ох обозначим через А2 и через В2— ее проекцию на ось Oy. Тогда ОА1 = х1, ОВ1 = y1, ОА2 = х2, ОВ2 = у2. Из точки Р проведем прямую, параллельную оси Ох, до пересечения с прямой A2Q в точке К. Рассмотрим треугольник PKQ. По теореме Пифагора имеем
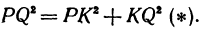
Но РК = А1А2, KQ = B1B2, как противоположные стороны прямоугольников; кроме того, на основании формулы (3 из § 1) направленные отрезки А1А2 и В1В2 будут равны
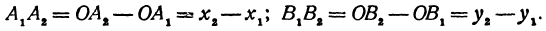
Подставляя полученные выражения в (*), получим
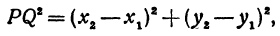
откуда
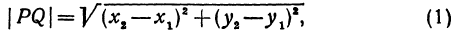
т. е. расстояние между двумя точками равно корню квадратному из суммы квадратов разностей координат.
Примечание:
Расстояние между двумя точками, так же как длина отрезка, всегда положительно, поэтому в формуле (1) перед квадратным корнем берут только знак плюс.
Пример:
Найти расстояние между точками Р (— 2, — 1) и Q (2, 2). Применяя формулу (1), получим
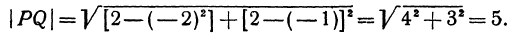
Пример:
Найти длину отрезка MN, если даны М (8, 2) и N(2, 10). Применяя формулу (1), получим
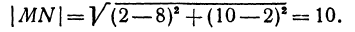
Задача:
Найти точку С, делящую отрезок PQ в отношении т : п, если известны координаты точек Р (х1, у1) и Q (х2, у2). По условию задачи надо найти такую точку С, чтобы было выполнено равенство
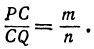
Решение:
Обозначим, как и выше, проекции точки Р на оси через А1 и В1, а проекции точки Q—через А2 и В2; тогда ОА1 = х1 , OB1 = y1, ОА2 =х2, ОВ2=у2 (рис. 11). Кроме того, обозначим координаты искомой точки С через х и у, а ее проекции на оси — через А и В, т. е. ОА = х, ОВ = у.
Так как прямые А1Р, АС и А2Q параллельны между собой, то на основании теоремы о пропорциональных отрезках можно записать, что
Но А1А = ОА — ОА1 = х—х1, АА2 = ОА2 — ОА = х2—х; поэтому, подставляя в равенство (*), будем иметь уравнение
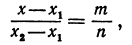
решая которое найдем абсциссу точки С:
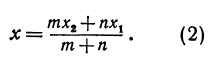
Рассуждая аналогично о проекциях на ось Оу, т. е. о точках В1, В и В2, получим ординату точки С, делящей отрезок в отношении т : п,
Итак, искомая точка С имеет координаты, определяемые равенствами (2) и (3).
Пример:
Найти точку, делящую в отношении 1:2 отрезок PQ, где Р (4, —3) и Q (8, 0). Здесь х1 = 4, у1 = — 3, х2 = 8, у2 = 0, т = 1, п = 2. Применяя формулы (2) и (3), получим:
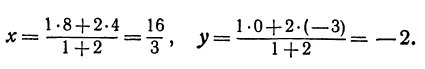
Пример:
Найти точку, делящую расстояние между точками А (4, 2) и B (8, 10) в отношении 3 : 1. Здесь х1=-4, у1 = 2, х2 = 8, у2= 10, т = 3, п = 1. По формулам (2) и (3) находим:
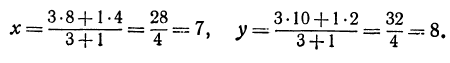
Следствие (из формул (2) и (3)). Если точка С делит отрезок РQ пополам, то т = n, поэтому
т. е. абсцисса середины отрезка равна средней арифметической абсцисс его начала и конца; ордината середины отрезка равна средней арифметической ординат его начала и конца.
Задача:
Даны три вершины треугольника: А (7, 0), В (4, 4) и С (7, 10). Найти длину биссектрисы угла A (рис. 12).
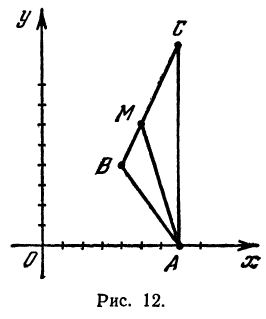
Найдем длины сторон АВ и АС. Для этого применим формулу (1):
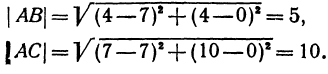
Обозначим точку пересечения биссектрисы угла А с противоположной стороной ВС через М, а ее координаты—через х и у. Помня, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам, можно утверждать, что точка М делит отрезок ВС в отношении 5 : 10 =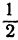 
; поэтому, применяя формулы (2) и (3), получим:
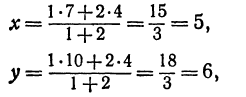
т. е. М (5, 6).
Теперь вычисляем длину биссектрисы между точками А(7, 0) и М(5, 6):
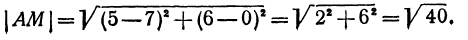
Задача:
Найти точку пересечения медиан треугольника, вершинами которого являются точки А(4, 6), В(—8, 10), С( —2, —6) (рис. 13).
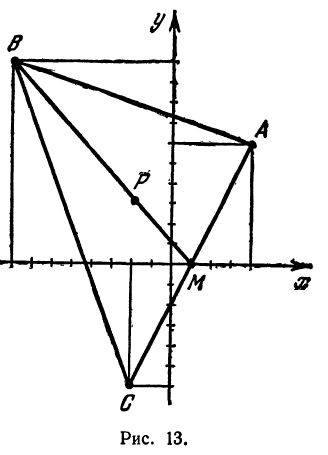
Точка пересечения медиан делит каждую из медиан в отношении 2:1, считая от вершины треугольника. Обозначим через М середину стороны АС; по формулам (4) и (5) можно найти ее координаты:
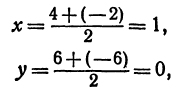
т. е. М(19 0). Точка Р пересечения медиан делит отрезок ВМ в отношении 2:1, поэтому ее координаты найдутся по формулам (2)
и (3):
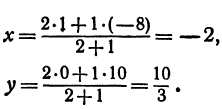
Итак, искомая точка
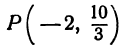
Задача:
Записать условие того, что точка М (х, у) находится на расстоянии По формуле (1) имеем
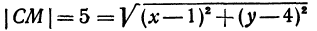
или, возводя обе части равенства в квадрат, получим
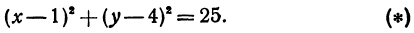
Это равенство есть уравнение с двумя неизвестными х и у. Этому уравнению удовлетворяют координаты любой точки, лежащей на расстоянии 5 от точки С. Иначе говоря, ему удовлетворяют координаты любой точки, принадлежащей геометрическому месту точек, расстояние которых от точки С равно 5. Это геометрическое место есть окружность.
Следовательно, можно сказать, что уравнение (*) есть уравнение окружности с центром в точке С и радиуса 5.
В следующих главах будут рассмотрены уравнения с двумя неизвестными х и у и те линии (геометрические места), точки которых имеют координаты, удовлетворяющие этим уравнениям.
Числовая ось
Числовой осью называют направленную прямую, на которой указывается начальная точка О и задается некоторый «эталон» длины Е. Каждой точке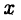 
этой прямой отвечает вещественное число, равное длине отрезка 
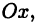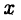если расположено правее точки О, и равное этой
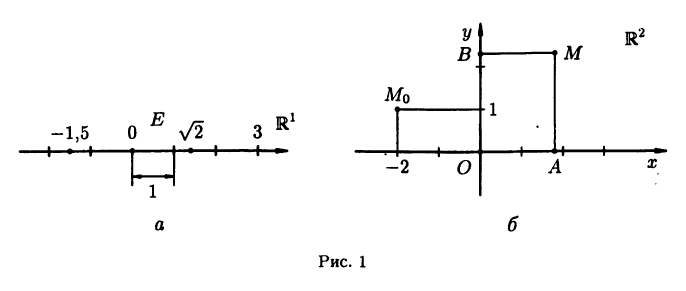
длине со знаком минус — в противном случае (см. рис. 1 а). Числовую ось будем обозначать 
(смысл этого обозначения прояснится ниже).
Указанное соответствие между точками числовой оси и множеством вещественных чисел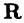 
является взаимно однозначным, т. е. каждой точке 
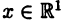соответствует единственное число 
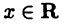, обратно, каждому числу 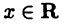соответствует единственная точка 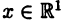Таким образом, множество 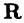. вещественных чисел можно отождествлять с числовой осью , чем мы будем впредь постоянно пользоваться.
Декартова система координат
Декартовой (прямоугольной) системой координат на плоскости называют две взаимно перпендикулярные числовые оси 
и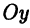 
, имеющие общее начало О и одинаковые единицы масштаба (см. рис. 1 б). Ось называют осью абсцисс, а ось 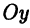— осью ординат. Плоскость 
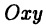называют координатной плоскостью и обозначают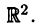 
Пусть М — произвольная точка координатной плоскости. Опустим из нее перпендикуляры МА и МВ на оси и 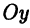соответственно. Декартовыми координатами точки М называют числа, которым соответствуют точки А к В. Например, точка 
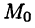имеет декартовы координаты 
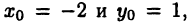что записывается в виде 
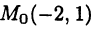Точка О имеет координаты (0,0).
Полярная система координат
В плоскости зададим луч — полярную ось, выходящий из точки О — полюса полярной системы координат (см. рис. 2 а). Произвольная точка М плоскости определяется парой чисел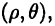 
называемой ее полярными координатами, где р — длина отрезка ОМ, а 
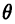— выраженный в радианах угол между ОМ и осью . Угол в считается положительным, если откладывается против часовой стрелки, и отрицательным в противоположном случае. Точка О имеет полярные координаты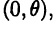 
где 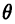— любой угол.
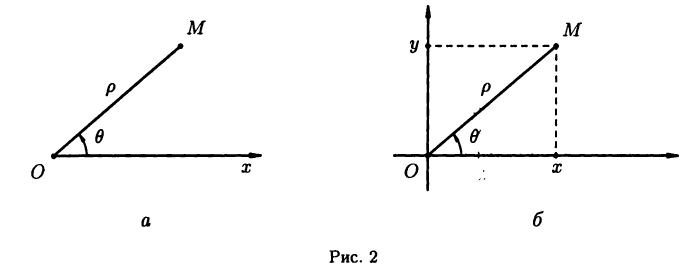
Полярные и декартовы координаты, заданные на одной плоскости (см. рис. 2 6), связаны очевидными равенствами:
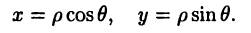
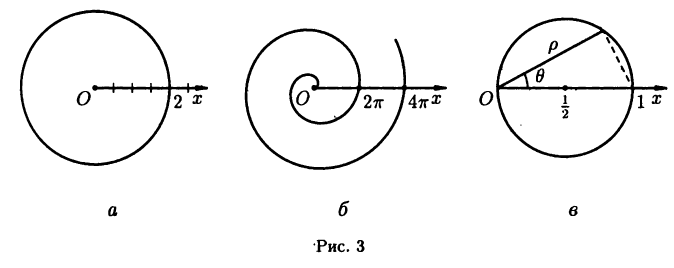
Полярные координаты удобны для задания многих кривых. Например, уравнение р=2 описывает окружность, изображенную на рис. За. Уравнение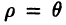 
описывает спираль Архимеда (рис . Уравнение 
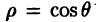описывает окружность с диаметром 1 и с центром в точке 
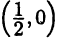(рис. Зв).
Системы координат в пространстве
Декартова система координат в пространстве определяется тремя взаимно перпендикулярными осям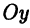и , и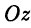 
, называемыми соответственно осями абсцисс, ординат и аппликат (см. рис. 4 а). Проcтранство 
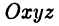обозначают 
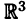. Положение точки М в 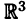определяется тройкой чисел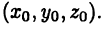 
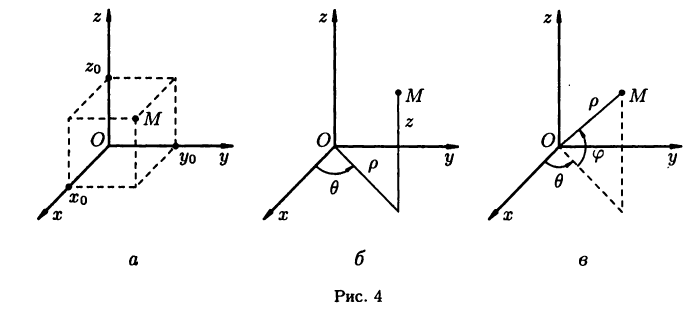
Аналогами полярной системы координат в пространстве служат цилиндрическая и сферическая системы координат.
Цилиндрическая система координат (рис. 4 б) представляет собой объединение полярной системы координат в плоскости 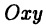с аппликатой z:
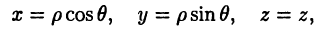
где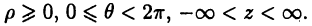 
Сферическая система координат (рис. 4 в) связана с декартовой системой равенствами
где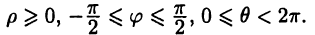 
Пространство
Пространство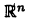 
На плоскости и в пространстве положение точки в декартовых координатах полностью определяется соответственно, парой и тройкой чисел вида [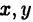
) и (x,y,z). Желая обобщить эти геометрические подходы, в анализе вводят понятие пространства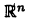
Упорядоченную систему из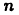 
вещественных чисел 
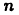называют -мерной точкой, а множество всех 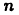-мерных точек называют 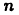—мерным пространством 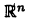или короче — пространством .
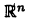Понятие пространства 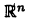естественно дополнить понятиями основных операций над его элементами. По определению полагают
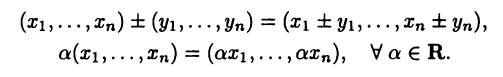
Наконец, обобщая известную из аналитической геометрии формулу, определяют расстояние между двумя точкам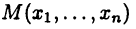и 
и 
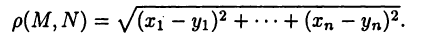
Прямую, плоскость и пространство можно рассматривать как пространства , 
и 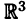соответственно. Ниже это будет практиковаться постоянно.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
Пример 1. Определить и построить на числовой оси области изменения переменных и
, заданные следующими неравенствами:
Рис. 1 Рис. 2
2) Избавляясь от знака абсолютной величины в неравенстве, содержащем , получим два неравенства:
и
Как обозначать числа с пи на числовой окружности?
Надеюсь, вы уже прочитали про числовую окружность и знаете, почему она называется числовой, где на ней начало координат и в какой стороне положительное направление. Если нет, то бегом читать ! Если вы, конечно, собираетесь находить точки на числовой окружности.
Обозначаем числа (2π), (π), (frac<π><2>), (-frac<π><2>), (frac<3π><2>)
Как вы знаете из прошлой статьи, радиус числовой окружности равен (1). Значит, длина окружности равняется (2π) (вычислили по формуле (l=2πR)). С учетом этого отметим (2π) на числовой окружности. Чтобы отметить это число нужно пройти от (0) по числовой окружности расстояние равно (2π) в положительном направлении, а так как длина окружности (2π), то получается, что мы сделаем полный оборот. То есть, числу (2π) и (0) соответствует одна и та же точка. Не переживайте, несколько значений для одной точки – это нормально для числовой окружности.
Теперь обозначим на числовой окружности число (π). (π) – это половина от (2π). Таким образом, чтобы отметить это число и соответствующую ему точку, нужно пройти от (0) в положительном направлении половину окружности.
Отметим точку (frac<π><2>) . (frac<π><2>) – это половина от (π), следовательно чтобы отметить это число, нужно от (0) пройти в положительном направлении расстояние равное половине (π), то есть четверть окружности.
Обозначим на окружности точки (-) (frac<π><2>) . Двигаемся на такое же расстояние, как в прошлый раз, но в отрицательном направлении.
Нанесем (-π). Для этого пройдем расстояние равное половине окружности в отрицательном направлении.
Теперь рассмотрим пример посложнее. Отметим на окружности число (frac<3π><2>) . Для этого дробь (frac<3><2>) переведем в смешанный вид (frac<3><2>) (=1) (frac<1><2>) , т.е. (frac<3π><2>) (=π+) (frac<π><2>) . Значит, нужно от (0) в положительную сторону пройти расстояние в пол окружности и еще в четверть.
Задание 1. Отметьте на числовой окружности точки (-2π),(-) (frac<3π><2>) .
Обозначаем числа (frac<π><4>), (frac<π><3>), (frac<π><6>)
Выше мы нашли значения в точках пересечения числовой окружности с осями (x) и (y). Теперь определим положение промежуточных точек. Для начала нанесем точки (frac<π><4>) , (frac<π><3>) и (frac<π><6>) .
(frac<π><4>) – это половина от (frac<π><2>) (то есть, (frac<π><4>) (=) (frac<π><2>) (:2)) , поэтому расстояние (frac<π><4>) – это половина четверти окружности.
(frac<π><4>) – это треть от (π) (иначе говоря, (frac<π><3>) (=π:3)), поэтому расстояние (frac<π><3>) – это треть от полукруга.
(frac<π><6>) – это половина (frac<π><3>) (ведь (frac<π><6>) (=) (frac<π><3>) (:2)) поэтому расстояние (frac<π><6>) – это половина от расстояния (frac<π><3>) .
Вот так они расположены друг относительно друга:
Замечание: Расположение точек со значением (0), (frac<π><2>) ,(π), (frac<3π><2>) , (frac<π><4>) , (frac<π><3>) , (frac<π><6>) лучше просто запомнить. Без них числовая окружность, как компьютер без монитора, вроде бы и полезная штука, а использовать крайне неудобно.
Разные расстояние на окружности наглядно:
Обозначаем числа (frac<7π><6>), (-frac<4π><3>), (frac<7π><4>)
Обозначим на окружности точку (frac<7π><6>) , для этого выполним следующие преобразования: (frac<7π><6>) (=) (frac<6π + π><6>) (=) (frac<6π><6>) (+) (frac<π><6>) (=π+) (frac<π><6>) . Отсюда видно, что от нуля в положительную сторону надо пройти расстояние (π), а потом еще (frac<π><6>) .
Отметим на окружности точку (-) (frac<4π><3>) . Преобразовываем: (-) (frac<4π><3>) (=-) (frac<3π><3>) (-) (frac<π><3>) (=-π-) (frac<π><3>) . Значит надо от (0) пройти в отрицательную сторону расстояние (π) и еще (frac<π><3>) .
Нанесем точку (frac<7π><4>) , для этого преобразуем (frac<7π><4>) (=) (frac<8π-π><4>) (=) (frac<8π><4>) (-) (frac<π><4>) (=2π-) (frac<π><4>) . Значит, чтобы поставить точку со значением (frac<7π><4>) , надо от точки со значением (2π) пройти в отрицательную сторону расстояние (frac<π><4>) .
Обозначаем числа (10π), (-3π), (frac<7π><2>) ,(frac<16π><3>), (-frac<21π><2>), (-frac<29π><6>)
Запишем (10π) в виде (5 cdot 2π). Вспоминаем, что (2π) – это расстояние равное длине окружности, поэтому чтобы отметить точку (10π), нужно от нуля пройти расстояние равное (5) окружностям. Нетрудно догадаться, что мы окажемся снова в точке (0), просто сделаем пять оборотов.
Из этого примера можно сделать вывод:
Числам с разницей в (2πn), где (n∈Z) (то есть (n) – любое целое число) соответствует одна и та же точка.
То есть, чтобы поставить число со значением больше (2π) (или меньше (-2π)), надо выделить из него целое четное количество (π) ((2π), (8π), (-10π)…) и отбросить. Тем самым мы уберем из числа, не влияющие на положение точки «пустые обороты».
Точке, которой соответствует (0), также соответствуют все четные количества (π) ((±2π),(±4π),(±6π)…).
Теперь нанесем на окружность (-3π). (-3π=-π-2π), значит (-3π) и (–π) находятся в одном месте на окружности (так как отличаются на «пустой оборот» в (-2π)).
Кстати, там же будут находиться все нечетные (π).
Точке, которой соответствует (π), также соответствуют все нечетные количества (π) ((±π),(±3π),(±5π)…).
Сейчас обозначим число (frac<7π><2>) . Как обычно, преобразовываем: (frac<7π><2>) (=) (frac<6π><2>) (+) (frac<π><2>) (=3π+) (frac<π><2>) (=2π+π+) (frac<π><2>) . Два пи – отбрасываем, и получается что, для обозначения числа (frac<7π><2>) нужно от нуля в положительную сторону пройти расстояние равное (π+) (frac<π><2>) (т.е. половину окружности и еще четверть).
Отметим (frac<16π><3>) . Вновь преобразования: (frac<16π><3>) (=) (frac<15π + π><3>) (=) (frac<15π><3>) (+) (frac<π><3>) (=5π+) (frac<π><3>) (=4π+π+) (frac<π><3>) . Ясно, что от нуля надо пройти расстояние равное (π+) (frac<π><3>) – и мы найдем место точки (frac<16π><3>) .
Нанесем на окружность число (-) (frac<21π><2>) .
(-) (frac<21π><2>) (= -) (frac<20π><2>) (-) (frac<π><2>) (=-10π-) (frac<π><2>) . Значит, место (-) (frac<21π><2>) совпадает с местом числа (-) (frac<π><2>) .
Обозначим (-) (frac<29π><6>) .
(-) (frac<29π><6>) (=-) (frac<30π><6>) (+) (frac<π><6>) (=-5π+) (frac<π><6>) (=-4π-π+) (frac<π><6>) . Для обозначение (-) (frac<29π><6>) , на числовой окружности надо от точки со значением (–π) пройти в положительную сторону (frac<π><6>) .
Единичная числовая окружность на координатной плоскости
п.1. Понятие тригонометрии
Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов. Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., – спроектирован с использованием тригонометрии.
Базовым объектом изучения в тригонометрии является угол.
Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.
п.2. Числовая окружность
Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.
 |
Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0). Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0. Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным . |
| Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90°, –120°, –180°. |  |
п.3. Градусная и радианная мера угла
Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).
В целом, более обоснованной и естественной для измерения углов является радианная мера.
 |
Найдем радианную меру прямого угла ∠AOB=90°. Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr. Длина дуги AB: (l_=frac<4>=frac<2pi r><4>=frac<pi r><2>.) Тогда радианная мера угла: $$ angle AOB=frac>=frac<pi r><2cdot r>=frac<pi> <2>$$ |
| 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 270° | 360° |
| (frac<pi><6>) | (frac<pi><4>) | (frac<pi><3>) | (frac<pi><2>) | (frac<2pi><3>) | (frac<3pi><4>) | (frac<5pi><6>) | (pi) | (frac<3pi><2>) | (2pi) |
п.4. Свойства точки на числовой окружности
Построим числовую окружность. Обозначим O(0;0), A(1;0)
 |
Каждому действительному числу t на числовой окружности соответствует точка Μ(t). При t=0, M(0)=A. При t>0 двигаемся по окружности против часовой стрелки, описывая дугу ⌒ AM=t. Точка M – искомая. При t Например: |
| Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<pi><4>, frac<pi><2>, frac<2pi><3>, pi), а также (-frac<pi><6>, -frac<pi><4>, -frac<pi><2>, -frac<2pi><3>, -pi) Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности. |
 |
| Отметим на числовой окружности точки, соответствующие (frac<pi><6>, frac<13pi><6>, frac<25pi><6>), и (-frac<11pi><6>). Все четыре точки совпадают, т.к. begin Mleft(frac<pi><6>right)=Mleft(frac<pi><6>+2pi kright)\ frac<pi><6>-2pi=-frac<11pi><6>\ frac<pi><6>+2pi=frac<13pi><6>\ frac<pi><6>+4pi=frac<25pi> <6>end |
 |
п.5. Интервалы и отрезки на числовой окружности
Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.
| Числовой промежуток | Соответствующая дуга числовой окружности |
| Отрезок | |
$$ -frac<pi> <6>lt t lt frac<pi> <3>$$  а также, с учетом периода $$ -frac<pi><6>+2pi klt tltfrac<pi><3>+2pi k $$ |
 |
| Интервал | |
$$ -frac<pi> <6>leq t leq frac<pi> <3>$$  а также, с учетом периода $$ -frac<pi><6>+2pi kleq tleqfrac<pi><3>+2pi k $$ |
 |
| Полуинтервал | |
$$ -frac<pi> <6>leq t ltfrac<pi> <3>$$  а также, с учетом периода $$ -frac<pi><6>+2pi kleq tltfrac<pi><3>+2pi k $$ |
 |
п.6. Примеры
Пример 1. Точка E делит числовую окружность во второй четверти в отношении 1:2.
Чему равны дуги AE, BE, EC, ED в градусах и радианах?
Угловая мера четверти 90°. При делении в отношении 1:2 получаем дуги 30° и 60° соответственно: begin BE=30^<circ>=frac<pi><6>.\ EC=60^<circ>=frac<pi><3>.\ AE=EC+CD=90^<circ>+30^<circ>=120^<circ>=frac<2pi><3>.\ ED=EC+CD=60^<circ>+90^<circ>=150^<circ>=frac<5pi><6>. end
Пример 2. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<pi><2>; frac<3pi><4>; frac<7pi><6>; frac<7pi><4>).
| Находим соответствующие углы в градусах и откладываем с помощью транспортира (положительные – против часовой стрелки, отрицательные – по часовой стрелке), отмечаем соответствующие точки на числовой окружности. begin -frac<pi><2>=-90^<circ>, frac<3pi><4>=135^<circ>\ frac<7pi><6>=210^<circ>, frac<7pi><4>=315^ <circ>end |  |
Пример 3. Найдите на числовой окружности точку, соответствующую данному числу: (-frac<11pi><2>; 5pi; frac<17pi><6>; frac<27pi><4>).
| Выделяем из дроби целую часть, отнимаем/прибавляем один или больше полных оборотов (2πk – четное количество π), чтобы попасть в промежуток от 0 до 2π. Далее – действуем, как в примере 2. begin -frac<11pi><2>=frac<-12+1><2>cdotpi=-6pi+frac<pi><2>rightarrow frac<pi><2>=90^<circ>\ 5pi=4pi+pirightarrow pi=180^<circ>\ frac<17pi><6>=frac<18-1><6>pi=3pi-frac<pi><6>rightarrow pi-frac<pi><6>=frac<5pi><6>\ frac<27pi><4>=frac<28-1><4>pi=7pi-frac<pi><4>rightarrow pi-frac<pi><4>=frac<3pi> <4>end |
 |
Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.
 |
Сравниваем каждое число с границами четвертей: begin 0, fracpi2approxfrac<3,14><2>=1,57, piapprox 3,14\ 3pi 3cdot 3,14\ frac<3pi><2>approx frac<3cdot 3,14><2>=4,71, 2piapprox 6,28 end |
(fracpi2lt 2lt pi Rightarrow ) угол 2 радиана находится во 2-й четверти
(pilt 4lt frac<3pi> <2>Rightarrow ) угол 4 радиана находится в 3-й четверти
(frac<3pi><2>lt 5lt 2pi Rightarrow ) угол 5 радиана находится в 4-й четверти
(7gt 2pi), отнимаем полный оборот: (0lt 7-2pilt fracpi2Rightarrow) угол 7 радиан находится в 1-й четверти.
Пример 5. Изобразите на числовой окружности множество точек ((kinmathbb)), запишите количество полученных базовых точек.
Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.
Как найти на числовой окружности п 12
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.
Единичной окружностью называют окружность радиуса 1.
Общий вид числовой окружности.
1) Ее радиус принимается за единицу измерения.
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти (см.рисунок). Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.
Соответственно:
первая четверть – это дуга AB
вторая четверть – дуга BC
третья четверть – дуга CD
четвертая четверть – дуга DA
4) Начальная точка числовой окружности – точка А.
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.
Числовая окружность на координатной плоскости.
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный – оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Значения x и y в четвертях числовой окружности:
x 0, y Основные величины числовой окружности:
Величина
в радианах
Величина
в радиусах
Имена и местонахождение основных точек числовой окружности:
Как запомнить имена числовой окружности.
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2π) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка – это 2π (крайняя правая точка на оси х, равная 1).
Как вы знаете, 2π – это длина окружности. Значит, половина окружности – это 1π или π. Ось х делит окружность как раз пополам. Соответственно, крайняя левая точка на оси х, равная -1, называется π.
Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность – это π, то половина полуокружности – это π/2.
Одновременно π/2 – это и четверть окружности. Отсчитаем три таких четверти от первой до третьей – и мы придем в крайнюю нижнюю точку на оси у, равной -1. Но если она включает три четверти – значит имя ей 3π/2.
2) Теперь перейдем к остальным точкам. Обратите внимание: все противоположные точки имеют одинаковый числитель – причем это противоположные точки и относительно оси у, и относительно центра осей, и относительно оси х. Это нам и поможет знать их значения точек без зубрежки.
Надо запомнить лишь значение точек первой четверти: π/6, π/4 и π/3. И тогда мы «увидим» некоторые закономерности:
– Относительно оси у в точках второй четверти, противоположных точкам первой четверти, числа в числителях на 1 меньше величины знаменателей. К примеру, возьмем точку π/6. Противоположная ей точка относительно оси у тоже в знаменателе имеет 6, а в числителе 5 (на 1 меньше). То есть имя этой точки: 5π/6. Точка, противоположная π/4, тоже имеет в знаменателе 4, а в числителе 3 (на 1 меньше, чем 4) – то есть это точка 3π/4.
Точка, противоположная π/3, тоже имеет в знаменателе 3, а в числителе на 1 меньше: 2π/3.
– Относительно центра осей координат все наоборот: числа в числителях противоположных точек (в третьей четверти) на 1 больше значения знаменателей. Возьмем опять точку π/6. Противоположная ей относительно центра точка тоже имеет в знаменателе 6, а в числителе число на 1 больше – то есть это 7π/6.
Точка, противоположная точке π/4, тоже имеет в знаменателе 4, а в числителе число на 1 больше: 5π/4.
Точка, противоположная точке π/3, тоже имеет в знаменателе 3, а в числителе число на 1 больше: 4π/3.
– Относительно оси х (четвертая четверть) дело посложнее. Здесь надо к величине знаменателя прибавить число, которое на 1 меньше – эта сумма и будет равна числовой части числителя противоположной точки. Начнем опять с π/6. Прибавим к величине знаменателя, равной 6, число, которое на 1 меньше этого числа – то есть 5. Получаем: 6 + 5 = 11. Значит, противоположная ей относительно оси х точка будет иметь в знаменателе 6, а в числителе 11 – то есть 11π/6.
Точка π/4. Прибавляем к величине знаменателя число на 1 меньше: 4 + 3 = 7. Значит, противоположная ей относительно оси х точка имеет в знаменателе 4, а в числителе 7 – то есть 7π/4.
Точка π/3. Знаменатель равен 3. Прибавляем к 3 на единицу меньшее число – то есть 2. Получаем 5. Значит, противоположная ей точка имеет в числителе 5 – и это точка 5π/3.
3) Еще одна закономерность для точек середин четвертей. Понятно, что их знаменатель равен 4. Обратим внимание на числители. Числитель середины первой четверти – это 1π (но 1 не принято писать). Числитель середины второй четверти – это 3π. Числитель середины третьей четверти – это 5π. Числитель середины четвертой четверти – это 7π. Получается, что в числителях середин четвертей – четыре первых нечетных числа в порядке их возрастания:
(1)π, 3π, 5π, 7π.
Это тоже очень просто. Поскольку середины всех четвертей имеют в знаменателе 4, то мы уже знаем их полные имена: π/4, 3π/4, 5π/4, 7π/4.
Особенности числовой окружности. Сравнение с числовой прямой.
Как вы знаете, на числовой прямой каждая точка соответствует единственному числу. К примеру, если точка А на прямой равна 3, то она уже не может равняться никакому другому числу.
На числовой окружности все иначе, поскольку это окружность. К примеру, чтобы из точки А окружности прийти к точке M, можно сделать это, как на прямой (только пройдя дугу), а можно и обогнуть целый круг, а потом уже прийти к точке M. Вывод:
Пусть точка M равна какому-то числу t. Как мы знаем, длина окружности равна 2π. Значит, точку окружности t мы можем записать двояко: t или t + 2π. Это равнозначные величины.
То есть t = t + 2π. Разница лишь в том, что в первом случае вы пришли к точке M сразу, не делая круга, а во втором случае вы совершили круг, но в итоге оказались в той же точке M. Таких кругов можно сделать и два, и три, и двести. Если обозначить количество кругов буквой k, то получим новое выражение:
t = t + 2πk.
Отсюда формула:
Если точка M числовой окружности равна числу t, то она равна и числу вида t + 2πk, где k – любое целое число:
M(t) = M(t + 2πk),
где k ∈ Z.
Число k называется параметром.
Уравнение числовой окружности
(второе уравнение – в разделе «Синус, косинус, тангенс, котангенс»):
[spoiler title=”источники:”]
http://reshator.com/sprav/algebra/10-11-klass/edinichnaya-chislovaya-okruzhnost-na-koordinatnoj-ploskosti/
http://raal100.narod.ru/index/0-287
[/spoiler]
