-
Общее уравнение
плоскости
Всякое уравнение
первой степени определяет в заданной
прямоугольной системе координат
плоскость.
Уравнение вида:
(27)
называется общим
уравнением плоскости. Вектор
,
перпендикулярный плоскости, называется
нормальным вектором плоскости.
-
Уравнение
плоскости, проходящей через точку
перпендикулярную вектору
Если плоскость
проходит через точку
перпендикулярно вектору
,
то её уравнение имеет вид:
(28)
-
Уравнение
плоскости, проходящей через три точки
в отрезках
Пусть плоскость
проходит через точки
,
,
.
Имеет вид:
(29)
Если плоскость
отсекает по осям координат соответственно
отрезку
,
,
и,
то её уравнение имеет вид:
(30)
-
Угол между
плоскостями. Условия параллельности
и перпендикулярности плоскостей
Угол
между плоскостями
и
определяется по формуле:
(31)
Условие параллельности
плоскостей:
(32)
Условие
перпендикулярности плоскостей:
(33)
-
Расстояние
от точки до плоскости
Расстояние от
точки
до плоскости
находится по формуле:
(34)
Пример 1. Составить
уравнение плоскости, проходящей через
точку
перпендикулярно вектору
.
Решение. Воспользуемся
уравнением (28). Здесь
;
;
;
;
;
.
Получим:
или
.
Пример 2. Найти
отрезки, отсекаемые плоскостью
на осях координат.
Решение. Преобразуем
данноё уравнение плоскости к уравнению
в отрезках (30) следующим образом:
;
Следовательно,
величины отрезков, отсекаемых на осях,
равны:
;
;
Пример 3. Найти
расстояние между параллельными
плоскостями
и
Решение. Возьмём
на одной из плоскостей произвольную
точку и определим её расстояние от
другой плоскости. Например, на первой
плоскости выберем точку
и найдём её расстояние до плоскости
,
пользуясь формулой (33):
Пример 4. Определить
угол, образованный плоскостями
и
.
Решение. Воспользуемся
формулой (31)
-
Вопросы для
самопроверки
Как определяется
общее уравнение плоскости?
Какой вектор
называется нормальным к плоскости и
как определяются его координаты из
общего уравнения плоскости?
Как записывается
уравнение плоскости, проходящей через
точку перпендикулярно вектору?
Запишите уравнения
плоскости через три точки; в отрезках.
Как определяется
угол между плоскостями? Сформулируйте
условия параллельности и перпендикулярности
плоскостей.
Как определяется
расстояние от точки до плоскости?
-
Примеры для
самостоятельного решения-
Составить
уравнение плоскости, проходящей через
точку
м перпендикулярной вектору
.
-
Составить
уравнение плоскости, проходящей через
точку
и отсекающей равны отрезки на осях
координат. -
Составить
уравнение плоскости, проходящей через
точки
.
Через точкупровести плоскость, параллельно
плоскости.
-
Составить
уравнение плоскости, проходящей через
точку
перпендикулярно плоскостям
и
.
-
Найти угол между
плоскостями
и
.
-
При каких
значениях
и
уравнения
и
определяют параллельные плоскости?
-
При каком значении
уравнение
и
определяют взаимно перпендикулярные
плоскости? -
Найти высоту
пирамиды
,
опущенную из вершинына грань АВС, если
,
,
,
.
Указание. Данную высоту можно найти
как расстояние от точкидо плоскости АВС.
-
Найти длину
перпендикуляра, опущенного из точки
на плоскость
.
-
Составить
уравнение плоскостей, параллельных
плоскости
и отстоящих от неё на расстоянии
-
-
Ответы к
примерам
4.7.1.
. 4.7.2.
.
4.7.3.
. 4.7.4.
.
4.7.5.
. 4.7.6.
.
4.7.7.
;
. 4.7.8.
.
4.7.9.
.
4.7.10.,
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.
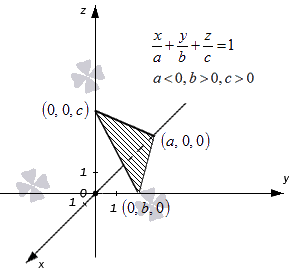
Уравнение плоскости в отрезках – описание и примеры
Уравнение плоскости в отрезках имеет вид xa+yb+zc=1 , где a, b и c – это действительные числа, отличные от нуля. Абсолютные величины чисел a, b и c равны длинам отрезков, которые отсекаются плоскостью на осях координат Oх, Oу и Oz в трехмерной системе координат Oхуz. Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.
Действительно, координаты точек a, 0, 0, 0, b, 0, 0, 0, c удовлетворяют уравнению плоскости в отрезках:
aa+0b+0c=1=1⇔1=10a+bb+0c=1=1⇔1=10a+0b+cc=1=1⇔1=1
Поясним этот момент, расположив заданные точки на графике.
Проиллюстрируем описанное выше примером.
Плоскость проходит через точки -2, 0, 0, 0, 3, 0 и 0, 0, -12 на осях координат в прямоугольной системе координат Oxyz. Необходимо записать уравнение плоскости в отрезках.
Решение
Определим положение отрезков, отсекаемых плоскостью на осях координат. На оси абсцисс откладываем в отрицательном направлении отрезок длиной 2 единицы. На оси ординат в положительном направлении откладываем отрезок длиной 3 . На оси аппликат в отрицательном направлении откладываем отрезок длиной 12 .
При этом, уравнение плоскости в отрезках будет иметь вид: x-2+y3+z-12=1 .
Ответ: x-2+y3+z-12=1
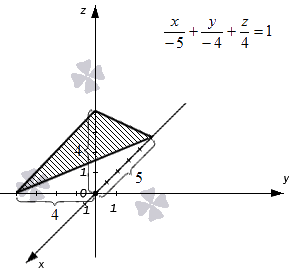
Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.
Плоскость в прямоугольной системе координат Oхуz задана уравнением плоскости в отрезках вида x-5+y-4+z4=1 . Необходимо изобразить эту плоскость на графике.
Решение
Изобразим оси координат, обозначаем начало координат и единичные отрезки на осях. Отмечаем длины отрезков, отсекаемых плоскостью, на каждой из осей. Соединяем концевые точки отрезков прямыми линиями. Полученная плоскость имеет вид треугольника. Она соответствует заданному уравнению плоскости в отрезках x-5+y-4+z4=1 .
Ответ:
Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки a, 0, 0, 0, b, 0, 0, 0, c и соединить их прямыми линиями.
Приведение общего уравнения плоскости к уравнению плоскости в отрезках
Мы имеем общее уравнение плоскости в пространстве вида Ax+By+Cz+D=0 . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.
Не получится перевести общее уравнение плоскости в пространстве в уравнение плоскости в отрезках в тех случаях, когда плоскость проходит через одну из координатных осей или располагается параллельно оси. Другими словами, мы можем работать лишь с полным уравнением плоскости вида Ax+By+Cz+D=0, где A≠0, B≠0, C≠0, D≠0 .
Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое D в правую часть уравнения с противоположным знаком.
Ax+By+Cz+D=0⇔Ax+By+Cz=-D
Так как D≠0 , то обе части полученного уравнения можно разделить на –D: A-Dx+B-Dy+C-Dz=1 .
Так как A≠0, B≠0, C≠0 , то мы можем отправить в знаменатели коэффициенты перед переменными x, y и z. Последнее уравнение эквивалентно равенству x-DA+y-DB+z-DC=1 . При этом мы использовали очевидное равенство pq=1qp, p, q∈R, p≠0, q≠0 .
В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить -DA=a, -DB=b, -DC=c.
Разберем решение примера.
Плоскость в прямоугольной системе координат Oxyz в пространстве задана уравнением вида 3x+9y-6z-6=0 . Переведем это уравнение в уравнение плоскости в отрезках.
Решение
Данное в условии задачи уравнение является полным уравнением плоскости. Это дает нам возможность привески его к уравнению плоскости в отрезках. Перенесем -6 в правую часть равенства, а затем разделим обе части равенства на 6:
3x+9y-6z-6=0⇔3x+9y+6z=63x+9y-6z=6⇔12x+32y-z=1
Коэффициенты при переменных x, y и z отправим в знаменатели: 12x+32y-z=1⇔x2+y23+z-1=1 . Полученное уравнение и есть уравнение плоскости в отрезках.
Ответ: x2+y23+z-1=1
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Окружность отсекает отрезки на осях
Какие отрезки на координатных осях отсекает плоскость 2x + 3y – 5 z + 30 = 0?
У точки, лежащей на оси Ox, координаты y и z равны нулю.
Полагая в уравнении плоскости y = z = 0, получим для определения величины отрезка, отсекаемого плоскостью на оси Oy, полагаем в уравнении плоскости x = 0 и z = 0 и получаем 3y + 30 = 0, или y = -10. Наконец, величину отрезка, отсекаемого на оси Oz, найдем, положив в уравнении плоскости x = 0 и y = 0. Получим -5z + 30 = 0 и z = 6.
Этим заканчивается решение задачи. Можно было бы поступить и проще, преобразовав данное уравнение к виду в отрезках на осях
Для этого перенесем в правую часть равенства свободный член. Данное уравнение запишется в виде 2x + 3y – 5z = -30.
Разделим теперь обе его части на -30 и получим
Величины отрезков, отсекаемых на координатных осях, равны:
Найти длину отрезка, отсекаемого окружностью x ^ 2 + y ^ 2 – 5x – 6y + 4 = 0 от оси ординат?
Математика | 5 – 9 классы
Найти длину отрезка, отсекаемого окружностью x ^ 2 + y ^ 2 – 5x – 6y + 4 = 0 от оси ординат.
Даны варианты ответа.
y1 – 2 = (6 + – √20) / 2 = 3 + – √5
длина отрезка = y2 – y1 = (3 + √5) – (3 – √5) = 3 – 3 + √5 + √5 = 2√5.
Найдите координаты точки пересечения отрезка АВ, А( – 4, 4)и В (2 ; 1)с осью ординат?
Найдите координаты точки пересечения отрезка АВ, А( – 4, 4)и В (2 ; 1)с осью ординат.
Окружность с центром О(5 ; 4) отсекает от прямой х + 2у – 3 = 0 хорду длиной 8?
Окружность с центром О(5 ; 4) отсекает от прямой х + 2у – 3 = 0 хорду длиной 8.
Вычислите длину окружности и площадь круга, ограничиваемой данной окружностью.
Составить уравнение прямой которая проходит через точку С (3 ; – 7) и отсекает на координатных осях, отличных от нуля отрезки одинаковой длины?
Составить уравнение прямой которая проходит через точку С (3 ; – 7) и отсекает на координатных осях, отличных от нуля отрезки одинаковой длины.
Сечение цилиндра параллельно его оси отсекает от окружности основания дугу в 120 радиус основания 6см?
Сечение цилиндра параллельно его оси отсекает от окружности основания дугу в 120 радиус основания 6см.
Сечение цилиндра плоскостью, параллельной оси, отсекает от окружности основания дугу в 120º?
Сечение цилиндра плоскостью, параллельной оси, отсекает от окружности основания дугу в 120º.
Найти площадь сечения, если высота цилиндра равна 7 см, а расстояние между осью цилиндра и секущей плоскостью равно 2см.
Даны точки А ( – 4 ; 4 ), В ( 2 ; 1)?
Даны точки А ( – 4 ; 4 ), В ( 2 ; 1).
Найдите координаты точки пересечения отрезка А В с осью ординат.
Как найти деаметр окружности если дана длинна?
Как найти деаметр окружности если дана длинна.
В цилиндре проведена параллельно его оси плоскость, отсекающая от окружности основания дугу в 120 градусов?
В цилиндре проведена параллельно его оси плоскость, отсекающая от окружности основания дугу в 120 градусов.
Высота цилиндра 12 см, расстояние плоскости от оси 4 см.
Найти площадь сечения.
В цилиндре проведена плоскость параллельная оси и отсекающая от окружности основания дугу в 120°?
В цилиндре проведена плоскость параллельная оси и отсекающая от окружности основания дугу в 120°.
Вычислите площадь сечения, если длинна оси равна 10 см, а её расстояние от секущей плоскости равно 2 см.
Являются ли графики функций у = kx и у = – kx симметричными относительно : а)оси абцисс б) оси ординат?
Являются ли графики функций у = kx и у = – kx симметричными относительно : а)оси абцисс б) оси ординат.
Вы зашли на страницу вопроса Найти длину отрезка, отсекаемого окружностью x ^ 2 + y ^ 2 – 5x – 6y + 4 = 0 от оси ординат?, который относится к категории Математика. По уровню сложности вопрос соответствует учебной программе для учащихся 5 – 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.
Уравнение прямой в отрезках на осях
Уравнение прямой в отрезках на осях позволяет строить прямую в координатной плоскости без каких-либо дополнительных вычислений.
при условии a≠0, b≠0, c≠0 (то есть прямая не параллельна ни одной из осей координат и не проходит через начало отсчёта).
Перепишем уравнение в виде
и разделим обе части на -с:
Это — уравнение прямой в отрезках на осях, так как числа m и n соответствуют длинам отрезков (с соответствующими знаками), которые прямая отсекает на осях координат (считая от начала отсчёта).
В самом деле, в точке пересечения с осью Ox y=0:
В точке пересечения с осью Oy x=0:
отсекает на оси Ox отрезок -2, на оси Oy — отрезок 4.
Отмечаем на координатной плоскости точки (-2; 0) и (0;4) и проводим через них прямую.
Прямая
отсекает на оси Ox отрезок 3, на оси Oy — отрезок -6.
Отмечаем точки (3;0) и (0;-6) и проводим через них прямую.
[spoiler title=”источники:”]
http://matematika.my-dict.ru/q/4563414_najti-dlinu-otrezka-otsekaemogo-okruznostu-x/
[/spoiler]
В 4:40 поступил вопрос в раздел Математика, который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку M (2, -3, 3) параллельно плоскости 3x+y-3z=0.
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике “Математика”. Ваш вопрос звучал следующим образом:
Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку M (2, -3, 3) параллельно плоскости 3x+y-3z=0.
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
2*x+8-8*y+10*z = 0-уравнение плоскости, которая проходит через данную точку параллельно данной плоскости. Теперь записываем уравнение плоскости в отрезках на осях, получаем длины отрезков.
——————-
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:
Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Евдокимова Любовь Германовна – автор студенческих работ, заработанная сумма за прошлый месяц 84 300 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
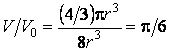
Таким образом,
плотность упаковки частицами пространства внутри вещества составляет .
ОТВЕТ: .
ЗАДАЧА 4. Определить
отрезки, отсекаемые на осях пространственной решетки плоскостью, заданной
индексами Миллера .
|
ДАНО: индексы |
|
А, В, |
АНАЛИЗ. Данная задача на основы кристаллографии. За единицы измерения
отрезков на координатных осях приняты периоды кристаллической решетки .
РЕШЕНИЕ. Запишем величины, обратные индексам плоскости . Общий знаменатель дробей 10. Умножим
дроби на общий знаменатель. Полученные числа определяют искомые отрезки .
ОТВЕТ: .
ЗАДАЧА 5. Какое наибольшее число линий может быть получено на
рентгенограмме, снятой на излучении с длиной волны Å
от кристалла простой кубической системы с параметром решетки Å.
АНАЛИЗ. Кристаллографические плоскости можно рассматривать как плоскости,
зеркально отражающие рентгеновские лучи. Расстояние d между параллельными плоскостями с индексами Миллера () для кубической системы
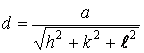
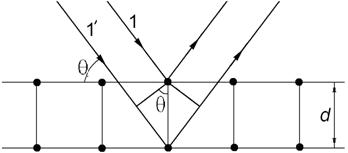
Рис. 3.2.7
Между лучами 1 и 1¢, падающими
под углом скольжения θ, возникает разность хода (рис.
3.2.7). При условии наблюдается максимум
первого порядка, который и фиксируется на рентгенограмме. Предполагается, что
образец имеет поликристаллическую структуру, и на его поверхность выходят
плоскости с разными индексами , а, следовательно,
и . Необходимо выделить все возможные
решения, вытекающие из условия .
Очевидно, что , а, следовательно,
. В нашем случае
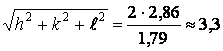
.
Составим таблицу возможных комбинаций .
Таблица
возможных комбинаций индексов Миллера .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
9 |
9 |
10 |
11 |