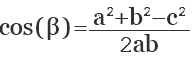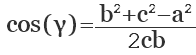Как найти величины углов треугольника 7 класс

Углы треугольника

Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.

α = 180°-β-γ

Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

a 2 = b 2 + c 2 + 2abc cos (α)

Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:

cos (α) = (b 2 + c 2 — a 2 ) / 2bc

,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.

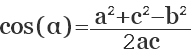
Нахождение углов треугольника по заданным сторонам

Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.

От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.

Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).

Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c” />
a” />
b” />

В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.

Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)

Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α	sin β	sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 – 2 bc · cos α

b 2 = a 2 + c 2 – 2 ac · cos β

c 2 = a 2 + b 2 – 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 – a 2

m_b = 1 2 √ 2 a 2 +2 c 2 – b 2

m_c = 1 2 √ 2 a 2 +2 b 2 – c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p – a ) b + c

l_b = 2√ acp ( p – b ) a + c

l_c = 2√ abp ( p – c ) a + b

где p = a + b + c 2 – полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b – c )( b + c – a )( c + a – b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k – коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://planetcalc.ru/534/

http://ru.onlinemschool.com/math/formula/triangle/

[/spoiler]

Как найти величину угла треугольника

Плоский треугольник в евклидовой геометрии составляют три угла, образованные его сторонами. Величины этих углов можно рассчитать несколькими способами. В силу того, что треугольник – одна из простейших фигур, существуют несложные формулы расчета, которые еще более упрощаются, если их применять к правильным и симметричным многоугольникам этого рода.

Инструкция

Если известны величины двух углов произвольного треугольника (β и γ), то величину третьего (α) можно определить исходя из теоремы о сумме углов в треугольнике. Она гласит, что эта сумма в евклидовой геометрии всегда равна 180°. То есть для нахождения единственного неизвестного угла в вершинах треугольника отнимайте от 180° величины двух известных углов: α=180°-β-γ.

Если речь идет о прямоугольном треугольнике, то для нахождения величины неизвестного острого угла (α) достаточно знать величину другого острого угла (β). Так как в таком треугольнике угол, лежащий напротив гипотенузы, всегда равен 90°, то для нахождения величины неизвестного угла отнимайте от 90° величину известного угла: α=90°-β.

В равнобедренном треугольнике тоже достаточно знать величину одного из углов, чтобы вычислить два других. Если известен угол (γ) между сторонами равной длины, то для вычисления обоих остальных углов найдите половину от разницы между 180° и величиной известного угла – эти углы в равнобедренном треугольнике будут равны: α=β=(180°-γ)/2. Из этого вытекает, что если известна величина одного из равных углов, то угол между равными сторонами можно определить как разницу между 180° и удвоенной величиной известного угла: γ=180°-2*α.

Если известны длины трех сторон (A, B, C) в произвольном треугольнике, то величину угла можно найти по теореме косинусов. Например, косинус угла (β), лежащего напротив стороны B, можно выразить как сумму возведенных в квадрат длин сторон A и C, уменьшенную на возведенную в квадрат длину стороны B и поделенную на удвоенное произведение длин сторон A и C: cos(β)=(A²+C²-B²)/(2*A*C). А чтобы найти величину угла, зная чему равен его косинус, надо найти его арк-функцию, то есть арккосинус. Значит β=arccos((A²+C²-B²)/(2*A*C)). Аналогичным способом можно найти величины углов, лежащих напротив остальных сторон в этом треугольнике.

Источники:

• величины углов

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Свойства углов треугольника

Треугольник – это центральная фигура геометрии. Он обладает многими удивительными свойствами. Два этих свойства, касающихся углов, мы сейчас повторим.

Пусть дан треугольник  с внутренними углами , , .

Теорема утверждает, что сумма внутренних углов треугольника равна  (см. Рис. 1).

Рис. 1. Иллюстрация к теореме о внутренних углах треугольника

Это теорема о внутренних углах треугольника.

Следующая теорема о внешнем угле треугольника.

Внешний угол треугольника равен сумме двух других внутренних углов, не смежных с ним (см. Рис. 2).

Рис. 2. Иллюстрация к теореме о внешнем угле треугольника

Из того, что сумма внутренних углов треугольника 180 градусов, вытекает наличие трех видов треугольников.

Виды треугольников

Первый – это остроугольный треугольник .

, ,

Например: (см. Рис. 3).

В сумме углы составляют , каждый из них меньше .

Рис. 3. Остроугольный треугольник

Тупоугольный треугольник (см. Рис. 4)

 – угол  тупой, т. е. лежит в пределах от 90 градусов до 180 градусов.

Например:

Тупым может быть только один угол.

Рис. 4. Тупоугольный треугольник

Прямоугольный треугольник (см. Рис. 5)

,

Например:

Рис. 5. Прямоугольный треугольник

Таким образом, мы рассмотрели все виды треугольников.

Теперь рассмотрим некоторые типовые задачи на углы треугольника.

Задача 1

Найдите угол  треугольника , если угол  равен 60 градусов, угол  равен 50 градусов (см. Рис. 6).

Рис. 6. Иллюстрация к задаче 1

Дано:

, , .

Найти: .

Решение

Ответ: .

Здесь мы воспользовались теоремой о внутренних углах треугольника.

Задача 2

Доказать, что углы при основании равнобедренного треугольника – острые (см. Рис. 7).

Дано: , .

Доказать: , .

Доказательство

Рис.7. Иллюстрация к задаче 2

В равнобедренном треугольнике углы при основании равны (по свойству равнобедренного треугольника): .

Пусть , тогда   . Это противоречит тому, что .

Что и требовалось доказать.

В предыдущих задачах фигурировали только внутренние углы треугольника. В следующей задаче присутствует внешний угол треугольника.

Задача 3

Найдите углы в треугольнике , если , внешний угол при вершине  равен 100 градусам (см. Рис. 8).

Дано: , , .

Найти:, , .

Решение

Рис. 8. Иллюстрация к задаче 3

Данный треугольник равнобедренный по условию.

Вспомним, что внешний угол  и внутренний угол  – смежные углы и в сумме осоставляют . Один из них дан, значит, можно найти другой, а если треугольник равнобедренный, то углы при основании равны , а, зная эти два угла, мы можем найти и третий угол.

Ответ: ; .

Задача 4

Найти сумму углов при всех вершинах пятиконечной звезды (см. Рис. 9).

Дано:  – звезда.

Найти: .

Решение

Рис. 9. Иллюстрация к задаче 4

Рассмотрим треугольник . В этом треугольнике угол при вершине  равен , так как угол  в этом треугольнике – внешний для треугольника .

 по той же теореме для треугольника .

При сложении всех трех углов треугольника получим:

Значит искомая сумма равняется .

Ответ: .

Примечание: данная сумма верна для пятиконечной звезды любой формы, с любыми углами.

Список литературы

1. Погорелов А.В. Геометрия. Учебник для 7-9 классов. – 2-е изд. – М.: 2014 – 240 с.

2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. – 5-е изд. – М.: Просвещение.

3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет портал «Школьный помощник» (Источник)

2. Интернет портал «Гипермаркет знаний» (Источник)

3. Интернет портал «Фестиваль педагогических идей» (Источник)

Домашнее задание

1. Чему равен угол при основании равнобедренного треугольника, если угол при его вершине на  больше угла при основании?

2. Определите величины углов равнобедренного треугольника , если внешний угол угла  при основании  равен .

3. Определите величины углов треугольника , если .

Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны

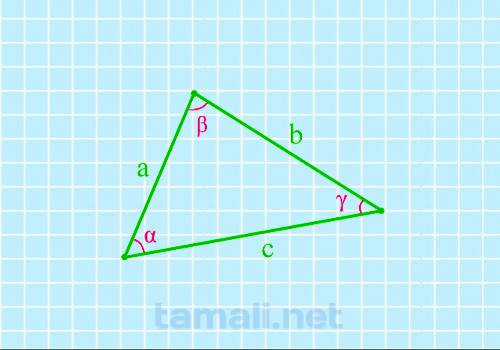
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

Угол прямоугольного треугольника через две стороны

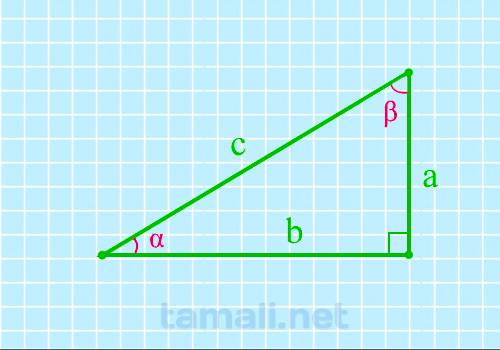
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

Острый угол прямоугольного треугольника через катет и площадь

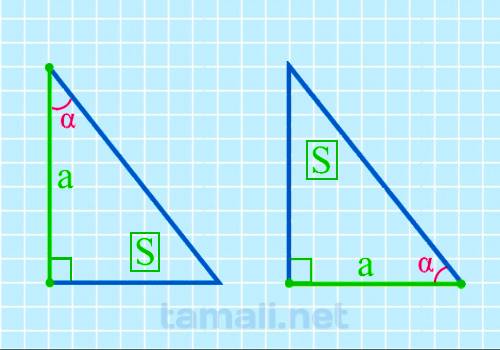
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

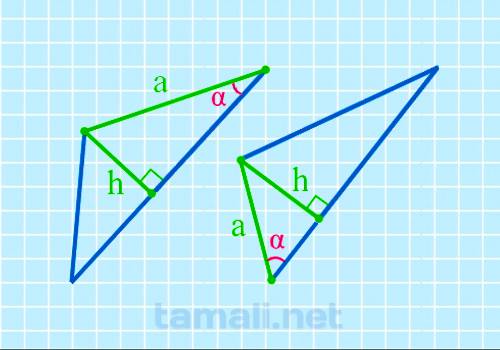
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

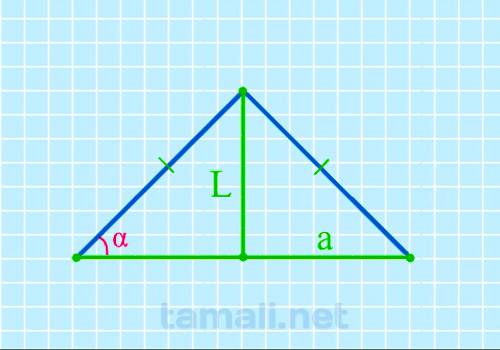
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

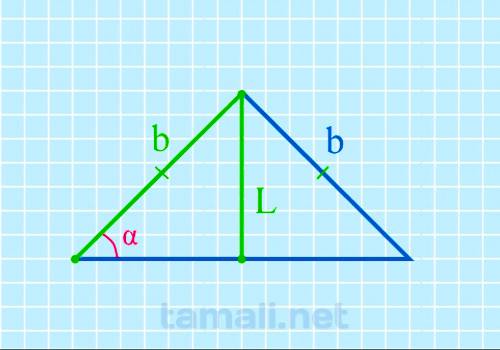
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

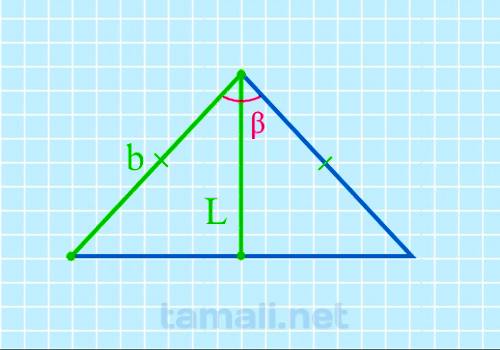
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

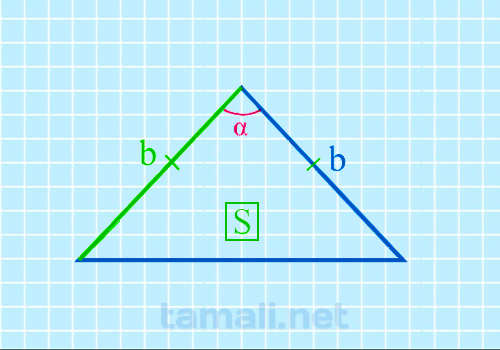
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.