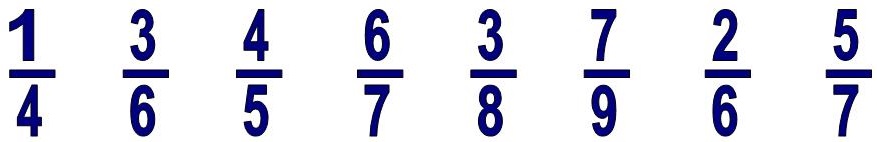Как найти верхнюю дробь вид

9 букв. Думаю, все, кто овладел азами математической науки, прекрасно осведомлён, что у дроби, записанной в виде двух чисел в столбик, разделенных горизонтальной черточкой, верхнее число носит название числитель, а нижнее является знаменателем. Поэтому в качестве ответа на заданный вопрос кроссворда выберу слово числитель. Оно как раз состоит из девяти букв и, считаю, вполне годится, чтобы заполнить клеточки кроссворда. автор вопроса выбрал этот ответ лучшим Галин­а Васил­ьна [163K] 7 лет назад  Дробь, где есть числитель и знаменатель называется простой. Числитель – это число, находящееся выше дробной черты и говорящее, сколько частей целого взято. На сколько разделено целое – об этом говорит знаменатель(расположен внизу, под дробной чертой) Nelli­4ka [114K] 6 лет назад  Конечно же, это числитель. Внизу расположен знаменатель. Объясню на пальцах (в прямом смысле): дана дробь – 7/10. Что это значит? Знаменатель “10” указывает на то, сколько частей в какой-либо искомой единице. На обеих руках у меня всего десять пальцев. А числитель “7” указывает на интересующее нас количество пальцев – 7. Если бы нам была дана дробь 6/10, мы имели бы полное право сократить дробь, т.е. пропорционально уменьшить значение и числителя, и знаменателя путем их деления на 2 (именно эта цифра является общим делителем для шести и десяти). Тогда бы у нас получилась следующая дробь – 3/5. Тагет­ес [135K] 7 лет назад  Часть математической дроби, а именно верхняя ее часть называется числитель, которая будет ответом в данном кроссворде, т.к. 1) заявлено 9 букв для правильного ответа, 2) по другому верхняя часть не называется. А если рассматривать нижнюю часть дроби, то ответом прошел бы знаменатель. Ну и для полноты картины (названиях частей дроби), то результат деления числителя на знаменатель – носит название частное. В данном случает ответ числитель У обыкновенных дробей, то есть таких дробей, у которых есть две части, верхняя и нижняя, разделенные горизонтальной или наклонной чертой, верхняя часть называется ЧИСЛИТЕЛЬ. Числитель в дроби может быть как больше нижней части – знаменателя, так и меньше. В первом случае дробь называется неправильной и выглядит примерно так: 7/2 или 30/15. Во втором случае дробь называется правильной и записывается примерно так: 2/7 или 15/30. Adgjm­p [140K] 7 лет назад  Две части дроби- верхняя и нижняя. В задании кроссворда надо дать опрежление верхней части дроби. Дробь делится на числи тель и знаменатель. Соответственно числитель будет верхней частью, а знаменатель нижней. Верным ответом на задание кроссворда ябляется слово- “числитель”, девять искомых букв. Птичк­а2014 [25.4K] 6 лет назад  Обычная дробь состоит из числителя сверху и знаменателя снизу, так же есть целая часть, которая находится слева и пишется прям напротив черточки дроби. Значит правильный ответ числитель, именно он находится сверху дроби и является его верхней частью. дед Мороз-шатун [34.8K] 8 лет назад  В простой математической дроби (в отличии от смешанной) имеется только числитель и знаменатель. При написании дроби числитель пишется сверху, а знаменатель соответственно снизу. Правильный ответ на этот вопрос – ч и с л и т е л ь – Rakot­sy [2.4K] 8 лет назад  Ясное дело что нижняя часть дроби называется знаменателем, а верхняя числителем. Ладле­н [266K] 6 лет назад  Да пришлось вспомнить счастливые школьные годы. Ведь в обыденной жизни, даже если и упоминается какая-нибудь дробь, то как -то не говорят, какой у нее числитель и знаменатель. Так что многие может и забывают об этом за ненадобностью. Но вот ваш вопрос заставил вспомнить школу. Так что если мне не изменяет память То число над чертой в дроби называлось числителем. Да много , что учат в школе, потом в обыденной жизни не применяется. УРАЛО­ЧКА74 [177K] 6 лет назад  Дробь состоит из числителя и знаменателя. Это надо запомнить. В верхней части дроби находится числитель, а в нижней части- знаменатель. Значит числитель и будет правильным ответом к вопросу. В слове 9 букв- всё сходится. Знаете ответ?

Числитель и знаменатель

Числитель дроби — это число, стоящее в записи обыкновенной дроби над дробной чертой, то есть сверху. Числитель показывает количество долей.

Знаменатель дроби — это число, стоящее в записи дроби под дробной чертой, то есть снизу. Знаменатель показывает, какие это доли и на сколько равных частей разделена единица.

Дробная черта — это горизонтальная черта в записи дроби, которая отделяет числитель и знаменатель друг от друга.

Вместе, числитель и знаменатель дроби, называются членами дроби.

Условились считать, что дробная черта означает деление верхнего числа на нижнее, поэтому:

Любую операцию деления можно записать в виде дроби. И наоборот, любую дробь можно записать в виде операции деления.

Как читать запись обыкновенных дробей

По этому правилу читаются все обыкновенные дроби.

Пример 1. Прочитайте дробь , назовите числитель и знаменатель.

Пример 2. Прочитайте дробь .

Пример 3. Прочитайте дробь .

Источник

Как проводить действия с дробями

В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.

Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.

Количество просмотров этой статьи: 32 117.

Действия с дробями не такие сложные, как кажутся, особенно если знать, что делать. Начните с изучения терминологии и основ, а затем перейдите к сложению, вычитанию, умножению и делению дробей. Как только вы поймете, что такое дроби и как с ними работать, вы будете быстро решать выражения с дробями.

Совет: преобразуйте смешанные числа в неправильные дроби, если вы их умножаете или делите.

Источник

Дроби и доли.

Дроби самая сложная тема для учеников начальных классов. Но даже самая трудная тема может стать простой и понятной. Для обучения детей нужно использовать фантазию и элементы игры. А главное – сохранять спокойствие.

В серьезных учебниках по математике есть знаки: и сложение, и вычитание, и умножение. А вот, привычного нам, с вами знака деления (:) – нет. Получается, что знаком деления (:) пользуются только ученики начальной школы? На самом деле – нет. Только этот знак можно писать и по-другому, вот такой чертой, она пишется посередине клетки:

Вот это все – деление.
Деление можно записывать не двумя точками, а горизонтальной полоской.
Так вот: любая математическая запись, в которой присутствует знак деления в виде черточки, называется дробью.
Слово «дробь» говорит само за себя – оно обозначает дробление или деление.
Для записи дробей используются цифры и черта, которую называют дробной.

Вы когда-нибудь видели военный парад? Идут солдаты стройными рядами, а впереди человек со знаменем (флагом) – знаменосец! И по знамени легко понять, к какому роду войск принадлежат эти солдаты. У дроби тоже есть «знаменосец» — это главное число, которое обозначает, на сколько равных частей разделили целое (предмет, фигуру или величину).

«Знаменосец» пишется под дробной чертой и называется ЗНАМЕНАТЕЛЬ.

А число, над чертой показывает, сколько таких частей взяли (или закрасили, или съели). Это число называют ЧИСЛИТЕЛЕМ.

читается – две третьих, можно заменить по-другому — 2 : 3.

Рассмотрим еще одно число: раньше мы не могли на уроке математики 1 разделить на 2. А теперь – умеем: 1 разделить на 2 – это не что иное, как одна вторая. Что же это значит? Если в математике мы с вами не делали этого ни разу, то в жизни вы это делаем постоянно. Предположим, у вас есть яблоко. И вам нужно разделить его между вами и другом. Т.е. одно яблоко разделить на 2.

Так что же за число такое – одна вторая, во-первых, это дробь потому что присутствует знак деления, во-вторых, оно меньше единицы.
Потому что нельзя один разделить на 2, чтобы получилось что-то больше 1.
В-третьих, оно обозначает, что мы целое разделили на 2 и взяли себе одну такую часть.

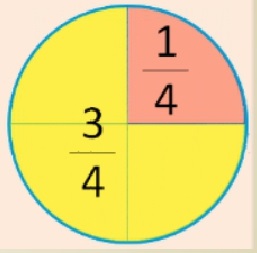
Давайте посмотрим на число:

По правилу, которое мы с вами вывели: три четвертых – это тоже самое, что три разделить на 4.

Давайте посмотрим, как это понять. Круг разделим на 4 равные части.
3 части закрасим желтым цветом. Это и есть три четвертых. Что же это значит?
Во-первых, это тоже дробь.
Во-вторых, она тоже меньше единицы.
И она обозначает, что круг мы разделили на 4 части
и закрасили желтым цветом – 3 таких части.

Итак,
как вы уже поняли: любая дробь будет иметь черту.
Ее так и называют – дробная черта. И обязательно будет стоять какое-то число над чертой и какое-то число под чертой.

Давайте научимся, как правильно читать дроби.
Читают их так: верхнее число всегда будет отвечать на вопрос: сколько?, а нижнее будет отвечать на вопрос: какая? или каких?

Сколько? – три, каких? – восьмых – три восьмых,
Сколько? – семь, каких? – девятых – семь девятых,
Сколько? – две, каких? – шестых – две шестых,
Сколько? – пять, каких? – седьмых – пять седьмых.

У чисел, которые вверху и внизу дроби есть свое научное название: верхнее число называется числитель, а нижнее – знаменатель.
Постарайтесь запомнить это. Это важно! Числитель – наверху, знаменатель – внизу.
Знаменатель показывает на сколько частей мы разделили наше целое, а числитель показывает – сколько частей целого мы с вами взяли.

Чтобы лучше запомнить, где числитель, где знаменатель, есть простая напоминалочка:
«ЧЕЛОВЕК ХОДИТ ПО ЗЕМЛЕ».
Ч – числитель – «над», З – знаменатель «под».

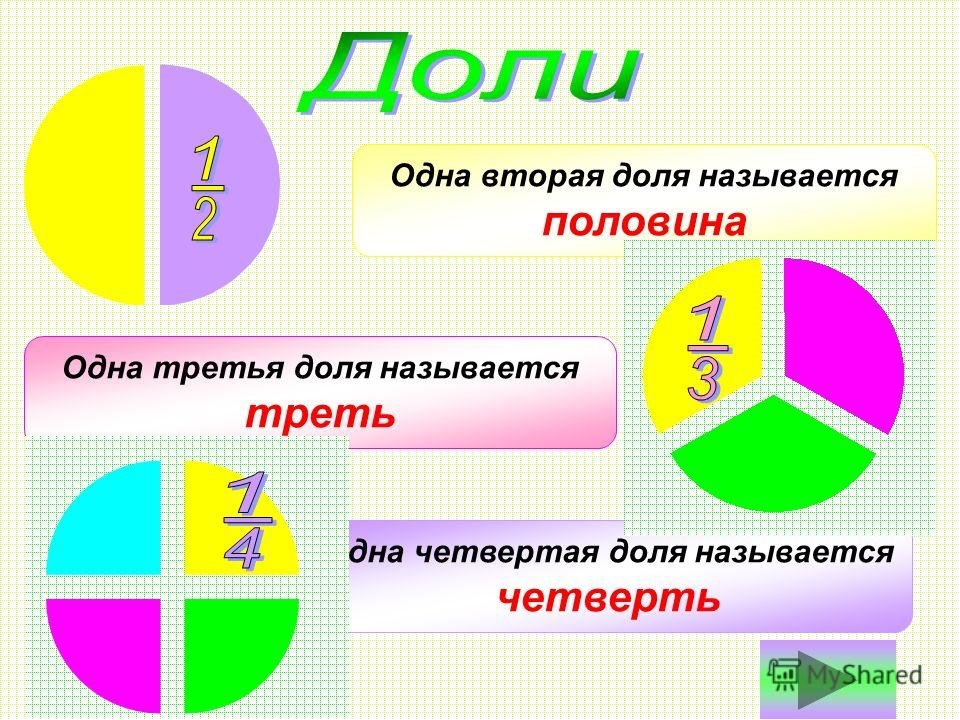
Есть одна разновидность дробей, которую в начальной школе выделяют в отдельную группу. Такие дроби называют долями. Если вам встретилось слово «доля», знайте, что это та же самая дробь, но только у нее числитель равен единице.

Мы постоянно сталкиваемся с ними в жизни.

Чаще всего мы встречаемся в жизни именно с половиной:

пол яблока — это одна вторая яблока, пол стакана – это одна вторая стакана.

Так же мы знакомы с одной третьей:

– это не что иное, как треть.
Треть грейфрута – это значит, разделили грейфрут на 3 части и взяли одну.

Точно так же мы с вами называем одну четвертую четвертью.
Например – школьная четверть. Мы с вами делим учебный год на 4 части и берем одну часть. Это и есть – четверть.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.9 / 5. Количество оценок: 81

Источник

Обыкновенные дроби

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

Виды дробей:

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 35.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Полученные числа запишем справа сверху над числителем.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

Источник

Числитель и знаменатель дроби

Числитель и знаменатель дроби. Виды дробей. Продолжаем рассматривать дроби. Сначала небольшая оговорка – мы, рассматривая дроби и соответствующие примеры с ними, пока будем работать только с числовым её представлением. Бывают ещё и дробные буквенные выражения (с числами и без них). Впрочем, все «принципы» и правила также распространяются и на них, но о таких выражениях поговорим в будущем отдельно. Рекомендую посетить эту страницу и изучать (вспоминать) тему дробей шаг за шагом.

Самое главное понять, запомнить и осознать, что ДРОБЬ – это ЧИСЛО.

Обыкновенная дробь – это число вида:

Число расположенное «сверху» (в данном случае m) называется числителем, число расположенное снизу (число n) называется знаменателем. У тех, кто только коснулся темы частенько возникает путаница – что как называется.

Вот вам приёмчик, как навсегда запомнить – где числитель, а где знаменатель. Данный приём связан со словесно-образной ассоциацией. Представьте себе банку с мутной водой. Известно, что по мере отстоя воды чистая вода остаётся сверху, а муть (грязь) оседает, запоминаем:

ЧИССС тая вода ВВЕРХУ ( ЧИССС литель сверху)

Гря ЗЗЗННН ая вода ВНИЗУ ( ЗННН аменатель внизу)

Так что, как только возникнет необходимость вспомнить, где числитель, а где знаменатель, то сразу зрительно представили банку с отстоянной водой, в которой сверху ЧИСтая вода, а снизу гряЗНая вода. Есть и другие приёмы для запоминания, если они вам помогут, то хорошо.

Примеры обыкновенных дробей:

Что означает горизонтальная черточка между числами? Это не что иное, как знак деления. Получается, что дробь можно рассматривать как бы как пример с действием делением. Просто записано это действие вот в таком виде. То есть, верхнее число (числитель) делится на нижнее (знаменатель):

Кроме того, есть ещё форма записи – дробь может записываться и так (через косую черту):

1/9, 5/8, 45/64, 25/9, 15/13, 45/64 и так далее…

Можем записать вышеуказанные нами дроби так:

Результат деления, как известно это число.

Уяснили – ДРОБЬ ЭТО ЧИСЛО.

Как вы уже заметили, у обыкновенной дроби числитель может быть меньше знаменателя, может быть больше знаменателя и может быть равен ему. Тут присутствует множество важных моментов, которые понятны интуитивно, без каких-либо теоретических изысков. Например:

1. Дроби 1 и 3 можно записать как 0,5 и 0,01. Забежим немного вперёд – это десятичные дроби, о них поговорим чуть ниже.

2. Дроби 4 и 6 в результате дают целое число 45:9=5, 11:1 = 11.

3. Дробь 5 в результате даёт единицу 155:155 = 1.

Какие выводы напрашиваются сами собой? Следующие:

1. Числитель при делении на знаменатель может дать конечное число. Может и не получится, разделите столбиком 7 на 13 или 17 на 11 — никак! Делить можно бесконечно, но об этом также поговорим чуть ниже.

2. Дробь в результате может дать целое число. Следовательно и любое целое число мы можем представить в виде дроби, вернее бесконечного ряда дробей, посмотрите, все эти дроби равны 2:

Ещё! Любое целое число мы всегда можем записать в виде дроби – само это число в числителе, единица в знаменателе:

3. Единицу мы всегда можем представить в виде дроби с любым знаменателем:

*Указанные моменты крайне важны для работы с дробями при вычислениях и преобразованиях.

А теперь о теоретическом разделении обыкновенных дробей. Их разделяют на правильные и неправильные.

Дробь у которой числитель меньше знаменателя называется правильной. Примеры:

Дробь у которой числитель больше знаменателя или равен ему называется неправильной. Примеры:

Смешанная дробь (смешанное число).

Смешанной дробью называется дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дробной его части. Примеры:

Смешанную дробь всегда можно представить в виде неправильной дроби и наоборот. Идём далее!

Десятичные дроби.

Выше мы их уже затронули, это примеры (1) и (3), теперь подробнее. Вот примеры десятичных дробей: 0,3 0,89 0,001 5,345.

Дробь, знаменатель которой есть степень числа 10, например 10, 100, 1000 и так далее, называется десятичной. Записать первые три указанные дроби в виде обыкновенных дробей несложно:

Четвёртая является смешанной дробью (смешанным числом):

Десятичная дробь имеет следующую форму записи — с начала целая часть, затем разделитель целой и дробной части точка или запятая и затем дробная часть, количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.

Данные дроби бывают конечными и бесконечными.

Примеры конечных десятичных дробей: 0,234; 0,87; 34,00005; 5,765.

Примеры бесконечных. Например число Пи это бесконечная десятичная дробь, ещё – 0,333333333333…. 0,16666666666…. и прочие. Также результат извлечения корня из чисел 3, 5, 7 и т.д. будет являться бесконечной дробью.

Дробная часть может быть цикличная (в ней присутствует цикл), два примера выше именно такие, ещё примеры:

0,123123123123…. цикл 123

0,781781781718…. цикл 781

0,0250102501…. цикл 02501

Записать их можно как 0,(123) 0,(781) 0,(02501).

Число Пи не является цикличной дробью как и, например, корень из трёх.

Ниже в примерах, будут звучать такие слова как «переворачиваем» дробь – это означает что числитель и знаменатель меняем местами. На самом деле у такой дроби есть название – обратная дробь. Примеры взаимно-обратных дробей:

Источник

Тема «Действия с алгебраическими дробями» вызывает у учащихся 7-8 классов определённые трудности, так как требует хороших знаний материала, изученного ранее: «Действия с обыкновенными дробями», «Преобразование многочленов», «Формулы сокращённого умножения». Если предшествующие знания по каким-то причинам сформированы недостаточно прочно, то под наплывом нового материала они как бы растворяются и, как следствие, являются тормозом для дальнейшего успешного обучения.

Успешно реализовывать задачу закрепления «старых» и формирования «новых» знаний позволяет визуализация учебного материала. Если учебная информация сопровождается определёнными рисунками, соответствующими формулами, зрительными подсказками, то её смысл становится видимым, понятным и, как следствие, лучше запоминается. Именно поэтому мы обратились к новым учебнику и задачнику для 7-го класса, выпущенных Санкт-Петербургским Институтом Продуктивного обучения Российской Академии Образования [1, 2].
Эти пособия отличается от других особым структурированием учебной информации небольшими порциями, которые можно охватить «одним взглядом»; теоретический материал сопровождается здесь умело подобранными иллюстрациями, необходимыми комментариями, замечаниями, выделением ключевых понятий.
Разнообразие заданий, таких как, «Алгоритмы и автоматы», серии, тесты, тренажеры, «Посмотрите и …», «Выберите ответ» и другие, предоставляет ученику определённую свободу выбора, а не загоняют его в жесткие рамки: «реши или найди ответ». Эти задания дают богатейший материал для индивидуальной работы со слабыми и сильными учащимися. Большое количество нестандартных упражнений, которые учат мыслить, творить, придумывать, находить выход из затруднительных ситуаций, предвидеть результат (исследовательские работы, комбинаторные задачи), – позволяет ученикам активизировать свою мыслительную деятельность, а учителю работать творчески.

В восьмом классе мурманского лицея № 1 по материалам данных учебника [1] и задачника [2] был проведён открытый урок «Многоэтажные дроби». Эта тема выбрана не случайно. В действующих учебниках она отражена мало (например, в учебнике под ред. С.А. Теляковского рассмотрен только один такой пример, решенный с помощью основного свойства дроби). Иногда «многоэтажность» заменяется традиционным действием деления, что приводит к громоздким и не всегда оправданным вычислениям. Однако на вступительных экзаменах в вузы часто встречаются задания, связанные с преобразованием многоэтажных дробей.

На уроке мы попытались реализовать идею составления алгоритма преобразования многоэтажной дроби самими учащимися.
Целью данного урока являлось:
1) создать алгоритм работы с многоэтажными дробями;
2) научиться использовать его при преобразовании выражений;
3) убедиться в том, что алгоритмы позволяют рационально выполнять математические операции, и что каждый сам может их создавать.

На уроке каждому лицеисту был выдан комплект специальных материалов, в которых учащиеся работали карандашом. В случае если задание было выполнено неверно, ученик мог исправить свои записи с помощью ластика и тут же записать правильное решение. Это позволило учащимся чувствовать себя раскованно, не бояться делать ошибки, не ждать ответов других учеников.
Знакомство с многоэтажными дробями началось в процессе выполнения упражнения, в котором необходимо было построить новые рациональные выражения с помощью заданных выражений (рис. 1-1). Лицеисты заполнили пропуски в двух первых примерах, остальные задания было предложено выполнить дома. После того, как учащиеся выполнили второй пример (рис. 1-1), состоялось обсуждение его структурных особенностей. Заметили, что первое слагаемое образовалось в результате деления дроби на дробь, что привело к необычному выражению – четырёхэтажной дроби.
Затем перешли к общим схемам строения многоэтажных дробей (рис. 1-2). Ещё раз обратили внимание на то, что под буквами подразумеваются рациональные выражения, что при делении дроби на дробь первая дробь является делимым, а вторая – делителем. В соответствующей многоэтажной дроби делимое становится числителем, а делитель – знаменателем. В результате получается четырёхэтажная дробь (схема А, рис. 1-2, слева). Символ деления здесь заменяется чертой, которую называют основной чертой дроби. Обратили внимание на значение и правило оформления основной черты дроби.
Далее обсудили схему В (рис. 1-2, справа), выяснили, сколько этажей имеет данная дробь, что записано в числителе, что в знаменателе, где расположена основная черта дроби. Схему С (рис. 1-2, внизу), лицеисты рассмотрели самостоятельно.

В примерах теста (рис. 1-3), необходимо было найти выражения многоэтажными дробями. Выполнить задания теста, то есть для каждого выражения найти верный ответ, записанный в верхней строке, учащимся было предложено дома.

Затем рассмотрели общую схему преобразования многоэтажной дроби (схема А, рис. 2-1, вверху), которая была также записана на доске, но без стрелок.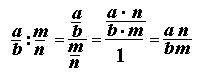

Алгоритм деления дроби на дробь был рассмотрен на предыдущих уроках (а также алгоритмы умножения и сложения дробей). Поэтому лицеисты уже знали, что стрелками обозначено действие умножение. Поставив стрелки в первой записи, они без труда, видя окончательный результат, расставили стрелки и во втором выражении.
После этого мы снова вернулись к рисунку 2 и схеме В (рис. 2-1, слева), лицеистам был задан вопрос: «А всегда ли надо (пусть даже мысленно) целое заменять дробью со знаменателем 1, нельзя ли и здесь создать мини-алгоритм?» После обсуждения пришли к правилу преобразования трёхэтажной дроби. В схеме С (рис. 2-1, справа), учащимся было предложено самим попробовать восстановить стрелку у первого выражения. Лицеисты быстро справились с этим заданием.
Затем перешли к практическим примерам 1 и 2 (рис. 2-2), где необходимо было заполнить пропуски, используя выработанный алгоритм (рис. 2-1). Это задание не вызвало особых затруднений у учащихся.
Далее рассмотрели более сложные примеры: в числителе или в знаменателе присутствует несколько множителей (рис. 2-3). Сначала разобрали случай, когда в числителях верхней и нижней дробей встречаются общие множители. Применив алгоритм работы с многоэтажными дробями, заметили, что общий множитель сокращается, если он присутствует в числителях обеих дробей. Случай, когда общий множитель есть в знаменателях обеих дробей, учащиеся разобрали самостоятельно и сами сделали соответствующий вывод.

Выполнив преобразование многоэтажной дроби по алгоритму, лицеисты убедились, что в подобных случаях сокращать нельзя. В примере 3 (рис. 2-3, внизу слева). необходимо было сначала сократить дробь, а затем применить алгоритм преобразования многоэтажной дроби. Учащиеся с большой заинтересованностью зачеркивали общие множители, рисовали стрелки и заполняли пропуски.
В четвертом задании лицеисты сразу же заметили общие множители в числителях обеих дробей и формулу сокращённого умножения в знаменателе нижней дроби. Разложив на множители и сократив знаменатели, а также числители, учащиеся довольно быстро получили верный результат. Задания 5, 6, 7 (рис. 2-4) лицеистам предлагалось выполнить дома.
Затем перешли к тождественным преобразованиям многоэтажных алгебраических дробей
. В примере 1 (рис. 3-1) предлагалось заполнить пропуски в числителях дробей и затем записать окончательный результат. Многие учащиеся при сложении целого и дроби применяли соответствующий алгоритм (ставили стрелки от m к 1). Данный пример не вызвал особых затруднений у лицеистов.
Задание «Посмотрите и найдите» № 2 (рис. 3-2, слева) поначалу испугало учащихся («значение такого сложного выражения надо найти устно?!»), но, после того, как преобразовали знаменатель первой многоэтажной дроби и увидели, что она равна 1, вторую дробь сократили довольно быстро и верно. Результат вычислений записали в рамочку внизу примера.
Выполнение примера № 3 (рис. 3-2, справа) заняло немного больше времени, так как не все сразу заметили противоположные выражения, при сокращении которых получается –1. Упражнение 4 (рис. 3-3) начали выполнять после того, как прочитали комментарий. Лицеисты самостоятельно заполняли пропуски в вычислениях, пользуясь алгоритмом. Затем все сверили свои результаты с решением этого примера, оформленным на обороте классной доски (рис. 3-4). Те из учащихся, кто выполнил задание 4 быстрее других, начали выполнять первые примеры упражнения 5 (рис. 3-5), которое было задано на дом.

Для того чтобы выяснить, как усвоен алгоритм преобразования многоэтажной дроби в конце урока была проведена игра. Каждый ученик получил листок с шуточными заданиями «Шторм на море» (рис. 4-1) и «Полицейские и воры» (рис. 4-2). Учащиеся самостоятельно преобразовывали «многоэтажную дробь»: сокращали (зачёркивали) общие множители, ставили стрелки и записывали получившийся результат в пустую рамочку. После выполнения всеми этого упражнения, сверили получившиеся результаты с ответами, оформленными на обороте классной доски. Одни учащиеся рисовали маяк, корабль, штурвал и якорь, другие записывали только начальные буквы этих слов (рис. 4-3). (На рисунках внизу: Ш – шериф, П – полицейский, М – мошенница, К – карманник). Все лицеисты без ошибок справились с этим необычным и интересным для них заданием.

Работать с визуальными учебными материалами учащимся очень нравится, так как на этих уроках они творят сами, не созерцают со стороны работу учителя и более сильных учащихся, а принимают активное участие в решении той или иной учебной задачи и видят результаты своей работы тут же. Подобные уроки проходят у детей эмоционально, они чувствуют себя первооткрывателями, радуются своим успехам, стремятся выполнить как можно больше разнообразных заданий, попробовать свои силы при решении довольно сложных упражнений. Так как на таких уроках мало пишется, но много думается, то польза от них колоссальная.

Распечатать комплект визуальных дидактических материалов по теме данной статьи.
Предлагаемые комплекты дидактических материалов на экране отражаются не совсем точно,
но распечатываются рисунки прекрасно!

1. Башмаков М. И. Многочлены и алгебраические дроби. Учебник алгебры для 7 кл. Выпуск 1. Конструктор книги Резник Н. А. – СПб.: Изд-во ЦПО «Информатизация образования», 2000.
2. Башмаков М.И., Резник Н.А. Задачник по алгебре для 7 класса общеобразовательной школы. – СПб.: Изд-во ЦПО «Информатизация образования», 2001.
3. Резник Н.А. Визуальные уроки. Компл. дидакт. матер. к шк. урокам. — СПб.: Свет, 1996.

Источник

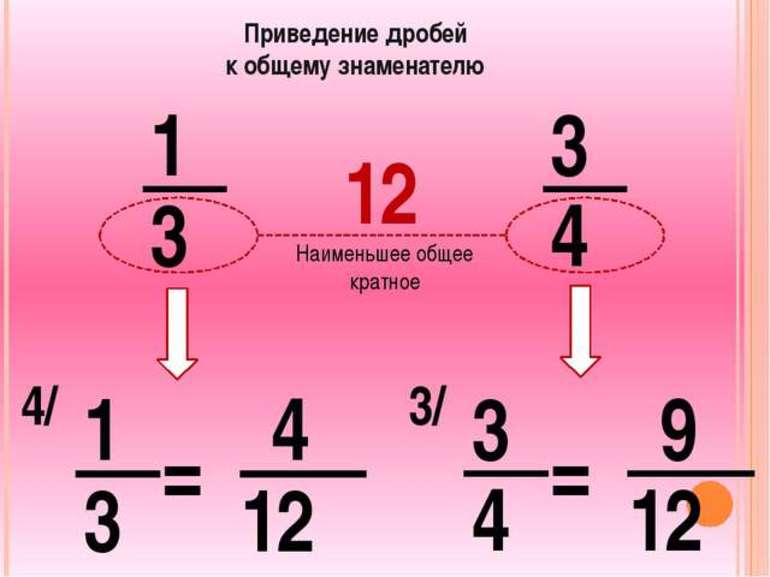
Общий знаменатель

Самый простой способ, как привести дробь к общему знаменателю, — верхнюю и нижнюю части первой дроби умножить на значение в знаменателе второй, а верхнюю и нижнюю часть второго дробного числа — на значение в знаменателе первой. Проверочное правило, действующее в этом случае: дробь не меняется, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.

Даны две дроби: 3/13 и 3/7. После выполнения необходимых действий получится: 3/13*7 = 21/91, 3/7*13 =39/91.

Общий знаменатель (ОЗ) — это любое натуральное число, которое является всеобщим кратным всех данных дробей. Иными словами, это значит, что ОЗ может быть любое число из натуральных, которое обязательно будет делиться на знаменатель каждого дробного числа. Допустим, есть две обычных дробных соотношения 4/8 и 5/10. ОЗ в этом случае может быть любым значением, кратным 8 и 10. А конкретно, это значения: 80, 160, 240, 320, 400 и так далее.

Дано 3 дробных значения: 1/5, 3/10 и 9/15. Вопрос: может ли ОЗ быть числом 330? Ответ: да, потому что оно делится на знаменатель каждого соотношения без остатка: 330/5 = 66, 330/10 = 33, 330/15 = 22.

НОЗ и НОК

При работе с дробями используются наименьший общий знаменатель (НОЗ) — это наименьшее натуральное число среди всех ОЗ ряда дробных чисел и наименьшее общее кратное (НОК) — это самый меньший общий делитель данного ряда чисел.

Наименьшее общее кратное — это НОЗ этого ряда. К нему можно прийти поиском НОК.

Например, необходимо провести следующую операцию для двух дробных значений: 7/16, 19/6. Нужно узнать, какой НОК у 16 и 6. Простые множители этих чисел:

16=8*2; 6= 3*2

НОК (16, 6) =8*2*3= 48.

Число 48 и есть искомый НОЗ.

Существует простое правило о том, как перевести дробное число к НОЗ. Вычисления проводятся по порядку:

1. Найти НОК.
2. Для каждого дробного числа из ряда определить дополнительный множитель. Определить его можно с помощью деления НОЗ на знаменатель каждой из дробей.
3. Умножить обе части каждой дроби на их дополнительные множители.

Пример. Есть 2 дробных значения: 3/14 и 18/30. Теперь можно воспользоваться правилом, для того чтобы найти НОЗ:

1. Найти НОК: 14 = 2*7; 30 = 5*2*3; НОК (14,32) = 5*2*7*3 = 210;
2. Найти дополнительные множители: 210/14 = 15; 210/30 = 7;
3. Перемножить верхнюю и нижнюю части с дополнительными множителями: 3*15/14*15 = 45/210; 18*7/30*7 = 126/210.

Примеры с несколькими дробями

Правило поиска ОЗ и НОЗ действует также и в отношении нескольких дробных чисел в ряде. Есть три значения: 3/9, 8/11 и 10/12. Для того чтобы переводить их, нужно совершать те же действия, которые представлены в правиле:

НОК (9; 11) = 99; НОК (99; 12) = 39; НОК (9; 11; 12) = 396;

396/9 = 44; 396/11 = 36; 396/12 = 33;

3*44/9*44 = 132/396; 8*36/11*36 =288/396; 10*33/12*33 =330/396;

НОЗ найден.

Приводить дробные соотношения к ОЗ требуется во многих случаях. Вычисление этой величины необходимо, чтобы получить разность дробей, провести их сложение, умножение или деление, а также при решении задач на доли и проценты, так как процентные соотношения — это обыкновенные выражения, которые содержат дробные соотношения.