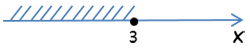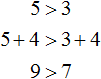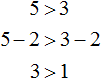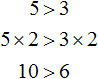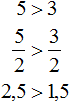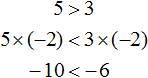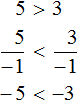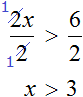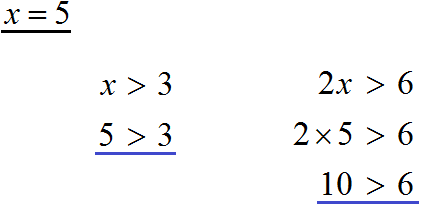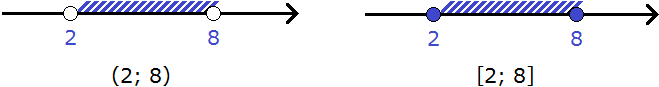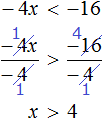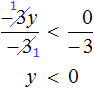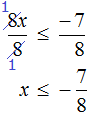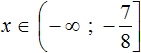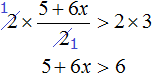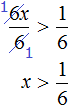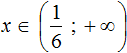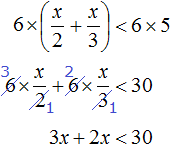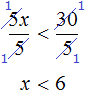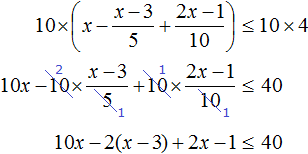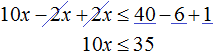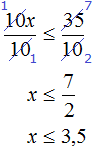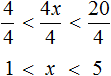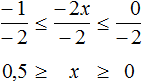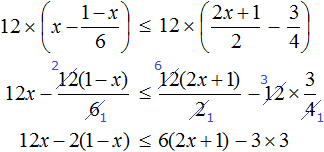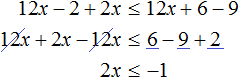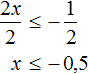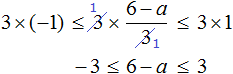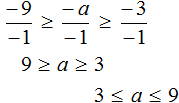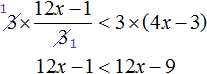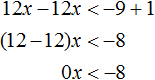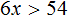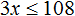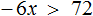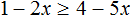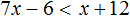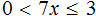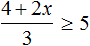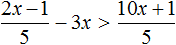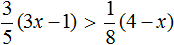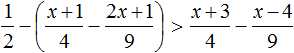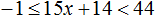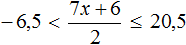Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для
сравнения величин.
| Символ | Название | Тип знака |
|---|---|---|
| > | больше |
строгий знак (число на границе не включается) |
| < | меньше |
строгий знак (число на границе не включается) |
| ≥ | больше или равно |
нестрогий знак (число на границе включается) |
| ≤ | меньше или равно |
нестрогий знак (число на границе включается) |
Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство
отличается от уравнения.
В отличии от уравнения в неравенстве вместо знака равно «=» используют любой
знак сравнения: «>», «<»,
«≤» или «≥».
Запомните!
Линейным
неравенством называют неравенство, в котором неизвестное стоит только в первой степени.
Рассмотрим пример линейного неравенства.
x − 6 < 8
Так как в неравенстве «x − 6 < 8»
неизвестное «x» стоит в первой степени, такое неравенство называют линейным.
Как решить линейное неравенство
Важно!
Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное
в первой степени с
коэффициентом «1».
При решении линейных неравенств используют правило переноса и правило деления неравенства на число.
Правило переноса в неравенствах
Также как и в уравнениях,
в неравенствах можно переносить
любой член неравенства из левой части в правую и наоборот.
Запомните!
При переносе из левой части в правую (и наоборот) член неравенства меняет свой знак на
противоположный.
Вернемся к нашему неравенству и используем правило переноса.
x − 6 < 8
x < 8 + 6
x < 14
Итак, мы получили ответ к неравенству «x < 14». Но что означает такой
ответ?
Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить,
понятие числовой оси.
Нарисуем числовую ось для неизвестного «x» и отметим на ней число «14».

Запомните!
При нанесении числа на числовую ось соблюдаются следующие правила:
Заштрихуем на числовой оси по полученному ответу «x < 14» все решения неравенства, то есть область
слева от числа «14».
Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство
«x − 6 < 8»
даст верный результат.
Возьмем, например число «12» из заштрихованной области и подставим его
вместо «x» в исходное неравенство «x − 6 < 8».
Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства.
Важно!
Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство
дают верный результат.
Решением неравенства
называют множество чисел из заштрихованной области на числовой оси.
В нашем примере ответ «x < 14» можно понимать так: любое число из
заштрихованной области (то есть любое число меньшее
«14») будет являться решением неравенства
«x − 6 < 8».
Правило умножения или деления неравенства на число
Рассмотрим другое неравенство.
2x − 16 > 0
Используем правило переноса и перенесём все числа без неизвестного, в правую часть.
2x − 16 > 0
2x > 16
Теперь нам нужно сделать так, чтобы при неизвестном «x»
стоял коэффициент «1». Для этого достаточно разделить и левую,
и правую часть на число «2».
Запомните!
При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть.
- Если неравенство умножается (делится) на положительное число,
то
знак самого неравенства остаётся прежним. - Если неравенство умножается (делится) на отрицательное число,
то
знак самого неравенства меняется на противоположный.
Разделим «2x > 16» на «2».
Так как «2» —
положительное число, знак неравенства останется прежним.
2x > 16 | (:2)
2x (:2) > 16 (:2)
x > 8
Ответ: x > 8
Рассмотрим другое неравенство.
9 − 3x ≥ 0
Используем правило переноса.
9 − 3x ≥ 0
−3x ≥ −9
Разделим неравенство на «−3».
Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный.
−3x ≥ −9
−3x ≥ −9 | :(−3)
−3x : (−3) ≤ −9 :(−3)
x ≤ 3
Ответ: x ≤ 3
Примеры решения линейных неравенств
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
16 ноября 2021 в 16:44
Алина Кирщина
Профиль
Благодарили: 0
Сообщений: 1
Алина Кирщина
Профиль
Благодарили: 0
Сообщений: 1
Как правильно написать «больше 15» символом? <15 или >15?
0
Спасибо
Ответить
24 ноября 2021 в 12:56
Ответ для Алина Кирщина
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 27
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 27
> 15 Острый конец символа «птичка» > смотрит в сторону меньшего числа
Еще можно запомнить, как что где больше вершин у символа «птички», там большее число находится. У символа > слева две вершины, а справа одна, значит слева находится большее число.
0
Спасибо
Ответить
29 ноября 2021 в 7:32
Ответ для Алина Кирщина
Фархад Асланов
Профиль
Благодарили: 0
Сообщений: 1
Фархад Асланов
Профиль
Благодарили: 0
Сообщений: 1
>15
0
Спасибо
Ответить
5 марта 2020 в 23:01
Лина Недзвецкая
Профиль
Благодарили: 0
Сообщений: 1
Лина Недзвецкая
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство:
log3
≤1
0
Спасибо
Ответить
20 августа 2020 в 1:16
Ответ для Лина Недзвецкая
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
0 < (3x − 5)/(x+1) ≤ 3.
(3x − 5)/(x+1) > 0 ⇔ x < − 1 ∪ x > 5/3;
(3x − 5)/(x+1) ≤ 3 ⇔ 8/(x+1) ≥ 0 ⇔ x > − 1.
{(−∞; −1) ∪ (5/3; +∞)} ∩ (−1; +∞) = (5/3; +∞).
0
Спасибо
Ответить
17 июля 2016 в 15:37
Sergey Gurzhiy
Профиль
Благодарили: 0
Сообщений: 1
Sergey Gurzhiy
Профиль
Благодарили: 0
Сообщений: 1
Решите неравенство
2^3-6x<1
0
Спасибо
Ответить
21 сентября 2016 в 13:44
Ответ для Sergey Gurzhiy
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Странно, что для 11класса, но всё же:
23 ? 6x<1
8 ? 6x<1
? 6x< ? 7
x>
1
Спасибо
Ответить
6 июня 2016 в 17:05
Катя Петрова
Профиль
Благодарили: 0
Сообщений: 1
Катя Петрова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
7 июня 2016 в 2:49
Ответ для Катя Петрова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Пусть 2x = y > 0.
Неравенство можно записать в виде
? 0.
Откуда y = 2 или 8 ? y < 9.
Стало быть, x = 1 или 3 ? x < log29.
0
Спасибо
Ответить
7 июня 2016 в 13:11
Ответ для Катя Петрова
Хачик Казанджян
Профиль
Благодарили: 0
Сообщений: 1
Хачик Казанджян
Профиль
Благодарили: 0
Сообщений: 1



-Tак как y>0, то сокращаем на y и преобразуем к виду
Учитывая, что y=2x получим x=1 или (3?x<log29) Ответ: (x=1)?(3?x<log2). или так {1?[3;log29)}
0
Спасибо
Ответить
8 июня 2016 в 12:10
Ответ для Катя Петрова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Списывать нехорошо.
0
Спасибо
Ответить
5 мая 2016 в 10:09
Влада Навдушевич
Профиль
Благодарили: 0
Сообщений: 1
Влада Навдушевич
Профиль
Благодарили: 0
Сообщений: 1
Как решить неравенство (х^2-4х+3)/(х^4-х^6) < или = 0
0
Спасибо
Ответить
8 июня 2016 в 12:28
Ответ для Влада Навдушевич
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
| (x — 1)(x — 3) |
| x4(1 — x)(1 + x) |
? 0.
и метод интервалов.
Ответ: (-oo; -1) U [3; +oo).
0
Спасибо
Ответить
3 августа 2015 в 16:54
Надие Рахимова
Профиль
Благодарили: 0
Сообщений: 1
Надие Рахимова
Профиль
Благодарили: 0
Сообщений: 1
область решения неравенства (х-4)>3х равна? решить
0
Спасибо
Ответить
31 августа 2016 в 10:31
Ответ для Надие Рахимова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
(x-4)>3x
x-4-3x>0
-4-2x>0
2x+4<0
2x<-4
x<-2
Проверка: Возьмём число меньшее -2, например -3
-3-4>-3 · 3
12>-9 Верно.
Ответ: x<-2
0
Спасибо
Ответить
Линейные неравенства с одной переменной. Равносильные неравенства
Неравенства вида ax>b или ax называют линейными неравенствами с одной переменной, где a и b некоторые числа, х – переменная (неизвестная), b – свободный член.
Решением неравенства с одной переменной называется значение переменной, при котором данное неравенство обращается в верное числовое неравенство.
Решить неравенство – это значит найти множество его решений или доказать, что их нет.
С помощью свойств числовых равенств можно решать уравнения, т. е. находить те значения переменной, при которых уравнение обращается в верное числовое равенство. Точно так же свойства числовых неравенств можно решать неравенства с переменной, т. е. находить те значения переменной, при которых неравенство с переменной обращается в верное числовое неравенство. Каждое такое значение переменной называют обычно решением неравенства с переменной.
Неравенства, имеющие одни и те же решения, называются равносильными.
Замена одного неравенства равносильным ему другим неравенством называется равносильным переходом от одного неравенства к другому.
При решении неравенств обычно заменяют данное неравенство другим, более простым, но равносильным данному; полученное неравенство снова заменяют более простым, равносильным данному неравенству и т.д. Такие замены осуществляются на основе следующих утверждений:
- Любой член неравенства можно перенести из одной части неравенства в другую с противоположенным знаком, не меняя при этом знак неравенства
- Обе части неравенства можно умножать или делить на одно и то же положительное число, не меняя при знак неравенства
- Обе части неравенства можно умножать или делить на одно и то же отрицательное число, при этом поменять знак неравенства на противоположенный знак
Применим эти правила для решения линейных неравенств, т. е. неравенств, сводящихся к виду ах + b > 0 (или ах + b < 0), где а и b – любые числа, за одним исключением:
Пример 1. Решить неравенство
Решение. Перенесем член 7х в левую часть неравенства, а член – 5 — в правую часть неравенства, не забыв при этом изменить знаки и у члена 7х, и у члена – 5 (руководствуемся правилом 1). Тогда получим
Разделим обе части последнего неравенства на одно и то же отрицательное число – 4, не забыв при этом перейти к неравенству противоположного смысла (руководствуясь правилом 3).
Получим . Это и есть решение заданного неравенства.
Как мы условились, для записи решения можно использовать обозначение соответствующего промежутка числовой прямой:
При решении линейных неравенств применяем свойства из вышеуказанной темы. Рассмотрим решение некоторых неравенств:
1) Решить неравенство:
Решение:
Ответ: [1;+)
2) Решить неравенство:
Решение:
Ответ: (-; 3,5)
3) Решить неравенство:
Решение:
Ответ: (-; -15)
Вопросы к конспектам
В каких значениях х дробь будет правильной?
Решите двойное неравенство: 7≤ 2х + 3 ≤ 11
Решите неравенство:
В каких значения х выражение 7,6 + 2х – (3х – 6,4) имеет положительные значения?
Найдите значения двойного неравенства: -12 < 2(x+3) < 4
Найдите при каких значениях переменной значения двучлена 9х + 3 больше значения двучлена 5х + 6
Решите неравенство: 5у + 9 ≤ 3 – 7у
Решите неравенство:
Последнее изменение: Четверг, 16 Февраль 2017, 23:57
Данный материал может показаться сложным для понимания. Рекомендуется изучать его маленькими частями.
Определения и свойства
Неравенством мы будем называть два числовых или буквенных выражения, соединенных знаками >, <, ≥, ≤ или ≠.
Пример: 5 > 3
Данное неравенство говорит о том, что число 5 больше, чем число 3. Острый угол знака неравенства должен быть направлен в сторону меньшего числа. Это неравенство является верным, поскольку 5 больше, чем 3.
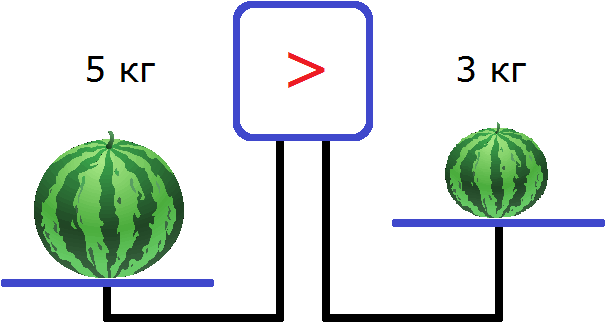
Если на левую чашу весов положить арбуз массой 5 кг, а на правую — арбуз массой 3 кг, то левая чаша перевесит правую, и экран весов покажет, что левая чаша тяжелее правой:
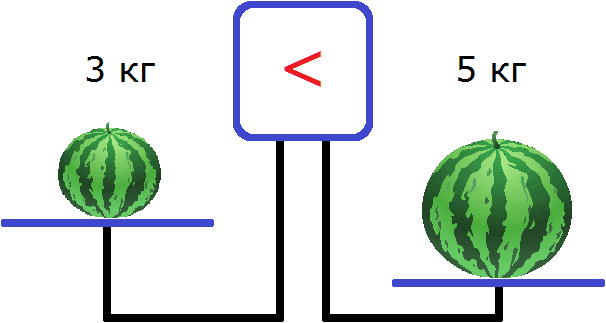
Если 5 > 3, то 3 < 5. То есть левую и правую часть неравенства можно поменять местами, изменив знак неравенства на противоположный. В ситуации с весами: большой арбуз можно положить на правую чашу, а маленький арбуз на левую. Тогда правая чаша перевесит левую, и экран покажет знак <
Если в неравенстве 5 > 3, не трогая левую и правую часть, поменять знак на <, то получится неравенство 5 < 3. Это неравенство не является верным, поскольку число 3 не может быть больше числа 5.
Числа, которые располагаются в левой и правой части неравенства, будем называть членами этого неравенства. Например, в неравенстве 5 > 3 членами являются числа 5 и 3.
Рассмотрим некоторые важные свойства для неравенства 5 > 3.
В будущем эти свойства будут работать и для других неравенств.
Свойство 1.
Если к левой и правой части неравенства 5 > 3 прибавить или вычесть одно и то же число, то знак неравенства не изменится.
Например, прибавим к обеим частям неравенства число 4. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем вычесть из обеих частей неравенства 5 > 3 какое-нибудь число, скажем число 2
Видим, что левая часть по-прежнему больше правой.
Из данного свойства следует, что любой член неравенства можно перенести из одной части в другую часть, изменив знак этого члена. Знак неравенства при этом не изменится.
Например, перенесём в неравенстве 5 > 3, член 5 из левой части в правую часть, изменив знак этого члена. После переноса члена 5 в правую часть, в левой части ничего не останется, поэтому запишем там 0
0 > 3 − 5
0 > −2
Видим, что левая часть по-прежнему больше правой.
Свойство 2.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то знак неравенства не изменится.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь положительное число, скажем на число 2. Тогда получим:
Видим, что левая часть по-прежнему больше правой.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь число. Разделим их на 2
Видим, что левая часть по-прежнему больше правой.
Свойство 3.
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Например, умножим обе части неравенства 5 > 3 на какое-нибудь отрицательное число, скажем на число −2. Тогда получим:
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Теперь попробуем разделить обе части неравенства 5 > 3 на какое-нибудь отрицательное число. Давайте разделим их на −1
Видим, что левая часть стала меньше правой. То есть знак неравенства изменился на противоположный.
Само по себе неравенство можно понимать, как некоторое условие. Если условие выполняется, то неравенство является верным. И наоборот, если условие не выполняется, то неравенство не верно.
Например, чтобы ответить на вопрос является ли верным неравенство 7 > 3, нужно проверить выполняется ли условие «больше ли 7, чем 3». Мы знаем, что число 7 больше, чем число 3. То есть условие выполнено, а значит и неравенство 7 > 3 верно.
Неравенство 8 < 6 не является верным, поскольку не выполняется условие «8 меньше, чем 6».
Другим способом определения верности неравенства является составление разности из левой и правой части данного неравенства. Если разность положительна, то левая часть больше правой части. И наоборот, если разность отрицательна, то левая часть меньше правой части. Более точно это правило выглядит следующим образом:
Число a больше числа b, если разность a − b положительна. Число a меньше числа b, если разность a − b отрицательна.
Например, мы выяснили, что неравенство 7 > 3 является верным, поскольку число 7 больше, чем число 3. Докажем это с помощью правила, приведённого выше.
Составим разность из членов 7 и 3. Тогда получим 7 − 3 = 4. Согласно правилу, число 7 будет больше числа 3, если разность 7 − 3 окажется положительной. У нас она равна 4, то есть разность положительна. А значит число 7 больше числа 3.
Проверим с помощью разности верно ли неравенство 3 < 4. Составим разность, получим 3 − 4 = −1. Согласно правилу, число 3 будет меньше числа 4, если разность 3 − 4 окажется отрицательной. У нас она равна −1, то есть разность отрицательна. А значит число 3 меньше числа 4.
Проверим верно ли неравенство 5 > 8. Составим разность, получим 5 − 8 = −3. Согласно правилу, число 5 будет больше числа 8, если разность 5 − 8 окажется положительной. У нас разность равна −3, то есть она не является положительной. А значит число 5 не больше числа 8. Иными словами, неравенство 5 > 8 не является верным.
Строгие и нестрогие неравенства
Неравенства, содержащие знаки >, < называют строгими. А неравенства, содержащие знаки ≥, ≤ называют нестрогими.
Примеры строгих неравенства мы рассматривали ранее. Таковыми являются неравенства 5 > 3, 7 < 9.
Нестрогим, например, является неравенство 2 ≤ 5. Данное неравенство читают следующим образом: «2 меньше или равно 5».
Запись 2 ≤ 5 является неполной. Полная запись этого неравенства выглядит следующим образом:
2 < 5 или 2 = 5
Тогда становится очевидным, что неравенство 2 ≤ 5 состоит из двух условий: «два меньше пять» и «два равно пять».
Нестрогое неравенство верно в том случае, если выполняется хотя бы одно из его условий. В нашем примере верным является условие «2 меньше 5». Значит и само неравенство 2 ≤ 5 верно.
Пример 2. Неравенство 2 ≤ 2 является верным, поскольку выполняется одно из его условий, а именно 2 = 2.
Пример 3. Неравенство 5 ≤ 2 не является верным, поскольку не выполняется ни одно из его условий: ни 5 < 2 ни 5 = 2.
Двойное неравенство
Число 3 больше, чем число 2 и меньше, чем число 4. В виде неравенства это высказывание можно записать так: 2 < 3 < 4. Такое неравенство называют двойным.
Двойное неравенство может содержать знаки нестрогих неравенств. К примеру, если число 5 больше или равно, чем число 2, и меньше или равно, чем число 7, то можно записать, что 2 ≤ 5 ≤ 7
Чтобы правильно записать двойное неравенство, сначала записывают член находящийся в середине, затем член находящийся слева, затем член находящийся справа.
Например, запишем, что число 6 больше, чем число 4, и меньше, чем число 9.
Сначала записываем 6
Слева записываем, что это число больше, чем число 4
Справа записываем, что число 6 меньше, чем число 9
Неравенство с переменной
Неравенство, как и равенство может содержать переменную.
Например, неравенство x > 2 содержит переменную x. Обычно такое неравенство нужно решить, то есть выяснить при каких значениях x данное неравенство становится верным.
Решить неравенство означает найти такие значения переменной x, при которых данное неравенство становится верным.
Значение переменной, при котором неравенство становится верным, называется решением неравенства.
Неравенство x > 2 становится верным при x = 3, x = 4, x = 5, x = 6 и так далее до бесконечности. Видим, что это неравенство имеет не одно решение, а множество решений.
Другими словами, решением неравенства x > 2 является множество всех чисел, бóльших 2. При этих числах неравенство будет верным. Примеры:
3 > 2
4 > 2
5 > 2
Число 2, располагающееся в правой части неравенства x > 2, будем называть границей данного неравенства. В зависимости от знака неравенства, граница может принадлежать множеству решений неравенства либо не принадлежать ему.
В нашем примере граница неравенства не принадлежит множеству решений, поскольку при подстановке числа 2 в неравенство x > 2 получается не верное неравенство 2 > 2. Число 2 не может быть больше самого себя, поскольку оно равно самому себе (2 = 2).
Неравенство x > 2 является строгим. Его можно прочитать так: «x строго больше 2″. То есть все значения, принимаемые переменной x должны быть строго больше 2. В противном случае, неравенство верным не будет.
Если бы нам было дано нестрогое неравенство x ≥ 2, то решениями данного неравенства были бы все числа, которые больше 2, в том числе и само число 2. В этом неравенстве граница 2 принадлежит множеству решений неравенства, поскольку при подстановке числа 2 в неравенство x ≥ 2 получается верное неравенство 2 ≥ 2. Ранее было сказано, что нестрогое неравенство является верным, если выполняется хотя бы одно из его условий. В неравенстве 2 ≥ 2 выполняется условие 2 = 2, поэтому и само неравенство 2 ≥ 2 верно.
Как решать неравенства
Процесс решения неравенств во многом схож с процессом решения уравнений. При решении неравенств мы будем применять свойства, которые изучили вначале данного урока, такие как: перенос слагаемых из одной части неравенства в другую часть, меняя знак; умножение (или деление) обеих частей неравенства на одно и то же число.
Эти свойства позволяют получить неравенство, которое равносильно исходному. Равносильными называют неравенства, решения которых совпадают.
Решая уравнения мы выполняли тождественные преобразования до тех пор, пока в левой части уравнения не оставалась переменная, а в правой части значение этой переменной (например: x = 2, x = 5). Иными словами, заменяли исходное уравнение на равносильное ему уравнение до тех пор, пока не получалось уравнение вида x = a, где a значение переменной x. В зависимости от уравнения, корней могло быть один, два, бесконечное множество, либо не быть совсем.
А при решении неравенств мы будем заменять исходное неравенство на равносильное ему неравенство до тех пор, пока в левой части не останется переменная этого неравенства, а в правой части его граница.
Пример 1. Решить неравенство 2x > 6
Итак, нужно найти такие значения x, при подстановке которых в 2x > 6 получится верное неравенство.
Вначале данного урока было сказано, что если обе части неравенства разделить на какое-нибудь положительное число, то знак неравенства не изменится. Если применить это свойство к неравенству, содержащему переменную, то получится неравенство равносильное исходному.
В нашем случае, если мы разделим обе части неравенства 2x > 6 на какое-нибудь положительное число, то получится неравенство, которое равносильно исходному неравенству 2x > 6.
Итак, разделим обе части неравенства на 2.
В левой части осталась переменная x, а правая часть стала равна 3. Получилось равносильное неравенство x > 3. На этом решение завершается, поскольку в левой части осталась переменная, а в правой части граница неравенства.
Теперь можно сделать вывод, что решениями неравенства x > 3 являются все числа, которые больше 3. Это числа 4, 5, 6, 7 и так далее до бесконечности. При этих значениях неравенство x > 3 будет верным.
4 > 3
5 > 3
6 > 3
7 > 3
Отметим, что неравенство x > 3 является строгим. «Переменная x строго больше трёх».
А поскольку неравенство x > 3 равносильно исходному неравенству 2x > 6, то их решения будут совпадать. Иначе говоря, значения, которые подходят неравенству x > 3, будут подходить и неравенству 2x > 6. Покажем это.
Возьмём, например, число 5 и подставим его сначала в полученное нами равносильное неравенство x > 3, а потом в исходное 2x > 6.
Видим, что в обоих случаях получается верное неравенство.
После того, как неравенство решено, ответ нужно записать в виде так называемого числового промежутка следующим образом:
В этом выражении говорится, что значения, принимаемые переменной x, принадлежат числовому промежутку от трёх до плюс бесконечности.
Иначе говоря, все числа, начиная от трёх до плюс бесконечности являются решениями неравенства x > 3. Знак ∞ в математике означает бесконечность.
Учитывая, что понятие числового промежутка очень важно, остановимся на нём подробнее.
Числовые промежутки
Числовым промежутком называют множество чисел на координатной прямой, которое может быть описано с помощью неравенства.
Допустим, мы хотим изобразить на координатной прямой множество чисел от 2 до 8. Для этого сначала на координатной прямой отмечаем точки с координатами 2 и 8, а затем выделяем штрихами ту область, которая располагается между координатами 2 и 8. Эти штрихи будут играть роль чисел, располагающихся между числами 2 и 8
Числа 2 и 8 назовём границами числового промежутка. Рисуя числовой промежуток, точки для его границ изображают не в виде точек как таковых, а в виде кружков, которые можно разглядеть.
Границы могут принадлежать числовому промежутку либо не принадлежать ему.
Если границы не принадлежат числовому промежутку, то они изображаются на координатной прямой в виде пустых кружков.
Если границы принадлежат числовому промежутку, то кружки необходимо закрасить.
На нашем рисунке кружки были оставлены пустыми. Это означало, что границы 2 и 8 не принадлежат числовому промежутку. Значит в наш числовой промежуток будут входить все числа от 2 до 8, кроме чисел 2 и 8.
Если мы хотим включить границы 2 и 8 в числовой промежуток, то кружки необходимо закрасить:
В данном случае в числовой промежуток будут входить все числа от 2 до 8, включая числа 2 и 8.
На письме числовой промежуток обозначается указанием его границ с помощью круглых или квадратных скобок.
Если границы не принадлежат числовому промежутку, то границы обрамляются круглыми скобками.
Если границы принадлежат числовому промежутку, то границы обрамляются квадратными скобками.
На рисунке представлено два числовых промежутка от 2 до 8 с соответствующими обозначениями:
На первом рисунке числовой промежуток обозначен с помощью круглых скобок, поскольку границы 2 и 8 не принадлежат этому числовому промежутку.
На втором рисунке числовой промежуток обозначен с помощью квадратных скобок, поскольку границы 2 и 8 принадлежат этому числовому промежутку.
С помощью числовых промежутков можно записывать ответы к неравенствам. Например, ответ к двойному неравенству 2 ≤ x ≤ 8 записывается так:
x ∈ [ 2 ; 8 ]
То есть сначала записывают переменную, входящую в неравенство, затем с помощью знака принадлежности ∈ указывают к какому числовому промежутку принадлежат значения этой переменной. В данном случае выражение x ∈ [ 2 ; 8 ] указывает на то, что переменная x, входящая в неравенство 2 ≤ x ≤ 8, принимает все значения в промежутке от 2 до 8 включительно. При этих значениях неравенство будет верным.
Обратим внимание на то, что ответ записан с помощью квадратных скобок, поскольку границы неравенства 2 ≤ x ≤ 8, а именно числа 2 и 8 принадлежат множеству решений этого неравенства.
Множество решений неравенства 2 ≤ x ≤ 8 также можно изобразить с помощью координатной прямой:
Здесь границы числового промежутка 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8.
В некоторых источниках границы, которые не принадлежат числовому промежутку, называют открытыми.
Открытыми их называют по той причине, что числовой промежуток остаётся открытым из-за того, что его границы не принадлежат этому числовому промежутку. Пустой кружок на координатной прямой математики называют выколотой точкой. Выколоть точку значит исключить её из числового промежутка или из множества решений неравенства.
А в случае, когда границы принадлежат числовому промежутку, их называют закрытыми (или замкнутыми), поскольку такие границы закрывают (замыкают) собой числовой промежуток. Закрашенный кружок на координатной прямой также говорит о закрытости границ.
Существуют разновидности числовых промежутков. Рассмотрим каждый из них.
Числовой луч
Числовым лучом называют числовой промежуток, который задаётся неравенством x ≥ a, где a — граница данного неравенства, x — решение неравенства.
Пусть a = 3. Тогда неравенство x ≥ a примет вид x ≥ 3. Решениями данного неравенства являются все числа, которые больше 3, включая само число 3.
Изобразим числовой луч, заданный неравенством x ≥ 3, на координатной прямой. Для этого отметим на ней точку с координатой 3, а всю оставшуюся справа от неё область выделим штрихами. Выделяется именно правая часть, поскольку решениями неравенства x ≥ 3 являются числа, бóльшие 3. А бóльшие числа на координатной прямой располагаются правее
Здесь точка 3 соответствует границе неравенства x ≥ 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≥ 3.
Точка 3, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≥ 3 принадлежит множеству его решений.
На письме числовой луч, заданный неравенством x ≥ a, обозначается следующим образом:
[ a ; +∞ )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница числового луча принадлежит ему, а другая нет, поскольку бесконечность сама по себе границ не имеет и подразумевается, что по ту сторону нет числа, замыкающего этот числовой луч.
Учитывая то, что одна из границ числового луча закрыта, данный промежуток часто называют закрытым числовым лучом.
Запишем ответ к неравенству x ≥ 3 с помощью обозначения числового луча. У нас переменная a равна 3
x ∈ [ 3 ; +∞ )
В этом выражении говорится, что переменная x, входящая в неравенство x ≥ 3, принимает все значения от 3 до плюс бесконечности.
Иначе говоря, все числа от 3 до плюс бесконечности, являются решениями неравенства x ≥ 3. Граница 3 принадлежит множеству решений, поскольку неравенство x ≥ 3 является нестрогим.
Закрытым числовым лучом также называют числовой промежуток, который задаётся неравенством x ≤ a. Решениями неравенства x ≤ a являются все числа, которые меньше a, включая само число a.
К примеру, если a = 2, то неравенство примет вид x ≤ 2. На координатной прямой граница 2 будет изображаться закрашенным кружком, а вся область, находящаяся слева, будет выделена штрихами. В этот раз выделяется левая часть, поскольку решениями неравенства x ≤ 2 являются числа, меньшие 2. А меньшие числа на координатной прямой располагаются левее
Здесь точка 2 соответствует границе неравенства x ≤ 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x ≤ 2.
Точка 2, являющаяся границей числового луча, изображена в виде закрашенного кружка, поскольку граница неравенства x ≤ 2 принадлежит множеству его решений.
Запишем ответ к неравенству x ≤ 2 с помощью обозначения числового луча:
x ∈ ( −∞ ; 2 ]
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x ≤ 2. Граница 2 принадлежит множеству решений, поскольку неравенство x ≤ 2 является нестрогим.
Открытый числовой луч
Открытым числовым лучом называют числовой промежуток, который задаётся неравенством x > a, где a — граница данного неравенства, x — решение неравенства.
Открытый числовой луч во многом похож на закрытый числовой луч. Различие в том, что граница a не принадлежит промежутку, как и граница неравенства x > a не принадлежит множеству его решений.
Пусть a = 3. Тогда неравенство примет вид x > 3. Решениями данного неравенства являются все числа, которые больше 3, за исключением числа 3
На координатной прямой граница открытого числового луча, заданного неравенством x > 3, будет изображаться в виде пустого кружка. Вся область, находящаяся справа, будет выделена штрихами:
Здесь точка 3 соответствует границе неравенства x > 3, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x > 3. Точка 3, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x > 3 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x > a, обозначается следующим образом:
( a ; +∞ )
Круглые скобки указывают на то, что границы открытого числового луча не принадлежат ему.
Запишем ответ к неравенству x > 3 с помощью обозначения открытого числового луча:
x ∈ ( 3 ; +∞ )
В этом выражении говорится, что все числа от 3 до плюс бесконечности, являются решениями неравенства x > 3. Граница 3 не принадлежит множеству решений, поскольку неравенство x > 3 является строгим.
Открытым числовым лучом также называют числовой промежуток, который задаётся неравенством x < a, где a — граница данного неравенства, x — решение неравенства. Решениями неравенства x < a являются все числа, которые меньше a, исключая число a.
К примеру, если a = 2, то неравенство примет вид x < 2. На координатной прямой граница 2 будет изображаться пустым кружком, а вся область, находящаяся слева, будет выделена штрихами:
Здесь точка 2 соответствует границе неравенства x < 2, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства x < 2. Точка 2, являющаяся границей открытого числового луча, изображена в виде пустого кружка, поскольку граница неравенства x < 2 не принадлежит множеству его решений.
На письме открытый числовой луч, заданный неравенством x < a, обозначается следующим образом:
( −∞ ; a )
Запишем ответ к неравенству x < 2 с помощью обозначения открытого числового луча:
x ∈ ( −∞ ; 2 )
В этом выражении говорится, что все числа от минус бесконечности до 2, являются решениями неравенства x < 2. Граница 2 не принадлежит множеству решений, поскольку неравенство x < 2 является строгим.
Отрезок
Отрезком называют числовой промежуток, который задаётся двойным неравенством a ≤ x ≤ b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x ≤ b примет вид 2 ≤ x ≤ 8. Решениями неравенства 2 ≤ x ≤ 8 являются все числа, которые больше 2 и меньше 8. При этом границы неравенства 2 и 8 принадлежат множеству его решений, поскольку неравенство 2 ≤ x ≤ 8 является нестрогим.
Изобразим отрезок, заданный двойным неравенством 2 ≤ x ≤ 8 на координатной прямой. Для этого отметим на ней точки с координатами 2 и 8, а располагающуюся между ними область выделим штрихами:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x ≤ 8. Точки 2 и 8, являющиеся границами отрезка, изображены в виде закрашенных кружков, поскольку границы неравенства 2 ≤ x ≤ 8 принадлежат множеству его решений.
На письме отрезок, заданный неравенством a ≤ x ≤ b обозначается следующим образом:
[ a ; b ]
Квадратные скобки с обеих сторон указывают на то, что границы отрезка принадлежат ему. Запишем ответ к неравенству 2 ≤ x ≤ 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8 включительно, являются решениями неравенства 2 ≤ x ≤ 8.
Интервал
Интервалом называют числовой промежуток, который задаётся двойным неравенством a < x < b, где a и b — границы данного неравенства, x — решение неравенства.
Пусть a = 2, b = 8. Тогда неравенство a < x < b примет вид 2 < x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая числа 2 и 8.
Изобразим интервал на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x < 8. Точки 2 и 8, являющиеся границами интервала, изображены в виде пустых кружков, поскольку границы неравенства 2 < x < 8 не принадлежат множеству его решений.
На письме интервал, заданный неравенством a < x < b, обозначается следующим образом:
( a ; b )
Круглые скобки с обеих сторон указывают на то, что границы интервала не принадлежат ему. Запишем ответ к неравенству 2 < x < 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, исключая числа 2 и 8, являются решениями неравенства 2 < x < 8.
Полуинтервал
Полуинтервалом называют числовой промежуток, который задаётся неравенством a ≤ x < b, где a и b — границы данного неравенства, x — решение неравенства.
Полуинтервалом также называют числовой промежуток, который задаётся неравенством a < x ≤ b.
Одна из границ полуинтервала принадлежит ему. Отсюда и название этого числового промежутка.
В ситуации с полуинтервалом a ≤ x < b ему (полуинтервалу) принадлежит левая граница.
А в ситуации с полуинтервалом a < x ≤ b ему принадлежит правая граница.
Пусть a = 2, b = 8. Тогда неравенство a ≤ x < b примет вид 2 ≤ x < 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, включая число 2, но исключая число 8.
Изобразим полуинтервал 2 ≤ x < 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 ≤ x < 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 ≤ x < 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде закрашенного кружка, поскольку левая граница неравенства 2 ≤ x < 8 принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде пустого кружка, поскольку правая граница неравенства 2 ≤ x < 8 не принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a ≤ x < b, обозначается следующим образом:
[ a ; b )
Видно, что с одной стороны граница обрамлена квадратной скобкой, а с другой круглой. Это связано с тем, что одна граница полуинтервала принадлежит ему, а другая нет. Запишем ответ к неравенству 2 ≤ x < 8 с помощью этого обозначения:
x ∈ [ 2 ; 8 )
В этом выражении говорится, что все числа от 2 до 8, включая число 2, но исключая число 8, являются решениями неравенства 2 ≤ x < 8.
Аналогично на координатной прямой можно изобразить полуинтервал, заданный неравенством a < x ≤ b. Пусть a = 2, b = 8. Тогда неравенство a < x ≤ b примет вид 2 < x ≤ 8. Решениями этого двойного неравенства являются все числа, которые больше 2 и меньше 8, исключая число 2, но включая число 8.
Изобразим полуинтервал 2 < x ≤ 8 на координатной прямой:
Здесь точки 2 и 8 соответствуют границам неравенства 2 < x ≤ 8, а выделенная штрихами область соответствует множеству значений x, которые являются решениями неравенства 2 < x ≤ 8.
Точка 2, являющаяся левой границей полуинтервала, изображена в виде пустого кружка, поскольку левая граница неравенства 2 < x ≤ 8 не принадлежит множеству его решений.
А точка 8, являющаяся правой границей полуинтервала, изображена в виде закрашенного кружка, поскольку правая граница неравенства 2 < x ≤ 8 принадлежит множеству его решений.
На письме полуинтервал, заданный неравенством a < x ≤ b, обозначается так: ( a ; b ]. Запишем ответ к неравенству 2 < x ≤ 8 с помощью этого обозначения:
x ∈ ( 2 ; 8 ]
В этом выражении говорится, что все числа от 2 до 8, исключая число 2, но включая число 8, являются решениями неравенства 2 < x ≤ 8.
Изображение числовых промежутков на координатной прямой
Числовой промежуток может быть задан с помощью неравенства или с помощью обозначения (круглых или квадратных скобок). В обоих случаях нужно суметь изобразить этот числовой промежуток на координатной прямой. Рассмотрим несколько примеров.
Пример 1. Изобразить числовой промежуток, заданный неравенством x > 5
Вспоминаем, что неравенством вида x > a задаётся открытый числовой луч. В данном случае переменная a равна 5. Неравенство x > 5 строгое, поэтому граница 5 будет изображаться в виде пустого кружкá. Нас интересуют все значения x, которые больше 5, поэтому вся область справа будет выделена штрихами:
Пример 2. Изобразить числовой промежуток (5; +∞) на координатной прямой
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью неравенства, а с помощью обозначения числового промежутка.
Граница 5 обрамлена круглой скобкой, значит она не принадлежит промежутку. Соответственно, кружок остаётся пустым.
Символ +∞ указывает, что нас интересуют все числа, которые больше 5. Соответственно, вся область справа от границы 5 выделяется штрихами:
Пример 3. Изобразить числовой промежуток (−5; 1) на координатной прямой.
Круглыми скобками с обеих сторон обозначаются интервалы. Границы интервала не принадлежат ему, поэтому границы −5 и 1 будут изображаться на координатной прямой в виде пустых кружков. Вся область между ними будет выделена штрихами:
Пример 4. Изобразить числовой промежуток, заданный неравенством −5 < x < 1
Это тот же числовой промежуток, который мы изобразили в предыдущем примере. Но в этот раз он задан не с помощью обозначения промежутка, а с помощью двойного неравенства.
Неравенством вида a < x < b, задаётся интервал. В данном случае переменная a равна −5, а переменная b равна единице. Неравенство −5 < x < 1 строгое, поэтому границы −5 и 1 будут изображаться в виде пустых кружка. Нас интересуют все значения x, которые больше −5, но меньше единицы, поэтому вся область между точками −5 и 1 будет выделена штрихами:
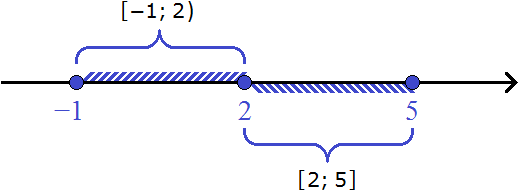
Пример 5. Изобразить на координатной прямой числовые промежутки [−1; 2) и [2; 5]
В этот раз изобразим на координатной прямой сразу два промежутка. Промежуток [−1; 2) является полуинтервалом, промежуток [2; 5] — отрезком.
У полуинтервала [−1; 2) левая граница принадлежит ему, а правая нет.
А у отрезка [2; 5] обе границы принадлежат ему.
Чтобы хорошо увидеть промежутки [−1; 2) и [2; 5], первый можно изобразить на верхней области, а второй на нижней. Так и поступим:
Граница 2 закрашена потому что она входит в промежуток [2; 5].
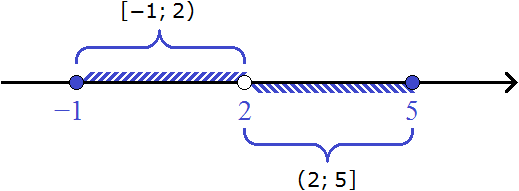
Пример 6. Изобразить на координатной прямой числовые промежутки [-1; 2) и (2; 5]
Квадратной скобкой с одной стороны и круглой с другой обозначаются полуинтервалы. Одна из границ полуинтервала принадлежат ему, а другая нет.
В случае с полуинтервалом [-1; 2) левая граница будет принадлежать ему, а правая нет. Значит левая граница будет изображаться в виде закрашенного кружка. Правая же граница будет изображаться в виде пустого кружка.
А в случае с полуинтервалом (2; 5] ему будет принадлежать только правая граница, а левая нет. Значит левая граница будет изображаться в виде пустого кружка. Правая же граница будет изображаться в виде закрашенного кружка.
Изобразим промежуток [-1; 2) на верхней области координатной прямой, а промежуток (2; 5] — на нижней:
Примеры решения неравенств
Неравенство, которое путём тождественных преобразований можно привести к виду ax > b (или к виду ax < b), будем называть линейным неравенством с одной переменной.
В линейном неравенстве ax > b, x — это переменная, значения которой нужно найти, а — коэффициент этой переменной, b — граница неравенства, которая в зависимости от знака неравенства может принадлежать множеству его решений либо не принадлежать ему.
Например, неравенство 2x > 4 является неравенством вида ax > b. В нём роль переменной a играет число 2, роль переменной b (границы неравенства) играет число 4.
Неравенство 2x > 4 можно сделать ещё проще. Если мы разделим обе его части на 2, то получим неравенство x > 2
Получившееся неравенство x > 2 также является неравенством вида ax > b, то есть линейным неравенством с одной переменной. В этом неравенстве роль переменной a играет единица. Ранее мы говорили, что коэффициент 1 не записывают. Роль переменной b играет число 2.
Отталкиваясь от этих сведений, попробуем решить несколько простых неравенств. В ходе решения мы будем выполнять элементарные тождественные преобразования с целью получить неравенство вида ax > b
Пример 1. Решить неравенство x − 7 < 0
Прибавим к обеим частям неравенства число 7
x − 7 + 7 < 0 + 7
В левой части останется x, а правая часть станет равна 7
x < 7
Путём элементарных преобразований мы привели неравенство x − 7 < 0 к равносильному неравенству x < 7. Решениями неравенства x < 7 являются все числа, которые меньше 7. Граница 7 не принадлежит множеству решений, поскольку неравенство строгое.
Когда неравенство приведено к виду x < a (или x > a), его можно считать уже решённым. Наше неравенство x − 7 < 0 тоже приведено к такому виду, а именно к виду x < 7. Но в большинстве школ требуют, чтобы ответ был записан с помощью числового промежутка и проиллюстрирован на координатной прямой.
Запишем ответ с помощью числового промежутка. В данном случае ответом будет открытый числовой луч (вспоминаем, что числовой луч задаётся неравенством x < a и обозначается как ( −∞ ; a)
x ∈ ( −∞ ; 7 )
На координатной прямой граница 7 будет изображаться в виде пустого кружка, а вся область, находящаяся слева от границы, будет выделена штрихами:
Для проверки возьмём любое число из промежутка ( −∞ ; 7 ) и подставим его в неравенство x < 7 вместо переменной x. Возьмём, например, число 2
2 < 7
Получилось верное числовое неравенство, значит и решение верное. Возьмём ещё какое-нибудь число, например, число 4
4 < 7
Получилось верное числовое неравенство. Значит решение верное.
А поскольку неравенство x < 7 равносильно исходному неравенству x − 7 < 0, то решения неравенства x < 7 будут совпадать с решениями неравенства x − 7 < 0. Подставим те же тестовые значения 2 и 4 в неравенство x − 7 < 0
2 − 7 < 0
−5 < 0 — Верное неравенство
4 − 7 < 0
−3 < 0 Верное неравенство
Пример 2. Решить неравенство −4x < −16
Разделим обе части неравенства на −4. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Мы привели неравенство −4x < −16 к равносильному неравенству x > 4. Решениями неравенства x > 4 будут все числа, которые больше 4. Граница 4 не принадлежит множеству решений, поскольку неравенство строгое.
Изобразим множество решений неравенства x > 4 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 3. Решить неравенство 3y + 1 > 1 + 6y
Перенесём 6y из правой части в левую часть, изменив знак. А 1 из левой части перенесем в правую часть, опять же изменив знак:
3y − 6y> 1 − 1
Приведём подобные слагаемые:
−3y > 0
Разделим обе части на −3. Не забываем, что при делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства y < 0 являются все числа, меньшие нуля. Изобразим множество решений неравенства y < 0 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 4. Решить неравенство 5(x − 1) + 7 ≤ 1 − 3(x + 2)
Раскроем скобки в обеих частях неравенства:
Перенесем −3x из правой части в левую часть, изменив знак. Члены −5 и 7 из левой части перенесем в правую часть, опять же изменив знаки:
Приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 8
Решениями неравенства являются все числа, которые меньше
. Граница
принадлежит множеству решений, поскольку неравенство
является нестрогим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 5. Решить неравенство
Умножим обе части неравенства на 2. Это позволит избавиться от дроби в левой части:
Теперь перенесем 5 из левой части в правую часть, изменив знак:
После приведения подобных слагаемых, получим неравенство 6x > 1. Разделим обе части этого неравенства на 6. Тогда получим:
Решениями неравенства являются все числа, которые больше
. Граница
не принадлежит множеству решений, поскольку неравенство
является строгим.
Изобразим множество решений неравенства на координатной прямой и запишем ответ в виде числового промежутка:
Пример 6. Решить неравенство
Умножим обе части на 6
После приведения подобных слагаемых, получим неравенство 5x < 30. Разделим обе части этого неравенства на 5
Решениями неравенства x < 6 являются все числа, которые меньше 6. Граница 6 не принадлежит множеству решений, поскольку неравенство является x < 6 строгим.
Изобразим множество решений неравенства x < 6 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 7. Решить неравенство
Умножим обе части неравенства на 10
В получившемся неравенстве раскроем скобки в левой части:
Перенесем члены без x в правую часть
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 10
Решениями неравенства x ≤ 3,5 являются все числа, которые меньше 3,5. Граница 3,5 принадлежит множеству решений, поскольку неравенство является x ≤ 3,5 нестрогим.
Изобразим множество решений неравенства x ≤ 3,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 8. Решить неравенство 4 < 4x < 20
Чтобы решить такое неравенство, нужно переменную x освободить от коэффициента 4. Тогда мы сможем сказать в каком промежутке находится решение данного неравенства.
Чтобы освободить переменную x от коэффициента, можно разделить член 4x на 4. Но правило в неравенствах таково, что если мы делим член неравенства на какое-нибудь число, то тоже самое надо сделать и с остальными членами, входящими в данное неравенство. В нашем случае на 4 нужно разделить все три члена неравенства 4 < 4x < 20
Решениями неравенства 1 < x < 5 являются все числа, которые больше 1 и меньше 5. Границы 1 и 5 не принадлежат множеству решений, поскольку неравенство 1 < x < 5 является строгим.
Изобразим множество решений неравенства 1 < x < 5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 9. Решить неравенство −1 ≤ −2x ≤ 0
Разделим все члены неравенства на −2
Получили неравенство 0,5 ≥ x ≥ 0. Двойное неравенство желательно записывать так, чтобы меньший член располагался слева, а больший справа. Поэтому перепишем наше неравенство следующим образом:
0 ≤ x ≤ 0,5
Решениями неравенства 0 ≤ x ≤ 0,5 являются все числа, которые больше 0 и меньше 0,5. Границы 0 и 0,5 принадлежат множеству решений, поскольку неравенство 0 ≤ x ≤ 0,5 является нестрогим.
Изобразим множество решений неравенства 0 ≤ x ≤ 0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 10. Решить неравенство
Умножим обе неравенства на 12
Раскроем скобки в получившемся неравенстве и приведем подобные слагаемые:
Разделим обе части получившегося неравенства на 2
Решениями неравенства x ≤ −0,5 являются все числа, которые меньше −0,5. Граница −0,5 принадлежит множеству решений, поскольку неравенство x ≤ −0,5 является нестрогим.
Изобразим множество решений неравенства x ≤ −0,5 на координатной прямой и запишем ответ в виде числового промежутка:
Пример 11. Решить неравенство
Умножим все части неравенства на 3
Теперь из каждой части получившегося неравенства вычтем 6
Каждую часть получившегося неравенства разделим на −1. Не забываем, что при делении всех частей неравенства на отрицательное число, знак неравенства меняется на противоположный:
Решениями неравенства 3 ≤ a ≤ 9 являются все числа, которые больше 3 и меньше 9. Границы 3 и 9 принадлежат множеству решений, поскольку неравенство 3 ≤ a ≤ 9 является нестрогим.
Изобразим множество решений неравенства 3 ≤ a ≤ 9 на координатной прямой и запишем ответ в виде числового промежутка:
Когда решений нет
Существуют неравенства, которые не имеют решений. Таковым, например, является неравенство 6x > 2(3x + 1). В процессе решения этого неравенства мы придём к тому, что знак неравенства > не оправдает своего местоположения. Давайте посмотрим, как это выглядит.
Раскроем скобки в правой части данного неравенство, получим 6x > 6x + 2. Перенесем 6x из правой части в левую часть, изменив знак, получим 6x − 6x > 2. Приводим подобные слагаемые и получаем неравенство 0 > 2, которое не является верным.
Для наилучшего понимания, перепишем приведение подобных слагаемых в левой части следующим образом:
Получили неравенство 0x > 2. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль не может быть больше, чем число 2. Значит неравенство 0x > 2 не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x > 2, то не имеет решений и исходное неравенство 6x > 2(3x + 1).
Пример 2. Решить неравенство
Умножим обе части неравенства на 3
В получившемся неравенстве перенесем член 12x из правой части в левую часть, изменив знак. Затем приведём подобные слагаемые:
Правая часть получившегося неравенства при любом x будет равна нулю. А ноль не меньше, чем −8. Значит неравенство 0x < −8 не имеет решений.
А если не имеет решений приведённое равносильное неравенство 0x < −8, то не имеет решений и исходное неравенство .
Ответ: решений нет.
Когда решений бесконечно много
Существуют неравенства, имеющие бесчисленное множество решений. Такие неравенства становятся верными при любом x.
Пример 1. Решить неравенство 5(3x − 9) < 15x
Раскроем скобки в правой части неравенства:
Перенесём 15x из правой части в левую часть, изменив знак:
Приведем подобные слагаемые в левой части:
Получили неравенство 0x < 45. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль меньше, чем 45. Значит решением неравенства 0x < 45 является любое число.
А если приведённое равносильное неравенство 0x < 45 имеет бесчисленное множество решений, то и исходное неравенство 5(3x − 9) < 15x имеет те же решения.
Ответ можно записать в виде числового промежутка:
x ∈ ( −∞; +∞ )
В этом выражении говорится, что решениями неравенства 5(3x − 9) < 15x являются все числа от минус бесконечности до плюс бесконечности.
Пример 2. Решить неравенство: 31(2x + 1) − 12x > 50x
Раскроем скобки в левой части неравенства:
Перенесём 50x из правой части в левую часть, изменив знак. А член 31 из левой части перенесём в правую часть, опять же изменив знак:
Приведём подобные слагаемые:
Получили неравенство 0x > −31. В левой части располагается произведение, которое будет равно нулю при любом x. А ноль больше, чем −31. Значит решением неравенства 0x < −31 является любое число.
А если приведённое равносильное неравенство 0x > −31 имеет бесчисленное множество решений, то и исходное неравенство 31(2x + 1) − 12x > 50x имеет те же решения.
Запишем ответ в виде числового промежутка:
x ∈ ( −∞; +∞ )
Задания для самостоятельного решения
Задание 1. Решите неравенство:
Задание 2. Решите неравенство:
Задание 3. Решите неравенство:
Задание 4. Решите неравенство:
Задание 5. Решите неравенство:
Задание 6. Решите неравенство:
Задание 7. Решите неравенство:
Задание 8. Решите неравенство:
Задание 9. Решите неравенство:
Задание 10. Решите неравенство:
Задание 11. Решите неравенство:
Задание 12. Решите неравенство:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x < b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x < 5 x − 2 ≥ 0 7 − 5 x < 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x < c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , < , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x < c |
|
x ∈ ( − ∞ ; c ) |
| x ≤ c |
|
x ∈ ( − ∞ ; c ] |
| x > c |
|
x ∈ ( c ; + ∞ ) |
| x ≥ c |
|
x ∈ [ c ; + ∞ ) |
Алгоритм решения линейного неравенства
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
a x < b a x ≤ b a x > b a x ≥ b
- Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a > 0 то неравенство приобретает вид x ≤ b a .
- Если a < 0 , то знак неравенства меняется на противоположный, неравенство приобретает вид x ≥ b a .
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3 ( 2 − x ) > 18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 − 3 x > 18
− 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 )
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как − 3 < 0 , знак неравенства поменяется на противоположный. x < 12 − 3 ⇒ x < − 4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ ( − ∞ ; − 4 )
№2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x + 4 ≥ 3 x + 3 − 14
6 x − 3 x ≥ 3 − 14 − 4
3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3 > 0, знак неравенства после деления меняться не будет.
x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x ∈ [ − 5 ; + ∞ )
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6 x − 1 ≤ 6 x − 1
6 x − 6 x ≤ − 1 + 1
0 ≤ 0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
Ответ:
- x – любое число
- x ∈ ( − ∞ ; + ∞ )
- x ∈ ℝ
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x + 6 − 9 x > − 8 x + 48
− 8 x + 8 x > 48 − 6
0 > 42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x ∈ ∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c < 0 a x 2 + b x + c ≤ 0 где a, b, c – некоторые числа, причем a ≠ 0, x – переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
- Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 .
- Отметить на числовой прямой корни трехчлена.
Если знак неравенства строгий > , < , точки будут выколотые.
Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение a x 2 + b x + c вместо x.
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.
Точки жирные, если знак неравенства нестрогий.
- Выбрать подходящие интервалы (или интервал).
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
- Записать ответ.
Примеры решения квадратных неравенств:
№1. Решить неравенство x 2 ≥ x + 12.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 ≥ x + 12
x 2 − x − 12 ≥ 0
x 2 − x − 12 = 0
a = 1, b = − 1, c = − 12
D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ .
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ )
№2. Решить неравенство − 3 x − 2 ≥ x 2 .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
− 3 x − 2 ≥ x 2
− x 2 − 3 x − 2 ≥ 0
− x 2 − 3 x − 2 = 0
a = − 1, b = − 3, c = − 2
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1
x 1 = − 2, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
− x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет − .
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ [ − 2 ; − 1 ]
№3. Решить неравенство 4 < x 2 + 3 x .
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
4 < x 2 + 3 x
− x 2 − 3 x + 4 < 0
− x 2 − 3 x + 4 = 0
a = − 1, b = − 3, c = 4
D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1
x 1 = − 4, x 2 = 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
− x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 < 0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервалы со знаком − .
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ )
№4. Решить неравенство x 2 − 5 x < 6.
Решение:
Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0.
x 2 − 5 x < 6
x 2 − 5 x − 6 < 0
x 2 − 5 x − 6 = 0
a = 1, b = − 5, c = − 6
D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49
D > 0 ⇒ будет два различных действительных корня
x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1
x 1 = 6, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x ∈ ( − 1 ; 6 )
№5. Решить неравенство x 2 < 4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x 2 < 4
x 2 − 4 < 0
x 2 − 4 = 0
( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2
x 1 = 2, x 2 = − 2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства < , выбираем в ответ интервал со знаком − .
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 2 ; 2 )
№6. Решить неравенство x 2 + x ≥ 0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0.
x 2 + x ≥ 0
x 2 + x = 0
x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1
x 1 = 0, x 2 = − 1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x 2 + x = 1 2 + 1 = 2 > 0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ )
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x − 1 x + 3 < 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
f ( x ) g ( x ) < 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
- Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя.
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
- Нанести нули числителя и нули знаменателя на ось x.
Вне зависимости от знака неравенства
при нанесении на ось x нули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x − 1 x + 3 > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравниваем числитель к нулю f ( x ) = 0.
x − 1 = 0
x = 1 – это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
- Приравниваем знаменатель к нулю g ( x ) = 0.
x + 3 = 0
x = − 3 – это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.
Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
№2. Решить неравенство 3 ( x + 8 ) ≤ 5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Привести неравенство к виду f ( x ) g ( x ) ≤ 0.
3 ( x + 8 ) ≤ 5
3 ( x + 8 ) − 5 x + 8 ≤ 0
3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 ( x + 8 ) x + 8 ≤ 0
3 − 5 x − 40 x + 8 ≤ 0
− 5 x − 37 x + 8 ≤ 0
- Приравнять числитель к нулю f ( x ) = 0.
− 5 x − 37 = 0
− 5 x = 37
x = − 37 5 = − 37 5 = − 7,4
x = − 7,4 – ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
- Приравнять знаменатель к нулю g ( x ) = 0.
x + 8 = 0
x = − 8 – это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
− 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 < 0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.
Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ )
№3. Решить неравенство x 2 − 1 x > 0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0.
- Приравнять числитель к нулю f ( x ) = 0.
x 2 − 1 = 0
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1
x 1 = 1, x 2 = − 1 – нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
- Приравнять знаменатель к нулю g ( x ) = 0.
x = 0 – это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
- Наносим нули числителя и нули знаменателя на ось x.
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
- Расставляем знаки на интервалах.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f ( x ) g ( x ) :
x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
- Выбираем подходящие интервалы и записываем ответ.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.
Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ )
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств – это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{ x + 4 > 0 2 x + 3 ≤ x 2
Алгоритм решения системы неравенств
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Примеры решений систем неравенств:
№1. Решить систему неравенств { 2 x − 3 ≤ 5 7 − 3 x ≤ 1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 3 ≤ 5
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 4 ;
Графическая интерпретация:
Точка 4 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
7 − 3 x ≤ 1
− 3 x ≤ 1 − 7
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 < 0, знак неравенства после деления меняется на противоположный.
x ≥ 2
Графическая интерпретация решения:
Точка 2 на графике жирная, так как знак неравенства нестрогий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x ∈ [ 2 ; 4 ]
№2. Решить систему неравенств { 2 x − 1 ≤ 5 1 < − 3 x − 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
2 x − 1 ≤ 5
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x ≤ 3
Графическая интерпретация:
Точка 3 на графике жирная, так как знак неравенства нестрогий.
- Решаем второе неравенство системы.
1 < − 3 x − 2
3 x < − 1 − 2
3 x < − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется.
x < − 1
Графическая интерпретация решения:
Точка -1 на графике выколотая, так как знак неравенства строгий.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x ∈ ( − ∞ ; − 1 )
№3. Решить систему неравенств { 3 x + 1 ≤ 2 x x − 7 > 5 − x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
3 x + 1 ≤ 2 x
3 x − 2 x ≤ − 1
x ≤ − 1
Графическая интерпретация решения:
- Решаем второе неравенство системы
x − 7 > 5 − x
x + x > 5 + 7
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется.
x > 6
Графическая интерпретация решения:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x ∈ ∅
№4. Решить систему неравенств { x + 4 > 0 2 x + 3 ≤ x 2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
- Решаем первое неравенство системы.
x + 4 > 0
x > − 4
Графическая интерпретация решения первого неравенства:
- Решаем второе неравенство системы
2 x + 3 ≤ x 2
− x 2 + 2 x + 3 ≤ 0
Решаем методом интервалов.
− x 2 + 2 x + 3 = 0
a = − 1, b = 2, c = 3
D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16
D > 0 – два различных действительных корня.
x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.
Графическая интерпретация решения второго неравенства:
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ .
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x ∈ ( − 4 ; − 1 ] ∪ [ 3 ; + ∞ )
Скачать домашнее задание к уроку 8.
Урок № 134
математика 6 «В» класс дата: 23.02.16.
Тема урока : «Решение
неравенств»
1. Цель: формирование навыков решение линейных неравенств с одной переменной и
их систем.
Задачи:
·
обобщить и систематизировать знания учащихся по
теме “Решение линейных неравенств и их систем»
·
активизировать познавательную деятельность,
развивать вычислительные навыки и логическое мышление учащихся.
·
воспитывать патриотизм, коммуникативные способности
учащихся при совместной работе, культуру умственного труда; создать на уроке
доброжелательную психологическую обстановку в отношениях “учитель – ученик”,
воспитать патриотизм, любовь к Родине.
Оборудование: компьютер, проектор, индивидуальные карточки с тестовыми заданиями,
презентация, флипчарт, музыкальные заставки.
Тип урока: урок закрепления пройденного
материала;
Вид урока: урок-путешествие в математическую страну « Неравенства»;
План урока:
I.
Организационный момент.(2 мин)
II.
Актуализация знаний. .
1. Устный счет «Математический диктант»(7 мин)
2. «Пазл» – работа по уровнем (5мин)
III.
Обобщение , закрепление и систематизация знаний «Путешествие»
3. «Графический диктант»(3мин)
4. Тестирование по группам с зашифрованной таблицей.(5мин)
5. Устный опрос по теории «Математическое домино»(5мин)
6. «Веселая рыбалка» с отгадыванием числового ребуса (5 мин)
7. Физкультминутка(1мин)
8. Загадка «Байтерека»(3мин)
9. Тренажер «верно-неверно».(3 мин)
10. «Найти
ошибки» с применением флипчарта (3мин)
IV.
Рефлексия (1 мин)
V.
Задание на дом (1 мин)
VI.
Выставление оценок(1мин)
ХОД УРОКА
1. Организационный момент
1) сообщение цели урока;
2) проверка готовности учащихся к восприятию
информации;
3) пояснение хода урока
4) рапорт дежурного.
Учитель: У каждого из Вас на столе ваши зачетные книжки и оценочная командировочная карта, где Вы будете фиксировать свои
достижения, и в конце оцените свою работу
Фамилия, имя
ученика(цы)__________________________________________________
|
Маршрут |
Ваша самооценка |
Ваши баллы |
Оценка учителя |
|
|
1 |
Устный счет «Математический диктант» |
|||
|
2 |
«ПАЗЛ» |
|||
|
3 |
«Графический диктант» |
|||
|
4 |
«Тестирование» |
|||
|
5 |
«Математическое домино» |
|||
|
6 |
«Веселая рыбалка» |
|||
|
7 |
«Загадка Байтерека» |
|||
|
8 |
Тренажер «Верно-неверное» |
|||
|
9 |
«Найти ошибки» |
|||
|
Итог урока |
||||
|
« от 40б и выше» -« 5» «26-35б» – «4» « 15-25б » – 3 Меньше 21б – зачет |
II. Актуализация опорных знаний
(Слайд № 1,2)
Эпиграф урока ( слайд №5)
« Когда человек не знает, к какой пристани он держит путь, для
него ни один ветер не будет попутным».
Класс разделен на три команды во главе с бригадирами,
имеющими право принимать окончательное решение по выполнению заданий. (Слайд
№6)
1. Математический диктант : (слайд №7)
Записать в виде неравенств утверждения:
а) сумма чисел
х и 17 больше 18;
б) разность чисел
13 и х меньше 2;
в) произведение чисел 17 и х больше 3;
г) удвоенная сумма чисел х и −3 не
больше 3;
д) полусумма чисел х и 3 не
больше их произведения;
е) удвоенное произведение х и −4 не
меньше их разности.
Взаимопроверка с помощью флипчарта 1 ( 6
баллов)
.
— Мы записали линейные неравенства.
— Что будет решением любого из этих
неравенств? Ответ: значение переменной, которое обращает его в верное.
— Как мы показываем множество
решений неравенства? Ответ: В виде числового промежутка.
4. Работа с флипчартами 2, 3, 4, 5, 6
2 — определить названия числовых
промежутков;( 4 балла)
Ответы: 1. Полуинтервал;2. Полуинтервал; 3.
Интервал; 4.отрезок
3 — запишите промежутки, изображенные
на рисунке; (4 балла)
Ответы:1/ I -6;3,7) 2/ I5;9I 3/
(-2,5;4I 4/ (-7;-1)
4— изобразите на координатной прямой
числовые промежутки ;(5 баллов)
5 — выберите из чисел те,
которые принадлежат промежутку; -3 балла
Ответы: -2; 0; 8,4.
2. Индивидуальная работа по уровнем «Пазл»
Учитель: «Мы с вами отправимся в путешествие самый
замечательный, современный и молодой город А. Какой это город вы узнаете
сейчас. Для этого Вам необходимо собрать пазл (индивидуальная работа по
карточкам. На данном этапе урока выработаем навыки решении линейных неравенств
с одной переменной » (слайд № 8,9)
Уровень А Уровень
В Уровень С
Решить неравенства . Решить неравенства .
Решить неравенства
1. .
Ответы:
Уровень А
Уровень В . Уровень С.
Перед посадкой в поезд нужно купить билеты. Билет считается купленным,
если команда на станции “Наблюдательная” ответит на заданные
вопросы.
3. Графический диктант (слайд №10)
(Учитель зачитывает математическое предложение, если учащиеся
с ним согласны, то ставят «1», а если нет, то» «0». По ключу, ребята проводят
взаимопроверку.)
1. Неравенство – это выражение, составленное с помощью знаков «+», « -_»,
«=».(неверно)
2. Если a>b, то b<a (верно)
3. Если a+c > b+c, то a<b(неверно)
4. Если a>b и c<0, то ac > bc
(неверно)
5. Если a>b и c>d, то a + c > b + c (верно)
6. Неравенства, имеющие одни и те же решения, называется
равносильными.(верно)
7. Для строгого неравенства используют знаки « больше или равно» и «
меньше равно», а для нестрогого – « меньше» и «больше». (неверно)
8. Решением системы неравенств является пересечение множеств решении всех
неравенств, заключенных в данной системе.( верно)
9. Число – 1 принадлежит ( – 1;
5 I ( неверно)
19. Число 3 принадлежит I-2;3I (верно)
Ключ для проверки : 0 1 0 0 1 1 0 1 0 1 (Слайд №10)
( макс. 10 баллов)
III.
Путешествие
Учитель: «Билеты куплены, ждем проверки билетов проводниками,
наша задача выполнить тестовые задания, чтоб проводники дали добро на
отправление.»
4. Тестирование
(проверка билетов) (слайд № 11)
ТЕСТ. Уровень А (6 примеров).
1.Записать неравенство в виде числового
промежутка: 2
X) C)
T)
Н)
2. Какой промежуток соответствует неравенству
7 ≤ х < 13?
А)[ 7; 13 ]; Б) (7; 13); О) [7; 13); К)
(7; 13]
3. Решите неравенство: 4х>28
A) x<7; P) x>7; C) X≥7; X) x≤7
4. Решите неравенство: 6х ≥ 12
К) ( – ∞; 2]; Б) (2 ; +∞); O) [ 2; +∞); Г) ( 2; 6]
5. Решите неравенство -2х < 4
Н) ( – ∞; 2]; Ш) (-2 ; ∞); Л) [ -2;
∞); Д) ( – 2; 4]
6. Решить систему неравенств
Е ( – 6;12]; О) (6 ; 12); У) [ -12; 6)
Ж) ( – 12; 6]
ТЕСТ. Уровень В: (
7 примеров)
1. Какой промежуток включает в себя все
решения неравенства 3 < х ≤ 4
М) ( 3; 4]; Б) [ -2; 5); И) ( -3; 2); Х)
( – ∞; 2] U [2; 4)
2. Решите неравенство: 3х ≥ 0
Г) ( 0; + ∞]; Н) [ 3; +∞); О) [ 0;+ ∞); Е)
( – ∞; 0]
3. Решите неравенство: -4х > -16
Л) ( – ∞; 4); О) (- ∞; 4]; Ц) [ -4; +∞);
З) ( 0; 4]
4. Решите неравенство: -2х < 5
О) (-∞; -2,5); Т) (-2,5; + ∞); Ч)(3; + ∞);
И) (7; + ∞)
5. Решите неравенство : х + 4 ≥ -1
У) (-∞;3); К) (-∞; -5); Д) [ -5; + ∞); Щ) (-
3; + ∞)
6. Решить систему неравенств:
А) нет решения; Е) (2;4]; Р) (2;4)
П) [2;4]
7. Найти число, принадлежащее промежутку
(-6; -3]
В) 3; А) -6; Ц) -3; Г) 6
ТЕСТ: Уровень С : ( 7 примеров)
1. Решить неравенства: 2х>22
А) х<11; К) х ≤ 11; О) х > 11 ;
С) х ≥ 11
2. Решить неравенства: -5х ≥30
T) (÷ П) [-6;
; Е) (6;
; В) (-
3. Решить неравенства: – 5х>-0,25
А) ; Л)
; Е)
; C)
4. Решить двойное неравенство:
Е) (-4;5); И) [-4;5); T) (-4;5]; C) [-4;5]
5. Решить линейное неравенство: 3х – 4 (х+1) <-8
– 5х
К) x < 1; Е) x> -1; Р) x> 1 ; Ч) x< -1.
6. Найти пересечение промежутков ; [-4;3) ∩
[-2;3)
Н) [-2;3); В) [-4;3) ; А) (3;5) ;
С) [-4;5)
7.Решить систему
неравенств:
Е) [1; 5) В) [-5;1] ; О) [-1;5)
; Л) [-1;5].
Схема ответов на тестовые задания: (Слайд №12)
Уровень А
|
Номера заданий |
1 |
2 |
3 |
4 |
5 |
6 |
|
Правильные ответы |
Х |
О |
Р |
О |
Ш |
О |
Уровень В
|
Номера заданий |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Правильные ответы |
М |
О |
Л |
О |
Д |
Е |
Ц |
Уровень С
|
Номера заданий |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Правильные ответы |
О |
Т |
Л |
И |
Ч |
Н |
О |
Выполняется самопроверка. Количество правильных ответов равно количеству
баллов. Учащимся необходимо занести в зачетную книжку.
5. Устный теоретический опрос «Математическое домино»
(слайд 13)
Учитель: -Поезд тронулся, дорога дальняя. Чтобы время
скоротать обычно, путешественники разгадывают кроссворды, играют в разные игры,
и мы тоже сыграем с вами в математическое домино, чтобы путь не показался
долгим и утомительным.
У каждого учащегося имеется карточка-домино. Карточка содержит
вопрос и ответ. Первым начинает ученик, у которого содержится слова «СТАРТ» и «ФИНИШ». Он задает стартовый вопрос. Каждый ученик должен внимательно следить за ходом
игры, чтобы не пропустить свой ответ. Ответив, ученик задает свой вопрос
и т.д. Учитель указывает на ошибку , если прозвучал неправильный ответ. Все
учащиеся одновременно следят и за тем, чтобы был дан правильный ответ. За игру в домино в оценочный лист вы себе поставите
один балл, если верно ответите на вопрос, и 0 баллов, если пропустите
свой ответ.
1. Финиш: Ответ: Решением системы неравенств с одной переменной называется
множество значение переменной, при котором верно каждое из неравенств системы.
Старт: Вопрос: Что такое неравенство?
2. Ответ: Запись, в котором числа и выражения
связаны знаками «<» , «>» называются неравенствами.
Вопрос: Назовите виды неравенства
3. Ответ: Строгие, нестрогие, двойные,
неравенства одного знака, неравенства противоположных знаков, линейные и
числовые неравенства
Вопрос: Какие неравенства называются строгими,
а какие нестрогими?
4. Ответ: Неравенства со знаками « » называется строгими, а со знаками «
» – нестрогими.
Вопрос: Назовите виды числовых промежутков
5. Ответ: Интервал, отрезок, полуинтервал,
луч, числовая прямая
Вопрос: Какие знаки используют для записи
числовых промежутков?
6. Ответ: для записи промежутков используют
круглые и квадратные скобки, Для строгого неравенства – круглые скобки, а для
нестрогого – квадратные.
Вопрос: Какой промежуток называется
пересечением числовых промежутков А и В ?
7. Ответ Пересечением числовых промежутков А и
В называют новый промежуток, содержащий только те числа, которые принадлежат и
промежутку А, и промежутку В:
Вопрос: Какой промежуток называется
объединением?
8. Ответ : Объединением промежутков А и В
называется новый промежуток состоящий только из тех чисел , принадлежащих хотя
бы одному из промежутков А или В.
Вопрос: Какие неравенства называются линейными
неравенствами с одной переменной?
9. Ответ: Неравенства вида ax>b, ax<b. называются линейными неравенствами с одной переменной.
Вопрос: Что значит решить неравенства?
10. Ответ: Решить неравенство – значит найти
множество его решений, или доказать , что их нет
Вопрос: Какие неравенства называются
равносильными?
11.Ответ: Равносильными называются неравенства,
имеющие одни и те же решения.
Вопрос: Что
является решением системы неравенств?
Станция «Балхаш» (слайд 14)
6. «Веселая рыбалка» (слайд 15) Решение линейных неравенств
Недалеко от этой станции есть «Озеро неизвестности», а в этом
озере водится необычная рыба. (Нарисовать рыбок с уравнениями)
Уровень А: М –
Уровень В: С –
Уровень С: О –
Итог: Вы узнаете, какую рыбу можно встречать в озере Балхаш
Ответ: СОМ (Слайд
№16)
7. Физкультминутка. Станция «Спортивная» (Слайд №17).
Поднимает руки класс – это раз
Повернулась голова – это два
Руки вниз – вперед смотри – это три
Руки в стороны, пошире, развернули на четыре
С силой их к плечам прижать и немного повращать – это пять
А на шесть – в ладоши хлопнуть
И на семь – ногою топнуть
А на восемь – подтянуться
И на девять – улыбнуться
Что ж заряд хороший есть?
Можно нам теперь и сесть.
– Станция « Астана» (слайд 18)
8. Загадка Байтерека. (слайд
№ 19)
Мы совершаем путешествие в одно из достопримечательности
Астаны «Байтерек». Монумент Байтерек был открыт в 2002 году, и стал знаком
истории Казахстана, нового этапа в жизни народа. Структура башни символизирует
три основы мироздания – подземный, земной и небесный миры. На глубине четыре с
половиной метра находится нижний уровень, где располагаются кафе, аквариумы и
мини-галерея «Байтерек».. Металлическая конструкция башни весит больше 1000
тонн и стоит на 500 сваях. На вершине находится огромный шар из стекла
диаметром 22 метра и весом 300 тонн. Высота сооружения составляет 97 , что символизирует 1997 год, год
провозглашения новой столицы
метров, с шаром, венчающим конструкцию . Общая высота составляет 105
метров. Архитектором столь амбициозного проекта стал, известный своими hi-tech
сооружениями, Норман Фостер.Чтобы решить загадку Байтерека нам надо выбрать
своего президента математики. Он должен решить систему неравенств. Числовой промежуток,
является числами, которые символизируют глубину подземного и высоту небесного
миров. ( -5 и 8)

Ответ: , 4,5м – глубина подземного уровня, а 8 метров – высота небесного
уровня, т.е шара.
9. Океанариум (слайд
№ 21)
Океанариум Развлекательного центра “Думан” – первый
и единственный в СНГ. Это единственный в мире Океанариум, удаленный от океана
более чем на 3000 километров. Емкость океанариума составляет 3 миллиона литров
воды, для приготовления которой понадобилось 120 тонн морской соли. Здесь живут
более 2000 морских обитателей, представляющих более 100 видов морской фауны из
различных уголков Земли.
9. Тренажер «Верно-неверно» (слайд № 23-27)( за
неправильные ответы аннулируются баллы)
Если 5>-4, то -4<5 (да)
Если 

– строгое неравенство (нет)
Если 

Верно ли, что промежуток является решением неравенства
, а промежуток
неравенства
.
10. Билет в торгово – развлекательный
центр «Хан – Шатыр» ( слайд № 26)
Учитель: «Хан Шатыр»
(как некоторые ошибочно считают, в переводе с казахского на русский «Ханский
шатёр», но на самом деле это словосочетание из ряда
“Царь-колокол”, “Царь-пушка”, т.е. Хан Шатыр – “Хан
среди шатров”) — крупный торгово-развлекательный центр в столице
Казахстана Астане. Открыт 6 июля 2010 года. Является самым большим шатром в
мире[1].
Учитель: «Математика учит преодолевать трудности и исправлять
собственные ошибки»
«Найти ошибку» ( по программе «Актив- студио) (флипчарт 6) (
1балл)
Уровень
А Уровень В
. 

Уровень С
Наш поезд возвращается назад
IV.
Итог урока.
V. Рефлексия. (Слайд №27) Выполните оценку вашего
настроения на сегодняшнем уроке с помощью смайликов, которое необходимо
заклеить на дереве.
VI.Домашнее задание: (Слайд №28) № 1094,1099,1101. Подготовиться к контрольной работе
Приложения к уроку.
1. МАТЕМАТИЧЕСКИЙ ДИКТАНТ
1. Записать в виде неравенства
а) сумма чисел х и 17больше 18
б) разность чисел 13 и х меньше 2
в) произведение чисел17 и х больше или равно
34
г) удвоенная сумма чисел х и 3 меньше или
равно 3
д) полусумма чисел х и 3 не больше их
произведения
е) удвоенное произведение -4 и х не меньше их
разности
2. Определить названия числовых промежутков
3. Записать промежутки
4. Изобразить на координатной прямой числовые
промежутки.
5. Выбрать из чисел те которые принадлежат
промежутку
6. Какому из интервалов принадлежит промежуток
«ПАЗЛ»
Уровень А Уровень
В Уровень С
Решить неравенства . Решить неравенства
. Решить неравенства
1. .
Ответы:
Уровень А Уровень
В . Уровень С.
Графический диктант
1.Неравенство – это выражение, составленное
с помощью знаков «+», « -_», «=».(неверно)
2.Если a>b, то b<a (верно)
3. Если a+c > b+c, то a<b(неверно)
4. Если a>b и c<0, то ac > bc (неверно)
5. Если a>b и c>d, то a + c > b + c (верно)
6. Неравенства, имеющие одни и те же
решения, называется равносильными.(верно)
Для строгого неравенства используют знаки «
больше или равно» и « меньше равно», а для нестрогого – « меньше» и «больше».
(неверно)
7. Решением системы неравенств является
пересечение множеств решении всех неравенств, заключенных в данной системе.(
верно)
8. Число – 1 принадлежит ( – 1; 5 I ( неверно)
9. Число 3 принадлежит I-2;3I (верно)
Ключ для проверки : 0 1 0 0 1 1 0 1 0 1
Тестирование
ТЕСТ. Уровень А
(6 примеров).
1.Записать неравенство в виде числового
промежутка: 2
X) C)
T)
Н)
2. Какой промежуток соответствует неравенству
7 ≤ х < 13?
А)[ 7; 13 ]; Б) (7; 13); О) [7; 13);
К) (7; 13]
3. Решите неравенство: 4х>28
A) x<7; P) x>7; C) X≥7; X) x≤7
4. Решите неравенство: 6х ≥ 12
К) ( – ∞; 2]; Б) (2 ; +∞); O) [ 2; +∞); Г) ( 2; 6]
5. Решите неравенство -2х < 4
Н) ( – ∞; 2]; Ш) (-2 ; ∞); Л) [ -2;
∞); Д) ( – 2; 4]
6. Решить систему неравенств
Е ( – 6;12]; О) (6 ; 12); У) [ -12;
Ж); г) ( – 12; 6]
ТЕСТ. Уровень В:
( 7 примеров)
1. Какой промежуток включает в себя все
решения неравенства 3 < х ≤ 4
М) ( 3; 4]; Б) [ -2; 5); И) ( -3; 2); Х)
( – ∞; 2] U [2; 4)
2. Решите неравенство: 3х ≥ 0
Г) ( 0; + ∞]; Н) [ 3; +∞); О) [ 0;+ ∞); Е)
( – ∞; 0]
3. Решите неравенство: -4х > -16
Л) ( – ∞; 4); О) (- ∞; 4]; Ц) [ -4; +∞);
З) ( 0; 4]
4. Решите неравенство: -2х < 5
О) (-∞; -2,5); Т) (-2,5; + ∞); Ч)(3; + ∞);
И) (7; + ∞)
5. Решите неравенство : х + 4 ≥ -1
У) (-∞;3); К) (-∞; -5); Д) [ -5; + ∞); Щ) (-
3; + ∞)
6. Решить систему неравенств:
А) нет решения; Е) (2;4]; Р) (2;4)
П) [2;4]
7. Найти число, принадлежащее промежутку (-6;
-3]
В) 3; А) -6; Ц) -3; Г) 6
ТЕСТ: Уровень С : ( 7 примеров)
1. Решить неравенства: 2х>22
А) х<11; К) х ≤ 11; О) х > 11 ;
С) х ≥ 11
2. Решить неравенства: -5х ≥30
T) (÷ П) [-6;
; Е) (6;
; В) (-
3. Решить неравенства: – 5х>-0,25
А) ; Л)
; Е)
; C)
4. Решить двойное неравенство:
Е) (-4;5); И) [-4;5); T) (-4;5]; C) [-4;5]
5. Решить линейное неравенство: 3х – 4 (х+1)
<-8 – 5х
К) x < 1; Е) x> -1; Р) x> 1 ; Ч) x< -1.
6. Найти пересечение промежутков ; [-4;3) ∩
[-2;3)
Н) [-2;3); В) [-4;3) ; А) (3;5) ;
С) [-4;5)
7.Решить систему
неравенств:
Е) [1; 5) В) [-5;1] ; О) [-1;5)
; Л) [-1;5].
Схема ответов на тестовые задания: (Слайд №12)
Уровень А
|
Номера заданий |
1 |
2 |
3 |
4 |
5 |
6 |
|
Правильные ответы |
Х |
О |
Р |
О |
Ш |
О |
Уровень В
|
Номера заданий |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Правильные ответы |
М |
О |
Л |
О |
Д |
Е |
Ц |
Уровень С
|
Номера заданий |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Правильные ответы |
О |
Т |
Л |
И |
Ч |
Н |
О |
«Математическое домино»
1. Финиш: Ответ: Решением системы неравенств с одной переменной называется
множество значение переменной, при котором верно каждое из неравенств системы.
Старт: Вопрос: Что такое неравенство?
2. Ответ: Запись, в котором числа и выражения
связаны знаками «<» , «>» называются неравенствами.
Вопрос: Назовите виды неравенства
3. Ответ: Строгие, нестрогие, двойные,
неравенства одного знака, неравенства противоположных знаков, линейные и
числовые неравенства
Вопрос: Какие неравенства называются строгими,
а какие нестрогими?
4. Ответ: Неравенства со знаками « » называется строгими, а со знаками «
» – нестрогими.
Вопрос: Назовите виды числовых промежутков
5. Ответ: Интервал, отрезок, полуинтервал,
луч, числовая прямая
Вопрос: Какие знаки используют для записи
числовых промежутков?
6. Ответ: для записи промежутков используют
круглые и квадратные скобки, Для строгого неравенства – круглые скобки, а для
нестрогого – квадратные.
Вопрос: Какой промежуток называется
пересечением числовых промежутков А и В ?
7. Ответ Пересечением числовых промежутков А и
В называют новый промежуток, содержащий только те числа, которые принадлежат и
промежутку А, и промежутку В:
Вопрос: Какой промежуток называется
объединением?
8. Ответ : Объединением промежутков А и В
называется новый промежуток состоящий только из тех чисел , принадлежащих хотя
бы одному из промежутков А или В.
Вопрос: Какие неравенства называются линейными
неравенствами с одной переменной?
9. Ответ: Неравенства вида ax>b, ax<b. называются линейными неравенствами с одной переменной.
Вопрос: Что значит решить неравенства?
10. Ответ: Решить неравенство – значит найти
множество его решений, или доказать , что их нет
Вопрос: Какие неравенства называются
равносильными?
11.Ответ: Равносильными называются
неравенства, имеющие одни и те же решения.
Вопрос: Что является решением системы
неравенств?
«Рыбалка»
Уровень А: М –
Уровень В: С –
Уровень С: О –
«Загадка Байтерека»
Тренажер «Верно-неверно» (слайд № 23-27)( за
неправильные ответы аннулируются баллы)
Если 5>-4, то -4<5 (да)
Если 

– строгое неравенство (нет)
Если 

Верно ли, что промежуток является решением неравенства
, а промежуток
неравенства
.
Приложение № 8 « Найти ошибки
Уровень
А Уровень В


Уровень С.
|
Ф.И. |
Ваша самооценка |
Ваши баллы |
Оценка учителя |
|
|
1 |
Устный счет |
|||
|
2 |
«ПАЗЛ» |
|||
|
3 |
«Графический |
|||
|
4 |
«Тестирование» |
|||
|
5 |
«Математическое |
|||
|
6 |
«Веселая рыбалка» |
|||
|
7 |
«Загадка Байтерека» |
|||
|
8 |
Тренажер |
|||
|
9 |
«Найти ошибки» |
|||
|
Итог урока |
||||
|
« от 40б и выше» -« «26-35б» – «4» « 15-25б » – 3 Меньше 21б – зачет |