Как решать задачи о прохождении тока через электрические схемы
В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про подбрасывания игральных кубиков и монеток, задачи про стрелков и станки.

В этой статье мы рассмотрим задачи вида
“задана схема электрической цепи с надежностью элементов (или вероятностями выхода из строя), найти вероятность работы цепи (или вероятность разрыва цепи)”.
Задачи могут иметь чуть разные формулировки, но принцип решения для них одинаков, и его мы изучим, чтобы суметь решать такие задачи со схемами любой сложности.
Далее:
- Базовые события, обозначения и формулы
- Последовательно или параллельно?
- Усложняем схему цепи
- Примеры решений
- На закуску: схема с мостиком
- Полезные ссылки
- Решебник
Понравилось? Добавьте в закладки
Базовые события, обозначения и формулы
Самое первое, с чего мы начнем – формализация задачи (и решение любой своей задачи рекомендую начинать с этого). А именно, мы введем основные события:
$X$ = (Цепь работает) = (Цепь пропускает ток) и противоположное ему:
$overline{X}$ =(Цепь не пропускает ток) = (Произошел разрыв в цепи).
$A_i$ = (Элемент i работает, пропускает ток) и $overline{A_i}$ =(Элемент i отказал, не пропускает ток), $i=1,2,…,n$.
Обычно в условии задачи известны вероятности работы элементов (надежности): $p(A_i)=p_i$ или вероятности отказа $p(overline{A_i})=q_i=1-p_i$, $i=1,2,…,n$.
Также напомним основные формулы (из темы действий с событиями, формулы сложения и умножения вероятностей), которые пригодятся в решении этого типа задач.
Для независимых в совокупности событий (а отказы/работа элементов цепи – именно такие):
$$
P(A cdot B) = P(A) cdot P(B); quad(1)
$$
$$
P(A+B) = P(A)+P(B)-P(A)cdot P(B); quad(2)
$$
$$
P(A_1+A_2+…+A_n)=1-P(overline{A_1})cdot P(overline{A_2})cdot … cdot P(overline{A_n}). quad(3)
$$
Последовательно или параллельно?
Еще немного времени посвятим теории, вспомним о том, как могут соединяться элементы в цепи.
Последовательное соединение

Элементы цепи “нанизаны” на провод один за другим (следуют один за другим, отсюда и “последовательно”). Если откажет один любой – ток в цепи прервётся. Или, иначе говоря, цепь работает тогда и только тогда, когда ВСЕ элементы работают. В терминах теории вероятностей получаем произведение событий: $X=A_1 cdot A_2 cdot A_3$, а вероятность работы цепи равна
$$
P(X)=P(A_1 cdot A_2 cdot A_3)= P(A_1) cdot P(A_2) cdot P(A_3) =p_1 cdot p_2 cdot p_3.
$$
Если в цепи последовательно соединены не три, а больше независимо работающих элементов, формула легко обобщается и получаем:
$$
P(X) = p_1 cdot p_2 cdot …cdot p_n; qquad P(overline{X})=1-p_1 cdot p_2 cdot …cdot p_n. quad(4)
$$
Параллельное соединение
Тут тоже сама схема дает нам подсказку, когда мы видим, что элементы в схеме расположены как бы на параллельных проводах, речь идет о параллельном соединении.
В этом случае если откажет, скажем, элемент 1, ток может пройти через 2. Если откажут 1 и 2, ток пройдет через 3. И только если ВСЕ элементы откажут, цепь разорвется.
Еще говорят, цепь работает, если работает хотя бы один элемент в ней, в терминах теории вероятностей – это сумма событий: $X=A_1+A_2+A_3$.
Используем формулу (3) чтобы записать вероятность работы такой цепи:
$$
P(A_1+A_2+A_3)=1-P(overline{A_1})cdot P(overline{A_2}) cdot P(overline{A_3})=1-q_1 cdot q_2 cdot q_3.
$$
И обобщим на случай $n$ параллельных элементов в цепи:
$$
P(X) = 1-q_1 cdot q_2 cdot …cdot q_n; qquad P(overline{X})=q_1 cdot q_2 cdot …cdot q_n. quad(5)
$$
Важно запомнить правило
Последовательному соединению соответствует произведение событий,
параллельному соединению – сумма событий.
Усложняем схему цепи
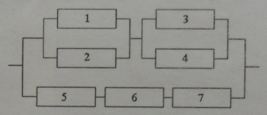
И все это была присказка к настоящему решению задач. Конечно, даже если у вас простая контрольная, схема с “тремя лампочками подряд” вряд ли попадется. Давайте посмотрим на типовые электрические схемы, для которых надо находить надежность в задачах:
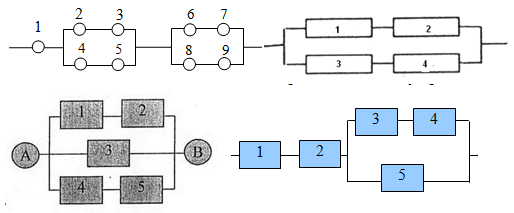
Как для таких схем выписывать вероятности? Нам нужно научиться делать декомпозицию: выделять уровни схемы и определять тип соединения на каждом уровне.
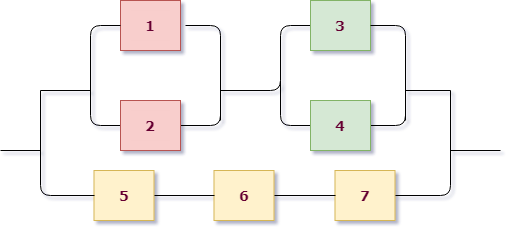
Возьмем для примера левую верхнюю схему:
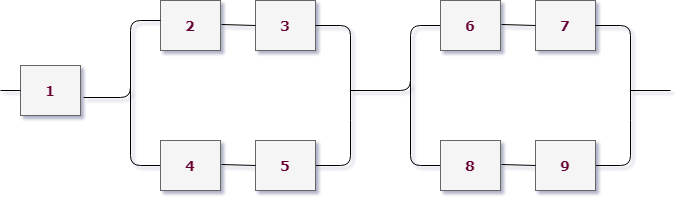
Работаем с первым уровнем схемы. Нужно мысленно выделить крупные части, которые между собой соединены одинаково (параллельно или последовательно). В данном случае видно три группы элементов, соединенных последовательно. Выделим для наглядности цветом:
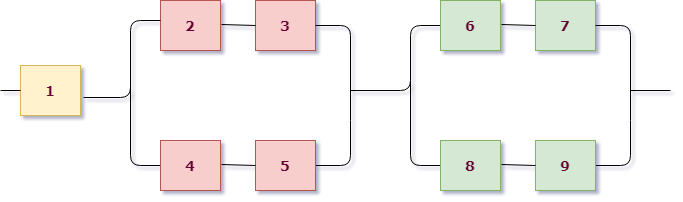
То есть тип схемы на первом уровне – последовательный:

Как мы уже знаем, если соединение последовательное, нужно перемножать события, то есть
$$
X=X_1 cdot X_2 cdot X_3,
$$
$X_1$ – работает первая группа элементов,
$X_2$ – работает вторая группа элементов,
$X_3$ – работает третья группа элементов.
Теперь смотрим на каждую группу. В первой группе всего один элемент, то есть она работает, когда работает первый элемент цепи ($X_1=A_1$). Мы дошли до элемента, разбор этой группы закончен.
А вот дальше интереснее. Рассмотрим поближе вторую группу:
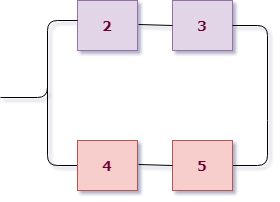
В ней сразу выделим цветом подгруппы элементов. Видно, что вторая группа имеет уже параллельную структуру из розовых и фиолетовых элементов (они “висят” на параллельных линиях, это второй уровень вложенности схемы). А вот внутри розовые соединены последовательно (розовая группа работает – $A_4 cdot A_5$), фиолетовые элементы также между собой последовательно (фиолетовая группа работает – $A_2 cdot A_3$). Это уже третий уровень вложенности и он заканчивается отдельными элементами, значит, разбор окончен.
Так как розовая и фиолетовая группа соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:
$$X_2 = A_2 cdot A_3 + A_4 cdot A_5.$$
Абсолютно аналогично разбирается третья подгруппа (она совпадает по структуре со второй):
$$X_3 = A_6 cdot A_7 + A_8 cdot A_9.$$
Сводим все в одну формулу и выпишем искомое событие (Цепь работает исправно):
$$
X=X_1 cdot X_2 cdot X_3 = A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right).
$$
Теперь переходим ко второму этапу решения задачи. Не забываем, что мы решаем задачу по теории вероятностей и надо определить вероятность того, что ток проходит в цепи. Будем использовать формулы (1)-(3).
Так как вероятность произведения для независимых событий равна произведению вероятностей, получим:
$$
P(X)= P left( A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right) right) =\
= P (A_1) cdot P left ( A_2 cdot A_3 + A_4 cdot A_5 right ) cdot P left( A_6 cdot A_7 + A_8 cdot A_9right) =
$$
Для множителей с суммой событий внутри используем формулу (2):
$$
= P (A_1) cdot left[ P(A_2 cdot A_3) + P(A_4 cdot A_5) – P(A_2 cdot A_3 cdot A_4 cdot A_5) right] cdot left[ P(A_6 cdot A_7) + P(A_8 cdot A_9) – P(A_6 cdot A_7 cdot A_8 cdot A_9)right] =
$$
И снова раскрываем вероятности произведений:
$$
= P (A_1) cdot left[ P(A_2) cdot P(A_3) + P(A_4) cdot P(A_5) – P(A_2) cdot P(A_3) cdot P(A_4) cdot P(A_5) right] cdot left[ P(A_6) cdot P(A_7) + P(A_8) cdot P(A_9) – P(A_6) cdot P(A_7) cdot P(A_8) cdot P(A_9)right].
$$
Перейдем к более компактной записи, положив $p_i=P(A_i)$:
$$
P(X)= p_1 cdot left[ p_2 cdot p_3 + p_4 cdot p_5 – p_2 cdot p_3 cdot p_4 cdot p_5 right] cdot left[ p_6 cdot p_7 + p_8 cdot p_9 – p_6 cdot p_7 cdot p_8 cdot p_9right].
$$
Если заданы надежности отдельных элементов $p_i$, подставляя их в формулу, можно найти вероятность работы схемы.
Алгоритм разбора схемы
- Выделяем в схеме основу: группы элементов, соединенные ТОЛЬКО последовательно или ТОЛЬКО параллельно между собой. Это верхний уровень. Записываем событие $X$ = (Цепь работает) как произведение или сумму соответственно.
- Каждую полученную группу анализируем также: ищем в ней подгруппы, соединенные только последовательно или только параллельно. Записываем событие соответственно типу соединения.
- Продолжаем до тех пор, пока не опустимся на уровень элементов (событий $A_i$).
- Подставляем все выражения в исходную формулу, получаем итоговую запись события $X$.
- Пользуясь формулами (1)-(3) выписываем вероятность события $P=P(X)$.
- Подставляем числовые значения $p_i, q_i$ и находим численное значение надежности схемы $P$.
- Если необходимо, находим вероятность отказа цепи $1-P$.
Примеры решений
Отработаем несколько раз этот алгоритм на примерах, чтобы он закрепился.
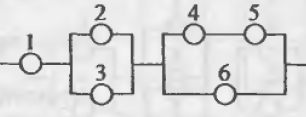
Пример 1. Дана схема включения элементов. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведенной схеме. Пусть событие $А_i$ означает безотказную работу за время Т элемента с номером $i$ ($i=1,2,3,…$), а событие $В$ – безотказную работу цепи. Требуется:
1) Написать формулу, выражающую событие $В$ через все события $А_i$.
2) Найти вероятность события $B$.
3) Вычислить $Р(В)$ при $р=0,6$.
Приступим к разбору схемы. Можно увидеть, что на первом уровне мы имеем три группы, соединенные последовательно: (1), (2,3) и (4,5,6) элементы. Выделим их цветом для наглядности:
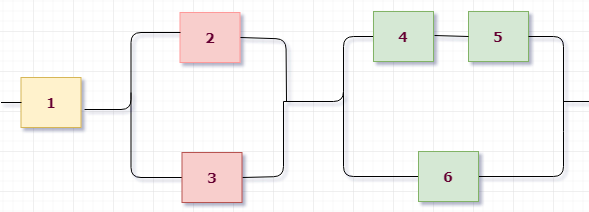
Значит, исходное событие можно представить в виде произведения трех событий $B=B_1 cdot B_2 cdot B_3$, где $B_i$ – работает $i$-aя группа элементов.
Первая группа элементов состоит из одного элемента, то есть $B_1=A_1$.
Вторая группа элементов состоит из двух элементов, соединенных параллельно (см. розовые), поэтому $B_2=A_2+A_3$.
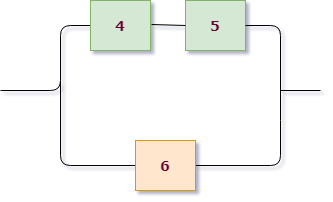
Третья группа элементов (см. зеленые) состоит из трех элементов, ее можно представить как параллельное соединение двух подгрупп: (4 и 5, соединены последовательно) и (6), поэтому $B_3=A_4 cdot A_5 + A_6$.
Подставляем все и получаем выражение для события $B$
$$
B=B_1 cdot B_2 cdot B_3 = A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6).
$$
Теперь выразим вероятность безотказной работы цепи за время T. Сначала применим формулу (1), чтобы раскрыть произведение:
$$
P(B)=P left( A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6) right) = P(A_1) cdot P left( A_2+A_3 right) cdot P left( A_4 cdot A_5 + A_6 right) =
$$
Раскроем вторую вероятность по формуле (3), а третью по формуле (2), получим:
$$= P(A_1) cdot left(1 – P(overline{A_2}) cdot P(overline{A_3}) right) cdot left( P(A_4) cdot P(A_5) + P(A_6) – P(A_4) cdot P(A_5) cdot P(A_6) right).$$
Подставляем $P(A_i)=p$ и получим:
$$
p(B)=pcdot(1-(1-p)cdot(1-p))cdot(pcdot p + p -p cdot p cdot p) = pcdotleft(1-(1-p)^2right)cdot left(p+p^2-p^3right).
$$
Осталось только найти значение при $p=0,6$:
$$
p(B)= 0,6cdotleft(1-(1-0,6)^2right)cdot left(0,6+0,6^2-0,6^3right) approx 0,375.
$$
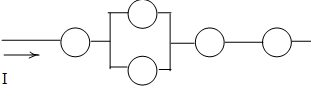
Пример 2. Найти вероятность обрыва цепи, если вероятность отказа каждого элемента равна 0,2, а отказы элементов – независимые события.
Пронумеруем элементы и сразу раскрасим схему, чтобы выделить ее структуру.
Это опять последовательная схема, но розовая группа состоит из двух элементов, соединенных параллельно, поэтому можем сразу выписать:
$$
X= A_1 cdot (A_2+A_3) cdot A_4 cdot A_5.
$$
Найдем вероятность этого события (работы цепи):
$$
P(X)= P left( A_1 cdot (A_2+A_3) cdot A_4 cdot A_5 right)= P(A_1) cdot P(A_2+A_3) cdot P(A_4) cdot P(A_5)= \
= P(A_1) cdot left( 1- P(overline{A_2}) cdot P(overline{A_3}) right) cdot P(A_4) cdot P(A_5).
$$
Вероятности отказа элементов цепи равна 0,2, вероятность работы элементов – 0,8, поэтому
$$
P(X)= 0,8 cdot left( 1- 0,2 cdot 0,2 right) cdot 0,8 cdot 0,8 = 0,492.
$$
Но в задаче требовалось найти вероятность обрыва цепи, это противоположное событие:
$$
P(overline{X}) = 1- P(X) = 1-0,492 = 0,508.
$$
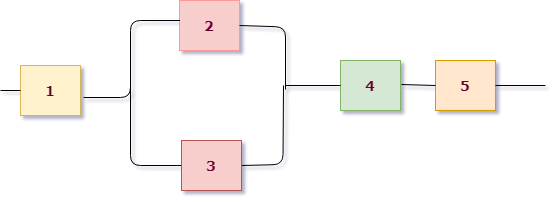
Пример 3. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность надежной работы элементов равна $p_1=p_2=p_3=p_4=0,8$, $p_5=p_6=p_7=0,9$.
Приступим к решению, сразу раскрасив схему. В этот раз схема на первом уровне имеет параллельное соединение: верхняя розово-зеленая группа и нижняя желтая находятся на параллельных линиях. Поэтому $X=X_1+X_2$, где $X_1$ – работает розово-зеленая линия, $X_2$ – работает желтая.
Для желтой группы, состоящей из трех последовательно расположенных элементов, сразу выписываем $X_2=A_5 cdot A_6 cdot A_7$.
Теперь рассмотрим верхнюю группу. Она состоит из двух подгрупп, связанных последовательно: розовой и зеленой. При этом каждая из них состоит из двух параллельно соединенных элементов. Записываем: розовая группа работает = $A_1+A_2$, зеленая группа работает = $A_3+A_4$, значит ток проходит через розово-зеленую группу $X_1 =(A_1+A_2) cdot (A_3+A_4)$.
Объединяем рассуждения и выписываем событие, соответствующее безотказной работе цепи:
$$
X=X_1+X_2 = (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7.
$$
Следующий шаг: выразить вероятность этого события. Во всех предыдущих примерах схема на первом уровне была последовательной, и событие выражалось как произведение. В этом случае схема на первом уровне параллельна, событие выглядит как сумма других событий, что немного усложняет выкладки. Для суммы событий можно использовать формулу (2) или (3), выбирая наиболее удобную в каждом конкретном случае.
В данном случае слагаемых всего два, поэтому возьмем формулу (2):
$$
P(X)= P left( (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7 right) = \
= P left( (A_1+A_2) cdot (A_3+A_4) right) + P left( A_5 cdot A_6 cdot A_7 right) – P left( (A_1+A_2) cdot (A_3+A_4) cdot A_5 cdot A_6 cdot A_7 right)
$$
Раскрываем все произведения по формуле (1):
$$
= P (A_1+A_2) cdot P(A_3+A_4) + P(A_5) cdot P(A_6) cdot P(A_7) – P (A_1+A_2) cdot P(A_3+A_4) cdot P(A_5) cdot P(A_6) cdot P(A_7) =
$$
По формуле (3) расписываем $P(A_1+A_2)=1-P(overline{A_1}) cdot P(overline{A_2}) = 1-q_1cdot q_2$ и $P(A_3+A_4)=1-P(overline{A_3}) cdot P(overline{A_4})= 1-q_3cdot q_4$.
Итого:
$$
P(X)= (1-q_1cdot q_2) cdot (1-q_3cdot q_4) + p_5 cdot p_6 cdot p_7 – \- (1-q_1cdot q_2) cdot (1-q_3cdot q_4) cdot p_5 cdot p_6 cdot p_7.
$$
Подставляем значения надежности элементов:
$$
P(X)= (1-0,2^2)^2 + 0,9^3 – (1-0,2^2)^2 cdot 0,9^3 approx 0,9788.
$$
Еще: другие уроки о решении задач по вероятности
На закуску: схема с мостиком
Для 99% учебных задач вам хватит той теории и примеров, что приведены выше: подробно изучите их и приступайте к своим примерам по аналогии. Но есть такие схемы, для которых нельзя выделить единую структуру на верхнем уровне – параллельную или последовательную, и весь алгоритм решения рушится.

Речь идет о схемах смешанного типа, еще их часто называют схемами с мостиком (мостиковые схемы). Типичная схема имеет такой вид:
Видно, что как ни крути, схему нельзя отнести ни к последовательным, ни к параллельным. Элемент №5 (мостик) “портит” тип схемы. Если его убрать (разорвать этот участок цепи), получим обычную параллельную структуру, а если предположить, что через этот участок всегда идет ток – последовательную (конкретные схемы изобразим ниже).
Поэтому для решения задачи о вычислении надежности подобной электросхемы используют формулу полной вероятности в форме теоремы разложения (см. подробнее тут, стр. 118)
Надежность цепи с избыточностью равна произведению вероятности безотказной работы $i$-го элемента цепи на вероятность безотказной работы оставшейся цепи (места подключения $i$-го элемента замкнуты накоротко) плюс произведение вероятности отказа того же $i$-го элемента на вероятность безотказной работы оставшейся цеии (места подключения $i$-го элемента разомкнуты).
То есть, для выделенного на схеме элемента-мостика рассматриваем две гипотезы:
$H_1$ = (Элемент 5 не пропускает ток), $P(H_1)=1- p_5 = q_5$;
$H_2$ = (Элемент 5 пропускает ток), $P(H_2)=p_5$.
Далее вычисляем надежность схемы при условии верности каждой из гипотез. Для наглядности нарисуем обе схемы:

Рассмотрим левую схему, верную при гипотезе $H_1$, через нее проходит ток, если $X|H_1 = A_1cdot A_3+ A_2cdot A_4$, вероятность
$$
P(X|H_1) = P(A_1cdot A_3+ A_2cdot A_4)= P(A_1cdot A_3)+ P(A_2cdot A_4) – P(A_1cdot A_3 cdot A_2cdot A_4)=\
=p_1 cdot p_3 + p_2 cdot p_4 – p_1 cdot p_2 cdot p_3 cdot p_4.
$$
Рассмотрим правую схему, верную при гипотезе $H_2$, и выпишем для нее аналогично событие и вероятность прохода тока:
$$
X|H_2 = (A_1+A_2)cdot (A_3+A_4),\
P(X|H_2) =P( (A_1+A_2)cdot (A_3+A_4)) = P(A_1+A_2)cdot P(A_3+A_4)=\ = (1-P(overline{A_1}) cdot P(overline{A_2})) cdot (1-P(overline{A_3}) cdot P(overline{A_4})) = (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$
Тогда по формуле полной вероятности, надежность схемы равна:
$$
P(X)=P(X|H_1)cdot P(H_1) + P(X|H_2)cdot P(H_2) = \
= q_5 (p_1 cdot p_3 + p_2 cdot p_4 – p_1 cdot p_2 cdot p_3 cdot p_4) + p_5 (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$
Аналогичным образом можно разбирать более сложные схемы (в которые более одного мостика), применяя на каждом этапе формулу полной вероятности (как бы вкладывая одну в другую).
Понравилось? Добавьте в закладки
Полезные ссылки по ТВ
|
|
Решебник по вероятности
А здесь вы найдете разные задачи по теории вероятностей с полными решениями (вводите часть текста для поиска своей задачи):
Практика
1. Расчет показателей безотказности
1.1 Вероятность безотказной работы
1.2 Вероятность отказа
1.3 Частота отказа
1.4 Интенсивность отказа
1.5 Средняя наработка до отказа
1.6 Среднее значение параметра потока отказов
1.7 Пример расчета показателей безотказности
2. Примеры расчета показателей надежности для различных законов распределения случайных величин
2.1 Экспоненциальный закон распределения
2.2 Закон распределения Вейбулла-Гнеденко
2.3 Закон распределения Рэлея
3. Примеры расчета показателей надежности сложных систем
3.1 Основное соединение элементов
3.2 Резервное соединение
1.1 Вероятность безотказной работы
Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа.
Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):
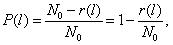
где N0 – число элементов в начале испытания; r(l) – число отказов элементов к моменту наработки.Следует отметить, что чем больше величина N0, тем с большей точностью можно рассчитать вероятность P(l).
В начале эксплуатации исправного локомотива P(0) = 1, так как при пробеге l = 0 вероятность того, что ни один элемент не откажет, принимает максимальное значение – 1. С ростом пробега l вероятность P(l) будет уменьшаться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность безотказной работы будет стремиться к нулю P(l→∞) = 0. Таким образом в процессе наработки величина вероятности безотказной работы изменяется в пределах от 1 до 0. Характер изменения вероятности безотказной работы в функции пробега показан на рис. 1.1.
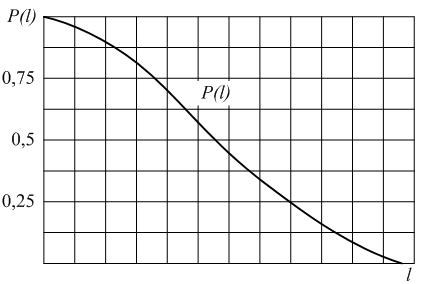
Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки
Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P(l), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента.
1.2 Вероятность отказа
Вероятностью отказа называют вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки произойдет хотя бы один отказ.
Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):
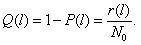
В начале эксплуатации исправного локомотива Q(0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q(l) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q(l→∞) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2.Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.
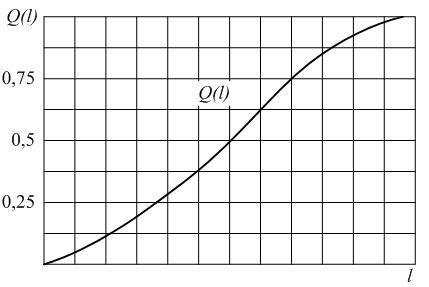
Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки
1.3 Частота отказов
Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы.
Частота отказов обозначается как 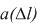 и определяется по формуле (1.3):
и определяется по формуле (1.3):
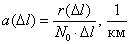
где – 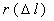 количество отказавших элементов за промежуток пробега
количество отказавших элементов за промежуток пробега 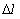 .
.
Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей.
Характер изменения частоты отказов в функции пробега показан на рис. 1.3.
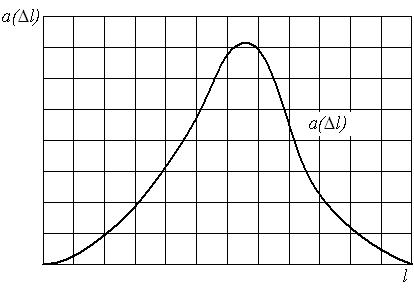
Рис. 1.3. График изменения частоты отказов в зависимости от наработки
1.4 Интенсивность отказов
Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени.
Интенсивность отказов обозначается как 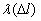 и определяется по формуле (1.4):
и определяется по формуле (1.4):
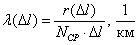
где 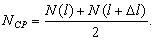
Как правило, интенсивность отказов 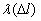 является неубывающей функцией времени. Интенсивность отказов обычно применяется для оценки склонности к отказам в различные моменты работы объектов.
является неубывающей функцией времени. Интенсивность отказов обычно применяется для оценки склонности к отказам в различные моменты работы объектов.
На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега.
Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки
На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс экс-плуатации элемента или объекта в целом.
Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера.
Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента.
Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной.
1.5 Средняя наработка до отказа
Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа.
Средняя наработка до отказа обозначается как L1 и определяется по формуле (1.5):
где li – наработка до отказа элемента; ri – число отказов.
Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента.
1.6 Среднее значение параметра потока отказов
Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени.
Среднее значение параметра потока отказов обозначается как Wср и определяется по формуле (1.6):
1.7 Пример расчета показателей безотказности
Исходные данные.
В течение пробега от 0 до 600 тыс. км., в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6.
Требуется.
Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени.
Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1.
Таблица 1.1.
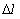 , тыс. км , тыс. км |
0 – 100 | 100 – 200 | 200 – 300 | 300 – 400 | 400 – 500 | 500 – 600 |
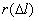 |
2 | 12 | 16 | 10 | 14 | 6 |
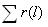 |
2 | 14 | 30 | 40 | 54 | 60 |
Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:
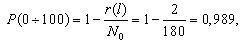
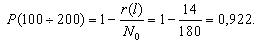
Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.
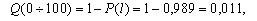
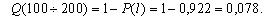
Произведем расчет частоты отказов по уравнению (1.3).
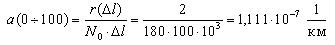
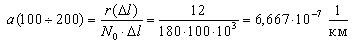
Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки.
Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:
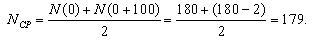
Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:
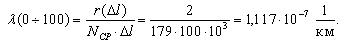
Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.
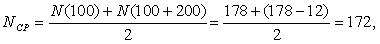
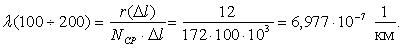
По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.
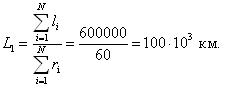
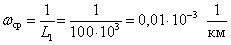
Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.).
Таблица 1.2.
 , тыс.км. , тыс.км. |
0 – 100 | 100 – 200 | 200 – 300 | 300 – 400 | 400 – 500 | 500 – 600 |
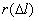 |
2 | 12 | 16 | 10 | 14 | 6 |
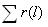 |
2 | 14 | 30 | 40 | 54 | 60 |
| P(l) | 0,989 | 0,922 | 0,833 | 0,778 | 0,7 | 0,667 |
| Q(l) | 0,011 | 0,078 | 0,167 | 0,222 | 0,3 | 0,333 |
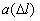 10-7, 1/км 10-7, 1/км |
1,111 | 6,667 | 8,889 | 5,556 | 7,778 | 3,333 |
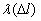 10-7, 1/км 10-7, 1/км |
1,117 | 6,977 | 10,127 | 6,897 | 10,526 | 4,878 |
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.
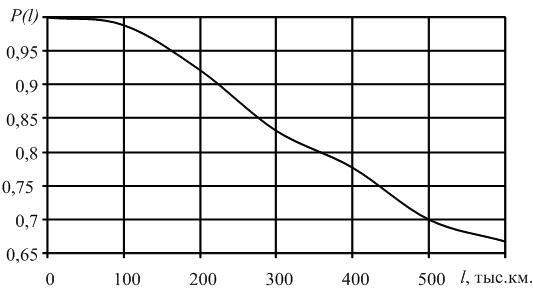
Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки
Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0.
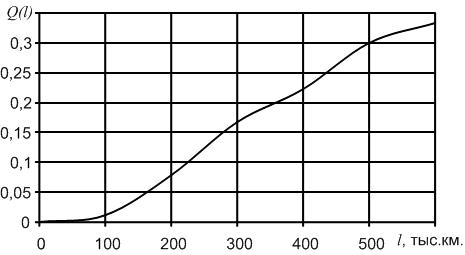
Рис. 1.6. График изменения вероятности отказа в зависимости от наработки
Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).
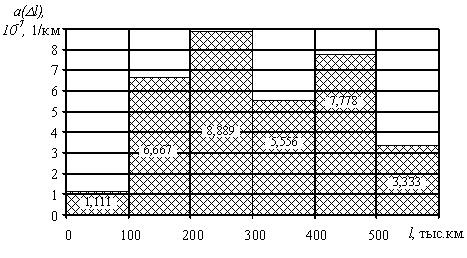
Рис. 1.7. График изменения частоты отказов в зависимости от наработки
На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки.
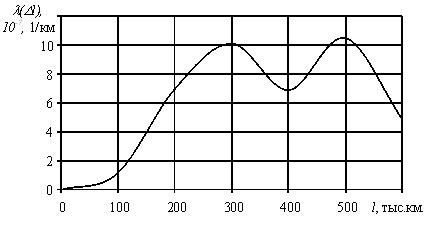
Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки
2.1 Экспоненциальный закон распределения случайных величин
Экспоненциальный закон достаточно точно описывает надежность узлов при внезапных отказах, имеющих случайный характер. Попытки применить его для других типов и случаев отказов, особенно постепенных, вызванных износом и изменением физико-химических свойств элементов показали его недостаточную приемлемость.
Исходные данные.
В результате испытания десяти топливных насосов высокого давления получены наработки их до отказа: 400, 440, 500, 600, 670, 700, 800, 1200, 1600, 1800 ч. Предполагая, что наработка до отказа топливных насосов подчиняется экспоненциальному закону распределения.
Требуется.
Оценить величину интенсивности отказов , а также рассчитать вероятность безотказной работы за первые 500 ч. и вероятность отказа в промежутке времени между 800 и 900 ч. работы дизеля.
Во-первых, определим величину средней наработки топливных насосов до отказа по уравнению:
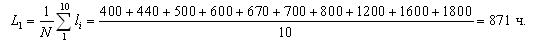
Затем рассчитываем величину интенсивности отказов:
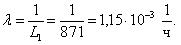
Величина вероятности безотказной работы топливных насосов при наработке 500 ч составит:
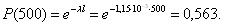
Вероятность отказа в промежутке между 800 и 900 ч. работы насосов составит:
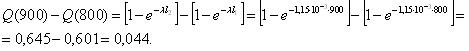
2.2 Закон распределения Вэйбулла-Гнеденко
Закон распределения Вейбулла-Гнеденко получил широкое распространение и используется применительно к системам, состоящим из рядов элементов, соединенных последовательно с точки зрения обеспечения безотказности системы. Например, системы, обслуживающие дизель-генераторную установку: смазки, охлаждения, питания топливом, воздухом и т.д.
Исходные данные.
Время простоя тепловозов в неплановых ремонтах по вине вспомогательного оборудования подчиняется закону распределения Вейбулла-Гнеденко с параметрами b=2 и a=46.
Требуется.
Необходимо определить вероятность выхода тепловозов из неплановых ремонтов после 24 ч. простоя и время простоя, в течение которого работоспособность будет восстановлена с вероятностью 0,95.
Найдем вероятность восстановления работоспособности локомотива после простоя его в депо в течение суток по уравнению:
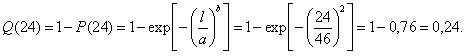
Для определения времени восстановления работоспособности локомотива с заданной величиной доверительной вероятности также используем выражение:
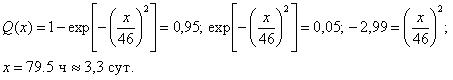
2.3 Закон распределения Рэлея
Закон распределения Рэлея используется в основном для анализа работы элементов, имеющих ярко выраженный эффект старения (элементы электрооборудования, различного рода уплотнения, шайбы, прокладки, изготовленные из резиновых или синтетических материалов).
Исходные данные.
Известно, что наработки контакторов до отказа по параметрам старения изоляции катушек можно описать функцией распределения Рэлея с параметром S = 260 тыс.км.
Требуется.
Для величины наработки 120 тыс.км. необходимо определить вероятность безотказной работы, интенсивность отказов и среднюю наработку до первого отказа катушки электромагнитного контактора.
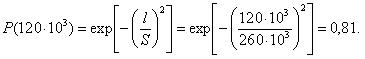
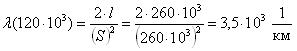
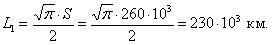
3.1 Основное соединение элементов
Система, состоящая из нескольких независимых элементов, связанных функционально таким образом, что отказ любого из них вызывает отказ системы, отображается расчетной структурной схемой безотказной работы с последовательно соединенными событиями безотказной работы элементов.
Исходные данные.
Нерезервированная система состоит из 5 элементов. Интенсивности их отказов соответственно равны 0,00007; 0,00005; 0,00004; 0,00006; 0,00004 ч-1
Требуется.
Необходимо определить показатели надежности системы: интенсивность отказов, среднее время наработки до отказа, вероятность безотказной работы, частота отказов. Показатели надежности P(l) и a(l) получить в интервале от 0 до 1000 часов с шагом в 100 часов.
Вычислим интенсивность отказа и среднюю наработку до отказа по следующим уравнениям:
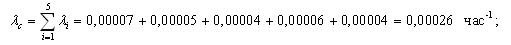
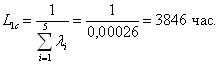
Значения вероятности безотказной работы и частоты отказов получим, используя уравнения приведенные к виду:
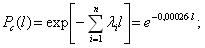
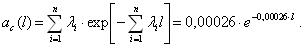
Результаты расчета P(l) и a(l) на интервале от 0 до 1000 часов работы представим в виде табл. 3.1.
Таблица 3.1.
| l, час | P(l) | a(l), час-1 |
| 0 | 1 | 0,00026 |
| 100 | 0,974355 | 0,000253 |
| 200 | 0,949329 | 0,000247 |
| 300 | 0,924964 | 0,00024 |
| 400 | 0,901225 | 0,000234 |
| 500 | 0,878095 | 0,000228 |
| 600 | 0,855559 | 0,000222 |
| 700 | 0,833601 | 0,000217 |
| 800 | 0,812207 | 0,000211 |
| 900 | 0,791362 | 0,000206 |
| 1000 | 0,771052 | 0,0002 |
Графическая иллюстрация P(l) и a(l) на участке до средней наработки до отказа представлена на рис. 3.1, 3.2.
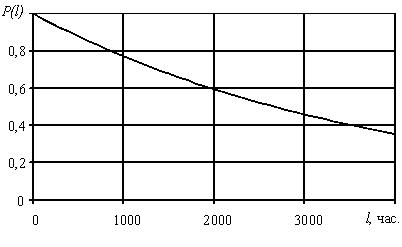
Рис. 3.1. Вероятность безотказной работы системы.
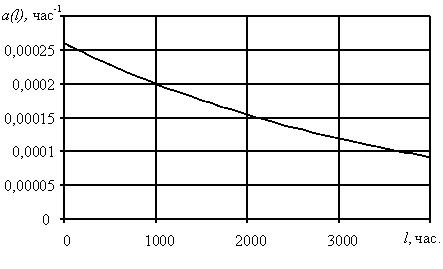
Рис. 3.2. Частота отказов системы.
3.2 Резервное соединение элементов
Исходные данные.
На рис. 3.3 и 3.4 показаны две структурные схемы соединения элементов: общего (рис. 3.3) и поэлементного резервирования (рис. 3.4). Вероятности безотказной работы элементов соответственно равны P1(l) = P ’1(l) = 0,95; P2(l) = P’2(l) = 0,9; P3(l) = P ’3(l) = 0,85.
Требуется.
Необходимо рассчитать надежность двух систем.
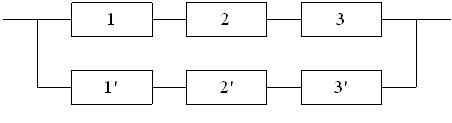
Рис. 3.3. Схема системы с общим резервированием.
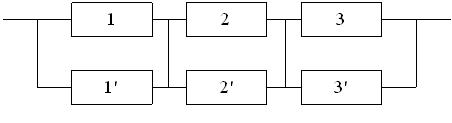
Рис. 3.4. Схема системы с поэлементным резервированием.
Вероятность безотказной работы блока из трех элементов без резервирования рассчитаем по выражению:
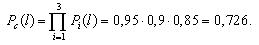
Вероятность безотказной работы той же системы при общем резервировании (рис. 3.3) составит:
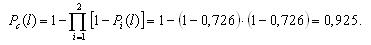
Вероятности безотказной работы каждого из трех блоков при поэлементном резервировании (рис. 3.4) будут равны:
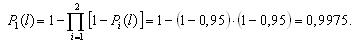
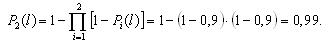
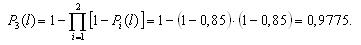
Вероятность безотказной работы системы при поэлементном резервировании составит:
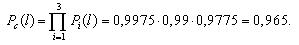
Таким образом, поэлементное резервирование дает более существенное увеличение надежности (вероятность безотказной работы возросла с 0,925 до 0,965, т.е. на 4%).
Исходные данные.
На рис. 3.5 представлена система с комбинированным соединением элементов. При этом вероятности безотказной работы элементов имеют следующие значения: P1=0,8; Р2=0,9; Р3=0,95; Р4=0,97.
Требуется.
Необходимо определить надежность системы. Также необходимо определить надежность этой же системы при условии, что резервные элементы отсутствуют.
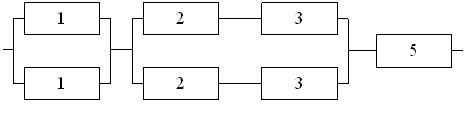
Рис.3.5. Схема системы при комбинированном функционировании элементов.
Для расчета в исходной системе необходимо выделить основные блоки. В представленной системе их три (рис. 3.6). Далее рассчитаем надежность каждого блока в отдельности, а затем найдем надежность всей системы.
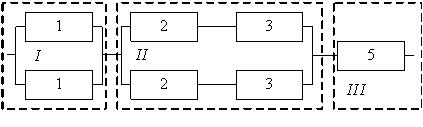
Рис. 3.6. Сблокированная схема.
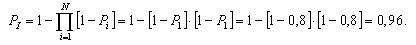
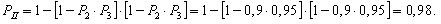
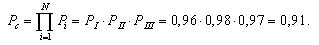
Надежность системы без резервирования составит:
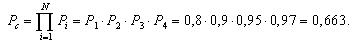
Таким образом, система без резервирования является на 28% менее надежной, чем система с резервированием.
Интенсивность
отказов всего изделия определяется по
следующей формуле:
![]() 1/ч,
1/ч,
где
![]() –
–
число типов элементов.![]() .
.
![]() –интенсивность
–интенсивность
отказов элементов i-того
типа. Эта величина определена согласно
табл. 1.2.
![]() –число
–число
элементов i-того
типа. Эта величина определена согласно
табл. 1.2.
![]()
Вероятность
безотказной работы изделия определяется
по следующей формуле:
![]() .
.
Поскольку
используется экспоненциальный закон
распределения,
![]() ,
,
следовательно
![]() .
.
1.5. Расчёт среднего времени наработки на отказ
Среднее время
наработки на отказ определяется по
следующей формуле:
![]() ч,
ч,
где
![]() –интенсивность
–интенсивность
отказов всего изделия.
![]() ,
,
ч.
2. Задача 2
РАСЧЁТ ПОКАЗАТЕЛЕЙ
НАДЁЖНОСТИ ЭЛЕКТРОТЕХНИЧЕСКОЙ УСТАНОВКИ
2.1. Исходные данные
Имеется
установка «А», состоящая из четырех
последовательно соединенных узлов.
Схема расчета надежности установки
изображена на рис. 2.1.
Все элементы установки равнонадежны и
для них справедлив экспоненциальный
закон распределения наработки до отказа.
Интенсивность отказов элементов
приведена в табл. 2.1.
В узле «г» число элементов, необходимых
для нормальной работы равно 2.
Требуется:
1.
Вычислить
и построить график изменения функции
надежности узлов «а», «б», «в» и «г»
установки «А» в течение 10000 ч с интервалом
2000 ч.
2.
По результатам
расчета вероятности безотказной работы
узлов «а», «б» и «в» сделать вывод об
эффективности различных видов
резервирования.
3.
Вычислить
и построить график изменения функции
надежности установки «А» в течение
10000 часов с интервалом 2000 ч.
4.
Определить
вероятность безотказной работы для
системы из двух параллельно включенных
установок «А» и «Б» по истечению года
эксплуатации, если вероятность безотказной
работы установки «Б» за год эксплуатации.
5.
Определить
годовую потребность запасных элементов
для общего количества установок
«С»
согласно табл. 2.1
при заданной вероятности обеспечения
запасными частями Pz
= 0,95
и согласно табл. 2.1.

Рис.2.1. Схема
надёжности установки
Таблица 2.1.
Исходные данные
|
Исходные |
Параметры |
|
Интенсивность |
12 |
|
Общее |
10 |
|
Вероятность |
0,93 |
|
Заданная |
0,999 |
2.2. Построение графика зависимости надёжности узлов установки «а» от времени работы
Установка «А»
состоит из четырёх узлов: «а», «б», «в»,
«г».
В
узле «а» было применено общее резервирование
с постоянным включением резерва и с
целой кратностью, поэтому вероятность
безотказной работы узла была определена
по формуле, представленной ниже:
Узел А:
![]() ,
,
где:
![]() –
–
интенсивность отказов основной или
резервной цепи, согласно рис. 2.1,![]()
![]() –число
–число
резервированных цепей (в горячем резерве
используется одна цепь).
На
основание вышеперечисленных постоянных,
функция
![]() примет следующий вид:
примет следующий вид:
![]()
С
помощью математического пакета MathCad
был получен график зависимости надёжности
узла «а» от текущего времени. Этот график
представлен на рис. 2.2.
******************************************************************
Пометь
графики, когда переписывать будешь. Ось
х – t,
ч. Ось У – Pa,Pб,Рв,Рг
(смотрая какой график) .
Если распечатывать будешь, достаточно
чёрной ручкой оси подправить.
******************************************************************

Рис.
2.2 Зависимость надёжности узла “а”
от времени
В
узле «б» было применено раздельное
резервирование с постоянно включением
резерва и с целой кратностью, поэтому
вероятность безотказной работы узла
была определена по формуле, представленной
ниже:
Узел
Б:
![]() ,
,
где:
![]() –
–
интенсивность отказов основной или
резервной цепи, согласно рис. 2.1,![]()
![]() –число
–число
резервированных цепей (используется
одна цепь),
![]() –число
–число
последовательно соединённых групп
элементов,
![]()
На
основание вышеперечисленных постоянных,
функция
![]() примет следующий вид:
примет следующий вид:
![]()
С
помощью математического пакета MathCad
был получен график зависимости надёжности
узла «б» от текущего времени. Этот график
представлен на рис. 2.3.

Рис.
2.3 Зависимость надёжности узла “б”
от времени
В
узле «в» было применено общее резервирование
с замезщением с целой кратностью, и
ненагруженном состоянии резерва поэтому
вероятность безотказной работы узла
была определена по формуле, представленной
ниже:
Узел
В:
![]()
где:
![]() –
–
интенсивность отказов основной или
резервной цепи, согласно рис. 2.1,![]()
![]() –число
–число
резервированных цепей (используется
одна цепь),
На
основание вышеперечисленных постоянных,
функция
![]() примет следующий вид:
примет следующий вид:
Узел
В: ![]()
С
помощью математического пакета MathCad
был получен график зависимости надёжности
узла «в» от текущего времени. Этот график
представлен на рис. 2.4.

Рис.
2.4 Зависимость надёжности узла “в”
от времени
******************************************************************
В
методичке формула плохо пропечатана
для узла г. Мог совершить ошибку в её
написании.
******************************************************************
В
узле «г» было применено общее резервирование
с дробной кратностью и постоянно
включенным резервом, и ненагруженном
состоянии резерва поэтому вероятность
безотказной работы узла была определена
по формуле, представленной ниже:
Узел
Г:
![]()
где:
![]() –
–
интенсивность отказов одной цепи,
согласно рис. 2.1,![]()
![]() –число
–число
элементов, необходимых для нормальной
работы. Согласно [1], k=2.
![]() –число
–число
элементов,
На
основании вышеперечисленных постоянных,
функция
![]() примет следующий вид:
примет следующий вид:
Узел
Г:
![]()
С
помощью математического пакета MathCad
был получен график зависимости надёжности
узла «г» от текущего времени. Этот график
представлен на рис. 2.5.

Рис.
2.5 Зависимость надёжности узла “г”
от времени
Наиболее
эффективный способ повышения надёжности
аппаратуры выбирается по наибольшей
величине вероятности безотказной работы
за год, поэтому ненагруженное дублирование
является наиболее надёжным способом
предотвращения отказов устройстве.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
09.06.20158.37 Mб19Kurbasova_Anglysky_dlya_tekhnicheskikh_vuzov.pdf
- #
- #
Вероятность безотказной работы — это вероятность того, что в пределах заданной наработки или заданном интервале времени отказ объекта не возникает. Вероятность безотказной работы вместе с интенсивностью отказов определяет безотказность объекта (при этом вероятность безотказной работы обратна вероятности отказа объекта).
Показатель вероятности безотказной работы определяется статистической оценкой:
где 


Вероятность безотказной работы группы взаимосвязанных объектов равна произведению вероятностей безотказной работы каждого объекта в этой группе:
где n — число объектов в группе.
Чем больше объектов в группе, тем ниже надежность всей группы, так как если

![P(t)=[P_{1}(t)]^{n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d25c6ea215cbba91fefc08e2a26bcc676c57bd40)
Среднее время безотказной работы системы[править | править код]
Среднее время безотказной работы (средняя наработка на отказ) 

Пределы несобственного интеграла изменяются от 0 до 





Вероятность 

Проинтегрировав выражение для 

Вероятность безотказной работы в зависимости от наработки
Графически полученное выражение для 


Здесь 
Типичные распределения времени безотказной работы[править | править код]
Основной источник: [1]
- Экспоненциальное распределение:
,
,
.
- Гамма-распределение:
,
,
.
- Распределение Вейбулла:
,
,
.
- Модифицированное распределение экстремального значения:
,
,
.
- Усечённое нормальное распределение:
,
,
,
.
- Логарифмически-нормальное распределение:
,
,
,
.
Примечания[править | править код]
- ↑ Барлоу Р., Прошан Ф. Математическая теория надежности. -М.: Советское радио, 1969.- С. 29-30
Литература[править | править код]
- Леликов О. П. Тема 2. Основные понятия и показатели надежности // Основы расчета и проектирования деталей и узлов машин. Конспект лекций по курсу “Детали машин”. — М.: Машиностроение, 2002. — С. 8-9. — 440 с. — 2000 экз. — ISBN 5-217-03077-1.
См. также[править | править код]
- Расчёт надёжности
- ГОСТ 27.002—89 (В викитеке)
- Вероятность безотказной работы по ГОСТ 27.002-89
Как вычисляется среднее время до отказа и вероятность безотказной работы?
Время на прочтение
4 мин
Количество просмотров 118K
Понятиям MTTF (Mean Time To Failure — среднее время до отказа) и другим терминам теории надежности посвящено большое количество статей, в том числе на Хабре (см., например, тут). Вместе с тем, редкие публикации «для широкого круга читателей» затрагивают вопросы математической статистики, и уж тем более они не дают ответа на вопрос о принципах расчета надежности электронной аппаратуры по известным характеристикам ее составных элементов.
В последнее время мне довольно много приходится работать с расчетами надежности и рисков, и в этой статье я постараюсь восполнить этот пробел, отталкиваясь от своего предыдущего материала (из цикла о машинном обучении) о пуассоновском случайном процессе и подкрепляя текст вычислениями в Mathcad Express, повторить которые вы сможете скачав этот редактор (подробно о нем тут, обратите внимание, что нужна последняя версия 3.1, как и для цикла по machine learning). Сами маткадовские расчеты лежат здесь (вместе с XPS- копией).
1. Теория: основные характеристики отказоустойчивости
Вроде бы, из самого определения (Mean Time To Failure) понятен его смысл: сколько (конечно, в среднем, поскольку подход вероятностный) прослужит изделие. Но на практике такой параметр не очень полезен. Действительно, информация о том, что среднее время до отказа жесткого диска составляет полмиллиона часов, может поставить в тупик. Гораздо информативнее другой параметр: вероятность поломки или вероятность безотказной работы (ВБР) за определенный период (например, за год).
Для того чтобы разобраться в том, как связаны эти параметры, и как, зная MTTF, вычислить ВБР и вероятности отказа, вспомним некоторые сведения из математической статистики.
Ключевое понятие теории надежности — это понятие отказа, измеряемое, соответственно, интервальным показателем
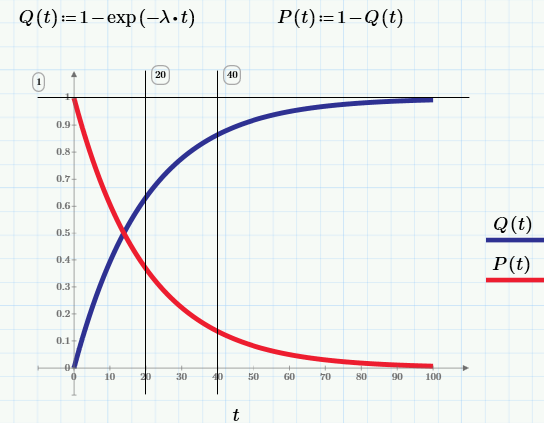
Q(t) = вероятность того, что изделие откажет к моменту времени t.
Соотвественно, вероятность безотказной работы (ВБР, в английской терминологии «reliability»):
P(t) = вероятность того, что изделие проработает без отказа от момента t0=0 до момента времени t.
По определению, в момент t0=0 изделие находится в работоспособном состоянии, т.е. Q(0)=0, а P(0)=1.
Оба параметра — это интервальные характеристики отказоустойчивости, т.к. речь идет о вероятности отказа (или наоборот, безотказной работы) на интервале (0,t). Если отказ рассматривать, как случайное событие, то, очевидно, что Q(t) — это, по определению, его функция распределения. А точечную характеристику можно определить, как
p(t)=dQ(t)/dt = плотность вероятности, т.е. значение p(t)dt равно вероятности, что отказ произойдет в малой окрестности dt момента времени t.
И, наконец, самая важная (с практической точки зрения) характеристика: λ(t)=p(t)/P(t)=интенсивность отказов.
Это (внимание!) условная плотность вероятности, т.е. плотность вероятности возникновения отказа в момент времени t при условии, что до этого рассматриваемого момента времени t изделие работало безотказно.
Измерить параметр λ(t) экспериментально можно путём испытания партии изделий. Если к моменту времени t работоспособность сохранило N изделий, то за оценку λ(t) можно принять процент отказов в единицу времени, происходящих в окрестности t. Точнее, если в период от t до t+dt откажет n изделий, то интенсивность отказов будет примерно равна
λ(t)=n/(N*dt).
Именно эта λ-характеристика (в пренебрежении ее зависимостью от времени) и приводится чаще всего в паспортных данных различных электронных компонент и самых разных изделий. Только сразу возникает вопрос: а как вычислить вероятность безотказной работы и при чем здесь среднее время до отказа (MTTF).
А вот при чем.
2. Экспоненциальное распределение
В терминологии, которую мы только что использовали, пока не было никаких предположений о свойствах случайной величины — момента времени, в который происходит отказ изделия. Давайте теперь конкретизируем функцию распределения значения отказа, выбрав в качестве нее экспоненциальную функцию с единственным параметром λ=const (смысл которого будет ясен через несколько предложений).
Дифференцируя Q(t), получим выражение для плотности вероятности экспоненциального распределения:
 ,
,
а из него – функцию интенсивности отказов: λ(t)=p(t)/P(t)=const=λ.
Что мы получили? Что для экспоненциального распределения интенсивность отказов – есть величина постоянная, причем совпадающая с параметром распределения. Этот параметр и является главным показателем отказоустойчивости и его часто так и называют λ-характеристикой.
Мало того, если теперь посчитать среднее время до первого отказа – тот самый параметр MTTF (Mean Time To Failure), то мы получим, что он равен MTTF=1/ λ.

Все это замечательные свойства экспоненциального распределения. Почему мы выбрали в качестве для описания отказов именно его? Да потому что это наиболее простая модель – модель пуассоновского потока событий, которая уже была нами рассмотрена в статье про анализ конверсии сайта. Поэтому-то в теории надежности наиболее часто используется показательное (экспоненциальное) распределение, для которого, как мы выяснили:
- надежность элементов можно оценить одним числом, т.к. λ=const;
- по известной λ довольно просто оценить остальные показатели надежности (например, ВБР для любого времени t);
- λ обладает хорошей наглядностью
- λ нетрудно измерить экспериментально
Но это еще не все, потому, что для экспоненциального распределения особенно легко делать расчет систем, состоящих из множества элементов. Но об этом – в следующей статье (продолжение следует).



