На этой странице вы узнаете
- Как кот может быть одновременно жив и мертв?
- Можно ли всегда выигрывать спор с монеткой?
- Если рандомно ответить на вопрос теста, какой шанс угадать ответ?
Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.
Вероятность
Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…
Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.
Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов.
Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат.
Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом.
По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив.
Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным. Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.
Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:
- выпадет орел;
- выпадет решка.

Эти два события образуют множество элементарных событий.
Множество элементарных событий — множество всех возможных результатов случайного эксперимента.
В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации.
Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран.
Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности.
Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу.
(P = frac{m}{n})
Вероятность можно обозначить, как P(x), где х — некоторое событие.
Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.
Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.
Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна (P = frac{2}{2} = 1), то есть мы точно выиграем спор.
Однако вероятность не так проста, и даже здесь подготовила ловушку.
В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет (frac{1}{6000}). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.
Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.
Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?
Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна
(frac{49}{140} = 0,35)
Выразим в процентах:
0,35 * 100% = 35%
Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.
Ответ: 0,35
Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой.
(P = frac{m}{n} * 100%)
Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.
Равновозможные и противоположные события
Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.
Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.
Вероятности появления событий равны.
Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий.
Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.
В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий.
Мы подбросили монету и выпал орел. Следовательно, не выпала решка.
А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными.
Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline{A}).
Заметим, что вероятность события A равняется 12, как и вероятность события (overline{A}). Чему равна их сумма?
)frac{1}{2} + frac{1}{2} = 1)
Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1.
(P(A) + P(overline{A}) = 1)
Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить.
Объединение и пересечение событий
Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим?
Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий.
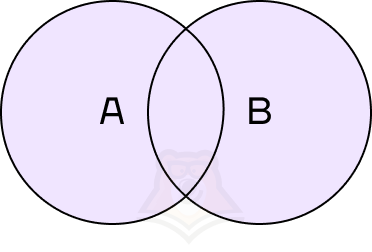
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег.
Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B).
Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?
Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.

Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B).
Несовместные и совместные события
Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.
Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно.
Несовместные события — такие события, появление одного из которых исключает появление другого.
Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.
Сформулируем определение суммы вероятностей двух несовместных событий.
Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:
(P(A cup B) = P(A) + P(B))
Если существуют несовместные события, то существуют и совместные.
Совместные события — события, наступление одного из которых не исключает наступления другого.
В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят? Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет.
Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”.
Найдем вероятность события А: (frac{1}{6}).
Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac{3}{6} = frac{1}{2})
Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А.
Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги.

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок.
Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:
(P(A cup B) = P(A) + P(B) — P(A cap B))
В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.
Независимые и зависимые события
Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем.
Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac{95}{100} = 0,95).
Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?
Ответим на вопрос: зависят ли булочки друг от друга?
Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.
Независимые события — такие события, появление одного из которых не зависит от появления другого события.
Определим вероятность независимых событий.
Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95.
А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:
(P(A cap B) = P(A) * P(B))
Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025.
В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”.
Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.
Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого.
Но если автоматы стоят рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.
Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

Нужная последовательность может быть в двух случаях:
- сначала вытащат фиолетовый кубик и потом снова фиолетовый;
- сначала вытащат оранжевый кубик, а потом фиолетовый.
Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac{5}{7}). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые.

Вероятность вытащить во второй раз фиолетовый кубик равна (frac{5}{7} * frac{4}{6} = frac{20}{42} = frac{10}{21}).

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac{2}{7}). В мешке останется шесть кубиков, пять из которых будут фиолетовыми.

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac{2}{7} * frac{5}{6} = frac{10}{42} = frac{5}{21}).
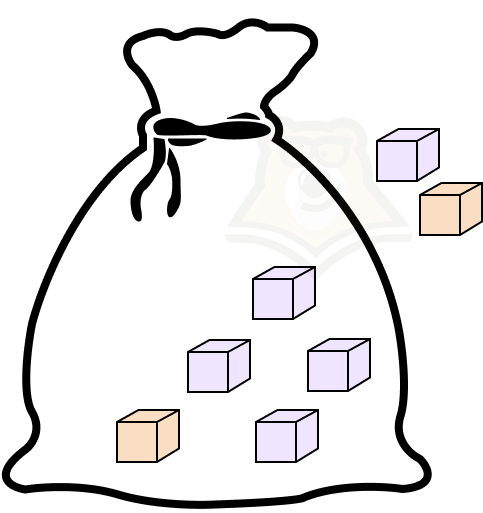
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы.
Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.
Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность.
Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:
(P(A cap B) = P(A) * P(B | A))
Формула Бернулли
Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?
Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac{1}{6}).
Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac{5}{6}).
Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k.
Чтобы решить задачу, нужно воспользоваться формулой Бернулли.
(P_n(k) = C_n^k * p^k * q^{n — k})
Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики».
Решим задачу, подставив значения в формулу:
(P_8(3) = C_8^3 * (frac{1}{6})^3 * (frac{5}{6})^5 = frac{8!}{5!3!} * frac{1}{6^3} * frac{5^5}{6^5} = frac{6 * 7 * 8}{1 * 2 * 3} * frac{5^5}{6^8} approx 0,1)
Фактчек
- Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
- События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
- События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
- События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A).
- Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Проверь себя
Задание 1.
Какие события являются несовместными?
- Подбрасывание монетки.
- Брак батареек в одной упаковке.
- “Миша идет” и “Миша стоит”.
- Случайное вытаскивание конфет из вазы.
Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?
- 0,17
- 1
- 0,83
- 1,17
Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?
- 1
- 0,216
- 0,45
- 1,5
Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.
- 0,3
- 0,001
- 2,7
- 0,729
Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой.
- 0,77
- 0,135
- 0,23
- -0,23
Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1
На чтение 16 мин Просмотров 126к. Опубликовано 25 мая, 2018
Вероятность — очень лёгкая тема, если концентрироваться на смысле задач, а не на формулах. Найти вероятность того что — не просто. И как решать задачи на вероятность?. Во-первых, что такое вероятность? Это шанс, что какое-то событие произойдёт. Если мы говорим, что вероятность некоторого события 50%, что это значит? Что оно либо произойдет, либо не произойдет — одно из двух. Таким образом подсчитать значение вероятности очень просто — нужно взять количество подходящих нам вариантов и разделить на количество всех возможных вариантов. Например, шанс получить решку при подбрасывании монеты это ½. Как мы получаем ½? Всего у нас два возможных варианта (орёл и решка), из них нам подходит один (решка), так мы и получаем вероятность ½.
![]()
Как мы уже с вами увидели, вероятность может быть выражена как в процентах, так и в обычных числах. Важно: на ЕГЭ вам нужно будет записать ответ в числах, не в процентах. Принято, что вероятность изменяется от 0 (никогда не произойдет) до 1 (абсолютно точно произойдет). Также можно сказать, что всегда
Вероятность подходящих событий + вероятность неподходящих событий = 1
Теперь мы точно понимаем, как считать вероятность отдельного события, и даже такие задачи есть в банке ФИПИ, но понятно, что на этом всё не заканчивается. Чтобы жизнь была веселее, в задачах на вероятность обычно происходят как минимум два события, и надо посчитать вероятность с учетом каждого из них.
Содержание
- Вероятность нескольких событий
- Задачи и решения задач на вероятность
- Вероятность нескольких событий
- Дополняющая вероятность
Вероятность нескольких событий
Подсчитываем вероятность каждого события в отдельности, затем между дробями ставим знаки:
1. Если нужно первое И второе событие, то умножаем.
2. Если нужно первое ИЛИ второе событие, то складываем.
Задачи и решения задач на вероятность
Задача 1. Среди натуральных чисел от 23 до 37 случайно выбирают одно число. Найдите вероятность того, что оно не делится на 5.
Решение:
Вероятность, это отношение благоприятных вариантов к общему их количеству.
Всего в этом промежутке 15 чисел. Из них на 5 делится всего 3, значит не делится 12.
Вероятность тогда: ![]()
Ответ: 0,8.
Задача 2. Для дежурства в столовой случайно выбирают двух учащихся класса. Какова вероятность того, что дежурить будут два мальчика, если в классе обучается 7 мальчиков и 8 девочек?
Решение: Вероятность, это отношение благоприятных вариантов к общему их количеству. В классе 7 мальчиков, это благоприятные варианты. А всего 15 учеников.
Вероятность что первый дежурный мальчик:
![]()
Вероятность что второй дежурный мальчик:
![]()
Раз оба должны быть мальчики, вероятности перемножим:
![]()
Ответ: 0,2.
Задача 3. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Решение: Пассажиру В. удобны 30 мест (12 + 18 = 30), а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30/300, т. е. 0,1.
Задача 4. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
Решение: Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна 15/25, т. е. 0,6.
Задача 5. В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам.
Решение: Из 35 билетов 28 не содержат вопроса по кислотам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам, равна 28/35, т. е. 0,8.
Задача 6. В среднем из 500 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение: Если из 500 насосов 2 подтекают, то 498 не подтекают. Следовательно, вероятность выбора хорошего насоса — 498/500, т. е. 0,996.
Задача 7. Вероятность того, что новый пылесос в течение года поступит в гарантийный ремонт, равна 0,065. В некотором городе из 1000 проданных пылесосов в течение года в гарантийную мастерскую поступило 70 штук.
На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение: Частота события «гарантийный ремонт» равна 70/1000, т. е. 0,07. Она отличается от предсказанной вероятности на 0,005 (0,07 – 0,065 = 0,005).
Задача 8. В чемпионате по гимнастике участвуют 50 спортсменок: 18 из России, 14 из Украины, остальные — из Белоруссии. Порядок, в котором выступают гимнастки, определяется жребием.
Найдите вероятность того, что спортсменка, выступающая первой, окажется из Белоруссии.
Решение: Всего участниц на чемпионате 50, а спортсменок из Белоруссии — 18 (50 – 18 – 14 = 18).
Вероятность того, что первой будет выступать спортсменка из Белоруссии — 18 из 50, т. е. 18/50, или 0,36.
Задача 9. Научная конференция проводится в 5 дней. Всего запланировано 80 докладов — первые три дня по 12 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой.
Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение: За первые три дня будут прочитаны 36 докладов (12 ∙ 3 = 36), на последние два дня планируется 44 доклада. Поэтому на последний день запланировано 22 докладов (44 : 2 = 22). Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 22/80, т. е. 0,275.
Задача 10.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 14 участников из России, в том числе Егор Косов.
Найдите вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России?
Решение: В первом туре Егор Косов может сыграть с 25 шахматистами (26 – 1 = 25), из которых 13 ― из России. Значит, вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России, равна 13/25, или 0,52.
Задача 11.
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение: Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек, т. е. 4/16, или 0,25.
Задача 12. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
Решение: Выбирают двоих туристов из пяти. Следовательно, вероятность быть выбранным равна 2/5, т. е. 0,4.
Задача 13. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение: На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист полетит первым рейсом вертолёта, равна 6/30, или 0,2.
Задача 14. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
Решение: Натуральных чисел от 10 до 19 десять, из них на 3 делятся три числа: 12, 15 и 18. Следовательно, искомая вероятность равна 3/10, т. е. 0,3.
Вероятность нескольких событий
Задача 1. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Стратор». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.
Решение:
Тип вопроса: совмещение событий.
Нас устроит следующий вариант: «Статор» не начинает первую игру, начинает вторую игру, не начинает третью игру. Вероятность такого развития событий равна произведению вероятностей каждого из этих событий. Вероятность каждого из них равна 0,5, следовательно: 0,5 · 0,5 · 0,5 = 0,125.
Задача 2. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей ― 1 очко, если проигрывает ― 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение:
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
| Игра №1 | Игра №2 | Вероятность данного варианта |
| 3 | 1 | 0,4 · 0,2 = 0,08 |
| 1 | 3 | 0,2 · 0,4 = 0,08 |
| 3 | 3 | 0,4 · 0,4 = 0,16 |
Вероятность происхождения какого-либо их этих 3-х вариантов равна сумме вероятностей каждого из вариантов: 0,08 + 0,08 + 0,16 = 0,32.
Задача 3. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того что Аня и Нина окажутся в одной группе.
Решение:
Тип вопроса: уменьшение групп.
Вероятность попадания Ани в одну из групп равна 1. Вероятность попадания Нины в ту же группу равна 2 из 20 (2 оставшихся места в группе, а человек осталось 20). 2/20 = 1/10 = 0,1.
Задача 4. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
Решение:
Способ №1
Тип задачи: уменьшение групп.
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая однорублевая монета попадет в один из карманов (групп) = 1.
Вероятность, что две двухрублевые монеты попадут в этот же карман = количество оставшихся мест в этом кармане/на количество оставшихся мест в обоих карманах = 2/5 = 0,4.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют в несколько вариантов:
Если Петя переложил в другой карман три из четырех рублевых монет (а двухрублевые не перекладывал), или если переложил в другой карман обе двухрублевые монеты и одну рублевую одним из трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
![]()
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: ![]()
Задача 5. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Решение:
Тип задачи: уменьшение групп.
Способ №1
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая двухрублевая монета попадет в один из карманов (групп) = 1. Вероятность, что вторая монета попадет в другой карман = количество оставшихся мест в другом/ на количество оставшихся мест в обоих карманах = 3/5 = 0,6.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
![]()
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: ![]()
Задача 6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно два раза.
Решение: Тип вопроса: нахождение желаемого и действительного совмещение событий Нас устраивают три варианта:
Орёл ― решка ― орёл;
Орёл ― орёл ― решка;
Решка ― орёл ― орёл;
Вероятность каждого случая ― 1/2, а каждого варианта ― 1/8 (1/2 ∙ 1/2 ∙ 1/2 = 1/8)
Нас устроит либо первый, либо второй, либо третий вариант. Следовательно, складываем их вероятности и получаем 3/8 (1/8 + 1/8 + 1/8 = 3/8), т. е. 0,375.
Задача 7. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение:
Тип вопроса: совмещение событий.
В любом случае А. будет играть как белыми, так и черными, поэтому нас устроит вариант, когда гроссмейстер А. выиграет, играя белыми (вероятность ― 0,5), а также играя чёрными (вероятность ― 0,34). Поэтому надо перемножить вероятности этих двух событий: 0,5 ∙ 0,34 = 0,17.
Задача 8. Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решение:
Тип вопроса: совмещение событий.
Вероятность того, что батарейка исправна, равна 0,98. Покупателю надо, чтобы и первая, и вторая батарейка были исправны: 0,98 · 0,98 = 0,9604.
Задача 9. На рок-фестивале выступают группы ― по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из США будет выступать после группы из Канады и после группы из Китая? Результат округлите до сотых.
Решение:
Тип вопроса: совмещение событий.
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (КИТ — Китай, КАН = Канада):
… США, КАН, КИТ …
… США, КИТ, КАН …
… КИТ, США, КАН …
… КАН, США, КИТ …
… КАН, КИТ, США …
… КИТ, КАН, США …
США находится после Китая и Канады в двух последних случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна:
![]()
≈ 0,33.
Дополняющая вероятность
Задача 1.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05.
Найдите вероятность того, что случайно выбранная батарейка будет забракована.
Решение:
Существуют 2 варианта, которые нам подходят:
Вариант А: батарейка забракована, она неисправна;
Вариант Б: батарейка забракована, она исправна.
Вероятность варианта А: 0,02 ∙ 0,97 = 0,0194;
Вероятность варианта Б: 0,05 ∙ 0,98 = 0,049;
Нас устроит либо первый, либо второй вариант: 0,0194 + 0,049 = 0,0684.
Задача 2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая — 40%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 5%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,6 · 0,03 = 0,018.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,4 · 0,05 = 0,02.
Вероятность того, что случайно купленное в магазине стекло окажется бракованным, равна 0,018 + 0,02 = 0,038.
Задача 3. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных.
Решение:
Предположим, у нас х тарелок изначально (ведь мы постоянно имеем дело с процентами, поэтому нам ничего не мешает оперировать конкретными величинами).
Тогда 0,1х — дефектные тарелки, а 0,9х — нормальные, которые поступят в магазин сразу. Из дефектных убирается 80%, то есть 0,08х, и остаётся 0,02х, которые тоже пойдут в магазин. Таким образом, общее количество тарелок на полках в магазине окажется: 0,9х + 0,02х = 0,92х. Из них нормальными будет 0,9х. Соответственно, по формуле вероятность будет 0,9х/0,92х ≈ 0,978.
Задача 4. По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,91. Вероятность того, что этот товар доставят из магазина Б, равна 0,89. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение. Вероятность того, что первый магазин не доставит товар, равна 1 − 0,91 = 0,09. Вероятность того, что второй магазин не доставит товар, равна 1 − 0,89 = 0,11. Вероятность происхождения двух этих событий одновременно равна произведению вероятностей каждого из них: 0,09 · 0,11 = 0,0099.
Задача 5. При изготовлении подшипников диаметром 70 мм вероятность того, что диаметр будет отличаться от заданного меньше чем на 0,01 мм, равна 0,961. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 69,99 мм или больше чем 70,01 мм.
Решение: Нам дана вероятность события, при котором диаметр будет в пределах между 69,99 мм и 70,01 мм, и она равна 0,961. Вероятность всех остальных вариантов мы можем найти по принципу дополняющей вероятности: 1 − 0,961 = 0,039.
Задача 6. Вероятность того, что на тесте по истории учащийся верно решит больше 9 задач, равна 0,68. Вероятность того, что верно решит больше 8 задач, равна 0,78. Найдите вероятность того, что верно решит ровно 9 задач.
Решение: Вероятность того, что Т. верно решит более 8 задач, включает в себя вероятность решения ровно 9 задач. При этом, события, при которых О. решит больше 9 задач, нам не подходят. Следовательно, отняв от вероятности решения более 9 задач вероятность решения более 8 задач, мы и найдём вероятность решения только 9 задач: 0,78 – 0,68 = 0,1.
Задача 7. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,88. Вероятность того, что окажется меньше 12 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 12 до 20.
Решение. Вероятность того, что в автобусе окажется меньше 21 пассажира, включает в себя вероятность, что в нём окажутся от 12 до 20 пассажиров. При этом события, при которых пассажиров будет меньше 12, нам не подходят. Следовательно, отняв от первой вероятности (менее 21) вторую вероятность (менее 12), мы и найдём вероятность того, что пассажиров будет от 12 до 20 : 0,88 – 0,66 = 0,22.
Задача 8. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 10 апреля погода в Волшебной стране хорошая. Найдите вероятность того, что 13 апреля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» — хорошая погода, «О» — отличная погода):
| 11 апреля | 12 апреля | 13 апреля | Вероятность данного варианта |
| X – 0,9 | X – 0,9 | O – 0,1 | 0,9 ·0,9 ·0,1 = 0,081 |
| X – 0,9 | O – 0,1 | O – 0,9 | 0,9 ·0,1 ·0,9 = 0,081 |
| O – 0,1 | O – 0,9 | O – 0,9 | 0,1 ·0,9 ·0,9 = 0,081 |
| O – 0,1 | X – 0,1 | O – 0,1 | 0,1 ·0,1 ·0,1 = 0,001 |
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 0,081 + 0,081 + 0,081 + 0,001 = 0,244.
Задача 9. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» ― хорошая погода, «О» ― отличная погода):
| 4 июля | 5 июля | 6 июля | Вероятность данного варианта |
| X – 0,8 | X – 0,8 | O – 0,2 | 0,8 · 0,8 · 0,2 = 0,128 |
| X – 0,8 | O – 0,2 | O – 0,8 | 0,8 · 0,2 · 0,8 = 0,128 |
| O – 0,2 | O − 0,8 | O − 0,8 | 0,2 · 0,8 · 0,8 = 0,128 |
| O – 0,2 | X – 0,2 | O – 0,2 | 0,2 · 0,2 · 0,2 = 0,008 |
Вероятность происхождения какого-либо их этих 4 ― х вариантов равна сумме вероятностей каждого из вариантов: 0,128 + 0,128 + 0,128 + 0,008 = 0,392.
События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).
Зачем нужна теория вероятности
Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.
Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.
В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.
Основные понятия теории вероятности
Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.

Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.
Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.
События А и В называется несовместными, если они не могут произойти одновременно.
Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом
.
Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом
.
Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.
- Вероятность принимает значения на отрезке от 0 до 1, т.е.
.
- Вероятность невозможного события равна 0, т.е.
.
- Вероятность достоверного события равна 1, т.e.
.
- Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е.
 .
.
Важным частным случаем является ситуация, когда имеется равновероятных элементарных исходов, и произвольные
из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле
. Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.
Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов , прямо в условии написано число всех исходов
.

Ответ получаем по формуле .
Пример задачи из ЕГЭ по математике по определению вероятности
На столе лежат 20 пирожков – 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?
Решение.
Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А – это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:
![]()
Ответ: 0,4
Независимые, противоположные и произвольные события
Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.
События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.
Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е. .
Теоремы сложения и умножения вероятностей, формулы
Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е.
.
Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае
.
Последние 2 утверждения называются теоремами сложения и умножения вероятностей.
Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.
Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение , которое обозначается символом 6! и читается “шесть факториал”.
В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов ![]() В нашем случае
В нашем случае .
Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .
В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам
![]()
В нашем случае .
И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину: . В общем случае ответ на этот вопрос дает формула для числа сочетаний из
элементов по
элементам:
![]()
В нашем случае .
Примеры решения задач из ЕГЭ по математике на определение вероятности
Задача 1. Из сборника под ред. Ященко.
На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение:
.
Ответ: 0,3.
Задача 2. Из сборника под ред. Ященко.
В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.
Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:
![]()
Ответ: 0,98.
Задача 3.
Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.
Решение:
Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие “У. верно решит ровно 9 задач” входит в условие “У. верно решит больше 8 задач”, но не относится к условию “У. верно решит больше 9 задач”.
Однако, условие “У. верно решит больше 9 задач” содержится в условии “У. верно решит больше 8 задач”. Таким образом, если мы обозначим события: “У. верно решит ровно 9 задач” – через А, “У. верно решит больше 8 задач” – через B, “У. верно решит больше 9 задач” через С. То решение будет выглядеть следующим образом:
![]() .
.
Ответ: 0,06.
Задача 4.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме “Тригонометрия”, либо к теме “Внешние углы”. По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:
![]()
Ответ: 0,35.
Задача 5.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.
Тогда укажем варианты таких событий. Примем обозначения: – лампочка горит,
– лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события “лампочка перегорела”, “лампочка горит”, “лампочка горит”:
![]() , где вероятность события “лампочка горит” подсчитывается как вероятность события, противоположного событию “лампочка не горит”, а именно:
, где вероятность события “лампочка горит” подсчитывается как вероятность события, противоположного событию “лампочка не горит”, а именно: ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий: ![]() .
.
Ответ: 0,975608.
Еще одну задачку вы можете посмотреть на рисунке:

Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.
Задачи на вычисление вероятностей обязательно входят и в ОГЭ, и в ЕГЭ… Именно поэтому я решил рассмотреть несколько задач на эту тему. Однако, прежде чем рассмотреть три задачи из Части 1 ВПР-2020 для 8-го класса по математике, считаю необходимым вспомнить самые азы теории вероятности, знакомство с которой начинается в 6-ом классе.
#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Часть I
Мы знаем, что события бывают трёх видов: достоверное, невозможное и случайное.
Достоверное событие — это событие, которое при данных условиях обязательно наступит.
Невозможное событие — это событие, которое при данных условиях никогда не наступит.
Случайное событие — это событие, которое при данных условиях может наступит, а может и не наступить.
Принято считать, что:
1) вероятность достоверного события равна 1 (или 100 %);
2) вероятность невозможного события равна 0 (или 0 %).
А как подсчитать вероятность случайного события? Ведь если оно с л у ч а й н о е, значит, не подчиняется никаким формулам, алгоритмам, закономерностям. Однако оказывается, что и в мире случайного действуют определённые законы, с помощью которых можно вычислять вероятности. Этим занимается раздел математики, который так и называется — теория вероятностей.
Пусть исход случайного события состоит из нескольких равновозможных вариантов, а само событие состоит в следующем: подкинули вверх монету, и она упала на землю «орлом» или «решкой». Это достоверное событие: монета обязательно упадёт на землю «орлом» или «решкой» — третьего варианта нет.
Оба исхода — выпадение «орла» или «решки» — равновозможны или, как говорят математики, равновероятны. Естественно считать, что вероятность события “выпадения «орла»” (обозначим это событие буквой А) равна вероятности события “выпадение «решки»” (обозначим это событие буквой В) и что их сумма равна вероятности события “выпадение «орла» или «решки»” (обозначим это событие буквой С). Последнее событие достоверное (третьего на дано!), его вероятность равна 1. Значит, вероятность выпадения «орла» равна 1/2 и вероятность выпадения «решки» тоже равна 1/2. Принято вероятность события обозначать буквой Р (поскольку «вероятность» по-французски —probabilite).
Таким образом в нашей задаче о бросании монеты получаем:
P(C) = 1; P(A) = P(B); P(A) + P(B) = P(C) => P(A) + P(B) = 1 и P(A) = P(B) = 1/2.
Если достоверное событие состоит из нескольких равновероятных возможностей, то вероятность случайного события можно вычислить
по следующему правилу:
Вероятность случайного события равна дроби, в знаменателе которой стоит число всех исходов, а в числителе — число всех благоприятных исходов.
P= (число всех благоприятных исходов)/(число всех исходов).
Вероятность часто записывают в процентах — значит, вероятность выпадения «орла» можно записать в виде
Р(А) = 1/2 или Р(А) = 50 %.
Рассмотрим несколько задач под из пособия «Всероссийская проверочная работа. Математика 8 класс : 20 вариантов. Практикум ФГОС / А.Р.Рязановский, Д.Г.Мухин, — М. : Издательство «Экзамен», 2020».
Перед условием задачи будем указывать № варианта, из которого эта задача взята. В данной статье мы рассмотрим задачи № 6.1 из вариантов 5, 8, 14. Как обычно, предлагаю читателю, прежде чем знакомиться с решением самостоятельно решить эти задачи.
В-т 5. Тося записала случайное двузначное число, меньшее 50. Найдите вероятность того, что это число больше 25.
В-т 8. Дима записал случайно трёхзначное число. Найдите вероятность того, что это число делится на 5.
В-т 14. Пять человек Григорий, Владимир, Екатерина, Софья и Нина. выбирают двоих для отправки в лагерь. Найдите вероятность того, что в лагерь попадут Софья и Нина.
РЕШЕНИЕ в-та 5.
1) 49 < 50, поэтому 49 – 9 = 40 — число двузначных чисел, удовлетворяющих этому условию.
2) 49 – 25 = 24 число двузначных чисел, которые больше 25, но меньше 50.
3) Р = 24/40 = 6/10 = 0,6.
ОТВЕТ. 0,6.
РЕШЕНИЕ в-та 8.
1) Имеется всего 999 – 99 = 900 трёхзначных чисел от 100 до 999.
2) рассмотрим последовательность трёхзначных чисел в обратном порядке от 999 до 100 — в этой последовательности каждое пятое число делится на 5: 900 : 5 = 180 — число чисел, кратных 5.
3) Р = 180/900 = 0,2.
ОТВЕТ. 0,2.
РЕШЕНИЕ в-та 14.
1) 5 × (5 – 1) : 2 = 10 – число пар, которое можно составить из пяти человек (см. статью «Турнирная задача, которая заставляет поломать голову как школьника, так и взрослого»).
2) Софья и Нина составляют одну пару из десяти — значит, Р = 0,1.
ОТВЕТ. 0,1.
Продолжение читайте здесь
Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.
Читайте наш канал в телеграм — по этой ссылке
Другие статьи автора:
❓ Что такое теория вероятностей?
Теория вероятностей использует случайные величины и распределения вероятностей для математической оценки неопределенных ситуаций. Понятие вероятности используется для присвоения числового описания вероятности наступления события. Вероятность можно определить как число благоприятных исходов, деленное на общее число возможных исходов события.
Определение теории вероятностей
Теория вероятностей – это область математики и статистики, которая занимается определением вероятностей, связанных со случайными событиями. Существует два основных подхода к изучению теории вероятностей: теоретический и экспериментальный. Теоретическая вероятность определяется на основе логических рассуждений без проведения экспериментов. В отличие от нее, экспериментальная вероятность определяется на основе исторических данных путем проведения повторных экспериментов.
Пример теории вероятностей
Предположим, нам необходимо определить вероятность выпадения числа 4 при бросании игральной кости. Число благоприятных исходов равно 1. Возможные исходы игральной кости – {1, 2, 3, 4, 5, 6}. Из этого следует, что всего существует 6 исходов. Таким образом, вероятность выпадения 4 при бросании игральной кости, используя теорию вероятности, можно вычислить как 1 / 6 ≈ 0,167.
🎲 Основы теории вероятностей
Мы можем понять эту область математики с помощью нескольких основных терминов, напрямую связанных с теорией вероятностей.
Случайный эксперимент
Случайный эксперимент в теории вероятностей – это испытание, которое повторяется несколько раз для получения четко определенного набора возможных результатов. Подбрасывание монеты является примером случайного эксперимента.
Пространство выборки
Пространство выборки можно определить как множество всех возможных исходов, полученных в результате проведения случайного эксперимента. Например, пространство выборки при подбрасывании симметричной монеты (fair coin), стороны которой – это орел и решка.
Событие
Теория вероятностей определяет событие как набор исходов эксперимента, который образует подмножество пространства выборки.
Примеры событий:
- Независимые – те, на которые не влияют другие события, являются независимыми.
- Зависимые – те, на которые влияют другие события.
- Взаимоисключающие – события, которые не могут произойти в одно и то же время.
- Равновероятные – два или более события, которые имеют одинаковые шансы произойти.
- Исчерпывающие – это события, которые равны выборочному пространству эксперимента.
Случайная величина
В теории вероятностей случайную переменную можно определить как величину, которая принимает значение при всех возможных исходах эксперимента.
Существует два типа случайных величин:
- Дискретная случайная величина – принимает точные значения, такие как 0, 1, 2…. Описывается кумулятивной функцией распределения и функцией массы вероятности.
- Непрерывная случайная величина – переменная, которая может принимать бесконечное число значений. Для определения характеристик этой переменной используются кумулятивная функция распределения и функция плотности вероятности.
Вероятность
Вероятность мы можем определить как численную вероятность наступления события. Вероятность того, что событие произойдет, всегда лежит между 0 и 1. Это связано с тем, что число желаемых исходов никогда не может превысить общее число исходов события. Теоретическая вероятность и эмпирическая вероятность используются в теории вероятностей для измерения шанса наступления события.

Условная вероятность
Ситуация, когда необходимо определить вероятность наступления события, притом что другое событие уже произошло.
Обозначается как P(A | B).
Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», на котором ты:
- Усвоишь специальную терминологию и сможешь читать статьи по Data Science без постоянных обращений к поисковику.
- Подготовишься к успешной сдачи вступительных экзаменов в Школу анализа данных Яндекс.
- Овладеешь математическим аппаратом, который необходим, чтобы стать специалистом в Data Science.
Ожидание
Ожидание случайной величины X можно определить как среднее значение результатов эксперимента, проводимого многократно. Ожидание обозначается как E[X]. Также известно как среднее значение случайной величины.
Дисперсия
Дисперсия – это мера, которая показывает, как распределение случайной величины изменяется относительно среднего значения. Дисперсия определяется как среднее квадратичное отклонение от среднего значения случайной величины. Обозначается как Var[X].
Функция распределения теории вероятностей
Распределение вероятностей или кумулятивная функция распределения – это функция, которая моделирует все возможные значения эксперимента, используя случайную переменную. Распределение Бернулли и биномиальное распределение – это примеры дискретных распределений вероятностей. Например, нормальное распределение представляет собой пример непрерывного распределения.
Массовая функция вероятности
Массовая функция вероятности определяется как вероятность того, что дискретная случайная величина будет в точности равна определенному значению.
Функция плотности вероятности
Функция плотности вероятности – это вероятность того, что непрерывная случайная величина принимает множество возможных значений.
Формулы теории вероятностей
В теории вероятностей существует множество формул, которые помогают рассчитать различные вероятности, связанные с событиями.
Наиболее важные формулы:
- Теоретическая вероятность: Число благоприятных исходов / Число возможных исходов.
- Эмпирическая вероятность: Число случаев, когда событие происходит / Общее число испытаний.
- Правило сложения: P(A ∪ B) = P(A) + P(B) – P(A∩B), где A и B – события.
- Правило комплементарности: P(A’) = 1 – P(A). P(A’) означает вероятность того, что событие не произойдет.
- Независимые события: P(A∩B) = P(A) ⋅ P(B).
- Условная вероятность: P(A | B) = P(A∩B) / P(B).
- Теорема Байеса: P(A | B) = P(B | A) ⋅ P(A) / P(B).
- Массовая функция вероятности: f(x) = P(X = x).
- Функция плотности вероятности: p(x) = p(x) = dF(x) / dx, где F(x) – кумулятивная функция распределения.
- Ожидание непрерывной случайной величины: ∫xf(x)dx, где f(x) является МФВ (Массовой функцией вероятности).
- Ожидание дискретной случайной величины: ∑xp(x), где p(x) – это ФПВ (Функцией плотности вероятности).
- Дисперсия: Var(X) = E[X2] – (E[X])2.
Применение теории вероятностей
Теория вероятностей используется во многих областях и помогает оценить риски, которые связаны с теми или иными решениями. Некоторые из направлений, где применяют теорию вероятностей:
- В финансовой отрасли теория вероятностей используется для создания математических моделей фондового рынка с целью прогнозирования будущих тенденций. Это помогает инвесторам вкладывать средства в наименее рискованные активы, которые дают наилучший доход.
- В потребительской индустрии теория вероятностей используется для снижения вероятности неудачи при разработке продукта.
- Казино использует теорию вероятностей для разработки азартных игр с максимизацией своей прибыли.
🏋️ Практические задания

Задача 1: При бросании двух игральных костей, какова вероятность того, что выпадет комбинация, сумма которой будет равна 8?
При бросании двух игральных костей существует 36 возможных исходов. Для получения суммы, равной 8, существует 5 благоприятных исходов: [(2, 6), (6, 2), (3, 5), (5, 3), (4, 4)]. Используя формулы теории вероятностей: Вероятность = Число благоприятных исходов / общее число возможных исходов = 5 / 36. Ответ: Вероятность получения суммы 8 при бросании двух игральных костей равна 5 / 36.
Задача 2: Какова вероятность вытащить карту королеву из колоды?
Колода карт имеет 4 масти. Каждая масть состоит из 13 карт. Таким образом, общее число возможных исходов = (4) * (13) = 52. Может быть, 4 королевы, по одной из каждой масти. Следовательно, количество благоприятных исходов = 4. Карточная вероятность = 4 / 52 = 1 / 13. Ответ: Вероятность получить королеву из колоды карт равна 1 / 13
Задача 3: Из 10 человек 3 купили карандаши, 5 купили тетради, а 2 купили и карандаши, и тетради. Если покупатель купил тетрадь, какова вероятность того, что он также купил карандаш?
Используя понятие условной вероятности, P(A | B) = P(A∩B) / P(B). Пусть A – событие, когда люди покупают карандаши, а B – событие, когда люди покупают тетради. P(A) = 3 / 10 = 0,3P(B) = 5 / 10 = 0,5P(A∩B) = 2 / 10 = 0,2. Подставим полученные значения в приведенную формулу, P(A | B) = 0,2 / 0,5 = 0,4. Ответ: Вероятность того, что покупатель купил карандаш, при условии, что он купил блокнот, равна 0,4.
В заключение
Подведем итоги:
- Теория вероятностей – это раздел математики, в котором рассматриваются вероятности случайных событий.
- Понятие вероятности объясняет возможность наступления того или иного события.
- Значение вероятности всегда лежит между 0 и 1.
- В теории вероятностей все возможные исходы случайного эксперимента составляют пространство выборки.
- Теория вероятностей использует такие важные понятия, как случайные величины и кумулятивные функции распределения для моделирования случайного события. Сюда же относится определение различных вероятностей, связанных с этим.
Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», который включает в себя:
- 47 видеолекций и 150 практических заданий.
- Консультации с преподавателями курса.
