Как найти вероятность цепочки в дереве вероятностей

Дерево вероятностей

В этой статье я покажу вам очень простой способ решения некоторых задач по теории вероятностей.
Рассмотрим задачу. Трое друзей Вася, Петя и Слава купили торт, и решили его съесть. Они разделили торт на три равных части. Внезапно появился четвертый друг Коля, и друзья решили отрезать ему по кусочку от своей доли. Вася отрезал 1/3 от своего куска, Петя 1/4, а Слава – половину. Какую часть всего торта получил в итоге Коля?

Изобразим ситуацию, описанную в задаче в виде такой схемы:

Сначала торт разрезали на три равные части, и каждому из трех друзей досталось по 1/3 торта.

Затем пришел Коля и каждый мальчик отрезал ему соответствующую часть своего куска:

Чтобы найти дробь от числа, нужно число умножить на эту дробь. То есть Вася отдает Коле часть торта, Петя –   часть торта, а Слава  часть торта.

В итоге Коля получит   часть тортa.

Когда мы ищем вероятность события,  мы ищем,  какую часть благоприятные исходы составляют от общего числа исходов. Если в задаче описывается последовательность случайных опытов, и следующий опыт зависит от исхода предыдущего, для разделения возможных сценариев  развития событий часто используют схему “дерева вероятностей”, аналогичную приведенной выше.

Решим еще одну задачу.

Две фабрики выпускают одинаковые стекла для автомобильных  фар. Первая фабрика выпускает 30% этих стекол, а вторая – 70%. Первая фабрика выпускает 4% бракованных  стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Изобразим ситуацию в виде дерева вероятностей:

Все стекла делятся на те, которые выпускает первая фабрика и на те, которые выпускает вторая:

Стекла, которые выпускает каждая фабрика делятся на бракованные и  пригодные. Из стекол, которые выпускает первая фабрика 4% бракованных, и из тех, которые выпускает вторая – 1% бракованных:

Нас интересуют бракованные стекла, которые выпускаются первой или второй фабрикой. Найдем, какую часть эти стекла составляют от всех стекол:

Ответ: 0,019

И.В. Фельдман, репетитор по математике.

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Теория вероятностей в заданиях ЕГЭ.
  Дерево вероятностей

• 

  2 слайд

  Задания домашней контрольной работы, вызвавшие затруднения
  1. Ков­бой Джон по­па­да­ет в муху на стене с ве­ро­ят­но­стью 0,9, если стре­ля­ет из при­стре­лян­но­го ре­воль­ве­ра. Если Джон стре­ля­ет из не­при­стре­лян­но­го ре­воль­ве­ра, то он по­па­да­ет в муху с ве­ро­ят­но­стью 0,4. На столе лежит 10 ре­воль­ве­ров, из них толь­ко 2 при­стре­лян­ные. Ков­бой Джон видит на стене муху, на­уда­чу хва­та­ет пер­вый по­пав­ший­ся ре­воль­вер и стре­ля­ет в муху. Най­ди­те ве­ро­ят­ность того, что Джон про­махнётся.
  2. Две фаб­ри­ки вы­пус­ка­ют оди­на­ко­вые стек­ла для ав­то­мо­биль­ных фар. Пер­вая фаб­ри­ка вы­пус­ка­ет 35  этих сте­кол, вто­рая – 65 . Пер­вая фаб­ри­ка вы­пус­ка­ет 3  бра­ко­ван­ных сте­кол, а вто­рая – 5 . Най­ди­те ве­ро­ят­ность того, что слу­чай­но куп­лен­ное в ма­га­зи­не стек­ло ока­жет­ся бра­ко­ван­ным.
  3. В волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится потом весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 9 мая погода в Волшебной стране отличная. Найдите вероятность того, что 12 мая в Волшебной стране будет отличная погода.

• 

  3 слайд

  Задания домашней контрольной работы, вызвавшие затруднения
  4. Аг­ро­фир­ма за­ку­па­ет ку­ри­ные яйца в двух до­маш­них хо­зяй­ствах. 85% яиц из пер­во­го хо­зяй­ства — яйца выс­шей ка­те­го­рии, а из вто­ро­го хо­зяй­ства — 65% яиц выс­шей ка­те­го­рии. Всего выс­шую ка­те­го­рию по­лу­ча­ет 80% яиц. Най­ди­те ве­ро­ят­ность того, что яйцо, куп­лен­ное у этой аг­ро­фир­мы, ока­жет­ся из пер­во­го хо­зяй­ства.
  5. Семья с детьми совершает прогулку по дорожкам парка. На каждой развилке они наудачу выбирают следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к киоску с мороженым А, другие к киоску с игрушками В, третьи к пруду с лебедями С. Найдите вероятность того, что семья выйдет к пруду с лебедями.
  6. В коробке лежат 3 красных и 7 черных шаров. Найдите вероятность того, что вынутые наугад 2 шара окажутся красными.
  7. В кар­ма­не у Пети было 4 мо­не­ты по рублю и 2 мо­не­ты по два рубля. Петя, не глядя, пе­ре­ло­жил какие-то 3 мо­не­ты в дру­гой кар­ман. Най­ди­те ве­ро­ят­ность того, что обе двух­рублёвые мо­не­ты лежат в одном кар­ма­не.

• 

  4 слайд

  Дерево вероятностей
  Если в задаче описывается последовательность случайных опытов, и следующий опыт зависит от исхода предыдущего, для разделения возможных сценариев развития событий часто используют схему “дерево вероятностей”

• 

• 

  6 слайд

  2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, а вторая – 70%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

    Ответ: 0,019

• 

  7 слайд

  3. В волшебной стране бывает два типа погоды: хорошая и отличная, причем погода, установившись утром, держится потом весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 9 мая погода в Волшебной стране отличная. Найдите вероятность того, что 12 мая в Волшебной стране будет отличная погода.

       Ответ: 0,756

• 

  8 слайд

  4. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 65 % яиц из первого хозяйства – яйца высшей категории, а из второго хозяйства – 85% яиц высшей категории. Всего высшую категорию получает 80 % яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

      Ответ: 0,25

• 

  9 слайд

  5. Семья с детьми совершает прогулку по дорожкам парка. На каждой развилке они наудачу выбирают следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к киоску с мороженым А, другие к киоску с игрушками В, третьи к пруду с лебедями С. Найдите вероятность того, что семья выйдет к пруду с лебедями.

       Ответ: 0,35

• 

  10 слайд

  6. В коробке лежат 3 красных и 7 черных шаров. Найдите вероятность того, что вынутые наугад 2 шара окажутся красными.
  Вероятность вынуть два определенных шара одновременно равна вероятности вынуть эти два шара последовательно без возвращения их в коробку.

• 

  11 слайд

  7. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.
  Обе двухрублевые монеты окажутся в одном кармане, если Петя переложил в другой карман три монеты по рублю, или две монеты по 2 рубля и одну монету по 1 рублю.

• 

  12 слайд

  7. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.

• 

  13 слайд

  РЕФЛЕКСИЯ
  Я знаю…

  Я умею…

  У меня вызывает трудность…

• 

  14 слайд

  Домашняя работа
  Выполнить контрольную работу №6073717 на сайте http://reshuege.ru/

Краткое описание документа:

Одним из важных разделов  ЕГЭ по математике  является решение  комбинаторных задач  путем организованного перебора возможных вариантов,  с использованием правила умножения, нахождение  вероятности случайных событий. 

Урок «Теория вероятностей в заданиях ЕГЭ. Дерево вероятностей» является вторым в разделе «Теория вероятностей», организованном при повторении и обобщении знаний при подготовке к ЕГЭ в 11классе. Урок построен с использованием приёмов информационно-коммуникационных технологий, а также беседы. 

Презентация составлена с использованием компьютерной программы Microsoft PowerPoint, что позволяет ярко представить материал с необходимой информацией. Использование презентации сокращает время обучения, и облегчает усвоение материала. 

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 262 584 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:
• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

РЕШЕНИЕ ЗАДАЧ НА ВЕРОЯТНОСТЬ С ПОМОЩЬЮ ДЕРЕВА ВАРИАНТОВ

Учитель математики высшей квалификационной категории Шутова О.Н.

город Ульяновск

Задачи на вероятность

1) Решение с помощью дерева возможных вариантов

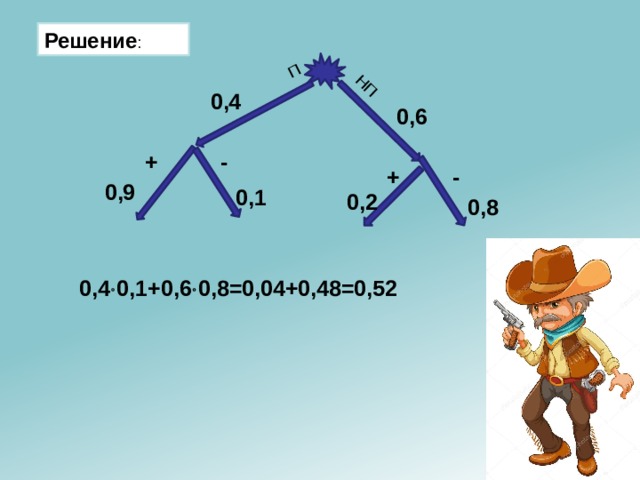
Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Макрос создан программистом Хансом Хофманом (Германия)

П

НП

Решение :

0,4

0,6

–

+

+

–

0,9

0,1

0,2

0,8

0,4  0,1+0,6  0,8=0,04+0,48=0,52

1) Решение с помощью дерева возможных вариантов

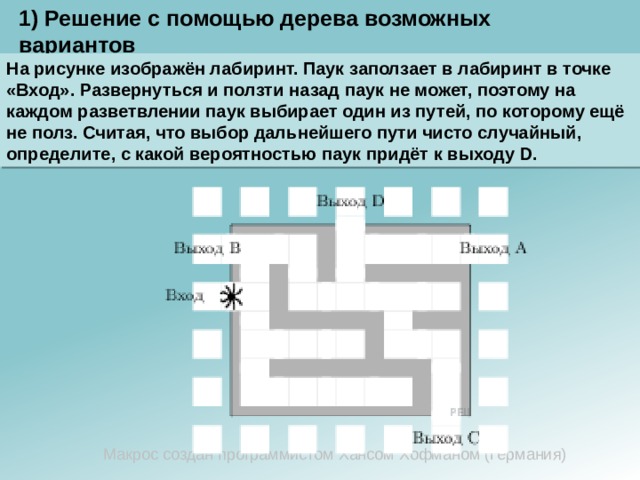
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.

Макрос создан программистом Хансом Хофманом (Германия)

1) Решение с помощью дерева возможных вариантов

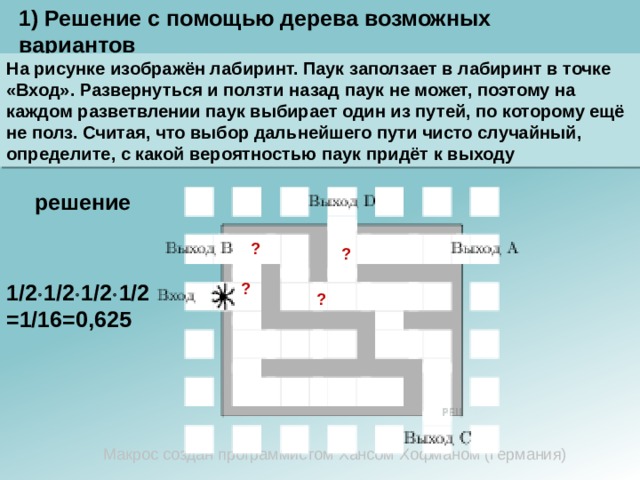
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу 

решение

?

?

1/2  1/2  1/2  1/2=1/16=0,625

?

?

Макрос создан программистом Хансом Хофманом (Германия)

Задачи на вероятность

1) Решение с помощью дерева возможных вариантов

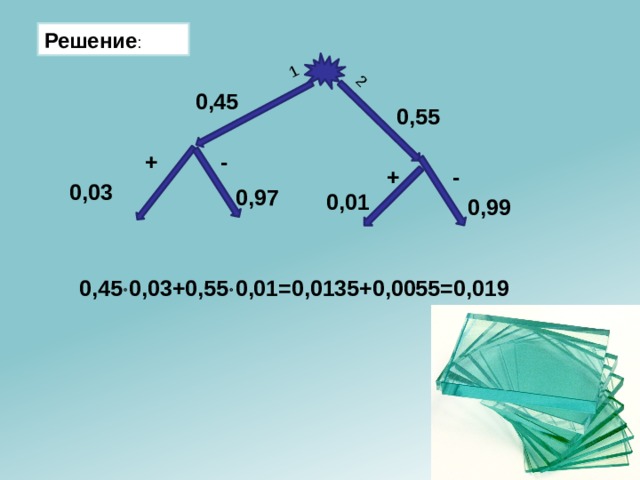
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Макрос создан программистом Хансом Хофманом (Германия)

1

2

Решение :

0,45

0,55

–

+

–

+

0,03

0,97

0,01

0,99

0,45  0,03+0,55  0,01=0,0135+0,0055=0,019

Задачи на вероятность

1) Решение с помощью дерева возможных вариантов

Нарисовать дерево возможных вариантов для вычисления значения дроби

(2х-у)/(х+у), если при х=1;2;3 переменная у=3;4

Макрос создан программистом Хансом Хофманом (Германия)

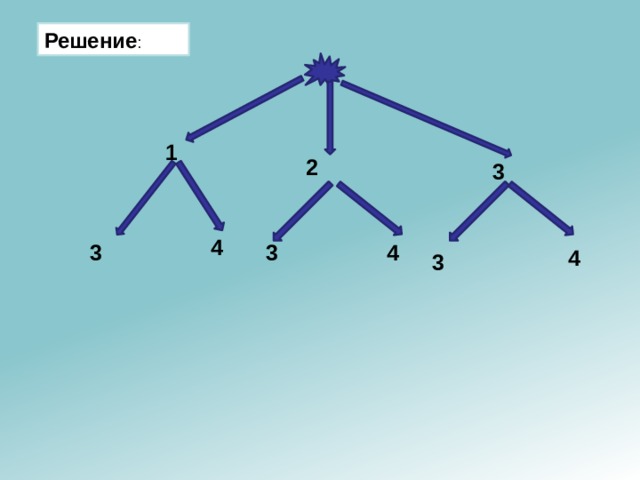
Решение :

1

2

3

4

4

3

3

4

3

Самостоятельная работа

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25 этих стекол, вторая – 75 Первая фабрика выпускает 4 бракованных стекол, а вторая – 2 Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 35 этих стекол, вторая – 65 Первая фабрика выпускает 3 бракованных стекол, а вторая – 5 Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

2. Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он по­па­да­ет в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

2. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,1. На столе лежит 10 револьверов, из них только 3 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Макрос создан программистом Хансом Хофманом (Германия)

Решение задач с помощью дерева вероятностей.
RAR / 5.92 Мб
Муниципальное общеобразовательное учреждение

Верхнедонская гимназия

Ст. Казанская

Ростовская область

Мастер-класс

«Решение задач с помощью дерева вероятностей»

 

Подготовила

учитель математики

Полиёва Е.И.

Ст. Казанская

Цели:

познакомить с понятием графа, вероятностного дерева;

рассмотреть методы решения задач с помощью графа, дерева вероятностей;

рассмотреть формы и методы закрепления знаний, умений и навыков

Оборудование:

интерактивная доска SmartBoard;

мультимедийный проектор;

персональный компьютер (ПК) учителя

презентация «Решение задач с помощью дерева вероятностей»

раздаточный материал (распечатать каждому ученику)

тренажер

самостоятельная работа

Слайд 1.

Слайд 2.

Слайд 4.

Решение задач. Тренажер. (приложение распечатать и выполнять на этих же листочках).

Данный материал предназначен для отработки умений и навыков по теме “Решение задач с помощью дерева вероятностей”. Тренажер можно использовать и на уроке, и на дополнительных заданиях по подготовке к ЕГЭ.

Задачи №1- №5 решаются совместно с учителем, №6 – №10 – самостоятельно с последующей проверкой.
 

Контроль усвоения материала. Самостоятельная работа.

Вероятность – это способ оценить, насколько вероятно, что событие произойдет, или насколько вероятно, что утверждение истинно. Древовидная диаграмма – это инструмент, который помогает людям эффективно рассчитывать вероятность и принимать решения на основе своих расчетов. Если вы студент-математик, математик или другой специалист, работающий со статистикой, вам будет полезно узнать об этой важной таблице. В этой статье мы рассмотрим определение диаграммы дерева вероятностей, объясним, как рассчитать вероятности с ее помощью, и дадим советы для успешного проведения расчетов.

Что такое диаграмма дерева вероятностей?

Диаграмма дерева вероятностей – это инструмент, который помогает людям рассчитать количество возможных исходов события и вероятность того, что они могут произойти. Это также организованное визуальное отображение этих результатов, где каждое дерево ветвь представляет собой другой результат. Умножая вероятности по ветвям, вы можете определить вероятность определенной серии событий. Вы можете проверить точность своей работы, убедившись, что все итоговые вероятности на древовидной диаграмме равны 1.0.

Например, при подбрасывании монеты первые две ветви представляют результаты первого броска монеты. Возможными исходами являются голова или решка , и вероятность каждого из них равна 0.5. Чтобы представить возможный исход каждого раза, когда вы можете подбросить монету еще раз, вы можете заполнить дальнейшие ветви дерева и вероятности. Древовидные диаграммы вероятности могут использоваться для расчета как независимых событий, например, броска монеты, так и зависимых событий, где каждое событие зависит от предыдущего.

Почему важны диаграммы дерева вероятностей?

Диаграммы дерева вероятностей важны, поскольку они могут быть полезными инструментами для следующих типов специалистов:

• Метеорологи: Специалисты в этой области могут использовать диаграмму дерева вероятностей для анализа погодных условий и прогнозирования вероятности определенных погодных условий, таких как дождь или снежная буря.

• Эпидемиологи: Вероятность является важной частью этой профессии, где члены команды рассчитывают и анализируют связь между воздействием и риском для здоровья.

• Статистики: Эти специалисты собирают и интерпретируют данные, чтобы помочь бизнесу в принятии решений высокого уровня, часто отвечают за управление финансовыми вероятностями и рисками.

• Оценщики стоимости: Люди в этой роли могут использовать диаграммы дерева вероятностей для рассмотрения вопроса о том, как сократить расходы, время и ресурсы, затраченные на производство продукта или предоставление услуги.

• Страховые андеррайтеры: Поскольку в обязанности этих специалистов входит оценка риска страхового клиента, полезно, когда они могут легко рассчитать вероятность риска.

• Аналитики по исследованию рынка: Представители этой профессии исследуют и собирают данные о потребительских рынках, чтобы помочь бизнесу в продвижении товаров и услуг, и используют вероятность для прогнозирования поведения потребителей.

• Астрономы: Эти специалисты собирают данные о космосе и небесных телах, используя вероятность для прогнозирования таких явлений, как солнечные вспышки, метеориты и космическая погода.

• Спортивные телеведущие: Эти профессионалы могут использовать вероятность при анализе спортивных событий и прогнозировании будущих спортивных событий для зрителей.

• Врачи: Люди на этой должности отвечают за оценку различных типов информации для пациентов, таких как здоровье беременности, продолжительность жизни и продолжительность болезни.

• Преподаватели математики: Преподаватели математики рассказывают учащимся о вероятности, чтобы подготовить их к решению обычных жизненных ситуаций и принятию повседневных решений.

Как рассчитать вероятности с помощью древовидных диаграмм

Хотя существует множество различных способов расчета вероятностей, древовидные диаграммы могут быть полезным графиком для визуализации и организации данных. Вот как использовать древовидные диаграммы для расчета вероятности события в шесть шагов:

1. Набросайте возможные исходы

Определив, какой ответ вы ищете, обрисуйте возможные исходы. Например, вы можете попытаться выяснить, сможет ли ваша баскетбольная команда Тигры выиграть сегодняшнюю игру. Это может зависеть от того, играете ли вы в Ястребов , высококвалифицированную команду, или в Ящеров , команду, в которой много новичков.

Сначала создайте точку с двумя стрелками, направленными от нее. Поскольку ваши возможные исходы – это игра Ястребов или Ящериц , вы можете написать эти исходы в конце каждой стрелки. Далее вы можете написать вероятность каждого исхода на линии стрелки.

2. Напишите вероятность каждого исхода

Поскольку вы обычно играете в The Lizards примерно 6 раз в 10 игр, вероятность того, что вы сыграете в The Lizards сегодня, равна 0.6. Вы можете вычесть 0.Отнимите 6 от 1, чтобы найти вероятность игры Ястребов , которая равна 0.4. На стрелке, указывающей на Ястребов , напишите 0.6. На стрелке, указывающей на Lizards, напишите 0.4. Быстрой проверкой для этого раздела является сложение ваших чисел, 0.6 и 0.4, чтобы убедиться, что они равны 1.0.

3. Создайте следующие ветви дерева

Играя в прошлом сезоне с командой The Lizards, вы выиграли игру восемь раз из десяти. Итак, если вы сегодня сыграете в The Lizards, вероятность того, что вы выиграете, равна 0.8. Это также означает, что вероятность того, что ваша команда проиграет игру, равна 0.2, так как в прошлом сезоне вы проиграли Ящерицам две игры из 10. После вашего Ящерицы создайте две новые стрелки, ветвящиеся вправо, ведущие к Выиграть и Проиграть результаты. На Выиграть стрелка, напишите 0.8. На Потерять стрелка, напишите 0.2.

Играя с Ястребами в прошлом сезоне, ваша команда выиграла игру пять раз из 10. Это означает, что вы также проиграли пять раз из 10. Во-первых, после того, как вы Ястребы создайте две новые стрелки, направленные вправо, ведущие к Выиграть и Проиграть исходы. На Победа стрелкой, напишите 0.5, и на Проиграть стрелке можно также написать 0.5. Чтобы проверить свою работу по ходу дела, вы можете добавить 0.5 с 0.5, чтобы убедиться, что оно равно 1.0.

4. Рассчитайте общую вероятность

Далее, пришло время вычислить общую вероятность путем умножения по ветвям дерева. Вы пытаетесь выяснить, насколько вероятно, что ваша команда сможет выиграть игру. Во-первых, умножьте вероятность того, что вы играете в The Lizards, 0.6, на вероятность того, что вы выиграете у Ящеров , 0.8. Это дает вам 0.48 выигрыша у The Lizards в сегодняшней игре.

Затем, в отдельном расчете, умножьте вероятность того, что вы играете в Ястребов , 0.4, к вероятности победы над Ястребами 0.5. Это дает вам 0.20 шансов на победу над Ястребами в сегодняшней игре.

5. Сложите соответствующие вероятности

Теперь вы можете сложить вероятности в столбце столбец дерева, чтобы найти свой окончательный результат, вероятность того, что вы можете выиграть сегодняшнюю игру в целом. Добавление 0.48, вероятность победы против Ящеров , с 0.20, шанс, что вы выиграете у Ястребов , даст вам результат 0.68 – вероятность того, что вы вообще выиграете игру. Вы можете умножить свой результат на 100, чтобы получить его в процентах, что может быть проще для понимания и представления другим. Исходя из ваших расчетов, вероятность того, что вы выиграете сегодняшнюю баскетбольную игру, составляет 68%.

6. Проверьте правильность своей работы

Проверка работы в данном случае означает расчет общей вероятности проигрыша игры, если вы играете с любой из команд, а затем сложение всех чисел в столбце, чтобы убедиться, что они равны 1.0. На Первом, чтобы найти вероятность того, что вы проиграете The Lizards в сегодняшней игре, умножьте 0.6 на 0.2, чтобы получить 0.12. Затем, чтобы найти вероятность проигрыша Ястребов в сегодняшней игре, умножьте 0.4 по 0.5, чтобы получить 0.20.

Затем, добавьте 0.12 и 0.20, чтобы получить 0.32, общая вероятность проигрыша в игре сегодня. Прибавьте 0.32 с 0.68, что является вероятностью выигрыша, и вы получаете 1.0. Этот метод проверки показывает, что вы выполнили расчеты правильно.

Советы по расчету вероятности с помощью древовидной диаграммы

Будь вы студент или профессионал, инструмент древовидной диаграммы может быть полезен вам в повседневной работе. Вот несколько советов по эффективному расчету вероятности с помощью древовидной диаграммы:

• Используйте лист бумаги: Подумайте о том, чтобы нарисовать диаграмму карандашом или ручкой и бумагой, по крайней мере, вначале. Физическое записывание информации и создание графика может помочь вам хорошо понять процесс и запомнить его на будущее.

• Сначала соберите всю информацию: Это помогает собрать и перечислить всю информацию, которую вы планируете использовать в диаграмме, прежде чем начать процесс рисования. Сюда входят измеряемые вами исходы и вероятности, которые вы уже знаете.

• Будьте внимательны к своим цифрам: Внимание к деталям – полезный навык при подсчете статистики. Обратите пристальное внимание на используемые числа и убедитесь, что каждый шаг на этом пути имеет правильное значение.

• Проверьте свою работу: При выполнении любого математического вычисления полезно проверить точность своей работы, используя метод проверки. Это может гарантировать, что вы представите правильные конечные результаты своему учителю, коллегам или руководителю.

• Поймите, что вероятность – это оценка: Хотя прогнозирование результатов до того, как они произойдут, может быть полезным и точным, всегда существует вероятность неожиданных событий. Старайтесь помнить об этом при использовании древовидной диаграммы, чтобы правильно управлять своими ожиданиями.

• Обратитесь за помощью: Если вы столкнулись с трудностями при попытке использовать древовидную диаграмму, попросите помощи у учителя, коллеги или надежного друга. Они могут дать вам совет о том, как легко завершить этот процесс.