Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Пусть нам задана функция плотности распределения непрерывной случайной величины. Тогда с её помощью мы можем найти вероятность того, что случайная величина попадет в интервал $(alpha ,beta )$.
Для начала вспомним несколько свойств функции распределения вероятности $F(x)$, которые понадобятся нам в дальнейшем.
Свойство 1: Для любых $X$ выполняется равенство:
Сформулируем и докажем следующую теорему:
Вероятность того, что непрерывная случайная величина $X$ примет значение из интервала $(alpha ,beta )$ равна значению определенного интеграла от $alpha $ до $beta $ плотности распределения $varphi (x)$.
Доказательство.
Используя свойство 1, имеем:
[Pleft(alpha le XИспользуя формулу Ньютона-Лейбница, получим:
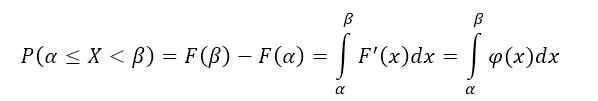
Рисунок 1.
Так как случайная величина $X$ непрерывна, то и функция распределения $F(x)$ также непрерывна. Следовательно, по свойству 2, получим:
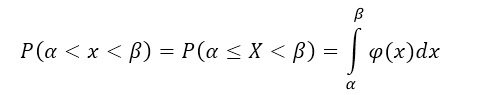
Рисунок 2.
ч. т. д.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Геометрически данную теорему можно интерпретировать следующим образом: Вероятность попадания случайной непрерывной величины $X$ в интервал $(alpha ,beta )$ равна площади криволинейной трапеции, ограниченной кривыми $y=varphi left(xright), x=alpha ,$ $x=beta $ и $y=0$ (рис. 1).
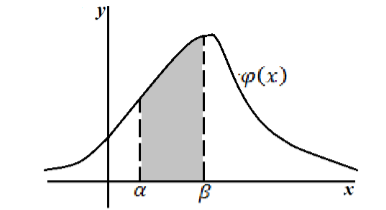
Рисунок 3. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(alpha ,beta )$.
Следствие 1: Если плотность распределения $varphi (x)$ – четная функция, а значения $alpha и beta $ равны по абсолютной величине (по модулю), причем $alpha ne beta $, то вероятность попадания непрерывной случайной величины в интервал $(alpha ,beta )$ можно найти по формуле:
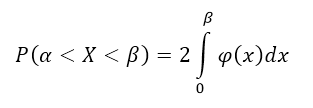
Рисунок 4.
«Вероятность попадания непрерывной величины в заданный интервал » 👇
Этот факт может быть легко показан геометрически:
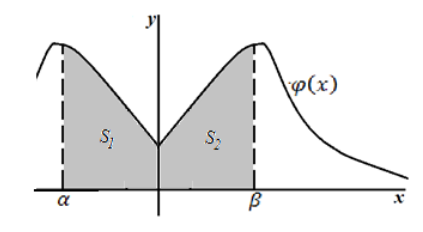
Рисунок 5.
Очевидно, что $S_1=S_2$.
Используя геометрический смысл плотности распределения, и получаем, что
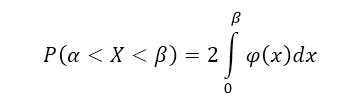
Рисунок 6.
Примеры задач на нахождение вероятности попадания непрерывной случайной величины в заданный интервал
Пример 1
Функция распределения имеет вид:
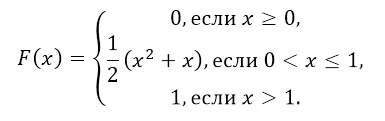
Рисунок 7.
Найти вероятности попадания случайной величины в интервал $(frac{1}{4},frac{1}{2})$.
Решение: Очевидно, что функция $F(x)$ непрерывна на сей области определения (в том числе непрерывна справа на всем интервале $(frac{1}{4},frac{1}{2})$). Значит по свойству 2, получим
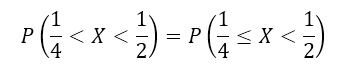
Рисунок 8.
Теперь, пользуясь свойством 1, получим:
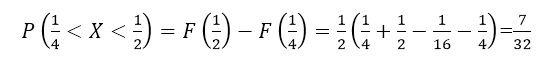
Рисунок 9.
Ответ: $frac{7}{32}$.
Пример 2
Плотность распределения задана в виде:
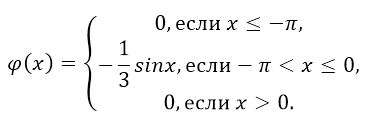
Рисунок 10.
Найти вероятности попадания случайной величины в интервал $(-frac{pi }{2},-frac{pi }{4})$.
Решение: Используя теорему 1, получим:
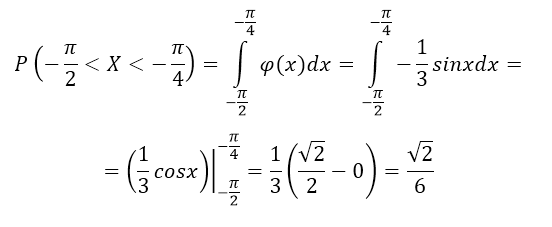
Рисунок 11.
Ответ: $frac{sqrt{2}}{6}$.
Пример 3
Функция плотности распределения имеет вид:
[varphi left(xright)=frac{1}{4x^2+4}]
Построить график плотности распределения и найти вероятность попадания случайной величины в интервал $left(-2,2right).$
Решение: Построим график функции $varphi left(xright)$:
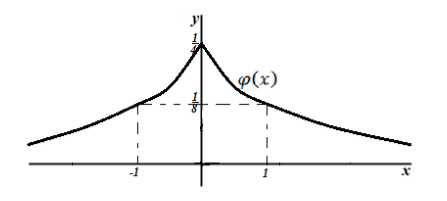
Рисунок 12.
Функция $varphi left(xright)$ четна, концы интервала $left(-2,2right)$ симметричны относительно начала координат, следовательно, по следствию 1, получаем:
[Pleft(-2Ответ: $frac{1}{2}arctg2.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
2.2.8. Вероятность попадания в промежуток
Найдём ![]() – вероятность того,
– вероятность того,
что случайная величина ![]() примет
примет
какое-нибудь значение из интервала ![]() .
.
В данном случае концы интервала (–1 и 5) находятся в области непрерывности функции распределения поэтому: ![]() .
.
И действительно, на данном интервале находятся значения ![]() , вероятности появления которых:
, вероятности появления которых: ![]() .
.
Вычислим вероятность ![]() . Оба
. Оба
конца этого промежутка не «попадают» в точки разрыва, поэтому:
![]() – вероятность того, что
– вероятность того, что
случайная величина ![]() примет
примет
значение из данного промежутка. И в самом деле – на нём находится единственное значение ![]() , которое может появиться с вероятностью
, которое может появиться с вероятностью ![]() .
.
Та же самая история с ![]() –
–
единственное, тут левый конец промежутка равен «минус» бесконечности:
![]() – самостоятельно
– самостоятельно
проанализируйте, какие значения ![]() , и с какими вероятностями располагаются на промежутке
, и с какими вероятностями располагаются на промежутке ![]()
Теперь более занятная ситуация, где нужно особо включать голову: если хотя бы один из концов ![]() промежутка «попадает» в точку
промежутка «попадает» в точку
разрыва функции ![]() , то указанную
, то указанную
выше формулу можно использовать лишь в одном случае из четырёх, а именно для неравенства:
![]()
Примечание: если ![]() , то
, то
левое неравенство становится строгим, но формула тоже применима.
Найдём ![]() . Как быть? – под
. Как быть? – под
правило не подходит! Вспоминаем теоремы тервера. По теореме сложения вероятностей несовместных событий:
![]() – вероятность того, что
– вероятность того, что
случайная величина ![]() примет
примет
значение из отрезка ![]() .
.
И действительно, этот отрезок включает в себя два значения ![]() , которые появляются с вероятностями
, которые появляются с вероятностями ![]() .
.
Тут же рассмотрим три других неравенства:
![]() , т.к. на интервале
, т.к. на интервале ![]() нет значений случайной величины.
нет значений случайной величины.
Да-да, так и пишем.
![]() – это «штатный» случай
– это «штатный» случай
(см. правило).
И для 2-го полуинтервала используем теорему сложения вероятностей несовместных событий:
![]()
Едем дальше:
![]() – поскольку там нет
– поскольку там нет
значений случайной величины.
Кстати, случай с нестрогим неравенством – есть «штатный» случай:
![]() , который можно оформить и
, который можно оформить и
так:
![]() – ведь на функции
– ведь на функции
распределения «свет клином не сошёлся».
И, наконец, типовая вероятность ![]() – того, что значение случайной величины
– того, что значение случайной величины ![]() отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение. И, как вы догадываетесь, эти характеристики нужно
отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение. И, как вы догадываетесь, эти характеристики нужно
вычислить. Но на самом деле не нужно, поскольку они уже рассчитаны в Задаче 87:
![]()
Раскрываем модуль:
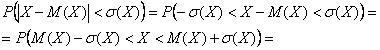
подставляем конкретные значения ![]() и пользуемся тем фактом, что они не «попадают» в точки разрыва функции
и пользуемся тем фактом, что они не «попадают» в точки разрыва функции
распределения:
![]()
![]() – искомая вероятность.
– искомая вероятность.
Напоминаю, что в типичном случае на интервале ![]() или вблизи него «сконцентрированы» наиболее вероятные значения случайной
или вблизи него «сконцентрированы» наиболее вероятные значения случайной
величины. Так сказать, «центр событий».
Ответ:
![]()
Аналогичное задание для самоконтроля, весь трафарет приведён выше:
Задача 94
Составить функцию распределения случайной величины ![]()

Выполнить чертёж. Найти вероятности следующих событий:
![]()
Подумайте над рациональным масштабом графика. Если возникают сомнению с нахождением вероятностей, помните – их всегда можно
пересчитать вручную, просто посмотрев на исходную табличку.
Решение и ответ там, где обычно.
И не успел я запостить этот материал на сайте (давно это было J), как от читателей стали поступать просьбы включить
в статью контрольный пример. Я даже прослезился (прямо как тот
профессор), и, конечно же, не смог вам отказать:
 2.2.9. Контрольное задание
2.2.9. Контрольное задание
 2.2.7. Функция распределения случайной величины
2.2.7. Функция распределения случайной величины
| Оглавление |
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
расчет вероятности помогает рассчитать вероятность для одного события, нескольких событий, двух событий, для серии событий, а также событий с условной вероятностью. Если вы хотите рассчитать вероятность a и b и для любого количества событий, то приведенный выше калькулятор вероятностей подойдет вам лучше всего!
Что ж, переходим к делу; просто прочтите этот пост, чтобы узнать, как рассчитать вероятность, различные уравнения вероятности, все формулы вероятности, статистический калькулятор вероятности и многое другое, что вам нужно знать о вероятности.
Итак, давайте начнем с наилучшего определения вероятности!
Что такое вероятность в статистике?
Под вероятностью понимается вероятность наступления события или нескольких событий. Вероятность – это то, что указывает на возможность достижения определенного результата и может быть рассчитано с помощью простой формулы вероятности.
Происхождение теории вероятностей начинается с изучения таких игр, как игра в кости, подбрасывание монет, карт и т. Д. Но в настоящее время вероятность имеет большое значение при принятии решений. Классическая теория показывает, что вероятность – это отношение благоприятного случая к общему количеству равновероятных случаев. Субъективный подход показывает, что вероятность события определяется человеком на основе имеющихся у него / нее свидетельств.
Исследование о вероятности:
Идея вероятности как полезной науки принадлежит известным французским математикам Блезу Паскалю и Пьеру де Ферма.
Согласно «Исчислению, том II» Тома М. Апостола, и Блез Паскаль, и Пьер де Ферма решали проблему с азартными играми в 1954 году. Они лучше всего работают при определении количества ходов, необходимых для получения 6 при броске двух кубиков. Да, дискуссии Паскаля и де Ферма заложили основу концепции теории вероятностей.
Какова формула вероятности?
Формула вероятности события следующая:
P (A) = количество благоприятных исходов / общее количество благоприятных исходов
Или формула вероятности:
P (A) = n (E) / n (S)
Где,
- P (A) называется вероятностью события «A»
- n (E) называется числом благоприятных исходов.
- n (S) называется числом событий в выборке
Примечание. Здесь благоприятный исход указывается как интересующий результат.
Теперь давайте посмотрим на основные формулы вероятности!
Каковы основные формулы вероятности?
Проведите вниз!
Диапазон вероятности:
0 ≤ P (A) ≤ 1
Правило сложения:
P (A∪B) = P (A) + P (B) – P (A∩B)
Правило дополнительных событий:
P (A ’) + P (A) = 1
Непересекающиеся события:
P (A∩B) = 0
Независимые мероприятия:
P (A∩B) = P (A) ⋅ P (B)
Условная возможность:
P (A | B) = P (A∩B) / P (B)
Формула Байеса:
Р (А | В) = Р (В | А) ⋅ Р (А) / Р (В)
Что ж, ближе к делу: вычисление обозначений вероятности становится простым с помощью статистических событий или калькулятора условной вероятности.
О калькуляторе вероятностей:
расчет вероятности – это продвинутый инструмент, который позволяет узнать вероятность одного события, нескольких событий, двух событий и для серии событий. Кроме того, этот калькулятор работает как калькулятор условной вероятности, так как помогает вычислить условную вероятность заданного входа. Короче говоря, определение вероятности становится простым с помощью этого калькулятора вероятностных событий. Помимо уравнения вероятности, вы можете легко найти вероятность с помощью этого калькулятора вероятностей.
как решать задачи на вероятность с помощью калькулятора:
Что ж, вы можете легко рассчитать условные или вероятностные события с помощью этого калькулятора вероятностных событий, поскольку он загружен с удобным интерфейсом, он на 100% бесплатен для вычисления вероятностей. Читать дальше!
Рассчитайте вероятность для одного события:
Вход:
- Прежде всего, вам нужно выбрать опцию «Single Probability» из выпадающего меню калькулятора.
- Затем вы должны ввести количество возможных результатов в специальное поле.
- Теперь вам нужно ввести количество произошедших событий (n) A в назначенное поле.
Вывод:
После этого нажмите кнопку «Рассчитать», расчет вероятности одного события сгенерирует:
- Вероятность наступления события P (A) как в десятичном, так и в процентах
- Вероятность события, которое не произойдет, P (A ‘) как в десятичном, так и в процентном выражении
Рассчитайте вероятность нескольких событий:
Вход:
- Прежде всего, вы должны выбрать опцию «Вероятность нескольких событий» из раскрывающегося меню этого калькулятора вероятности для нескольких событий.
- Сразу после этого вы должны ввести количество событий (n) A в заданные поля
- Затем вы должны ввести количество событий (n) B в специальное поле этого калькулятора.
Вывод:
После того, как вы ввели все вышеперечисленные параметры, нажмите кнопку «Рассчитать», и этот расчет вероятности нескольких событий сгенерирует:
- Вероятность наступления события P (A) как в десятичном, так и в процентах
- Вероятность события, которое не произойдет, P (A ‘) как в десятичном, так и в процентном выражении
- Вероятность наступления события B P (B) как в десятичном, так и в процентном выражении
- Вероятность того, что событие B не произойдет, P (B ‘) как в десятичном, так и в процентном выражении
- Вероятность наступления обоих событий P (A ∩ B) как в десятичной, так и в процентной форме.
- Вероятность наступления любого из событий P (A ∪ B) как в десятичной, так и в процентной форме.
- Условная вероятность P (A | B) как в десятичной, так и в процентной форме
Рассчитайте вероятность двух событий:
Вход:
- Во-первых, вы должны выбрать опцию «Вероятность двух событий» в раскрывающемся меню этого калькулятора вероятности двух событий.
- Затем вам нужно выбрать формат ввода, хотите ли вы добавить значения в десятичном формате или в процентах.
- Сразу после этого вы должны добавить значение вероятности P (A) в обозначенное поле.
- Затем вы должны добавить значение вероятности P (B) в обозначенное поле.
Вывод:
После того, как вы добавите все значения в указанные поля, нажмите кнопку вычислить, калькулятор вероятности двух событий сгенерирует:
- Вероятность того, что событие не произойдет P (A ‘)
- Вероятность того, что событие B не произойдет P (B ‘)
- Вероятность наступления обоих событий P (A ∩ B)
- Вероятность наступления любого из событий P (A ∪ B)
- Вероятность появления A или B, но не обоих P (AΔB)
- Вероятность того, что ни A, ни B не встретятся P ((A∪B) ‘)
- Вероятность появления B, но не A
Калькулятор покажет все указанные выше значения как в десятичном, так и в процентном формате.
Рассчитайте вероятность серии событий:
Вход:
- Прежде всего, вы должны выбрать опцию «Вероятность серии событий» в соответствующем поле этого калькулятора вероятности серии событий.
- Затем вы должны ввести значение вероятности и количество повторов для «События А» в предназначенное для этого поле.
- Сразу после этого вы должны добавить значение вероятности и количество повторов для «События B» в данное поле.
Вывод:
После того, как вы ввели все значения в обозначенные поля, просто нажмите кнопку «Рассчитать», и эта вероятность мгновенно выдаст следующие результаты:
- Вероятность появления А 2 раза
- Вероятность того, что А не произойдет
- Вероятность возникновения А
- Вероятность появления B 4 раза
- Вероятность того, что B не произойдет
- Вероятность появления B
- Вероятность того, что A встречается 2 раза, а B – 4 раза
- Вероятность того, что не произойдет ни A, ни B
- Вероятность появления как A, так и B
- Вероятность появления A 2 раза, но не B
- Вероятность появления B 4 раза, но не A
- Вероятность появления A, но не B
- Вероятность появления A, но не B
Вычислить условную вероятность P (A | B):
Вход:
- Прежде всего, вы должны выбрать опцию «Условная вероятность P (A | B)» в специальном поле этого калькулятора условной вероятности.
- Затем вы должны ввести значение вероятности a и b в обозначенное поле.
- Затем вы должны ввести значение вероятности P (B) в предназначенное для этого поле.
Вывод:
После этого просто нажмите кнопку вычислить, калькулятор условной вероятности сгенерирует:
- Условная вероятность P (A | B) как в десятичной, так и в процентной форме
К счастью, найти вероятность a и b становится легко с помощью этого калькулятора условной вероятности.
Каковы различные типы вероятностных событий:
Прочтите, чтобы узнать о различных типах вероятностных событий:
Простое событие:
Если событие E содержит только одну точку выборки из пространства выборки, оно называется простым событием или элементарным событием. Помните, что это событие, которое содержит только один результат.
Пример вероятности единичного события:
Предположим, вы бросаете кубик, вероятность выпадения 2 на кубике считается простым событием и задается как E = {2}.
Сложное событие:
Если в пространстве для выборки имеется более одной точки выборки, то это считается сложным событием. Это событие предполагает объединение двух или более событий вместе и определение вероятности такой комбинации событий.
Пример сложного события по вероятности:
Когда вы бросаете кубик, существует вероятность появления четного числа, которая называется составным событием, поскольку существует более одной возможности, есть три возможности, которые равны E = {2,4,6}.
Определенное событие:
Определенное событие называется событием, которое обязательно произойдет в любом данном эксперименте. Вероятность такого события равна 1.
Невозможное событие:
Когда событие не может произойти, это означает, что событие не может произойти, тогда это считается невозможным событием. Вероятность невозможного события обозначается как 0.
Пример невозможного события по вероятности:
Карта, которую вы вытащили из колоды, красного и черного цвета, считается невозможным.
Равно вероятные события:
Если результаты эксперимента равновероятны, то они считаются равновероятными событиями.
Пример равновероятных событий по вероятности:
Когда вы подбрасываете монету, вероятность выпадения орла и решки одинакова.
Бесплатные мероприятия:
Для события E ненаступление события называется дополнительным событием. Обычно говорят, что дополнительные события – это события, которые не могут произойти одновременно.
Пример вероятности дополнительных событий:
Когда бросается кубик, получение нечетного и четного лиц считается дополнительными событиями.
Взаимоисключающие события:
Два события называются взаимоисключающими вероятностными событиями, когда оба не могут произойти одновременно. Помните, что взаимоисключающие вероятностные события всегда имеют разный исход. Два простых события всегда считаются взаимоисключающими, тогда как два составных события могут быть, а могут и не быть!
Если A и B – два события, тогда;
(A ∩ B) = Ø
и,
Вероятность пересечения
P (A ∩ B) = 0
Вероятность союза
Р (А ∪ В) = Р (А) + Р (В)
Зависимые вероятностные события и независимые вероятностные события (примеры задач):
Опишем оба термина простыми словами:
- Зависимые вероятностные события связаны друг с другом
- Независимые вероятностные события не связаны между собой, значит, вероятность того, что одно произойдет, не влияет на другое.
Вероятность двух событий, происходящих вместе – зависимая вероятность:
Здесь уравнение вероятности, которое вы используете, немного отличается.
P (A и B) = P (A) • P (B | A)
Где;
- P (B | A) просто обозначено как «вероятность B, если A произошло»)
Пример проблемы:
Если 85% сотрудников имеют медицинскую страховку, из 85% только 45% имели отчисления выше 1000 долларов. Итак, какой процент людей имел франшизу выше 1000 долларов?
Шаг 1:
- Вам нужно преобразовать проценты двух событий в десятичные числа, давайте посмотрим на пример.
85% = 0,85.
45% = 0,45.
Шаг 2:
- Теперь вам нужно умножить десятичные дроби из шага 1 вместе.
0,85 x 0,45 = 0,3825 или 38,35 процента.
Таким образом, вероятность того, что у физических лиц будет франшиза более 1000 долларов, составляет 38,35%.
Вот как рассчитать вероятность того, что два события произойдут вместе!
Вероятность двух событий, происходящих вместе – Независимая вероятность:
Все, что вам нужно, это использовать определенную формулу правила умножения. Вам следует умножить вероятность первого события на второе. Например, если вероятность события A 2/9 и события B равна 3/9, то вероятность того, что оба события происходят одновременно, равна (2/9) * (3/9) = 6/81 = 2/27.
Пример проблемы:
Шансы получить работу, на которую вы подали заявку, составляют 45%, а шансы получить квартиру, на которую вы подавали заявку, составляют 75%, тогда как насчет вероятности того, что вы получите и новую работу, и новую квартиру?
Шаг 1:
- Вам следует преобразовать ваши проценты двух событий в десятичные числа, давайте взглянем на приведенный выше пример.
45% = 0,45.
75% = 0,75.
Шаг 2:
- Теперь вам нужно умножить десятичные дроби из шага 2 вместе:
0,45 x 0,65 = 0,3375 или 33,75 процента.
Итак, вероятность получить работу и квартиру составляет 33,75%.
Вероятность A и B:
Вероятность A и B означает, что вы хотите знать вероятность двух событий, которые происходят одновременно. Существуют разные формулы, которые полностью зависят от того, есть ли у вас зависимые события или независимые события.
Формула для вероятности A и B (независимых событий): p (A и B) = p (A) * p (B)
Помните, что если вероятность одного события не влияет на другое, значит, у вас независимое событие. Итак, как уже упоминалось ранее, вам нужно умножить вероятность одного на вероятность другого.
Формула для вероятности A и B (зависимых событий): p (A и B) = p (A) * p (B | A)
Помимо этих уравнений вероятностей, вы можете просто добавить параметры в указанный выше калькулятор вероятностей, чтобы определить вероятность событий.
Как рассчитать вероятность (вручную, шаг за шагом)?
Помимо уравнений вероятности, вы можете просто добавить параметры в приведенный выше калькулятор вероятностей, чтобы определить вероятность событий. Но, если вы хотите рассчитать вероятность вручную, то прочтите!
Все, что вам нужно, чтобы рассчитать вероятность:
- Прежде всего, вы должны определить одно событие с одним исходом.
- Затем вы должны определить общее количество возможных результатов.
- Затем вам нужно разделить количество событий на количество возможных результатов.
Давайте копать глубже!
Шаг № 1: Определите одно событие с одним результатом:
Первым шагом к вычислению вероятности является определение вероятности, которую вы хотите вычислить. Это может быть указано как событие, предположим, что вероятность дождливой погоды, или выпадение определенного числа на кубике. Событие должно иметь хотя бы один возможный исход. Например, если вы хотите найти вероятность выпадения тройки с кубиком при первом броске, вы должны выяснить, что есть возможный результат: означает, что вы либо бросаете тройку, либо не бросаете тройку.
Шаг № 2: Определите общее количество результатов:
Затем вы должны определить количество результатов, которые могут возникнуть в результате события, которое вы определили на первом шаге. Если мы говорим о примере броска кубика, то всего может произойти 6 исходов, поскольку на кубике 6 чисел. Итак, ясно, что для одного события – выпадения трех – может произойти 6 различных результатов.
Шаг № 3: Разделите количество событий на количество возможных результатов:
После того как вы определили вероятностное событие вместе с соответствующими результатами, вам нужно разделить общее количество событий на общее количество возможных исходов. Например, бросок кубика один раз и выпадение тройки можно считать вероятностью одного события. Таким образом, вы можете продолжать бросать кубик – следовательно, каждый бросок будет считаться одним событием.
Итак, из приведенного выше примера результат в дроби: 1/6.
Как рассчитать вероятность с несколькими случайными событиями?
Хотите мгновенно рассчитать вероятность нескольких событий, а затем просто расчет вероятности для нескольких событий. Несомненно, вычисление вероятности с несколькими случайными событиями очень похоже на вычисление вероятности с одним событием, однако есть лишь несколько дополнительных шагов, которые нужно придерживаться, чтобы достичь окончательного решения. Следующие ниже шаги показывают, как рассчитать вероятность нескольких событий:
- Прежде всего, вы должны определить каждое событие, которое вы будете рассчитывать.
- Затем вам нужно рассчитать вероятность каждого события.
- Наконец, вам нужно умножить все вероятности вместе
Часто задаваемые вопросы (о вероятности):
Как найти вероятности с процентами?
Если вы хотите рассчитать вероятность в процентах, вам следует решить задачу, как обычно, то есть вам нужно преобразовать свой ответ в процент.
Например;
Если количество желаемых результатов разделить на количество возможных событий, равное 0,25, тогда вам следует умножить ответ на 100, чтобы получить 25%. Если есть вероятность определенного исхода в процентной форме, тогда вам просто нужно разделить процент на 100, а теперь умножить его на количество событий, чтобы вычислить вероятность.
Как рассчитать вероятность на калькуляторе?
Все, что вам нужно для ввода значений в указанные выше поля, калькулятор вероятностей сделает все за вас в течение нескольких секунд.
Каковы 3 типа вероятности?
Три типа вероятности следующие:
- Классический
- Определение относительной частоты
- Субъективная вероятность
Каковы 5 правил вероятности?
Основные правила вероятности:
- Правило вероятности первое – (Для любого события A, 0 ≤ P (A) ≤ 1)
- Правило вероятности два – (Сумма вероятностей всех возможных исходов равна 1)
- Правило вероятности третье – (Правило дополнения)
Вероятности, связанные с несколькими событиями:
- Правило вероятности четвертое (правило сложения для непересекающихся событий)
Нахождение P (A и B) с помощью логики:
- Правило вероятности пятое – (Общее правило сложения)
Как я могу определить вероятность при выборе случайных чисел?
Запомните все это на основе диапазона генератора случайных чисел. Например, если диапазон от 1 до 9, то вероятность получения определенного числа считается равной 1/9.
Если я брошу кубик 6 раз, какова вероятность?
Вероятность того, что он хотя бы раз выпадет на 6, составляет 66,5%.
Если я брошу обычный шестигранный кубик, какова вероятность получить 5?
Тогда ваш ответ будет 1/6, или примерно 17%.
Если один раз бросить шестигранный кубик, какова вероятность выпадения 1 или 2?
2/6, после подбрасывания кубика вероятность получить 1 равняется 1/6, а вероятность получения 2 также равна 1/6. Таким образом, 1/6 + 1/6 = 2/6 или 1/3 или 0,333.
Как рассчитать вероятность футбольных матчей?
На самом деле, ты не можешь. Единственное, от чего можно уйти, так это их умения. Помните, что игроки тоже люди, и у них может быть плохой день, а это значит, что они играют не так хорошо, как обычно!
Где мы используем вероятность в реальной жизни?
Вот примеры вероятности из реальной жизни:
- Прогноз погоды
- Среднее значение по крикету
- Политика
- Подбрасывание монеты или кубика
- Страхование
- Вы скорее всего погибнете в результате несчастного случая
- Лотерейные билеты
- Играя в карты
Вывод:
Помните, что вероятность – это то, что дает вам информацию о вероятности того, что что-то произойдет. Итак, просто воспользуйтесь приведенным выше калькулятором вероятностей, чтобы вычислить вероятность событий или в соответствии с условиями!
Other languages: Probability Calculator, olasılık hesaplama, kalkulator prawdopodobieństwa, kalkulator probabilitas, wahrscheinlichkeitsrechner, 確率 計算, 확률 계산기, pravděpodobnost kalkulačka, calculo de probabilidade, calcul de probabilité, calculo de probabilidad, calcolo probabilità, todennäköisyys laskuri, sandsynlighedsregning, sannsynlighetskalkulator.
17 авг. 2022 г.
читать 2 мин
Вероятность описывает вероятность того, что некоторое событие произойдет.
Мы можем рассчитать вероятности в Excel, используя функцию PROB , которая использует следующий синтаксис:
ПРОБ(x_диапазон, вероятностный_диапазон, нижний_предел, [верхний_предел])
куда:
- x_range: диапазон числовых значений x.
- prob_range: диапазон вероятностей, связанных с каждым значением x.
- нижний_предел: нижний предел значения, для которого вы хотите получить вероятность.
- upper_limit: Верхний предел значения, для которого вы хотите получить вероятность. По желанию.
В этом руководстве представлено несколько примеров использования этой функции на практике.
Пример 1: Вероятность игры в кости
На следующем изображении показана вероятность выпадения кубика с определенным значением при данном броске:

Поскольку кости с одинаковой вероятностью выпадут на каждом значении, вероятность одинакова для каждого значения.
На следующем рисунке показано, как найти вероятность того, что кубик выпадет на число от 3 до 6:

Вероятность оказывается равной 0,5 .
Обратите внимание, что аргумент верхнего предела является необязательным. Таким образом, мы могли бы использовать следующий синтаксис, чтобы найти вероятность того, что кости приземлятся только на 4:
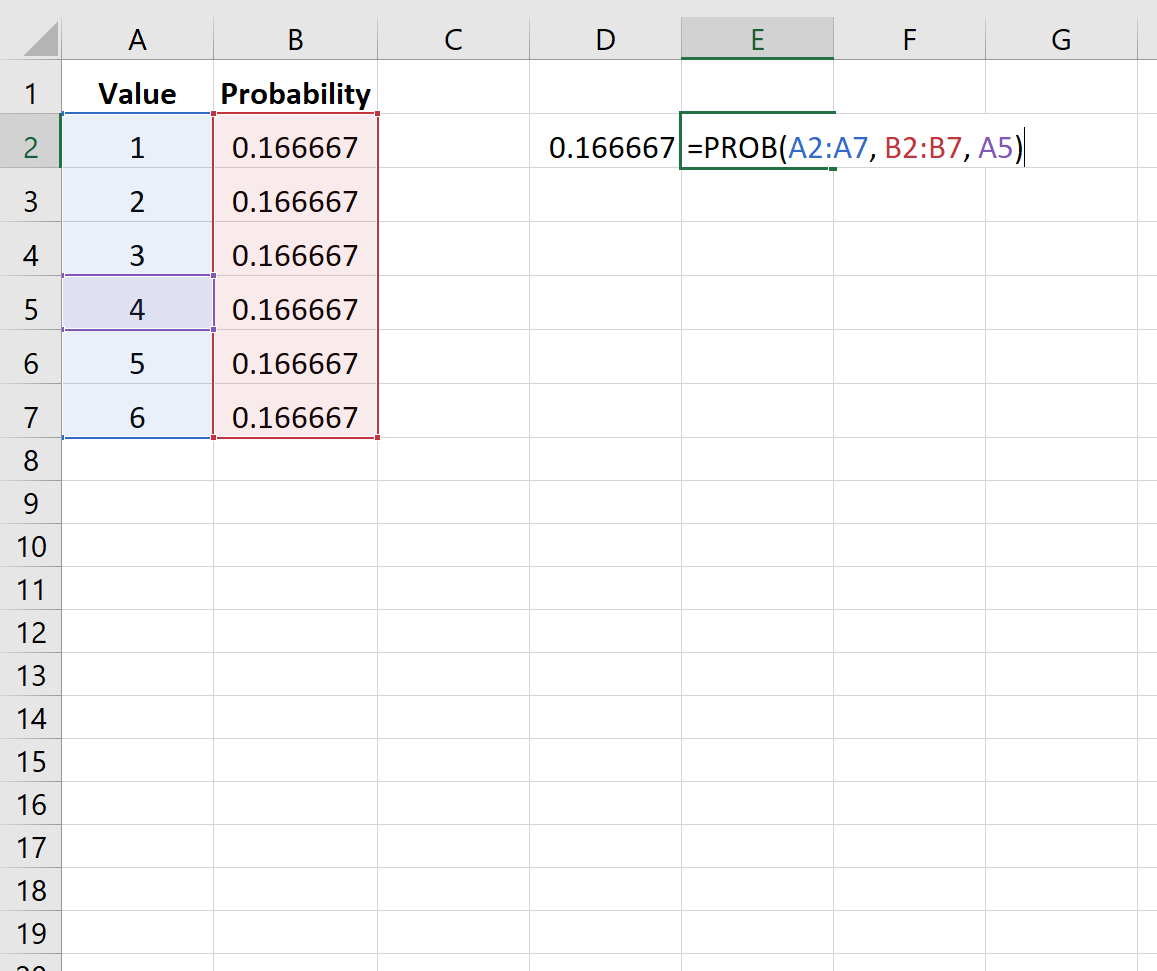
Вероятность оказывается равной 0,166667 .
Пример 2: Вероятность продаж
На следующем изображении показана вероятность того, что компания продаст определенное количество товаров в предстоящем квартале:

На следующем рисунке показано, как найти вероятность того, что компания совершит 3 или 4 продажи:
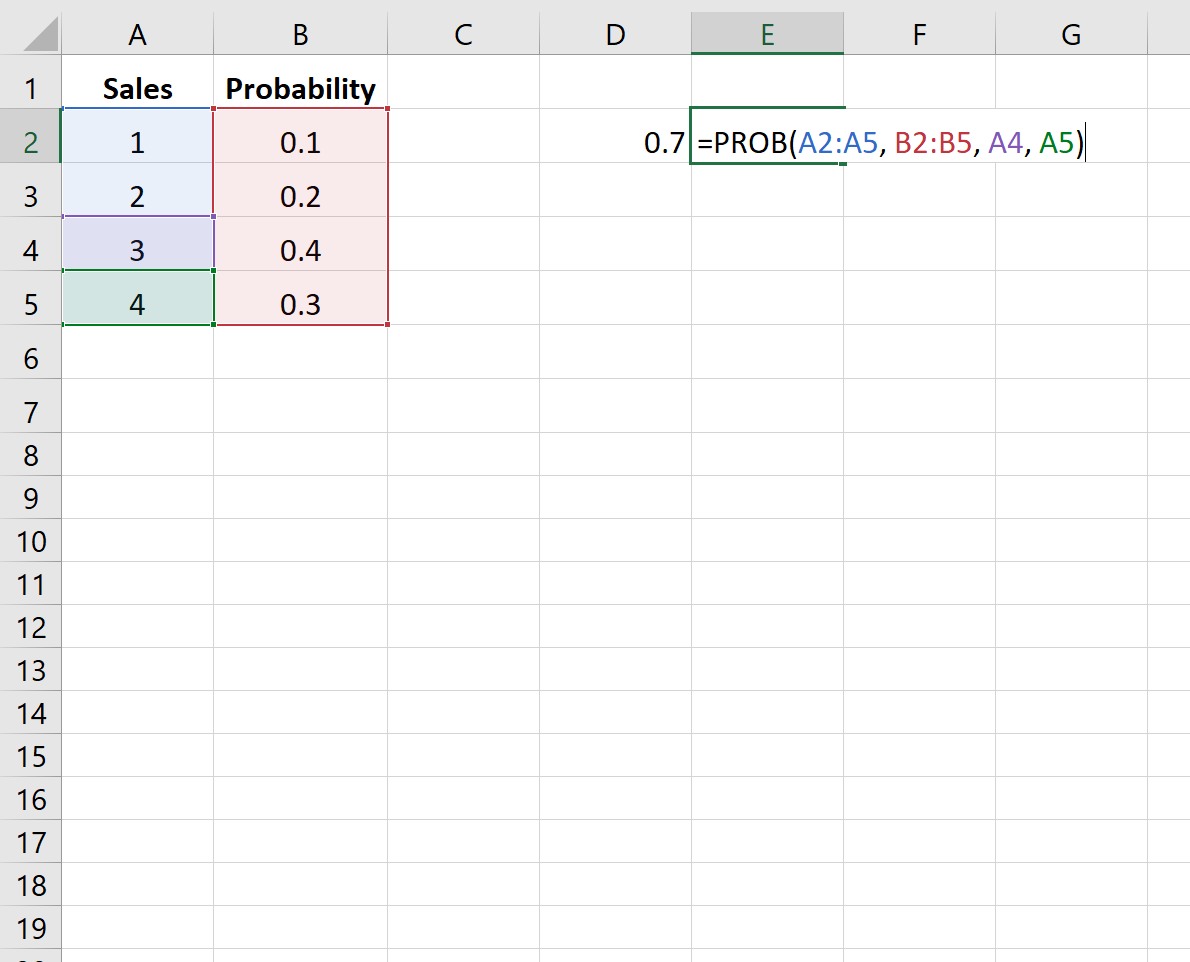
Вероятность оказывается равной 0,7 .
Дополнительные ресурсы
Как рассчитать относительную частоту в Excel
Как рассчитать кумулятивную частоту в Excel
Как создать частотное распределение в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Содержание:
Нормальный закон распределения:
Нормальный закон распределения имеет плотность вероятности
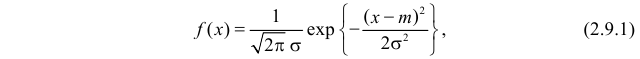
где 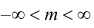
График функции плотности вероятности (2.9.1) имеет максимум в точке 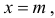 а точки перегиба отстоят от точки
а точки перегиба отстоят от точки  на расстояние
на расстояние 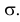 При
При 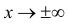 функция (2.9.1) асимптотически приближается к нулю (ее график изображен на рис. 2.9.1).
функция (2.9.1) асимптотически приближается к нулю (ее график изображен на рис. 2.9.1).
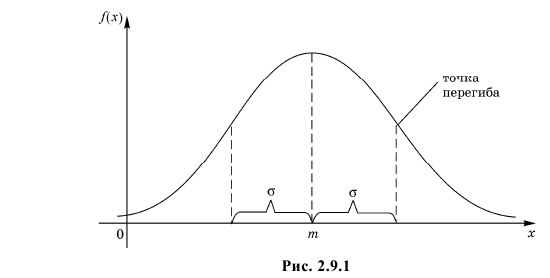
Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр  равен математическому ожиданию нормально распределенной случайной величины, а дисперсия
равен математическому ожиданию нормально распределенной случайной величины, а дисперсия 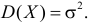 Если
Если 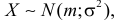 т.е. X имеет нормальный закон распределения с параметрами
т.е. X имеет нормальный закон распределения с параметрами  и
и 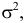 то
то 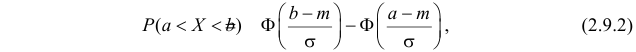
где 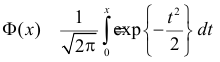 – функция Лапласа
– функция Лапласа
Значения функции 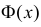 можно найти по таблице (см. прил., табл. П2). Функция Лапласа нечетна, т.е.
можно найти по таблице (см. прил., табл. П2). Функция Лапласа нечетна, т.е. 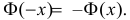 Поэтому ее таблица дана только для неотрицательных
Поэтому ее таблица дана только для неотрицательных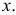 График функции Лапласа изображен на рис. 2.9.2. При значениях
График функции Лапласа изображен на рис. 2.9.2. При значениях 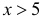 она практически остается постоянной. Поэтому в таблице даны значения функции только для
она практически остается постоянной. Поэтому в таблице даны значения функции только для 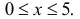 При значениях
При значениях 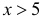 можно считать, что
можно считать, что 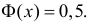
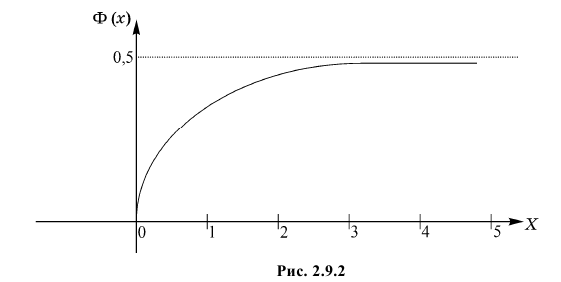
Если 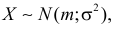 то
то
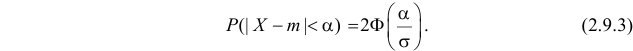
Пример:
Случайная величина X имеет нормальный закон распределения 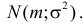 Известно, что
Известно, что 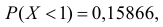 а
а 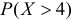
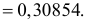 Найти значения параметров
Найти значения параметров 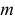 и
и 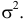
Решение. Воспользуемся формулой (2.9.2): 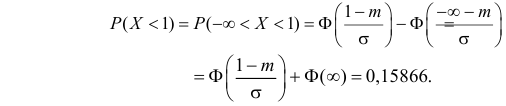
Так как 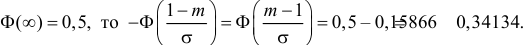 По таблице функции Лапласа (см. прил., табл. П2) находим, что
По таблице функции Лапласа (см. прил., табл. П2) находим, что 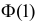
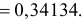 Поэтому
Поэтому 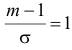 или
или 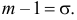
Аналогично 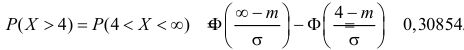 Так как
Так как 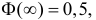 то
то 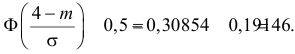 По таблице функции Лапласа (см. прил., табл. П2) находим, что
По таблице функции Лапласа (см. прил., табл. П2) находим, что 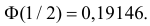 Поэтому
Поэтому 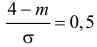 или
или 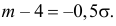 Из системы двух уравнений
Из системы двух уравнений 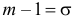 и
и 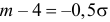 находим, что
находим, что 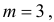 а
а 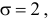 т.е.
т.е. 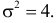 Итак, случайная величина X имеет нормальный закон распределения N(3;4).
Итак, случайная величина X имеет нормальный закон распределения N(3;4).
График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.
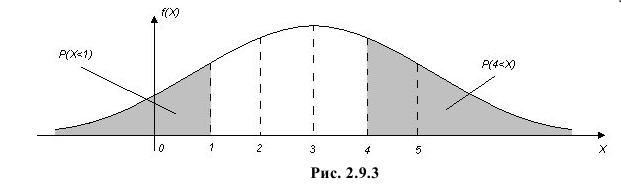
Ответ. 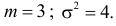
Пример:
Ошибка измерения X имеет нормальный закон распределения, причем систематическая ошибка равна 1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?
Решение. По условиям задачи 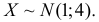 Вычислим сначала вероятность того, что в одном измерении ошибка не превзойдет 2 мк. По формуле (2.9.2)
Вычислим сначала вероятность того, что в одном измерении ошибка не превзойдет 2 мк. По формуле (2.9.2)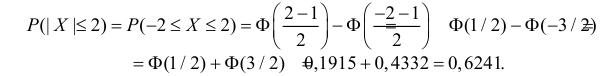
Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.
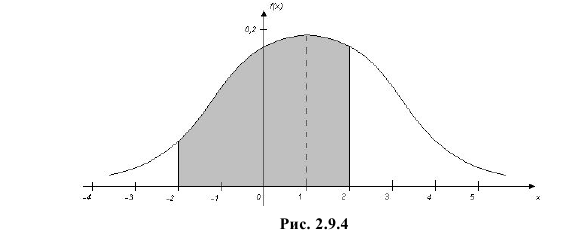
Каждое измерение можно рассматривать как независимый опыт. Поэтому по формуле Бернулли (2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна 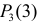
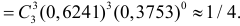
Ответ. 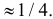
Пример:
Функция плотности вероятности случайной величины X имеет вид 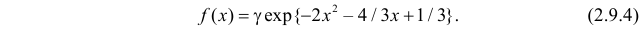
Требуется определить коэффициент 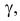 найти
найти 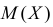 и
и 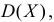 определить тип закона распределения, нарисовать график функции
определить тип закона распределения, нарисовать график функции 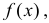 вычислить вероятность
вычислить вероятность 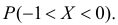
Замечание. Если каждый закон распределения из некоторого семейства законов распределения имеет функцию распределения , 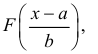 где
где 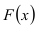 – фиксированная функция распределения, a
– фиксированная функция распределения, a 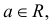
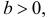 то говорят, что эти законы распределения принадлежат к одному виду или типу распределений. Параметр
то говорят, что эти законы распределения принадлежат к одному виду или типу распределений. Параметр 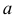 называют параметром сдвига,
называют параметром сдвига, 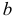 – параметром масштаба.
– параметром масштаба.
Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице: 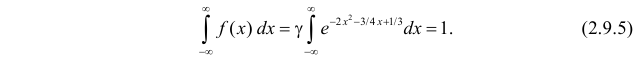
Преобразуем выражение в показателе степени, выделяя полный квадрат: 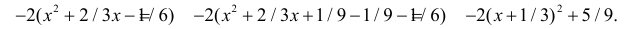
Тогда (2.9.5) можно записать в виде 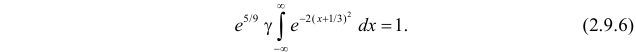
Сделаем замену переменных так, чтобы 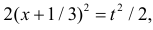 т.е.
т.е. 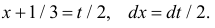 Пределы интегрирования при этом останутся прежними. Тогда (2.9.6) преобразуется к виду
Пределы интегрирования при этом останутся прежними. Тогда (2.9.6) преобразуется к виду

Умножим и разделим левую часть равенства на 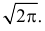 Получим равенство
Получим равенство 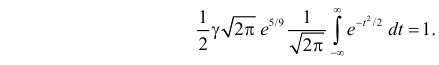
Так как 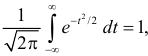 как интеграл по всей числовой оси от функции плотности вероятности стандартного нормального закона распределения N(0,1), то приходим к выводу, что
как интеграл по всей числовой оси от функции плотности вероятности стандартного нормального закона распределения N(0,1), то приходим к выводу, что

Поэтому
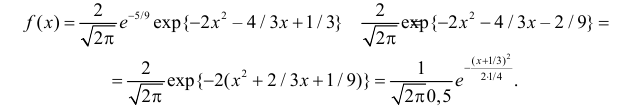
Последняя запись означает, что случайная величина имеет нормальный закон распределения с параметрами 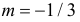 и
и 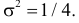 График функции плотности вероятности этого закона изображен на рис. 2.9.5. Распределение случайной величины X принадлежит к семейству нормальных законов распределения. По формуле (2.9.2)
График функции плотности вероятности этого закона изображен на рис. 2.9.5. Распределение случайной величины X принадлежит к семейству нормальных законов распределения. По формуле (2.9.2)
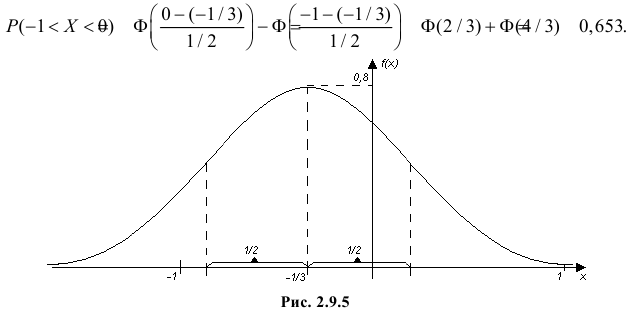
Ответ. 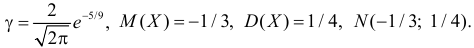
Пример:
Цех на заводе выпускает транзисторы с емкостью коллекторного перехода 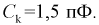 Сколько транзисторов попадет в группу
Сколько транзисторов попадет в группу 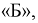 если в нее попадают транзисторы с емкостью коллекторного перехода от 1,80 до 2,00 пФ. Цех выпустил партию в 1000 штук.
если в нее попадают транзисторы с емкостью коллекторного перехода от 1,80 до 2,00 пФ. Цех выпустил партию в 1000 штук.
Решение.
Статистическими исследованиями в цеху установлено, что 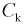 можно трактовать как случайную величину, подчиняющуюся нормальному закону.
можно трактовать как случайную величину, подчиняющуюся нормальному закону.
Чтобы вычислить количество транзисторов, попадающих в группу 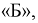 необходимо учитывать, что вся партия транзисторов имеет разброс параметров, накрывающий всю (условно говоря) числовую ось. То есть кривая Гаусса охватывает всю числовую ось, центр ее совпадает с
необходимо учитывать, что вся партия транзисторов имеет разброс параметров, накрывающий всю (условно говоря) числовую ось. То есть кривая Гаусса охватывает всю числовую ось, центр ее совпадает с 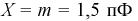 (т. к. все установки в цеху настроены на выпуск транзисторов именно с этой емкостью). Вероятность попадания отклонений параметров всех транзисторов на всю числовую ось равна 1. Поэтому нам необходимо фактически определить вероятность попадания случайной величины
(т. к. все установки в цеху настроены на выпуск транзисторов именно с этой емкостью). Вероятность попадания отклонений параметров всех транзисторов на всю числовую ось равна 1. Поэтому нам необходимо фактически определить вероятность попадания случайной величины 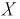 в интервал
в интервал 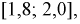 а затем пересчитать количество пропорциональной вероятности.
а затем пересчитать количество пропорциональной вероятности.
Для расчета этой вероятности надо построить математическую модель. Экспериментальные данные говорят о том, что нормальное распределение можно принять в качестве математической модели. Эмпирическая оценка (установлена статистическими исследованиями в цеху) среднего значения 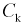
дает 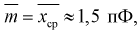 оценка среднего квадратического отклонения
оценка среднего квадратического отклонения 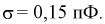
Обозначая 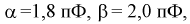 подставим приведенные значения в (6.3):
подставим приведенные значения в (6.3):
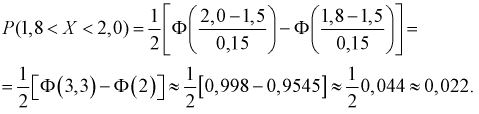
Тогда количество транзисторов 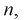 попавших в интервал [1,8; 2,0] пФ, можно найти так:
попавших в интервал [1,8; 2,0] пФ, можно найти так: 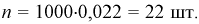 Таким образом можно планировать и рассчитывать количество транзисторов, попадающих в ту или иную группу.
Таким образом можно планировать и рассчитывать количество транзисторов, попадающих в ту или иную группу.
Нормальное распределение и его свойства
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста… Но не будем спешить, сначала посмотрим, как можно построить такой график.
Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, “от 180 до 181 включительно”.
После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если
Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:
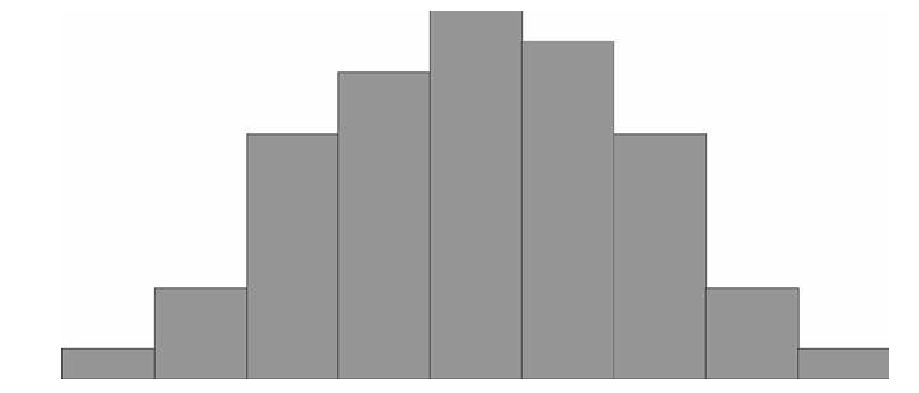
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, “оплывет” вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади “ломтика” кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста – достоверное событие. А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых, от величины такого диапазона – чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых, от того, насколько “популярен” выбранный нами рост. Напомним, что мода – самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения.
И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны.
Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной).
Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире. Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением. Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение 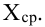 и отклонение s. Кроме того, любой житель города с вероятностью 68% попадет в диапазон роста
и отклонение s. Кроме того, любой житель города с вероятностью 68% попадет в диапазон роста 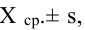 с вероятностью 95% – в диапазон
с вероятностью 95% – в диапазон 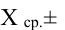
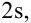 и с вероятностью 99,7% – в диапазон
и с вероятностью 99,7% – в диапазон 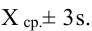
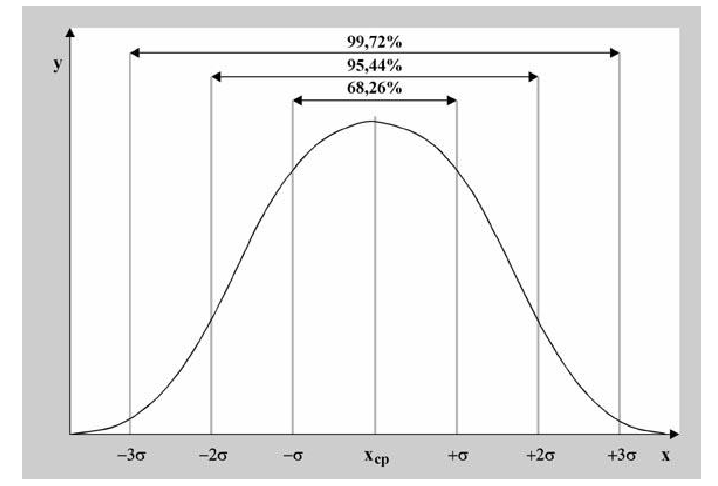
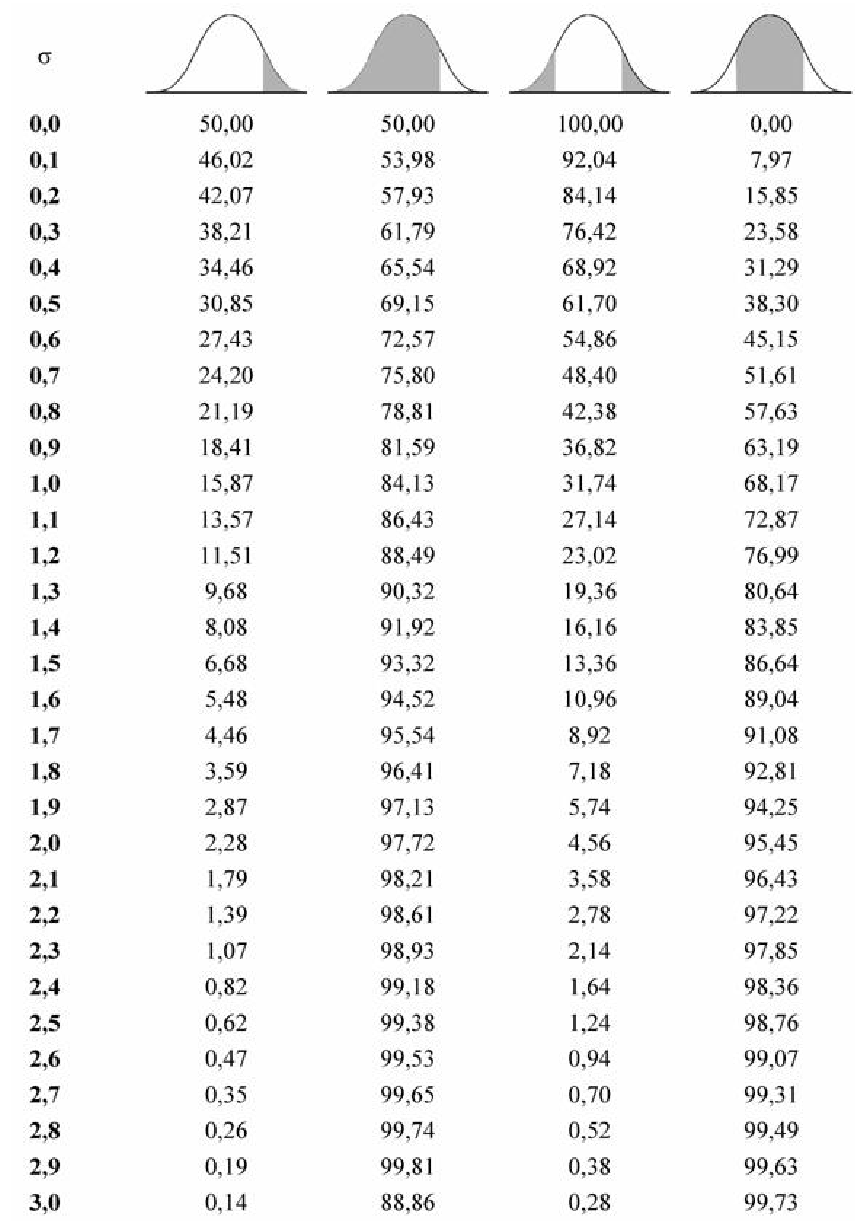
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный (заштрихованный) диапазон
Нормальный закон распределения
Нормальный закон распределения случайных величин, который иногда называют законом Гаусса или законом ошибок, занимает особое положение в теории вероятностей, так как 95 % изученных случайных величин подчиняются этому закону. Природа этих случайных величин такова, что их значение в проводимом эксперименте связано с проявлением огромного числа взаимно независимых случайных факторов, действие каждого из которых составляет малую долю их совокупного действия. Например, длина детали, изготавливаемой на станке с программным управлением, зависит от случайных колебаний резца в момент отрезания, от веса и толщины детали, ее формы и температуры, а также от других случайных факторов. По нормальному закону распределения изменяются рост и вес мужчин и женщин, дальность выстрела из орудия, ошибки различных измерений и другие случайные величины.
Определение: Случайная величина X называется нормальной, если она подчиняется нормальному закону распределения, т.е. ее плотность распределения задается формулой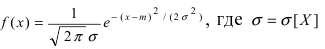 – средне-квадратичное отклонение, a m = М[Х] – математическое ожидание.
– средне-квадратичное отклонение, a m = М[Х] – математическое ожидание.
Приведенная дифференциальная функция распределения удовлетворяет всем свойствам плотности вероятности, проверим, например, свойство 4.:
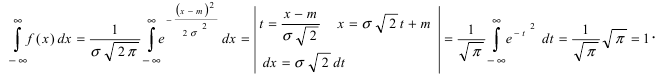
Выясним геометрический смысл параметров 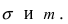 Зафиксируем параметр
Зафиксируем параметр 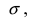 и будем изменять параметр m. Построим графики соответствующих кривых (Рис. 8).
и будем изменять параметр m. Построим графики соответствующих кривых (Рис. 8). 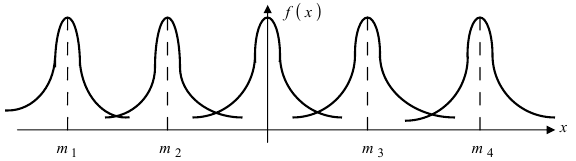
Рис. 8. Изменение графика плотности вероятности в зависимости от изменения математического ожидания при фиксированном значении средне-квадратичного отклонения. Из рисунка видно, кривая 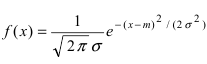 получается путем смещения кривой
получается путем смещения кривой 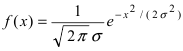 вдоль оси абсцисс на величину m, поэтому параметр m определяет центр тяжести данного распределения. Кроме того, из рисунка видно, что функция
вдоль оси абсцисс на величину m, поэтому параметр m определяет центр тяжести данного распределения. Кроме того, из рисунка видно, что функция 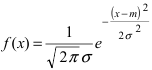 достигает своего максимального значения в точке
достигает своего максимального значения в точке 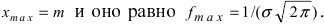 Из этой формулы видно, что при уменьшении параметра
Из этой формулы видно, что при уменьшении параметра 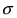 значение максимума возрастает. Так как площадь под кривой плотности распределения всегда равна 1, то с уменьшением параметра
значение максимума возрастает. Так как площадь под кривой плотности распределения всегда равна 1, то с уменьшением параметра 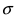 кривая вытягивается вдоль оси ординат, а с увеличением параметра
кривая вытягивается вдоль оси ординат, а с увеличением параметра 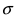 кривая прижимается к оси абсцисс. Построим график нормальной плотности распределения при m = 0 и разных значениях параметра
кривая прижимается к оси абсцисс. Построим график нормальной плотности распределения при m = 0 и разных значениях параметра 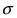 (Рис. 9):
(Рис. 9): 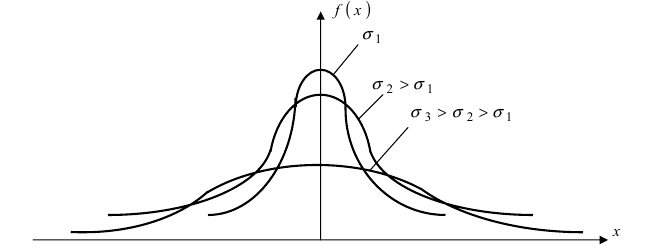
Рис. 9. Изменение графика плотности вероятности в зависимости от изменения средне-квадратичного отклонения при фиксированном значении математического ожидания.
Интегральная функция нормального распределения имеет вид: 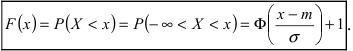
График функции распределения имеет вид (Рис. 10): 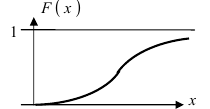
Рис. 10. Графика интегральной функции распределения нормальной случайной величины.
Вероятность попадания нормальной случайной величины в заданный интервал
Пусть требуется определить вероятность того, что нормальная случайная величина попадает в интервал 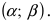 Согласно определению
Согласно определению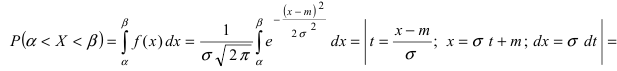 пересчитаем пределы интегрирования
пересчитаем пределы интегрирования 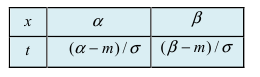
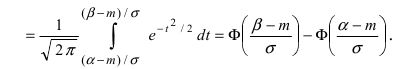 Следовательно,
Следовательно,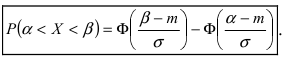
Рассмотрим основные свойства функции Лапласа Ф(х):
- Ф(0) = 0 – график функции Лапласа проходит через начало координат.
- Ф (-х) = – Ф(х) – функция Лапласа является нечетной функцией, поэтому
- таблицы для функции Лапласа приведены только для неотрицательных значений аргумента.
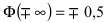 – график функции Лапласа имеет горизонтальные асимптоты
– график функции Лапласа имеет горизонтальные асимптоты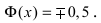
Следовательно, график функции Лапласа имеет вид (Рис. 11): 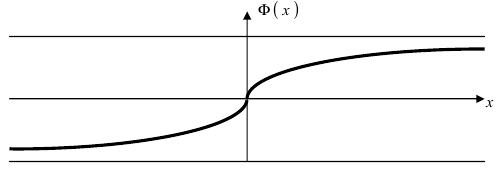
Рис. 11. График функции Лапласа.
Пример №1
Закон распределения нормальной случайной величины X имеет вид: 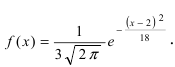 Определить вероятность попадания случайной величины X в интервал (-1;8).
Определить вероятность попадания случайной величины X в интервал (-1;8).
Решение:
Согласно условиям задачи 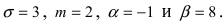 Поэтому искомая вероятность равна:
Поэтому искомая вероятность равна: 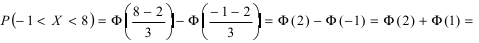 0,4772 + 0,3413 = 0,8185.
0,4772 + 0,3413 = 0,8185.
Вычисление вероятности заданного отклонения
Вычисление вероятности заданного отклонения. Правило 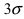 .
.
Если интервал, в который попадает нормальная случайная величина X, симметричен относительно математического ожидания 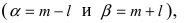 то, используя свойство нечетности функции Лапласа, получим
то, используя свойство нечетности функции Лапласа, получим
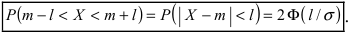
Данная формула показывает, что отклонение случайной величины Х от ее математического ожидания на заданную величину l равна удвоенному значению функции Лапласа от отношения / к среднему квадратичному отклонению. Если положить 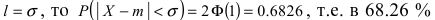 случаях нормальная случайная величина X отличается от своего математического ожидания на величину равную среднему квадратичному отклонению. Если
случаях нормальная случайная величина X отличается от своего математического ожидания на величину равную среднему квадратичному отклонению. Если 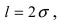 то вероятность отклонения равна
то вероятность отклонения равна 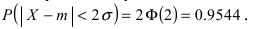 Наконец, в случае
Наконец, в случае 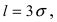 то вероятность отклонения равна
то вероятность отклонения равна 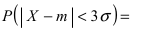
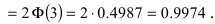 Из последнего равенства видно, что только приблизительно в 0.3 % случаях отклонение нормальной случайной величины X от своего математического ожидания превышает
Из последнего равенства видно, что только приблизительно в 0.3 % случаях отклонение нормальной случайной величины X от своего математического ожидания превышает 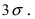 Это свойство нормальной случайной величины X называется правилом “трех сигм”. На практике это правило применяется следующим образом: если отклонение случайной величины X от своего математического ожидания не превышает
Это свойство нормальной случайной величины X называется правилом “трех сигм”. На практике это правило применяется следующим образом: если отклонение случайной величины X от своего математического ожидания не превышает 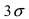 то эта случайная величина распределена по нормальному закону.
то эта случайная величина распределена по нормальному закону.
Показательный закон распределения
Определение: Закон распределения, определяемый фу нкцией распределения:
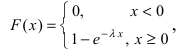 называется экспоненциальным или показательным.
называется экспоненциальным или показательным.
График экспоненциального закона распределения имеет вид (Рис. 12): 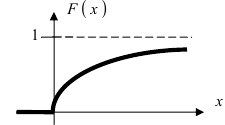
Рис. 12. График функции распределения для случая экспоненциального закона.
Дифференциальная функция распределения (плотность вероятности) имеет вид: 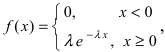 а ее график показан на (Рис. 13):
а ее график показан на (Рис. 13): 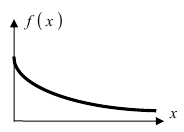
Рис. 13. График плотности вероятности для случая экспоненциального закона.
Пример №2
Случайная величина X подчиняется дифференциальной функции распределения 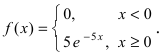 Найти вероятность того, что случайная величина X попадет в интервал (2; 4), математическое ожидание M[Х], дисперсию D[X] и среднее квадратичное отклонение
Найти вероятность того, что случайная величина X попадет в интервал (2; 4), математическое ожидание M[Х], дисперсию D[X] и среднее квадратичное отклонение 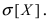 Проверить выполнение правила “трех сигм” для показательного распределения.
Проверить выполнение правила “трех сигм” для показательного распределения.
Решение:
Интегральная функция распределения 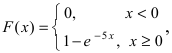 следовательно, вероятность того, что случайная величина X попадет в интервал (2; 4), равна:
следовательно, вероятность того, что случайная величина X попадет в интервал (2; 4), равна: 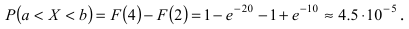 Математическое ожидание
Математическое ожидание 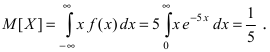 Вычислим значение величины М
Вычислим значение величины М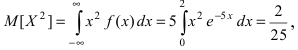 тогда дисперсия случайной величины X равна
тогда дисперсия случайной величины X равна 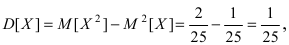 а средне-квадратичное
а средне-квадратичное
отклонение 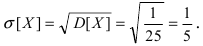 Для проверки правила “трех сигм” вычислим вероятность заданного отклонения:
Для проверки правила “трех сигм” вычислим вероятность заданного отклонения:
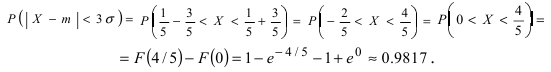
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин

