Ожидаемая продолжительность жизни: что это такое?
В бурных обсуждениях повышения пенсионного возраста часто фигурирует вроде бы понятное и в то же время странное понятие — «ожидаемая продолжительность жизни«. Это стандартный и общепринятый демографический показатель, но который довольно сложно воспринимать и часто его воспринимают неправильно.
К примеру, если ожидаемая продолжительность жизни для российских мужчин составляет 67,5 лет, а возраст выхода на пенсию — 65 лет, то наивно можно предположить, что ожидаемое время жизни на пенсии равно 2,5 годам (67,5 — 65), но такой расчет будет неверным. Правильная цифра ожидаемой продолжительности жизни для мужчины 65 лет составит 13,9 лет. Честно признаюсь: до недавнего времени сам не до конца ясно понимал, как делаются подобные расчеты, сейчас разобрался и готов объяснить.
Давайте сначала посмотрим на официальные данные Росстата по показателю ожидаемой продолжительности жизни. Все графики будем приводить отдельно для мужчин и для женщин, так как между ними существуют очень большие различия.
В 2017 году ожидаемая продолжительность жизни для мужчин, по данным Росстата, составляла 67,51 лет и для женщин — 77,64 года. Что это вообще означает и как рассчитывается?
Все начинается со смертности
Это может показаться странным, но единственными исходными данными, которые необходимы для расчета ожидаемой продолжительности жизни являются так называемые «возрастные коэффициенты смертности«. Фактически это таблица, в которой указана доля умерших (обычно — за год) от общего количества людей, которые находились в данной возрастной группе. Вот к примеру, возрастные коэффициенты смертности за 2016 год:
В самой левой части графики возрастной коэффициент для мужчин в возрасте «0» (то есть, родившихся) составляет 6,6 человек. Это означает, что в 2016 году на 1000 родившихся младенцев мужского пола в течение первого года жизни умерло 6,6 человек. Для младенцев женского пола показатель равен 5,4 человека. И так далее. К сожалению, Росстат в стандартном виде представляет данные не по единичным годам, а по пятилеткам — группа «5-10 лет», группа «10-14», группа «15-19» лет и так далее. Видно, что возрастные коэффициенты довольно низкие в возрасте с 1 года до примерно 30 лет, затем начинают постепенно увеличиваться. Причем во всех возрастных группах мужчин в среднем умирает больше, чем женщин. . Это интересный вопрос, почему такое наблюдается. Ученые считают, что помимо социальных (вредные привычки, рискованное поведение и проч.), существуют биологические причины, почему женщины живут дольше, чем мужчины
Вероятность дожития
На основе коэффициентов смертности мы можем посчитать вероятность дожития — вероятность того, что если человек вступил в определенную возрастную группу, то он доживет до ее границы. Если человек вступил в возрастную группу, то вероятность дожить до конца срока этой возрастной группы составляет (100% — коэффициент смертности).
Обратите внимание: мы предполагаем, что показатели смертности останутся неизменными в течение всего рассматриваемого период, хотя фактически берутся данные только за один определенный год.
Рассмотрим пример. Для тех же младенцев мужского пола вероятность дожития с 0 до 1 года составляет 99,34% (100% — 6,6/1000), для женщин — 99,46% (100%- 5,4/100). Мы считаем, что общее количество родившихся равно 100%.
Возьмем следующую возрастную группу — «1-4 год». Коэффициент смертности для мужчин равен 0,4, значит вероятность дожития в этой возрастной группе — 99,96% (100% — 0,4/1000). В данном случае мы считаем, что 100% — это те, младенцы, которые были живы к первому году жизни. Если необходимо посчитать вероятность вновь родившегося младенца дожить до 5 лет, то нам необходимо перемножить две вероятности дожития — «до 1 год» и «от 1 до 4%, то есть 99,34% * 99,96% = 99,30%. Так можно итеративно продолжать по следующим возрастным группам. Чтобы перейти в следующую возрастную группу, человеку необходимо дожить до возраста ее начала.
Разумеется, если имеются данные коэффициентов смертности по отдельным годам, то аналогичным образом вероятность дожития можно посчитать точнее, чем если использовать 5-летние когорты. К счастью, Центр демографических исследований РЭШ предоставляет однолетние возрастные коэффициенты смертности, на основе которых мы рассчитаем накопленные вероятности дожития. . Первоисточником этих данных тоже является Росстат. Но сотрудники РЭШ «добыли» эти данные и предоставили их для анализа в удобном виде.
К примеру, на графике (можно навести на него мышкой, чтобы увидеть количественные значения) видно, что для младенцев мужского пола 2017 года рождения вероятность дожить до 65 лет составляет 62% (84% — для женского пола) при условии, что все возрастные коэффициенты смертности останутся на уровне 2017 года в течение жизни этого младенца.
Ожидаемая продолжительность жизни — это некоторый статистический конструкт, который отражает просто текущие показатели смертности в одной цифре. Конечно можно было бы подсчитать подобные вероятности точно. Но для этого надо подождать лет 100 для того, чтобы дождаться пока, все (или почти все) люди 2017 года рождения не умрут. Так как этого сделать сейчас невозможно, то демографы используют подобные вычисления, основанные на допущениях. Конечно можно ожидать, что в будущем коэффициенты смертности будут снижаться, и это приведет к росту фактической средней продолжительности жизни. Однако для этого тоже надо делать допущения относительно того, как будут изменяться коэффициенты смертности в будущем. Эти допущения также будут субъективными. Поэтому оценки вероятность дожить до определенного возраста, рассчитанные на текущих коэффициентах смертности, представляют собой скорее нижнюю оценку вероятности.
Если же мы сохраним подобные консервативные допущения («в будущем коэффициенты смертности не улучшатся и останутся на уровне 2017 года»), то можно рассчитать вероятность дожития до возраста Y, начиная с любого возраста X, последовательно перемножая коэффициенты дожития.
Ожидаемая же продолжительность жизни рассчитывается как произведение двух векторов: 1) разницы в накопленных вероятностях дожития по возрастам 2) вектор возрастов (в нашем случае от 0 до 100 лет). Для особо любопытных — ссылка на лист Excel, в котором показан расчет.
Для примера я использовал данные РЭШ и рассчитал ожидаемую продолжительность жизни для мужчин в 2017 году. Получилось 67,80 лет. Это немного не совпадает с показателем Росстата (67,51), но достаточно точно. Исходя из процедуры расчета становится понятно, что не обязательно начинать расчет с 0 лет. Начинать можно с произвольного возраста X и рассчитать ожидаемую продолжительность жизни в возрасте X. Логика остается той же самой. Берем разницу накопленных векторов дожития и перемножаем с вектором лет (в данным случае вектор начинается с 0 в возрасте X). Таким образом мы получаем взвешенную по коэффициентам смертности последующих лет ожидаемую продолжительность жизни в возрасте X.
Какова моя вероятность дожить до Y лет? Какова ожидаемая продолжительность жизни в возрасте X?
Возможно, все это звучит слишком сложно и технично. Чтобы было максимально понятно и интересно, мы сделали калькулятор, который позволяет рассчитать ожидаемую продолжительность жизни, начиная с любого возраста и вероятность дожить от возраста X до возраста Y. Мы использовали коэффициенты смертности, которые отличаются в зависимости от пола и региона проживания. Регион проживания также важен, так как существуют большие отличия в показателях смертности между субъектами РФ. Разница в ожидаемой продолжительности жизни между лучшими по этому показателями регионами (Северный Кавказ, Москва) и худшими (некоторые регионы Сибири и Дальнего Востока) достигает 12-15 лет.
Калькулятор ожидаемой продолжительности жизни и вероятности дожития
доступен здесь или здесь (в полном экране)

К примеру, если вы мужчина в возрасте 35 лет, проживающий в Москве, то вероятность дожить до 65 лет (планируемый стандартный возраст выхода на пенсию) составляет 75,3% (для женщин — 89,1%). Ожидаемая продолжительность жизни в этом возрасте составляет 42,7 лет (для женщин — 47,8 лет). Можно посмотреть любые другие сочетание возрастов и регионов проживания.
Имеются следующие данные о возрастных коэффициентах смертности:
для детей, в возрасте до одного года – 26,2‰ (К0),
для детей, достигших возраста один год – 6,5‰ (К1),
для детей, достигших возраста два года – 4,0‰ (К2),
для детей, достигших возраста три года – 2,5‰ (К3),
для детей, достигших возраста четыре года – 0,6‰ (К4).
Сумма предстоящих человеко-лет жизни для совокупности родившихся (10 тыс. чел.) составляет 636 600.
Составьте таблицу смертности для данных возрастных групп и определите среднюю ожидаемую продолжительность предстоящей жизни для возраста 0, 1, 2, 3 и 4 года.
Решение:
Таблицы смертности и средней продолжительности жизни, таблицы дожития – система взаимосвязанных упорядоченных по возрасту рядов чисел, организованных как описание процесса уменьшения с возрастом под действием смертности некоторого абстрактного поколения с фиксированной начальной численностью, именуемой корнем таблицы.
Макет таблицы смертности имеет вид:
| Возраст, лет | Число доживших до возраста х, лет | Вероятность дожить до следующего возраста | Вероятность смерти в течение года | Число живущих в возрасте х | Предстоящее число чел.-лет жизни | Средняя продолжительность предстоящей жизни | Коэффициент дожития |
|---|---|---|---|---|---|---|---|
| х | lx | px | qx | Lx | Tx | ex0 | Px |
В нашей задаче численность поколения условно равна 10 000 чел.
На основе возрастных коэффициентов смертности можно определить вероятность смерти в течение года для каждого года жизни (qх):
q0 = 0,0262
q1 = 0,0065
q2 = 0,0040
q3 = 0,0025
q4 = 0,0006
Затем определим вероятность дожития от возраста х до возраста х + 1 (рх):
p0 = 1 – q0 = 1 – 0,0262 = 0,9738
p1 = 1 – q1 = 1 – 0,0065 = 0,9935
p2 = 1 – q2 = 1 – 0,0040 = 0,9960
p3 = 1 – q3 = 1 – 0,0025 = 0,9975
p4 = 1 – q4 = 1 – 0,0006 = 0,9994
Теперь рассчитаем число доживающих до возраста х (lx) :
l0 = 10 000 (по условию)
l1 = l0 × p0 = 10 000 × 0,9738 = 9 738
l2 = l1 × p1 = 9 738 × 0,9935 = 9 675
l3 = l2 × p2 = 9 675 × 0,9960 = 9 636
l4 = l3 × p3 = 9 636 × 0,9975 = 9 612
l5 = l4 × p4 = 9 612 × 0,9994 = 9 606
Найдём число живущих в возрасте х лет (Lх), представляющее собой среднюю арифметическую из числа доживающих до возраста х и до возраста х + 1:
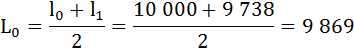
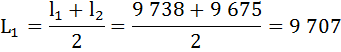
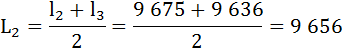
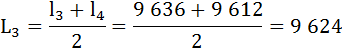
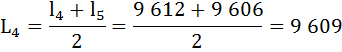
Определим число предстоящих человеко-лет жизни (Тх) для разных возрастов.
По условию задания
Т0 = 636 600
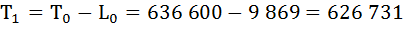
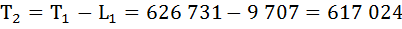
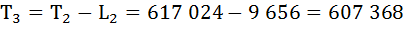
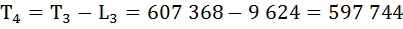
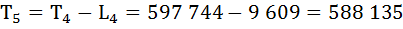
Рассчитаем среднюю продолжительность предстоящей жизни населения по формуле:
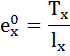
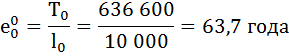
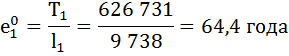
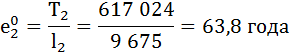
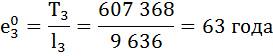
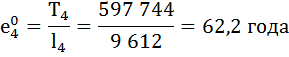
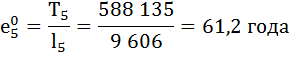
Коэффициент передвижки Px – вероятность для индивидуума в интервале возраста от х до х+1 прожить 1 год и попасть в интервал от х+1 до х+2 – определяется по формуле:
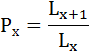
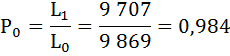
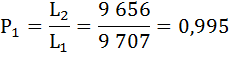
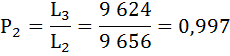
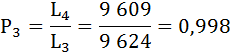
Полученные результаты занесём в таблицу:
| х | lx | px | qx | Lx | Tx | e0x | Px |
|---|---|---|---|---|---|---|---|
| 0 | 10 000 | 0,9738 | 0,0262 | 9 869 | 636 600 | 63,7 | 0,984 |
| 1 | 9 738 | 0,9935 | 0,0065 | 9 707 | 626 731 | 64,4 | 0,995 |
| 2 | 9 675 | 0,9960 | 0,0040 | 9 656 | 617 024 | 63,8 | 0,997 |
| 3 | 9 636 | 0,9975 | 0,0025 | 9 624 | 607 368 | 63 | 0,998 |
| 4 | 9 612 | 0,9994 | 0,0006 | 9 609 | 597 744 | 62,2 | – |
| 5 | – | – | – | – | 588 135 | 61,2 | – |
| – | – | – | – | – | – | – | – |
| 100 | – | – | – | – | – | – | – |
| 636 600 |
Условие задачи взято из: Социально-экономическая статистика: Практикум/Под ред. В. Н. Салина, Е. П. Шпаковской: Учеб. пособие. – М.:Финансы и статистика, 2003. – 192 с.

Утверждение теоремы непосредственно следует из определения условной вероятности и допускает распространение на случай большего числа сомножителей:
P( A1A2A3…Ak )=P A1 ·P A2 /A1 ·P A3 /A2A1 ·…·P Ak /Ak –1…A3A2A1 .
Пример 4.1 Вероятность дожить человеку до 20 лет равна 0,96; вероятность дожить человеку до 60 лет равна 0,69. Какова вероятность дожить до 60 лет человеку 20 – летнего возраста?
Решение: Обозначим через «0–20» – событие, состоящее в том, что родившийся человек доживет до 20-ти лет; «0–60» – родившийся человек доживет до 60-ти лет; «20–60» – двадцатилетний доживет до 60 лет (разумеется, при условии, что до 20-ти лет он дожил). По условию:
0,96=P(«0–20»); 0,69=P(«0–60»)=P(«0–20» «20–60»).
Тогда вероятность дожить до 60 лет человеку 20 – летнего возраста определяется как условная вероятность:
|
P «0 |
– 60» |
0,69 |
|||
|
P(«20–60»/«0–20»)= |
=0,719. |
||||
|
P «0 |
– 20» |
0,96 |
■
Пример 4.2 Слово «лотос», составленное из букв – кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наудачу извлекаются одна за другой три буквы. Какова вероятность того, что при этом появится слово «сто»?
Решение: Введем обозначения для событий: A1 – первой извлечена буква «с»; A2 – второй извлечена буква «т»; A3 – третьей извлечена буква «о»; А – получилось слово «сто». Очевидно, A A1A2A3 . Тогда:
P A P A1 ·P A2 /A1 ·P A3 /A2A1 51 ·41 ·23 301 .
■
Если появление события А не зависит от того, произошло или нет событие В, то условная вероятность А в предположении, что событие В
41

наступило, будет равна вероятности А, т.е. P(A/B)=P(A). Подставляя в формулу умножения вероятностей вместо P(A/B) вероятность P(A), получим: P(AB)=P(A)·P(B).
Если это соотношение выполняется, то события А и В называются независимыми.
Утверждение 1. Пусть события А и В – независимы. Тогда независимы также события A и В, А и B , A и B .
Пример 4.3 Известно, что P(A)=0,6; P( A B )=0,8; P( A B )=0,5. Найти
P(B), P(A/B), P(B/A) и выяснить, зависимы ли события A и B? Решение: Используя расширенную формулу сложения:
P( A B )=P(A)+ P(B) – P( A B ), можно найти вероятность события B:
P(B)= P( A B )+P( A B ) – P(A)=0,8+0,5–0,6=0,7.
|
Далее |
по |
формуле для условной вероятности |
имеем: P(A/B)= |
||||||||||
|
P A B |
0,5 |
5 |
≈0,714; P(B/A)= |
P A B |
0,5 |
5 |
≈0,833. |
||||||
|
P B |
0,7 |
7 |
P A |
0,6 |
6 |
Поскольку P( A B )=0,5 и P(A)·P(B)=0,6·0,7=0,42, то
P( A B )≠P(A)·P(B); следовательно, события A и B – зависимы.
■
Несколько событий называют попарно независимыми, если каждые два из них независимы.
Несколько событий называют независимыми в совокупности,
если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Отметим, что требование независимости событий в совокупности сильнее требования их попарной независимости.
Утверждение 2. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
P A1A2…Ak P A1 ·P A2 · …· P Ak .
42

A1 , A2 ,…, Ak
Если события A1 , A2 ,…, Ak – независимы в совокупности, то и противоположные им события A1 , A2 ,…, Ak также независимы в совокупности.
Теорема 2. Вероятность появления хотя бы одного из событий A1 , A2
,…, Ak , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий:
P A 1– P A1 ·P A2 ·…· P Ak .
Следствие. Если события имеют одинаковую
вероятность, равную p, то вероятность появления хотя бы одного из этих событий P A =1–qk , где q=1-p.
Пример 4.4 По одной и той же мишени стреляют одновременно двое. Вероятность попадания для первого стрелка равна 0,7; для второго – 0,6. Определить вероятность поражения цели.
Решение: Данную задачу можно решить тремя способами, приведем каждый из них. Введем обозначения: A1 – событие, состоящее в том, что первый стрелок попал в цель; A2 – второй попал; А – цель поражена.
1) P A P( A1A2 A1A2 A1A2 ) =P A1A2 P A1A2 P A1A2
несовместн ые события
=P A1 P A2 P A1 P A2 P A1 P A2 0,7·0,6+0,3·0,6+0,7·0,4= =0,42+0,18+0,28=0,88.
|
P A P |
=P A |
P A |
– P A A =0,7+0,6–0,7·0,6= |
||||
|
2) |
A A |
||||||
|
1 2 |
1 |
2 |
1 2 |
||||
|
совместные |
=1,3–0,42=0,88.
3) P A 1–P A1 P A2 1–0,3·0,4=1–0,12=0,88.
■
Пример 4.5 На связке 5 ключей. К замку подходит только один ключ. Найти вероятность того, что: а) потребуется не более двух попыток
43

открыть замок, если опробованный ключ в дальнейших испытаниях не участвует; б) нужный ключ окажется последним.
Решение: а) Обозначим через: A событие – «потребуется не более двух попыток»; 1 – «первая попытка успешна»; 1 ·2 – «с первой попытки замок не открылся, а со второй – открылся». Тогда:
P(A)= P(1+ 1 ·2)=P(1)+ P( 1 ·2)= P(1)+ P( 1 )·P(2 / 1 )= 51 54 · 41 = 52 =0,4.
б) Событие «нужный ключ окажется последним» означает, что первый ключ не подошел, и второй ключ замок не открыл, …, четвертый ключ не подошел, а пятому – «уже деваться некуда» ( 1 · 2 · 3 · 4 ·5). Представляя данное событие в виде произведения зависимых событий, получим:
P( 1 · 2 · 3 · 4 ·5)= P ( 1 )·P( 2 / 1 )·P( 3 / 1 2 )·P( 4 / 1 23 )·P(5/ 1 234 )= = 54 · 34 · 23 · 21 ·1= 51 =0,2.
■
Пример 4.6 Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,8.
Решение: Обозначим через Аi – событие, состоящее в том, что i–ая бомба достигла цели; соответственно через Ai – противоположное событие (бомба пролетела мимо). Разрушение моста означает, что хотя бы одна бомба достигнет цели. События A1 , A2 , A3 , A4 – независимы,
следовательно, независимыми будут и противоположные им события. Поэтому искомая вероятность равна:
P A 1– P A1 P A2 P A3 P A4 1-(1–0,3)(1–0,4)(1–0,6)(1–0,8)=0,9664.
■
Теорема 3. Если событие A может произойти только при условии появления одного из событий (гипотез) B1 , B2 , …,Bn , образующих полную группу, то вероятность события A равна сумме произведений
44
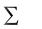
вероятностей каждого из этих событий (гипотез) на соответствующие условные вероятности события A:
n
P(A) P(Bi ) P(A / Bi ).
i 1
Указанная формула называется формулой полной вероятности.
Пример 4.7 В коробку побросали n шариков, закрыли ее и хорошенько потрясли. Затем добавили один белый шар, перемешали все шары и наудачу извлекли один шар. Определить вероятность того, что извлеченный шар – белый, если все гипотезы о первоначальном составе шаров – равновероятны?
Решение: Обозначим через Bi – гипотезу, состоящую в том, что
|
первоначально в коробке |
было i |
белых шаров, |
по условию: |
|||||
|
P B |
P B |
… P B |
1 |
. Так как все события |
B |
,B |
, …,B – |
|
|
0 |
1 |
n |
n 1 |
0 |
1 |
n |
||
попарно несовместны, то, после добавления одного белого шара, вероятность извлечения белого шара определяем по формуле полной вероятности:
|
P A P B P A / B … P B |
P A / B |
1 |
( |
1 |
2 |
… 1) |
|||||||||||
|
0 |
0 |
n |
n |
n 1 |
n 1 |
n 1 |
|||||||||||
|
1 |
· |
1 n 1 |
· (n 1) |
n 2 |
. |
||||||||||||
|
n 1 |
2(n 1) |
2(n 1) |
|||||||||||||||
■
В тесной связи с формулой полной вероятности находится так называемая формула Байеса. Она относится к той же ситуации, что и формула полной вероятности (событие A может наступить только вместе с одним из n попарно несовместных событий B1 ,B2 , …,Bn ).
Допустим, что опыт уже произведен, и нам известно, что событие A наступило. Сам по себе этот факт еще не позволяет сказать, какое из событий B1 , B2 , …,Bn имело место в проделанном опыте. Можно,
45

однако, поставить такую задачу: найти вероятности P B1 / A , …,
P Bn / A каждой из гипотез в предположении, что наступило событие A
(такие вероятности называются апостериорными в отличие от вероятностей P(B1 ) , …,P(Bn ) , вычисляемых до опыта и называемых
априорными).
С одной стороны, вероятность совмещения двух зависимых событий определяется по формуле: P(ABi ) P(A / Bi ) P(Bi ) , а с другой стороны, имеем: P(Bi A) P(Bi / A) P(A) . Приравнивая правые части, получим: P(Bi / A) P(A) P(A / Bi ) P(Bi ) , откуда следует:
P(Bi / A) P(A / Bi ) P(Bi ) ,
P A
где знаменатель рассчитывается по формуле полной вероятности. Таким образом, апостериорная вероятность определяется по формуле:
|
P(Bi / A) |
P(A / Bi ) P(Bi ) |
, |
|
n |
||
|
P(A / Bi ) P(Bi ) |
||
|
i 1 |
которая называется формулой Байеса. Запомнить ее нетрудно: в знаменателе стоит выражение для полной вероятности события A, а в числителе – одно из слагаемых этого выражения. Формула Байеса дает возможность «пересмотреть» вероятности гипотез с учетом наблюдавшегося результата опыта.
Пример 4.8 Известно, что 5% мужчин и 0,2% женщин – дальтоники. Какова доля мужчин среди дальтоников?
Решение: Обозначим событие, состоящее в том, что выбранный наудачу человек оказался: дальтоником через D; женщиной – F; мужчиной – M. По условию: P(D/M)=0,05 и P(D/F)=0,002. Требуется найти вероятность того, что выбранный наудачу дальтоник оказался
P M ·P D/M
мужчиной P(M/D). По формуле Байеса: P(M/D)= ,
P D
46

где знаменатель вычисляется по формуле полной вероятности:
P D P M ·P D/M P F ·P D/F = 21 ·0,05+ 21 ·0,002=0,026.
1·0,05
Тогда искомая вероятность будет равна: P(M/D)= 20,026 =0,96, т.е.
среди дальтоников 96% мужчин.
■
Пример 4.9 Страховая компания разделяет застрахованных по группам риска: малый риск, средний риск и высокий риск. Среди этих клиентов 50% относятся к группе малого риска, 30% – к группе среднего риска и 20% – к группе высокого риска. Вероятность необходимости выплачивать страховую выплату для клиентов первой группы равна 0,01; для второй группы – 0,04 и для третьей – 0,09. Какова вероятность того, что:
а) клиент получит страховую выплату за период страхования; б) получивший страховую выплату клиент относится к группе малого риска?
Решение: Обозначим событие, состоящее в том, что клиент относится к i–ой группе риска через Bi ; событие, состоящее в том, что клиент получит страховую выплату за период страхования – А. По условию:
P B1 0,5 ; P B2 0,3; P B3 0,2 .
Вероятности страховых выплат для клиентов каждой группы – это апостериорные вероятности гипотез B1 , B2 и B3 :
P(A/B1 )=0,01; P(A/B2 )=0,04 и P(A/B3 )=0,09.
а) Вероятность получения клиентом страховой выплаты за период страхования вычисляется по формуле полной вероятности:
P A P B1 P A/B1 P B2 P A/B2 P B3 P A/B3 .
P A =0,5·0,01+0,3·0,04+0,2·0,09=0,035.
47
б) Так как клиент уже получил страховую выплату, значит, речь идет об апостериорной вероятности, которую вычисляют по формуле Байеса:
|
P B /A |
P B1 P A/B1 |
0,5·0,01 |
≈0,143. |
|
|
P A |
||||
|
1 |
0,035 |
|||
|
■ |
Пример 4.10 При обследовании больного имеется подозрение на одно из двух заболеваний B1 и B2 . Их вероятности в данных условиях:
P B1 0,6 и P B2 0,4 . Для уточнения диагноза назначается анализ,
результатом которого является положительная или отрицательная реакция. В случае болезни B1 вероятность положительной реакции равна 0,9, отрицательной – 0,1; в случае B2 положительная и отрицательная реакции равновероятны. Анализ произвели дважды, и оба раза реакция оказалась отрицательной (событие A). Найдите вероятность каждого заболевания после проделанных анализов.
|
Решение: В случае заболевания |
B1 |
событие |
A происходит с |
||||||||||
|
вероятностью 0,1·0,1=0,01, а в случае заболевания B2 – с вероятностью |
|||||||||||||
|
0,5·0,5=0,25. |
Следовательно, по |
формуле |
Байеса имеем: |
||||||||||
|
P B1 |
/ A |
P A / B1 P B1 |
0,01 0,6 |
≈0,06; |
|||||||||
|
P A / B1 P B1 P A / B2 P B2 |
0,01 0,6 0,25 0,4 |
||||||||||||
|
P B2 |
/ A |
0,25·0,4 |
≈0,94. |
■ |
|||||||||
|
0,01 |
0,6 0,25 |
0,4 |
|||||||||||
Задачи для самостоятельного решения:
4.1Известно, что P(A)>0,5; P(B)>0,8. Могут ли такие события A и B: а) быть несовместными; б) быть противоположными;
в) верно ли неравенство P( A B )>0,2?
4.2Вероятность для человека, поступившего в университет, закончить первый курс равна P; вероятность проучиться успешно до пятого курса и
48
закончить его равна Q. Какова вероятность для второкурсника успешно закончить пятый курс?
4.3При включении зажигания двигатель начинает работать с вероятностью 0,6. Найти вероятность того, что:
а) двигатель начнет работать при третьем включении зажигания; б) для запуска двигателя придется включать зажигание не более трѐх раз.
4.4Два охотника стреляют по летящей утке. Шансы попадания оцениваются для первого охотника как 90%, а для второго – 80%. Найти вероятность того, что птичке не спастись.
4.56 шаров (4 белых и 2 чѐрных) случайным образом раскидали в два ящика по три шара в каждый.
а) Какова вероятность того, что ровно один чѐрный шар попал в первый ящик?
б) Из первого ящика достали шар, он оказался белым. Какова вероятность того, что ровно один чѐрный шар попал в первый ящик?
4.6Из ящика, содержащего чѐрные и белые шары, 100 раз подряд извлекли чѐрный шар. Какова вероятность того, что и в 101-й раз будет извлечен чѐрный шар? Рассмотреть два случая: выбор шаров производился без возвращения; выборка была с возвращением.
4.7При обследовании на СПИД вероятность обнаружить ВИЧ у инфицированного человека равна 0,9. Вероятность принять здорового человека за больного равна 0,01. Пусть доля инфицированных по отношению ко всему населению равна 0,0001. Найдите условную вероятность того, что человек не инфицирован, если при обследовании у него обнаружен ВИЧ.
4.8Страховая компания разделяет застрахованных водителей на три группы по вероятности попадания в дорожную аварию. Среди застрахованных водители группы с низкой вероятностью составили
49
25%, со средней – 60% и с высокой – 15%. Ниже приведена таблица вероятностей попадания водителей каждой группы в аварию:
|
Вероятность попадания в аварию |
|||
|
Риск водителя |
|||
|
низкая |
средняя |
высокая |
|
|
1 авария в год |
0,01 |
0,03 |
0,10 |
|
2 аварии в год |
0 |
0,01 |
0,05 |
|
3 аварии в год |
0 |
0 |
0,01 |
|
4 аварии в год |
0 |
0 |
0 |
Требуется найти:
а) если случайно выбранный водитель не попадал в аварию в течение года, какова вероятность того, что он принадлежит к группе водителей с высокой вероятностью попадания в дорожную аварию?
б) если случайно выбранный водитель не попадал в аварию в течение четырех лет, какова вероятность того, что он принадлежит к группе водителей с низкой вероятностью попадания в дорожную аварию?
4.9Институт дистанционного обучения отправил учебники в три своих филиала. Вероятность своевременной доставки в первый филиал равна 0,9; во второй – 0,95; в третий – 0,8. Найти вероятности следующих событий:
а) только один филиал получит учебники вовремя; б) хотя бы один филиал получит учебники с опозданием.
4.10Фирма имеет три источника поставки комплектующих – заводы А, В и С. На долю завода А приходится 50% общего объема поставок; В – 30% и С – 20%. Из практики известно, что 10% поставляемых заводом А деталей бракованных, заводом В – 5% и заводом С – 6%. Определите вероятности следующих событий:
а) взятая наугад деталь была получена от завода А; б) взятая наугад и оказавшаяся бракованной деталь, была получена от завода А.
50
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Какова вероятность, что вы умрете невероятной смертью и что такое предел Хейфлика
Статистика — штука без эмоций, сплошная математика. Есть скучные формулы вычисления вероятности того, например, что вы доживете до 75 лет, а потом и до 85, или что уже в этом году в вас попадет молния, и вы останетесь живы. Более того, эти теоретические значения подкреплены вполне реальными историями из жизни, что добавляет им значимости, а нам седых волос.

Getty Images
Классическая формула теории вероятностей до безобразия проста. Допустим, мы хотим выяснить, каковы шансы умереть сегодня. Для этого берем общую численность населения в России (по данным ООН — 146 574 000 человек) и делим на количество умерших сегодня (4500 человек). Отношение 1:33000 и будет искомой вероятностью. Вероятность в том числе лежит в основе расчетов на рынке ценных бумаг, матанализа азартных игр и даже наличия разумной жизни во Вселенной.
Шансы погибнуть в авиакатастрофе составляют 1:4000000, а вероятность смерти от падения с кровати составляет в среднем 1:1500000
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Все прекрасно знают, что самолет — самый безопасный вид транспорта и бла-бла-бла. Не убедительно? А если мы скажем, что шансы погибнуть в авиакатастрофе составляют 1:4000000 и примерно равны тому, что вам на голову упадет не какой-нибудь кирпич, а целый астероид? Живите теперь с этим. Более того, есть масса историй, когда после падения авиалайнера были выжившие. В 1985 году Boeing 747 компании Japan Air Lines врезался в гору Оцутакава, и большинство из 524 человек остались живы! Правда, из-за несогласованности в действиях спасателей и несвоевременно оказанной помощи практически все погибли от полученных травм и переохлаждения. Но это уже совсем другая история… И не забывайте про «правило пяти рядов»: даже при аварии шансы выжить в разы выше, если сесть не далее пятого ряда от аварийного выхода.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Если отталкиваться от авиакатастроф, то есть еще одна занятная цифра для сравнения. Вероятность смерти от падения с кровати составляет в среднем 1:1500000: только в США ежегодно регистрируют порядка 400 таких случаев. В России отдельной статистики по подобным происшествиям нет, но это не значит, что такие истории нам не угроза. В Питере скончался 45-летний мужчина после падения с дивана, а в Севастополе 8-летний мальчик упал с кровати и получил черепно-мозговую травму, не совместимую с жизнью.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Но вернемся к астероидам. Ежегодно в опасной близости от Земли пролетает около 150 небесных тел. Падение одного из них может произойти в любой момент. Ученые подсчитали, что астероид Апофис может свалиться на наши головы в 2068 году, и если это произойдет, то 300-метровое небесное тело сравняет с землей всю Москву и область впридачу. Правда, эксперты успокаивают: учитывая все современные технологии предотвращения подобных катастроф, нам ничего не угрожает. С другой стороны, все мы прекрасно помним Челябинский метеорит: небольшой кусок, отколовшийся от 17-метрового астероида, разрушившегося в результате торможения в атмосфере Земли (по официальной версии). Обнаружили его только после входа в атмосферу, за несколько секунд до падения. Так что не расслабляемся.
По статистике, женщины в шесть раз реже погибают от ударов молний, а средний возраст пострадавших — 35 лет
Если вероятность столкновения с астероидом ничтожно мала, то мы для вас приготовили кое-что более опасное. Если вы мужчина — остерегайтесь молний, так как вы в группе риска. По статистике, женщины в шесть раз реже погибают от ударов молний, а средний возраст пострадавших — 35 лет. В общей сложности вероятность схватить разряд в несколько сотен тысяч воль составляет 1:600000. Но и тут не стоит паниковать: три случая из пяти с хорошим концом. Более того, есть люди, в которых молния попадала не один, не два и не три раза — и как с гуся вода!
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
В кубинца Хорхе Маркеса молния била пять раз. Сильнейшие ожоги, выбитые пломбы и опаленная макушка — последствия столкновения с природным явлением. Но парень жив, черт бы его побрал! Насчет того, что молния дважды не бьет в одно место: в Техасе любитель бездорожья укрылся от грозы под деревом (неужели мама в детстве не говорила, что так делать нельзя?), где, конечно же, его настигла молния. Парень без сознания грохнулся на землю. Но на этом его беды не закончились: молния шарахнула уже по лежавшему в отключке бедолаге второй раз. И что вы думаете? После госпитализации у парня диагностировали лишь небольшой ожог ноги, который зажил через пару недель. Но рекордсменом в этой дисциплине вот уже долгое время является рейнджер из Кентукки Рой Кливленд Салливан, о чем даже свидетельствует запись в Книге рекордов Гиннесса. Этот человек-громоотвод получал разряд — внимание! — семь раз. А знаете, от чего умер этот егерь? В возрасте 71 года пустил себе пулю в висок из-за неразделенной любви (при том, что жена Роя была на 30 лет моложе).
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Статистика суицидов говорит, что с вероятностью 1:580 вы в этом году сведете счеты с жизнью. Но не обольщайтесь, если вы таки решитесь на самоубийство, то вероятность успеха равна 1:14.Один англичанин, от которого ушла жена, пытался шесть раз наложить на себя руки: вешался, травился, нырял в ванную с феном… И что вы думаете? На седьмой попытке он пустил в квартиру газ — не сработало. Тогда он зажег спичку, и раздался громадный взрыв. Недосамоубийцу — целого и невредимого, в отличие от его дома — осудили на два года условно за поджог.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Если верить статистике, то самые лютые убийцы не обстоятельства, не астероиды с самолетами, а наши с вами организмы. Вероятность умереть от недуга выше всего. В топе болезни сердца (1:4), следом рак (1:6) и расстройства работы мозга (1:7). Но и здесь не все так печально: в случае инфаркта или инсульта вероятность полного выздоровления равна 1:3 — не густо, но и не безнадежно.
Статистика по возрасту говорит, что в 65 лет шанс прожить еще десять лет 1:2, а если вы и этот рубеж перевалили, то шансы протянуть еще столько же сокращаются вдвое — 1:4. И не забывайте, что если вы не попали ни в одну из вероятностей, не болеете, за вами не гонится насильник с топором и все у вас хорошо, то есть так называемый предел Хейфлика. Ваши клетки не вечны, и умирают примерно после полсотни делений. Так что рано или поздно у организма попросту истечет срок эксплуатации.
