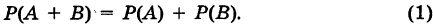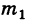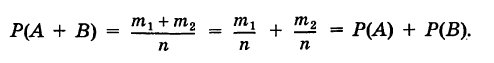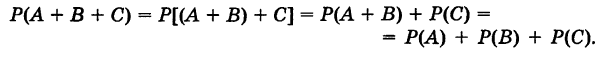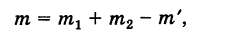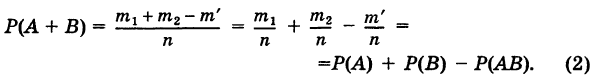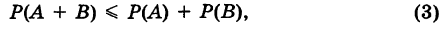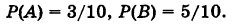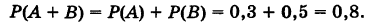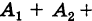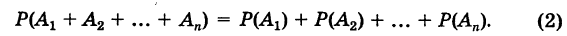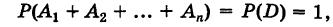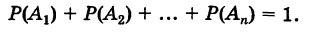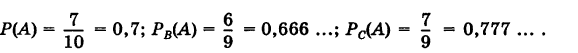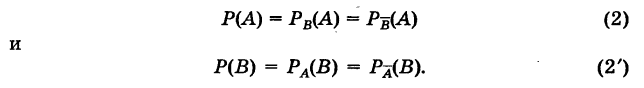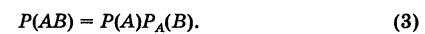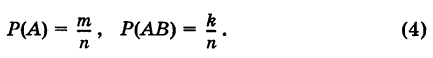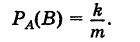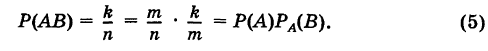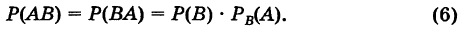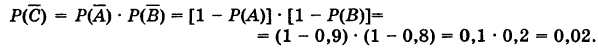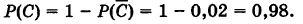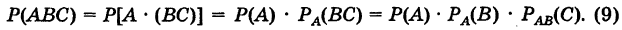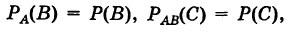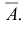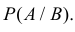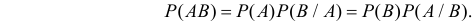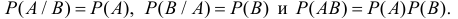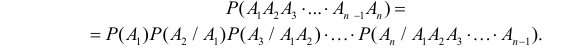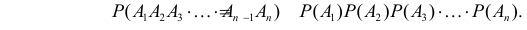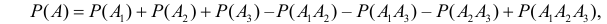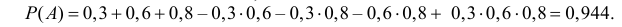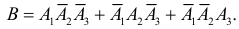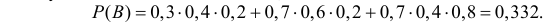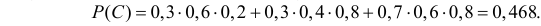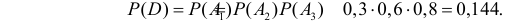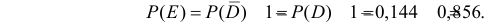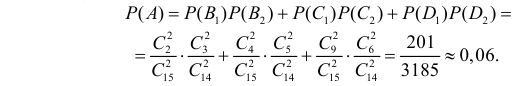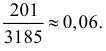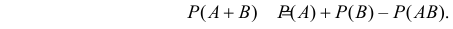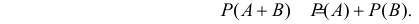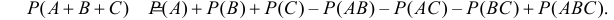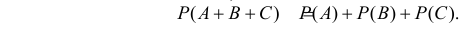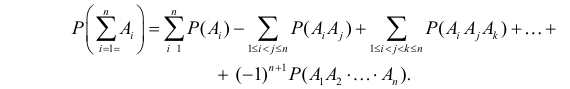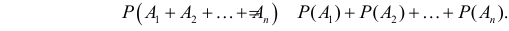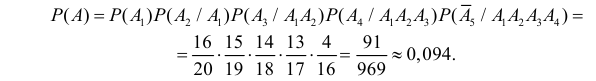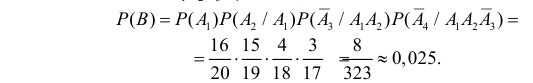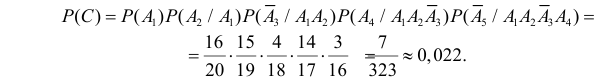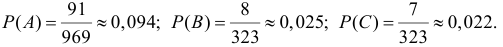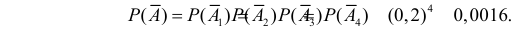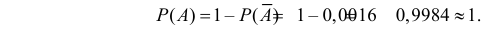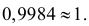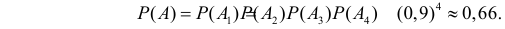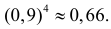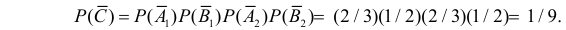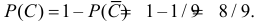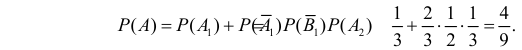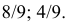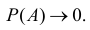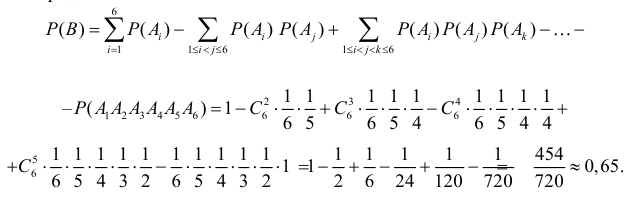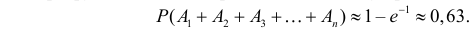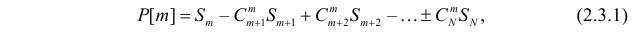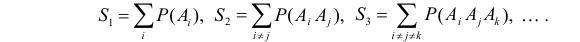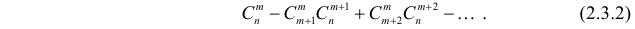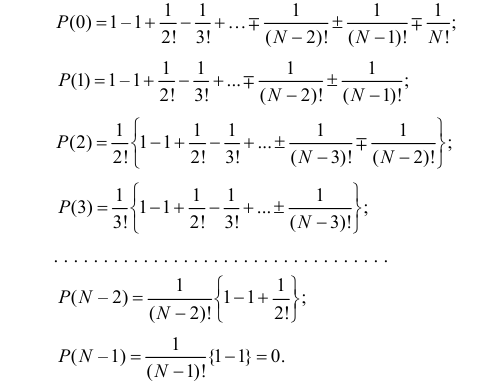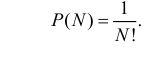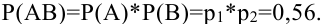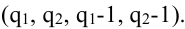Понравилось? Добавьте в закладки
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записывается как $A subset B$.
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается очевидно: А = В.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
$$P(A+B)=P(A)+P(B).$$
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
$$Pleft(sum_{i=1}^{n}A_i right)=sum_{i=1}^{n} P(A_i).$$
Если случайные события $A_1, A_2, …, A_n$ образуют полную группу несовместных событий, то имеет место равенство
$P(A_1)+P(A_2)+…+P(A_n)=1.$ Такие события (гипотезы) используются при решении задач на полную вероятность.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
$$P(A+B)=P(A)+P(B)-P(Acdot B).$$
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
$$P(Acdot B)=P(A)cdot P(B).$$
Вероятность произведения зависимых событий вычисляется по формуле условной вероятности.
Примеры решений задач с событиями
Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.
Решение. Обозначим события: А – вынули белый шар из первого ящика, 


В – белый шар из второго ящика, 


Нам нужно, чтобы произошло одно из событий 



Тогда искомая вероятность по теореме сложения будет

Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания.
Решение.
Пусть А – попадание первого стрелка, 
В – попадание второго стрелка, 
Тогда 



Найдем нужные вероятности.
а) АВ – двойное попадание,
б) 

в) А+В – хотя бы одно попадание,

г) 

См. обучающую статью “решение задач о стрелках”
Пример. Решить задачу, применяя теоремы сложения и умножения. Мастер обслуживает 3 станка, работающих независимо друг от друга. Вероятность того, что первый станок потребует внимания рабочего в течение смены, равна 0,4, второй – 0,6, третий – 0,3. Найти вероятность того, что в течение смены: а) ни один станок не потребует внимания мастера, б) ровно 1 станок потребует внимания мастера.
Решение.
Вводим базовые независимые события $A_i$ = (Станок $i$ потребовал внимания рабочего в течение смены), $i=1, 2, 3$. По условию выписываем вероятности: $p_1=0,4$, $p_2=0,6$, $p_3=0,3$. Тогда $q_1=0,6$, $q_2=0,4$, $q_3=0,7$.
Найдем вероятность события $X$=(Ни один станок не потребует внимания в течение смены):
$$
P(X)=Pleft(overline{A_1} cdot overline{A_2} cdot overline{A_3}right)= q_1 cdot q_2 cdot q_3 =
0,6cdot 0,4 cdot 0,7 = 0,168.
$$
Найдем вероятность события $Z$= (Ровно один станок потребует внимания в течение смены):
$$
P(Z)= \ = P(A_1) cdot Pleft(overline{A_2} right) cdot Pleft(overline{A_3} right) + Pleft(overline{A_1}right) cdot P(A_2) cdot Pleft(overline{A_3} right) + Pleft(overline{A_1} right) cdot Pleft(overline{A_2} right) cdot P(A_3)=\
= p_1 cdot q_2 cdot q_3 + q_1 cdot p_2 cdot q_3 + q_1 cdot q_2 cdot p_3 =\ =
0,4cdot 0,4 cdot 0,7+0,6cdot 0,6 cdot 0,7+0,6cdot 0,4 cdot 0,3 = 0,436.
$$
См. обучающую статью “решение задач о станках”
Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.
Решение.
А – формула содержится в первом справочнике;
В – формула содержится во втором справочнике;
С – формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
1.
2. 
3.
Вероятность наступления хотя бы одного события
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий?
Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.
Теорема. Вероятность появления хотя бы одного из событий $A_1, A_2, …, A_n$, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
$$
P(A)=1-Pleft(overline{A_1}right)cdot Pleft(overline{A_2}right)cdot … cdot Pleft(overline{A_n}right)= 1-q_1 cdot q_2 cdot … cdot q_n.
$$
Если события $A_1, A_2, …, A_n$ имеют одинаковую вероятность $p$, то формула принимает простой вид:
$$
P(A)=1-(1-p)^n=1-q^n.
$$
Примеры решений на эту тему
Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события 


Вероятности событий, противоположных событиям 




Искомая вероятность 
Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).
Решение. События “машина работает” и “машина не работает” (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице:
Отсюда вероятность того, что машина в данный момент не работает, равна
Искомая вероятность
Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.
Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
Решение. Обозначим через А событие “при n выстрелах стрелок попадает в цель хотя бы один раз”. События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула 
Приняв во внимание, что, по условию, 

Прологарифмируем это неравенство по основанию 10:
Итак, 
См. обучающую статью “решение задач с хотя бы один…”
Содержание:
Теорема сложения вероятностей:
Теорема: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т. е. если АВ = 0, то
Доказательство: Пусть из общего числа п всех возможных и равновозможных элементарных исходов испытания
Следствие. Вероятность суммы конечного числа попарно несовместных событий равна сумме вероятностей этих событий.
Пусть, например, события А, В и С попарно несовместны, т. е. события АВ, АС, ВС невозможны.
Имеем
Замечание. Пусть теперь события А и В совместны. Тогда число благоприятных элементарных исходов для события А + В будет
где 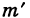
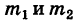
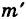
Поэтому, в общем случае имеем
Следствие. Так как Р(АВ) 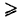
т. е. вероятность суммы двух событий никогда не превосходит суммы вероятностей этих событий.
Это утверждение, очевидно, справедливо также и для нескольких событий.
Пример:
В урне находятся 2 белых, 3 красных и 5 синих одинаковых по размеру шаров. Какова вероятность, что шар, случайным образом извлеченный из урны, будет цветным (не белым)?
Решение:
Пусть событие А — извлечение красного шара из урны, а событие В — извлечение синего шара. Тогда событие А + В есть извлечение цветного шара из урны. Очевидно, имеем
Так как события А и В несовместны (извлекается только один шар), то по теореме сложения имеем
Полная группа событий:
Определение: Система событий
называется полной группой событий для данного испытания, если любым исходом его является одно и только одно событие этой группы.
Иными словами, для полной группы событий (1) выполнены следующие условия:
1)событие 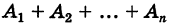
2)события 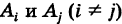
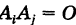
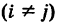
Простейшим примером полной группы событий является пара событий: А и А.
Теорема: Сумма вероятностей событий полной группы равна единице.
Доказательство: Для полной группы (1) событие 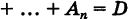
Но
поэтому из (2) имеем
Теорема умножения вероятностей:
Определение: Вероятность события А при условии, что произошло событие В, называется условной вероятностью события А и обозначается так:
Замечание. Вероятность каждого события А в данном испытании связана с наличием известного комплекса условий. При определении условной вероятности мы предполагаем, что в этот комплекс условий обязательно входит событие В. Таким образом, мы фактически имеем другой, более обременительный комплекс условий, соответствующий испытанию в новой обстановке. Вероятность 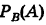
Пример:
В урне находятся 7 белых и 3 черных шара.
Какова вероятность: 1) извлечения из урны белого шара (событие А); 2) извлечения из урны белого шара после удаления из нее одного шара, который является белым (событие В) или черным (событие С)?
Решение:
Здесь
Таким образом, условная вероятность события может быть как меньше, так и больше вероятности этого события.
Определение: Два события А и В называются независимыми, если вероятность каждого из них не зависит от появления или непоявления другого, т. е.
В противном случае события называются зависимыми.
Теорема: Вероятность произведения (совмещения) двух событий А и В равна произведению вероятности одного из них на условную вероятность другого, в предположении, что первое имеет место, т. е.
Доказательство: Пусть событию А благоприятствуют т, а событию АВ благоприятствуют k равновозможных элементарных исходов из общего их количества 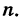
Но если событие А произошло, то в этой ситуации возможны лишь те m элементарных исходов, которые благоприятствовали событию А, причем k из них, очевидно, благоприятствуют событию В. Таким образом,
Отсюда на основании равенств (4) имеем
Теорема доказана.
Так как ВА = АВ, то имеем также
Замечание. Формула (5) формально остается верной, если событие А невозможно.
Следствие. Для любых двух событий А и В справедливо равенство
Теорема: Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий:
Действительно, полагая, что 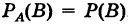
Пример:
Вероятность поражения цели первым стрелком (событие A)равна 0,9, а вероятность поражения цели вторым стрелком (событие B)равна 0,8. Какова вероятность того, что цель будет поражена хотя бы одним стрелком?
Решение:
Пусть С — интересующее нас событие; противоположное событие 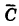
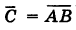
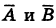
Отсюда вероятность того, что цель будет поражена хотя бы одним стрелком, есть
Теорема допускает обобщение на случай нескольких событий. Например, для случая трех событий А, В и С имеем
Определение: События называются независимыми в совокупности, если каждое из них и любое произведение остальных (включающее либо все остальные события, либо часть из них) есть события независимые.
События, независимые в совокупности, очевидно, попарно независимы между собой; обратное неверно.
Теорема: Вероятность произведения конечного числа независимых в совокупности событий равна произведению вероятностей этих событий.
Действительно, например, для трех независимых в совокупности событий А, В и С из формулы (9), учитывая, что
имеем
и т.п.
Теоремы сложения и умножения вероятностей
В теории вероятностей события рассматривают на фоне комплекса условий, которые его порождают. Проще говоря, событие – это результат опыта, который проистекает в природе по воле человека, независимо от нее или ей вопреки. Рассмотрим множество событий, которые можно наблюдать в эксперименте при фиксированном комплексе условий. На множестве таких событий определим следующие понятия.
Суммой событий A и B называется событие, состоящее в появлении хотя бы одного из событий A или B . Сумму событий A и B обозначают через A + B .
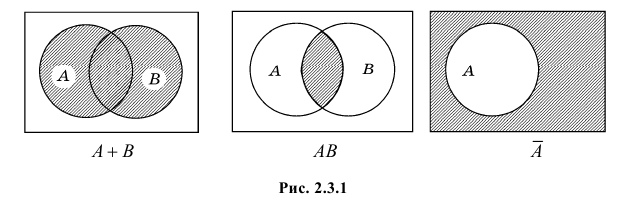
Приведенные понятия можно проиллюстрировать следующим образом.
Пусть комплекс условий состоит в том, что внутрь прямоугольника наугад бросают точку. Обозначим через А попадание точки внутрь левого круга, а через В – внутрь правого круга. Тогда события 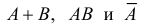
Произведением событий A и B называют событие, состоящее в появлении событий А и В в одном и том же опыте. Обозначают произведение событий A и B через AB.
Событие, состоящее в не появлении события A, называется противоположным событием и обозначается через
Если в каждом опыте два события A и B всегда либо оба происходят, либо оба не происходят, то такие события называют равносильными или эквивалентными и записывают: A = B .
Говорят, что события 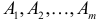
Словесные рассуждения можно перевести в символическую запись с помощью соответствий: «или» 


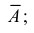

Вероятность события A, вычисленная при условии, что событие B произошло, называется условной вероятностью события A и обозначается через
Теорема умножения вероятностей
Вероятность произведения событий равна вероятности одного события, умноженной на вероятность другого события, вычисленную при условии, что первое событие произошло, т.е.
События называются независимыми, если появление одного из них не изменяет вероятности появления другого. Если события независимы, то
Для любого конечного числа событий вероятность произведения событий равна произведению вероятностей этих событий, причем вероятность каждого следующего события вычисляется при условии, что предыдущие события произошли, т.е.
Если события независимы, то
Итак, перед вычислением вероятности произведения событий необходимо установить, зависимы события или нет.
Пример №1
Вероятности попадания в цель при одном выстреле для первого, второго и третьего стрелков равны соответственно 0,3; 0,6; 0,8. Все три стрелка выстрелили в цель. Какова вероятность того, что:
а) цель поражена;
б) произошло только одно попадание;
в) произошло ровно два попадания;
г) попадут все три стрелка;
д) будет хотя бы один промах?
Решение. Обозначим через 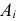
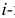
а) Поражение цели (событие A) равносильно появлению хотя бы одного из событий A1 или A2 или A3. Поэтому 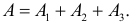
так как события независимы, то
б) Рассмотрим три случая:
1) 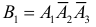
2) 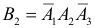
3) 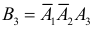
Только одно попадание в цель (событие В) равносильно реализации хотя бы одного из несовместных событий B1 или B2 или B3 . Поэтому
В силу независимости событий 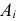
в) Два попадания в цель (событие C) равносильны реализации хотя бы одного из несовместных случаев: 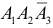
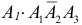
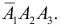
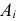
г) Все три стрелка попадут в цель (событие D), если произойдут события 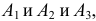
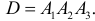
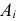
д) Хотя бы один промах (событие Е) равносилен появлению хотя бы одного из событий 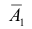
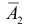
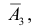
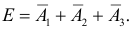
Ответ. а) 0,944; б) 0,332; в) 0,468; г) 0,144; д) 0,856.
Замечание. Значительное число вероятностных задач связано с теорией стрельб. В связи с этим уместно вспомнить изречение немецкого военного теоретика Карла Клаузевица (1780–1830): «Никакая человеческая деятельность не соприкасается со случаем так всесторонне и так часто, как война».
Пример №2
В первой урне два белых шара, четыре синих и девять красных, а во второй соответственно три, пять и шесть. Из каждой урны наугад выбирают два шара. Какова вероятность того, что будут выбраны шары одного цвета?
Решение. Событие, состоящее в выборе шаров одного цвета, обозначим через A. Обозначим через 
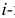
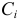
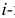
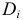
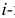
Событие A произойдет, если из первой урны будут выбраны два белых шара (событие B1) и из второй урны будут выбраны тоже два белых шара (событие B2) или из первой урны извлекут два синих шара (событие C1) и из второй урны будут выбраны тоже два синих шара (событие C2) или из первой урны будут выбраны два красных шара (событие D1) и из второй урны будут выбраны тоже два красных шара (событие D2). Поэтому 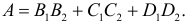
Ответ.
Теорема сложения вероятностей
Вероятность суммы событий A и B равна сумме вероятностей этих событий без вероятности их совместного появления:
События называются несовместными, если их появление в одном и том же опыте невозможно. Если события A и B несовместны, то
Для трех совместных событий теорема сложения вероятностей имеет вид:
Если события несовместны, то
Теорему сложения можно обобщить на любое конечное число слагаемых:
Если события несовместны, то
Итак, прежде чем вычислять вероятность суммы событий следует выяснить, совместны они или нет.
Указание. Желателен следующий порядок решения задач и оформления записи:
а) обозначения событий;
б) анализ взаимосвязей событий и их символическая запись;
в) вычисление вероятностей.
Пример №3
Из 20 изделий четыре имеют скрытые дефекты. Изделия выбирают наугад по одному и проверяют. Найдите вероятности следующих событий:
A – первым бракованным изделием окажется пятое по счету проверяемое изделие;
B – первыми бракованными изделиями окажутся третье и четвертое проверяемые изделия;
C – первыми бракованными изделиями окажутся третье и пятое по счету изделия.
Решение. Обозначим через 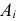
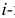
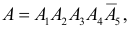
Событие B произойдет, если первые два изделия будут годными, а третье и четвертое окажутся бракованными. Символически это можно записать в виде 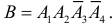
Аналогично, 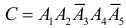
Ответ.
Пример №4
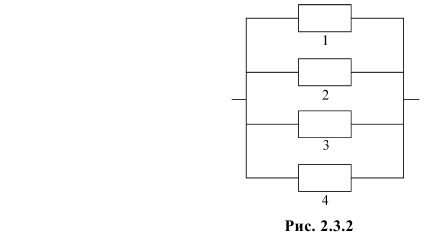
Имеется система соединенных между собой элементов (скажем, участок электрической цепи, поточная линия и т.д., см. рис. 2.3.2). Вероятность безотказной работы каждого элемента в течение заданного времени (надежность) равна 0,8. Элементы выходят из строя независимо друг от друга. Какова надежность системы?
Решение. Пусть событие А состоит в безотказной работе системы в течение заданного времени, а 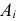
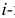
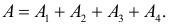
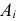
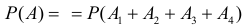
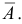
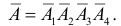
Тогда
Ответ.
Пример №5
Имеется система соединенных между собой элементов (электрическая цепь, поточная линия и т.д., см. рис. 2.3.3). Вероятность безотказной работы (надежность) каждого элемента равна 0,9. Элементы выходят из строя независимо друг от друга. Какова надежность системы?
Решение. Пусть событие А состоит в безотказной работе системы, а 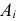
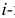
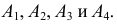
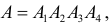
Ответ.
Пример №6
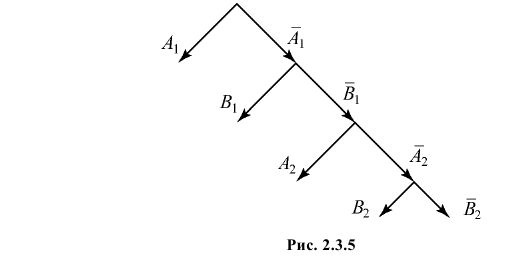
Два стрелка по очереди стреляют в цель до первого попадания. Вероятность попадания в цель при одном выстреле равна для них соответственно 1/3 и 1/2. Каждый стрелок имеет право только на два выстрела. Какова вероятность того, что цель будет поражена? Какова вероятность того, что цель поразит первый стрелок?
Решение. Обозначим через 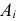
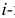

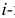
Цель не будет поражена (событие 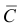
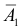
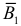
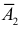
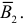
Поэтому вероятность поражения цели
Цель поразит первый стрелок (событие A), если он попадет при первом выстреле или при первом выстреле он не попадет в цель и второй стрелок при своем первом выстреле не попадет в цель и после этого первый стрелок попадет в цель. Поэтому 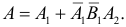
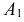
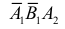
Ответ.
Пример №7
Урна содержит шесть занумерованных шаров с номерами от одного до шести. Шары извлекаются по одному без возвращения. Пусть событие A состоит в том, что шары будут извлечены в порядке их номеров, а событие B в том, что хотя бы один раз номер шара совпадет с порядковым номером его извлечения. Найти вероятности событий A и B и определить предельные вероятности этих событий при неограниченном увеличении числа шаров в урне.
Решение. а) Обозначим через 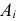
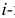
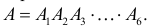
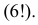
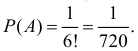
Событие B произойдет, если появится хотя бы одно из событий A1 или A2 или … или A6. Поэтому 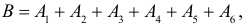
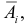
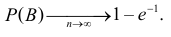
Заметим, что искомая вероятность является частичной суммой ряда Тейлора функции 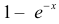
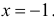
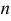
Ответ. 
Теорема. Пусть имеем группу событий 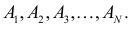
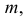
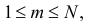
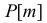
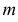
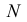
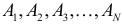
где
К формуле (2.3.1) приводят следующие соображения. Пусть E – элементарный исход опыта. Предположим, что этот исход включен в 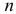
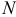
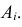
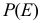
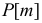
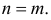
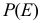
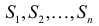
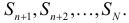
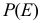
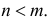
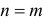
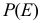
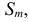
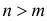
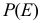
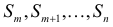
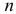
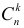
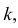
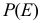
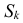
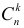
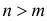
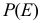
Но 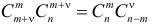
В последнем выражении в скобке имеем разложение бинома 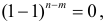
Продолжим решение примера. Установлено, что вероятность ровно 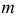
Здесь равенство нулю означает невозможность получить 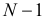
Всё о теореме умножения вероятностей
При оценки вероятности наступления какого-либо случайного события очень важно предварительно хорошо представлять, зависит ли вероятность наступления интересующего нас события от того, как развиваются остальные события. В случае классической схемы, когда все исходы равновероятны, мы уже можем оценить значения вероятности интересующего нас отдельного события самостоятельно. Мы можем сделать это даже в том случае, если событие является сложной совокупностью нескольких элементарных исходов. А если несколько случайных событий происходит одновременно или последовательно? Как это влияет на вероятность реализации интересующего нас события?
Если я несколько раз кидаю игральную кость, и хочу, чтобы выпала “шестерка”, а мне все время не везет, значит ли это, что надо увеличивать ставку, потому что, согласно теории вероятностей, мне вот-вот должно повезти? Увы, теория вероятности не утверждает ничего подобного. Ни кости, ни карты, ни монетки не умеют запоминать, что они продемонстрировали нам в прошлый раз. Им совершенно не важно, в первый раз или в десятый раз сегодня я испытываю свою судьбу. Каждый раз, когда я повторяю бросок, я знаю только одно: и на этот раз вероятность выпадения “шестерки” снова равна одной шестой. Конечно, это не значит, что нужная мне цифра не выпадет никогда. Это означает лишь то, что мой проигрыш после первого броска и после любого другого броска – независимые события.
События А и В называются независимыми, если реализация одного из них никак не влияет на вероятность другого события. Например, вероятности поражения цели первым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события “первое орудие поразило цель” и “второе орудие поразило цель” независимы.
Если два события А и В независимы, и вероятность каждого из них известна, то вероятность одновременного наступления и события А, и события В (обозначается АВ) можно посчитать, воспользовавшись следующей теоремой.
Теорема умножения вероятностей для независимых событий: Р(АВ) = Р(А)*Р(В) – вероятность одновременного наступления двух независимых событий равна произведению вероятностей этих событий.
Пример №8
Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: 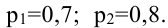
Решение:
Как мы уже видели события А (попадание первого орудия) и В (попадание второго орудия) независимы, т.е.
Что произойдет, с нашими оценками, если исходные события не являются независимыми? Давайте немного изменим предыдущий пример.
Пример №9
Два стрелка на соревнованиях стреляют по мишеням, причем, если один из них стреляет метко, то соперник начинает нервничать, и его результаты ухудшаются. Как превратить эту житейскую ситуацию в математическую задачу и наметить пути ее решения? Интуитивно понятно, что надо каким-то образом разделить два варианта развития событий, составить по сути дела два сценария, две разные задачи. В первом случае, если соперник промахнулся, сценарий будет благоприятный для нервного спортсмена и его меткость будет выше. Во втором случае, если соперник прилично реализовал свой шанс, вероятность поразить мишень для второго спортсмена снижается.
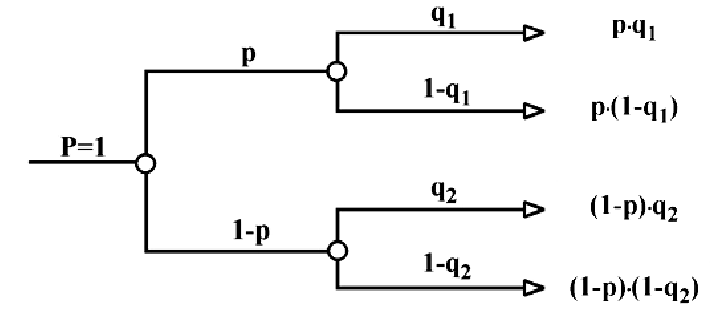
Для разделения возможных сценариев (их часто называют гипотезами) развития событий мы будем часто использовать схему “дерева вероятностей”. Эта схема похожа по смыслу на дерево решений, с которым Вам, наверное, уже приходилось иметь дело. Каждая ветка представляет собой отдельный сценарий развития событий, только теперь она имеет собственное значение так называемой условной вероятности
Эта схема очень удобна для анализа последовательных случайных событий.
Остается выяснить еще один немаловажный вопрос: откуда берутся исходные значения вероятностей в реальных ситуациях? Ведь не с одними же монетами и игральными костями работает теория вероятностей? Обычно эти оценки берутся из статистики, а когда статистические сведения отсутствуют, мы проводим собственное исследование. И начинать его нам часто приходится не со сбора данных, а с вопроса, какие сведения нам вообще нужны.
Пример №10
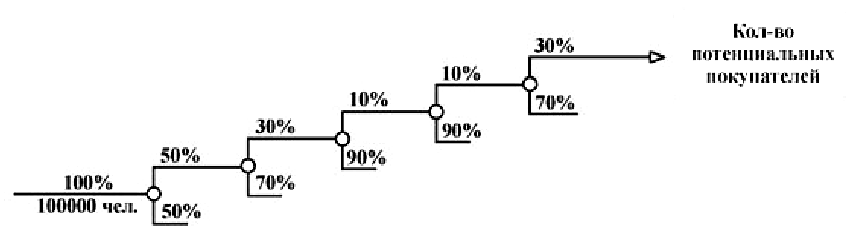
Допустим, нам надо оценить в городе с населением в сто тысяч жителей объем рынка для нового товара, который не является предметом первой необходимости, например, для бальзама по уходу за окрашенными волосами. Рассмотрим схему “дерева вероятностей”. При этом значение вероятности на каждой “ветке” нам надо приблизительно оценить. Итак, наши оценки емкости рынка: 1) из всех жителей города женщин 50%, 2) из всех женщин только 30% красят волосы часто, 3) из них только 10% пользуются бальзамами для окрашенных волос, 4) из них только 10% могут набраться смелости попробовать новый товар, 5) из них 70% обычно покупает все не у нас, а у наших конкурентов.
Решение:
По закону перемножения вероятностей, определяем вероятность интересующего нас события А={житель города покупает у нас этот новый бальзам} = 0,00045. Умножим это значение вероятности на число жителей города. В результате имеем всего 45 потенциальных покупательниц, а если учесть, что одного пузырька этого средства хватает на несколько месяцев, не слишком оживленная получается торговля.
И все-таки польза от наших оценок есть. Во-первых, мы можем сравнивать прогнозы разных бизнес-идей, на схемах у них будут разные “развилки”, и, конечно, значения вероятности тоже будут разные. Во-вторых, как мы уже говорили, случайная величина не потому называется случайной, что она совсем ни от чего не зависит. Просто ее точное значение заранее не известно. Мы знаем, что среднее количество покупателей может быть увеличено (например, с помощью рекламы нового товара). Так что имеет смысл сосредоточить усилия на тех “развилках”, где распределение вероятностей нас особенно не устраивает, на тех факторах, на которые мы в состоянии повлиять. Рассмотрим еще один количественный пример исследования покупательского поведения.
Пример №11
За день продовольственный рынок посещает в среднем 10000 человек. Вероятность того, что посетитель рынка заходит в павильон молочных продуктов, равна 1/2. Известно, что в этом павильоне в среднем продается в день 500 кг различных продуктов. Можно ли утверждать, что средняя покупка в павильоне весит всего 100 г?
Обсуждение:
Конечно, нельзя. Понятно, что не каждый, кто заходил в павильон, в результате что-то там купил.
Как показано на схеме, чтобы ответить на вопрос о среднем весе покупки, мы должны найти ответ на вопрос, какова вероятность того, что человек, зашедший в павильон, что-нибудь там купит. Если таких данных в нашем распоряжении не имеется, а нам они нужны, придется их получить самим, понаблюдав некоторое время за посетителями павильона. Допустим, наши наблюдения показали, что только пятая часть посетителей павильона что-то покупает. Как только эти оценки нами получены, задача становится уже простой. Из 10000 человек, пришедших на рынок, 5000 зайдут в павильон молочных продуктов, покупок будет только 1000. Средний вес покупки равен 500 грамм. Интересно отметить, что для построения полной картины происходящего, логика условных “ветвлений” должна быть определена на каждом этапе нашего рассуждения так же четко, как если бы мы работали с “конкретной” ситуацией, а не с вероятностями. Задачи для самопроверки 1. Пусть есть электрическая цепь, состоящая из п последовательно соединенных элементов, каждый из которых работает независимо от остальных.
Известна вероятность р невыхода из строя каждого элемента. Определите вероятность исправной работы всего участка цепи (событие А). 2. Студент знает 20 из 25 экзаменационных вопросов. Найдите вероятность того, что студент знает предложенные ему экзаменатором три вопроса. 3. Производство состоит из четырех последовательных этапов, на каждом из которых работает оборудование, для которого вероятности выхода из строя в течение ближайшего месяца равны соответственно 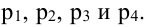
Всё о теореме сложения вероятностей
В этом разделе мы начнем применять на практике математический аппарат теории вероятностей для оценки вероятности наступления интересующего нас случайного события, которое, в свою очередь, является некоторой комбинацией других случайных событий.
Классическое определение вероятности Р(А) события А как отношения числа благоприятных элементарных исходов m к числу всех элементарных исходов п предполагает, что все элементарные исходы равновероятны. Однако, это условие далеко не всегда выполняется, поэтому мы сейчас введем еще одно определение вероятности – статистическое (или частотное).
Как оценить вероятность интересующего нас события, если в процессе испытания элементарные исходы вовсе не обязаны быть равновероятными? Строго говоря, необходимо было бы много раз проделать интересующий нас опыт и узнать частоту реализации различных элементарных исходов.
В пределе, при увеличении числа испытаний, отношение числа m реализованных событий А к общему количеству испытаний n и будет определять вероятность 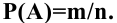
Теорема сложения вероятностей для несовместных событий:
Р(А + В) = Р(А) + Р(В) – вероятность наступления в результате эксперимента хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий.
Обсуждение:
Напомним, что события А и В называются несовместными, если в результате опыта они не могут появиться вместе. (Пожалуйста, не путайте их с независимыми событиями, которые мы обсуждали в прошлом разделе. Независимые события могут спокойно сосуществовать друг с другом.)
Пример №12
По статистике, в прошлом году 10% жителей нашего города встретили Новый год в отъезде, 40% ходили в гости или в ресторан, оставаясь в городе, остальные встречали Новый год дома. Считая, что эта тенденция сохранится, посчитайте вероятность того, что житель нашего города встретит Новый год дома.
Решение:
Здесь можно смело пользоваться теоремой сложения вероятностей, т.к. события встречи Нового года в разных местах одним и тем же человеком – несовместны. Поэтому все, кто встретит Новый год в гостях или в другом городе (они составят вместе 40% + 10%), не смогут встретить его дома. Принимая общее число жителей города за 100%, найдем, что 50% оставалось дома в прошлый раз. Полагая, что эти же пропорции сохранятся и в этом году, найдем, что вероятность встретить Новый год дома для жителя нашего города равна Р=0,5. (Заметим, что в данном случае нам было удобно посчитать сначала вероятность обратного события, а потом вычесть результат из 100%.)
Что произойдет, с нашими оценками, если исходные события не являются несовместными? Давайте немного изменим предыдущий пример.
Пример №13
Владелец фирмы частных такси хочет сделать прогноз количества клиентов на новогоднюю ночь. Пусть, по его сведениям, в прошлом году Новый год встретили дома 50%, в компании друзей или родственников, но не выезжая из города – 80%, в отъезде были 10%. Почему у него получилось в сумме больше 100%?
Видимо, каких-то жителей он посчитал больше одного раза. Скорее всего, тех, кто сидел дома, но, одновременно, принимал друзей или родственников, которые пришли к нему в гости. Поскольку эти события не являются несовместными, просто складывая вероятности, он завышает свои оценки.
Впрочем, это относится не только к оценке вероятности события, но и к решению любых задач на подсчет элементов объединения двух множеств путем сложения. Если множества частично перекрываются, сумма их элементов будет больше, чем реальное количество элементов, поскольку при арифметическом сложении элементы этого “перекрытия” мы невольно посчитали дважды, и как входящие в первое множество, и как входящие во второе. Выход здесь один: мы должны заметить, что множества частично “перекрываются”, посчитать число элементов в их общей части и вычесть это число из суммы (т.к. при суммировании мы его посчитали дважды).
В случае подсчета вероятности события С, которое наступает или при наступлении события А, или при наступлении события В, если А и В не являются несовместными, можно воспользоваться следующей теоремой:
Общая теорема сложения вероятностей:
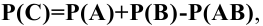
- Формула полной вероятности
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Комбинаторика – правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Методы математической статистики
Теория вероятности — подробнее
Что такое вероятность?
Рассмотрим пример. Допустим, мы бросаем игральную кость. Что это за кость такая, знаешь? Так называют кубик с цифрами на гранях. Сколько граней, столько и цифр: от ( 1) до ( 6).
Итак, мы бросаем кость и хотим, чтобы выпало ( 5) или ( 6). И нам выпадает ( 5).
В теории вероятностей говорят, что произошло благоприятное событие.
Если бы выпало ( 6), событие тоже было бы благоприятным. Итого может произойти всего два благоприятных события.
А сколько неблагоприятных?
Раз всего возможных событий ( 6), значит, неблагоприятных из них ( 6-2=4) события (это если выпадет ( 1,text{ }2,text{ }3) или ( 4)).
Вероятностью называется отношение количества благоприятных событий к количеству всех возможных событий.
То есть вероятность показывает, какая доля из всех возможных событий приходится на благоприятные.
Обозначают вероятность латинской буквой ( p) (видимо, от английского слова probability — вероятность).
Принято измерять вероятность в процентах (см. темы «Дроби, рациональные числа» и «Проценты»).
Для этого значение вероятности нужно умножать на ( 100%).
В примере с игральной костью вероятность ( p=frac{благоприятных}{всего}=frac{2}{6}=frac{1}{3}).
А в процентах: ( p=frac{1}{3}cdot 100%=frac{100}{3}%approx 33,3%).
И еще события бывают зависимыми друг от друга и независимыми. Начнем с зависимых событий.
Зависимые события
Например, ты решил зайти к знакомому, помнишь подъезд и даже этаж на котором он живет. А вот номер и расположение квартиры забыл. И вот стоишь ты на лестничной клетке, а перед тобой ( 3) двери на выбор.
Каков шанс (вероятность) того, что если ты позвонишь в первую дверь, тебе откроет твой друг? Всего квартиры ( 3), а друг живет только за одной из них. С равным шансом мы можем выбрать любую дверь.
Но каков этот шанс?
Дверей ( 3), нужная дверь ( 1). Вероятность угадать, позвонив в первую дверь: ( frac{1}{3}). То есть один раз из трех ты точно угадаешь.
Мы хотим узнать, позвонив ( 1) раз, как часто мы будем угадывать дверь? Давай рассмотри все варианты:
1. Ты позвонил в 1-ю дверь
2. Ты позвонил в 2-ю дверь
3. Ты позвонил в 3-ю дверь
А теперь рассмотрим все варианты, где может находиться друг:
а. За 1ой дверью
б. За 2ой дверью
в. За 3ей дверью
Сопоставим все варианты в виде таблицы. Галочкой обозначены варианты, когда твой выбор совпадает с местоположением друга, крестиком – когда не совпадает.
Как видишь, всего возможно ( 9) вариантов местоположения друга и твоего выбора, в какую дверь звонить.
А благоприятных исходов всего ( 3). То есть ( 3) раза из ( 9) ты угадаешь, позвонив в дверь ( 1) раз, т.е. ( frac{3}{9}=frac{1}{3}).
Это и есть вероятность – отношение благоприятного исхода (когда твой выбор совпал с местоположение друга) к количеству возможных событий.
Определение – это и есть формула. Вероятность принято обозначать p, поэтому:
( displaystyle p=frac{text{благоприятных}}{всего})
Такую формулу писать не очень удобно, поэтому примем за ( displaystyle {{N}_{б}}) – количество благоприятных исходов, а за ( N) – общее количество исходов.
( displaystyle p=frac{{{N}_{б}}}{N})
Вероятность можно записывать в процентах, для этого нужно умножить получившийся результат на ( 100%):
( displaystyle p=frac{{{N}_{б}}}{N}cdot 100%)
Наверное, тебе бросилось в глаза слово «исходы».
Поскольку математики называют различные действия (у нас такое действие – это звонок в дверь) экспериментами, то результатом таких экспериментов принято называть исход.
Ну а исходы бывают благоприятные и неблагоприятные.
Давай вернемся к нашему примеру. Допустим, мы позвонили в одну из дверей, но нам открыл незнакомый человек. Мы не угадали. Какова вероятность, что если позвоним в одну из оставшихся дверей, нам откроет наш друг?
Если ты подумал, что ( displaystyle frac{1}{3}), то это ошибка. Давай разбираться.
У нас осталось две двери. Таким образом, у нас есть возможные шаги:
1. Позвонить в 1-ую дверь
2. Позвонить во 2-ую дверь
Друг, при всем этом, точно находится за одной из них (ведь за той, в которую мы звонили, его не оказалось):
а. Друг за 1-ой дверью
б. Друг за 2-ой дверью
Давай снова нарисуем таблицу:
Как видишь, всего есть ( 4) варианта, ( 2) из которых – благоприятны. То есть вероятность равна ( displaystyle frac{2}{4}=frac{1}{2}).
А почему не ( displaystyle frac{1}{3})?
Рассмотренная нами ситуация – пример зависимых событий. Первое событие – это первый звонок в дверь, второе событие – это второй звонок в дверь.
А зависимыми они называются потому что влияют на следующие действия. Ведь если бы после первого звонка в дверь нам открыл друг, то какова была бы вероятность того, что он находится за одной из двух других?
Правильно, ( 0%).
Но если есть зависимые события, то должны быть и независимые? Верно, бывают.
Правило умножения вероятностей независимых событий
Что такое независимые события ты уже знаешь.
А если нужно найти вероятность того, что два (или больше) независимых события произойдут подряд?
Можно конечно посчитать, но есть способ проще.
Допустим мы хотим знать, какова вероятность того, что бросая монетку ( 2) раза, мы два раза увидим орла?
Мы уже считали: ( p=0,25).
А если бросаем монетку ( 3) раза? Какова вероятность увидеть орла ( 3) раза подряд?
Всего возможных вариантов ( 8):
- Орел-орел-орел
- Орел-орел-решка
- Орел-решка-орел
- Орел-решка-решка
- Решка-орел-орел
- Решка-орел-решка
- Решка-решка-орел
- Решка-решка-решка
Не знаю, как ты, но я ( 3) раза ошибся, составляя этот список. Ух! А подходит нам только ( 1) вариант (первый).
( displaystyle p=frac{{{N}_{б}}}{N}=frac{1}{8})
Для 5 бросков можешь составить список возможных исходов сам. Но математики не столь трудолюбивы, как ты.
Поэтому они сначала заметили, а потом доказали, что вероятность определенной последовательности независимых событий каждый раз уменьшается на вероятность одного события.
Другими словами,
Вероятность определенной последовательности независимых событий равна произведению вероятностей каждого из событий
Рассмотрим на примере все той же, злосчастной, монетки.
Вероятность выпадения орла в ( 1) испытании? ( displaystyle frac{1}{2}). Теперь мы бросаем монетку ( 5) раз.
Какова вероятность выпадения ( 5) раз подряд орла?
( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}={{left( frac{1}{2} right)}^{5}}=frac{1}{32})
Это правило работает не только, если нас просят найти вероятность того, что произойдет одно и то же событие несколько раз подряд.
Если бы мы хотели найти последовательность РЕШКА-ОРЕЛ-РЕШКА, при ( 3) бросках подряд, мы поступили бы также.
Вероятность выпадения решка – ( displaystyle frac{1}{2}), орла – ( displaystyle frac{1}{2}).
Вероятность выпадения последовательности РЕШКА-ОРЕЛ-РЕШКА-РЕШКА:
( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}={{left( frac{1}{2} right)}^{4}}=frac{1}{16})
Можешь проверить сам, составив таблицу.
Правило сложения вероятностей несовместных событий
Так стоп! Новое определение.
Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента.
Ряд несовместных событий образуют полную группу событий.
Давай разбираться. Возьмем нашу изношенную монетку и бросим её ( 3) раза. Возможные варианты:
- Орел-орел-орел
- Орел-орел-решка
- Орел-решка-орел
- Орел-решка-решка
- Решка-орел-орел
- Решка-орел-решка
- Решка-решка-орел
- Решка-решка-решка
Так вот, несовместные события – это определенная, заданная последовательность событий. ( 1),text{ }2),text{ }3),text{ }4)ldots text{ }8)) – это несовместные события.
Вероятности несовместных событий складываются.
Если мы хотим определить, какова вероятность двух (или больше) несовместных событий, то мы складываем вероятности этих событий.
Нужно понять, что выпадение орла или решки – это два независимых события.
Если мы хотим определить, какова вероятность выпадения последовательности ( 1)) (или любой другой), то мы пользуемся правилом умножения вероятностей.
Какова вероятность выпадения при первом броске орла, а при втором и третьем решки?
( displaystyle p=frac{1}{2}cdot frac{1}{2}cdot frac{1}{2}=frac{1}{8})
Но если мы хотим узнать, какова вероятность выпадения одной из нескольких последовательностей, например, когда орел выпадет ровно ( 1) раз, т.е. варианты ( 4),text{ }6)) и ( 7)), то мы должны сложить вероятности этих последовательностей.
Всего вариантов ( 8), нам подходит ( 3).
( displaystyle p=frac{{{N}_{б}}}{N}=frac{3}{8})
То же самое мы можем получить, сложив вероятности появления каждой последовательности:
( displaystyle p={{p}_{4}}+{{p}_{6}}+{{p}_{7}}=frac{1}{8}+frac{1}{8}+frac{1}{8}=frac{3}{8})
Таким образом, мы складываем вероятности, когда хотим определить вероятность некоторых, несовместных, последовательностей событий.
Правило, помогающее не запутаться, когда умножать, а когда складывать:
Опишите, что должно произойти, используя союзы «И» или «ИЛИ». Затем вместо «И» ставим знак умножения, а вместо «ИЛИ» — сложения.
Возвратимся к примеру, когда мы подбросили монетку ( 3) раза, и хотим узнать вероятность увидеть орла ( 1) раз.
Что должно произойти?
Должны выпасть:
(орел И решка И решка) ИЛИ (решка И орел И решка) ИЛИ (решка И решка И орел).
Вот и получается:
( displaystyle left( frac{1}{2}cdot frac{1}{2}cdot frac{1}{2} right)+left( frac{1}{2}cdot frac{1}{2}cdot frac{1}{2} right)+left( frac{1}{2}cdot frac{1}{2}cdot frac{1}{2} right)=frac{1}{8}+frac{1}{8}+frac{1}{8}=frac{3}{8})
Давай рассмотрим несколько примеров.
Каждый год я участвую примерно в сотне собеседований в образовательных проектах JetBrains: собеседую абитуриентов в Computer Science Center и корпоративную магистратуру ИТМО (кстати, набор на программу идёт прямо сейчас). Все собеседования устроены по одному шаблону: мы просим на месте порешать задачи и задаём базовые вопросы по дисциплинам, которые студенты изучали в университетах. Большинство вопросов, которые мы задаём, довольно простые — нужно дать определение некоторого понятия, сформулировать свойство или теорему. К сожалению, у значительной доли студентов все эти определения выветриваются сразу после экзаменов в университетах. Казалось бы, что тут удивительного? В современном мире любое определение можно за пару секунд нагуглить, если это нужно. Но невозможность восстановить базовое определение свидетельствует о непонимании сути предмета.
Если непонимание алгебры или математического анализа может мало влиять на вашу жизнь, то непонимание теории вероятностей делает из вас лёгкую мишень для обмана и манипулирования. Суждения о вероятностях различных событий настолько глубоко вошли в нашу повседневную жизнь, что умение правильно рассуждать и отличать правду от невежества или манипуляции является необходимым. В этом небольшом обзоре мы поговорим о базовых понятиях теории вероятностей, научимся правильно формулировать утверждения про простые случайные процессы и разберём несколько парадоксов. Часть материала позаимствована из брошюры А. Шеня «Вероятность: примеры и задачи», которую я очень рекомендую для самостоятельного изучения.
Перед тем, как говорить об определениях, нам нужно договориться о том, откуда же в нашем мире берётся случайность. Например, почему мы считаем, что подбрасывание монеты — это случайный процесс? С точки зрения классической физики, описывающей процессы в макромире, всё детерминировано, поэтому по параметрам подброса монеты можно однозначно определить, какой стороной она упадёт. Однако на практике оказывается, что измерить и учесть все силы, которые действуют на монетку фактически, невозможно, и поэтому результат этого эксперимента принято считать случайным. Важно понимать, что этот вопрос не является вопросом теории вероятностей. Теория вероятностей работает с моделями — для неё монетка, у которой орёл и решка выпадают одинаково часто, и монетка, у которой орлов в два раза больше, чем решек, — это просто две разные модели. Вопрос о том, какая из моделей больше соответствует наблюдаемой действительности — это вопрос нашего опыта (опыт показывает, что частота орла и решки примерно одинаковая). Таким образом, первым делом мы должны договориться о модели.
Определения
Для определения модели, которая позволит нам говорить о вероятностях, нужно описать вероятностное пространство.
Вероятностное пространство в самом простом конечном случае состоит из множества элементарных исходов
и набора неотрицательных чисел
, таких что их сумма равна
. Довольно часто все исходы считаются равновероятными, т.е.
. В более сложном бесконечном случае нужно отдельно выделять множество интересующих нас событий и задавать вероятности событий при помощи функции, называемой вероятностной мерой. Событием называется множество, состоящее из элементарных событий, т.е. любое подмножество
. Вероятность события
, обозначается
, — это сумма всех таких
, что
. В частности, вероятность пустого события
равна нулю, а события
равна 1. В случае, когда все исходы считаются равновероятными, вероятность события просто равна отношению количества исходов, содержащихся в событии, к общему количеству элементарных исходов, т.е.
.
Вероятность любого события заключена между 0 и 1. Если вероятность события нулевая, то такое событие называется невозможным, если же вероятность события равна единице, то такое событие называется достоверным.
Важно, что без определения вероятностного пространства нельзя (в математическом смысле) говорить о вероятности чего-либо.
Замечание
На основе определения вероятностного пространства легко провести разделение между теорией вероятностей и статистикой: теория вероятностей предсказывает частоты на основе знания вероятностного пространства, а статистика решает обратную задачу — на основе наблюдаемых частот определяет параметры неизвестного вероятностного пространства.
Пример: подбрасывание монетки
Будем считать, что монетка
чеканная
«правильная» или «симметричная», т.е. она одинаково часто выпадает орлом и решкой, а на ребро никогда не встаёт. Тогда множество элементарных исходов состоит из двух элементов,
. Так как мы договорились, что монетка «правильная», то разумно считать, что
. Теперь давайте перечислим все возможные события и их вероятности.
- Не выпадет ни орёл, ни решка. Это соответствует событию
,
.
- Выпадет орёл,
,
.
- Выпадет решка,
,
.
- Выпадет орёл или решка,
,
.
Пример: подбрасывание игрального кубика
Как и в случае с монеткой мы будем предполагать, что игральный кубик выпадает всеми гранями одинаково часто. Тогда множество элементарных исходов состоит из шести элементов,
, все их вероятности равны
. Количество различных событий в этом эксперименте равно
(это количество всех подмножеств множества из 6 элементов). Удивительным образом вопрос «сколько существует различных событий в эксперименте с подбрасывание игрального кубика?», по моим наблюдения, ставит в тупик 9 из 10 абитуриентов.
Давайте рассмотрим некоторые примеры событий.
- Выпадет 1,
,
.
- Выпадет число большее трёх,
,
.
- Выпадет число кратное трём,
,
.
Пример: два подбрасывания монетки
В тех же предположениях о «симметричености» монеты мы определим множество элементарных исходов как множество упорядоченных пар
Симметриченость монетки позволяет нам заключить, что все элементарные исходы равновероятны, т.е.
.
Примеры событий.
- В первом броске выпадет решка,
,
.
- Выпадет хотя бы одна решка,
,
.
- Монетка дважды выпадет одной стороной,
,
.
Пример: выбираем случайное число из календаря 2020 года
Множество элементарных исходов
. Как выбрать вероятности? Это зависит от того, как устроен эксперимент. Например, мы можем вырвать случайный лист отрывного календаря и посмотреть число на нем. Наиболее точной моделью, описывающей этот эксперимент, было бы вероятностное пространство с
исходами, где одинаковые числа разных месяцев различаются. И тогда вероятность того, что выпадет число 1, была бы суммой вероятностей элементарных исходов, соответствующих первым числам разных месяцев, т.е.
. Но мы можем для удобства рассмотреть более простое множество элементарных исходов
с 31 исходом, но с разными вероятностями:
,
,
.
Пример события: «выпавшее число месяца делится на 10». Это соответствует событию
.
Замечание
Как только мы определили вероятностное пространство (т.е. определились с множеством
и вероятностями, которые мы приписываем элементарным исходам), то вопрос о вероятности некоторого события становится чисто арифметическим. Другими словами, как только мы выбрали некоторую математическую модель, которая с нашей точки зрения описывает физический процесс, то вероятности всех событий однозначно определены.
Задачи для самопроверки
В каждой задаче следует сначала описать вероятностное пространство, а уже только потом производить вычисления.
- Бросаем два игральных кубика: красный и синий. Определите вероятность того, что цифры на красном и синем кубиках совпадут.
- В этом же эксперименте с кубиками нужно найти наиболее вероятную сумму цифр на кубиках.
- Наудачу выбирается одно число от 1 до 20. Считая все числа равновозможными, определите вероятность того, что выбранное число:
- чётно;
- делится на 3;
- делится и на 2, и на 3;
- не делится ни на 2, ни на 3;
- имеет сумму цифр 9;
- имеет сумму цифр, делящуюся на 3.
Пример вероятностного пространства, не соответствующего физическому миру
Рассмотрим следующий эксперимент: подбрасываем две монетки и смотрим на то, какими сторонами они выпали. Можно было бы сказать, что в данной задаче всего три исхода: две решки, два орла и орёл и решка. Если предполагать, что все исходы равновозможны, то получается, что вероятность выпадения двух орлов равна 1/3. Математика не запрещает нам рассматривать такое вероятностное пространство, но экспериментальная проверка подсказывает, что в физическом мире ответ скорее ближе к 1/4. Поэтому не стоит по умолчанию предполагать все исходы равновозможными, иначе мы получим 1/2 в ответ на вопрос о вероятности встречи динозавра.
Формула суммы вероятностей
Будем называть два события несовместными, если их пересечение равно пустому множеству. Т.е., нет исходов, которые соответствовали бы обоим событиям. Пример: события «на игральном кубике выпало чётное число» и «на игральном кубике выпала единица или тройка» несовместны.
Несовместные события обладают следующим свойством. Пусть
и
— два несовместных события. Вероятность того, что произойдёт хотя бы одно из них, равна сумме вероятностей
и
, другими словами
, событие
также называют суммой событий
и
и обозначают
. Это свойство не выполняется для произвольных событий. Например, события «на игральном кубике выпало чётное число» и «на игральном кубике выпало число больше четырёх» не несовместны и сумма их вероятностей (5/6) больше вероятности их суммы (4/6).
Рассмотрим следующую задачу. В мешке лежат шарики трёх цветов: белые, жёлтые и чёрные. Причём известно, что белых
от общего числа, а жёлтых —
. Какова вероятность того, что случайно вытащенный шар будет светлым? Аккуратный подсчёт показывает, что если в мешке
шаров, то рассматриваемому событию соответствует
шаров, т.е.
от общего числа шаров. События «вытащен белый шар» и «вытащен жёлтый шар» несовместны, поэтому вероятность, что шар будет светлым равна сумме вероятностей этих событий.
События называются противоположными, если всегда происходит ровно одно из них. Из этого определения можно заключить, что во-первых, эти события несовместны, а во-вторых, их суммарная вероятность равна 1. Событие, противоположное событию
, выражается, как
(если все элементарные исходы имеют положительную вероятность, то это единственное такое событие).
Задача для самопроверки
Наудачу выбирается число
от 1 до 100. Рассмотрим следующие события:
- число
чётно;
- число
нечётно;
- число
делится на 4;
- число
имеет остаток 2 при делении на 4;
- число
имеет остаток 1 при делении на 4.
Какие из этих событий несовместны? (укажите все пары)
Формула включений и исключений
Как определить вероятность суммы двух событий, которые не являются несовместными? Рассмотрим следующий пример. Среди учеников школы
процентов знают французский язык и
знают немецкий. Доля тех, кто владеет обоими языками всего
. Какова доля учеников, знающих хотя бы один из этих двух языков? Если нарисовать диаграмму, если мы сложим доли знающих французский и знающих немецкий, то мы дважды посчитаем тех, кто знает оба языка. Поэтому ответ:
.
Этот же вопрос можно сформулировать и на языке теории вероятностей: с какой вероятностью случайно выбранный школьник знает хотя бы один из двух языков? Аналогичное рассуждение приводит нас к следующей формуле:
где
— это пересечение событий
и
, т.е. это событие состоящее из тех элементарных исходов, которые входят одновременно и в
, и в
(такое событие также называют произведением событий
и
и обозначают
).
Задача для самопроверки
Известно, что ученики класса, имеющие двойки по алгебре, составляют 25%, а ученики, имеющие двойки по геометрии, составляют 15%. Сколько учеников имеют двойки и по алгебре, и по геометрии, если ученики, не имеющие двоек ни по одному из предметов, составляют 70%?
Условная вероятность
Снова рассмотрим задачу про учеников и иностранные языки. Какая доля среди школьников знающих немецкий знает и французский? Ответ легко вычислить, посмотрев на картинку. Нужно вычислить отношение количества школьников знающих оба языка к количеству школьников знающих немецкий, т.е.
. Переходя к языку теории вероятностей можно задаться следующим вопросом: какова вероятность, что случайно выбранный школьник знает французский при условии, что он знает немецкий? Пусть события
и
соответствуют тому, что случайно выбранный школьник знает французский и немецкий соответственно. Тогда искомая вероятность называется условной вероятностью наступления
при условии
и обозначается
. По аналогии получаем следующую формулу для условной вероятности:
Какова вероятность, что случайно выбранный школьник знает немецкий при условии, что он знает французский?
Из формулы условной вероятности можно получить формулу для вероятности произведения двух событий.
Словами: чтобы найти вероятность того, что произойдут оба события
и
, надо умножить вероятность события
на условную вероятность события
при известном
.
Задача для самопроверки
В классе 50% мальчиков; среди мальчиков 60% любит мороженое. Какова доля мальчиков, любящих мороженое, среди учеников класса? Как это переформулировать на языке теории вероятностей?
Независимость
Рассмотрим эксперимент с бросанием двух игральных кубиков: красного и синего. В этом эксперименте имеются 36 исходов, которые мы считаем равновозможными. Вероятность того, что на красном кубике выпадет тройка, равна
(6 исходов из 36), вероятность того, что на синем кубике выпадет тройка, тоже равна
. Какова вероятность того, что на синем кубике выпадет тройка при условии, что на красном выпала тройка? По формуле условной вероятности нужно посчитать отношение вероятности выпадения тройки на обоих кубиках к вероятности выпадения тройки на красном. Получаем
. Заметим, что наличие информации о том, что на красном кубике выпала тройка, никак не влияет на вероятность выпадения тройки на синем. Такие события будем называть независимыми. Будем говорить, что события
и
независимы, если
(В этом определении предполагаются, что обе вероятности событий
и
строго больше нуля.)
Альтернативное определение можно получить, если воспользоваться определением условной вероятности: два события называются независимыми, если вероятность их произведения равна произведению их вероятностей.
Задачи для самопроверки
- Являются ли события «знать немецкий» и «знать французский» независимыми?
- Бросаем один игральный кубик. Являются ли независимыми события:
- «выпало чётное» и «выпало нечётное»,
- «выпало чётное» и «выпало 2»,
- «выпало чётное» и «выпало кратное трём».
Следующий шаг — это разговор про формулу Байеса, которая выводится из определения условной вероятности. Перепишем определение:
И подставив это в определение получаем формулу Байеса
которая позволяет менять местами событие и условие под знаком вероятности. Думаю, что про применение формулы Баейса нужно писать отдельный пост, например, такой.
На этом мы закончим с определениями и перед тем, как перейти к парадоксам, давайте обсудим, а в каких случаях мы можем говорить о вероятности.
Когда мы можем говорить о вероятности?
Предлагаю рассмотреть несколько вопросов, которые проиллюстрируют важность формулировок.
Какова вероятность того, что гуляя по улице вы встретите динозавра?
Я думаю, что всем ясно, что это не 1/2. Но всё же, как правильно ответить на этот вопрос? Проблема этого вопроса в том, что он сформулирован некорректно — из него нельзя однозначным образом определить вероятностное пространство, а следовательно и о вероятности говорить нельзя. Можно предложить какую-нибудь другую формулировку вопроса, в которой это будет очевидно. Например, начиная с завтрашнего дня на каждой улице города каждую минуту с вероятностью 0.00001 материализуется динозавр и существует в течение часа, никуда не уходя. В данной формулировке понятен случайный процесс и можно оценить вероятность встречи, если определить, как устроена прогулка, сколько длится и сколько улиц она затрагивает.
Вы подбросили монетку и не подглядывая накрыли её рукой. Какова вероятность того, что монетка повёрнута орлом вверх?
Очень хочется сказать, что в данном случае уж точно вероятность — 1/2. Однако, строго говоря, никакого случайного процесса уже нет. Монетка уже упала какой-то стороной. От того, что вы чего-то не знаете, не значит, что это что-то случайное. Например, если вы не знаете решение уравнения — это не значит, что его решением с одинаковой вероятностью может быть любое число. Поэтому в данном случае описать вероятностное пространство не получится. Можно переформулировать вопрос, например, так: «Какова вероятность, что вы угадаете сторону монетки, если наугад равновероятно выберите орёл или решку?». В такой формулировке уже ясно, что является случайным процессом (выбор орла или решки), как определить вероятностное пространство и получить ответ 1/2. При этом, в такой формулировке уже совершенно неважно, была монетка «честной» или нет.
Замечание. Нашу уверенность в чём-то тоже можно описывать в терминах теории вероятностей — это делается в рамках Байесовской интерпретации теории вероятностей. Эта интерпретации позволяет использовать аппарат теории вероятностей для оценки нашей уверенности в истинности каких-то утверждений (не обязательно случайных) основываясь на информации, которая нам известна. Однако стоит заметить, что в этом случае понятие вероятности становится субъективным — у одного и того же события с точки зрения разных наблюдателей может быть разная вероятность. Например, в покере вы можете считать вероятность выпадения пиковой дамы положительной (так как вы не видите её на столе и в своей руке), а ваш противник, у которого в руке уже есть пиковая дама, будет оценивать вероятность её выпадения как нулевую. При этом можно придумать и такой вариант, в котором обе оценки окажутся отличными от «реальной», объктивной, вероятности. В этом нет противоречия, т.к. в это три различные величины (игроки обладают разной информацией, а объективная вероятность в данном случае соответствует полной информации).
Вы проснулись утром. Какова вероятность того, что сегодня воскресенье?
Думаю, что вы уже поняли, что ответ 1/7 — неправильный, а точнее, вопрос некорректный. Не понятно, что является случайный процессом. Для того, чтобы получить 1/7 нужно уточнить вопрос, например, так: вы засыпаете в воскресенье вечером и случайным образом просыпаетесь в любое утро на следующей неделе, какова вероятность, что вы проснётесь в воскресенье? Но даже с этим уточнением, если спросить вас о дне недели уже после того, как вы проснулись (после того, как случайный выбор был сделан), то такой вопрос останется некорректным — иначе придётся предполагать, что вы находитесь в суперпозиции всех дней недели до тех пор, пока не посмотрите на календарь.
Я написал на доске некоторое (конкретное) число и утверждаю, что дважды успешно проверил его на простоту вероятностным алгоритмом, который ошибается с вероятность менее 1%. С какой вероятностью это число простое?
Хотелось бы сказать, что это число простое с вероятностью более 99.99%. Однако, с математической точки зрения число может быть либо простым, либо нет. Поэтому так говорить некорректно. После того, как алгоритм завершил работу, ничего случайного в этой постановке задачи уже нет, следовательно нет и вероятности. Правильно было бы сказать, что вы уверены на 99.99%, что это число простое, но и это вы можете заявить только в том случае, если доверяете мне на 100% 🙂
Парадоксы
В этом разделе мы попробуем разобрать несколько известных «парадоксов» теории вероятностей и понять, что в них либо нет противоречий, либо вопросы поставлены некорректно.
Парадокс Монти-Холла
Этот очень известный парадокс. Об него было сломано много копий, в том числе даже именитые математики давали неправильный ответ.
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?
Как подсказывает Википедия, для того, чтобы задача была определена корректно, нам требуется уточнить, что участнику игры заранее известны следующие правила:
- автомобиль равновероятно размещён за любой из трёх дверей;
- ведущий знает, где находится автомобиль;
- ведущий в любом случае обязан открыть дверь с козой (но не ту, которую выбрал игрок) и предложить игроку изменить выбор;
- если у ведущего есть выбор, какую из двух дверей открыть, он выбирает любую из них с одинаковой вероятностью.
Если вы не знакомы с этим парадоксом, то я предлагаю вам несколько минут подумать о том, каким будет правильный ответ.
Для того, чтобы ответить на заданный вопрос, давайте разберёмся, что тут является случайным процессом. По уточнению видно, что случайный процесс упоминается только в пунктах 1 и 4: «автомобиль равновероятно размещён за любой из трёх дверей» и «если у ведущего есть выбор, какую из двух дверей открыть, он выбирает любую из них с одинаковой вероятностью». Вопрос, на который мы должны научиться отвечать, звучит так: «Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор». Т.е. нас спрашивают о том, какая из двух стратегий даёт большую вероятность выигрыша. Замечу, что условие номер 4 никак не влияет на факт выигрыша игрока, поэтому нет смысла включать его в вероятностное пространство. Поэтому предлагается выбрать вероятностное пространство с множеством элементарных исходов
, соответствующим номеру двери, за которым находится автомобиль, и вероятностями
. Теперь рассмотрим две стратегии игрока: «оставить выбранную дверь», обозначим
, и «сменить дверь», обозначим
.
Мы не знаем, как игрок делает выбор первой двери, но нам и не нужно это знать. Достаточно проверить, как работает стратегия при всех выборах первой двери. Обозначим через
дверь, которую игрок выбрал изначально, а через
— дверь, за которой спрятан автомобиль. Тогда для любого
событие «игрок выиграл при использовании стратегии
» соответствует тому, что он угалад правильную дверь с первой попытки. Говоря формально, нас интересует событие
, т.е.
, и его вероятность
. Событие «игрок выиграл при использовании стратегии
» соответствует противоположному событию
, т.е.
, и его вероятность
. Осталось ещё раз отметить, что, если этот анализ верен для любого выбора
, поэтому верен и при любой стратегии выбора первой двери. Кроме того, заметим, что мы никак не использовали условие 4.
Как видите, никаких неоднозначностей тут нет, парадоксом эта задача называется только потому, что ответ может не соответствовать интуиции. Но так в математике случается довольно часто.
Парадокс мальчика и девочки
Цитирую Википедию.
Впервые задача была сформулирована в 1959 году, когда Мартин Гарднер опубликовал один из самых ранних вариантов этого парадокса в журнале Scientific American под названием «The Two Children Problem», где привёл следующую формулировку:
- У мистера Джонса двое детей. Старший ребёнок — девочка. Какова вероятность того, что оба ребёнка — девочки?
- У мистера Смита двое детей. Хотя бы один ребёнок — мальчик. Какова вероятность того, что оба ребёнка — мальчики?
Сам Гарднер изначально давал ответ
и
соответственно, но впоследствии понял, что ситуация во втором случае неоднозначна. Ответом на второй вопрос может быть и
в зависимости от того, как было выяснено, что один из детей — мальчик.
Вероятностное пространоство задано
и все вероятности равны
. В первом случае нам известно, что выполнено событие
. Поэтому при условии
вероятность двух девочек равна 1/2.
Во втором случае всё сложнее, т.к. не понятно, как мы узнали, что у мистера Смита один из детей мальчик. Можно предположить два варианта:
- Выбирается случайный человек с двумя детьми и его спрашивают, есть ли среди его детей мальчик. Тогда вероятность двух мальчиков получится 1/3, т.к. это соответствует вероятности ММ при условии события
.
- Выбирается случайный человек с двумя детьми, выбирается случайный его ребёнок (старший или младший) и спрашивается его пол. Этот эксперимент соответствует другому вероятностному пространству, в котором нужно ещё учесть выбор того ребёнка, про которого спрашивают. В нём будет 8 элементарных исходов, и нам подойдут четыре из них (ММ и спросили про старшего, ММ и спросили про младшего, МД и спросили про старшего, ДМ и спросили про младшего). Нам подходят два исхода, поэтому ответом будет 1/2.
Парадокс Спящей Красавицы
Обсуждение этого парадокса мотивировано вот этим постом на хабре, который вызвал широкое обсуждение, но описание этого парадокса есть и в википедии.
Испытуемой («Спящей Красавице») делается укол снотворного. Бросается симметричная монетка. В случае выпадения орла её будят, и эксперимент на этом заканчивается. В случае выпадения решки её будят, делают второй укол (после чего она забывает о побудке) и будят на следующий день, не бросая монеты (в таком случае эксперимент идёт два дня подряд). Вся эта процедура Красавице известна, однако у неё нет информации, в какой день её разбудили.
Представьте себя на месте Спящей Красавицы. Вас разбудили. Какова вероятность того, что монетка упала решкой?
Предлагается рассмотреть два альтернативных решения с разными результатами.
Решение 1
У вас нет никакой информации о результате выпадения монеты и предыдущих побудках. Поскольку известно, что монетка честная, можно предположить, что вероятность выпадения решки равна
.
Решение 2
Проведём эксперимент 1000 раз. Спящую Красавицу будят в среднем 500 раз с орлом и 1000 раз с решкой (т.к. при выпадении решки Спящую Красавицу спрашивают 2 раза). Поэтому вероятность выпадения решки равна
.
Кажется, что оба решения могут претендовать на звание правильного. Однако, при попытке определить вероятностное пространство нас ожидают серьёзные трудности. Что же является случайным процессом? Дело в том, что когда Спящая Красавица просыпается, никакого случайного процесса уже нет. Выбор уже сделан. Ей не известен результат этого выбора, но ничего случайного уже нет. Это возвращает нас к примеру с динозавром. Если вы не знаете, есть ли за углом динозавр, то это не значит, что он там есть с вероятностью 1/2. Поэтому «Решение 1» отвечает не на вопрос про вероятность, а на вопрос про степень уверенности Спящей Красавицы. А «Решение 2» предлагает рассмотреть совершенно другой эксперимент, в котором задаётся в общем-то совершенно другой вопрос, на который предлагается ответить внешнему наблюдателю до начала эксперимента.
Для того, чтобы придать этому вопросу математический смысл и получить желаемый ответ 2/3, придётся воспользоваться каким-нибудь философским приёмом, вроде «подселения душ». Например, так: вы заходите в аппарат переселения душ, после этого подбрасывается монетка для Спящей Красавицы, которая создаёт две параллельные вселенные: одну, где монетка выпала орлом, и другую, где выпала решкой. Суммарно в пространстве-времени этих двух альтернативных вселенных есть три различных пробуждения Спящей Красавицы. Аппарат по переселению душ с вероятностью 1/3 подселяет вашу душу в тело Спящей Красавицы незадолго до одного из этих пробуждений. Какова вероятность, что вы проснетесь в параллельной вселенной, где выпала решка?
Как видите, для придания математического смысла этому вопросу, придётся хорошенько пофантазировать, но этим занимаются не математики, а философы (подробнее в этом посте). Утверждать, что «оба решения правильные», некорректно с математической точки зрения.
Задача для самопроверки
Объясните, почему в задаче о детях моряка, с которой начинается этот пост, вопрос поставлен некорректно (т.е. ни 1/2, ни 1/3 не являются правильным ответом).
Бесконечный случай
Когда мы переходим к бесконечному случаю, т.е. рассматриваем эксперименты с бесконечным числом элементарных исходов, то всё становится значительно сложнее. Я не буду вдаваться в детали и даже не буду определять вероятностное пространство для бесконечного случая, т.к. это требует более сложной математики. Однако, для иллюстрации отмечу, что в бесконечном случае могут быть такие (плохие) множества элементарных исходов, которые не имеют вероятности (неизмеримые множества). При этом для всех хороших (измеримых) событий вероятность определена однозначно. Поэтому и те «парадоксы», которые возникают в бесконечном случае, тоже возникают из-за неоднозначности выбора вероятностного пространства. Хорошим наглядным примером служит парадокс Бертрана, показывающий, как казалось бы эквивалентные (на самом деле нет) вероятностные пространства приводят к разным результатам.
Вместо заключения
Даже если вы не собираетесь никуда поступать или проходить собеседования на технические позиции в IT-компании, то вы всё равно можете захотеть освежить знания по математике, которые могут пригодиться в программировании. Могу посоветовать онлайн-курс СS центра по теории вероятностей, который читает А.И. Храбров.
БОНУС
Приглашаю всех послушать лекция Александра Шеня «Генераторы «случайных чисел»: теория и практика» в это воскресенье 26 апреля в 14:00 в Computer Science клубе. Лекция будет читаться в zoom-е, для участия нужно записаться на курс или подписаться на рассылку.
Сложение и умножение вероятностей
- Сложение вероятностей несовместных событий
- Вероятность противоположного события
- Умножение вероятностей независимых событий
- Вероятность появления хотя бы одного события
- Примеры
п.1. Сложение вероятностей несовместных событий
События называют несовместными, если они не могут произойти одновременно в результате одного опыта.
Например:
1) Нельзя одновременно A = «получить 5» и B = «получить 2» на экзамене. События A и B – несовместны.
2) Нельзя одновременно C = «достать туз» и D = «достать шестерку» из колоды карт. События C и D – несовместны.
Вероятность появления одного из двух несовместных событий A или B равна сумме вероятностей этих событий: $$ mathrm{ P(Avee B)=P(A) + P(B) } $$
Если обобщить на любое количество событий:
Вероятность появления нескольких несовместных событий A1 или A2 или …Ak равна сумме вероятностей этих событий: $$ mathrm{ P(A_1vee A_2vee … vee A_k)=P(A_1) + P(A_2) + … + P(A_k) } $$
Например:
Стрелок может попасть в «10» с вероятностью P(10) = 0,3, в «9» – с вероятностью P(9) = 0,2. Значит, попасть в «10 или 9» он может с вероятностью:
P(«10 или 9») = 0,3 + 0,2 = 0,5
п.2. Вероятность противоположного события
Пространство элементарных событий образует полную группу событий.
Сумма вероятностей всех событий, образующих полную группу, равна единице. $$ mathrm{ Omega={A_1, A_2, …, A_k}, P(A_1) + P(A_2) + … + P(A_k) = 1 } $$
Например:
При бросании кубика Ω = {1; 2; … ; 6} – полная группа событий.
Вероятности выпадения каждой грани: (mathrm{p_1=p_2=…=p_6=frac16})
Сумма всех вероятностей: (mathrm{p_1+p_2+…+p_6=6cdot frac16=1})
Два случайных события A и B называют противоположными, если они несовместны и образуют полную группу событий: $$ mathrm{ Omega=left{A;Bright}, B=overline{A}, } $$ Сумма вероятностей противоположных событий равна единице. $$ mathrm{ P(A) + P(B) = P(A) + P(overline{A}) = 1 } $$
Например:
Вероятность попадания стрелка в мишень p = 0,8.
Противоположное событие: стрелок не попадёт в мишень. Его вероятность:
q = 1 – p = 0,2.
п.3. Умножение вероятностей независимых событий
Два случайных события A и B называют независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Вероятность совместного появления двух независимых событий A и B равна произведению вероятностей этих событий: $$ mathrm{ P(A wedge B) = P(A) cdot P(B) } $$
Если обобщить на любое количество событий:
Вероятность совместного появления нескольких независимых событий A1 и A2 и … Ak равна произведению вероятностей этих событий: $$ mathrm{ P(A_1wedge A_2wedge …wedge A_k)=P(A_1)cdot P(A_2)cdot … cdot P(A_k) } $$
Например:
Вероятность попадания стрелка в мишень p = 0,8.
Стрелок делает три выстрела подряд.
1) Какова вероятность, что он попал все три раза?
Каждый выстрел является независимым событием, поэтому вероятность трёх удачных выстрелов подряд:
P3 = P(+, +, +) = p · p · p = 0,83 = 0,512
2) Какова вероятность, что он не попал ни разу?
Вероятность промаха равна q = 1 – p = 0,2.
Вероятность трёх промахов подряд:
P0 = P(–, –, –) = q · q · q = 0,23 = 0,008
3) Какова вероятность, что он попал только один раз?
Стрелок мог попасть при первом выстреле, а затем два раза промахнуться, или при втором выстреле (промахнуться на первом и третьем), или при третьем (промахнувшись два раза поначалу). Сложение и умножение вероятностей даёт итоговую вероятность одного попадания:
P1 = P(+,–,–) + P(–,+,–) + P(–,–,+) =
p · q · q + q · p · q + q · q · p = 3pq2 = 3 · 0,8 · 0,22 = 0,096
4) Какова вероятность, что он промахнулся один раз?
Аналогичные предыдущему пункту рассуждения приводят к такому выражению для вероятности двух попаданий (одного промаха):
P2 = P(–,+,+) + P(+,–,+) + P(+,+,–) =
q · p · p + p · q · p + p · p · q = 3p2q = 3 · 0,82 · 0,2 = 0,384
Мы получили следующий закон распределения для возможного количества попаданий из трёх выстрелов:
Количество попаданий, X
0
1
2
3
Вероятность, Px
0,008
0,096
0,384
0,512
X = {0; 1; 2; 3} образует полную группу событий. Сумма всех вероятностей:
P0 +P1 + P2 + P3 = 0,008 + 0,096 + 0,384 + 0,512 = 1
п.4. Вероятность появления хотя бы одного события
Вероятность появления хотя бы одного из событий A1, A2, …, Ak, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий: $$ mathrm{ P(A)=1-q_1cdot q_2cdot … cdot q_{k}, q_{i}=1-p_{i} } $$
Например:
Студент сдаёт два экзамена.
Вероятность сдать первый экзамен равна p1 = 0,7 второй – p2 = 0,6.
Тогда вероятность сдать хотя бы один экзамен: P = 1 – q1q2 = 1 – 0,3 · 0,4 = 0,88.
п.5. Примеры
Пример 1. Подбрасывают четыре игральных кубика. Какова вероятность, что на каждом из них выпадет нечётное число очков?
Для кубика Ω = {1; 2; 3; 4; 5; 6} – пространство элементарных событий.
Выпадение нечётного числа A = {1; 3; 5}. Вероятность выпадения нечётного числа для одного кубика: (mathrm{p=frac{k}{n}=frac36=frac12}).
Результаты подбрасывания 4-х кубиков являются независимыми. Вероятность, что на каждом выпадет нечётное число: $$ mathrm{ P=pcdot pcdot pcdot p=p^4=frac{1}{2^4}=frac{1}{16} } $$ Ответ: (frac{1}{16}).
Пример 2. На полигоне испытываются три ракеты.
Вероятность успешного испытания для каждой из ракет: p1 = 0,8, p2 = 0,75, p3 = 0,6.
Какова вероятность, что хотя бы одна ракета пройдёт испытания успешно?
Найдём вероятность того, что ни одна из ракет не пройдёт испытаний:
q1 = 1 – p1 = 0,2, q2 = 1 – p2 = 0,25, q3 = 1 – p3 = 0,4
q1 · q2 · q3 = 0,2 · 0,25 · 0,4 = 0,02
Тогда, искомая вероятность (противоположное событие):
P = 1 – q1 · q2 · q3 = 1 – 0,02 = 0,98
Ответ: 0,98.
Мораль: инвестору нужно показывать сразу несколько сырых проектов.
Пример 3. В системе пожарной сигнализации установлены два независимых датчика. Вероятность срабатывания каждого из датчиков при пожаре: p1 = 0,6; p2 = 0,7. Найдите вероятность того, что при пожаре:
1) сработает ровно один датчик;
2) сработает хотя бы один датчик.
Вероятности отказов: q1 = 1 – p1 = 0,4; q2 = 1 – p2 = 0,3.
1) Событие «сработает ровно один датчик» является суммой двух событий «первый сработал, второй – отказал» или «первый отказал, второй – сработал». Вероятность:
P1 = p1q2 + q1p2 = 0,6 · 0,3 + 0,4 · 0,7 = 0,46
2) Найдем вероятность отказа обоих датчиков:
P0 = q1q2 = 0,4 · 0,3 = 0,12
Событие «сработает хотя бы один датчик» является противоположным отказу обоих датчиков. Вероятность:
P1 ∨ 2 = 1 – P0 = 1 – 0,12 = 0,88
Ответ: 1) 0,46; 2) 0,88.
Пример 4. У админа в ящике 11 плат, из которых 3 – бракованные.
Наугад берётся 2 платы. Какова вероятность того, что хотя бы одна из них – рабочая?
Найдём вероятность того, что обе выбранные платы – бракованные.
Выбрать 2 платы из 3 бракованных можно (mathrm{C_3^2=C_3^1=3}) способами.
Выбрать 2 платы из общей совокупности можно (mathrm{C_{11}^2=frac{11cdot 10}{1cdot 2}=55}) способами.
Вероятность взять обе бракованные платы из ящика: (mathrm{P_{2 text{бр}}=frac{C_3^2}{C_2^{11}}=frac{3}{55}})
Значит, вероятность того, что хотя бы одна плата не будет бракованной (противоположное событие):
(mathrm{P=1-P_{2 text{бр}}=1-frac{3}{55}=frac{52}{55}}).
Ответ: (mathrm{frac{52}{55}}).
Пример 5*. Парадокс дней рождения
В классе учится k человек. Исследуйте вероятность того, что хотя бы у двух одноклассников дни рождения совпадают.
Считаем, что в году n = 365 дней.
Пусть день рождения одного из учеников известен (один день в году – «занят»).
Тогда вероятность того, что день рождения второго ученика не совпадает с днём рождения первого: (mathrm{q_2=1-frac{1}{365}}) («заняты» два дня).
Вероятность того, что день рождения третьего ученика не совпадает с днями рождения первых двух: (mathrm{q_3=1-frac{2}{365}}) («заняты» три дня). И т. д.
Для всех k учеников вероятность того, что все дни рождения разные: begin{gather*} mathrm{ widetilde{p}(k)=q_2cdot q_3cdot … cdot q_{k}=left(1-frac{1}{365}right)left(1-frac{2}{365}right)…left(1-frac{k-1}{365}right)= }\ mathrm{ =frac{364cdot 363cdot … cdot(365-k+1)}{365^{k-1}}= frac{365cdot 364cdot 363cdot … cdot(365-k+1)}{365^{k}}= frac{365!}{365^{k}(365-k)!} } end{gather*} Значит, вероятность того, что хотя бы у двух одноклассников дни рождения совпадают: begin{gather*} mathrm{ p(k)=1-widetilde{p}(k)=1-frac{365!}{365^{k}(365-k)!} } end{gather*}
Таким образом, в классе из 30 человек вероятность совпадения дней рождения равна 70,63%. А в группе из 50 человек она достигает 97,04%.