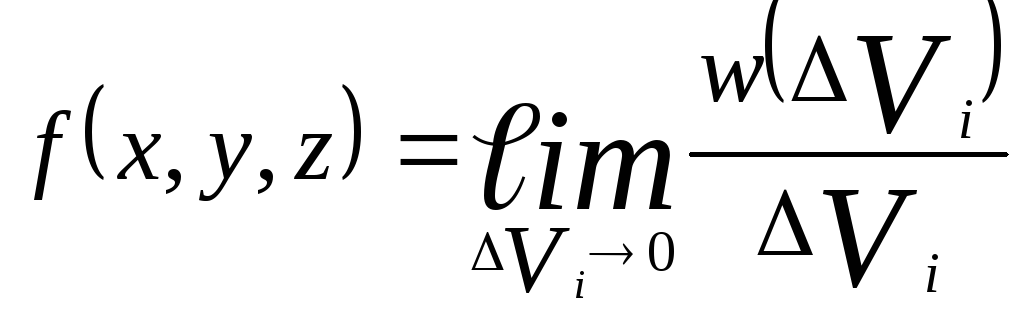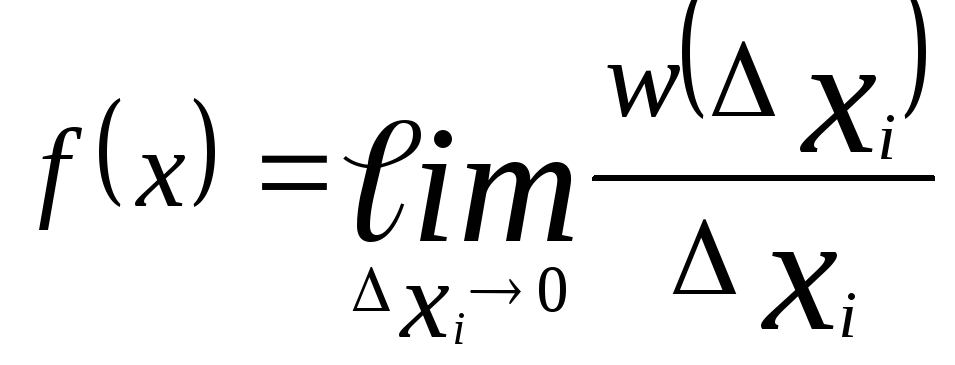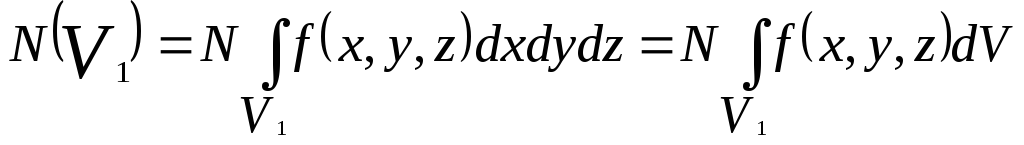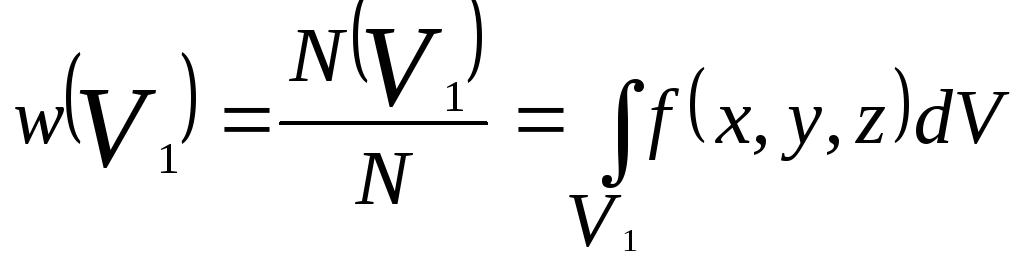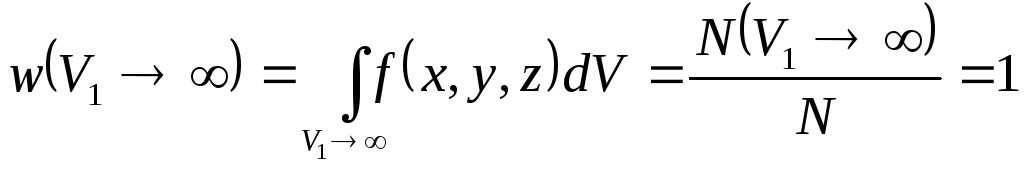3.СТАТИСТИЧЕСКОЕ
ОПИСАНИЕ СВОЙСТВ ИДЕАЛЬНОГО ГАЗА.
3.1. Основные
понятия теории вероятностей
Для изучения
макросистем применяют статистические
методы, использующие понятия и величины,
относящиеся не к отдельным частицам, а
к большим совокупностям частиц. Подробно
о статистическом описании систем и
теории вероятностей можно прочитать в
[2,4,12,14,16].
Многие законы
молекулярной физики, удобно трактовать,
пользуясь понятием вероятности.
К этому
понятию прибегают, когда речь идет о
случайных событиях.
Случайным
событием
называют такое событие, которое при
некоторых условиях может произойти или
не произойти.
Относительной
частотой
случайного события называют отношение
числа n
появления
данного события к общему числу N
проведённых
испытаний, в каждом из которых могло
проявиться или не проявиться данное
событие.
Например, при
одинаковых условиях было произведено
три серии бросания монет: в первой серии
было 10 бросаний, число монет, упавших
орлом вверх, равно 4; во второй серии
было 20 бросаний, число монет, упавших
орлом вверх, равно 12; в третьей серии
было 12 бросаний, число монет, упавших
орлом вверх, равно 6. Событие – падение
монеты орлом вверх. Относительная
частота события в сериях будет: в первой
серии
,
во второй серии
,
в третьей серии
.
Данный пример, а
также другие наблюдения различных
явлений показывают, что, если число
испытаний невелико, то относительные
частоты появления события в каждой
серии могут существенно отличаться
одна от другой. Если же число опытов в
сериях велико, то относительные частоты
отличаются мало. Опыт показывает, что
существует такое число w
, называемое
вероятностью
случайного события, что относительные
частоты события при большом числе
испытаний мало отличаются от этого
числа.
Вероятностью
w
случайного события,
называется предел, к которому стремится
отношение числа опытов, приводящих к
его осуществлению, к общему числу опытов
при беспредельном увеличении последнего:
(3.1)
Вероятность
случайного события может изменяться в
следующих границах
.
Вероятность
невозможного
события
равна нулю, вероятность
достоверного события
равна единице.
Два события А и В
называют несовместимыми
или непересекающимися,
если при проведении некоторого испытания
они не могут произойти одновременно.
Суммой,
или объединением,
двух событий называют наступление
одного из двух событий А или В и записывают
в виде:
С = А+В или
(Здесь
–
знак объединения).
Вероятность
наступления одного из несовместимых
событий А или В определяется законом
сложения вероятностей
(3.2)
Пример.
Вероятность нахождения частицы в объёме
V1
равна w1
=0,3 ,
вероятность нахождения её в объёме V2
равна w2
=0,2 . Какова
вероятность нахождения частицы в любом
из этих объёмов или в объёме V1
или в объёме
V2
?
Решение.
Частица не
может находиться одновременно сразу в
двух объёмах, эти события несовместимы,
следовательно
w
= w1
+ w2
, w
= 0,3+0,2 = 0,5
Два события
называются независимыми,
если наступление одного из них не влияет
на вероятность наступления другого.
Произведением,
или пересечением,
двух событий называют одновременное
или последовательное наступление обоих
событий А и В и записывают в виде:
С = А.В
или
(Здесь
–
знак пересечения).
Для двух независимых
событий выполняется закон умножения
вероятностей.
(3.3)
Пример.
Вероятность обнаружения частиц одного
сорта в объёме V1
равна w1
= 0.8 ,
вероятность обнаружения их в объёме V2
равна w2
= 0,5. Эти
события независимы. Какова вероятность
обнаружить частицы данного сорта и в
объёме V1
и в объёме
V2
одновременно?
Решение.
Так как данные события независимы, то
можно использовать теорему умножения
вероятностей: w1
=0,8 , w2
=0,5, тогда
w
= 0,8.0,5
=0,4. В 40% будут наблюдаться одновременно
эти два события.
В физике многие
микропараметры являются случайными
величинами, поэтому необходимо
представление о среднем значении
случайной величины. Среднее арифметическое
значение случайной величины тесно
связано с вероятностью. Пусть N
– число наблюдений величины Х. Пусть в
N1
случаях
величина Х имеет значение Х1
, в N2
случаях –
Х2
и так далее. Среднее
арифметическое значение Х
будет равно:
(3.4)
Так как
,
то можно записать среднее значение
случайной величины Х через относительные
частоты
(3.5)
При очень больших
N
относительная частота мало отличается
от вероятности. Среднее арифметическое
значение случайной величины называют
в этом случае математическим
ожиданием и
записывают в виде:
(3.6)
Кроме среднего
значения случайной величины, важно
знать насколько сильно отличаются её
значения от среднего. Для характеристики
разброса значений случайной величины
от среднего используют среднеквадратичное
отклонение от среднего
или стандартное
отклонение.
При большом числе наблюдений стандартную
ошибку можно определить по формуле:
(3.7)
Стандартная
ошибка имеет те же единицы измерения,
что и случайная величина и показывает
интервал, в котором оказывается случайная
величина.
Другой характеристикой
разброса значений случайной величины
от среднего является дисперсия
σ2,
равная квадрату стандартной ошибки.
Она отражает «площадь» разброса случайной
величины и измеряется в квадратных
единицах измерения случайной величины.
Если явления
характеризуются непрерывно меняющимися
величинами, то определение вероятности
по формуле (3.1) не имеет смысла. Например,
не имеет смысла спрашивать, какова
вероятность того, что скорость частицы
равна 10 м/с, так как скорость – непрерывная
случайная величина и может принимать
любые значения, сколь угодно мало
отличающиеся от заданной. Множество
событий в таком случае не является
счётным, и их вероятностное описание
осуществляется с помощью плотности
вероятности.
Рассмотрим понятие плотности вероятности
на физическом примере. Пусть в некотором
сосуде находится газ. При различных
актах наблюдения молекула оказывается
в различных точках. В этом случае всё
пространство (в том числе и вне объёма
сосуда) делят (см. [2]) на небольшие объёмы
Vi
(i
= 1,2,3,..). Число таких объёмов бесконечно.
Число актов наблюдений N.
При каждом акте наблюдения молекула
окажется обнаруженной в одном из объёмов
Vi
. Пусть при N
актах наблюдений ()
молекула обнаружена Ni
раз в объёме
Vi
. Тогда вероятность обнаружения молекулы
в объёме Vi
равна
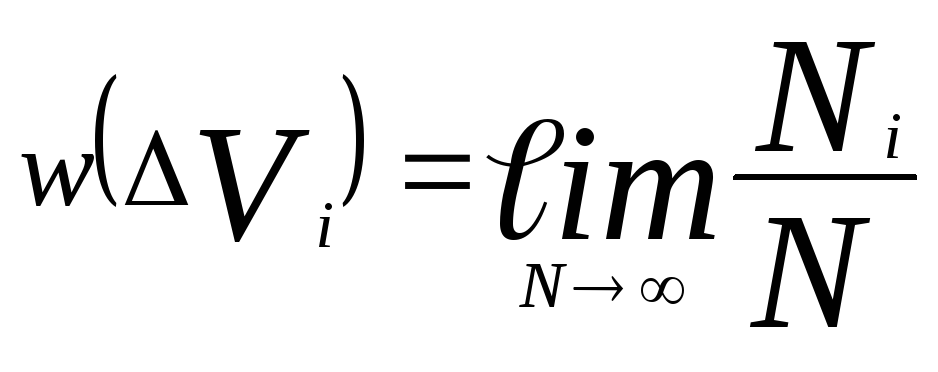
Внутри сосуда эта вероятность даже при
равных объёмах различна (не постоянна),
зависит от объёма Vi
. Поэтому для определения вероятности
нахождения молекулы в объёме Vi
используют
понятие
плотности вероятности, определяя
её как предел отношения вероятности
нахождения частицы в объёме Vi
к величине этого объёма, при стремлении
последнего к нулю:
(3.8)
Здесь x,
y,
z
– координаты точки, к которой стягивается
бесконечно малый объём. Таким образом,
плотность
вероятности
это вероятность нахождения молекулы в
бесконечно малом объёме вблизи некоторой
точки, отнесённая к этому объёму; то
есть она определяется так же, как и
другие «плотности». Для одномерного
случая:
(3.9)
Здесь х
– координата точки, к которой стягивается
бесконечно малый интервал хi
. Вблизи
разных координат плотность вероятности
может быть различной. Если изобразить
графически распределение плотностей
вероятностей, то кривая зависимости
будет называться кривой распределения
плотностей вероятностей или дифференциальным
законом распределения.
Если произвести
N
наблюдений, то в бесконечно малом объёме
dV
в окрестностях точки (x,
y,
z)
молекула будет обнаружена в dN
случаях:
или
Для одномерного
случая:
(3.10)
Поскольку число
молекул очень велико,
имеет смысл вероятности нахождения
молекулы вблизи точки с координатой x
в интервале dx.
Если подсчитать
число случаев N(V1)
обнаружения молекул в конечном объёме
V1
, то оно
будет связано с плотностью вероятности
следующим образом:
Вероятность быть
обнаруженной в объёме V1
для молекулы
определяется формулой:
(3.11)
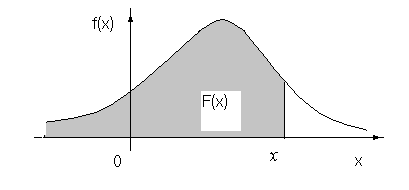
Н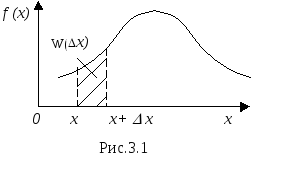
рисунке 3.1, где изображено дифференциальное
распределение случайной величины Х,
вероятность частицы быть обнаруженной
в интервале x
вблизи некоторого значения x
(одномерный случай) численно равна
площади заштрихованной криволинейной
трапеции. Знание плотности вероятности
позволяет найти вероятность для любой
области, в которой плотность определена.
Поскольку вероятность для непрерывной
случайной величины определяют через
плотность вероятности, то и среднее
значение непрерывной случайной величины
определяют тоже через плотность
вероятности. Для непрерывной случайной
величины x
, которая
может принимать любые значения в
интервале от 0 до a
, среднее
значение можно определить по формуле:
.
Усреднение можно
проводить по ансамблю
или по
времени [2,4,5,16].
Возьмём очень
большое число N
a
совершенно
одинаковых сосудов с одинаковым числом
молекул N
в каждом из них. Сосуд с заключёнными в
нём N
молекулами можно назвать статистической
системой. Совокупность статистических
систем называется статистическим
ансамблем.
Вычислить среднее по ансамблю значение
некоторой
случайной величины x
, связанной с молекулой, можно по формуле:
,
где N
a
– число
систем в ансамбле, xi
– значение
случайной величины, характеризующей
молекулу в i
– той системе ансамбля. При большом N
a
, как
показано в [2], среднее по ансамблю равно
математическому ожиданию случайной
величины х.
Вычислить среднее
по времени значение
некоторой случайной величины х
в одной из систем ансамбля можно,
проследив за ней в течение очень большого
промежутка времени. Тогда
можно
вычислить по формуле:
В 1871 году Л. Больцман
высказал эргодическую
гипотезу,
согласно которой среднее по ансамблю
равно среднему по времени
.
Доказательство справедливости этой
гипотезы до настоящего отсутствует.
Кроме дифференциального
распределения некоторой случайной
величины х,
используют понятие интегрального
распределения
этой величины.
Пусть f(x)
есть распределение плотности вероятности
некоторой случайной величины х,
которая может принимать любые значения
(),
тогда функция F(x)
называется функцией распределения
вероятностей или интегральным законом
распределения. Значение F(x)
, определяемое
по формуле:
,
(3.12)
показывает
вероятность того, что случайная величина
Х не превышает значения
x.
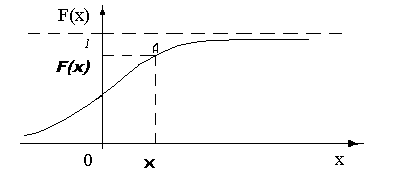
На рис.3.2 (б)
представлен вид интегрального
распределения, соответствующий
дифференциальному распределению,
изображённому на рис.3.2(а). Заштрихованная
часть на рис 3,2 (а) равна значению F(x)
и означает вероятность того, что случайная
величина Х не превышает значения х.
На рис. 3.2(б)
эта вероятность равна ординате точки
А.
Рис.3.2 а
Рис.3.2 б
Из рис.3.2 (б) видно,
что при
значение
.
Это определяется условием нормировки:
.
Для трёхмерного случая:
(3.13)
Условие нормировки
можно пояснить на примере всё тех же
частиц газа в пространстве. Если выбрать
объём, охватывающий всё пространство,
то при каждом испытании частица окажется
в какой-то точке пространства (факт
существования частицы) и, следовательно,
.
Вероятность найти частицу будет равна
единице:
Вероятность
попадания случайной величины Х в заданный
интервал
равна
приращению функции распределения на
этом интервале:
или
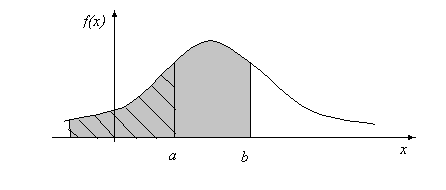
Графически
это изображено на рис. 3.3, где вероятность
попадания случайной величины x
в заданный интервал
численно равна площади криволинейной
трапеции в интервале.
Рис.3.3
- Авторы
- Файлы
- Литература
Хаустов П.А.
1
1 Ставропольский государственный аграрный университет
1. Трофимова Т.И., Курс физики: учебное пособие для вузов. – М.: Издательский центр «Академия», 2008. – 560 с.
2. Рабочая тетрадь «Математическая логика и теория алгоритмов» (учебное пособие) / Т.А. Гулай, С.В. Мелешко, И.А. Невидомская, А.А. Яновский. // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 8-2. – С. 169.
3. Яновский А.А., Симоновский А.Я., Савченко П.И. моделирование гидрогазодинамических процессов в кипящей магнитной жидкости // Информационные системы и технологии как фактор развития экономики региона: сб. науч. трудов. – Ставрополь, 2013. – С. 159-163.
4. Яновский А.А. Управление теплообменными процессами при кипении магнитной жидкости на неограниченной поверхности при помощи магнитного поля/ Яновский А.А., Симоновский А.Я. // Физическое образование в вузах. – 2012. – Т.18, №1. – С. 35-36.
5. Яновский А.А., Симоновский А.Я. Математическое моделирование формы пузырька пара в кипящей магнитной жидкости // Научно-практическая конференция «Финансово-экономические и учетно-аналитические проблемы развития региона». – Ставрополь, 2013. – С. 490-493
6. Яновский А.А. Тепло- и массоперенос поле в кипящей магнитной жидкости в однородном магнитном поле / Яновский А.А., Симоновский А.Я., Чуенкова И.Ю. // Труды XI Международной конференции «Перспективные технологии, оборудование и аналитические системы для материаловедения и наноматериалов». 2014. Ч.1. Курск. – С. 252-257.
7. Яновский А.А. К вопросу о теплообмене в кипящей магнитной жидкости / Яновский А.А., Симоновский А.Я., Холопов В.Л. // В сборнике: ХI Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики сборник докладов. Составители: Д.Ю. Ахметов, А.Н. Герасимов, Ш.М. Хайдаров. 2015. – С. 4336-4338.
8. Яновский А.А., Спасибов А.С. Математическое моделирование процессов в кипящих намагничивающихся средах // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 183-186.
Теория вероятности представляет собой раздел математики, изучающей закономерности массовых случайных явлений. Однако, область ее применения не ограничивается одной только математикой, а активно используется в различных областях науки, например в различных разделах физике, о чем пойдет речь в данной статье. На рубеже девятнадцатого и двадцатого веков многие ученые пытались, с точки зрения классической физики, объяснить принцип поведения электронов и других элементарных частиц, однако их попытки потерпели неудачу, ввиду того, что фотоны и электроны проявляли то свойства волн (интерференция), то свойства частиц (отражение, преломление), то есть имели некий дуализм, который впоследствии был назван корпускулярно-волновым. Только в 1926 году получилось устранить, казавшуюся невозможность сочетания этих свойств, а наука, изучающая поведение таких частиц, получила название квантовой, однако из-за несовершенных приборов было невозможно полностью описать их поведение, и тут на помощь пришла теория вероятности. То есть надо было только вычислить вероятность, того что мы получим определенный результат. Однако позже выяснилось, что обычное сложение вероятностей по законам теории Лапласа не подходит, ввиду очень малых размеров исследуемых объектов. Но, не подчиняясь законам, само понятие вероятности не претерпевает изменений, то есть вероятность p наступления события A будет равно отношению благоприятных исходов опыта m к общему числу проведенных опытов:

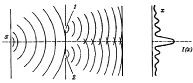
Следовательно, нам стоит лишь изменить способ вычисления вероятности в квантовой механики. Для нахождения такой формулы проводилось множество экспериментов, в основном мысленных, в данной статье я опишу один из них. Предположим, что у нас есть схема, которая состоит из слабого источника электронов (S), расположенного в некой области точки А, экран B с двумя отверстиями и за линией C детектор электронов, фиксирующий пролет частиц.
Рис. 1. Схема опыта
В результате электрон, выпущенный из источника, пролетает через одно из отверстий и регистрируется детектором, который может быть расположен на расстоянии х от C. В итоге мы имеем функцию x от вероятности p, то есть возможность попадания электрона в точку х. Данный график будет представлять собой сложную кривую и должен подчиняться функции плотности распределения вероятности, имеющей вид:
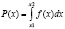
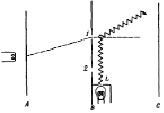
По теории вероятности, частица, летящая из источника в некоторую точку x, должна проходить через одно из открытых отверстий. Применяя формулу сложения вероятностей 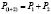
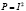

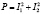
Рис. 2. Явление интерференции
И тут возникает парадокс, прослеживая пролеты частиц и регистрируя через какое отверстие он пролетает и проверив экспериментально правильность построение кривых b и с, в итоге получим кривую d, которая будет равна формуле сложения вероятностей:
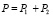
Таким образом, теория вероятности сыграла очень важную роль в становлении квантовой физики, ввиду отсутствия нужного оборудования, только она помогла в понимании поведения элементарных частиц.
Рис. 3. Схема опыта с осветителем
Библиографическая ссылка
Хаустов П.А. ТЕОРИЯ ВЕРОЯТНОСТИ В КВАНТОВОЙ ФИЗИКЕ // Международный студенческий научный вестник. – 2016. – № 3-3.
;
URL: https://eduherald.ru/ru/article/view?id=15033 (дата обращения: 20.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Видео
Вероятность в квантовой механике
Физик Алексей Акимов о суперпозиционных состояниях, эксперименте Шрёдингера и вычислении вероятности в квантовой механике
Над материалом работали

Добавить в закладки
Вы сможете увидеть эту публикацию в личном кабинете
Журнал «Вояджеры»
Понятие вероятности появилось в физике в связи с развитием кинетической теории газов. Когда было установлено, что газ состоит из большого числа движущихся частиц, то возник вопрос о том, с какими скоростями движутся частицы газа — его молекулы.
Английский физик Дж. Максвелл построил первую теорию идеального газа, в которой состояние газа задавалось не положением и скоростью каждой частицы, а функцией распределения — вероятностью найти молекулу с заданной скоростью в заданном месте сосуда. Для того чтобы упростить изложение, предположим, что сосуд разбит на маленькие кубические ячейки с ребром, например, в 1 мм и что нас интересуют не точные координаты молекулы, а лишь то, в какой ячейке она находится. Скорости мы тоже будем задавать не точно, а считая, например, все скорости молекулы, двигающейся здесь вдоль оси ОХ, отличающиеся не более чем на 1 мм/с, одинаковыми. Тогда и скорости представляется возможным задавать ячейками, на которые можно разбить трехмерную диаграмму; по осям ее отложены компоненты скоростей vx, v3y, vz, а точка изображает скорость частицы. Если на молекулы газа не действуют никакие силы, например сила тяжести или электрическое поле, то молекула будет одинаково часто бывать в любом месте сосуда. Мы говорим, что вероятность найти молекулу в любой ячейке одна и та же. Обозначим эту вероятность через wi. Очевидно, что сумма wi, взятая по всем ячейкам, равна 1, так как вероятность найти молекулу в какой-либо ячейке равна 1. Если в сосуде находится N молекул, то в одной ячейке будет находиться в среднем wiN молекул. wi не зависит от номера ячейки; i — плотность газа, постоянная вдоль сосуда.
Совсем иначе выглядит вероятность найти молекулу с заданной скоростью или вероятность найти точку в заданной ячейке на диаграмме скоростей.
Так как энергия газа — Е Джоулей — определена, то, грубо говоря, на каждую молекулу приходится примерно E/N Джоулей, и в газе должно быть мало молекул, энергия которых сильно отличается от этой величины. Клетки на диаграмме скоростей не равноправны, и распределение по скоростям не равновероятно. Такое распределение вероятностей и нашел Максвелл.
Из теории Максвелла следовало, что большая часть молекул газа имеет скорость
v* = (m/(2πkT))1/2 где k — постоянная Больцмана, Т — абсолютная температура, m — масса молекул. Это значение называют наиболее вероятной скоростью.
Понятие вероятности оказалось очень плодотворным. С ее помощью можно рассчитывать различные процессы, в которых участвуют много частиц и в которых роль отдельных частиц становится незаметной. Это такие процессы, как теплопроводность, перемешивание — диффузия, химические реакции и многие другие. Их изучает статистическая физика.
До создания квантовой механики считалось, что появление вероятностей связано обычно с большим числом частиц, координаты и скорости которых практически нельзя измерить.
Оказалось, однако, что даже для одной определенной частицы нельзя точно измерить координату и импульс одновременно и что результат опыта можно предсказать только в вероятностной форме.
Так как нет возможности точно измерить траекторию частицы, значит, нельзя и дать точный ответ на вопрос о том, на какой угол отклонится летящий протон в поле атомного ядра. Можно лишь указать вероятность его отклонения на тот или иной угол. Нельзя сказать также, когда распадается определенный радиоактивный атом, можно лишь указать вероятность того, что он распадается через t секунд. Известно, что число атомов уменьшается по закону Nt = N0e-λt, если при t=0 было N0 атомов. Постоянная λ в этой формуле называется постоянной распада (см. Радиоактивность) . Таким образом, хотя и нельзя установить, какие именно атомы распадутся, утверждение о законе распада большого числа атомов оказывается вполне определенным.
Вероятности появляются еще в одном разделе физики — в теории измерений. Никакое измерение не дает абсолютно точного значения измеряемой величины. Точное значение отличается от измеренного, и теория может лишь оценить вероятность того или иного отклонения. Оценка вероятности ошибки из анализа совокупности повторных измерений — важная задача экспериментальной физики.
В таблицах пишут, например, что скорость света равна 2,997924580 (1,2)•108 м/с; величина в скобках называется стандартным отклонением.
В данном случае из теории вероятности следует, что истинная скорость света не может отличаться от написанной более чем на 1,2 единицы в последнем знаке с вероятностью 68,3%.
Дело в том, что в любом опыте существует большое количество неучтенных факторов. В случае скорости света такими факторами могут быть непостоянство температуры, неточность в измерении длины волны и т. д., но они могут сказываться лишь в восьмом знаке после запятой. Степень достоверности этого утверждения и оценивается вероятностью.
Теория вероятности очень важна при вычислении достоверных значений основных физических величин.
Молекулярная физика
1. Понятие о вероятности 2. Понятие о распределении. 3. Функция распределения
Понятие о вероятности • Закон Больцмана, как и барометрическую формулу, удобно трактовать с несколько иной точки зрения, а именно, пользуясь понятием вероятности. • К этому термину прибегают в тех случаях, когда речь идет о случайных событиях, т. е. таких, условия наступления которых неизвестны и которые поэтому нельзя заранее с уверенностью предсказать.
Понятие о вероятности • Приобретая, например, билет в автобусе, мы обычно заранее не знаем, будет ли его номер четным или нечетным. Поэтому такое «событие» , как приобретение билета именно с четным номером, можно считать событием случайным. Если мы, например, приобретем 10 билетов, то в их числе могут оказаться и три, и шесть, и восемь билетов с четными номерами. Но может случиться и так, что среди них не окажется ни одного четного, или, наоборот, четными окажутся все 10 билетов. • Однако в этой кажущейся полнейшей произвольности есть и определенная закономерность. Она заключается в том, что, если повторять опыт (покупки билетов) достаточно большое число раз, то приблизительно в половине случаев билет будет иметь четный номер. И чем больше будет число таких «опытов» , тем ближе к половине будет доля билетов с четными номерами. В таком случае и говорят, что вероятность приобретения билета с четным номером равна 1/2. • Точно так же, бросая много раз монету, мы можем быть уверены, что приблизительно в половине случаев она упадет обращенной вверх стороной с гербом. И это будет тем вероятнее, чем больше будет число бросаний.
Понятие о вероятности • Эти и другие подобные им опыты позволяют нам дать следующее определение вероятности: вероятностью события называется предел, к которому стремится отношение числа опытов, приводящих, к его осуществлению, к общему числу опытов при беспредельном увеличении последнего. • Если из N опытов (или наблюдений) N’ приводят к реализации интересующего нас события, то вероятность W этого события выражается формулой:
Понятие о вероятности • В рассмотренном нами случае с номерами билетов вероятность четного номера равна 1/2. Такова же, конечно, и вероятность нечетного номера. Сумма этих двух вероятностей равна единице. Она очевидно дает нам вероятность «события» , заключающегося в том, что билет будет иметь или четный, или нечетный номер. Но такое событие неизбежно, так что вероятность, равная единице, означает достоверность. Наоборот, если какое-то событие невозможно (например, полное отсутствие номера), то его вероятность равна нулю.
Понятие о вероятности • В примере с билетами (так же как и с бросанием монет) «опыт» (покупка билета) может привести к одному из двух исходов: номер билета может быть четным или нечетным, и оба эти исхода являются равновозможными. Но так бывает не всегда. Например, из того факта, что при выстреле в цель возможно лишь два исхода — попадание или промах, не следует, что вероятность попадания равна 1/2, так как попадание и промах не являются равновозможными результатами выстрела. И если будет произведено очень много выстрелов, то отношение числа попаданий к числу выстрелов едва ли будет равно половине: у искусного стрелка, снабженного хорошо пристрелянным оружием, оно будет близким к единице, у плохого оно может мало отличаться от нуля. Однако, хотя вероятности каждого из двух возможных исходов выстрела и не равны 1/2, их сумма (для данного стрелка) и в этом случае равна единице: о том, что выстрел приведет к какому-то исходу — попаданию или промаху, можно утверждать с полной определенностью!
Теорема сложения вероятностей • Рассмотрим теперь еще один пример, который позволит нам сформулировать одно из важных положений теории вероятностей и, кроме того, дать еще одно определение самой величины вероятности. Пусть в ящике лежат 20 вполне одинаковых по своим размерам и весу гладких шаров и пусть 5 из них выкрашены в белый цвет, а остальные — в черный. Если мы теперь извлечем из ящика один шар, то ясно, что, поскольку во всем, кроме цвета, шары друг от друга не отличаются, вероятность вынуть один какой-нибудь шар равна вероятности вынуть любой другой. Для каждого шара, который мы пожелали бы как-нибудь отметить, вероятность быть вынутым равна, очевидно, 1/20. • Посмотрим теперь, какова вероятность того, что будет вынут белый шар? Так как для каждого шара (все равно, белого или черного) вероятность быть вынутым равна 1/20, а всего белых шаров пять (и нам все равно, какой из них будет вынут), то искомая вероятность равна сумме вероятностей для всех белых шаров:
Теорема сложения вероятностей • Этот результат выражает одно из важных положений теории вероятностей — теорему сложения вероятностей, которая гласит: если W 1, W 2, W 3 и т. д. — вероятности нескольких исключающих друга событий, то вероятность того, что осуществится какое-нибудь одно из них, равна сумме вероятностей всех этих событий.
Теорема сложения вероятностей • Вероятность осуществления одного из исключающих друга событий, равна сумме вероятностей всех этих событий.
Понятие о вероятности • Значит, сумма вероятностей нескольких событий дает нам вероятность того, что наступит или одно событие, или другое, или третье и т. д. При этом предполагается, что эти события, или хотя бы два из них, не могут произойти одновременно. Так, в нашем примере 5/20 — это вероятность того, что будет вынут один из белых шаров, а так как операция извлечения шара производится только один раз, то если вынут один какой-нибудь белый шар, то не может быть вынут никакой другой. • Приведенный пример позволяет дать новое определение вероятности, несколько отличающееся от прежнего. Мы нашли, что вероятность того, что будет вынут белый шар, равна 5/20. Но число 20 — это число всех возможных исходов операции извлечения шара, а число 5 — это число случаев (из возможных 20), благоприятствующих наступлению данного события — появлению белого шара. Это и позволяет определить вероятность данного события как отношение числа случаев, благоприятствующих его наступлению, к общему числу возможных случаев, если все случаи равновозможны.
Понятие о вероятности • Это определение вероятности принадлежит Лапласу. Оно, как легко видеть, не противоречит прежнему определению. Для приведенного только что определения вероятности существенно, чтобы все случаи были равновозможны, равновероятны. Именно так обстоит дело в нашем примере с шарами. • При физических применениях теории вероятностей обычно тоже приходится иметь дело с равновероятными событиями.
Понятие о вероятности • Вернемся теперь к формуле закона Больцмана Из того, что здесь было сказано о вероятности, ясно, что величина n/n 0 в этой формуле как раз и имеет смысл вероятности. Ведь любая из n 0 молекул может обладать потенциальной энергией U. Значит, n 0 — это общее число возможных случаев. В действительности же энергией U обладают n молекул. Следовательно, n — это число, которое мы раньше назвали числом «благоприятствующих» случаев. Поэтому отношение n/n 0 , которое мы называли долей молекул, обладающих энергией U, есть в то же время и вероятность того, что любая из n 0 молекул обладает такой энергией.
Теорема умножения вероятностей • Нам остается изложить еще одно важное положение теории вероятностей — теорему умножения вероятностей. Она относится к случаю, когда определяется вероятность сложного события, состоящего в совмещении двух или больше независимых событий. События называются независимыми, если вероятность любого из них не зависит от того, наступит или не наступит любое другое. • Обращаясь к прежним примерам с билетами и стрелком, мы можем, например, поставить такую задачу: какова вероятность того, что стрелок, отправляясь к стрельбищу на автобусе, приобретет билет с четным номером, а вслед затем его первый выстрел увенчается попаданием? Ясно, что эти два события являются независимыми.
Теорема умножения вероятностей • Допустим, что для нашего стрелка вероятность W 1 попадания равна 0, 8. Это значит, что в среднем из 10 посещений стрельбища он в восьми случаях первым выстрелом попадает в цель. Но при этом только в половине из них он приобретет в то же время билет с четным номером, так как вероятность W 2 получить четный билет равна 1/2. Значит, искомая вероятность W 12 сложного события — совпадения четного номера и успешного выстрела — равна произведению вероятностей каждого из них:
Теорема умножения вероятностей • Вероятность совмещения двух или нескольких независимых, событий равна произведению вероятностей каждого из них в отдельности.
Понятие о распределении • В основные уравнения кинетической теории идеальных газов входит, как мы знаем, средняя кинетическая энергия молекул, которая в свою очередь определяется их средней квадратичной скоростью. Смысл средней квадратичной скорости заключается в том, что это — та скорость, которой должны были бы обладать все молекулы (если бы величины их скоростей были одинаковы, а направления равновероятны), чтобы давление газа было тем, каким оно в действительности является. На самом деле, однако, скорости молекул не одинаковы, и мы это даже принимали во внимание при выводе основного уравнения. На это указывают и опытные факты. Так, например, в опытах Штерна, в которых измерялась скорость молекул, смещенная полоска оказывалась не резкой, а размытой изза того, что молекулы с разными скоростями попадали в разные места мишени. Об этом свидетельствует и рассмотренный закон распределения молекул по высоте в поле тяжести (барометрическая формула). Если бы все молекулы имели одинаковые скорости, распределение было бы совсем иным.
Опыт Штерна
Понятие о распределении • В самом деле, представим себе, что все молекулы, находящиеся у поверхности Земли, имеют одинаковые скорости, вертикальная составляющая которых равна и. Эти молекулы поднялись бы до высоты х, определяемой условием • т. е. до высоты • после чего они вернулись бы к Земле с первоначальной кинетической энергией, т. е. они вели бы себя так же, как ведет себя любое брошенное вверх тело. При таких условиях атмосфера имела бы на высоте х резкую границу, за пределами которой ее не было бы. Опыт же показывает, что атмосфера резкой границы не имеет, ее плотность убывает с высотой в соответствии с барометрической формулой. Предположение о равенстве скоростей всех молекул противоречит, таким образом, опыту.
Понятие о распределении • Благодаря беспорядочным движениям молекул и их взаимным столкновениям молекулы газа каким-то образом распределяются по скоростям, так что среди них имеются как очень быстрые, так и очень медленные. • Несмотря на полную хаотичность молекулярных движений, несмотря на случайный характер столкновений и вызываемых ими изменений скорости молекул, их распределение по скоростям, как показывают теория и опыт, оказывается не случайным, не произвольным, а вполне определенным. На его характер не влияют ни столкновения между молекулами, ни даже внешние поля. Оно оказывается однозначным и единственно возможным. И это не только не противоречит представлению о хаотичности молекулярных движений, но именно ею и обусловлено.
Понятие о распределении • Прежде чем приступить к выводу закона распределения молекул по скоростям, выясним сущность задачи о распределении. Определить распределение молекул по скоростям означает, как будто бы, определить число молекул, обладающих той или иной заданной скоростью. Однако в такой постановке вопрос не имеет смысла, так как вероятное число молекул, имеющих точно (математически точно!) заданную скорость, равно нулю. Ведь число различных значений скорости бесконечно большое. Число же молекул конечное. Поэтому число молекул, приходящихся на долю каждого произвольно заданного значения скорости, равно нулю. Вследствие этого вопрос должен быть сформулирован “иначе: сколько молекул (или какая часть молекул) обладает скоростями, лежащими в некотором интервале вблизи заданной скорости?
Понятие о распределении • Именно так всегда и ставятся статистические задачи. Если, например, требуется найти распределение населения страны по возрасту, то это не значит, что нужно определить вероятное число людей, имеющих тот или иной точно (математически точно) заданный возраст. Такой вопрос не имеет смысла, так как число различных значений возраста бесконечно большое, а число людей конечное. Можно лишь определить вероятное число людей, возраст которых лежит в определенном интервале значений. • Когда в повседневной речи мы говорим, что такому-то человеку 18 лет, то мы не хотим этим сказать, что ему ровно 18 лет, 0 дней, 0 минут, 0 секунд. Наше утверждение означает лишь, что его возраст лежит в интервале между 18 и 19 годами. Точно так же, когда, например, Министерство образования, планируя работу школ в учебном году, интересуется числом детей семилетнего возраста, поступающих в школу, то оно интересуется не детьми, которым 1 сентября в 8 часов утра исполнится ровно 7 лет. Его на самом деле интересует число детей, чей возраст лежит между семью и восемью годами.
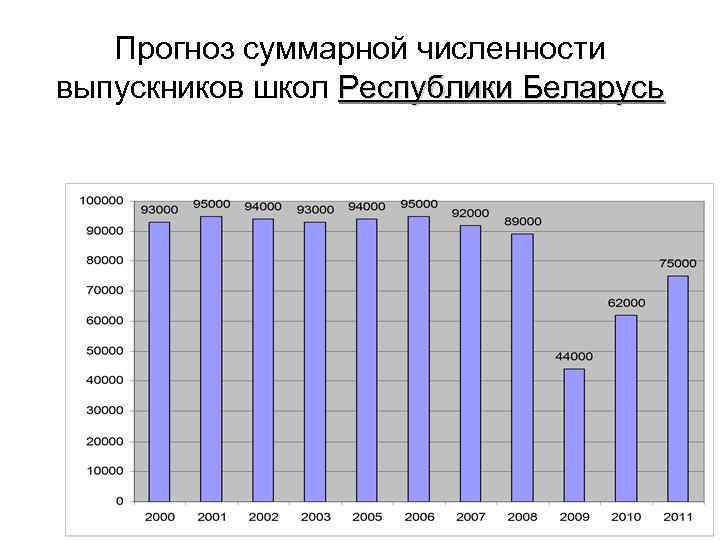
Прогноз суммарной численности выпускников школ Республики Беларусь
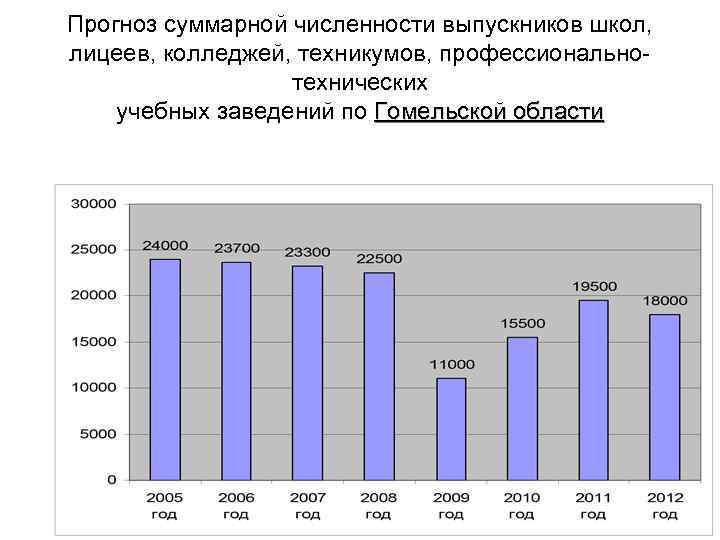
Прогноз суммарной численности выпускников школ, лицеев, колледжей, техникумов, профессиональнотехнических учебных заведений по Гомельской области
Функция распределения • Изучая распределение частиц по скоростям, мы тоже будем искать число частиц, скорости которых (или компоненты скорости) лежат в определенном интервале значений скорости (или компонент скорости). • Очевидно, что число частиц в единице объема, скорости которых лежат в некотором интервале от до , тем больше, чем больше интервал, т. е. • или • где а — коэффициент пропорциональности.
Функция распределения • Ясно также, что зависит и от самой скорости, так как в одинаковых по величине интервалах, но при различных абсолютных значениях скорости, число частиц будет различным, как не одинаково, например, число людей в интервале возрастов от 99 до 100 лет и от 30 до 31 года, хотя размеры интервалов в обоих случаях одинаковы. Это значит, что в последней формуле коэффициент пропорциональности должен быть функцией скорости
Функция распределения • Наконец, величина должна быть также пропорциональна числу частиц п в единице объема. Поэтому формула для должна иметь вид: • Ее обычно записывают в таком виде:
Функция распределения • Величина — в этой формуле представляет собой • долю частиц в единице объема газа, скорости которых лежат в интервале от до. • Функция называется функцией распределения. Нашей задачей и является найти вид этой функции. Смысл ее ясен из формулы. В самом деле, • при
Функция распределения • Это значит, что равна доле частиц, скорости которых заключены в единичном интервале скоростей вблизи скорости. • Переходя к пределу, можно формулу переписать в виде:
Функция распределения • Из того, что говорилось выше о вероятности, следует, что • величина в формуле имеет смысл • вероятности: это вероятность того, что любая из молекул газа, содержащихся в единице его объема, обладает скоростью, лежащей в интервале вблизи скорости • . • Величине же функции распределения можно приписать смысл вероятности любой молекуле газа в единице его объема иметь скорость, заключенную в единичном интервале вблизи скорости. Ее называют поэтому плотностью вероятности.
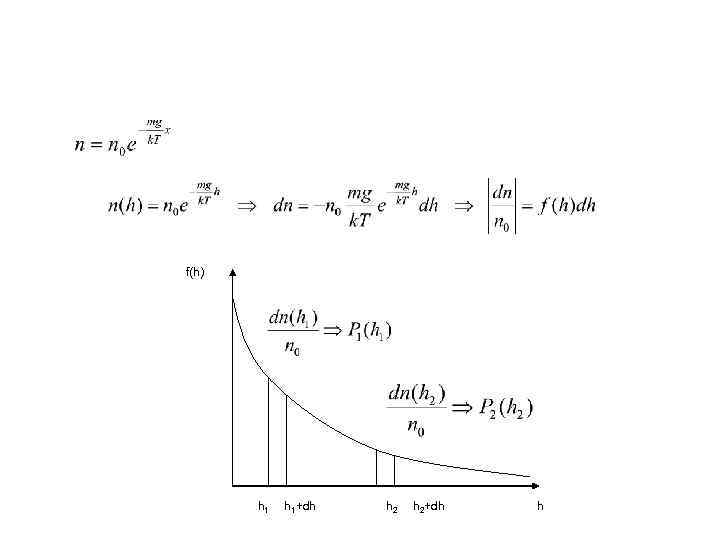
Функция распределения • Полученная ранее барометрическая формула обязана своим видом тому, что скорости молекул не одинаковы, а определенным образом распределены по скоростям. Характер этого распределения как раз и зависит от вида функции. Пользуясь уже известной барометрической формулой, мы и определим вид функции распределения, приводящей к зависимости плотности молекул от высоты:
Функция распределения • Заметим, что функция распределения может быть найдена и другими путями. Максвелл получил ее (1859 г. ) из соображений, основанных на теории вероятностей. Больцман (1877 г. ) вывел эту функцию из рассмотрения столкновений газовых молекул, благодаря которым и устанавливается распределение. Как следствие этой формулы может быть получена и барометрическая формула. Мы же для простоты расчета воспользуемся уже выведенной барометрической формулой, чтобы найти
f(h) h 1+dh h 2+dh h