Теорема сложения вероятностей. Теорема умножения вероятностей.
Составитель преподаватель кафедры высшей математики Ищанов Т.Р.
Тeория. Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же опыте; в противном случае события называются совместными.
Пример 1. При бросании игральной кости выпадение 3 очков и 6 очков события несовместные, так как они одновременно не могут произойти в одном и том же опыте.
Пример 2. А — появление четырех очков при бросании игральной кости; В-появление четного числа очков. События А и В совместные, так появление одного из них не исключает появление другого в одном и том же испытании.
Два события называются независимыми, если вероятность появления одного из них не влияет на вероятность появления другого события, в противном случае события зависимы.
Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С – появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то «АВС» – выпадение «герба» во всех трех испытаниях.
Условной вероятностью ![]() называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению, равна :
называют вероятность события В, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению, равна :
![Rendered by QuickLaTeX.com [P_A (B)=(P(AB))/(P(A))]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-2b271052355966bddf4571d791108b5d_l3.png)
где (Р(А)>0).
Пример 3. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).
Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность
![Rendered by QuickLaTeX.com [P_A(B)=frac35.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-45d2458ed4fda43d2e8d4d1fe65c8120_l3.png)
Этот же результат можно получить по формуле
![Rendered by QuickLaTeX.com [P_A(B)=frac{P(AB)}{P(A)},qquad (P(A)>0).]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-06443f20c38227785ecdf55f3b259b51_l3.png)
Действительно, вероятность появления белого шара при первом испытании
![Rendered by QuickLaTeX.com [P(A)=frac36=frac12.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-a3bfed995241412e3df42ad7debd8df5_l3.png)
Найдем вероятность Р (АВ) того, что в первом испытании появится черный шар, а во втором—белый. Общее число исходов — совместного появления двух шаров, безразлично какого цвета, равно числу размещений
![]()
Из этого числа исходов событию AВ благоприятствуют ![]() исходов. Следовательно,
исходов. Следовательно,
![]()
Искомая условная вероятность
![]()
Как видим, получен прежний результат.
Теорема умножения вероятностей (для зависимых событий). Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
![Rendered by QuickLaTeX.com [P(AB)=P(A)P_A (B)]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-d8bed58df57964ee40f607ea897bcf80_l3.png)
Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
![]()
где ![]() — вероятность события An, вычисленная в предположении, что события A1, A2, A3, … , An-1 наступили.
— вероятность события An, вычисленная в предположении, что события A1, A2, A3, … , An-1 наступили.
В частности, для трех событий ![]() . Заметим, что порядок, в котором расположены события, может быть выбран любым, т. е. безразлично какое событие считать первым, вторым и т.д.
. Заметим, что порядок, в котором расположены события, может быть выбран любым, т. е. безразлично какое событие считать первым, вторым и т.д.
Пример 4. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический.
Решение. Вероятность того, что первый валик окажется конусным (событие А), ![]() .
.
Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик— конусный, т. е. условная вероятность ![]() .
.
По теореме умножения, искомая вероятность
![Rendered by QuickLaTeX.com [P(AB)=P(A)P_A(B)=frac{3}{10}cdot frac79=frac{7}{30}.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-2a48d2fde43c873f6f47505d67d0e169_l3.png)
Пример 5. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Найти вероятность того, что при первом испытании появится белый шар (событие А), при втором — черный (событие В) и при третьем—синий (событие С).
Решение. Вероятность появления белого шара в первом испытании ![]()
Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т. е. условная вероятность ![]()
Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что в первом испытании появился белый шар, а во втором — черный, т. е. условная вероятность ![]()
Искомая вероятность
![Rendered by QuickLaTeX.com [P(ABC)=P(A)P_A(B)P_{AB}(C)=frac{5}{12}cdot frac{4}{11}cdotfrac{3}{10}=frac{1}{22}.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-e8515cc3dbf87c662e4db308b45c91ed_l3.png)
Теорема умножения вероятностей (для независимых событий). Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
![]()
Суммой А+В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то А+В – попадание при первом выстреле, или при втором, или в обоих выстрелах. В частности, если два события А и В – несовместные, то А+В – событие, состоящее в появлении одного из этих событий, безразлично какого. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.
Теорема сложения вероятностей (для несовместных событий). Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
![]()
Пример 6. В урне 30 шаров: 10 красных, 5 синих и 15 белых. Найти вероятность появления цветного шара.
Решение Появление цветного шара означает появление либо красного, либо синего шара. Вероятность появления красного шара (событие A) P (A) = 10/30 = 1/3. Вероятность появления синего шара (событие B) P (B) = 5/30 = 1/6. События A и B несовместны (появление шара одного цвета исключает появление шара другого цвета), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 1/3 + 1/6 = 0,5.
Пример 7. Стрелок стреляет по мишени, разделенной на 3 области. Вероятность попадания в первую область равна 0,45, во вторую – 0,35.Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.
Решение. Событие A – «стрелок попал в первую область» и B – «стрелок попал во вторую область» — несовместны (попадание в одну область исключает попадание в другую), поэтому теорема сложения применима. Искомая вероятность P (A + B) = P (A) + P (B) = 0,45 + 0,35 = 0,80.
Теорема сложения вероятностей (для совместных событий). Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
![]()
Для трех событий A, B, C имеем:
![]()
Замечание 1. При использовании полученной формулы следует иметь в виду, что события А и В могут быть как независимыми, так и зависимыми. Для независимых событий:
![]()
Пример 8. Вероятности попадания в цель при стрельбе первого и второго орудий соответственно равны: p1 = 0,7; p2 = 0,8. Найти вероятность попадания при одном залпе (из обоих орудий) хотя бы одним из орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результата стрельбы из другого орудия, поэтому события А (попадание первого орудия) и В (попадание второго орудия) независимы. Вероятность события АВ (оба орудия дали попадание) Р (АВ)=Р (А)*Р(В) = 0,7*0,8 = 0,56. Искомая вероятность Р(А+В)=Р(А) + Р(В)—Р(АВ) = 0,7 + 0,8 — 0,56=0,94.
Замечание. Так как в настоящем примере события А и В независимые, то можно было воспользоваться формулой ![]() . В самом деле, вероятности событий, противоположных событиям А и В, т. е. вероятности промахов, таковы:
. В самом деле, вероятности событий, противоположных событиям А и В, т. е. вероятности промахов, таковы:
![]()
Искомая вероятность того, что при одном залпе хотя бы одно орудие даст попадание, равна ![]() . Как и следовало ожидать, получен тот же результат.
. Как и следовало ожидать, получен тот же результат.
Для зависимых событий: ![]()
Вероятность появления хотя бы одного события.
Теорема. Вероятность появления хотя бы одного из событий A1, A2, …, An, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий ![]() :
:
![]()
Частный случай. Если события ![]() имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий:
имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий:
![]()
Практический материал.
1.(6.4.12) В урне 4 белых и 3 черных шара. Из нее вынимают 2 шара. Найти вероятность того, что оба шара белые. Рассмотреть выборки: а) без возвращения; б) с возвращением.
2. Вероятность наступления некоторого случайного события в каждом опыте одинакова и равна 0,2. Опыты проводятся последовательно до наступления этого события. Определить вероятность того, что: а) придется проводить четвертый опыт; б) будет проведено четыре опыта. Ответ: а) P (A)=0,83 ; б) P (B)=0,83·0,2
3. Три стрелка одновременно стреляют по одной мишени. Вероятности попадания при одном выстреле соответственно равны 0,7; 0,8 и 0,9. Найти вероятности того, что при одновременном залпе этих стрелков в мишени будет: а) только одно попадание; б) хотя бы одно попадание. Ответ: а) 0,092; б) 0,994
4. Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8. (Указание: Задача обратная примеру 8). Ответ: 0,7
5. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное. Ответ: 0,18
6. Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность. Ответ: 0,432
Полезная страница? Сохрани или расскажи друзьям
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записывается как $A subset B$.
События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записывается очевидно: А = В.
Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
$$P(A+B)=P(A)+P(B).$$
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
$$Pleft(sum_{i=1}^{n}A_i right)=sum_{i=1}^{n} P(A_i).$$
Если случайные события $A_1, A_2, …, A_n$ образуют полную группу несовместных событий, то имеет место равенство
$P(A_1)+P(A_2)+…+P(A_n)=1.$ Такие события (гипотезы) используются при решении задач на полную вероятность.
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.
Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
$$P(A+B)=P(A)+P(B)-P(Acdot B).$$
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
$$P(Acdot B)=P(A)cdot P(B).$$
Вероятность произведения зависимых событий вычисляется по формуле условной вероятности.
Примеры решений задач с событиями
Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.
Решение. Обозначим события: А – вынули белый шар из первого ящика,  ;
;
 – вынули черный шар из первого ящика,
– вынули черный шар из первого ящика,  ;
;
В – белый шар из второго ящика,  ;
;
 – черный шар из второго ящика,
– черный шар из второго ящика,  .
.
Нам нужно, чтобы произошло одно из событий  или
или  . По теореме об умножении вероятностей
. По теореме об умножении вероятностей
 ,
,  .
.
Тогда искомая вероятность по теореме сложения будет
 .
.
Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) двойного промаха, в) хотя бы одного попадания; г) одного попадания.
Решение.
Пусть А – попадание первого стрелка,  ;
;
В – попадание второго стрелка,  .
.
Тогда  – промах первого,
– промах первого,  ;
;
 – промах второго,
– промах второго,  .
.
Найдем нужные вероятности.
а) АВ – двойное попадание, 
б) 
 – двойной промах,
– двойной промах,  .
.
в) А+В – хотя бы одно попадание,
 .
.
г)  – одно попадание,
– одно попадание,
 .
.
См. обучающую статью “решение задач о стрелках”
Пример. Решить задачу, применяя теоремы сложения и умножения. Мастер обслуживает 3 станка, работающих независимо друг от друга. Вероятность того, что первый станок потребует внимания рабочего в течение смены, равна 0,4, второй – 0,6, третий – 0,3. Найти вероятность того, что в течение смены: а) ни один станок не потребует внимания мастера, б) ровно 1 станок потребует внимания мастера.
Решение.
Вводим базовые независимые события $A_i$ = (Станок $i$ потребовал внимания рабочего в течение смены), $i=1, 2, 3$. По условию выписываем вероятности: $p_1=0,4$, $p_2=0,6$, $p_3=0,3$. Тогда $q_1=0,6$, $q_2=0,4$, $q_3=0,7$.
Найдем вероятность события $X$=(Ни один станок не потребует внимания в течение смены):
$$
P(X)=Pleft(overline{A_1} cdot overline{A_2} cdot overline{A_3}right)= q_1 cdot q_2 cdot q_3 =
0,6cdot 0,4 cdot 0,7 = 0,168.
$$
Найдем вероятность события $Z$= (Ровно один станок потребует внимания в течение смены):
$$
P(Z)= \ = P(A_1) cdot Pleft(overline{A_2} right) cdot Pleft(overline{A_3} right) + Pleft(overline{A_1}right) cdot P(A_2) cdot Pleft(overline{A_3} right) + Pleft(overline{A_1} right) cdot Pleft(overline{A_2} right) cdot P(A_3)=\
= p_1 cdot q_2 cdot q_3 + q_1 cdot p_2 cdot q_3 + q_1 cdot q_2 cdot p_3 =\ =
0,4cdot 0,4 cdot 0,7+0,6cdot 0,6 cdot 0,7+0,6cdot 0,4 cdot 0,3 = 0,436.
$$
См. обучающую статью “решение задач о станках”
Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.
Решение.
А – формула содержится в первом справочнике;
В – формула содержится во втором справочнике;
С – формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
1. 
2.  .
.
3. 
Вероятность наступления хотя бы одного события
Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий?
Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.
Теорема. Вероятность появления хотя бы одного из событий $A_1, A_2, …, A_n$, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
$$
P(A)=1-Pleft(overline{A_1}right)cdot Pleft(overline{A_2}right)cdot … cdot Pleft(overline{A_n}right)= 1-q_1 cdot q_2 cdot … cdot q_n.
$$
Если события $A_1, A_2, …, A_n$ имеют одинаковую вероятность $p$, то формула принимает простой вид:
$$
P(A)=1-(1-p)^n=1-q^n.
$$
Примеры решений на эту тему
Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p1 = 0,8; p2 = 0,7; p3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события  (попадание первого орудия),
(попадание первого орудия),  (попадание второго орудия) и
(попадание второго орудия) и  (попадание третьего орудия) независимы в совокупности.
(попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям  ,
,  и
и  (т. е. вероятности промахов), соответственно равны:
(т. е. вероятности промахов), соответственно равны:
 ,
,  ,
, 
Искомая вероятность  .
.
Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).
Решение. События “машина работает” и “машина не работает” (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: 
Отсюда вероятность того, что машина в данный момент не работает, равна 
Искомая вероятность 
Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.
Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?
Решение. Обозначим через А событие “при n выстрелах стрелок попадает в цель хотя бы один раз”. События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула  .
.
Приняв во внимание, что, по условию,  (следовательно,
(следовательно,  ), получим
), получим

Прологарифмируем это неравенство по основанию 10:

Итак,  , т.е. стрелок должен произвести не менее 5 выстрелов.
, т.е. стрелок должен произвести не менее 5 выстрелов.
См. обучающую статью “решение задач с хотя бы один…”
ВЕРОЯТНОСТЕЙ
4.1. Теорема сложения вероятностей
Теорема 4.1.Вероятность появления
одного из двух несовместных событий,
безразлично какого, равна сумме
вероятностей этих событий:
![]() .
.
(4.1)
Следствие.Вероятность появления
одного из нескольких попарно несовместных
событий, безразлично какого, равна сумме
вероятностей этих событий:
![]() .
.
Теорема 4.2.Вероятность появления
хотя бы одного из двух совместных событий
равна сумме вероятностей этих событий
без вероятности их совместного появления
![]() . (4.2)
. (4.2)
Теорема 4.3.Сумма вероятностей
противоположных событий равна единице:
![]() .
.
(4.3)
Пример 4.1.На стеллаже библиотеки
в случайном порядке расставлено 15
учебников, причем 5 из них в переплете.
Библиотекарь берет наудачу 3 учебника.
Найти вероятность того, что хотя бы два
учебника окажется в переплете;
Решение.1) ПустьA– событие, заключающееся в том, что хотя
бы два учебника из трех отобранных будет
в переплете. СобытиеAбудет состоять из двух несовместных
событий:A1–
событие, состоящее в том, что из трех
отобранных учебников два в переплете,
а один – нет;A2– событие, состоящее в том, что из трех
отобранных учебников все три в переплете.
Тогда![]() .
.
Поскольку события A1иA2несовместны,
то по теореме 4.1. получаем
![]() .
.
Вероятности событий A1иA1находим,
используя классическое определение
вероятностей.
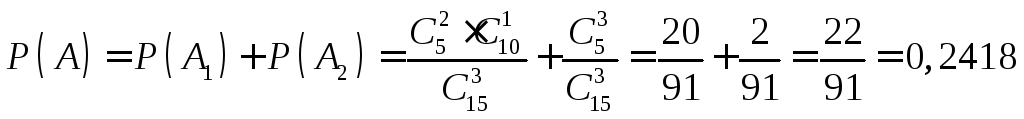 .
.
4.2. Теорема умножение вероятностей
Пусть при выполнении некоторого комплекса
условий могут произойти случайные
события AиB.
Их вероятность соответственно обозначим
черезP(A)
иP(B).
Допустим, что стало известно о наступлении
событияA, а относительно
событияBданных не
получено. Таким образом, комплекс условий
для наступления событияBизменился, вероятность наступления
событияBможет стать
другой, отличной отP(B).
Если, например, при бросании игральной
кости вероятность выпадения единицы
равна 1/6, то после того, как стало известно,
что выпало нечетное число очков, эта
вероятность стала равна 1/3.
Событие, состоящее в том, что случится
событие B, когда
известно, что произошло событиеA,
будем обозначать символомB/A.
Соответствующая вероятностьP(B/A)
называетсяусловной вероятностьюсобытияBпри условии,
что событиеAпроизошло.
В следующей теореме мы введем формулу
для вычисления условной вероятности.
Теорему примем без доказательства.
Теорема 4.4.
![]() .
.
(4.4)
Аналогично
![]() .
.
(4.5)
Теорема 4.5(теорема умножения
вероятностей).
Вероятность совместного наступления
двух событий (вероятность произведения
двух событий) равна произведению
вероятности одного из них на условную
вероятность другого при условии, что
первое уже произошло:
![]() .
.
(4.6)
Пример 4.2.Из урны, в которойmчерных иnбелых шаров,
извлекают два шара. Чему равна вероятность
того, что:
а) оба шара белых;
б) шары разного цвета.
Решение.а) ПустьA1– событие, состоящее в том, что первый
шар белый,A2–
событие, состоящее в том, что второй шар
белый. Тогда
![]() .
.
б) Пусть A1B2– событие, состоящее в том, что первый
шар белый, а второй – черный,B1A2– событие, состоящее в том, первый шар
черный, а второй – белый. Тогда
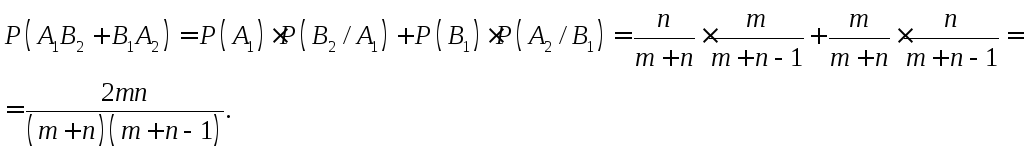
Теорему умножения вероятностей легко
распространить на случай, когда событий
больше двух.
Следствие.Вероятность совместного
появления нескольких событий равна
произведению вероятности одного из них
на условные вероятности всех остальных,
причем вероятность каждого последующего
события вычисляется в предположении,
что все предыдущие события уже появились:
![]() ,
,
где
![]() – вероятность событияAn,
– вероятность событияAn,
вычисленная в предположении, что событияA1,A2,
…,An-1наступили.
В частности для трех событий будем
иметь:
![]() .
.
Заметим, что порядок, в котором расположены
события, может быть выбран любым.
Безразлично, какое событие считать
первым, вторым и т.д.
Определение 4.1.Два события называютсянезависимыми, если вероятность
одного из них не зависит от появления
или не появления другого, т.е.
![]() или
или![]() .
.
Два события называются зависимыми,
если вероятность появления одного из
них зависит от наступления или не
наступления другого события.
Теорема умножения вероятностей, которая
была доказана выше, рассматривалась
для зависимых событий. Сформулируем
теорему умножения вероятностей (без
доказательства) для независимых событий.
Теорема 4.6.Вероятность совместного
появления двух независимых событий
равна произведению вероятностей этих
событий:
![]() .
.
(4.7)
Пример 4.3.Студент может уехать в
университет или автобусом, который
ходит через каждые 20 мин, или маршрутным
такси, которое ходит через каждые 10 мин.
Какова вероятность того, что студент,
подошедший к остановке, уедет в течение
ближайших пяти минут?
Решение.ПустьA– событие, заключающееся в том, что
студент, подошедший к остановке, уедет
в течение ближайших пяти минут. СобытиеAбудет состоять из
двух совместных событий:A1– событие, состоящее в том, что студент
в течение пяти минут уедет автобусом;A2– событие,
состоящее в том, что студент в течение
пяти минут уедет маршрутным такси.
Совместность этих событий заключается
в том, что к остановке одновременно
может подойти как автобус, так и маршрутное
такси. Но эти события независимые.
Поэтому по т.4.2. и по т.4.6. имеем
![]() .
.
Пусть в результате испытания может
появиться nсобытий
независимых в совокупности, либо
некоторые их них (в частности, только
одно или ни одного), причем вероятности
появления каждого из событий известны.
Как найти вероятность того, что наступит
хотя бы одно из этих событий? Например,
если в результате испытания могут
появиться три события, то появление
хотя бы одного из этих событий означает
наступление либо одного, либо двух, либо
трех событий. Ответ на поставленный
вопрос дает следующая теорема.
Теорема 4.7.Вероятность появления
хотя бы одного из событийA1,A2, …,An,
независящих в совокупности, равна
разности между единицей и произведением
вероятностей противоположных событий![]() :
:
![]() .
.
(4.8)
Пример 4.4(Условие примера4.1.).
На стеллаже библиотеки в случайном
порядке расставлено 15 учебников, причем
5 из них в переплете. Библиотекарь берет
наудачу 3 учебника. Найти вероятность
того, что хотя бы один из взятых учебников
окажется в переплете;
Решение.1) ПустьA– событие, заключающееся в том, что хотя
бы один из трех отобранных учебников
будет в переплете. Рассмотрим
противоположное событие![]() – состоящее в том, что ни один из трех
– состоящее в том, что ни один из трех
взятых учебников не будет в переплете.
СобытияAи![]() образуют полную группу событий. Значит,
образуют полную группу событий. Значит,![]() .
.
Тогда
![]() .
.
Пример 4.5.Вероятности попадания в
цель при стрельбе из трех орудий таковы:p1=0,8,p2=0,7,p3=0,9. Найти
вероятность:
а) только одного попадания при одном
залпе из всех орудий;
б) хотя бы одного попадания при одном
залпе из всех орудий.
Решение.а) ПустьA– событие, состоящее в том, что при одном
залпе из всех орудий было только одно
попадание. Вероятность попадания в цель
каждым из орудий не зависит от результатов
стрельбы из других орудий. СобытиеAвозможно при появлении одного из попарно
несовместных событийA1,
илиA2, илиA3.
A1– событие,
состоящее в том, что произошло попадание
в цель первым орудием, т.е. первое орудие
попало, второе и третье – нет, значит,
![]() ;
;
A2– событие,
состоящее в том, что произошло попадание
в цель вторым орудием, т.е. второе орудие
попало, а первое и третье – нет,
![]() ;
;
A3– событие,
состоящее в том, что произошло попадание
в цель третьим орудием, т.е. третье орудие
попало, а первое и второе – нет,
![]() .
.
Таким образом, получаем
![]() .
.
События B1,B2,B3независимы.
Используя теоремы сложения и умножения
вероятностей, получаем:
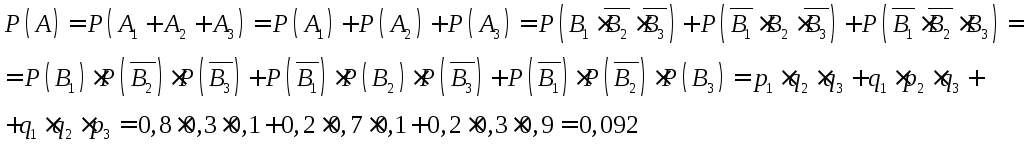 гдеq1,q2,q3– соответствующие
гдеq1,q2,q3– соответствующие
вероятности промаха каждым орудием.
б) Пусть C– событие,
состоящее в том, что при одном залпе из
всех орудий было хотя бы одно попадание.
Рассмотри противоположное событие![]() ,
,
состоящее в том, что при одном залпе не
было ни одного попадания, т.е.![]() .
.
СобытияCи![]() образуют полную группу, поэтому сумма
образуют полную группу, поэтому сумма
их вероятностей равна единице.
Следовательно, получаем
![]() .
.
Теоремы сложения и умножения вероятностей
широко используются при расчете
вероятности безотказной работы или
вероятности разрыва электрической
цепи, если даны, например, вероятности
отказа каждого узла, входящего в
электрическую схему. Как известно,
соединения приборов в электрической
цепи возможно двумя способами: параллельномилипоследовательном.
Пусть два прибора Z1иZ2соединены
последовательно. Вероятность отказа
каждого прибора соответственно равноp1иp2.
Поставим вопрос: какова вероятность
того, что электрическая схема выйдет
из строя? Какова вероятность того, что
электрическая схема будет работать
некоторое время безотказно?
Вероятности безотказной работы каждого
прибора в течение некоторого времени
будут равны
![]() .
.
Пусть A– событие,
состоящее в том, что схема выйдет из
строя,![]() – событие, состоящее в том, что схема
– событие, состоящее в том, что схема
будет работать безотказно. Тогда

Пусть два прибора Z1иZ2соединены
параллельно. Вероятность отказа каждого
прибора соответственно равноp1иp2. Поставим
вопрос: какова вероятность того, что
электрическая схема выйдет из строя?
Какова вероятность того, что электрическая
схема будет работать некоторое время
безотказно?
Вероятности безотказной работы каждого
прибора в течение некоторого времени
будут равны
![]() .
.
Пусть A– событие,
состоящее в том, что схема выйдет из
строя,![]() – событие, состоящее в том, что схема
– событие, состоящее в том, что схема
будет работать безотказно. Тогда

Пример 4.6.Дана электрическая схема,
в которой вероятность отказов узлов![]() ,
,
за времяTравнаp1=0,2;p2=0,1;p3=0,2;p4=0,4. Схема
выходит из строя, если цепь разомкнута.
Определить вероятность того, что цепь
не пропустит электрический ток.

Решение.Пусть![]() событие, заключающееся
событие, заключающееся
в том, что в цепи тока нет. Цепь разобьем
на два участка:![]() и
и![]() ,
,
которые соединены последовательно.

![]() ,
,
где![]() и
и![]() вероятность того,
вероятность того,
что ток есть.
Тогда
![]() .
.
Участок
![]() разбиваем на два участка:
разбиваем на два участка:![]() и
и![]() ,
,
которые соединены параллельно. Пусть![]() событие, заключающееся
событие, заключающееся
в том, что на этом участке ток есть. Тогда
![]() ,
,
где
![]() вероятность того,
вероятность того,
что на участке![]() тока нет,
тока нет,![]() вероятность того,
вероятность того,
что на участке![]() тока нет.
тока нет.
По условию p1=0,2.
Участок![]() есть последовательное
есть последовательное
соединение двух элементов![]() и
и![]() .
.
Тогда
![]() .
.
Далее
![]() .
.
Следовательно,
![]() .
.
Почему в одной ситуации вероятности складываются, в другой – умножаются, а в третьей – вообще всё сложнее ?
Приветствую Вас, уважаемые Читатели! В одном из прошлых материалов, где я рассказывал про доску Гальтона – механическое устройство, которое визуализирует биномиальное распределение, я использовал три незыблемых правила манипулирования вероятностью. В этом материале хотелось бы поговорить об этом подробнее. Поехали!
Что такое событие?
Согласно словарю Ожегова событие – это “то, что произошло, то или иное значительное явление, факт общественной, личной жизни“. Глобально события можно разделить на два вида: детерминированные и вероятностные.
- Первые – это те события, исход которых можно предсказать и описать до факта его совершения. Например, если Вы бросите камень с 9-го этажа, то можете быть уверены, что он упадёт на Землю.
- Вторые – это те, которые даже при одинаковых начальных условиях могут привести к неожиданному или случайному исходу. Классическим примером случайного события является бросок монеты: до того, как монета не упадет, мы можем только предполагать, какой стороной она окажется к верху.
Однако и во втором случае есть место детерминированности. Мы на 100% уверены, что событий может быть только два: “Орёл” или “Решка”.
События “Орёл” и “Решка” образуют т.н. называемую полную группу событий. Математически это можно записать следующим образом:
Есть еще много различных классификаций “событий”, но я позволю остановиться на этом
Несовместные события
Что еще нужно сказать о событиях “Орёл” и “Решка” ? Самое главное – это то, что появление одного из них исключает выпадение другого. В теории вероятностей такие события принято называть несовместными, а в случае двух исходов, как в нашем случае, – противоположными.
Для несовместных событий действует теорема о сложении вероятностей:
- Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
В случае с подбрасыванием монетки это звучит так: вероятность получить или “Орёл” или “Решку” равно сумме вероятностей каждого исхода. Здесь ключевую роль играет союз “ИЛИ”, ведь именно он вербально задаёт несовместимость событий.
Независимые события
Казалось бы, следует перейти к понятию совместного события, однако логика требует иначе. Давайте представим, что мы параллельно подбрасываем две монеты. Зависит ли исход каждого испытания друг от друга?
Да, можно пытаться хитрить, но природу не обманешь….
Очевидно, что нет. Таким образом два события называются независимыми, если появление одного из них, не изменяет вероятность появления другого.
Правило вычисления вероятности независимых событий называется теоремой об умножении вероятностей:
Здесь уже главенствует союз “И” : вероятность наступления и того, и другого события равно произведению вероятностей наступления каждого из них по отдельности (независимые события!).
На конкретном примере вероятность выпадения двух “Орлов” или двух “Решек” при одновременном подбрасывании двух монет равняется 1/2*1/2 = 1/4.
Совместные события
Продолжим подбрасывать параллельно две монеты и попытаемся ответить на вопрос, а чему равна вероятность выпадения хотя бы одного “Орла” или “Решки” ?
- Очевидно, что, если складывать вероятности, то получим 1/2+1/2 = 1, что противоречит здравому смыслу. Ведь легко представить ситуацию, когда мы загадаем “Орла”, а две монеты выпадут “Решкой”.
- Умножение вероятностей так же не работает, ведь мы ищем вероятность хотя бы одного, а не одновременного выполнения событий.
Ответ: совместить два подхода и использовать формулу:
Таким образом, вероятность равняется 1/2+1/2 – 1/2*1/2 = 3/4.
События такого вида называются совместными – возникновение каждого из них не исключает возникновение другого. Естественно, что указанная выше формула распространяется и на произвольное количество событий, разве что будет немного посложнее.
Осталось рассмотреть еще один важный класс событий – зависимые, но это я сделаю в одном из следующих материалов. Спасибо за внимание!
- Ставьте “Нравится” и подписывайтесь на канал прямой сейчас, чтобы не пропустить следующие публикации.
- TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.
Содержание:
Основные теоремы теории вероятностей:
Теоремы сложения вероятностей
Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 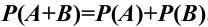
Доказательство.
Докажем теорему для схемы случаев. Пусть всевозможные исходы опыта сводятся к совокупности случаев, которые можно наглядно изобразить в виде 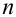
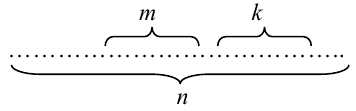
Теорема 1 (Обобщенная теорема сложения несовместных событий) Вероятность суммы 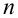 несовместных событий равна сумме вероятностей этих событий:
несовместных событий равна сумме вероятностей этих событий: 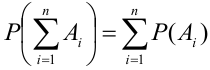 .
.
Доказательство (методом математической индукции).
Предположим, что теорема справедлива для 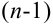 несовместного события:
несовместного события: 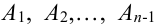 , т.е. справедливо равенство:
, т.е. справедливо равенство: 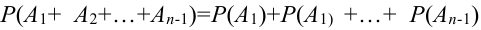 . Докажем, что теорема будет справедлива для
. Докажем, что теорема будет справедлива для 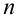 несовместных событий.
несовместных событий.
Обозначим  .
.
Имеем 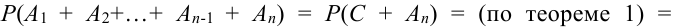
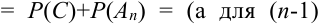 несовместного события теорема доказана) =
несовместного события теорема доказана) = 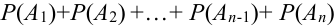 . (что и треб. доказать)
. (что и треб. доказать)
Следствие 1. Если события 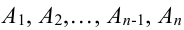 образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
образуют полную группу несовместных событий, то сумма их вероятностей равна единице: 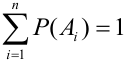 .
.
Доказательство.
Т.к. события 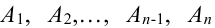 образуют полную группу несовместных событий, то, по определению, появление хотя бы одного из них – достоверное событие:
образуют полную группу несовместных событий, то, по определению, появление хотя бы одного из них – достоверное событие: 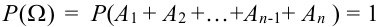 .
.
Т.к. события несовместные, то к ним применима обобщенная теорема сложения:
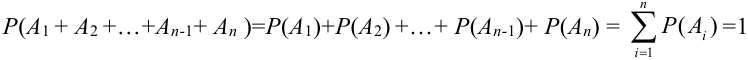 , (что и треб, доказать).
, (что и треб, доказать).
Следствие 2. Сумма вероятностей противоположных событий равна единице: 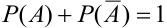
Доказательство.
События А, 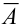 – противоположные, т.е. по определению образуют полную группу несовместных событий, тогда по следствию 1,
– противоположные, т.е. по определению образуют полную группу несовместных событий, тогда по следствию 1, 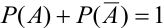 .
.
Замечание. Следствие 2 – частный случай следствия 1. На практике весьма часто оказывается легче вычислить вероятность противоположного события, чем прямого.
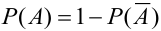 .
.
В формулировке таких задач встречаются слова «хотя бы», «не менее», «по крайней мере» и др.
Пример:
Из колоды карт (36) наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.
Решение.
1 способ (по теореме 1′).
Событие А = {из 3 карт окажется хотя бы один туз}.
Хотя бы один – это либо один, либо два, либо три, т.е. событие А может быть представлено в виде суммы трех событий: 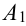 = {из 3 карт окажется один туз},
= {из 3 карт окажется один туз}, 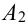 = {из 3 карт окажется два туза},
= {из 3 карт окажется два туза}, 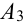 = {из 3 карт окажется три туза}.
= {из 3 карт окажется три туза}.
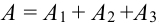 .
.
Т.к. события несовместны, то по теореме 1′: 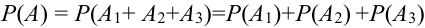 .
.
Найдем отдельно вероятности событий.
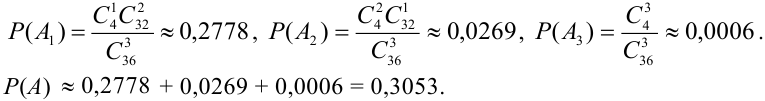
2 способ (по следствию 2).
Событие 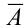 = {из 3 вынутых карт не окажется ни одного туза}.
= {из 3 вынутых карт не окажется ни одного туза}.
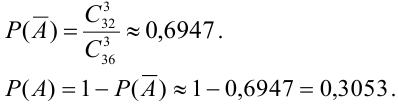
Теорема 2. Вероятность суммы двух совместных событий равна сумме вероятностей этих
событий без вероятности их произведения (совместного осуществления): 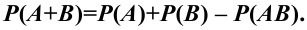
Доказательство (геометрическое)
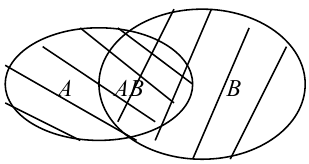
События отождествляют с множествами. Два раза накладываем «лепесток» друг на друга, поэтому и отнимаем его. (что и треб. доказать)
Теорема 2 ( Обобщенная теорема сложения совместных событий).
Вероятность суммы 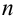 совместных событий равна
совместных событий равна 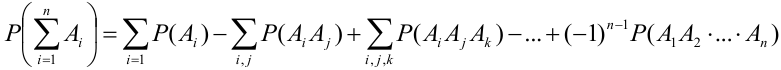 , где суммы распространяются на различные значения индексов.
, где суммы распространяются на различные значения индексов.
Для трех совместных событий теорема запишется в виде:
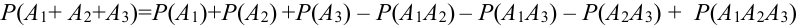
Доказательство для трех событий (геометрическое):
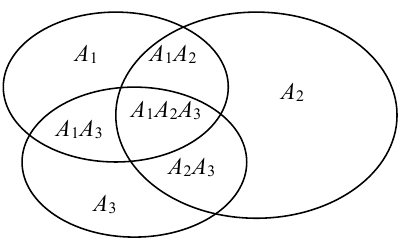
События отождествляют с множествами (см. рис.). (что и треб. доказать)
Замечание. Аналогичную формулу можно написать для произведения совместных событий:
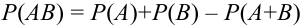
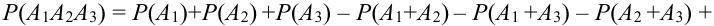
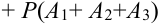
Пример:
Для поражения самолета необходимо, чтобы были поражены оба двигателя (события 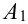 и
и 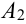 ) или была поражена кабина пилота (событие
) или была поражена кабина пилота (событие 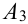 ). Требуется выразить вероятность поражения самолета (событие А) через вероятности событий
). Требуется выразить вероятность поражения самолета (событие А) через вероятности событий 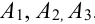 .
.
Решение.
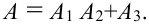 Т.к. события совместны, то по теореме 2 следует, что
Т.к. события совместны, то по теореме 2 следует, что
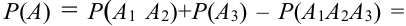 (по замечанию) =
(по замечанию) =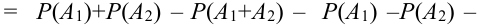
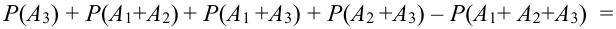
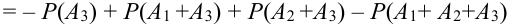 .
.
Теоремы умножения вероятностей
Определение 21. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Определение 22. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Примеры:
1) А = {появление решки на первой монете}, В = {появление решки на второй монете}. А и В – независимы.
2) А = {рождение мальчика у Тани}, В = {рождение мальчика у Лены}. А и В – независимы.
3) В урне 2 белых и 1 черный шар. Двое Таня и Ваня вынимают из урны по одному шару. Зависимы или независимы события: А = {появление белого шара у Тани}, В = {появление белого шара у Вани}?
Решение.
Найдем вероятности событий. 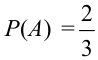 до известия о событии В. После известия о событии В данная вероятность
до известия о событии В. После известия о событии В данная вероятность 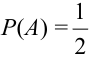 . Следовательно, А и В зависимые.
. Следовательно, А и В зависимые.
Определение 23. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Определение 24. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.
Определение 25. Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается 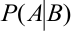 .
.
В Примере 3): 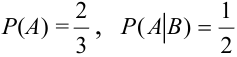 .
.
Условие независимости события А от события В: 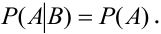
Условие зависимости события А от события В: 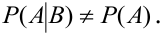
Теорема 3. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
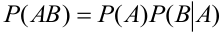
Доказательство.
Докажем для схемы урн истинность тождества формулы.
Пусть всевозможные исходы опыта сводятся к 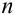 случаям, которые изобразим в виде точек:
случаям, которые изобразим в виде точек:
Пусть событию А благоприятствует 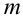 случаев, событию В –
случаев, событию В – 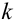 случаев, а т.к. события А и В совместны (мы не предполагали их несовместность), то событиям А и В одновременно благоприятствует
случаев, а т.к. события А и В совместны (мы не предполагали их несовместность), то событиям А и В одновременно благоприятствует 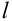 случаев.
случаев.
Тогда, вероятности данных событий равны: 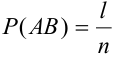 ,
, 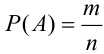 .
.
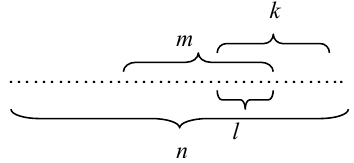
Вычислим условную вероятность 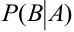 , т.е. условную вероятность события В в предположении, что А имело место. Если известно, что А произошло, то из ранее возможных
, т.е. условную вероятность события В в предположении, что А имело место. Если известно, что А произошло, то из ранее возможных 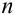 случаев остаются возможными только те, которые благоприятствовали событию А. Из них
случаев остаются возможными только те, которые благоприятствовали событию А. Из них 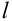 случаев благоприятны событию В, следовательно,
случаев благоприятны событию В, следовательно, 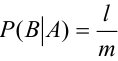 , т.е.
, т.е.
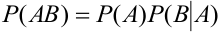 — истинно, т.к.
— истинно, т.к. 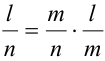 — истинное тождество. (что и треб, доказать).
— истинное тождество. (что и треб, доказать).
Замечание 1. При применении теоремы вполне безразлично, какое из событий А или В считать первым, а какое вторым, т.е. теорему можно записать в виде: 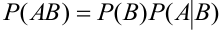
Замечание 2. В общем случае при 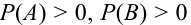 условная вероятность выражается формулой:
условная вероятность выражается формулой: 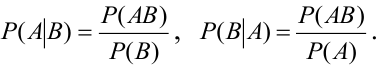
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.
Замечание 3. Зависимость и независимость событий всегда взаимны.
Замечание 4. Условные вероятности обладают всеми свойствами, присущими обычным вероятностям:
1. 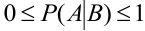 ,
,
2. если наступление события В исключает возможность осуществления А, т.е. 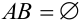 , то
, то 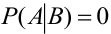 если событие В ведет к обязательному осуществлению А, т.е.
если событие В ведет к обязательному осуществлению А, т.е. 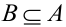 , то
, то 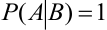 .
.
3. Если 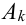 – несовместные события, т.е.
– несовместные события, т.е. 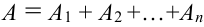 , то
, то 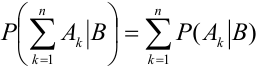 .
.
4. 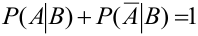 .
.
Замечание 5. Если А и В независимы, то независимы также события 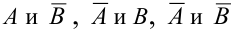 .
.
Теорема 3. ( Обобщенная теорема умножения зависимых событий).
Вероятность произведения нескольких зависимых событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что всс предыдущие имели место:
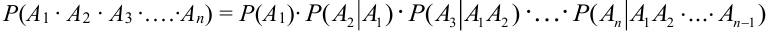 .
.
Теорема 4. {теорема умножения независимых событий).
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: 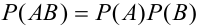 .
.
Теорема 4. ( Обобщенная теорема умножения независимых событий).
Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий:
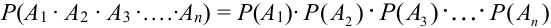 .
.
Пример:
Из колоды карт последовательно вынуты две карты. Найти: а) вероятность того, что вторая карта окажется тузом (неизвестно, какая карта была вынута вначале), б) вероятность того, что вторая карта будет тузом, если первоначально тоже был вынут туз.
Решение.
Обозначим А = {появление туза вторым}, В = {появление туза первым}.
а) 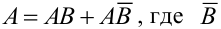 = {появление первым не туза}. События АВ и АВ – несовместны, тогда по теореме 1 следует, что
= {появление первым не туза}. События АВ и АВ – несовместны, тогда по теореме 1 следует, что 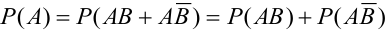 = (события А и В, А и
= (события А и В, А и 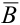 — зависимые, применим теорему 3) =
— зависимые, применим теорему 3) = 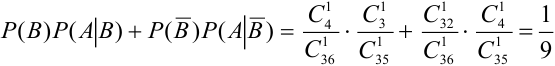 .
.
б) Если вынутая первая карта – туз , то в колоде осталось 35 карт и среди них только три туза, следовательно, 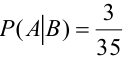 .
.
Или можно было найти эту вероятность, используя формулу условной вероятности:
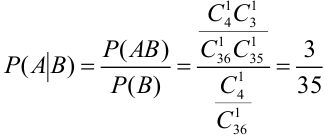
Пример:
В урне 2 белых и 3 черных шара. Из урны вынимают подряд 2 шара. Найти вероятность того, что а) оба белые, б) оба белые, если после первого вынимания шар возвращают обратно в урну, и шары перемешиваются.
Решение.
Обозначим: А = {появление двух белых шаров}, В = {появление белого шара при первом вынимании}, С = {появление белого шара при втором вынимании}.
а) 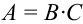 . События В и С – зависимы, тогда по теореме 3 следует, что
. События В и С – зависимы, тогда по теореме 3 следует, что
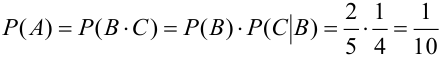 .
.
б) 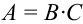 . События В и С – независимы, тогда по теореме 4 следует, что
. События В и С – независимы, тогда по теореме 4 следует, что 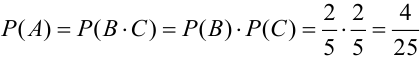 .
.
Теорема 5. Вероятность наступления события А, состоящего в появлении хотя бы одного из событий 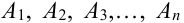 , независимых в совокупности, равна разности между 1 и произведением вероятностей противоположных событий:
, независимых в совокупности, равна разности между 1 и произведением вероятностей противоположных событий: 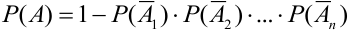
Если все 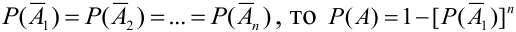 .
.
Пример:
Производится три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно 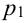 = 0,4;
= 0,4; 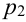 = 0,5;
= 0,5; 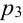 = 0,7. Найти вероятность того, что в результате этих трех выстрелов в мишени будет хотя бы одна пробоина.
= 0,7. Найти вероятность того, что в результате этих трех выстрелов в мишени будет хотя бы одна пробоина.
Решение.
Обозначим А = {хотя бы одно попадание в цель}.
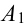 = {попадание в цель при первом выстреле},
= {попадание в цель при первом выстреле}, 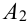 = {попадание в цель при втором выстреле},
= {попадание в цель при втором выстреле}, 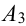 = {попадание в цель при третьем выстреле}.
= {попадание в цель при третьем выстреле}. 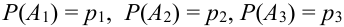 .
.
Можно расписать в алгебре событий данное событие в виде суммы произведений: 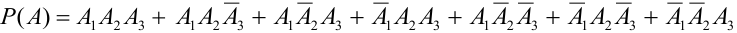 и найти вероятности слагаемых, где множители – независимые события. Но это нецелесообразно.
и найти вероятности слагаемых, где множители – независимые события. Но это нецелесообразно.
Перейдем от прямого события к противоположному: 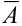 = { ни одного попадания в цель}:
= { ни одного попадания в цель}:
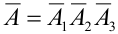 ,
,
где 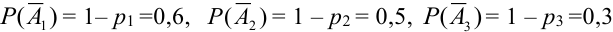 .
.
Тогда по теореме 5:
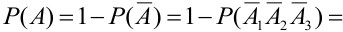 (т.к. события независимые, то по теореме 4) =
(т.к. события независимые, то по теореме 4) = 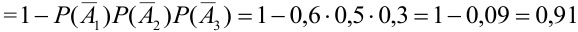 .
.
Основные формулы для вычисления вероятностей
Ограниченность классического и статистического способов определения вероятности событий, приемлемых, главным образом, для определения вероятности простых событий, приводит к тому, что в подавляющем большинстве случаев ни один из этих способов в чистом виде для решения задачи определения наступления событий применить не удаётся.
Например, требуется определить вероятность поражения движущегося танка. Определить эту вероятность по частоте наступления события на практике невозможно – необходимо провести большое число стрельб. При этом надо не только определить вероятность попадания в движущийся танк (что сделать не сложно), но и определить вероятность поражения его экипажа, если будет иметь место попадание в танк (а это выполнить на практике невозможно).
Факт сложности или невозможности определения вероятности сложных событий явился стимулом разработки аппарата теории вероятностей, с помощью которого вероятность определяется не прямым, а косвенным методом через вероятность более простых событий.
Сущность косвенного метода определения вероятности сложного события заключается в следующем: вначале анализируют условия испытания и устанавливают события 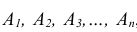 от которых зависит наступление события В, как комбинацию
от которых зависит наступление события В, как комбинацию 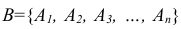 . Определяют вероятности наступления простых событий
. Определяют вероятности наступления простых событий 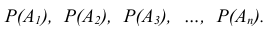 . После чего определяют вероятности интересующего события В как функцию известных или заданных вероятностей.
. После чего определяют вероятности интересующего события В как функцию известных или заданных вероятностей.
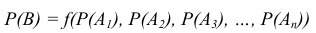
Однако определению вероятности наступления сложного события как комбинации более простых событий должны предшествовать твёрдые знания правил применения рассмотренных в лекции теорем сложения (объединения) и умножения (пересечения) событий.
Этому вопросу и будет посвящён вопрос нашего занятия.
Пример:
Для того что бы вывести из строя артиллерийскую батарею необходимо поразить либо два взвода с орудиями либо центр управления огнём. Используя операции сложения (объединения) и умножения (пересечения) событий представим сложное событие D={ поражение артиллерийской батареи} как комбинацию простых событий. Результат проиллюстрируем диаграммой Эйлера-Венна.
Решение:
Обозначим через событие А = {поражение первого взвода орудий}, через событие В = {поражение второго взвода орудий}, С = {поражение центра управления огнём}. Тогда событие D = {поражение артиллерийской батареи} определится как поражение либо центра управления огнём (событие С) либо одновременно первого взвода орудий (событие А) и второго взвода орудий (событие В), т.е. будет иметь место следующая комбинация событий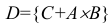 (рисунок 1).
(рисунок 1).
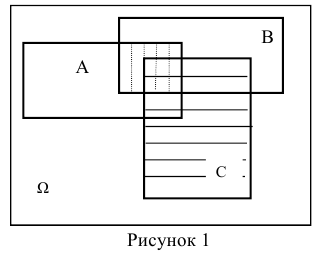
Для решения такого типа задач необходимо усвоить ряд основных свойств, которыми обладают действия над событиями.
Операции сложения (объединения) и умножения (пересечения) событий обладают рядом свойств, аналогичным свойствам сложения и умножения чисел.
1. Переместительное свойство:
А + В = В + А; 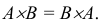
2. Сочетательное свойство:
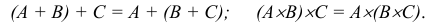
3. Распределительное свойство:
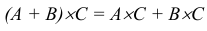 (рисунок 2).
(рисунок 2).
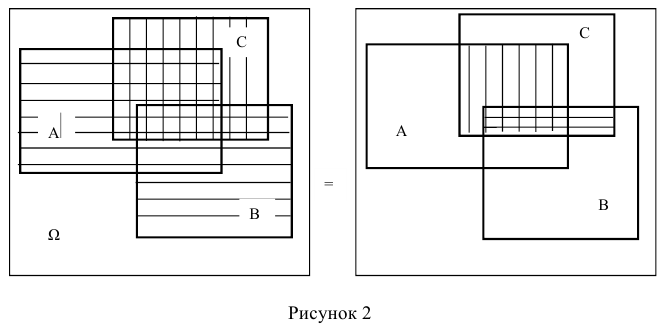
4. Операции прибавления пустого множества и умножения на пустое множество аналогичны операциям над числами, если считать пустое множество за ноль.
Ряд операций над событиями уже не обладают свойствами по аналогии с арифметическими действиями, например:
5. 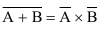 (рисунок 3)
(рисунок 3)
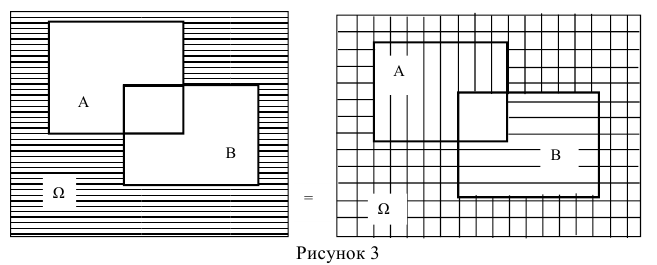
6. 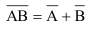 (рисунок 4).
(рисунок 4).
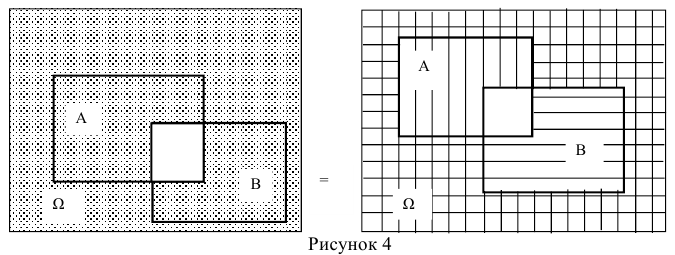
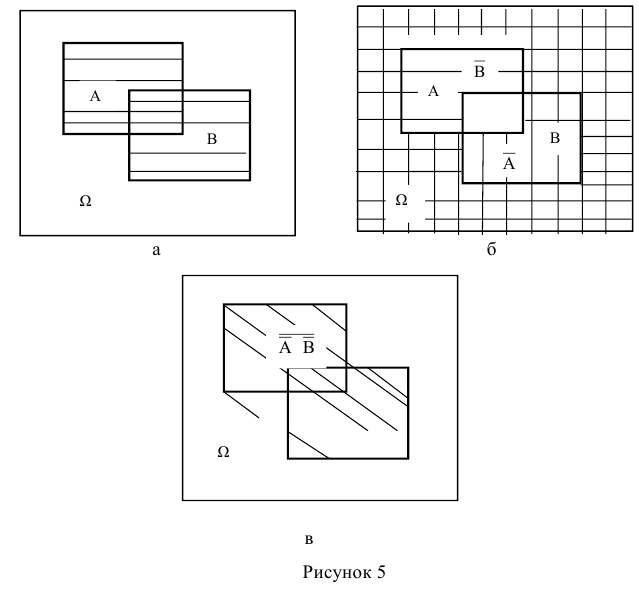
7. 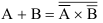 (рисунок 5)
(рисунок 5)
Основные теоремы теории вероятностей: сложение, умножение, формула полной вероятности
На предыдущей лекции мы говорили о том, что достаточно часто определить вероятность сложного события трудно или вообще невозможно. Для чего научились представлять события, как комбинацию других более простых событий используя понятия суммы (объединения) или произведения (пересечения) событий.
Вспомним пример, рассматриваемый нами на предыдущей лекции:
Для того что бы вывести из строя артиллерийскую батарею необходимо поразить либо два взвода с орудиями либо центр управления огнём. Используя для решения задачи правила сложения и умножения событий сложное событие – поражение артиллерийской батареи, заключающееся в поражении либо двух взводов орудий либо центра управления огнём, было представлено как следующая комбинация событий 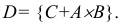
На сегодняшнем занятии мы ответим на следующий вопрос: как определить вероятность сложного события представляющего собой функцию известных или заданных вероятностей
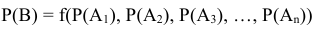
При определении вероятностей сложных событий пользуются теоремами сложения и умножения вероятностей. Эти теоремы теоретически могут быть доказаны только для таких событий, вероятность появления которых может быть определена классическим способом. Для других событий эти теоремы принимаются как аксиомы. Поэтому мы не будем показывать доказательство этих теорем, а ограничимся только понятием «правила», понимая при этом ряд теорем и следствий из них, с помощью которых определяется вероятность комбинации событий.
Правила сложения вероятностей
Аксиома: Вероятность суммы или наступления хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий (аддитивность Р):
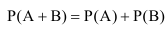
Данную аксиому иногда называют «теоремой сложения», так как для опытов, сводящихся к «схеме случаев», она может быть доказана.
Эта аксиома легко обращается на любое число несовместных событий: вероятность суммы несовместных событий равна сумме вероятностей этих событий:
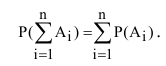
Пример №1
Вероятность попадания в башню танка при одном выстреле- 0,2, в его корпус – 0,1, в ходовую часть – 0,025. Найти вероятность попадания в танк при одном выстреле.
Решение:
Обозначим интересующее нас событие через А = {попадание в танк}, тогда 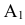 = {попадание в башню танка},
= {попадание в башню танка}, 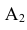 = {попадание в корпус танка},
= {попадание в корпус танка}, 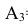 ={попадание в ходовую часть}.
={попадание в ходовую часть}.
Очевидно, что попадание в танк наступит тогда, когда снаряд попадёт либо в башню, либо в корпус, либо в ходовую часть танка. Таким образом, интересующее нас событие А будет являться суммой событий 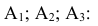
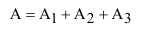
А так как события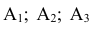 несовместные (наступление одного из них исключает появление другого), то вероятность наступления события А определится как:
несовместные (наступление одного из них исключает появление другого), то вероятность наступления события А определится как:
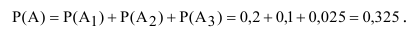
Вывод: полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 325 случаях из 1000 будет получено попадание в танк.
Из данной аксиомы вытекают два важных следствия.
Следствие 1. Если события 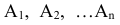 образуют полную группу несовместных событий
образуют полную группу несовместных событий 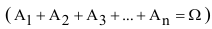 , то сумма их вероятностей равна единице.
, то сумма их вероятностей равна единице.
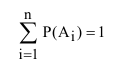
Следствие 2. Сумма вероятностей противоположных событий равна 1.
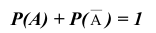
Для совместных событий аксиома примет следующий вид:
Вероятность суммы, или наступление хотя бы одного из двух совместных событий, равна сумме вероятности этих событий без вероятности произведения этих событий:
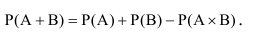
Справедливость этого тождества наглядно следует из его геометрической интерпретации (рисунок 1).
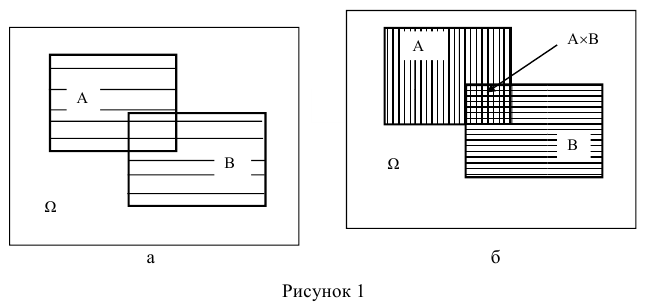
На диаграмме Эйлера-Венна вероятность наступления событий А (или
В) по существу есть площадь области, при попадании случайной точки в которую, наступает событие А (или В). Тогда вероятность комбинации А + В будет соответствовать площади заштрихованной области (рисунок 1 .а). Чтобы получить такую же по площади область, необходимо из площади областей наступления событий А и В вычесть площадь их совместного появления АхВ (рисунок 1.6).
Пример №2
Вероятность подавления батареи противника из-за потерь только в личном составе составляет 0,15; вследствие повреждения материальной части – 0,45; а из-за потерь одновременно в личном составе и материальной части – 0,25. Какова вероятность подавления артиллерийской батареи?
Решение: Пусть событие А = {подавление личного состава батареи}, а событие В= {повреждения материальной части}. Тогда одновременное подавление личного состава и повреждение материальной части будут являться совместным наступлением событий А и В или 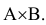
Вероятность наступления события А по условию задачи равна 0,15 (Р(А)=0,15), вероятность наступления события В равна 0,45 (Р(В)=0,45), вероятность совместного наступления события А и В равна 0,25 (Р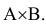 )=0,25).
)=0,25).
Требуется найти вероятность события С ={подавления батареи противника}, которое будет заключаться либо в подавлении личного состава батареи, либо в повреждении материальной части либо того и другого, или Р(А+В).
Применив теорему сложения вероятностей, получим:
Р(С) = Р(А + В) = Р(А) + Р(В) – Р(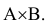 ) = 0,15 + 0,45 – 0,25 = 0,35.
) = 0,15 + 0,45 – 0,25 = 0,35.
Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 35 случаях из 100 батарея противника будет подавлена, т.е. поражён либо личный состав, либо повреждена техника, либо и то и другое.
Правила умножения вероятностей
Перед рассмотрением правил умножения вероятностей введём ряд новых понятий, которые необходимы для логического понимания производимых над событиями действий.
Событие А называется независимым от события В, если вероятность наступления события А не зависит от того, произошло ли событие В.
Событие А называется зависимым от события В, если вероятность наступления события А меняется в зависимости от того, произошло событие В или нет.
Факт зависимости или независимости события устанавливают из анализа условий испытания. В теории вероятностей под зависимостью случайных событий понимают не причинную зависимость, при которой два события выступают по отношению друг к другу как причина и следствие, а вероятностную или стохастическую зависимость (стохастическая зависимость [stochastic dependence] – зависимость между случайными величинами, проявляющаяся в том, что изменение закона распределения одной из них происходит под влиянием изменения закона распределения другой). Смысл вероятностной или стохастической зависимости двух событий состоит в том, что при наступлении одного из них другое наступает чаще или реже, чем наступает вообще при реализации данного комплекса условий.
В качестве примеров зависимых событий можно привести следующие:
Пример №3
Реализация комплекса условий: выстрел по танку; событие А= {попадание в танк}; реализация комплекса условий – попадание в танк; событие В = {поражение экипажа танка}.
Для появления интересующего события В = {поражение экипажа танка} при реализации комплекса условий – выстрел по танку необходимо появления события А = {попадание в танк}, в то же время при реализации комплекса условий события А = {попадание в танк} не всегда может наступить событие В = {поражение экипажа танка}.
Раз нам требуется определить вероятность совместного наступления двух зависимых событий, одно из которых может наступить только при том условии, что имело место другое из них, введём понятие условной вероятности события.
Вероятность события В, вычисленная при условии, что имело место другое событие А называется условной вероятностью события В по отношению к событию А (обозначается 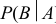 )).
)).
Теорема: Вероятность произведения или совместного наступления двух любых случайных событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
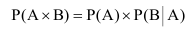
Пример №4
Вероятность попадания в танк при одном выстреле равна 0,8; вероятность поражения экипажа танка при попадании в танк равна 0,7. Определить вероятность поражения экипажа танка при одном выстреле.
Решение:
Пусть событие А = {попадание в танк при одном выстреле}, а событие В = {поражение экипажа танка}. Интересующее нас событие С = {поражение экипажа танка при одном выстреле} будет иметь место только в том случае, если наступит событие А, при этом наступление события С возможно только тогда, когда одновременно наступят события А и В.
Вероятность наступления события А по условию задачи равна 0,8 (Р(А)=0,8); вероятность наступления события В равна 0,7 (Р(В)=0,7).
Требуется найти вероятность поражения экипажа танка при одном выстреле, которая будет являться произведением вероятностей попадания в танк при одном выстреле и поражении экипажа танка при условии что имело место попадание в него, т.е. Р(С)=Р(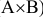 ).
).
Применив теорему умножения вероятностей, получим:
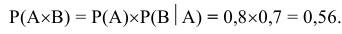
Вывод: полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях по одному выстрелу в каждом в среднем в 56 случаях из 100 экипаж танка будет поражён.
Правило умножения вероятностей легко обращается на случай произвольного числа событий:
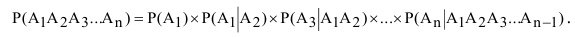
Из данной теоремы вытекает ряд важных следствий.
Следствие 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
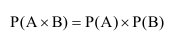
Пример №5
По цели в тире производят по одному выстрелу два студента. Вероятность попадания в цель первого студента равна 0,7, второго – 0,4. Найти вероятность того, что в цель попадут оба студента.
Решение:
Пусть событие А={попадание в цель первым студентом}, а событие В={попадание в цель вторым студентом}, тогда интересующее нас событие С={попадание в цель и первым и вторым студентом}.
Вероятность наступления события А по условию задачи равна 0,7 (Р(А)=0,7), вероятность наступления события В равна 0,4 (Р(В)=0,4).
Попадание в цель вторым студентом не зависит от того, попадёт ли в цель первый студент и наоборот, а следовательно события А и В -независимы. Применив следствие из теоремы умножения для независимых событий, получим:
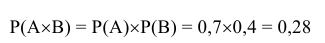
Вывод: полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях в среднем в 28 случаях из 100 в цель попадут оба студента.
Зависимость и независимость событий всегда взаимны. Если событие А не зависит от события В, то и событие В не зависит от события А. Таким образом, можно уточнить данное ранее определение независимых событий. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Из рассмотренных выше правил сложения и умножения вероятностей вытекает ещё одно очень важное следствие: если противоположное событие распадается на меньшее число вариантов, чем прямое событие, то имеет смысл при вычислении вероятностей переходить к противоположному событию:
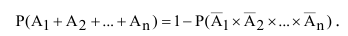
Пример №6
Два орудия, начиная с первого, ведут последовательно огонь по цели до получения первого попадания. При этом первое орудие может произвести два выстрела, а второе – только один. Вероятность попадания в цель при первом выстреле первого орудия – 0,4; вторым выстрелом – 0,8; вероятность попадания в цель вторым орудием – 0,6. Чему равна вероятность поражения цели?
Решение:
Обозначим за событие 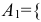 попадание в танк первым орудием с первого выстрела}, за событие
попадание в танк первым орудием с первого выстрела}, за событие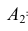 = {попадание в танк первым орудием со второго выстрела};В={ попадание в танк вторым орудием}. Тогда интересующее нас событие С={поражение танка} определится как:
= {попадание в танк первым орудием со второго выстрела};В={ попадание в танк вторым орудием}. Тогда интересующее нас событие С={поражение танка} определится как:
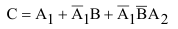
Так как события 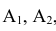 В несовместны и независимы, то вероятность наступления события С будет равна:
В несовместны и независимы, то вероятность наступления события С будет равна:
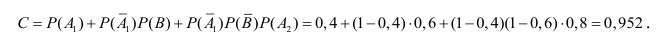
Вывод: полученный результат означает, что при проведении достаточно большого числа испытаний в аналогичных условиях в среднем в 95 случаях из 100, танк будет поражён.
Формула полной вероятности
При изложении третьего вопроса лекции преподаватель на примере поражения движущегося танка обозначает проблему определения вероятности сложного события (давая при этом понятие гипотезы).
После чего преподаватель доводит условие задачи (Пример 7), формулу для вычисления полной вероятности события (без её вывода) и условия её применения.
При постановке задачи и пояснения физической сущности вопроса преподаватель использует оверхэд-проектор и подготовленные слайды.
Решение задачи преподаватель проводит на доске, особое внимание при этом обращая на методику её решения и порядок записи. В заключении решения задачи преподаватель под запись доводит вывод, отражающий физическую сущность полученного результата.
При решении ряда практических задач вычисление вероятности некоторого сложного события можно существенно облегчить, если связать наступление этого события с наступлением единственно возможных и несовместных событий, под которыми понимаются гипотезы о всех возможных исходах испытаний.
Пусть, например, производится выстрел по танку (рисунок 2).
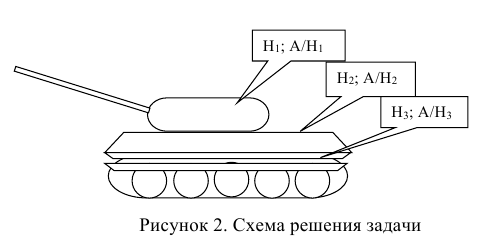
Известно, что башня танка, его корпус или ходовая часть имеют не только различные размеры, форму и т.д., что усложняет попадание, но и различную степень уязвимости. Первое приводит к тому, что вероятность попадания в различные отсеки танка будет различной, а второе – к тому, что различной будет и вероятность поражения танка при попадании в его башню, корпус или ходовую часть, а, следовательно, и вероятность поражения танка в целом. Поэтому для облегчения вычисления вероятности поражения танка Р(А) представляется целесообразным ввести гипотезы о возможном исходе стрельбы.
Дадим определение:
Под гипотезами понимают полную группу единственно возможных несовместных событий, которые могут наступить в результате проведения испытаний.
В условиях нашей задачи гипотезы о возможном исходе стрельбы будут следующие:
- •
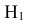 ={попадание в башню танка};
={попадание в башню танка}; - •
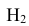 ={попадание в корпус танка};
={попадание в корпус танка}; - •
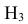 = {попадание в ходовую часть танка};
= {попадание в ходовую часть танка}; - •
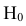 ={ промах}.
={ промах}.
Вероятности этих гипотез 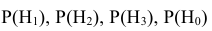 можно определить и не проводя стрельбу по танку, достаточно, например, провести стрельбу его макету. Далее можно поставить задачу определения условных вероятностей поражения танка при попадании в различные его отсеки, т.е. поставить задачу определения условных вероятностей поражения танка при реализации выбранных гипотез:
можно определить и не проводя стрельбу по танку, достаточно, например, провести стрельбу его макету. Далее можно поставить задачу определения условных вероятностей поражения танка при попадании в различные его отсеки, т.е. поставить задачу определения условных вероятностей поражения танка при реализации выбранных гипотез: 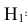 ={npH попадании в башню танка};
={npH попадании в башню танка}; 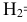 ={при попадании в корпус танка}; Нз= {при попадании в ходовую часть танка}:
={при попадании в корпус танка}; Нз= {при попадании в ходовую часть танка}:
- •
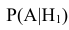 – вероятность поражения танка при попадании в башню;
– вероятность поражения танка при попадании в башню; - •
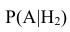 – вероятность поражение танка при попадании в корпус;
– вероятность поражение танка при попадании в корпус; - •
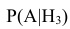 – вероятность поражение танка при попадании в ходовую часть.
– вероятность поражение танка при попадании в ходовую часть.
Указанные условные вероятности возможно определить опытным путём, проводя полигонные стрельбы по танку.
Пример №7
Ведётся стрельба из орудия по танку. Известно, что при попадании снаряда в башню вероятность поражения танка равна 0,8; при попадании в корпус – 0,6; при попадании в ходовую часть – 0,5.
Известны также вероятности попадания снаряда в каждый из отсеков танка. Вероятность попадания в башню танка равна 0,2. Вероятность попадания в корпус равна 0,3; вероятность попадания в ходовую часть равна 0,1.
Требуется определить вероятность поражения танка при одном выстреле.
Вычислить вероятность наступления интересующего нас события позволяет формула, получившая особое название формулы полной вероятности.
Полная вероятность события равна сумме парных произведений вероятностей каждой из гипотез на отвечающие им условные вероятности наступления этого события.
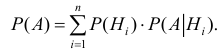
Данная формула является следствием из обеих теорем – теорем сложения и умножения вероятностей.
При определении полной вероятности необходимо следить, чтобы были учтены все гипотезы о возможном исходе испытания, при которых может наступить интересующее нас событие, т.е. гипотезы должны составлять полную группу несовместных событий. Свидетельством полного учёта всех гипотез является выполнение равенства
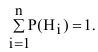
Если данное равенство не выполняется, то это означает, что учтены не все гипотезы о возможных исходах испытания.
Таким образом оказывается, что знания вероятностей гипотез 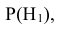
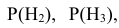 о возможных исходах стрельбы и условных вероятностей наступления интересующего нас события А – поражение танка при осуществлении этих гипотез
о возможных исходах стрельбы и условных вероятностей наступления интересующего нас события А – поражение танка при осуществлении этих гипотез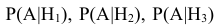 является достаточным для вычисления вероятности поражения танка, т.е. наступления интересующего нас события А.
является достаточным для вычисления вероятности поражения танка, т.е. наступления интересующего нас события А.
Вернёмся к решению примера.
Решение:
Таким образом, возможные гипотезы об исходах стрельбы:
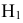 = {попадание в башню танка};
= {попадание в башню танка};
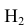 = {попадание в корпус танка};
= {попадание в корпус танка};
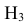 = {попадание в ходовую часть}.
= {попадание в ходовую часть}.
По условию задачи вероятности гипотез будут равны:
гипотеза 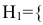 попадания в башню танка} – равна 0,2 (Р(
попадания в башню танка} – равна 0,2 (Р(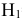 ) = 0,2);
) = 0,2);
гипотеза 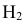 ={попадание в корпус танка} – равна 0,3 (Р(
={попадание в корпус танка} – равна 0,3 (Р(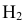 ) = 0,3);
) = 0,3);
гипотеза Нз ={попадание в ходовую часть} – равна 0,1 (Р(Нз) = 0,1).
Интересующее нас событие А = {поражение танка}. По условию задачи вероятность поражения танка при реализации гипотез:
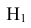 = {попадание в башню танка} равна 0,8 (Р(А|
= {попадание в башню танка} равна 0,8 (Р(А|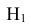 ) = 0,8);
) = 0,8);
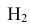 = {попадание в корпус танка} равна 0,6 (Р(А|
= {попадание в корпус танка} равна 0,6 (Р(А|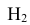 ) = 0,6);
) = 0,6);
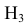 = {попадание в ходовую часть} равна 0,5 (Р(А|
= {попадание в ходовую часть} равна 0,5 (Р(А|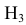 ) = 0,5).
) = 0,5).
Проверим, все ли гипотезы об исходах стрельбы учтены:
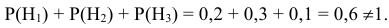
Следовательно, имеющиеся гипотезы не составляют полной группы событий и не учтено событие 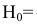 {промах}, вероятность которого можно определить как вероятность противоположного попаданию в танк события -промаху –
{промах}, вероятность которого можно определить как вероятность противоположного попаданию в танк события -промаху – 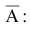
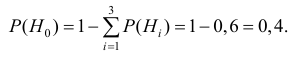
Таким образом, вероятность гипотезы 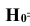 ={промах} равна 0,4. (Р|
={промах} равна 0,4. (Р|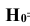 ) =0,4).
) =0,4).
Вероятность поражения танка при реализации гипотезы 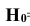 ={промах} равна 0. (Р(А|
={промах} равна 0. (Р(А|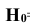 ) = 0).
) = 0).
Применяя формулу полной вероятности для решения задачи получим:
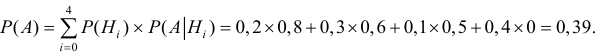
Следовательно, полная вероятность поражения танка при одном выстреле равна
Р(А) = 0,39 = 39%.
Вывод: Полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях в среднем в 39 случаях из 100 танк окажется поражённым.
Формула Байеса, вероятность появления хотя бы одного события
Пусть имеется полная группа несовместных гипотез 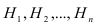 с известными вероятностями их наступления
с известными вероятностями их наступления 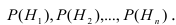 Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности
Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности
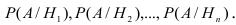
Требуется определить какие вероятности имеют гипотезы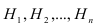 относительно события А, т.е. условные вероятности
относительно события А, т.е. условные вероятности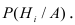
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, делённому на полную вероятность этого события.
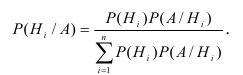
Эта формула называется формулой Байеса.
Доказательство.
По Теореме умножения вероятностей получаем:
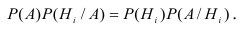
Тогда если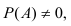
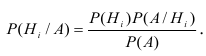
Для нахождения вероятности Р(А) используем формулу полной вероятности.
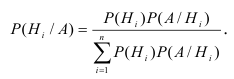
Если до испытания все гипотезы равновероятны с вероятностью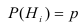 , то формула Байеса примет вид:
, то формула Байеса примет вид:
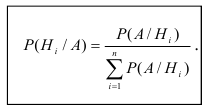
Пример №8
Известно, что 30% приборов собирает специалист высшей квалификации, 70% приборов – специалист средней квалификации. Вероятность того, что прибор, собранный специалистом высшей квалификации, надёжен, равна 0,9. Для специалиста средней квалификации эта вероятность равна 0,8. Взятый наудачу прибор оказался надёжным. Найти вероятность того, что этот прибор собран специалистом высшей квалификации.
Решение: пусть событие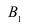 – появление прибора, собранного специалистом высшей квалификации; событие
– появление прибора, собранного специалистом высшей квалификации; событие 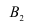 – появление прибора, собранного специалистом средней квалификации. Вероятности этих событий равны соответственно
– появление прибора, собранного специалистом средней квалификации. Вероятности этих событий равны соответственно 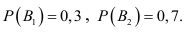
Пусть событие А означает появление надёжного прибора. По условию примера вероятность события А при условии, что появится прибор, собранный специалистом высшей квалификации, = 0,9. Аналогично вероятность появления надёжного прибора при условии, что появится прибор, собранный специалистом средней квалификации,
= 0,9. Аналогично вероятность появления надёжного прибора при условии, что появится прибор, собранный специалистом средней квалификации,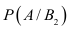 = 0,8.
= 0,8.
Искомая вероятность появления прибора, собранного специалистом высшей квалификации, т.е. события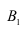 при условии, что появилось событие А, определяется по формуле
при условии, что появилось событие А, определяется по формуле
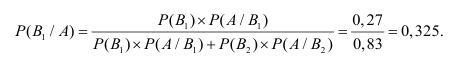
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Генеральная и выборочная совокупности
- Ковариация в теории вероятности
- Функциональные преобразования двухмерных случайных величин
- Правило «трех сигм» в теории вероятности
- Производящие функции
