Как найти вероятность наступления только одного события

Вероятность появления только одного события

Пример
4. Пусть даны
три независимых события
,,,
их вероятности соответственно равны,,
и.
Найти вероятность появления только
одного события.

 Пусть:

событие
–
появилось только событие(ине появились)

событие
–
появилось только событие(ине появились)

событие

–
появилось только событие(ине появились)

Таким
образом, чтобы найти вероятность
появления только одного из событий
,,,
будем искать вероятность

так
как события
,,несовместны.

События

,,– независимы,,– независимы.

Обозначим
,,.

Тогда
,
т.е.

(появления
только одного события ) =.˜

Формула полной вероятности.

Пусть
некоторое событие

может произойти вместе с одним из
несовместных событий
,
составляющих полную группу событий.
Пусть известны вероятности этих событийи условные вероятности наступления
события

при наступлении события
:

.

Теорема.
Вероятность
события
,
которое может произойти вместе с одним
из событий
,
равна сумме парных произведений
вероятностей каждого из этих событий
на соответствующие им условные вероятности
наступления события
.

Пример
5. В двух
ящиках содержатся по 20 деталей, причем
в первом 17 стандартных деталей, а во
втором 15 стандартных деталей. Из второго
ящика наудачу извлечена одна деталь и
переложена в первый ящик. Найти вероятность
того, что наудачу извлеченная деталь
из первого ящика, окажется стандартной.

 Опыт
можно разбить на два этапа:первый
– перекладывание детали,

второй
– выбор детали.

Гипотезы:

–
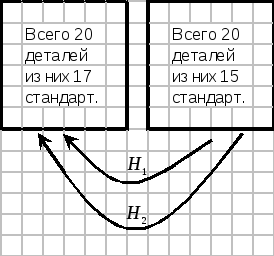
переложена стандартная деталь;

–
переложена нестандартная деталь.

,

.

,

.

.
˜

Пример
6. Один из
трех стрелков производит два выстрела.
Вероятность попадания в цель при одном
выстреле для первого стрелка равна 0,4,
для второго – 0,6, для третьего – 0,8. Найти
вероятность того, что в цель попадут
два раза.



Вероятность
того, что выстрелы производит первый,
второй или третий стрелок равна
.

Вероятности
того, что один из стрелков, производящих
выстрелы, два раза попадает в цель,
равны:

–
для первого стрелка:

–
для второго стрелка:

–
для третьего стрелка:

Искомая
вероятность равна:

.


Формула Байеса (формула гипотез)

Пусть
имеется полная группа несовместных
гипотез
с известными вероятностями их наступления.
Пусть в результате опыта наступило
событие
,
условные вероятности которого по каждой
из гипотез известны, т.е. известны
вероятности
.

Требуется
определить какие вероятности имеют
гипотезы
относительно события
,
то есть условные вероятности
.

Теорема.
Вероятность
гипотезы после испытания равна
произведению вероятности гипотезы до
испытания на соответствующую ей условную
вероятность события, которое произошло
при испытании, деленному на полную
вероятность этого события.

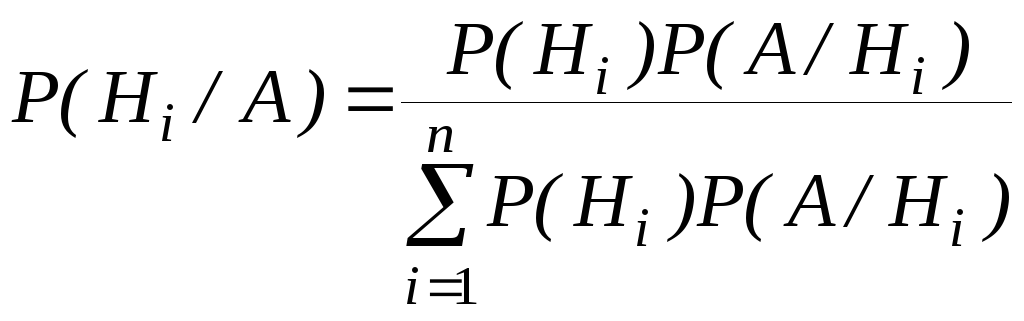
Эта
формула называется формулой
Байеса.

.

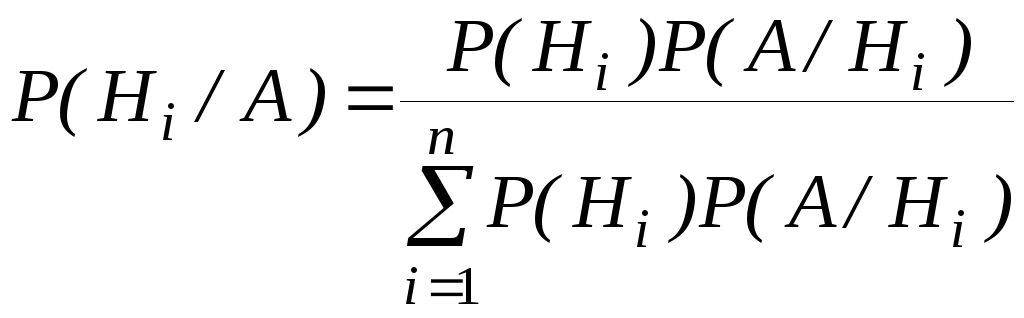Пример
7. Детали,
изготовляемые цехом завода, попадают
для проверки их на стандартность к
одному из двух контролеров. Вероятность
того, что деталь попадет к первому
контролеру равна 0,6, ко второму равна
0,4. Вероятность того, что деталь будет
признана стандартной первым контролером
равна 0,94, а вторым – 0,98. Годная деталь
при проверке была признана стандартной.
Найти вероятность того, что ее проверил
первый контролер.

 Гипотезы:

– деталь проверил первый контролер;

–
деталь проверил второй контролер.

Событие
–
деталь признана стандартной.

Как
видно до испытания
,
а после.˜

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решение задач с формулировкой “хотя бы один”

Поговорим о задачах, в которых встречается фраза “хотя бы один”. Наверняка вы встречали такие задачи в домашних и контрольных работах, а теперь узнаете, как их решать. Сначала я расскажу об общем правиле, а потом рассмотрим частный случай независимых событий и схемы Бернулли, выпишем формулы и примеры для каждого.

Общая методика и примеры

Общая методика для решения задач, в которых встречается фраза “хотя бы один” такая:

1. Выписать исходное событие $A$ = (Вероятность того, что … хотя бы …).
2. Сформулировать противоположное событие $bar{A}$.
3. Найти вероятность события $P(bar{A})$.
4. Найти искомую вероятность по формуле $P(A)=1-P(bar{A})$.

А теперь разберем ее на примерах. Вперед!

Пример 1. В ящике находится 25 стандартных и 6 бракованных однотипных деталей. Какова вероятность того, что среди трёх наудачу выбранных деталей окажется хотя бы одна бракованная?

Действуем прямо по пунктам.
1. Записываем событие, вероятность которого надо найти прямо из условия задачи:
$A$ =(Из 3 выбранных деталей хотя бы одна бракованная).

2. Тогда противоположное событие формулируется так $bar{A}$ = (Из 3 выбранных деталей ни одной бракованной) = (Все 3 выбранные детали будут стандартные).

3. Теперь нужно понять, как найти вероятность события $bar{A}$, для чего еще раз посмотрим на задачу: говорится об объектах двух видов (детали бракованные и нет), из которых вынимается некоторое число объектов и изучаются (бракованные или нет). Это задача решается с помощью классического определения вероятности (точнее, по формуле гипергеометрической вероятности, подробнее о ней читайте в статье).

Для первого примера запишем решение подробно, далее будем уже сокращать (а полные инструкции и калькуляторы вы найдете по ссылке выше).

Сначала найдем общее число исходов – это число способов выбрать любые 3 детали из партии в 25+6=31 деталей в ящике. Так как порядок выбора несущественнен, применяем формулу для числа сочетаний из 31 объектов по 3: $n=C_{31}^3$.

Теперь переходим к числу благоприятствующих событию исходов. Для этого нужно, чтобы все 3 выбранные детали были стандартные, их можно выбрать $m = C_{25}^3$ способами (так как стандартных деталей в ящике ровно 25).

Вероятность равна:

$$
P(bar{A})=frac{m}{n}=frac{C_{25}^3 }{C_{31}^3} = frac{23 cdot 24cdot 25}{29cdot 30cdot 31} =frac{2300}{4495}= 0.512.
$$

4. Тогда искомая вероятность:

$$
P(A)=1-P(bar{A})=1- 0.512 = 0.488.
$$

Ответ: 0.488.

Пример 2. Из колоды в 36 карт берут наудачу 6 карт. Найти вероятность того, что среди взятых карт будут: хотя бы две пики.

1. Записываем событие $A$ =(Из 6 выбранных карт будут хотя бы две пики).

2. Тогда противоположное событие формулируется так $bar{A}$ = (Из 6 выбранных карт будет менее 2 пик) = (Из 6 выбранных карт будет ровно 0 или 1 пиковые карты, остальные другой масти).

Замечание. Тут я остановлюсь и сделаю небольшое замечание. Хотя в 90% случаях методика “перейти к противоположному событию” работает на отлично, существуют случаи, когда проще найти вероятность исходного события. В данном случае, если искать напрямую вероятность события $A$ потребуется сложить 5 вероятностей, а для события $bar{A}$ – всего 2 вероятности. А вот если бы задача была такая “из 6 карт хотя бы 5 – пиковые”, ситуация стала бы обратной и тут проще решать исходную задачу. Если опять попытаться дать инструкцию, скажу так. В задачах, где видите “хотя бы один”, смело переходите к противоположному событию. Если же речь о “хотя бы 2, хотя бы 4 и т.п.”, тут надо прикинуть, что легче считать.

3. Возвращаемся к нашей задаче и находим вероятность события $bar{A}$ с помощью классического определения вероятности.

Общее число исходов (способов выбрать любые 6 карт из 36) равно $n=C_{36}^6$ (калькулятор сочетаний тут).

Найдем число благоприятствующих событию исходов. $m_0 = C_{27}^6$ – число способов выбрать все 6 карт непиковой масти (их в колоде 36-9=27), $m_1 = C_{9}^1cdot C_{27}^5$ – число способов выбрать 1 карту пиковой масти (из 9) и еще 5 других мастей (из 27).

Тогда:

$$
P(bar{A})=frac{m_0+m_1}{n}=frac{C_{27}^6+C_{9}^1cdot C_{27}^5 }{C_{36}^6} =frac{85215}{162316}= 0.525.
$$

4. Тогда искомая вероятность:

$$
P(A)=1-P(bar{A})=1- 0.525 = 0.475.
$$

Ответ: 0.475.

Пример 3. В урне 2 белых, 3 черных и 5 красных шаров. Три шара вынимают наугад. Найти вероятность того, что среди вынутых шаров хотя бы два будут разного цвета.

1. Записываем событие $A$ =(Среди вынутых 3 шаров хотя бы два разного цвета). То есть, например, “2 красных шара и 1 белый”, или “1 белый, 1 черный, 1 красный”, или “2 черных, 1 красный” и так далее, вариантов многовато. Попробуем правило перехода к противоположному событию.

2. Тогда противоположное событие формулируется так $bar{A}$ = (Все три шара одного цвета) = (Выбраны 3 черных шара или 3 красных шара) – всего 2 варианта получилось, значит, этот способ решения упрощает вычисления. Кстати, все шары белого цвета не могут быть выбраны, так как их всего 2, а вынимается 3 шара.

3. Общее число исходов (способов выбрать любые 3 шара из 2+3+5=10 шаров) равно $n=C_{10}^3=120$.

Найдем число благоприятствующих событию исходов. $m = C_{3}^3+C_{5}^3=1+10=11$ – число способов выбрать или 3 черных шара (из 3), или 3 красных шара (из 5).

Тогда:

$$
P(bar{A})=frac{m}{n}=frac{11}{120}.
$$

4. Искомая вероятность:

$$
P(A)=1-P(bar{A})=1- frac{11}{120}=frac{109}{120} = 0.908.
$$

Ответ: 0.908.

Частный случай. Независимые события

Идем дальше, и приходим к классу задач, где рассматривается несколько независимых событий (стрелки попадают, лампочки перегорают, машины заводятся, рабочие болеют с разной вероятностью каждый и т.п.) и нужно “найти вероятность наступления хотя бы одного события”. В вариациях это может звучать так “найти вероятность, что хотя бы один стрелок из трех попадет в цель”, “найти вероятность того, что хотя бы один автобус из двух вовремя приедет на вокзал”, “найти вероятность, что хотя бы один элемент в устройстве из четырех элементов откажет за год” и т.д.

Если в примерах выше речь шла о применении формулы классической вероятности, здесь мы приходим к алгебре событий, используем формулы сложения и умножения вероятностей (небольшая теория тут).

Итак, рассматриваются несколько независимых событий $A_1, A_2,…,A_n$, вероятности наступления каждого известны и равны $P(A_i)=p_i$ ($q_i=1-p_i$). Тогда вероятность того, что в результате эксперимента произойдет хотя бы одно из событий, вычисляется по формуле

$$
P=1-q_1cdot q_2 cdot …cdot q_n. quad(1)
$$

Строго говоря, эта формула тоже получается применением основной методики “перейти к противоположному событию”. Ведь действительно, пусть $A$=(Наступит хотя бы одно событие из $A_1, A_2,…,A_n$), тогда $bar{A}$ = (Ни одно из событий не произойдет), что значит:

$$
P(bar{A})=P(bar{A_1} cdot bar{A_2} cdot … bar{A_n})=P(bar{A_1}) cdot P(bar{A_2}) cdot … P(bar{A_n})=\
=(1-P(A_1)) cdot (1-P(A_2)) cdot … (1-P(A_n))=\
=(1-p_1) cdot (1-p_2) cdot … (1-p_n)=q_1cdot q_2 cdot …cdot q_n,\
$$
откуда и получаем нашу формулу
$$
P(A)=1-P(bar{A})=1-q_1cdot q_2 cdot …cdot q_n.
$$

Пример 4. Узел содержит две независимо работающие детали. Вероятности отказа деталей соответственно равны 0,05 и 0,08. Найти вероятность отказа узла, если для этого достаточно, чтобы отказала хотя бы одна деталь.

Событие $A$ =(Узел отказал) = (Хотя бы одна из двух деталей отказала). Введем независимые события: $A_1$ = (Первая деталь отказала) и $A_2$ = (Вторая деталь отказала). По условию $p_1=P(A_1)=0,05$, $p_2=P(A_2)=0,08$, тогда $q_1=1-p_1=0,95$, $q_2=1-p_2=0,92$. Применим формулу (1) и получим:

$$
P(A)=1-q_1cdot q_2 = 1-0,95cdot 0,92=0,126.
$$

Ответ: 0,126.

Пример 5. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом справочнике, равна 0,8, во втором – 0,7, в третьем – 0,6. Найти вероятность того, что формула содержится хотя бы в одном справочнике.

Действуем аналогично. Рассмотрим основное событие
$A$ =(Формула содержится хотя бы в одном справочнике). Введем независимые события:
$A_1$ = (Формула есть в первом справочнике),
$A_2$ = (Формула есть во втором справочнике),
$A_3$ = (Формула есть в третьем справочнике).

По условию $p_1=P(A_1)=0,8$, $p_2=P(A_2)=0,7$, $p_3=P(A_3)=0,6$, тогда $q_1=1-p_1=0,2$, $q_2=1-p_2=0,3$, $q_3=1-p_3=0,4$. Применим формулу (1) и получим:

$$
P(A)=1-q_1cdot q_2cdot q_3 = 1-0,2cdot 0,3cdot 0,4=0,976.
$$

Ответ: 0,976.

Пример 6. Рабочий обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что в течение смены первый станок потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвёртый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера.

Думаю, вы уже уловили принцип решения, вопрос только в количестве событий, но и оно не оказывает влияния на сложность решения (в отличие от общих задач на сложение и умножение вероятностей). Только будьте внимательны, вероятности указаны для “потребует внимания”, а вот вопрос задачи “хотя бы один станок НЕ потребует внимания”. Вводить события нужно такие же, как и основное (в данном случае, с НЕ), чтобы пользоваться общей формулой (1).

Получаем:
$A$ = (В течение смены хотя бы один станок НЕ потребует внимания мастера),
$A_i$ = ($i$-ый станок НЕ потребует внимания мастера), $i=1,2,3,4$,
$p_1 = 0,7$, $p_2 = 0,4$, $p_3 = 0,6$, $p_4 = 0,75$.

Искомая вероятность:

$$
P(A)=1-q_1cdot q_2cdot q_3 cdot q_4= 1-(1-0,7)cdot (1-0,4)cdot (1-0,6)cdot (1-0,75)=0,982.
$$

Ответ: 0,982. Почти наверняка мастер будет отдыхать всю смену;)

Частный случай. Повторные испытания

Думаете, дальше будет сложнее? Напротив, случаи все более частные, решения и формулы все более простые.

Итак, у нас есть $n$ независимых событий (или повторений некоторого опыта), причем вероятности наступления этих событий (или наступления события в каждом из опытов) теперь одинаковы и равны $p$. Тогда формула (1) упрощается к виду
:

$$
P=1-q_1cdot q_2 cdot …cdot q_n = 1-q^n.
$$

Фактически мы сужаемся к классу задач, который носит название “повторные независимые испытания” или “схема Бернулли”, когда проводится $n$ опытов, вероятность наступления события в каждом из которых равна $p$. Нужно найти вероятность, что событие появится хотя бы раз из $n$ повторений:

$$
P=1-q^n. quad(2)
$$

Подробнее о схеме Бернулли можно прочитать в онлайн-учебнике, а также посмотреть статьи-калькуляторы о решении различных подтипов задач (о выстрелах, лотерейных билетах и т.п.). Ниже же будут разобраны задачи только с “хотя бы один”.

Пример 7. Пусть вероятность того, что телевизор не потребует ремонта в течение гарантийного срока, равна 0,9. Найти вероятность того, что в течение гарантийного срока из 3 телевизоров хотя бы один не потребует ремонта.

Решения короче вы еще не видели.
Просто выписываем из условия: $n=3$, $p=0,9$, $q=1-p=0,1$.
Тогда вероятность того, что в течение гарантийного срока из 3 телевизоров хотя бы один не потребует ремонта, по формуле (2):

$$
P=1-0,1^3=1-0,001=0,999
$$

Ответ: 0,999.

Пример 8. Производится 5 независимых выстрелов по некоторой цели. Вероятность попадания при одном выстреле равна 0,8. Найти вероятность того, что будет хотя бы одно попадание.

Опять, начинаем с формализации задачи, выписывая известные величины. $n=5$ выстрелов, $p=0,8$ – вероятность попадания при одном выстреле, $q=1-p=0,2$.
И тогда вероятность того, что будет хотя бы одно попадание из пяти выстрелов равна:
$$
P=1-0,2^5=1-0,00032=0,99968
$$

Ответ: 0,99968.

Думаю, с применением формулы (2) все более чем ясно (не забудьте почитать и о других задачах, решаемых в рамках схемы Бернулли, ссылки были выше). А ниже я приведу чуть более сложную задачу. Такие задачи встречаются пореже, но и их способ решения надо усвоить. Поехали!

Пример 9. Производится n независимых опытов, в каждом из которых некоторое событие A появляется с вероятностью 0,7. Сколько нужно сделать опытов для того, чтобы с вероятностью 0,95 гарантировать хотя бы одно появление события A?

Имеем схему Бернулли, $n$ – количество опытов, $p=0,7$ – вероятность появления события А.

Тогда вероятность того, что произойдет хотя бы одно событие А в $n$ опытах, равна по формуле (2):
$$
P=1-q^n=1-(1-0,7)^n=1-0,3^n
$$
По условию эта вероятность должна быть не меньше 0,95, поэтому:

$$
1-0,3^n ge 0,95,\
0,3^n le 0,05,\
n ge log_{0,3} 0,05 = 2,49.
$$

Округляя, получаем что нужно провести не менее 3 опытов.

Ответ: минимально нужно сделать 3 опыта.

Полезные ссылки

• Калькуляторы на схему Бернулли
• Основные формулы комбинаторики
• Примеры решений задач по теории вероятностей
• Заказать свои задачи на вероятность

В решебнике вы найдете более 1000 задач со словами “хотя бы …”:

На этой странице вы узнаете

• Как кот может быть одновременно жив и мертв? 
• Можно ли всегда выигрывать спор с монеткой? 
• Если рандомно ответить на вопрос теста, какой шанс угадать ответ?

Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.

Вероятность

Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…

Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться. 

Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов. 

Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат. 

Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:

• выпадет орел;
• выпадет решка. 

Эти два события образуют множество элементарных событий. 

Множество элементарных событий — множество всех возможных результатов случайного эксперимента. 

В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации. 

Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран. 

Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности. 

Вероятность — отношение количества благоприятных событий к количеству всех возможных событий. 

Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу. 

(P = frac{m}{n})

Вероятность можно обозначить, как P(x), где х — некоторое событие. 

Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.

Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.

Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%. 

Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?

Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна 
(frac{49}{140} = 0,35)

Выразим в процентах:  
0,35 * 100% = 35%

Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ. 

Ответ: 0,35

Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой. 

(P = frac{m}{n} * 100%)

Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.

Равновозможные и противоположные события

Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными. 

Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие. 

Вероятности появления событий равны. 

Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий. 

Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них. 

В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий. 

Мы подбросили монету и выпал орел. Следовательно, не выпала решка. 

А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными. 

Противоположные события — такие события, если при не наступлении одного обязательно наступает второе. 

Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline{A}). 

Заметим, что вероятность события A равняется 12, как и вероятность события (overline{A}). Чему равна их сумма?

)frac{1}{2} + frac{1}{2} = 1) 

Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1. 

(P(A) + P(overline{A}) = 1)

Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить. 

Объединение и пересечение событий 

Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим? 

Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий. 

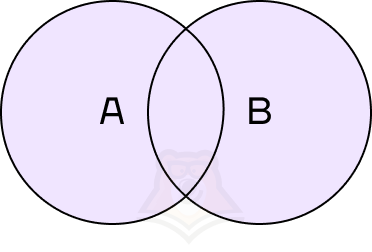
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег. 

Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B). 

Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?

Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям. 

Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B). 

Несовместные и совместные события

Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.

Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно. 

Несовместные события — такие события, появление одного из которых исключает появление другого. 

Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности. 

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.

Сформулируем определение суммы вероятностей двух несовместных событий. 

Если существуют несовместные события, то существуют и совместные. 

Совместные события — события, наступление одного из которых не исключает наступления другого. 

В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят?  Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет. 

Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”. 

Найдем вероятность события А: (frac{1}{6}). 

Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac{3}{6} = frac{1}{2})

Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А. 

Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги. 

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок. 

В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике. 

Независимые и зависимые события 

Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем. 

Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac{95}{100} = 0,95). 

Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?

Ответим на вопрос: зависят ли булочки друг от друга? 

Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми. 

Независимые события — такие события, появление одного из которых не зависит от появления другого события. 

Определим вероятность независимых событий. 

Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95. 

А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:

(P(A cap B) = P(A) * P(B))

Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025. 

В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”. 

Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой. 

Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого. 

Но если автоматы стоят  рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого. 

Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

Нужная последовательность может быть в двух случаях:

• сначала вытащат фиолетовый кубик и потом снова фиолетовый;
• сначала вытащат оранжевый кубик, а потом фиолетовый. 

Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac{5}{7}). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые. 

Вероятность вытащить во второй раз фиолетовый кубик равна (frac{5}{7} * frac{4}{6} = frac{20}{42} = frac{10}{21}). 

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac{2}{7}). В мешке останется шесть кубиков, пять из которых будут фиолетовыми. 

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac{2}{7} * frac{5}{6} = frac{10}{42} = frac{5}{21}). 

В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы. 

Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.

Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А. 

Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.   

Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность. 

Формула Бернулли

Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?

Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac{1}{6}). 

Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac{5}{6}). 

Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k. 

Чтобы решить задачу, нужно воспользоваться формулой Бернулли. 

(P_n(k) = C_n^k * p^k * q^{n — k}) 

Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики». 

Решим задачу, подставив значения в формулу:

(P_8(3) = C_8^3 * (frac{1}{6})^3 * (frac{5}{6})^5 = frac{8!}{5!3!} * frac{1}{6^3} * frac{5^5}{6^5} = frac{6 * 7 * 8}{1 * 2 * 3} * frac{5^5}{6^8} approx 0,1) 

Фактчек

• Вероятность — отношение количества благоприятных событий к количеству всех возможных событий. 
• События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе. 
• События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
• События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A). 
• Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А. 

Проверь себя

Задание 1. 
Какие события являются несовместными?

1. Подбрасывание монетки.
2. Брак батареек в одной упаковке.
3. “Миша идет” и “Миша стоит”.
4. Случайное вытаскивание конфет из вазы. 

Задание 2. 
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?

1. 0,17
2. 1
3. 0,83
4. 1,17 

Задание 3. 
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?

1. 1
2. 0,216
3. 0,45
4. 1,5 

Задание 4. 
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут. 

1. 0,3
2. 0,001
3. 2,7
4. 0,729 

Задание 5. 
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой. 

1. 0,77
2. 0,135
3. 0,23
4. -0,23

Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1

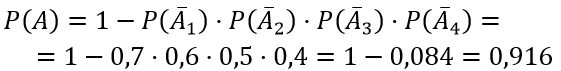
Почему в одной ситуации вероятности складываются, в другой – умножаются, а в третьей – вообще всё сложнее ?

Приветствую Вас, уважаемые Читатели! В одном из прошлых материалов, где я рассказывал про доску Гальтона – механическое устройство, которое визуализирует биномиальное распределение, я использовал три незыблемых правила манипулирования вероятностью. В этом материале хотелось бы поговорить об этом подробнее. Поехали!

Что такое событие?

Согласно словарю Ожегова событие – это “то, что произошло, то или иное значительное явление, факт общественной, личной жизни“. Глобально события можно разделить на два вида: детерминированные и вероятностные.

• Первые – это те события, исход которых можно предсказать и описать до факта его совершения. Например, если Вы бросите камень с 9-го этажа, то можете быть уверены, что он упадёт на Землю.
• Вторые – это те, которые даже при одинаковых начальных условиях могут привести к неожиданному или случайному исходу. Классическим примером случайного события является бросок монеты: до того, как монета не упадет, мы можем только предполагать, какой стороной она окажется к верху.

Однако и во втором случае есть место детерминированности. Мы на 100% уверены, что событий может быть только два: “Орёл” или “Решка”.

События “Орёл” и “Решка” образуют т.н. называемую полную группу событий. Математически это можно записать следующим образом:

Есть еще много различных классификаций “событий”, но я позволю остановиться на этом

Несовместные события

Что еще нужно сказать о событиях “Орёл” и “Решка” ? Самое главное – это то, что появление одного из них исключает выпадение другого. В теории вероятностей такие события принято называть несовместными, а в случае двух исходов, как в нашем случае, – противоположными.

Для несовместных событий действует теорема о сложении вероятностей:

• Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

В случае с подбрасыванием монетки это звучит так: вероятность получить или “Орёл” или “Решку” равно сумме вероятностей каждого исхода. Здесь ключевую роль играет союз “ИЛИ”, ведь именно он вербально задаёт несовместимость событий.

Независимые события

Казалось бы, следует перейти к понятию совместного события, однако логика требует иначе. Давайте представим, что мы параллельно подбрасываем две монеты. Зависит ли исход каждого испытания друг от друга?

Да, можно пытаться хитрить, но природу не обманешь….

Очевидно, что нет. Таким образом два события называются независимыми, если появление одного из них, не изменяет вероятность появления другого.

Правило вычисления вероятности независимых событий называется теоремой об умножении вероятностей:

Здесь уже главенствует союз “И” : вероятность наступления и того, и другого события равно произведению вероятностей наступления каждого из них по отдельности (независимые события!).

На конкретном примере вероятность выпадения двух “Орлов” или двух “Решек” при одновременном подбрасывании двух монет равняется 1/2*1/2 = 1/4.

Совместные события

Продолжим подбрасывать параллельно две монеты и попытаемся ответить на вопрос, а чему равна вероятность выпадения хотя бы одного “Орла” или “Решки” ?

• Очевидно, что, если складывать вероятности, то получим 1/2+1/2 = 1, что противоречит здравому смыслу. Ведь легко представить ситуацию, когда мы загадаем “Орла”, а две монеты выпадут “Решкой”.
• Умножение вероятностей так же не работает, ведь мы ищем вероятность хотя бы одного, а не одновременного выполнения событий.

Ответ: совместить два подхода и использовать формулу:

Таким образом, вероятность равняется 1/2+1/2 – 1/2*1/2 = 3/4.

События такого вида называются совместными – возникновение каждого из них не исключает возникновение другого. Естественно, что указанная выше формула распространяется и на произвольное количество событий, разве что будет немного посложнее.

Осталось рассмотреть еще один важный класс событий – зависимые, но это я сделаю в одном из следующих материалов. Спасибо за внимание!

• Ставьте “Нравится” и подписывайтесь на канал прямой сейчас, чтобы не пропустить следующие публикации.
• TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.