Как найти вероятность ошибки р

5.6. Вероятность ошибки р

Если следовать подразделению статистики на описательную и аналитическую, то задача аналитической статистики – предоставить методы, с помощью которых можно было бы объективно выяснить,
например, является ли наблюдаемая разница в средних значениях или взаимосвязь (корреляция) выборок случайной или нет.

Например, если сравниваются два средних значения выборок, то можно сформулировать две предварительных гипотезы:

• Гипотеза 0 (нулевая): Наблюдаемые различия между средними значениями выборок находятся в пределах случайных отклонений.

• Гипотеза 1 (альтернативная): Наблюдаемые различия между средними значениями нельзя объяснить случайными отклонениями.

В аналитической статистике разработаны методы вычисления так называемых тестовых (контрольных) величин, которые рассчитываются по определенным формулам на основе данных,
содержащихся в выборках или полученных из них характеристик. Эти тестовые величины соответствуют определенным теоретическим распределениям
(t-pacnpeлелению, F-распределению, распределению X2 и т.д.), которые позволяют вычислить так называемую вероятность ошибки. Это вероятность равна проценту ошибки,
которую можно допустить отвергнув нулевую гипотезу и приняв альтернативную.

Вероятность определяется в математике, как величина, находящаяся в диапазоне от 0 до 1. В практической статистике она также часто выражаются в процентах. Обычно вероятность обозначаются буквой р:

0 < р < 1

Вероятности ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая.
В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения,
тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности.
Обычно в исследованиях используют 5% вероятность ошибки.

Существует общепринятая терминология, которая относится к доверительным интервалам вероятности:

• Высказывания, имеющие вероятность ошибки р <= 0,05 – называются значимыми.
• Высказывания с вероятностью ошибки р <= 0,01 – очень значимыми,
• А высказывания с вероятностью ошибки р <= 0,001 – максимально значимыми.

В литературе такие ситуации иногда обозначают одной, двумя или тремя звездочками.

Вероятность ошибки	Значимость	Обозначение
р > 0.05	Не значимая	ns
р <= 0.05	Значимая	*
р <= 0.01	Очень значимая	**
р <= 0.001	Максимально значимая	***

В SPSS вероятность ошибки р имеет различные обозначения; звездочки для указания степени значимости применяются лишь в немногих случаях. Обычно в SPSS значение р обозначается Sig. (Significant).

Времена, когда не было компьютеров, пригодных для статистического анализа, давали практикам по крайней мере одно преимущество. Так как все вычисления надо было выполнять вручную,
статистик должен был сначала тщательно обдумать, какие вопросы можно решить с помощью того или иного теста. Кроме того, особое значение придавалось точной формулировке нулевой гипотезы.

Но с помощью компьютера и такой мощной программы, как SPSS, очень легко можно провести множество тестов за очень короткое время. К примеру, если в таблицу сопряженности свести 50 переменных
с другими 20 переменными и выполнить тест X², то получится 1000 результатов проверки значимости или 1000 значений р. Некритический подбор значимых величин может
дать бессмысленный результат, так как уже при граничном уровне значимости р = 0,05 в пяти процентах наблюдений, то есть в 50 возможных наблюдениях, можно ожидать значимые результаты.

Этим ошибкам первого рода (когда нулевая гипотеза отвергается, хотя она верна) следует уделять достаточно внимания. Ошибкой второго рода называется ситуация,
когда нулевая гипотеза принимается, хотя она ложна. Вероятность допустить ошибку первого рода равна вероятности ошибки р. Вероятность ошибки второго рода тем меньше, чем больше вероятность ошибки р.

Ошибки первого и второго рода

Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.

Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.

Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.

Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.

Замечание 1.
Правильное решение может быть принято
также в двух случаях:

1. гипотеза принимается,
   причём и в действительности она
   правильная;

2. гипотеза отвергается,
   причём и в действительности она неверна.

Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).

Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия

Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.

Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.

Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:.

Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.

Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.

Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии,
то наблюдаемое значение критерия.

Критическая
область. Область принятия гипотезы.
Критические точки

После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.

Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.

Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.

Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.

Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.

Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.

Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.

Правосторонней
называют критическую область, определяемую
неравенством
>,
где— положительное число.

Левосторонней
называют критическую область, определяемую
неравенством
<,
где— отрицательное число.

Односторонней
называют правостороннюю или левостороннюю
критическую область.

Двусторонней
называют критическую область, определяемую
неравенствами
где.

В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):

,
или равносильным неравенством
.

Отыскание
правосторонней критической области

Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?

Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее,
была равна принятому уровню значимости:
Р(>)=.

Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.

Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>,
то нулевую гипотезу отвергают; если же<,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.

Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение

Р(>)=?
(*)

Поскольку вероятность
события
>мала (— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.

Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.

Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».

На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.

Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.

Отыскание
левосторонней и двусторонней критических
областей***

Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<(<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<)=.

Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее,
была равна принятому уровню значимости:

.
(*)

Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и(>0),
то

Учитывая (*), получим
.

Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.

Дополнительные
сведения о выборе критической области.
Мощность критерия

Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.

Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.

Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.

Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.

Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.

Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.

Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
иневозможно; если уменьшить,
тобудет возрастать. Например, если принять=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.

Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.

Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.

Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.

Маркетинг – та сфера, где больше всего любят работать с большими данными (англ. big data), однако излюбленный инструмент маркетологов – A/B-тестирование – предполагает использование малых данных (англ. small data). При этом какие бы цифры ни были получены по итогам теста, все сводится к анализу статистической выборки и определению статистической значимости результатов эксперимента. Неотъемлемой частью данного исследования является P-значение, о котором мы хотим рассказать в этой статье.

Что такое P-значение

P-value или p-значение – одна из ключевых величин, используемых в статистике при тестировании гипотез. Она показывает вероятность получения наблюдаемых результатов при условии, что нулевая гипотеза верна, или вероятность ошибки в случае отклонения нулевой гипотезы.

Этот термин первым упомянул в своих работах К. А. Браунли в 1960 году. Он описал p-уровень значимости как показатель, который находится в обратной зависимости от истинности результатов. Чем выше р-value, тем ниже степень доверия в выборке зависимости между переменными.

Другими словами, в статистике p-значение – это наименьшее значение уровня значимости, при котором полученная проверочная статистика ведет к отказу от основной (нулевой) гипотезы.

Значение p-уровня чаще всего соответствует статистической значимости, равной 0,05. Если значение р меньше 0,05, нулевую гипотезу отклоняют. При этом чем меньше это значение, тем лучше, т. к. растет предполагаемая значимость альтернативной гипотезы и «сила» отвержения нулевой.

Часто p-значение понимают неправильно. Например, если значение р = 0,05, можно сказать о том, что существует 5% вероятности, что результат получен случайно и не соответствует действительности.

Кратко о главном

• Р-значение показывает вероятность того, что наблюдаемая разница в результатах могла быть случайной.
• Значение p применяется как альтернатива выбранным уровням достоверности для тестирования идей или в дополнение к ним.
• Со снижением p-значения повышается статистическая значимость разницы, полученной в ходе исследования.

Статистическая значимость

Эксперимент начинается с формулирования нулевой гипотезы. Она показывает, что два исследуемых явления никаким образом не связаны друг с другом.

Эксперимент проводится с целью выявить или показать какое-либо влияние или тип взаимодействия рассматриваемых явлений. Если в итоге анализа подтверждается нулевая гипотеза, значит, тест провалился.

Чтобы правильно интерпретировать результаты, рассчитывают показатель статистической значимости.

Статистическая значимость – это критерий, с помощью которого можно определить, необходимо ли отвергнуть или принять ту или иную гипотезу.

Перед началом тестирования следует установить порог значимости (альфа). Если значение р меньше альфа, можно говорить о том, что наш результат является статистически значимым. Это говорит о том, что наблюдаемое явление действительно имело место, и нулевую гипотезу нужно отклонить.

Порог значимости альфа устанавливается обычно на уровне 0,05 или 0,01. Выбор значения определяется поставленной задачей.

Порог значимости равен 0,05, а p-значение – 0,02. Т. к. установленное значение альфа больше p-уровня, делаем вывод, что это статистически значимый результат.

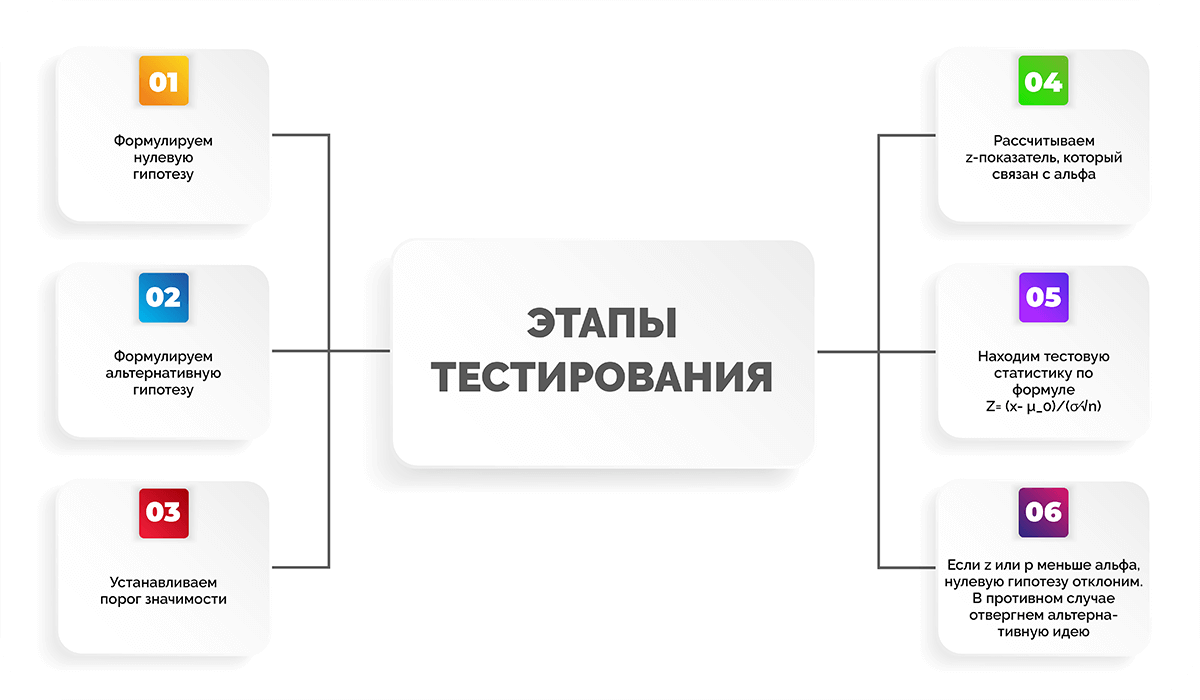
Все тестирование можно разделить на несколько этапов:

1. Формулируем нулевую гипотезу.
2. Формулируем альтернативную гипотезу.
3. Устанавливаем порог значимости.
4. Рассчитываем z-показатель, который связан с альфа.
5. Находим тестовую статистику по формуле .
6. Если z-показатель или p-значение меньше уровня альфа, нулевую гипотезу отклоним. В противном случае отвергнем альтернативную идею.

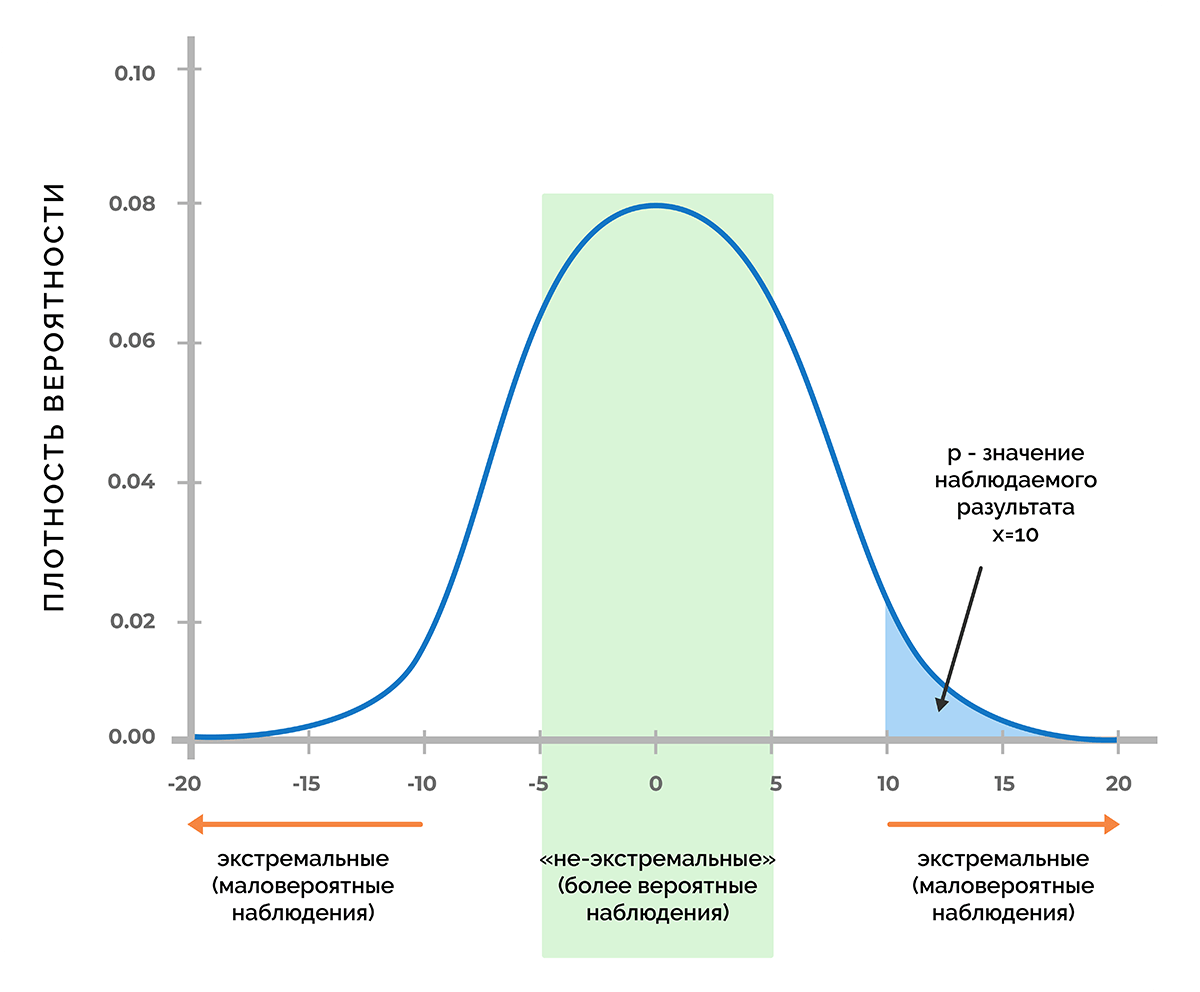
Если идет речь о явлениях, которые управляются случайными процессами, обычно это приводит к нормальному распределению значений. В этом случае нулевую гипотезу представляют в виде кривой Гаусса, которая отражает распределение ожидаемых наблюдений. Это распределение актуально в случае, если одна переменная в эксперименте не зависит от другой.

Порог вероятности

В основе статистической значимости лежит вероятность получения определенного результата при верности нулевой гипотезы. Чтобы разобрать смысл этого определения, предположим, что в процессе тестирования получили некое число х. Это может быть любая метрика, например, прибыль от продаж, величина конверсии, количество довольных покупателей и т. д.

Используя функцию плотности вероятности, которая связана с нулевой гипотезой, можно выяснить, удастся ли получить число х (или любое другое значение, которое маловероятнее, чем х) с вероятностью менее 5% (p < 0,05) или менее 1% (p < 0,01), или другого порога, при котором p меньше заданного уровня значимости.

Таким образом, p-критерий отражает вероятность получения результата, который равен или является более экстремальным, чем фактически наблюдаемый результат, в случае отсутствия взаимосвязи между исследуемыми переменными.

Доверительные уровни

Доверительный уровень значимости выбирается перед запуском статистического эксперимента. Чаще всего используются значения 90%, 95% или 99%.

Ниже в таблице приводим критические p-значения, а также z-оценки для разных доверительных уровней.

Доверительный уровень	Стандартное отклонение (z-оценка)	Вероятность (p-уровень)
90%	< -1,65 или > +1,65	< 0,10
95%	< -1,96 или > +1,96	< 0,05
99%	< -2,58 или > +2,58	< 0,01

Значения, которые находятся в пределах области нормального распределения z-оценки (стандартного отклонения), представляют ожидаемый результат.

Проверка статистических гипотез

Проверка гипотезы – это статистическое исследование, которое проводится, чтобы подтвердить или опровергнуть какую-либо гипотезу (простую или сложную).

Можно предположить, что посадочная страница с красной кнопкой CTA даст больше конверсий, чем текущая версия лендинга с синей. Проверить это можно путем тестирования, в котором будут участвовать нулевая и альтернативная гипотезы.

Нулевая гипотеза – первоначальное условие, при котором нет никакой разницы между текущей и новой версиями лендинга в плане конверсии

Альтернативная гипотеза – подразумевает, что изменение цвета кнопки на странице является причиной роста конверсии.

В статистике применяется рандомизация и нормализация нулевой гипотезы.

Рандомизация нулевой гипотезы – пространственная модель данных, которую мы наблюдаем, является одним из многих вариантов пространственных организаций данных. При этом все другие варианты не будут заметно отличаться от наблюдаемых.

Нормализация нулевой гипотезы подразумевает, что наблюдаемые значения являются одним из многих случайных вариантов выборок. При этом ни пространственное расположение данных, ни их значения не установлены.

Благодаря значению p можно увидеть, насколько нулевая гипотеза правдоподобна с учетом данных выборки. Таким образом, если нулевая гипотеза подтвердится, p-значение будет свидетельствовать об отсутствии увеличения конверсии вследствие изменения цвета кнопки.

Подход p-value к проверке гипотез

Значение р может использоваться для выявления доказательства для отклонения нулевой (первоначальной) гипотезы в ходе эксперимента.

Мы уже упоминали выше о том, что уровень значимости обозначается до начала исследования, чтобы определить, насколько малое значение p нужно получить для опровержения нулевой гипотезы. Однако в разных случаях разные люди могут использовать разные уровни значимости, поэтому при интерпретации итогов двух разных тестирований другими людьми могут возникать трудности. Решить эту проблему помогает p-value.

Рассмотрим пример, в котором в компании провели исследование, в ходе него сравнили доходность двух активов. Тест и анализ проводили два специалиста, которые брали за основу одни и те же самые исходные данные, но использовали разные уровни значимости. Есть вероятность, что эти люди сделают противоположные выводы о различии активов. Предположим, что один специалист для отклонения нулевой гипотезы взял уровень достоверности 90%, а другой – 95%. При этом среднее значение p наблюдаемой разницы между результатами равнялось 0,08, что отвечает уровню достоверности 92%. В таком случае первый специалист выявит значимое различие между двумя доходами, а второй статистически значимой разницы не обнаружит.

Чтобы избежать подобной ситуации, можно сообщить значение p-value эксперимента и дать возможность независимым наблюдателям самостоятельно оценивать статистическую значимость итоговых данных. Данный подход к проверке утверждений стали называть «подход p-value».

Как рассчитать P-value

Чаще всего p-значения определяют с помощью таблиц p-value или специализированного статистического ПО. Также помогает в этом калькулятор на тематических сайтах. Подобные расчеты основываются на известном или предполагаемом распределении вероятностей определенной статистики. Определение среднего значения р зависит от отклонения между выбранным эталонным и тестовым значением. При этом учитывается нормальное распределение вероятностей статистики.

Что касается ручного математического расчета значения р, существуют разные способы, которые рассмотрим далее в статье.

Как рассчитать p-значение, используя тестовую статистику

Распределение тестовой статистики происходит с предполагаемым условием, что верна нулевая гипотеза. Чтобы выразить вероятность того, что статистика эксперимента будет такой же экстремальной, как значение x для выборки, используется кумулятивная функция распределения.

Левосторонний эксперимент:
P-value = cdf (x)

Правосторонний эксперимент:
P-value = 1 – cdf (x)

Двусторонний эксперимент:
P-value = 2 × мин {{cdf (x), 1 – cdf (x)}}

Ручной расчет значения p затрудняют распространенные распределения вероятностей, которыми характеризуется проверка гипотез. Для расчета примерных показателей cdf удобнее использовать статистическую таблицу или ПК.

Пошаговый алгоритм расчета p-значения

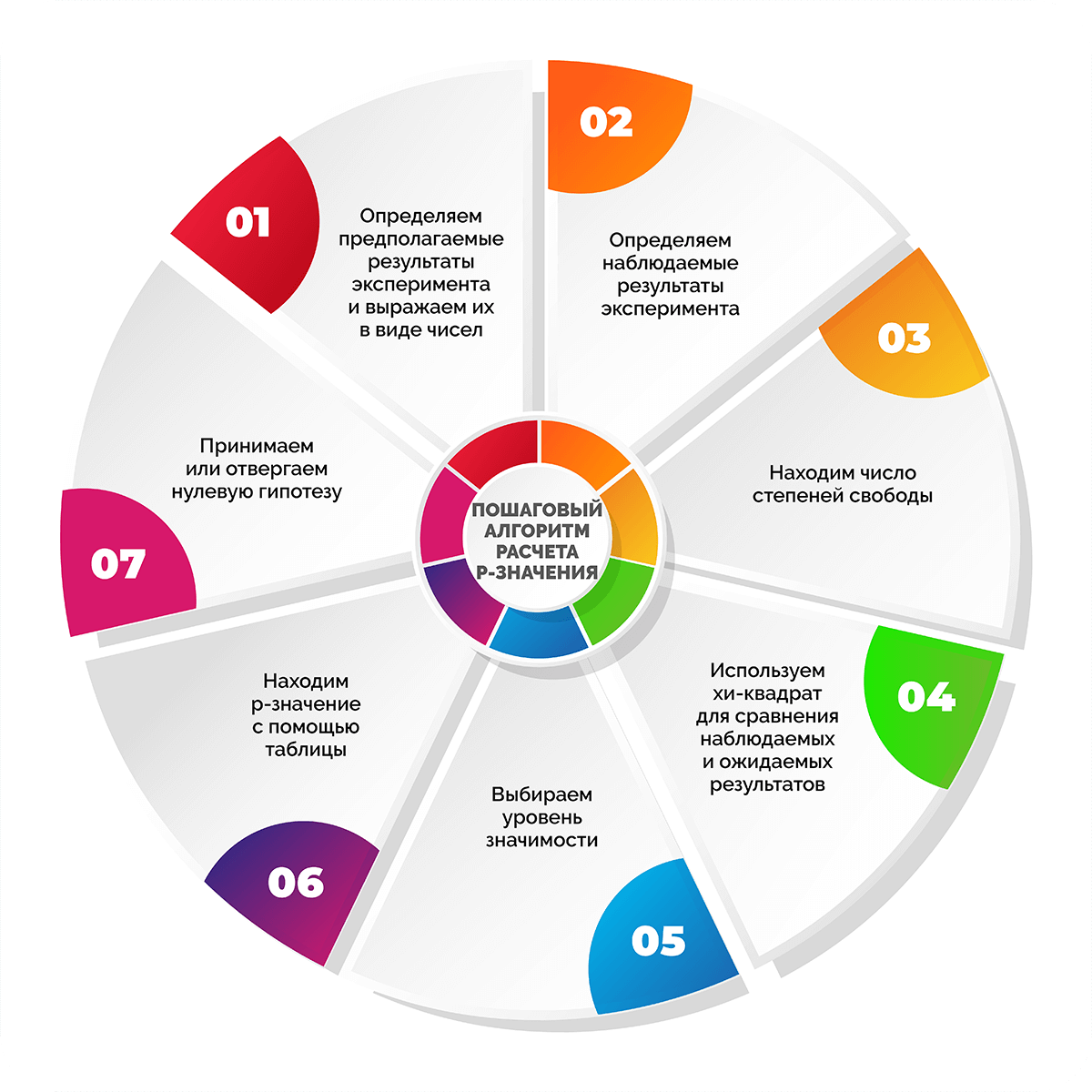
Шаг 1. Определяем предполагаемые результаты эксперимента и выражаем их в виде чисел

Как правило, на начало исследования уже есть видение того, какие числа можно считать приемлемыми. Выводы могут быть основаны на опыте проведения предыдущих экспериментов, наборах достоверных данных или общих сведеньях из научной литературы и других источников.

Опыт работы с лендингами показывает, что посадочные страницы с CTA-кнопкой на первом экране приводят примерно вдвое больше покупателей, чем версии без таких кнопок. Необходимо определить, действительно ли наличие кнопки влияет на посетителей сайта. Для этого будем анализировать конверсии в покупку. Если взять условные 300 конверсий, то предполагается, что 200 из них произойдут благодаря лендингам с CTA-кнопкой, а 100 – сайтам без кнопки при условии, что пользователи требовательны к наличию кнопок.

Шаг 2. Определяем наблюдаемые результаты эксперимента

Теперь нужно провести тест и получить реальные, т. е. наблюдаемые значения, которые таже будут выражаться в числовом формате. Если в экспериментальных условиях реальные цифры не совпадут с ожидаемыми, то будет два варианта – или это обусловлено действиями в ходе эксперимента, или получилось случайно. В данном случае цель определения p-value – понять, действительно ли наблюдаемые значения отличаются от ожидаемых настолько, что нулевая гипотеза не будет опровергнута.

Предположим, что мы выбрали 300 случайных конверсий с наших сайтов, на которых либо была кнопка на первом экране, либо ее не было. Определили, что 220 конверсий произошли благодаря лендингам с кнопкой и 80 – без нее. Результаты отличаются от ожидаемых, которые составляли 200 и 100 соответственно. Теперь предстоит узнать, действительно ли к изменению в значениях привел наш тест (добавление кнопки на первый экран) или это случайное отклонение. Определить это поможет p-значение.

Шаг 3. Находим число степеней свободы

Число степеней свободы показывает, насколько может измениться эксперимент. При этом степень изменяемости зависит от количества исследуемых категорий.

Число степеней свободы = n – 1, где n – количество анализируемых переменных или категорий.

В нашем эксперименте 2 условия и, соответственно, две категории результатов: для лендингов без кнопки на первом экране и для лендингов с ней.

Число степеней свободы = 2 – 1 = 1.

Если бы в эксперименте мы сравнивали посадочные станицы с CTA-кнопкой, без кнопки и с pop-up окном, то получили бы 2 степени свободы и т. д.

Шаг 4. Используем хи-квадрат для сравнения наблюдаемых и ожидаемых результатов

Хи-квадрат (х²) – числовое отражение разницы между наблюдаемыми (фактическими) и ожидаемыми значениями тестирования.

где:

о – наблюдаемое значение;
е – ожидаемое значение.

Подставляем наши цифры в уравнение и учитываем, что нужно подсчитать дважды – для двух видов лендинга.

х² = ((220 – 200)²/200) + ((80 – 100)2/100) = ((20)²/200)) + ((-20)²/100) = (400/200) + (400/100) = 2 + 4 = 6.

Шаг 5. Выбираем уровень значимости

Уровень значимости отражает степень уверенности в полученных результатах. Если статистическая значимость низкая, это говорит о низкой вероятности случайного получения экспериментальных результатов.

Для большинства тестов достаточно статистической значимости, равной 0,05 или 5%. При этом будет вероятность 95%, что исследователь получил значимый результат вследствие проведенных мероприятий, а не случайно.

В нашем случае примем статистическую значимость, равную 0,05.

Шаг 6. Находим p-значение с помощью таблицы

Для облегчения расчетов статисты применяют специализированные таблицы. Они довольно простые и позволяют легко найти значение р, зная число степеней свободы и хи-значение. Слева по вертикали располагаются значения числа степеней свободы. Вверху по горизонтали находятся p-значения. По данным таблицы сначала находят нужное число степеней свободы, затем в соответствующем ему ряду выбирают первое значение, которое превышает расчетное значение хи-квадрата. Число в верхней горизонтальной строке будет соответствовать p-значению. При этом нужное значение р находится в диапазоне чисел между найденным и следующим за ним слева.

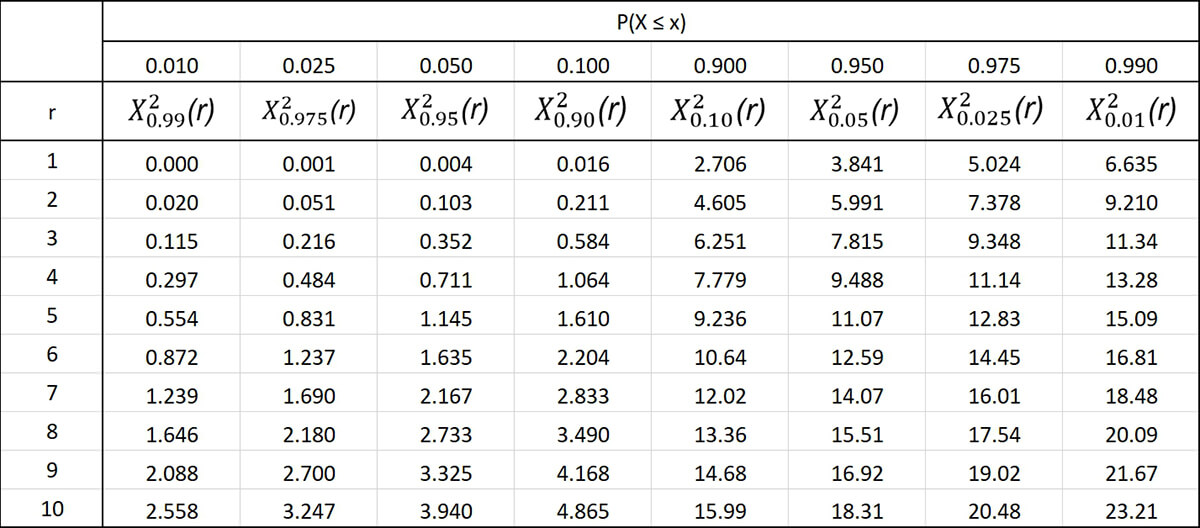
В нашем примере всего одна степень свободы, а хи-квадрат равен 6. Поэтому в таблице выбираем первую строку и движемся по ней слева направо до тех пор, пока не увидим первое значение больше 6 – это число 6,635. Оно соответствует p-значению 0,01, а значит, наше p-значение находится в диапазоне между 0,01 и 0,025.

Шаг 7. Принимаем или отвергаем нулевую гипотезу

Если найденное приблизительное значение p меньше уровня значимости, можно заключить, что вероятна связь между экспериментальными переменными и полученными результатами. В противном случае нельзя утверждать с уверенностью, связаны ли результаты с манипуляцией переменными или стали случайностью.

В нашем эксперименте диапазон значений р 0,01-0,025 определенно меньше установленной статистической значимости 0,05, что позволяет отклонить нулевую гипотезу. А значит, можно сделать вывод, что посадочные страницы с CTA-кнопкой на 1-м экране конвертируют лучше, чем аналогичные версии без такой кнопки. Вероятность того, что рост конверсий на лендингах с кнопкой является случайностью, составляет не больше 1-2,5%.

Как интерпретировать P-значение

P-уровень тесно связан с уровнем статистической значимости. Последний таже определяет исход эксперимента.

• Если p-значение меньше уровня значимости, то нулевую гипотезу можно смело отклонить и считать истинной альтернативную гипотезу.
• Если p-значение больше уровня значимости, это означает, что в ходе эксперимента выявили недостаточно оснований для отклонения нулевой гипотезы.

Отвержение нулевой гипотезы говорит о том, что в процессе исследования была обнаружена закономерная связь между тестируемыми переменными.

P-значение – это…

• вероятность того, что в ходе исследования наблюдения были случайными. То есть, если p = 0,05, есть 5% вероятности того, что наблюдаемое явление случайно и 95% вероятности того, что результат является следствием созданных условий;
• вероятность того, что будет сделан неверный вывод о взаимосвязи переменных. Если р = 0,05, то на каждые 100 экспериментов, где наблюдалась взаимосвязь, 95 их них действительно была, а 5 – нет.

Что нужно помнить о P-значениях

1. «Неожиданность» определяет тот, кто проводит эксперимент. Подводит итоги теста по факту тот, кто его проводит. Чем выше значение р, тем чаще вы будете получать неожиданные результаты.
2. Применение p-значения имеет довольно извилистую логику. Чтобы оценить аргументы в пользу отклонения нулевой гипотезы, необходимо изначально считать, что она верна. Именно это является причиной путаницы.
3. По значению p невозможно оценить вероятность того, что один исследуемый вариант лучше другого. Также по этому показателю нельзя понять, какая вероятность того, что предпочтение одного варианта другому ошибочно. На самом деле, p-значение показывает лишь вероятность того, что при верности нулевой гипотезы удастся вычислить результат, отличный от нуля.
4. Значимость p-значения при подведении итогов сплит-тестов – тема неутихающих споров в научном сообществе. Большинство маркетологов остаются приверженцами классической проверки на статистическую значимость и отстаивают ее как «золотой стандарт». При этом специалисты по статистике приводят аргументы в пользу других методов проверки, что провоцирует жаркие дебаты.
5. Всегда можно получить существенное (высшее) значение p. Есть типичная ошибка, которая зависит с одной стороны от объема выборки, с другой – от изменений генеральной совокупности данных. Если во втором случае повлиять на изменения никак нельзя, то собирать и накапливать данные ничто не мешает. Но есть ли польза от такого количества сведений? Сам факт того, что у полученного параметра высокое p-значение, практического значения не имеет.
6. Не стоит волноваться раньше времени. В первую очередь нужно собрать данные, которые помогут сформировать рабочую идею. Всегда трудно делать выбор между вариантами, которые почти не отличаются друг от друга. Если выделить предпочтительный вариант проблематично из-за похожих результатов, можно просто выбрать один из них и не беспокоиться о том, правильный ли это выбор.
7. P-значение не повод прекращать тест. Для получения достоверных результатов, которые позволят интерпретировать p-значение, необходимо вычислить размер выборки, затем провести эксперимент. В процессе тестирования предстоит выбрать время, когда пора его закончить. При этом оно не должно быть связано с достижением статистической значимости или высокого показателя p-значения. Главное – получить реальные результаты в конце теста, например, обеспечить рост прибыли, оптимизировать конверсию и т. д.

Примеры интерпретации P-значений

На нескольких примерах рассмотрим, как правильно интерпретировать p-значения при проверке разных идей.

По мнению интернет-провайдера, 90% пользователей довольны качеством предоставляемых услуг. Чтобы это проверить, была собрана простая выборка, куда вошли 500 случайных абонентов. 85% дали утвердительный ответ на вопрос об удовлетворенности услугами провайдера. По данным выборки удалось вычислить p-значение, равное 0,018.

Если выдвинуть гипотезу о том, что 90% пользователей действительно довольны обслуживанием провайдера, получим реальную наблюдаемую разницу или более экстремальную разницу, которая составит 1,8% потребителей услуг вследствие ошибки случайной выборки.

Ресторан вводит услугу доставки еды и утверждает, что время доставки составляет около 30 минут или меньше. Однако есть мнение, что реальный срок доставки превышает заявленное время. Для проверки этих вариантов были отобраны случайные заказы еды с доставкой и проведены расчеты. По результатам выяснили, что среднее время доставки составляет 40 минут (больше на 10 минут, чем заявляет ресторан), а p-значение равно 0,03.

Результаты показывают, что в случае, когда нулевая гипотеза верна, т. е. доставка еды занимает 30 минут или меньше, есть вероятность 3%, что среднее время доставки будет как минимум на 10 минут больше из-за эффекта случайности.

Отдел маркетинга разрабатывает новый скрипт продаж для менеджеров. Предполагается, что с его помощью компания будет продавать минимум на 30% больше, чем со старым скриптом. Чтобы это проверить, собирается простая случайная выборка из 100 контактов с клиентами по новому скрипту и 100 – по старому. В результате эксперимента новый скрипт привел 60 покупателей, а старый – 45. Вычислили среднее значение p, равное 0,011.

Если взять за основу мнение, что новый скрипт приводит столько же клиентов, сколько и старый, или меньше, будет получена крайняя разница в 1,1% тестирований вследствие случайной ошибки выборки.

Часто задаваемые вопросы

P-значение – вероятность того, что исследуемая статистика удовлетворит конкретным условиям. Поскольку вероятности отрицательными не бывают, отрицательного значения p тоже быть не может.

Если p-значение высокое, это свидетельствует о том, что статистика эксперимента для другой выборки будет иметь столь же экстремальное значение, как и в тестируемой выборке. При высоком p-значении отвергнуть нулевую гипотезу нельзя.

Если получено низкое p-значение, это значит, что вероятность получить такое же критическое значение, как и наблюдаемое в текущей выборке, в тестовой статистике для другой выборки окажется очень низкой. При низком p-значении нулевую гипотезу отвергают и принимают альтернативную.

Некоторые считают, что p-значения показывают вероятность совершить ошибку при отклонении истинной нулевой гипотезы (ошибка первого типа) – это заблуждение. P-значения не свидетельствуют о частоте вероятных ошибок по двум причинам:

1. При расчете p-значения в основе утверждение, что верна нулевая гипотеза, а разница в итоговых данных обусловлена случайностью. То есть величина p-значения не отражает вероятность того, что ноль будет ложным или истинным, т. к. с учетом изначального предположения он полностью верен.
2. Несмотря на то, что при низком p-значении при условии истинности нулевого значения выборочные данные маловероятны, p-значение все еще не может четко показать, какой из вариантов имеет большую вероятность стать истиной: когда нуль действительно является ложным или когда нуль является верным, но выборка нечеткая.

Заключение

Несмотря на то, что при интерпретации результатов исследований часто допускают ошибки, неправильно используя статистическую значимость, она продолжает оставаться важным методом в экспериментах. P-значение или p-value является одной из обязательных составляющих при оценке результатов тестирования. Именно этот показатель дает возможность понять, с какой вероятностью полученные итоги удовлетворяют определенным значениям.

Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter

Автор статьи: Попов Олег Александрович.

При копировании или цитировании ссылка на сайт и автора обязательна!

В самой
простой интерпретации р-уровень — это
вероятность ошибки.

Рассмотрим его
более подробно. В исследовании мы
оперируем понятиями рабочей и нулевой
гипотезы, которые обозначаются и
интерпретируются следующим образом:

H₁
— рабочая гипотеза. Это гипотеза о
значимости различий (взаимосвязи,
влияния). Обычно, в исследованиях
стремятся проверить эту гипотезу.

H₀
— нулевая гипотеза. Гипотеза об отсутствии
различий (взаимосвязи, влияния). Эту
гипотезу в исследовании стремятся
опровергнуть.

р – это вероятность
принять нулевую гипотезу (какова
вероятность того, что различия
отсутствуют?). Поэтому, для большинства
статистических методов чем меньше это
значение, тем более достоверен
статистический показатель. Причем
большинство показателей сконструированы
именно так, чтобы проверять достоверность
рабочей, а не нулевой гипотезы.

Нулевая
гипотеза принимается, если мы считаем
различие (зависимость, взаимосвязь)
случайным явлением. Для психологии
приняты три стандартных значения
вероятности ошибки:

р ≤
0,01 — вероятность принять нулевую
гипотезу менее 1%

р ≤
0,05 — вероятность менее 5% (от 0,02 до 0,05).

р ≤ 0,1 — вероятность
менее 10% (от 0,06 до 0,1).

Иначе говоря —
вероятность сделать ошибочный вывод
может быть 1%, 5%, 10%.

Для
психологии, социологии и т. п.
традиционно принято использовать
р≤0,05. Для точных наук
только р≤0,01 и даже р≤0,001. Если исследование
не пилотажное, то значение р от 0,06 до
0,1 мы считаем тенденцией, т. е.
предполагаем, что если увеличим, улучшим
выборку или улучшим метод, или исключим
побочные факторы то вероятность ошибки
станет меньше. Но только предполагаем.

Для всех
статистических показателей можно узнать
значение р (сам метод расчета очень
сложный, поэтому обычно пользуются уже
рассчитанными таблицами или используют
программы). При этом можно пойти двумя
путями:

1. Узнать значение
   р и по нему судить значим ли полученный
   показатель.

2. Рассчитать
   показатель, посмотреть в таблицу
   критических значений и найти критическое
   значение для конкретного р и количества
   человек.

Приведём
пример.

1. Был
   рассчитал коэффициент корреляции r
   = 0,8. Для него был высчитано
   р = 0,001. Это говорит, что данный коэффициент
   значим, т. к. р≤0,01.

2. Был
   рассчитал коэффициент корреляции r =
   0,8. Значение р мы считать не умеем,
   поэтому пользуемся таблицей критических
   значений. Известно что выборка для
   расчетов была 100 человек и для нас
   вполне достаточно значения р≤0,05. В
   таблице ищем: для количества человек
   100 и р≤0,05 критическое значение равно
   0,197, т. е. r_крит
   = 0,197. Наше значение коэффициента 0,8,
   что намного больше критического, а
   значит мы делаем вывод, что полученное
   значение достоверно на уровне р≤0,05.

Все
программы статистического анализа
могут рассчитывать вероятность ошибки,
поэтому обращаться к таблицам критических
значений не нужно. При расчетах вручную
это неизбежно.

Если вы хотите узнать принципы расчета вероятности ошибки, глубже понять ее сущность, читайте статью про статистический смысл вероятности ошибки.

Вам нужны расчеты с аналитическими выводами? Обращайтесь!

принятия решения

Определим вероятность
ошибки 
и вероятность правильного обнаружения
D = 1 – 
как функция порога с^*
. Как известно, ошибка первого рода
возникает тогда, когда принимается
решение о наличии сигнала s(t) в принятой
реализации в то время, как _{сигнал
отсутствует. Вероятность этого события
равна}

_.
(5.1)

_{Для
упрощения расчетов произведем нормирование
случайной величины V , сдвинув V на
величину условного математического
ожидания при отсутствии сигнала M[V
/
s=0]
и пронормировав полученное выражение
относительно условного среднеквадратического
отклонения 
v0
при отсутствии сигнала}.

Сдвиг и нормировка
производится как левой, так и правой
частей неравенства (5.1). В результате
преобразований формула (5.1) примет вид

(5.2)

где

,

. (5.3)

Вероятность
правильного обнаружения D = 1 – 
как функция порога с^*
есть вероятность превышения случайной
величиной V порога с
^*, но при
наличии сигнала в принятой реализации:

.

Точно также, как
и в предыдущем случае , производится
смещение случайной величины V на величину
условного математического ожидания
_{M(
V
/
s

0
)
и нормировка ее относительно условного
среднеквадратического отклонения Z,
равного 
v1}, но
при наличии сигнала. В результате получим
вероятность правильного обнаружения

(5.4)

где

,

. _(5.5)

В интегральной
форме вероятность ошибки 
и вероятность правильного решения D =
1-
имеют вид

,
( 5.10 )

,
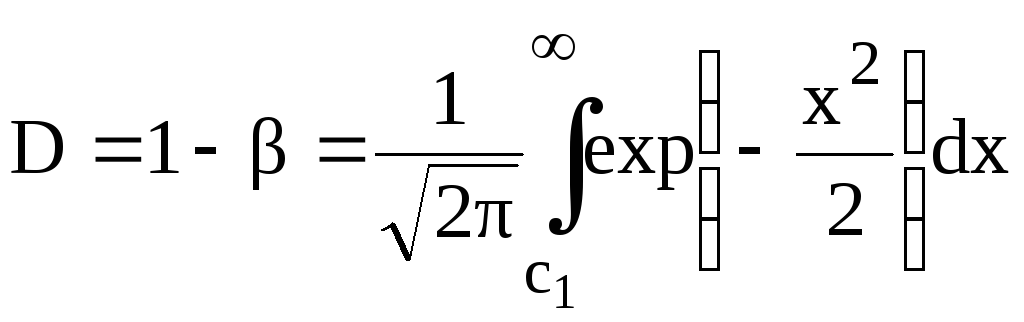
(5.11 )

где
с ₀
и с ₁
вычисляются
при помощи формул (4.18), (4.19), (4.24), (4.25),
(4.29), (5.3), (5.5).

Формулы (5.10) и
(5.11) позволяют построить рабочую
характеристику приемника при использовании
непрерывных наблюдений на интервале
(0,
)
.

6. Методика эксперимента

1. Для того, чтобы
снять рабочую характеристику, необходимо
измерить вероятность правильного
обнаружения D=1-
и вероятность ошибки первого рода .
Эти вероятности измеряются методом
статистических испытаний. Для измерения
D=1-
в течение времени Тн периодически
воспроизводится передача “1” по каналу
связи при заданном отношении сигнал/шум
и фиксированном значении порога.
(Переключатель П₁
в положении “Сигн.+Шум”, а переключатель
П₂
в положениях “Е₁“,
“Е₂
“, “Е₃
“).

В качестве оценки
вероятности правильного обнаружения
берется отношение числа импульсов на
выходе приемника N_i
к общему числу сигналов N^*,
поступивших на вход приемника за время
измерения Тн, т.е. D^*=
N_i
/ N^*
.

Для измерения 
в течение времени Тн периодически
воспроизводится передача “0” по каналу
связи с определенным уровнем шума.
(Переключатель П₁
в положении “Сигн.+Шум”, а переключатель
П₂
в положении “0”). Вероятность ложной
тревоги вычисляется как отношение числа
ошибочных решений N_i
к общему числу испытаний за время Тн:
^*
= N_i
/ N^*.

При N^*


оценки ^*
и D^*
стремятся к своим истинным значениям

и D. Следовательно, результаты измерений
тем точнее, чем больше время измерения.
Отношение N_i/N^*
измеряется частотомером. Для этого
импульсы с выхода приемника N_i
подаются на вход А, а с выхода N^*
– на вход Б частотомера. Переключатель
частотомера “Род работы” устанавливается
в положение “Отношение частот A/B”.
Время измерения Тн задается переключателем
“Время счета”. При этом на цифровом
индикаторе частотомера будет высвечиваться
значение ^*
или D^*
в зависимости от положения переключателя
П₁.

Рекомендуется
регистрировать значения 
и D при одном и том же значении порога
С^*.
Для этого при фиксированном значении
порога С^*
переключатель П₁
поставить в положение “Сигн.+Шум” и
манипулировать переключателем П₂
.

Для того, чтобы
вычислить значение порога триггера
Шмидта приведем правило решения (4.16) к
виду

.

Выходное
напряжение интегратора pавно

Здесь К постоянный
множитель, учитывающий коэффициент
передачи перемножителя и интегратора.
Поэтому величина порога С_Т^*
триггера Шмидта связана с порогом С
выражением

(6.1)

Значение
К для каждой установки написано на
передней панели.

2. В пункте 8 ЗАДАНИЯ
необходимо построить правила ₁
, ₂
, ₃
проверки
гипотез о состоянии источника. Согласно
правилу _j
интервал значений порогов (С_min^*
, C_max^*
) разбивается
точкой С_j
на область
(С_min ^*,
C_j )
– приема гипотезы Н₀
, и область
(С_j ,
C_max^*
) – приема
гипотезы Н₁
. Примем С₂
= С_Б
, где С_Б
– порог
Байеса, найденный в пункте 7, а пороги
C₁
и С₃
определим по формулам

C₁
= С₂
– k₀
(С₂
– С_min
) , C₃
= С₂
+ k₀
(С_max
– С₂
) ,

где 0 < k₀
< 1 и
задается преподавателем.

3. При расчетах
вероятностей 
, D=1-
и порога С можно воспользоваться как
экспериментальными данными , так и
построенными графиками. Погрешность
представления ,
D и С зависит от качества интерполяции
и качества построения графиков.
Вероятности 
и D по графику определяются следующим
образом:

– для известного
С в произвольном месте чертежа под углом

к оси абсцисс проводится прямая,
удовлетворяющая уравнению tg

= C ,

– построенная
прямая переносится параллельно самой
себе до касания с выбранной рабочей
характеристикой,

– в точке касания
определяются вероятности 
и D.

З А Д А Н И Е

1. Ознакомиться с
описанием экспериментальной установки,
методикой эксперимента, получить от
преподавателя значения априорной
вероятности P₀
состояния источника, матрицу потерь П,
отношение сигнал/шум и коэффициент k₀
.

2. Поставить
переключатель П₁
в положение “Сигн.”. Какому состоянию
канала соответствует это положение ?

Поставить
переключатель П₂
в положение “Е₁
“.

Пронаблюдать и
зарисовать осциллограммы напряжений
в контрольных точках КТ₁,
КТ₂
, КТ₃.
Объяснить изменение формы сигнала в
контрольной точке КТ₃
при изменении порога.

Измерить амплитуду
и длительность радиосигнала в контрольной
точке КТ₁
во всех положениях переключателя П₂
. По результатам измерений вычислить
энергию сигнала E
_s .

3. Поставить
переключатель П₁
в положение “Сигн.+Шум”.

Пронаблюдать
форму напряжений в тех же точках при
положениях Е₁,
Е₂,
Е₃
переключателя П₂.
Какому состоянию канала соответствует
эти положения ?

Для каждого
положения переключателя П₂
вычислить отношение сигнал/шум. В
положении переключателя П₂
“0” пронаблюдать форму напряжений в
контрольных точках. Объяснить изменение
формы сигналов в точке КТ₃
при изменении порога.

4. Снять зависимость
вероятности правильного обнаружения
D и вероятности ошибки 
от величины порога при трех значениях
отношения сигнал/шум.

5. По полученным
данным построить рабочие характеристики
приемника на плоскости (,
D) для трех значений отношения сигнал/шум,
пересчитав предварительно пороги С_Т^*
триггера Шмидта в пороги С, пользуясь
соотношением (6.1).

* Расчет вероятностей
ошибок _i
, _i
для различных правил 
принятия решения по заданному
преподавателем энергии сигнала и
рассчитанным порогам триггера Шмидта
С_Тi
произвести по схеме

6. Вычислить
вероятности 
и D по формулам (5.10) и (5.11) для заданного
преподавателем отношения сигнал/шум
при тех же значениях порогов, что и в
пункте 5.

Построить
теоретическую рабочую характеристику
на том же графике, что и экспериментальная
рабочая характеристика и сравнить
теоретическую кривую с экспериментальной.

7. Критерий Байеса.
Для заданной преподавателем матрицы
потерь П, априорного распределения
состояния источника P₀
и отношения сигнал/шум построить средний
риск как функцию порога по формуле
(2.7), приведя его к виду

R(C) = P₁
П₁₁
+ P₀
П₀₀
+ 
(С) P₀
(П₁₀
– П₀₀)
– D(C) P₁
(П₀₁
– П₁₁).

Определить порог
С_Б
, при котором функция риска достигает
минимум, и соответствующие ему вероятности

и D .

Для найденных 
и D проверить формулу (3.16).

8. Минимаксный
критерий. Задать три правила ₁
, ₂
, ₃
проверки
гипотез о состоянии источника. Выбрать
наилучшее правило.

9. Критерий максимума
апостериорной вероятности. По заданной
априорной вероятности P₀
состояния
источника для каждого отношения
сигнал/шум по экспериментальным кривым
найти пороги С_МАВ
i и вероятности
((d_i),
D(d_i)),
соответствующие им. Построить график
D(d_i)
и объяснить его поведение.

10. Критерий максимума
правдоподобия. Для каждого отношения
сигнал/шум по экспериментальным кривым
найти пороги С_1МП
, С_2МП
, С_3МП
и
соответствующие им вероятности ((d₁)
, D(d₁)),
((d₂)
, D(d₂)),
((d₃),
D(d₃)).
Построить график С_МП(d_i)
и объяснить его поведение.

11. Критерий
Неймана-Пирсона. Положим вероятность
ошибки первого рода равна вероятности
,
найденной в п. 8. Определить порог С_Н-П
и вероятность
правильного обнаружения D по
экспериментальной кривой и теоретически
для отношения сигнал/шум, заданного в
п.1. Сравнить полученные результаты.

12. Построить таблицу
для заданного в п.1. отношения сигнал/шум

Критерий	Априорные данные	Порог	 , D
Байеса
min max
МАВ
МП
Неймана-Пирсона

Сравнить полученные
результаты. При каких условия критерии
min max, МАВ. МП приводятся к критерию
Байеса.

29

Соседние файлы в папке Лаб. 1204

• #
• #