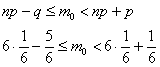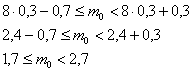Как найти вероятность промаха при каждом выстреле

Решение задач о выстрелах и попаданиях в цель

В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про бросание игральных костей и задачи о подбрасывании монет.

Перейдем еще к одному типу задач: про стрелков, которые делают выстрелы по целям (или мишеням), причем вероятности попаданий для каждого стрелка обычно заданы, а нужно найти вероятность ровно одного попадания, или не более двух попаданий, или всех трех и так далее, в зависимости от конкретной задачи.

Основной метод решения подобных задач – использование теорем о сложении и умножении вероятностей, который мы и разберем на примерах ниже. А перед примерами вы найдете онлайн калькулятор, который поможет решить подобные задачи буквально в один клик! Удобно решать самому? Посмотрите видеоурок и скачайте бесплатный шаблон Excel для решения задач о выстрелах.

Онлайн решение задачи про попадание в цель

Выберите количество стрелков и затем введите в поля вероятности $p_i$ их попаданий в цель (десятичный разделитель – точка):

Видеоурок и шаблон Excel

Посмотрите наш ролик о решении задач с выстрелами: как использовать Excel для решения типовых задач с 2, 3 и 4 стрелками (выстрелами).

Расчетный файл Эксель из видео можно бесплатно скачать.

Два стрелка

Начнем традиционно с более простых задач, а именно, с двух стрелков. Пусть первый стрелок попадает в цель с вероятностью $p_1$, а второй – с вероятностью $p_2$ (конкретные числа см. в примерах ниже). Соответственно, сразу можно сделать вывод, что промахиваются они с вероятностями $q_1=1-p_1$ и $q_2=1-p_2$.

Чтобы иметь возможность оперировать с событиями, нужно сначала их (события) ввести. Кстати, сразу заметим, что события эти независимые (то есть вероятность попадания первого стрелка не зависит от того, как стреляет второй и наоборот). Итак, пусть:

Событие $A_1$ = (Первый стрелок попал в цель),

Событие $A_2$ = (Второй стрелок попал в цель).

Соответственно, события $overline{A_1}$, $overline{A_2}$ обозначают промах первого и второго стрелка (не попал в цель).

Сразу можно выписать все, что нам стало известно к этому времени о данных событиях, в терминах теории вероятности (так сказать, формализуем задачу, чтобы легче было ее решать дальше):
$$
P(A_1)=p_1, quad P(A_2)=p_2, quad Pleft(overline{A_1}right)=1-p_1=q_1, quad Pleft(overline{A_2}right)=1-p_2=q_2.
$$

Теперь можно переходить к подсчету вероятностей попаданий. Например, пусть событие $X$ =(При двух выстрелах не было ни одного поражения цели). Вопрос, когда такое случится? Ясно, что когда ни первый стрелок, ни второй не попадут в цель, то есть одновременно произойдут события $overline{A_1}$ и $overline{A_2}$, что можно записать как произведение событий: $X=overline{A_1} cdot overline{A_2}$. Согласно теореме умножения вероятностей независимых событий, вероятность произведения событий равна произведению соответствующих вероятностей, или:
$$
P(X)=Pleft(overline{A_1} cdot overline{A_2}right)= Pleft(overline{A_1}right) cdot Pleft(overline{A_2}right) = q_1 cdot q_2. qquad (1)
$$

Рассмотрим еще одно событие $Y$ =(При двух выстрела ровно один стрелок попадет в цель). Как можно записать это событие через уже известные нам $A_1$ и $A_2$? Подумаем, когда такое событие произойдет:
1. Когда первый стрелок попадет в цель (событие $A_1$) и одновременно с этим второй стрелок промахнется (событие $overline{A_2}$), то есть получили произведение событий $A_1 cdot overline{A_2}$.

2. Когда второй стрелок попадет в цель (событие $A_2$) и одновременно с этим первый стрелок промахнется (событие $overline{A_1}$), то есть получили произведение событий $overline{A_1} cdot A_2$.

Так как других вариантов для получения одного попадания нет, а эти два варианта – несовместные (они не могут произойти одновроменно, или первая ситуация, или вторая), то по теореме сложения вероятностей несовместных событий:
$$
P(Y) = Pleft(A_1 cdot overline{A_2} + overline{A_1} cdot A_2right)= Pleft(A_1 cdot overline{A_2} right)+ Pleft( overline{A_1} cdot A_2right) =
$$
дальше уже по известной теореме умножения вероятностей раскрываем скобки:
$$
= P(A_1) cdot left(overline{A_2} right) + Pleft( overline{A_1} right) cdot P(A_2) = p_1 cdot q_2 + q_1 cdot p_2.
$$
Мы получили формулу, позволяющую найти вероятность в точности одного попадания в цель:
$$
P(Y) = p_1 cdot q_2 + q_1 cdot p_2. qquad (2)
$$

Если вы одолели последние пару абзацев, дальше все будет проще, поверьте:). Просто нужно привыкнуть к формулам, а потом они сами будут подсказывать вам верный ход решения.

Ну и наконец, найдем вероятность события $Z$ = (Оба стрелка попадут в цель), которое, как вы наверное и сами уже поняли, можно выразить так: $Z = A_1 cdot A_2$. Итоговая формула:
$$
P(Z) = P(A_1 cdot A_2) = P(A_1) cdot P(A_2)= p_1 cdot p_2. qquad (3)
$$

Большая теоретическая часть окончена, теперь можно решать примеры как орешки.

Пример 1. Два одновременно стреляют по мишени. Вероятность попадания по мишени у первого стрелка равна 0,6, у второго – 0,7. Какова вероятность того, что в мишени будет только одна пробоина?

Не будем повторять все выкладки выше, для этого мы их и делали подробно. Сразу перейдем к решению. Так как нужно найти вероятность всего одного попадания, используем формулу (2), где по условию $p_1=0,6$, $p_2=0,7$, значит $q_1=1-p_1=0,4$, $q_2=1-p_2=0,3$. Получаем:
$$
P = p_1 cdot q_2 + q_1 cdot p_2 = 0,6 cdot 0,3 + 0,4 cdot 0,7 = 0,46.$$

Пример 2. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8, производят по одному выстрелу. Найти вероятность того, что мишень поражена дважды.

Опять же, нужно только применить формулу (3) с данными задачи $p_1=0,7$, $p_2=0,8$ и сразу получим ответ:
$$
P = p_1 cdot p_2=0,7 cdot 0,8 = 0,56.
$$

Пример 3. Производятся два выстрела по цели, вероятности попадания равны 0,3 и 0,4. Найти вероятность того, что хотя бы один выстрел попал в цель.

На этот раз задача будет решена не в одно, а в два действия, но пусть это вас не пугает. Как обычно, в задачах содеражащих фразу “хотя бы один…” мы помимо основного события: $Q$ = (Хотя бы один выстрел попал в цель) вводим сразу противоположное событие $overline{Q}$ = (Ни один выстрел не попал в цель, 0 попаданий). А дальше уже известно, применяем формулу (1), которая выведена выше:
$$
P(overline{Q}) = q_1 cdot q_2= (1-0,3) cdot (1-0,4) =0,7 cdot 0,6 = 0,42.
$$
Вероятность нужного нам события тогда равна:
$$
P(Q) = 1- P(overline{Q}) = 1 – 0,42 = 0,58.
$$

Три стрелка

К двум устрелявшимся стрелкам наконец присоединяется третий, бодрый и полный сил. А мы принимаемся за вывод формул. Напомню общую постановку задачи: три стрелка, вероятности попаданий в цель которых равны $p_1$, $p_2$ и $p_3$, делают по одному выстрелу и подсчитывают число попаданий. Наша задача – вычислить вероятности 1, 2, 3 или ни одного попадания.

Начало одинаковое – формализуем задачу и вводим независимые события:

Событие $A_1$ = (Первый стрелок попал в цель),

Событие $A_2$ = (Второй стрелок попал в цель),

Событие $A_3$ = (Третий стрелок попал в цель).

Известно, что:
$$
P(A_1)=p_1, quad P(A_2)=p_2, quad P(A_3)=p_3, \ Pleft(overline{A_1}right)=1-p_1=q_1, quad Pleft(overline{A_2}right)=1-p_2=q_2, quad Pleft(overline{A_3}right)=1-p_3=q_3.
$$

Вероятность того, что не будет ни одного попадания, вычисляется абсолютно аналогично случаю для двух стрелков, только добавляется третий сомножитель (см. формулу (1)), так как все трое должны промахнуться:
$$
P_0=Pleft(overline{A_1} cdot overline{A_2} cdot overline{A_3}right)= Pleft(overline{A_1}right) cdot Pleft(overline{A_2}right) cdot Pleft(overline{A_3}right)= q_1 cdot q_2 cdot q_3. qquad (4)
$$

Желающие потренироваться в выводе формул могут на этом этапе самостоятельно попытаться выписать вероятности для 2 и 3 попаданий (соответственно, $P_2$ и $P_3$), и сравнить с теми формулами, что я приведу ниже:
$$
P_2 = P(X_2)= \
= P(A_1) cdot P(A_2) cdot Pleft(overline{A_3} right) + P(A_1)cdot Pleft(overline{A_2} right) cdot P(A_3) + Pleft(overline{A_1} right) cdot P(A_2) cdot P(A_3)=\
= p_1 cdot p_2 cdot q_3 + p_1 cdot q_2 cdot p_3 + q_1 cdot p_2 cdot p_3. qquad (6)
$$

$$
P_3 = P(X_3)= P(A_3) cdot P(A_2) cdot P(A_3) = p_1 cdot p_2 cdot p_3. qquad (7)
$$

Теперь, вооружившись формулами до зубов, снова возвращаемся к задачнику и решаем примеры буквально в одну строчку (конечно, если вы оформляете эти работы для сдачи преподавателю, используйте в решении и вывод формул, приведенный выше).

Пример 4. Три стрелка производят по одному выстрелу. Вероятности попадания 1-го, 2-го и 3-го стрелков соответственно равны: 0,2, 0,3 и 0,4. Найти вероятность получения одного попадания?

Так как речь идет об одном попадании, используем формулу (5), куда подставляем значения из условия задачи:
$$
p_1=0,2, quad p_2=0,3, quad p_3=0,4, quad q_1=0,8, quad q_2=0,7, quad q_3=0,6
$$
Получаем:
$$
P_1 = p_1 cdot q_2 cdot q_3 + q_1 cdot p_2 cdot q_3 + q_1 cdot q_2 cdot p_3=\
= 0,2 cdot 0,7cdot 0,6 + 0,8 cdot 0,3 cdot 0,6 + 0,8 cdot 0,7 cdot 0,4 = 0,452.
$$

Пример 5. 3 стрелка делают по одному выстрелу в мишень. Вероятности попадания для каждого стрелка соответственно равны 0,8; 0,7; 0,5. Определите вероятность того, что в мишени окажется ровно 2 пробоины.

Так как речь идет о двух попаданиях, используем формулу (6), куда подставляем значения из условия задачи:
$$
p_1=0,8, quad p_2=0,7, quad p_3=0,5, quad q_1=0,2, quad q_2=0,3, quad q_3=0,5
$$
Получаем:
$$
P_2 = p_1 cdot p_2 cdot q_3 + p_1 cdot q_2 cdot p_3 + q_1 cdot p_2 cdot p_3 = \
= 0,8 cdot 0,7 cdot 0,5 + 0,8 cdot 0,3 cdot 0,5 + 0,2 cdot 0,7 cdot 0,5 = 0,47.
$$

Пример 6. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8; для второго и третьего орудий эти вероятности соответственно равны 0,7 и 0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.

Надеюсь, вас не смутили орудия вместо стрелков? На самом деле, не суть важно, что происходит: три стрелка вышли на линию, или три пушки готовят залп, или три снайпера целятся в одного террориста. С точки зрения теории вероятностей, все формулы остаются прежними.

Поэтому смело приступаем к решению. Требуется найти вероятность события $A$ = (Будет хотя бы одно попадания при одновременном залпе из всех орудий), поэтому введем для простоты расчетов противоположное событие $overline{A}$ = (Все три орудия дали промашку), вероятность которого найдем по формуле (4), подставляя значения:
$$
p_1=0,8, quad p_2=0,7, quad p_3=0,9, quad q_1=0,2, quad q_2=0,3, quad q_3=0,1
$$
Получаем:
$$
Pleft(overline{A} right) = P_0 = q_1 cdot q_2 cdot q_3 = 0,2 cdot 0,3 cdot 0,1 = 0,006.
$$
Искомая вероятность:
$$
P(A) = 1 – Pleft(overline{A} right) = 1 – 0,006 = 0,994.
$$

Задачи на формулу Бернулли

Когда я писала первый вариант статьи, этого раздела не было. Но ведь задачи, когда выстрелы попадают в цель с одинаковой вероятностью, встречаются весьма и весьма часто и фактически являются частным и более простым случаем разобранных выше. Так что перед вами дополнительный раздел, надеюсь, он окажется полезным:).

Итак, вернемся к нашим стрелкам. Теперь будем считать, что вероятность попадания в цель при каждом выстреле одинакова и равна $p$, число выстрелов равно $n$ и конечно, как и прежде, выстрелы попадают в цель независимо друг от друга. Хм… Что-то знакомое? Конечно! Это схема независимых повторных испытаний, иначе говоря, схема Бернулли.

Ну вот, скажете вы, только научились решать одним способом, и тут на тебе, “схема Бернулли”!

А я отвечу, что в ней как минимум пара преимуществ:

• нужно запомнить всего одну формулу вместо нескольких (см. выше)
• теперь количество стрелков может быть не только 2, 3 или 4 (что уже громоздко), а практически любое – 5, 10, 12…

Пора приступать. Сначала сама формула, а потом разберем несколько примеров для закрепления пройденного:).

Пусть производится $n$ выстрелов, вероятность попадания в цель каждом из которых равна $p$. Вероятность, что окажется в точности $k$ попаданий, можно вычислить по формуле Бернулли:
$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot p^k cdot q^{n-k}.
$$

Пример 7. Стрелок производит 4 выстрела, вероятность попадания при каждом из них равна $p=0,8$. Найти вероятность того, что:
1) Стрелок попадёт 3 раза
2) Стрелок попадёт не менее 3-ёх раз.

Вот она, типовая задача на формулу Бернулли. Наши параметры: $n=4$ (число выстрелов), $p=0,8$ (вероятность попадания при одном выстреле), $q=1-p=0,2$ (вероятность промаха).

1) Вероятность того, что стрелок попадёт 3 раза:

$$
P_4(3)=C_4^3 cdot 0,8^3 cdot 0,2^{4-3} = 4 cdot 0,8^3 cdot 0,2 =0,41.
$$

2) Вероятность того, что стрелок попадёт не менее 3-ёх раз из 4 (то есть или 3, или 4 раза – складываем вероятности соответствующих событий):

$$
P_4(k ge 3) =P_4(3) + P_4(4)=0,41+ C_4^4 cdot 0,8^4 cdot 0,2^{0} = 0,41+0,8^4 =0,819.
$$

И это все! Проще некуда, но не забывайте, что задачи разные, где-то формула Бернулли подходит (повторяем: вероятности одинаковые, события независимые и повторные), а где-то – нет (как в разобранных в начале этой статьи задачах).

Пример 8. Вероятность попасть в десятку у данного стрелка при одном выстреле равна 0,2. Определить вероятность выбивания не менее 20 очков при десяти выстрелах.

И опять проверяем выполнение условий схемы Бернулли: вероятности одинаковые (да, $p=0,2$), выстрелы независимые, число выстрелов задано ($n=10$).

Сформулируем вопрос задачи математически: что значит выбито не менее 20 очков? Это значит, что в 10 выстрелах было не менее 2 попаданий в цель (то есть 2, 3, 4,…, 10). Что-то многовато…

В таком случае проще подсчитать сначала вероятность противоположного события: “В 10 выстрелах было менее 2 попаданий в цель” (то есть 0 или 1). Вот тут полегче, давайте посчитаем:

$$
P_{10}(k lt 2) =P_{10}(0) + P_{10}(1)=C_{10}^{0} cdot 0,2^{0} cdot 0,8^{10}+ C_{10}^{1} cdot 0,2^{1} cdot 0,8^{9} =\
=0,8^{10}+ 10 cdot 0,2 cdot 0,8^{9} =0,376.
$$

Тогда искомая вероятность выбить не менее 20 очков будет:

$$
P_{10}(k ge 2) =1-P_{10}(k lt 2)=1-0,376=0,624.
$$

Пригодится: онлайн калькулятор для таких задач

Другие задачи про выстрелы и попадания

Конечно же, не все задачи про выстрелы можно решать по данным формулам (точнее, не все вписываются в эту схему напрямую), это лишь один из популярных классов задач. Для полноты изложения я приведу еще несколько типовых задач с немного отличающимся решением. Задачи из существенно других разделов (например, на формулу Байеса или построение ряда распределения случайной величины) будут разобраны в других статьях.

Пример 9. Вероятность того, что стрелок попадет в цель при одном выстреле, равна 0,7. Производится пять независимых выстрелов. Какова вероятность того, что в мишени окажется хотя бы одна пробоина?

Требуется найти вероятность события $A$ = (В мишени окажется хотя бы одна пробоина), поэтому вводим сначала противоположное событие $overline{A}$ = (Все пять выстрелов не попали в цель). Если обозначить вероятность попадания в цель как $p=0,7$ (она одинакова при каждом выстреле), а вероятность промаха как $q=1-p=0,3$, то вероятность всех пяти промахов будет
$$
Pleft(overline{A} right) = q^5 = 0,3^5.
$$
Искомая вероятность:
$$
P(A) = 1 – Pleft(overline{A} right) = 1 – 0,3^5 = 0,998.
$$

Общий случай: как найти вероятность наступления хотя бы одного события

Пример 10. Два стрелка стреляют по мишени по одному разу. Вероятность того, что оба попали равна 0,42, а вероятность того что оба промахнулись, 0,12. Найти вероятность попадания в мишень каждым стрелком при одном выстреле.

Если обозначить вероятности попадания первым и вторым стрелком соответственно как $p_1$ и $p_2$, то, используя формулы (1) и (3), запишем условие задачи в виде системы уравнений:
$$
P_2 = p_1 cdot p_2 = 0,42;\
P_0 = (1-p_1) cdot (1-p_2) = 0,12.\
$$
Решая эту систему, найдем искомые вероятности попадания для каждого стрелка: $p_1 = 0,6$ и $p_2 = 0,7$ (или наоборот, $p_1 = 0,7$ и $p_2 = 0,6$).

Пример 11. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Если обозначить вероятность попадания в цель как $p$ (она одинакова при каждом выстреле), а вероятность промаха как $q=1-p$, то вероятность 4 промахов при четырех выстрелах будет равна $q^4$, а соответственно вероятность хотя бы одного попадания в цель при четырех выстрелах – $1-q^4$. Получаем уравнение:
$$
1-q^4=0,9984;\
q^4=0,0016;\
q=0,2;\
p=1-q=0,8.
$$
Нашли вероятность попадания в цель при одном выстреле, она равна 0,8.

Пример 12. Два стрелка независимо выстрелили по мишени по два раза. Меткость первого стрелка равна 0,8; второго – 0,7. Найти вероятность того, что в мишень попадут все четыре пули.

Все 4 пули попадут в мишень, если первый стрелок попадет оба раза (вероятность попадания при одном выстреле у него $p_1=0,8$), и одновременно второй стрелок попадет оба раза (вероятность попадания при одном выстреле у него $p_2=0,7$). По правилу умножения вероятностей
$$
P = p_1 cdot p_1 cdot p_2 cdot p_2 = 0,8 cdot 0,8 cdot 0,7 cdot 0,7 = 0,3136.
$$

Полезная информация

Онлайн калькуляторы Онлайн учебник Более 200 примеров Решенные контрольные

Формулы и таблицы Сдача тестов Решение на заказ Онлайн помощь

Решебник по вероятности

В решебнике вы найдете более 700 задач о выстрелах и попаданиях с полными решениями (вводите часть текста для поиска своей задачи):

Теория
вероятностей.

       
Задачи на «Стрельбу».

№ 1. Стрелок  стреляет  по 
мишени  один  раз.  В  случае  промаха 
стрелок  делает второй
выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 
0,8.  Найдите  вероятность  того,  что  мишень 
будет  поражена  (либо  первым  либо вторым
выстрелом).

Решение. Первый способ.

 Пусть A –
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на стрел­ком с пер­во­го вы­стре­ла, B –
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на со вто­ро­го вы­стре­ла.
Ве­ро­ят­ность со­бы­тия A равна P(A) = P₁(A)
= 0,8. Со­бы­тие B на­сту­па­ет, если, стре­ляя пер­вый раз,
стре­лок про­мах­нул­ся P₁() =1 –
0,8 = 0,2, а, стре­ляя вто­рой раз, попал P₂(A) = 0,8. Это не­за­ви­си­мые
со­бы­тия, их ве­ро­ят­ность равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: P(B)
= P₁() ∙ P₂(A)
= 0,2·0,8 = 0,16. Со­бы­тия A и B не­сов­мест­ные, ве­ро­ят­ность
их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: P (A + B) = P(A) + P(B) = 0,8 + 0,16 =
0,96.

Ответ:
0,96.

Второй способ. Пусть A –
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на стрел­ком
при одном выстреле, B – со­бы­тие,
со­сто­я­щее в том, что ми­шень по­ра­же­на (либо  первым 
либо вторым выстрелом).

Так как вероятность попасть
в мишень при одном выстреле равна 0,8, то есть P(A) = 0,8, то ве­ро­ят­ность
того, что, стре­ляя пер­вый раз, стре­лок про­мах­нул­ся, равна P₁() = 1 – 0,8 =  0,2. Ве­ро­ят­ность
того, что, стре­ляя второй  раз, стре­лок про­мах­нул­ся, равна P₂() = 1 – 0,8 =  0,2. Ве­ро­ят­ность
того, что, стре­лок про­мах­нул­ся оба раза,  равна P₁() ∙ P₂() = 0,2∙0,2 = 0,04. Ве­ро­ят­ность
противоположного события (хотя бы один раз не промахнется) равна P(B)= 1 – 0,04 = 0,96.

Ответ: 0,96.

№
2. Стрелок  4  раза 
стреляет  по  мишеням. Вероятность  попадания  в 
мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок первый раз попал

 в мишень, а последние 3 раза промахнулся.

Решение. Пусть A – со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на
стрел­ком при одном выстреле, B – со­бы­тие, со­сто­я­щее в том, что ми­шень
по­ра­же­на.

Так
как вероятность попасть
в мишень при одном выстреле равна 0,7, то
вероятность попадания при первом выстреле равна P₁(A) = 0,7, тогда ве­ро­ят­ность того, что, стре­ляя
второй раз, стре­лок про­мах­нул­ся, равна P₂() = 1 – 0,7 =  0,3. Ве­ро­ят­ность того,
что, стре­ляя третий  раз, стре­лок про­мах­нул­ся, равна P₃() = 1 – 0,8 =  0,2. Ве­ро­ят­ность того,
что, стре­ляя четвертый раз, стре­лок про­мах­нул­ся, равна P₃() = 1 – 0,8 =  0,2. Все события
независимы. Ве­ро­ят­ность того, что стрелок первый раз попал в мишень, а последние 

3 раза промахнулся.
P(B)= P₁(A)∙ P₂()∙ P₃()∙ P₄() = 0,7∙0,3∙0,3∙0.3 = 0,0189

Ответ: 0,0189.

№ 3.
Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7
, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень
попадает только один из стрелков.

Решение. Пусть A₁ –
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на первым стрелком, A₂ –
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на вторым стрелком. С – со­бы­тие, со­сто­я­щее в том, что в ми­шень попал только один из стрелков, то есть (первый попадет и второй промажет) либо (первый промажет и
второй попадет).

Вероятность попадания в мишень первым стрелком р
(А₁)=0,7, вероятность его промаха
р ()=1-р(А₁)=1-
0,7 = 0,3.

 Вероятность попадания в мишень вторым стрелком р
(А₂)=0,8, вероятность его промаха
 р ()=1-р(А₂)=1
– 0,8 = 0,2.
р (С) = р(А₁)∙р () + р(А₂)∙р
() = 0,7∙0,2 +
0,8∙0,3 = 0,38

Ответ.0,38.

№ 4. Каждый
из трех стрелков стреляет в мишень по одному разу, причем вероятность попадания
1 стрелка составляет 80%, второго – 70%, третьего – 60%. Найдите вероятность
того, что двое из трех стрелков попадет в мишень.

Решение.

 Пусть A₁ – со­бы­тие, со­сто­я­щее в том,
что ми­шень по­ра­же­на первым стрелком, A₂ – со­бы­тие, со­сто­я­щее
в том, что ми­шень по­ра­же­на вторым стрелком. A₃ – со­бы­тие,
со­сто­я­щее в том, что ми­шень по­ра­же­на третьим стрелком. С – со­бы­тие, со­сто­я­щее в том, что в ми­шень попали только двое из трех из стрелков,

Вероятность попадания в мишень первым стрелком р
(А₁)=0,8, вероятность его промаха
р ()=1-р(А₁)=1-
0,8 = 0,2.

 Вероятность попадания в мишень вторым стрелком р
(А₂)=0,7, вероятность его промаха
 р ()=1-р(А₂)=1
– 0,7 = 0,3.

Вероятность попадания в мишень третьим стрелком р
(А₃)=0,6, вероятность его промаха
 р ()=1-р(А₂)=1
– 0,6 = 0,4.

Чтобы
вычислить вероятность (двое из трех попали), надо вычислить вероятности, когда:

1. Промахнулся только первый стрелок, а второй и
третий попали.
2. Промахнулся только второй стрелок,  а первый
и третий попали.
3. Промахнулся только третий стрелок, а первый и
второй попали.
Вероятность того, что промахнулся только первый
стрелок, а второй и третий попали: P₁ = р ()∙ р (А₂)∙ р (А₃)=  0,2∙0,7∙0,6 = 0,084.
Вероятность того, что промахнулся только второй
стрелок, а первый и третий попали P₂ = р (А₁) ∙ р () р (А₃)= 0,8∙0,3∙0,6 = 0,144.
Вероятность того, что промахнулся только третий
стрелок, а первый и второй попали P₃ = р (А₁) ∙ р (А₂) ∙ р () = 0,8∙0,7∙0,4
= 0,224.
Отсюда вероятность (2 из 3 попали) р (С) = P₁+ P₂+ P₃ = 0,084+0,144+0,224 = 0,452
Ответ: 0,452

№5. Стрелок
3 раза стреляет по мишеням. Вероятность попадания в мишень при  одном выстреле равна 0,8.
Найдите вероятность того, что стрелок первые 2 раза попал  в мишени, а последний раз
промахнулся.

Решение. Пусть A – со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на
стрел­ком при одном выстреле, B – со­бы­тие, со­сто­я­щее в том, что ми­шень
по­ра­же­на.

Так
как вероятность попасть
в мишень при одном выстреле равна 0,8, то
вероятность попадания при первом выстреле равна P₁(A) = 0,8, вероятность попадания при втором выстреле
равна P₂(A)
= 0,8, ве­ро­ят­ность того, что, стре­ляя третий раз, стре­лок про­мах­нул­ся,
равна P₃() = 1 – 0,8 =  0,2.

Все события независимы. Ве­ро­ят­ность того, что стрелок первые 2 раза попал  в мишени, а последний раз
промахнулся.

P(B)= P₁(A)∙ P₂(А)∙ P₃() = 0,8∙0,8∙0,2 = 0,128

Ответ: 0,128

№ 6. Биатлонист 5 раз стреляет по мишеням.
Вероятность попадания в мишень при одном выстреле 0,8. Какова вероятность,
что он попал в мишень 4 раза и один промахнулся? 

Решение.

Промахнуться он мог первым, вторым, ..пятым выстрелом.
ХОООО; ОХООО; ООХОО; ОООХО; ООООХ.
Вероятность каждого исхода равна 0,8⁴ ∙ 0,2 .
Суммируем вероятности: p = 5∙(0,8⁴ ∙ 0,2) = 0,8⁴ =
0,4096.
Ответ.0,4096.

№ 7.  Три стрелка стреляют
в цель. Вероятность попадания в цель для первого, второго и третьего стрелка
соответственно равна 0,6; 0,7 и 0,75; Определить вероятность хотя бы одного попадания
в цель, если каждый стрелок сделает по одному выстрелу.

Решение.

 Пусть A₁ –
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на первым стрелком, A₂ –
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на вторым стрелком. A₃ –
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на третьим стрелком. С – со­бы­тие, со­сто­я­щее в том, что в ми­шень попали хотя бы один раз.

Вероятность попадания в мишень первым стрелком р
(А₁)=0,6, вероятность его промаха
р ()=1-р(А₁)=1-
0,6 = 0,4.

 Вероятность попадания в мишень вторым стрелком р
(А₂)=0,7, вероятность его промаха
 р ()=1-р(А₂)=1
– 0,7 = 0,3.

Вероятность попадания в мишень третьим стрелком р
(А₃)=0,75, вероятность его промаха
 р ()=1-р(А₂)=1
– 0,75= 0,25.

Посчитаем вероятность события: никто не попал
(то есть  все промазали):

Р= р ()∙ р ()∙ р ()=
0,4∙0,3∙0,25= 0,03.
Вероятность хотя бы одного попадания в цель,
если каждый стрелок сделает по одному выстрелу р (С) = 1 – Р = 1 – 0,03 = 0,97.

Ответ .0,97.

№ 8. Три стрелка один за
другим стреляют в цель. Вероятность попадания первого – 0,8. Второго – 0,75.
Третьего 0,7.
Какова вероятность того, что попадут все три стрелка?

Решение.

 Пусть A₁ –
со­бы­тие, со­сто­я­щее в том, что цель по­ра­же­на первым стрелком, A₂ –
со­бы­тие, со­сто­я­щее в том, что цель по­ра­же­на вторым стрелком. A₃ –
со­бы­тие, со­сто­я­щее в том, что цель по­ра­же­на третьим стрелком. С – со­бы­тие, со­сто­я­щее в том, что в цель попали все три стрелка.

Вероятность попадания в мишень первым стрелком р
(А₁)=0,8. Вероятность попадания в мишень вторым стрелком р (А₂)=0,75.
Вероятность попадания в мишень третьим стрелком р (А₃)=0,7.

Вероятность того, что в цель попали все три стрелка:

р (С) = р (А₁)∙ р (А₁)∙ р
(А₁)=0,8∙0,75∙0,7= 0,42

Ответ. 0,42.

 № 9. Ковбой Джон попадает в муху на стене с
вероятностью 0,9, если стреляет

 из пристрелянного револьвера.
Если Джон стреляет из не пристрелянного револьвера, то он попадает в муху с
вероятностью 0,2. На столе лежит 10 револьверов,  из них только 4
пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый
попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон
промахнётся.

Решение.1 способ.

 Пусть A₁ –
со­бы­тие, со­сто­я­щее в том, что ковбой берет пристрелянный револьвер, A₂ –
со­бы­тие, со­сто­я­щее в том, что ковбой берет не пристрелянный револьвер. В₁–
со­бы­тие, со­сто­я­щее в том, что ковбой попадает в муху из пристрелянного
револьвера. В₂– со­бы­тие, со­сто­я­щее в том, что ковбой попадает в
муху из не пристрелянного револьвера. С –
со­бы­тие, со­сто­я­щее в том, что Джон  не промахнётся.

Вероятность того, что ковбой схватит пристрелянный револьвер
р (А₁) = 0,4. Вероятность того, что ковбой попадает в муху из
пристрелянного револьвера р (В₁) = 0,9. Вероятность того, что попадется пристрелянный револьвер и
Джон попадет, равна Р₁= р (А₁)∙
р (В₁)  = 0,4∙0,9 = 0,36.

Вероятность того, что ковбой схватит не  пристрелянный
револьвер р (А₂) = 0,6. Вероятность того, что ковбой попадает в муху
из не пристрелянного револьвера р (В₂) = 0,2. Вероятность того, что попадется не пристрелянный револьвер
и Джон попадет, равна Р₁= р (А₂)∙
р (В₂) = 0,6∙0,2 = 0,12.

Вероятность
того, что Джон  не промахнётся р(С) = Р₁
+ Р₂ = 0,36 +0,12 = 0,48.

Вероятность противоположного
события Джон  промахнётся р()= 1 – р(С) =
1 – 0,48 = 0.52.

Ответ. 0,52.

2 способ.

 Пусть A₁ –
со­бы­тие, со­сто­я­щее в том, что ковбой берет пристрелянный револьвер. A₂ –
со­бы­тие, со­сто­я­щее в том, что ковбой берет не пристрелянный револьвер. В₁–
со­бы­тие, со­сто­я­щее в том, что ковбой попадает в муху из пристрелянного
револьвера. В₂– со­бы­тие, со­сто­я­щее в том, что ковбой попадает в
муху из не пристрелянного револьвера. – со­бы­тие, со­сто­я­щее в
том, что ковбой промахнется из пристрелянного револьвера. – со­бы­тие, со­сто­я­щее в
том, что ковбой промахнется из не пристрелянного револьвера. С – со­бы­тие, со­сто­я­щее в том, что Джон  
промахнётся.

 Вероятность
того, что ковбой схватит пристрелянный револьвер р (А₁) = 0,4.
Вероятность того, что ковбой попадает в муху из пристрелянного револьвера р (В₁)
= 0,9, вероятность промаха Р() =  1 – р (В₁) = 1 – 0,9 = 0,1.Вероятность
того, что попадется пристрелянный револьвер и Джон промахнется, равна Р₁=
р (А₁)∙ р () = 0,4∙0,1 = 0,04.

Вероятность того, что ковбой схватит не  пристрелянный
револьвер р (А₂) = 0,6. Вероятность того, что ковбой попадает в муху
из не пристрелянного револьвера р (В₂) = 0,2, вероятность промаха Р() =  1 – р (В₁) = 1 – 0,2 = 0,8.Вероятность
того, что попадется не пристрелянный револьвер и Джон промахнется, равна Р₂=
р (А₂) ∙ р () = 0,6∙0,8= 0,48.

 Вероятность того, что Джон  промахнётся р(С) =
Р₁ + Р₂ = 0,04 +0,48 = 0,52.

Ответ. 0,52.

№10. При ар­тил­ле­рий­ской стрель­бе ав­то­ма­ти­че­ская си­сте­ма де­ла­ет
вы­стрел по цели. Если цель не уни­что­же­на, то си­сте­ма де­ла­ет по­втор­ный
вы­стрел. Вы­стре­лы по­вто­ря­ют­ся до тех пор, пока цель не будет уни­что­же­на.
Ве­ро­ят­ность уни­что­же­ния не­ко­то­рой цели при пер­вом вы­стре­ле равна
0,4, а при каж­дом по­сле­ду­ю­щем — 0,6. Сколь­ко вы­стре­лов по­тре­бу­ет­ся
для того, чтобы ве­ро­ят­ность уни­что­же­ния цели была не менее 0,98?

Решение. Переформулируем вопрос задачи:

Сколько
выстрелов потребуется для того, чтобы вероятность промаха была бы меньше 1
-0,98 = 0,02?

При
первом  выстреле вероятность промаха  1- 0,4 = 0,6.

При
каждом последующем выстреле вероятность промаха 1 – 0,6 = 0,4.

При
двух выстрелах вероятность промаха  0,6∙0,4 = 0,24  (первый
выстрел – промах и второй выстрел – промах).

При
трех выстрелах вероятность промаха

0,6∙0,4∙0,4
= 0,096

При
четырех выстрелах вероятность промаха

0,6∙0,4∙0,4 ∙0,4=
0,0384

При
пяти выстрелах вероятность промаха

0,6∙0,4∙0,4 ∙0,4∙0,4 = 0,01536

Замечаем,
что  0,015360,2

Итак,
пяти выстрелов достаточно, чтобы ве­ро­ят­ность уни­что­же­ния цели была
не менее 0,98.

Ответ:
5.

№11. При
артиллерийской стрельбе автоматическая система делает выстрел по цели. Если
цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются
до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой
цели при первом выстреле равна 0,6, а при каждом последующем — 0,8. Сколько
выстрелов потребуется для того, чтобы вероятность уничтожения цели была не
менее 0,95?

Сколько бы не было сделано выстрелов, все эти события (каждый
отдельный выстрел) будут независимыми. При совершении независимых событий (в
данном случае группы выстрелов) одновременно вероятность такого события будет
равна произведению вероятностей этих независимых событий.

Вероятность поразить цель при первом выстреле равна 0,6.

Значит, вероятность промахнуться при первом выстреле равна 0,4.

Вероятность поразить цель при каждом последующем выстреле (втором
ит.д.) равна 0,8.

Значит, вероятность промаха при каждом последующем выстреле равна
0,2.

Необходимо поставить  вопрос: каким образом может быть
поражена
цель?              

Цель может быть поражена либо при первом выстреле, либо вторым
выстрелом, либо третьим, либо четвёртым, либо пятым выстрелом и т.д. …

Все перечисленные события независимые. Найдём их вероятности.

При первом:

Вероятность поражения равна 0,6.

При втором:

Вероятность поражения равна  0,4 ∙ 0,8 = 0,32 (мимо -попал).

То есть, вероятность поражения цели не более, чем двумя выстрелами
равна  0,6 + 0,32 = 0,92 < 0,95

При третьем:

Вероятность поражения равна  0,4 ∙ 0,2 ∙ 0,8 = 0,064 (мимо
–мимо -попал).

То есть, вероятность поражения цели не более, чем тремя выстрелами
равна  0,6 + 0,32 + 0,064 = 0,984 > 0,95

Таким образом, необходимо сделать три выстрела, чтобы мишень была
поражена  с вероятностью не менее  0,95.

Ответ: 3

№
12. Вероятность  попасть  в  мишень  равна  0,6.
 Произведено  три  выстрела.  Какова  вероятность, что
мишень была поражена не менее  двух раз?

Решение: 

Вероятность
того, что все три  выстрела попадут в цель, равна P₁=0,6³=0,216.

Вероятность
того, что мишень будет поражена два раза, равна P₂=3∙(0,4∙0,6∙0,6)=3∙0,144=0,432. 
Здесь умножили на 3, потому что возможны три варианта (попал – не попал 
-попал, попал – попал – не попал и не попал-попал-попал). Тогда искомая
вероятность равна P=P1+P₂=0,216 +0,432 = 0,648.

Ответ
0.648.

Решение задач о выстрелах и попаданиях в цель

Задачи про стрелков, которые делают выстрелы по целям (или мишеням), причем вероятности попаданий для каждого стрелка обычно заданы, а нужно найти вероятность ровно одного попадания, или не более двух попаданий, или всех трех и так далее, в зависимости от конкретной задачи.

Основной метод решения подобных задач – использование теорем о сложении и умножении вероятностей, который мы и разберем на примерах ниже.

Два стрелка

Пример 1. Два одновременно стреляют по мишени. Вероятность попадания по мишени у первого стрелка равна 0,6, у второго – 0,7. Какова вероятность того, что в мишени будет только одна пробоина?

Не будем повторять все выкладки выше, для этого мы их и делали подробно. Сразу перейдем к решению. Так как нужно найти вероятность всего одного попадания, используем формулу (2), где по условию p1=0,6p1=0,6, p2=0,7p2=0,7, значит q1=1−p1=0,4q1=1−p1=0,4, q2=1−p2=0,3q2=1−p2=0,3. Получаем:

P=p1⋅q2+q1⋅p2=0,6⋅0,3+0,4⋅0,7=0,46.P=p1⋅q2+q1⋅p2=0,6⋅0,3+0,4⋅0,7=0,46.

Пример 2. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8, производят по одному выстрелу. Найти вероятность того, что мишень поражена дважды.

Опять же, нужно только применить формулу (3) с данными задачи p1=0,7p1=0,7, p2=0,8p2=0,8 и сразу получим ответ:

P=p1⋅p2=0,7⋅0,8=0,56.P=p1⋅p2=0,7⋅0,8=0,56.

Пример 3. Производятся два выстрела по цели, вероятности попадания равны 0,3 и 0,4. Найти вероятность того, что хотя бы один выстрел попал в цель.

На этот раз задача будет решена не в одно, а в два действия, но пусть это вас не пугает. Как обычно, в задачах содеражащих фразу “хотя бы один…” мы помимо основного события: QQ = (Хотя бы один выстрел попал в цель) вводим сразу противоположное событие Q¯¯¯¯Q¯ = (Ни один выстрел не попал в цель, 0 попаданий). А дальше уже известно, применяем формулу (1), которая выведена выше:

P(Q¯¯¯¯)=q1⋅q2=(1−0,3)⋅(1−0,4)=0,7⋅0,6=0,42.P(Q¯)=q1⋅q2=(1−0,3)⋅(1−0,4)=0,7⋅0,6=0,42.

Вероятность нужного нам события тогда равна:

P(Q)=1−P(Q¯¯¯¯)=1−0,42=0,58.P(Q)=1−P(Q¯)=1−0,42=0,58.

Три стрелка

К двум устрелявшимся стрелкам наконец присоединяется третий, бодрый и полный сил. А мы принимаемся за вывод формул. Напомню общую постановку задачи: три стрелка, вероятности попаданий в цель которых равны p1p1, p2p2 и p3p3, делают по одному выстрелу и подсчитывают число попаданий. Наша задача – вычислить вероятности 1, 2, 3 или ни одного попадания.

Пример 4. Три стрелка производят по одному выстрелу. Вероятности попадания 1-го, 2-го и 3-го стрелков соответственно равны: 0,2, 0,3 и 0,4. Найти вероятность получения одного попадания?

Так как речь идет об одном попадании, используем формулу (5), куда подставляем значения из условия задачи:

p1=0,2,p2=0,3,p3=0,4,q1=0,8,q2=0,7,q3=0,6p1=0,2,p2=0,3,p3=0,4,q1=0,8,q2=0,7,q3=0,6

Получаем:

P1=p1⋅q2⋅q3+q1⋅p2⋅q3+q1⋅q2⋅p3==0,2⋅0,7⋅0,6+0,8⋅0,3⋅0,6+0,8⋅0,7⋅0,4=0,452.P1=p1⋅q2⋅q3+q1⋅p2⋅q3+q1⋅q2⋅p3==0,2⋅0,7⋅0,6+0,8⋅0,3⋅0,6+0,8⋅0,7⋅0,4=0,452.

Пример 5. 3 стрелка делают по одному выстрелу в мишень. Вероятности попадания для каждого стрелка соответственно равны 0,8; 0,7; 0,5. Определите вероятность того, что в мишени окажется ровно 2 пробоины.

Так как речь идет о двух попаданиях, используем формулу (6), куда подставляем значения из условия задачи:

p1=0,8,p2=0,7,p3=0,5,q1=0,2,q2=0,3,q3=0,5p1=0,8,p2=0,7,p3=0,5,q1=0,2,q2=0,3,q3=0,5

Получаем:

P2=p1⋅p2⋅q3+p1⋅q2⋅p3+q1⋅p2⋅p3==0,8⋅0,7⋅0,5+0,8⋅0,3⋅0,5+0,2⋅0,7⋅0,5=0,47.P2=p1⋅p2⋅q3+p1⋅q2⋅p3+q1⋅p2⋅p3==0,8⋅0,7⋅0,5+0,8⋅0,3⋅0,5+0,2⋅0,7⋅0,5=0,47.

Пример 6. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8; для второго и третьего орудий эти вероятности соответственно равны 0,7 и 0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.

Надеюсь, вас не смутили орудия вместо стрелков? На самом деле, не суть важно, что происходит: три стрелка вышли на линию, или три пушки готовят залп, или три снайпера целятся в одного террориста. С точки зрения теории вероятностей, все формулы остаются прежними.

Поэтому смело приступаем к решению. Требуется найти вероятность события AA= (Будет хотя бы одно попадания при одновременном залпе из всех орудий), поэтому введем для простоты расчетов противоположное событие A¯¯¯¯A¯ = (Все три орудия дали промашку), вероятность которого найдем по формуле (4), подставляя значения:

p1=0,8,p2=0,7,p3=0,9,q1=0,2,q2=0,3,q3=0,1p1=0,8,p2=0,7,p3=0,9,q1=0,2,q2=0,3,q3=0,1

Получаем:

P(A¯¯¯¯)=P0=q1⋅q2⋅q3=0,2⋅0,3⋅0,1=0,006.P(A¯)=P0=q1⋅q2⋅q3=0,2⋅0,3⋅0,1=0,006.

Искомая вероятность:

P(A)=1−P(A¯¯¯¯)=1−0,006=0,994.P(A)=1−P(A¯)=1−0,006=0,994.

Другие задачи про выстрелы и попадания

Конечно же, не все задачи про выстрелы можно решать по данным формулам (точнее, не все вписываются в эту схему напрямую), это лишь один из популярных классов задач. Для полноты изложения я приведу еще несколько типовых задач с немного отличающимся решением.

Пример 7. Вероятность того, что стрелок попадет в цель при одном выстреле, равна 0,7. Производится пять независимых выстрелов. Какова вероятность того, что в мишени окажется хотя бы одна пробоина?

Требуется найти вероятность события AA = (В мишени окажется хотя бы одна пробоина), поэтому вводим сначала противоположное событие A¯¯¯¯A¯ = (Все пять выстрелов не попали в цель). Если обозначить вероятность попадания в цель какp=0,7p=0,7 (она одинакова при каждом выстреле), а вероятность промаха как q=1−p=0,3q=1−p=0,3, то вероятность всех пяти промахов будет

P(A¯¯¯¯)=q5=0,35.P(A¯)=q5=0,35.

Искомая вероятность:

P(A)=1−P(A¯¯¯¯)=1−0,35=0,998.P(A)=1−P(A¯)=1−0,35=0,998.

Пример 8. Два стрелка стреляют по мишени по одному разу. Вероятность того, что оба попали равна 0,42, а вероятность того что оба промахнулись, 0,12. Найти вероятность попадания в мишень каждым стрелком при одном выстреле.

Если обозначить вероятности попадания первым и вторым стрелком соответственно как p1p1 и p2p2, то, используя формулы (1) и (3), запишем условие задачи в виде системы уравнений:

P2=p1⋅p2=0,42;P0=(1−p1)⋅(1−p2)=0,12.P2=p1⋅p2=0,42;P0=(1−p1)⋅(1−p2)=0,12.

Решая эту систему, найдем искомые вероятности попадания для каждого стрелка: p1=0,6p1=0,6 и p2=0,7p2=0,7 (или наоборот, p1=0,7p1=0,7 и p2=0,6p2=0,6).

Пример 9. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Если обозначить вероятность попадания в цель как pp (она одинакова при каждом выстреле), а вероятность промаха как q=1−pq=1−p, то вероятность 4 промахов при четырех выстрелах будет равна q4q4, а соответственно вероятность хотя бы одного попадания в цель при четырех выстрелах – 1−q41−q4. Получаем уравнение:

1−q4=0,9984;q4=0,0016;q=0,2;p=1−q=0,8.1−q4=0,9984;q4=0,0016;q=0,2;p=1−q=0,8.

Нашли вероятность попадания в цель при одном выстреле, она равна 0,8.

Пример 10. Два стрелка независимо выстрелили по мишени по два раза. Меткость первого стрелка равна 0,8; второго – 0,7. Найти вероятность того, что в мишень попадут все четыре пули.

Все 4 пули попадут в мишень, если первый стрелок попадет оба раза (вероятность попадания при одном выстреле у него p1=0,8p1=0,8), и одновременно второй стрелок попадет оба раза (вероятность попадания при одном выстреле у него p2=0,7p2=0,7). По правилу умножения вероятностей

P=p1⋅p1⋅p2⋅p2=0,8⋅0,8⋅0,7⋅0,7=0,3136.



Что такое независимые испытания? Практически всё понятно уже из самого названия. Пусть производится несколько испытаний. Если вероятность появления некоего события  в каждом из них не зависит от исходов остальных испытаний, то… заканчиваем фразу самостоятельно! При этом под словосочетанием «независимые испытания» часто подразумевают повторные независимые испытания – когда они осуществляются друг за другом. Простейшие примеры:

– монета подбрасывается 10 раз;
– игральная кость подбрасывается 20 раз.

Совершенно ясно, что вероятность выпадения орла либо решки в любом испытании не зависит от результатов других бросков. Аналогичное утверждение, естественно, справедливо и для кубика.  А вот последовательное извлечение карт из колоды не является серией независимых испытаний – очевидно, это цепочка зависимых событий. Однако если карту каждый раз возвращать обратно, то это тоже будут повторные независимые испытания.

И у нас в гостях очередной Терминатор, который абсолютно равнодушен к своим удачам / неудачам, и поэтому его стрельба представляет собой образец стабильности 🙂

Задача 65
Стрелок совершает 4 выстрела по мишени. Вероятность попадания при каждом выстреле постоянна и равна . Найти вероятность того, что:
а) стрелок попадёт только один раз, б) стрелок попадёт 2 раза.

Решение: условие сформулировано в общем виде и вероятность попадания в мишень при каждом выстреле считается известной. Она равна  (если совсем тяжко, присвойте параметру какое-нибудь конкретное значение, например, ).

Коль скоро мы знаем , то легко найти вероятность промаха в каждом выстреле:
, то есть, «ку» – это тоже известная нам величина.

а) Рассмотрим событие «Стрелок попадёт только один раз» и обозначим его вероятность через  (индексы понимаются как «1 попадание из 4»).  Данное событие состоит в 4 несовместных исходах: стрелок попадёт в 1-й или во 2-й, или в 3-й, или в 4-й попытке. По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:

Упростим результат с помощью комбинаторной формулы количества сочетаний:
 способами можно выбрать попытку, в которой стрелок попал, и, поскольку в каждом исходе имеет место 1 попадание и 3 промаха, то:
 – вероятность того, что стрелок попадёт только 1 раз из 4.

…как-то так «с лёгкой руки» я начал называть повторные независимые испытания «попытками», что не в каждой задаче может быть корректным в содержательном плане… …ну да ладно.
б) Рассмотрим событие «Стрелок попадёт два  раза» и обозначим его вероятность через  («2 попадания из 4»). Здесь исходов будет уже больше, попадания возможны:

в 1-й и 2-й попытках
или
в 1-й и 3-й попытках,
или
в 1-й и 4-й попытках,
или
во 2-й и 3-й попытках,
или
во 2-й и 4-й попытках,
или
в 3-й и 4-й попытках.

Таким образом, по тем же теоремам сложения и умножения вероятностей:

Можно ли так решать задачу? Безусловно, можно. Но что делать, если серия состоит из 5, 6 или бОльшего количества выстрелов? Тут уже будут получаться десятки слагаемых, запись которых отнимет много времени и места. В этой связи гораздо рациональнее придерживаться более компактной схемы:
 способами (перечислены выше) можно выбрать 2 попытки, в которых произойдут попадания.

И, поскольку в любом исходе ровно 2 попадания и 2 промаха, то:
 – вероятность того, что стрелок попадёт 2 раза из 4.

Ответ:

Итак – вероятность того, что будет 1 попадание из 4, равна , вероятность того, что будет 2 попадания из 4, равна , …не замечаете ли вы закономерности?

Только что на конкретном примере мы повторили путь Якоба Бернулли, который несколько веков назад вывел формулу, названную позже в его честь:

За примером далеко ходить не будем:

Задача 66
Найти вероятность того, что при 10 бросках монеты орёл выпадет 3 раза.

Решение: сначала немного порассуждаем: всего проводится 10 повторных независимых испытаний. Сколькими способами можно выбрать 3 испытания из 10, в которых выпадет орёл? Считаем:
 способами.

Это что же получается, нужно записывать 120 слагаемых, в каждом из которых 10 множителей?! Конечно, нет! – ведь есть формула Бернулли:

, в данном случае:

 – всего испытаний;
 – количество испытаний, в которых должен появиться орёл;
 – вероятность появления орла в каждом испытании;
 – вероятность появления решки в каждом испытании.

Таким образом:
 – вероятность того, что при 10 бросках монеты орёл выпадет ровно 3 раза.

Ответ:

Следует отметить, что повторный характер независимых испытаний не является «жизненно важным» условием для применения формулы Бернулли. Рассмотрим похожую задачу:
Найти вероятность того, что при броске 10 монет орёл выпадет на 3 монетах.

Здесь испытания не повторяются, а скорее, производятся одновременно, но, тем не менее, работает та же самая формула: .

Решение будет отличаться смыслом и некоторыми комментариями, в частности:
 способами можно выбрать 3 монеты, на которых выпадет орёл.
 – вероятность выпадения орла на каждой из 10 монет
и т.д.

Однако на практике подобные задачи встречаются не столь часто, и, видимо, по этой причине  формула Бернулли чуть ли не стереотипно ассоциируется только с повторными испытаниями. Хотя, как только что было показано, повторяемость вовсе не обязательна.
Следующая задача для самостоятельного решения:

Задача 67
Игральную кость бросают 6 раз. Найти вероятность того, что 5 очков:

а) не выпадут (выпадут 0 раз);
б) выпадут 2 раза;
в) выпадут 5 раз.

Результаты округлить до 4 знаков после запятой.

Очевидно, что в рассматриваемых примерах некоторые события более вероятны, а некоторые – менее вероятны. Так, например, при 6 бросках кубика даже безо всяких расчётов интуитивно понятно, что вероятности событий пунктов «а» и «бэ» значительно больше вероятности того, что «пятёрка» выпадет 5 раз. И на уровне интуиции легко сделать вывод, что наивероятнейшее количество появлений «пятёрки» равно единице – ведь всего граней шесть, и при 6 бросках кубика каждая из них должна выпасть в среднем по одному разу. Желающие могут вычислить вероятность  и посмотреть, будет ли она больше «конкурирующих» значений  и .

Теперь сформулируем строгий критерий на этот счёт:

Найдём наивероятнейшее число  появлений «пятёрки» при 6 бросках кубика. Сначала вычислим:
 – целое число, таким образом, это частный случай 1-го пункта и .
Как вариант, можно воспользоваться общей формулой:

 – полученному неравенству удовлетворяет единственное целое значение .
В целях закрепления материала решим пару задач:

Задача 68
Вероятность того, что при броске мяча баскетболист попадёт в корзину, равна 0,3. Найти наивероятнейшее число попаданий при 8 бросках и соответствующую вероятность.

Решение: для оценки наивероятнейшего числа попаданий используем двойное неравенство . В данном случае:

 – всего бросков;
 – вероятность попадания в корзину при каждом броске;
 – вероятность промаха при каждом броске.

Таким образом, наивероятнейшее количество попаданий при 8 бросках находится в следующих пределах:

Поскольку левая граница (1,7) – дробное число (пункт № 1 критерия – см. выше), то существует единственное наивероятнейшее значение, и, очевидно, что это .

Используя формулу Бернулли ,  вычислим вероятность того, что при 8 бросках будет ровно 2 попадания:
 

Ответ:  – наивероятнейшее количество попаданий при 8 бросках,  – соответствующая вероятность.

Аналогичное задание для самостоятельного решения:

Задача 69
Монета подбрасывает 9 раз. Найти вероятность наивероятнейшего числа появлений орла

Решение и ответ в конце книги.

А сейчас немного отвлёчёмся и рассмотрим весьма любопытную ситуацию: предположим, что во всех 9 испытаниях выпал орёл. Что, кстати, не являются каким-то уж сильно невероятным событием:  😉

Вопрос: какая сторона монеты вероятнее всего выпадет в 10-м испытании?

Как вы думаете?

…ответьте на этот вопрос и перейдите на следующую страницу.

Правильный ответ: вероятности останутся равными! Почему? Причина была сформулирована в начале параграфа: поскольку испытания независимы, то вероятность выпадения орла либо решки в любом испытании не зависит от результатов других испытаний!

Однако игры разума таковы, что у многих людей напрашивается следующий вывод: раз орёл выпал много раз подряд, то теперь выпадение решки гораздо (!) вероятнее. Этот психологический феномен получил название Ошибка игрока. Если подбрасывать монету тысячи, десятки тысяч раз, то соотношение орлов / решек будет примерно равным (о чём мы ещё поговорим). Но в этом процессе неоднократно встретятся эпизоды, когда монету «заклинит» на какой-то одной грани, и КАК ИМЕННО распределятся эти «необычные» серии на длинной дистанции – никто не знает.

К слову, о «необычности». Любая случайная последовательность девяти орлов/решек так же вероятна, как и выпадение 9 орлов! Проверить данный факт легче лёгкого: запишем произвольную последовательность исходов, например:
Орёл/Решка/Решка/Орёл /Решка/ Орёл /Решка/ Орёл /Орёл

По теореме умножения вероятностей независимых событий, вероятность появления этой цепочки:
, что в точности равно вероятности выпадения девяти орлов !

И здесь мы сталкиваемся со второй иллюзией – человек склонен считать «красивые» комбинации чем-то из ряда вон выходящим и чуть ли не фантастическим. Но на самом деле ничего необычного, например, в комбинации О/О/О/Р/Р/Р/О/О/О  – нет, и она может запросто появиться в серии испытаний.

Вероятность получить, скажем, пиковый «Ройял-флеш» в покересоставляет 1:2598960, однако мало кто задумывается, что с той же вероятностью приходит ЛЮБАЯ, в том числе, совершено «мусорная» комбинация из пяти карт! И с этой точки зрения «сверхъестественная» комбинация  10, В, Д, К, Т пик ничем не примечательна – встречалась «в истории» наряду с другими очень много раз. И поэтому «Ройял-флеш» может запросто оказаться у вас или у вашего соперника.

Кстати, к теме нашего разговора относятся и типичные ситуации в играх, в частности, в картах – когда «карта идёт», и наоборот – когда постоянно сдают «один мусор» или «фатально не везёт». Такие «полосы» встречаются у каждого игрока, и никакой мистики в этом нет. Да что там игры, в жизни то же самое – пресловутые «чёрные и белые полосы».

На просторах Интернета часто встречается популярный «секрет выигрыша» в рулетку, известный также под названием «Мартингейл». Краткая суть системы состоит в следующем: «Ставьте на красное. Если выпало чёрное, удваивайте ставку и снова ставьте на красное. Если снова выпало чёрное, то ещё раз удваивайте ставку и снова ставьте на красное и т.д.». Казалось бы – вот оно, золотое дно, ведь красных секторов целых 18 из 37! (+ 18 черных и 1 зеро в европейской рулетке). И уж «красное» должно (!) выпасть если не на 5-й, то на 10-й раз точно, что позволит отыграть всё ранее поставленное с прибылью!

Ничего подобного!

Вероятность выпадения красного сектора в любом испытании постоянна  и никак не зависит от результатов предыдущих испытаний. Постоянна – и проигрышна (т.к. поставленные на «красное» деньги с вероятностью  проигрываются, а в случае успеха удваиваются). Длинная серия «чёрного» обязательно появятся (рано или поздно) и разорит даже Билла Гейтса. Поэтому данный «секрет», как и все остальные системы игры в рулетку – не работает.

«Ошибка игрока» совершается и многими участниками лотерей. Она состоит в том, что люди пытаются предугадать числа на основе статистики предыдущих тиражей. Чистой воды химера и пустая трата времени – если, например, № 8 не выпадал 50 раз подряд, то он с таким же успехом может не выпасть ещё 150 раз (это не ирония). Однако если провести десятки тысяч тиражей, то количество появлений всех номеров будет примерно равным, но В КАКОМ ПОРЯДКЕ И КАКИМИ СЕРИЯМИ будет выпадать та же «восьмёрка» на длинной дистанции – никто предсказать не может.

А теперь ответим на один важный вопрос:

Как правильно играть в азартные игры и лотереи? – в чём главный секрет?

Наверное, многие ожидают услышать от меня что-нибудь вроде: «Лучше вообще не играть», «Открыть собственное казино», «Организовать лотерею» и т.п. Ну почему же не играть? Игра – это одно из развлечений, а за развлечения, как известно, нужно… совершенно верно! Поэтому средства, на которые вы играете, следует считать платой за развлечение, но ни в коем случае трагической потерей. Что касается лотерей, то билет лучше покупать опять же ради развлечения и наобум. Или «по наитию». Правда, лично я никогда не слышал, чтобы кто-то из «счастливчиков» рассказывал о своём предчувствии.

Естественно, перечисленные советы не относятся к хроническим лудоманам и им как раз таки «Лучше вообще не играть». И после столь увлекательного отступления рассмотрим ещё несколько задач по теме:

Задача 70
Среди изделий, произведенных на станке-автомате, в среднем бывает 60% изделий первого сорта. Какова вероятность того, что среди 6 наудачу отобранных изделий будет:

а) от 2 до 4 изделий первого сорта;
б) не менее 5 изделий первого сорта;
в) хотя бы одно изделие более низкого сорта.

Вероятность производства первосортного изделия не зависит от качества других выпущенных изделий, поэтому в задаче речь идёт о независимых испытаниях. Пожалуйста, не подходите формально и не пренебрегайте подобным анализом условия, а то может статься, события-то зависимые или задача вообще о другом.

Решение: вероятность зашифрована под проценты, которые, напоминаю, нужно разделить на сто:  – вероятность того, что выбранное изделие будет 1-го сорта. Тогда:  – вероятность того, что оно не будет первосортным.

а) Событие «Среди 6 наудачу отобранных изделий будет от 2 до 4 изделий первого сорта» состоит в трёх несовместных исходах: среди  изделий будет 2 первосортных или 3 первосортных, или 4 первосортных.

С исходами удобнее разделаться по отдельности. Трижды используем формулу Бернулли :

 

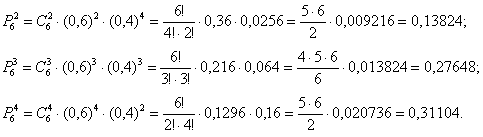
По теореме сложения вероятностей несовместных событий:
 – вероятность того, что среди 6 наудачу отобранных изделий будет от 2 до 4 изделий первого сорта.

Решение можно было записать и «одной строкой», что мы и сделаем в следующем пункте:

б) Событие «Среди 6 наудачу отобранных изделий будет не менее 5 изделий первого сорта» состоит в двух несовместных исходах: первосортных изделий будет пять или шесть. По формуле Бернулли и теореме сложения вероятностей несовместных событий:

 – искомая вероятность.

в) Вероятность того, что «Среди 6 наудачу отобранных изделий будет хотя бы одно изделие более низкого сорта» удобно найти через вероятность противоположного события («Все изделия будут первосортными»), которая уже известна:

 – вероятность того, что среди шести отобранных изделий окажется хотя бы одно низкосортное.

Ответ: , и подобных задач пруд пруди.

Давайте заодно вспомним такое полезное понятие, как полная группа событий. Что осталось не найденным? Остались не найденными вероятности двух событий. Не хотел я лишний раз заострять внимание на Калькуляторе по теории вероятностей, который приложен к книге, но быстроты ради воспользуюсь:

 – но на чистовике так, конечно, делать не нужно – обязательно расписывайте вычисления подробно!

Проверка:
,
что и требовалось проверить

Небольшое задание для самостоятельного решения:

Задача 71
Производится 8 выстрелов по цели, в каждом из которых вероятность попадания равна 0,1. Для разрушения цели требуется хотя бы два попадания. Найти вероятность того, что цель будет разрушена

Формула Бернулли очень удобна, но с другой стороны, обладает и рядом недостатков. В частности, при достаточно больших значениях  и  её применение затруднено ввиду огромных значений факториалов. В этом случае используют теоремы Лапласа. В другой распространённой на практике ситуации вероятность  достаточно мала, а количество испытаний  весьма велико. Здесь вопрос разрешается с помощью формулы Пуассона, с неё и начнём:

1.10. Формула Пуассона

1.8. Формулы Байеса

| Оглавление |



Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

забыли пароль? Помощь сайту

Задачи о выстрелах и вероятность попадания в мишень создана: 25.01.2023 в 00:14 …………………………………………  ( +3188 )  liliana : Вероятность попадания стрелком в мишень при каждом выстреле не зависит от результатов предыдущих выстрелов и равна 0,8. Стрелок сделал 5 выстрелов. Найти вероятности следующих событий: а) мишень поражена одной пулей; б) мишень поражена двумя пулями;  в) зарегистрировано хотя бы одно попадание; г) зарегистрировано не менее трех попаданий. Решение. Вероятность попадания при одном выстреле равна 0.8, а вероятность не попадания равна 0,2. а) По ф-ле Бернулли Р=0,8*0,24 *С51=0,8*0,24*5 =0,0064  (1 раз попал и 4 раза не попал) б) По формуле Бернулли Р=0,8*0,8*0,23  *C52 = 0,82*0,23*5!/(3!*2!)=0,0512 в) Рассмотрим противоположное событие – не попал ни разу р=0,25.   Тогда вероятность попадания хотя бы 1 раз равна Р= 1- 0,25     г) не менее трех означает, что  попал 3 или 4 или 5 раз Р = С53*0,83*0,32 + С54*0,84*0,21 + 0,85 Хочу написать ответ