Как найти вероятность разрыва цепи

Как решать задачи о прохождении тока через электрические схемы

В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про подбрасывания игральных кубиков и монеток, задачи про стрелков и станки.

В этой статье мы рассмотрим задачи вида
“задана схема электрической цепи с надежностью элементов (или вероятностями выхода из строя), найти вероятность работы цепи (или вероятность разрыва цепи)”.

Задачи могут иметь чуть разные формулировки, но принцип решения для них одинаков, и его мы изучим, чтобы суметь решать такие задачи со схемами любой сложности.

Далее:

• Базовые события, обозначения и формулы
• Последовательно или параллельно?
• Усложняем схему цепи
• Примеры решений
• На закуску: схема с мостиком
• Полезные ссылки
• Решебник

Базовые события, обозначения и формулы

Самое первое, с чего мы начнем – формализация задачи (и решение любой своей задачи рекомендую начинать с этого). А именно, мы введем основные события:

$X$ = (Цепь работает) = (Цепь пропускает ток) и противоположное ему:

$overline{X}$ =(Цепь не пропускает ток) = (Произошел разрыв в цепи).

$A_i$ = (Элемент i работает, пропускает ток) и $overline{A_i}$ =(Элемент i отказал, не пропускает ток), $i=1,2,…,n$.

Обычно в условии задачи известны вероятности работы элементов (надежности): $p(A_i)=p_i$ или вероятности отказа $p(overline{A_i})=q_i=1-p_i$, $i=1,2,…,n$.

Также напомним основные формулы (из темы действий с событиями, формулы сложения и умножения вероятностей), которые пригодятся в решении этого типа задач.

Для независимых в совокупности событий (а отказы/работа элементов цепи – именно такие):

$$
P(A cdot B) = P(A) cdot P(B); quad(1)
$$
$$
P(A+B) = P(A)+P(B)-P(A)cdot P(B); quad(2)
$$
$$
P(A_1+A_2+…+A_n)=1-P(overline{A_1})cdot P(overline{A_2})cdot … cdot P(overline{A_n}). quad(3)
$$

Последовательно или параллельно?

Еще немного времени посвятим теории, вспомним о том, как могут соединяться элементы в цепи.

Последовательное соединение

Элементы цепи “нанизаны” на провод один за другим (следуют один за другим, отсюда и “последовательно”). Если откажет один любой – ток в цепи прервётся. Или, иначе говоря, цепь работает тогда и только тогда, когда ВСЕ элементы работают. В терминах теории вероятностей получаем произведение событий: $X=A_1 cdot A_2 cdot A_3$, а вероятность работы цепи равна

$$
P(X)=P(A_1 cdot A_2 cdot A_3)= P(A_1) cdot P(A_2) cdot P(A_3) =p_1 cdot p_2 cdot p_3.
$$

Если в цепи последовательно соединены не три, а больше независимо работающих элементов, формула легко обобщается и получаем:

$$
P(X) = p_1 cdot p_2 cdot …cdot p_n; qquad P(overline{X})=1-p_1 cdot p_2 cdot …cdot p_n. quad(4)
$$

Параллельное соединение

Тут тоже сама схема дает нам подсказку, когда мы видим, что элементы в схеме расположены как бы на параллельных проводах, речь идет о параллельном соединении.

В этом случае если откажет, скажем, элемент 1, ток может пройти через 2. Если откажут 1 и 2, ток пройдет через 3. И только если ВСЕ элементы откажут, цепь разорвется.

Еще говорят, цепь работает, если работает хотя бы один элемент в ней, в терминах теории вероятностей – это сумма событий: $X=A_1+A_2+A_3$.

Используем формулу (3) чтобы записать вероятность работы такой цепи:

$$
P(A_1+A_2+A_3)=1-P(overline{A_1})cdot P(overline{A_2}) cdot P(overline{A_3})=1-q_1 cdot q_2 cdot q_3.
$$

И обобщим на случай $n$ параллельных элементов в цепи:

$$
P(X) = 1-q_1 cdot q_2 cdot …cdot q_n; qquad P(overline{X})=q_1 cdot q_2 cdot …cdot q_n. quad(5)
$$

Важно запомнить правило

Последовательному соединению соответствует произведение событий,
параллельному соединению – сумма событий.

Усложняем схему цепи

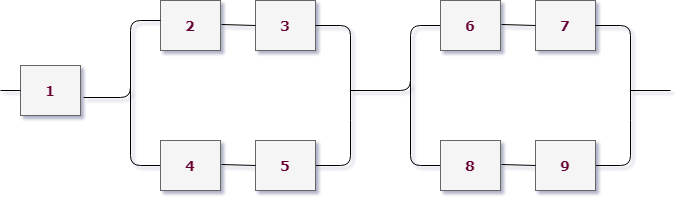
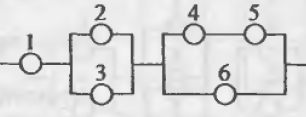
И все это была присказка к настоящему решению задач. Конечно, даже если у вас простая контрольная, схема с “тремя лампочками подряд” вряд ли попадется. Давайте посмотрим на типовые электрические схемы, для которых надо находить надежность в задачах:

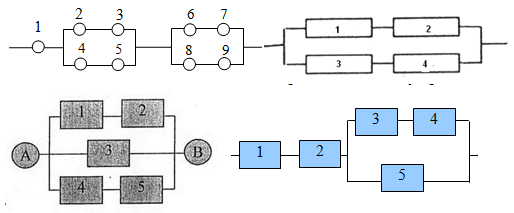
Как для таких схем выписывать вероятности? Нам нужно научиться делать декомпозицию: выделять уровни схемы и определять тип соединения на каждом уровне.

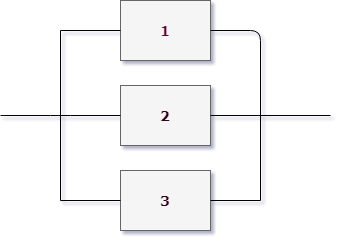
Возьмем для примера левую верхнюю схему:

Работаем с первым уровнем схемы. Нужно мысленно выделить крупные части, которые между собой соединены одинаково (параллельно или последовательно). В данном случае видно три группы элементов, соединенных последовательно. Выделим для наглядности цветом:

То есть тип схемы на первом уровне – последовательный:

Как мы уже знаем, если соединение последовательное, нужно перемножать события, то есть

$$
X=X_1 cdot X_2 cdot X_3,
$$

$X_1$ – работает первая группа элементов,
$X_2$ – работает вторая группа элементов,
$X_3$ – работает третья группа элементов.

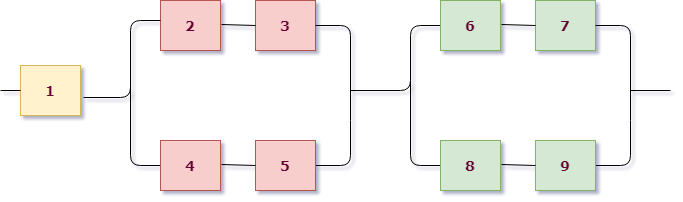
Теперь смотрим на каждую группу. В первой группе всего один элемент, то есть она работает, когда работает первый элемент цепи ($X_1=A_1$). Мы дошли до элемента, разбор этой группы закончен.

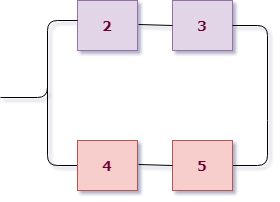
А вот дальше интереснее. Рассмотрим поближе вторую группу:

В ней сразу выделим цветом подгруппы элементов. Видно, что вторая группа имеет уже параллельную структуру из розовых и фиолетовых элементов (они “висят” на параллельных линиях, это второй уровень вложенности схемы). А вот внутри розовые соединены последовательно (розовая группа работает – $A_4 cdot A_5$), фиолетовые элементы также между собой последовательно (фиолетовая группа работает – $A_2 cdot A_3$). Это уже третий уровень вложенности и он заканчивается отдельными элементами, значит, разбор окончен.

Так как розовая и фиолетовая группа соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:

$$X_2 = A_2 cdot A_3 + A_4 cdot A_5.$$

Абсолютно аналогично разбирается третья подгруппа (она совпадает по структуре со второй):

$$X_3 = A_6 cdot A_7 + A_8 cdot A_9.$$

Сводим все в одну формулу и выпишем искомое событие (Цепь работает исправно):

$$
X=X_1 cdot X_2 cdot X_3 = A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right).
$$

Теперь переходим ко второму этапу решения задачи. Не забываем, что мы решаем задачу по теории вероятностей и надо определить вероятность того, что ток проходит в цепи. Будем использовать формулы (1)-(3).

Так как вероятность произведения для независимых событий равна произведению вероятностей, получим:

$$
P(X)= P left( A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right) right) =\
= P (A_1) cdot P left ( A_2 cdot A_3 + A_4 cdot A_5 right ) cdot P left( A_6 cdot A_7 + A_8 cdot A_9right) =
$$

Для множителей с суммой событий внутри используем формулу (2):

$$
= P (A_1) cdot left[ P(A_2 cdot A_3) + P(A_4 cdot A_5) – P(A_2 cdot A_3 cdot A_4 cdot A_5) right] cdot left[ P(A_6 cdot A_7) + P(A_8 cdot A_9) – P(A_6 cdot A_7 cdot A_8 cdot A_9)right] =
$$

И снова раскрываем вероятности произведений:

$$
= P (A_1) cdot left[ P(A_2) cdot P(A_3) + P(A_4) cdot P(A_5) – P(A_2) cdot P(A_3) cdot P(A_4) cdot P(A_5) right] cdot left[ P(A_6) cdot P(A_7) + P(A_8) cdot P(A_9) – P(A_6) cdot P(A_7) cdot P(A_8) cdot P(A_9)right].
$$

Перейдем к более компактной записи, положив $p_i=P(A_i)$:

$$
P(X)= p_1 cdot left[ p_2 cdot p_3 + p_4 cdot p_5 – p_2 cdot p_3 cdot p_4 cdot p_5 right] cdot left[ p_6 cdot p_7 + p_8 cdot p_9 – p_6 cdot p_7 cdot p_8 cdot p_9right].
$$

Если заданы надежности отдельных элементов $p_i$, подставляя их в формулу, можно найти вероятность работы схемы.

Алгоритм разбора схемы

• Выделяем в схеме основу: группы элементов, соединенные ТОЛЬКО последовательно или ТОЛЬКО параллельно между собой. Это верхний уровень. Записываем событие $X$ = (Цепь работает) как произведение или сумму соответственно.
• Каждую полученную группу анализируем также: ищем в ней подгруппы, соединенные только последовательно или только параллельно. Записываем событие соответственно типу соединения.
• Продолжаем до тех пор, пока не опустимся на уровень элементов (событий $A_i$).
• Подставляем все выражения в исходную формулу, получаем итоговую запись события $X$.
• Пользуясь формулами (1)-(3) выписываем вероятность события $P=P(X)$.
• Подставляем числовые значения $p_i, q_i$ и находим численное значение надежности схемы $P$.
• Если необходимо, находим вероятность отказа цепи $1-P$.

Примеры решений

Отработаем несколько раз этот алгоритм на примерах, чтобы он закрепился.

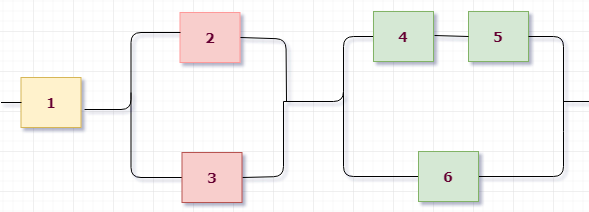
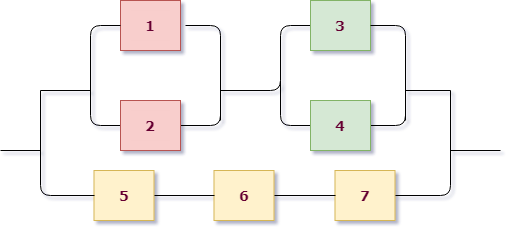
Пример 1. Дана схема включения элементов. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведенной схеме. Пусть событие $А_i$ означает безотказную работу за время Т элемента с номером $i$ ($i=1,2,3,…$), а событие $В$ – безотказную работу цепи. Требуется:
1) Написать формулу, выражающую событие $В$ через все события $А_i$.
2) Найти вероятность события $B$.
3) Вычислить $Р(В)$ при $р=0,6$.

Приступим к разбору схемы. Можно увидеть, что на первом уровне мы имеем три группы, соединенные последовательно: (1), (2,3) и (4,5,6) элементы. Выделим их цветом для наглядности:

Значит, исходное событие можно представить в виде произведения трех событий $B=B_1 cdot B_2 cdot B_3$, где $B_i$ – работает $i$-aя группа элементов.

Первая группа элементов состоит из одного элемента, то есть $B_1=A_1$.

Вторая группа элементов состоит из двух элементов, соединенных параллельно (см. розовые), поэтому $B_2=A_2+A_3$.

Третья группа элементов (см. зеленые) состоит из трех элементов, ее можно представить как параллельное соединение двух подгрупп: (4 и 5, соединены последовательно) и (6), поэтому $B_3=A_4 cdot A_5 + A_6$.

Подставляем все и получаем выражение для события $B$

$$
B=B_1 cdot B_2 cdot B_3 = A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6).
$$

Теперь выразим вероятность безотказной работы цепи за время T. Сначала применим формулу (1), чтобы раскрыть произведение:

$$
P(B)=P left( A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6) right) = P(A_1) cdot P left( A_2+A_3 right) cdot P left( A_4 cdot A_5 + A_6 right) =
$$

Раскроем вторую вероятность по формуле (3), а третью по формуле (2), получим:

$$= P(A_1) cdot left(1 – P(overline{A_2}) cdot P(overline{A_3}) right) cdot left( P(A_4) cdot P(A_5) + P(A_6) – P(A_4) cdot P(A_5) cdot P(A_6) right).$$

Подставляем $P(A_i)=p$ и получим:

$$
p(B)=pcdot(1-(1-p)cdot(1-p))cdot(pcdot p + p -p cdot p cdot p) = pcdotleft(1-(1-p)^2right)cdot left(p+p^2-p^3right).
$$

Осталось только найти значение при $p=0,6$:

$$
p(B)= 0,6cdotleft(1-(1-0,6)^2right)cdot left(0,6+0,6^2-0,6^3right) approx 0,375.
$$

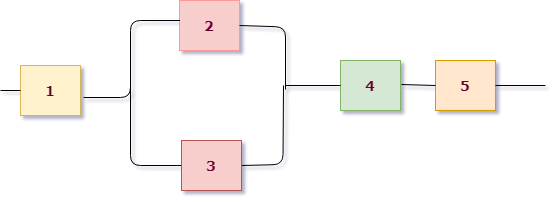
Пример 2. Найти вероятность обрыва цепи, если вероятность отказа каждого элемента равна 0,2, а отказы элементов – независимые события.

Пронумеруем элементы и сразу раскрасим схему, чтобы выделить ее структуру.

Это опять последовательная схема, но розовая группа состоит из двух элементов, соединенных параллельно, поэтому можем сразу выписать:

$$
X= A_1 cdot (A_2+A_3) cdot A_4 cdot A_5.
$$

Найдем вероятность этого события (работы цепи):

$$
P(X)= P left( A_1 cdot (A_2+A_3) cdot A_4 cdot A_5 right)= P(A_1) cdot P(A_2+A_3) cdot P(A_4) cdot P(A_5)= \
= P(A_1) cdot left( 1- P(overline{A_2}) cdot P(overline{A_3}) right) cdot P(A_4) cdot P(A_5).
$$

Вероятности отказа элементов цепи равна 0,2, вероятность работы элементов – 0,8, поэтому

$$
P(X)= 0,8 cdot left( 1- 0,2 cdot 0,2 right) cdot 0,8 cdot 0,8 = 0,492.
$$

Но в задаче требовалось найти вероятность обрыва цепи, это противоположное событие:

$$
P(overline{X}) = 1- P(X) = 1-0,492 = 0,508.
$$

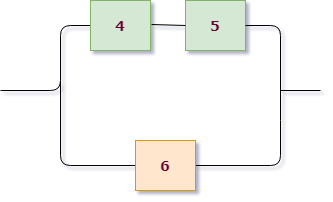
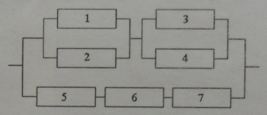
Пример 3. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность надежной работы элементов равна $p_1=p_2=p_3=p_4=0,8$, $p_5=p_6=p_7=0,9$.

Приступим к решению, сразу раскрасив схему. В этот раз схема на первом уровне имеет параллельное соединение: верхняя розово-зеленая группа и нижняя желтая находятся на параллельных линиях. Поэтому $X=X_1+X_2$, где $X_1$ – работает розово-зеленая линия, $X_2$ – работает желтая.

Для желтой группы, состоящей из трех последовательно расположенных элементов, сразу выписываем $X_2=A_5 cdot A_6 cdot A_7$.

Теперь рассмотрим верхнюю группу. Она состоит из двух подгрупп, связанных последовательно: розовой и зеленой. При этом каждая из них состоит из двух параллельно соединенных элементов. Записываем: розовая группа работает = $A_1+A_2$, зеленая группа работает = $A_3+A_4$, значит ток проходит через розово-зеленую группу $X_1 =(A_1+A_2) cdot (A_3+A_4)$.

Объединяем рассуждения и выписываем событие, соответствующее безотказной работе цепи:

$$
X=X_1+X_2 = (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7.
$$

Следующий шаг: выразить вероятность этого события. Во всех предыдущих примерах схема на первом уровне была последовательной, и событие выражалось как произведение. В этом случае схема на первом уровне параллельна, событие выглядит как сумма других событий, что немного усложняет выкладки. Для суммы событий можно использовать формулу (2) или (3), выбирая наиболее удобную в каждом конкретном случае.

В данном случае слагаемых всего два, поэтому возьмем формулу (2):

$$
P(X)= P left( (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7 right) = \
= P left( (A_1+A_2) cdot (A_3+A_4) right) + P left( A_5 cdot A_6 cdot A_7 right) – P left( (A_1+A_2) cdot (A_3+A_4) cdot A_5 cdot A_6 cdot A_7 right)
$$

Раскрываем все произведения по формуле (1):

$$
= P (A_1+A_2) cdot P(A_3+A_4) + P(A_5) cdot P(A_6) cdot P(A_7) – P (A_1+A_2) cdot P(A_3+A_4) cdot P(A_5) cdot P(A_6) cdot P(A_7) =
$$

По формуле (3) расписываем $P(A_1+A_2)=1-P(overline{A_1}) cdot P(overline{A_2}) = 1-q_1cdot q_2$ и $P(A_3+A_4)=1-P(overline{A_3}) cdot P(overline{A_4})= 1-q_3cdot q_4$.

Итого:

$$
P(X)= (1-q_1cdot q_2) cdot (1-q_3cdot q_4) + p_5 cdot p_6 cdot p_7 – \- (1-q_1cdot q_2) cdot (1-q_3cdot q_4) cdot p_5 cdot p_6 cdot p_7.
$$

Подставляем значения надежности элементов:

$$
P(X)= (1-0,2^2)^2 + 0,9^3 – (1-0,2^2)^2 cdot 0,9^3 approx 0,9788.
$$

Еще: другие уроки о решении задач по вероятности

На закуску: схема с мостиком

Для 99% учебных задач вам хватит той теории и примеров, что приведены выше: подробно изучите их и приступайте к своим примерам по аналогии. Но есть такие схемы, для которых нельзя выделить единую структуру на верхнем уровне – параллельную или последовательную, и весь алгоритм решения рушится.

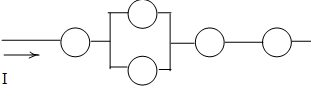
Речь идет о схемах смешанного типа, еще их часто называют схемами с мостиком (мостиковые схемы). Типичная схема имеет такой вид:

Видно, что как ни крути, схему нельзя отнести ни к последовательным, ни к параллельным. Элемент №5 (мостик) “портит” тип схемы. Если его убрать (разорвать этот участок цепи), получим обычную параллельную структуру, а если предположить, что через этот участок всегда идет ток – последовательную (конкретные схемы изобразим ниже).

Поэтому для решения задачи о вычислении надежности подобной электросхемы используют формулу полной вероятности в форме теоремы разложения (см. подробнее тут, стр. 118)

Надежность цепи с избыточностью равна произведению вероятности безотказной работы $i$-го элемента цепи на вероятность безотказной работы оставшейся цепи (места подключения $i$-го элемента замкнуты накоротко) плюс произведение вероятности отказа того же $i$-го элемента на вероятность безотказной работы оставшейся цеии (места подключения $i$-го элемента разомкнуты).

То есть, для выделенного на схеме элемента-мостика рассматриваем две гипотезы:
$H_1$ = (Элемент 5 не пропускает ток), $P(H_1)=1- p_5 = q_5$;
$H_2$ = (Элемент 5 пропускает ток), $P(H_2)=p_5$.

Далее вычисляем надежность схемы при условии верности каждой из гипотез. Для наглядности нарисуем обе схемы:

Рассмотрим левую схему, верную при гипотезе $H_1$, через нее проходит ток, если $X|H_1 = A_1cdot A_3+ A_2cdot A_4$, вероятность

$$
P(X|H_1) = P(A_1cdot A_3+ A_2cdot A_4)= P(A_1cdot A_3)+ P(A_2cdot A_4) – P(A_1cdot A_3 cdot A_2cdot A_4)=\
=p_1 cdot p_3 + p_2 cdot p_4 – p_1 cdot p_2 cdot p_3 cdot p_4.
$$

Рассмотрим правую схему, верную при гипотезе $H_2$, и выпишем для нее аналогично событие и вероятность прохода тока:

$$
X|H_2 = (A_1+A_2)cdot (A_3+A_4),\
P(X|H_2) =P( (A_1+A_2)cdot (A_3+A_4)) = P(A_1+A_2)cdot P(A_3+A_4)=\ = (1-P(overline{A_1}) cdot P(overline{A_2})) cdot (1-P(overline{A_3}) cdot P(overline{A_4})) = (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$

Тогда по формуле полной вероятности, надежность схемы равна:

$$
P(X)=P(X|H_1)cdot P(H_1) + P(X|H_2)cdot P(H_2) = \
= q_5 (p_1 cdot p_3 + p_2 cdot p_4 – p_1 cdot p_2 cdot p_3 cdot p_4) + p_5 (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$

Аналогичным образом можно разбирать более сложные схемы (в которые более одного мостика), применяя на каждом этапе формулу полной вероятности (как бы вкладывая одну в другую).

Полезные ссылки по ТВ

Онлайн калькуляторы Онлайн учебник Более 200 примеров Решенные контрольные

Формулы и таблицы Сдача тестов Решение на заказ Онлайн помощь

Решебник по вероятности

А здесь вы найдете разные задачи по теории вероятностей с полными решениями (вводите часть текста для поиска своей задачи):

Пример 3.1. Разрыв
электрической цепи происходит в том
случае, когда выходит из строя хотя бы
один из трех последовательно соединенных
элементов. Определить вероятность того,
что не будет разрыва цепи, если элементы
выходят из строя соответственно с
вероятностями 0,3; 0,4 и 0,6. Как изменится
искомая вероятность, если первый элемент
не выходит из строя?

Решение.

Введем в рассмотрение
событие А,
состоящее в том, что не будет разрыва
цепи. Искомая вероятность равна
вероятности того, что не выйдут из строя
все три элемента. Пусть событие A_k
означает, что k-й
элемент не выйдет из строя (k=1,
2, 3). Тогда

A=A₁
A₂
A₃,
т.е. P(A)
= Р(A₁
A₂
A₃).

Так как события
независимы, то

P(A)=Р(A₁)Р(A₂)Р(A₃)=0,7*0,6*0,4=0,168.

Если первый элемент
не выходит из строя, то

p=Р(A₂
A₃)=0,24.

Пример
3.2. Определить
вероятность того, что выбранное наудачу
изделие является первосортным, если
известно, что 4% всей продукции являются
браком, а 75% небракованных изделий
удовлетворяют требованиям первого
сорта.

Решение.

Пусть событие А
состоит в том, что выбранное изделие
небракованное, а событие В—
в том, что выбранное изделие первосортное.

Дано:

Р (A)
=1—0,04 =0,96,

Р(B|A)
= 0,75.

Искомая вероятность
p
= Р(АВ)
= 0,96*0,75 = 0,72.

Пример 3.3. Партия
из ста деталей подвергается выборочному
контролю. Условием непригодности всей
партии является наличие хотя бы одной
бракованной детали среди пяти проверяемых.
Какова вероятность для данной партии
быть непринятой, если она содержит 5%
неисправных деталей?

Решение.

Введем в рассмотрение
событие А,
состоящее в том, что в партии является
в наличии хотя бы одна бракованная
деталь среди пяти проверяемых.

Найдем вероятность
q
противоположного события
,
которое заключается в том, что партия
деталей будет принята. Данное событие
является произведением пяти событий

А
= А₁А₂А₃А₄А₅
,

где A_k
(k
= 1, 2, 3, 4, 5)
означает, что k-я
проверенная деталь доброкачественная.

Вероятность события
A₁
равна

P(A₁)=,

так как всего
деталей 100, а исправных 95.

После осуществления
события A₁
деталей останется 99, среди которых
исправных 94, поэтому

Р(A₂|A₁)=
.

Аналогично

Р(A₃|
A₂A₁)=
,

Р(A₄|
A₃A₂A₁)=
,

Р(A₅|
A₄A₃
A₂A₁)=
.

По общей формуле
находим

Искомая вероятность
=l—q
= 0,23.

3.4. Задачи для самостоятельной работы

3.1. Два стрелка,
для которых вероятности попадания в
мишень равны соответственно 0,7 и 0,8,
производят по одному выстрелу. Определить
вероятность хотя бы одного попадания
в мишень.

(Ответ:
p
= 0.94)

3.2. Вероятность
выхода из строя k-го
блока вычислительной машины за время
Т
равна p_k,
(k=l,
2, …, n).
Определить вероятность выхода из строя
за указанный промежуток времени хотя
бы одного из n
блоков этой машины, если работа всех
блоков взаимно независима.

(Ответ:
p
=
)

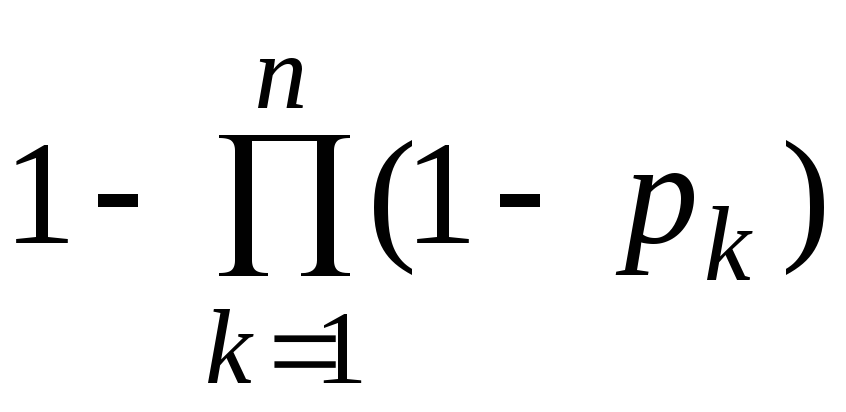
3.3. Вероятность
наступления события в каждом опыте
одинакова и равна 0,2. Опыты производятся
последовательно до наступления события.
Определить вероятность того, что придется
производить четвертый опыт.

(Ответ:
p
= 0.512)

3.4. Вероятность
того, что изготовленная на первом станке,
деталь будет первосортной, равна 0,7. При
изготовлении такой же детали на втором
станке эта вероятность равна 0,8. На
первом станке изготовлены две детали,
на втором три. Найти вероятность того,
что все детали первосортные.

(Ответ:
p
= 0.251)

3.5. Разрыв
электрической цепи может произойти
вследствие выхода из строя элемента К
или двух элементов K₁
и К₂,
которые выходят из строя независимо
друг от друга соответственно с
вероятностями 0,3; 0,2 и 0,2. Определить
вероятность разрыва электрической
цепи.

(Ответ:
p
= 0.328)

3.6. Вероятность
того, что в результате четырех независимых
опытов событие А
произойдет хотя бы один раз, равна
половине. Определить вероятность
появления события при одном опыте, если
она во всех опытах остается неизменной.

(Ответ:
p

3.7. В круг радиуса
R
вписан равносторонний треугольник.
Какова вероятность того, что четыре
наугад поставленные в данном круге
точки окажутся внутри треугольника?

(Ответ:
p
=
)

3.8. События A
и В
несовместны, Р(A)0
и Р(B).
Зависимы ли данные события?

(Ответ:
События зависимы)

3.9. На участке АВ
для мотоциклиста-гонщика имеются 12
препятствий, вероятность остановки на
каждом из которых равна 0,1. Вероятность
того, что от пункта В
до конечного пункта С
мотоциклист проедет без остановки,
равна 0,7. Определить вероятность того,
что на участке АС
не будет ни одной остановки.

(Ответ:
p
= 0,197)

3.10. Три игрока
играют на следующих условиях. Сначала
против первого последовательно ходят
второй и третий игроки. При этом первый
игрок не выигрывает, а вероятности
выигрыша для второго и третьего игроков
одинаковы и равны 0,3. Если первый игрок
не проигрывает, то он делает по одному
ходу против второго и третьего игроков
и выигрывает у каждого из них с вероятностью
0,4. После этого игра заканчивается.
Определить вероятность того, что в
результате такой игры первый игрок
выиграет хотя бы у одного партнера.

(Ответ:
p
=
0,314)

3.11. Вероятность
поражения первой мишени для данного
стрелка равна 2/3. Если при первом выстреле
зафиксировано попадание, то стрелок
получает право на второй выстрел по
другой мишени. Вероятность поражения
обеих мишеней при двух выстрелах равна
0,5. Определить вероят­ность поражения
второй мишени.

(Ответ:
p
=0,75 )

3.12. С помощью шести
карточек, на которых написано по одной
букве, составлено слово «карета».
Карточки перемешиваются, а затем наугад
извлекаются по одной. Какова вероятность,
что в порядке поступления букв образуется
слово «ракета»?

(Ответ:
p
=
)

3.13. Абонент забыл
последнюю цифру номера телефона и потому
набирает ее наудачу. Определить
вероятность того, что ему придется
звонить не более, чем в три места. Как
изменится вероятность, если известно,
что последняя цифра нечетная?

(Ответ:
p
=
;
если известно, что последняя цифра
нечетная, то p
=
)

3.14. В обществе из
2n
человек одинаковое число мужчин и
женщин. Места за столом занимаются
наудачу. Определить вероятность того,
что два лица одного пола не займут места
рядом.

(Ответ:
p
=
)

3.15. Общество,
состоящее из пяти мужчин и десяти женщин,
наудачу разбивается на пять групп по
три человека. Найти вероятность того,
что в каждой группе будет по одному
мужчине.

(Ответ:
p
=)

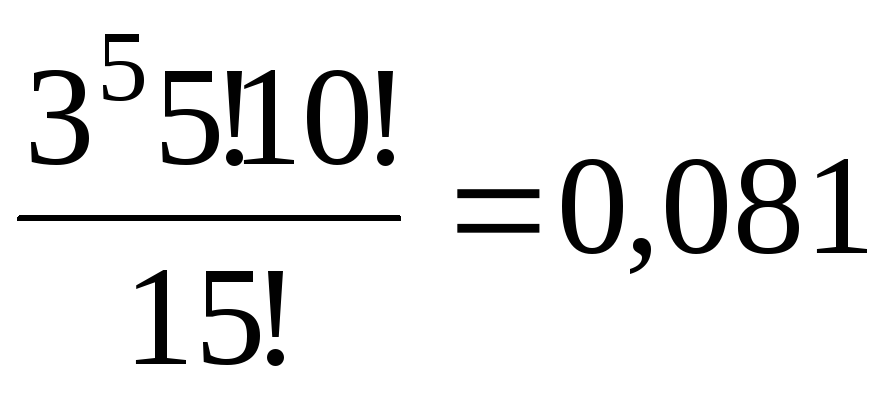
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Помогите с математикой,пожалуйста!

мариша

Профи

(522),
на голосовании

12 лет назад

Разрыв электрической цепи происходит в том случае, когда выходит из строя хотя бы один из трех последовательно соединенных элементов. Определить вероятность того, что не будет разрыва цепи, если известно, что элементы выходят из строя соответственно с вероятностями 0.3, 0.4 и 0.6. Как изменится вероятность, если первый элемент не выходит из строя?

Найти вероятность разрыва цепи

11.03.2018, 09:43. Показов 18287. Ответов 3

---

0

В задачах, использующих вероятностные количественные характеристики, приходится по вероятностям одних событий оценивать вероятности других событий. Для этого используются различные соотношения, в основе которых лежат теоремы сложения и умножения вероятностей.

Событие А называется независимым от события В, если вероятность появления события А не зависит от того, произошло событие В или нет; в противном случае такие события называются зависимыми. Например, вероятность события того, что во второй раз из урны, содержащей белые и черные шары, будет вынут белый шар, не зависит от того, какой шар был вынут в первый раз, если он был возвращен обратно. Однако если первый шар не был возвращен обратно, то результат второго извлечения уже будет зависеть от первого, ибо состав шаров в урне уже изменится в зависимости от результата первого извлечения.

Вероятность произведения независимых событий A и B равна произведению вероятностей этих событий:

. (16.1)

Пример 16.1. Алмазы, возможно, вскоре станут использовать в качестве полупроводников в спутниках связи. Эксперты предсказывают, что алмазные микросхемы будут более быстродействующими, термо – и радиационностойкими, что особенно важно для приборов, работающих в космосе. По оценкам экспертов, вероятности этих трех событий равны 0,9; 0,9 и 0,95 соответственно. Предполагается, что обсуждением проекта по разработке алмазных микросхем стоит вести лишь в том случае, если имеется хотя бы 70% уверенности в том, что они будут обладать всеми тремя указанными свойствами. Должен ли обсуждаться проект?

Решение. Пусть A – событие, состоящее в том, что алмазные микросхемы будут более быстродействующими, B – событие, состоящее в том, что алмазные микросхемы будут более термостойкими, C – событие, состоящее в том, что алмазные микросхемы будут более радиационностойкими. Поскольку события A, B и С независимы, то, используя теорему умножения вероятностей (2.3), получим

.

Таким образом, поскольку 0,7695>0,7, то предложенный проект следует обсуждать.

Пример 16.2. Дана электрическая цепь:

Вероятность выхода из строя элемента А равна 0,1, элемента В – 0,2, элемента С – 0,3. Найти вероятность разрыва цепи.

Решение. В данном случае разрыв цепи произойдет только тогда, когда выйдут из строя все элементы цепи, т. е. и элемент А, и элемент В, и элемент С. При помощи алгебры событий разрыв цепи можно описать следующим образом: . Поскольку эти события независимы, то

Вероятность события A, вычисленная при условии, что имело место другое событие B, называется условной вероятностью события A и обозначается или .

Вероятность произведения двух событий A и B равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже имело место:

. (16.2)

Пример 16.3. Одна из наиболее сложных проблем рыночных исследований – отказ потребителей отвечать на вопросы о потребительских предпочтениях, либо, если опрос проводится по месту жительства, – отсутствие их дома на момент опроса. Предположим, что исследователь рынка с вероятностью в 0,94 верит, респондент согласится отвечать на вопросы анкеты, если окажется дома. Он также полагает, что вероятность того, что этот человек будет дома, равна 0,65. Имея такие данные, оцените процент заполненных анкет.

Решение. Пусть A – событие того, что респондент окажется дома. Вероятность этого события . Пусть B – событие того, что респондент согласится отвечать на вопросы. По условию задачи задана условная вероятность , т. е. вероятность того, что он согласится отвечать на вопросы, если он будет дома. Тогда, согласно теореме умножения вероятностей зависимых событий (2.4), вероятность того, что человек будет дома и согласится отвечать на вопросы, будет равна

,

Т. е. процент заполненных анкет будет равен 61%.

Пример 16.4. Вероятность попадания в цель при отдельном выстреле (событие А) равна 0,8. Какова вероятность поражения цели, если в 2% случаях бывают осечки, т. е. в 2% случаях выстрела не происходит?

Решение. Пусть событие В состоит в том, что выстрел произошел, тогда событие означает противоположное событие, т. е. что произошла осечка. По условию P()=0,02, отсюда получаем P(B)=1–P()=0,98. По условию задачи PB(A)=0,8. Поражение цели означает совмещение событий В и А, т. е. что выстрел произойдет и даст попадание. Поэтому

P(AB) = P(B)PB(A) = 0,98×0,8 = 0,784.

Пример 16.5. В коробке девять одинаковых радиоламп, три из которых были в употреблении. В течение рабочего дня мастеру для ремонта пришлось взять две радиолампы. Какова вероятность того, что обе радиолампы были в употреблении?

Решение. Вероятность того, что первая взятая радиолампа была в употреблении (событие А), равна P(A)=3/9. После того как событие А произошло в коробке осталось 8 радиолам, из которых две были в употреблении. Поэтому для события В, состоящего в том, что вторая радиолампа была в употреблении, условная вероятность PA(B)=2/8. Следовательно, вероятность появления двух ламп, бывших в употреблении, равна:

P(AB) = P(A)PA(B) = .

Заметим, что данную задачу можно решить и комбинаторным способом:

P(AB) = .

Понятие условной вероятности позволяет естественным образом определить независимость событий. Говорят, что событие А независимо от события В, если имеет место равенство

PB(A) = P(A),

Т. е. если наступление события В не влияет на вероятность наступления события А. Если событие А не зависит от В, то и событие В также не зависит от А. Таким образом, свойство независимости взаимно. Поэтому за определение независимости двух событий А и В можно принять условие (16.1).

Упражнения

16.1. Вероятность того, что завтра цены на потребительские товары вырастут, равна 0,3; вероятность того, что завтра поднимется цена на серебро, равна 0,2, а вероятность одновременного роста цен на потребительские товары и серебро составляет 0,06. Являются ли цены на потребительские товары и серебро независимыми друг от друга? Поясните ответ.

Ответ. Да, т. к. 0,3×0,2=0,23.

16.2. Иностранная фирма, производящая автомобили, интересуется российским рынком. Для изучения вкусов потенциальных покупателей проводится опрос, в котором выясняются наиболее желательные характеристики автомобиля. Предположим, что результаты опроса показали: 35% потенциальных покупателей в основном оценивают автомобиль по его техническим характеристикам, 50% – по его дизайну, 25% – считают важным и то, и другое. Основываясь на этой информации, ответьте, являются ли два вида предпочтений потенциальных покупателей независимыми друг от друга? Объясните почему?

Ответ. Нет, не являются, т. к. 0,35×0,5¹0,25.

16.3. Аудиторская фирма размещает рекламу в журнале “Коммерсант”. По оценкам фирмы, 60% людей, читающих журнал, являются потенциальными клиентами фирмы. Выборочный опрос показал также, что 85% людей, которые читают журнал, помнят о рекламе фирмы, помещенной в конце журнала. Оцените, чему равен процент людей, которые являются потенциальными клиентами фирмы и могут вспомнить ее рекламу?

Ответ. 0,85×0,6=0,51, т. е. 51%.

16.4. Консультационная фирма получила приглашение для выполнения двух видов работ от двух международных корпораций. Руководство фирмы оценивает вероятность получения заказа от фирмы А (событие А) равной 0,45. Также, по мнению руководителей фирмы, в случае, если фирма заключит договор с компанией А, то с вероятностью в 90% компания В даст фирме консультационную работу. С какой вероятностью компания получит оба заказа?

Ответ. 0,45×0,9=0,405.

16.5. Вероятность наступления события А в каждом опыте одинакова и равна 0,4. Опыты производятся последовательно до наступления события А. Определить вероятность того, что понадобится ровно 3 опыта.

Ответ. 0,4×0,4×0,6=0,096.

< Предыдущая		Следующая >