Как найти вероятность случайного события 6 класс

Представим
себе такую историю…

Саша
и Паша встретились по дороге в школу, и между ними завязался такой разговор.

–
Вероятно, меня сегодня вызовут к доске на уроке математики, – сказал Саша.

–
Вполне вероятно, что и меня тоже сегодня вызовут к доске на уроке математики, –
продолжил Паша.

–
Тебя недавно спрашивали, – возразил Саша, – а меня давно не спрашивали. Значит,
маловероятно, что тебя вызовут к доске сегодня, а вот меня вызовут с большей
вероятностью.

–
Согласен, – произнёс Паша, – но вероятность всё же есть, что меня тоже могут
вызвать к доске.

–
А давай спросим у Мудряша, кого же из нас скорее всего вызовут к доске, –
предложил Саша.

–
Давай – согласился Паша.

–
Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним
устные задания, – предложил Мудряш.

–
Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было
получиться!

–
Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – В вашем разговоре
прозвучали такие слова, как «вероятно», «вполне вероятно», «маловероятно»,
«с большей вероятностью». Все эти слова связаны со словом «вероятность».
Давайте разберёмся, что же такое вероятность.

–
Итак, – продолжил Мудряш, – многое в нашей жизни, несмотря на то, что мы
планируем заранее, зависит от случая. Купив лотерейный билет, мы можем
выиграть, а можем не выиграть. Сегодня на уроке математики учитель может
вызвать вас к доске, а может и не вызвать. Снег может выпасть, а может и не
выпасть, чёрный кот может перебежать дорогу перед вами, а может и передумать.
Всё это события. И каждое из этих событий в одних и тех же условиях могло
произойти, а могло и не произойти.

Запомните! Событие,
которое при данных условиях может наступить, а может и не наступить, называют
случайным.

–
Разве в нашей жизни всегда происходят только случайные события? – спросил Паша.

–
Вообще, событие бывает трёх видов: достоверное, невозможное и случайное,
– продолжил Мудряш. – Событие, которое при данных условиях обязательно
наступит, называют достоверным. Например, вы знаете, что
после понедельника всегда наступает вторник. Это достоверное событие. Событие,
которое при данных условиях никогда не наступит, называют невозможным.
Например, вода на озере замёрзнет при + 20^о. Данное событие никогда
не произойдёт при таком условии, значит, это событие невозможное.

А
вы можете привести примеры достоверных и невозможных событий? – спросил у ребят
Мудряш.

–
Достоверными будут такие события: вода на озере замёрзнет при – 20^о,
так как вода замерзает при минусовой температуре; дата рождения моего друга –
число меньшее, чем 32, так как в каждом месяце не более 31 дня, – привёл
примеры Паша.

–
А невозможными будут такие события: среди ночи выглянуло солнце, при бросании
игрального кубика выпадет 7 очков, – сказал Саша.

–
Молодцы! – похвалил ребят Мудряш. – Но всё же в жизни всё не так чётко и ясно.
Чаще всего мы сталкиваемся именно со случайными событиями, одни из которых
более вероятны, другие — менее вероятны.

–
А эти случайные события нельзя заранее предугадать? – спросил Паша.

–
Хороший вопрос! – сказал Мудряш. – Очень часто нам важно знать, на сколько или
во сколько раз одно случайное событие вероятнее другого. Существует специальная
наука, которая занимается оценками вероятностей случайных событий. Называется
эта наука теорией вероятностей.

Итак,
вероятность наступления достоверного события можно охарактеризовать как
стопроцентную, а вероятность наступления невозможного события — как нулевую.
Так как 100 % – это  величины
(в свою очередь, ),
то договорились о следующем: вероятность достоверного события считается
равной 1, вероятность невозможного события считается равной 0. Тогда вероятность
случайного события может быть любым числом от 0 до 1.

–
Давайте проведём небольшой эксперимент, – предложил Мудряш. – Будем
подбрасывать монету, например рубль. Скажите, в результате этого эксперимента
какие события могут произойти?

–
Монета может упасть решкой вверх, – предположил Саша.

–
Или монета может упасть орлом вверх, – сказал Паша.

–
Правильно! – согласился Мудряш. – Случай «монета встала на ребро» считаем
невероятным и не учитываем. Эксперимент с монетой – это достоверное событие:
монета обязательно упадёт орлом или решкой вверх, третьего варианта не дано. Но
оба исхода – выпадение орла или выпадение решки – равновозможны,
или ещё можно сказать равновероятны. В результате эксперимента
может произойти как первое событие, так и второе. Тогда вероятность каждого
из этих событий будет равна отношению числа благоприятных случаев к числу
равновозможных случаев.

Допустим,
нас интересует исход выпадение орла – это благоприятный для нас случай. Тогда вероятность
этого события будет равна отношению благоприятных случаев (таких случаев – 1) к
числу всех равновозможных случаев (их 2), то есть равна .
То же самое мы можем сказать и о вероятности события выпадение решки. Она тоже
равна .

–
Давайте проведём ещё один эксперимент, – предложил Мудряш. – Будем подбрасывать
игральный кубик. Скажите, какие события могут произойти в результате этого
эксперимента?

–
В результате эксперимента с игральным кубиком можно получить один из 6 исходов:
выпадет 1, 2, 3, 4, 5 или 6 очков, – сказал Паша.

–
Хорошо! – согласился Мудряш. – Все эти 6 исходов равновозможны, и один из них
обязательно произойдёт. Если нас интересует событие, например выпадение 2
очков, то вероятность данного события будет равна .

–
А теперь представьте, что нас интересуют следующие события: первое — выпадение
чётного числа очков; второе — выпадение числа очков, кратного числу 3.
Определите вероятность этих событий.

–
Событию выпадение чётного числа очков благоприятствуют 3 случая: выпадение 2, 4
или 6 очков, – начал Саша. – Тогда вероятность этого события равна отношению
числа случаев, благоприятствующих этому событию (их 3), к числу всех
равновозможных случаев (их 6). Значит, вероятность выпадения чётного числа
очков равна  или
.

–
Событию выпадение числа очков, кратного числу 3, благоприятствуют только 2
случая: выпадение 3 или 6 очков, – сказал Паша. – Тогда вероятность этого
события равна отношению числа случаев, благоприятствующих этому событию (их 2),
к числу всех равновозможных случаев (их 6). Следовательно, вероятность
выпадения числа очков, кратного числу 3, равна  или
.

–
Молодцы! – похвалил ребят Мудряш. – Приведённые примеры иллюстрируют следующее.
Если эксперимент заканчивается одним из  равновозможных
исходов, из которых  являются
благоприятными для наступления данного события, то вероятность этого события
равна .

–
А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько
заданий.

Задание
первое: в коробке лежит 3 красных и 7 синих шаров. Наугад
вынимают 1 шар. Какова вероятность того, что этот шар окажется: красным; синим?

Решение: представим
себе, что шары пронумерованы числами от 1 до 10, так как всего у нас 7 + 3 = 10
шаров в коробке. Тогда при вынимании шара может произойти 10 равновозможных
исходов: вынули шар с номером один, вынули шар с номером 2 и так далее. В
первом случае благоприятных исходов будет только 3 (ведь в коробке только 3 красных
шара). Поэтому искомая вероятность равна .

Во
втором случае благоприятных исходов будет 7, так как в коробке лежит 7 синих
шаров. Поэтому искомая вероятность равна .

Задание
второе: в коробке лежит 10 карточек, пронумерованных числами
от 1 до 10. Какова вероятность того, что наугад будет вытянута карточка с
чётным числом?

Решение: при
вынимании карточек может произойти десять равновозможных исходов: вынули карточку
с номером 1, вынули карточку с номером 2 и так далее. Но благоприятных исходов
будет только 5: вынули карточку с номером 2, вынули карточку с номером 4,
вынули карточку с номером 6, вынули карточку с номером 8 или вынули карточку с
номером 10. Значит, искомая вероятность равна  или
.

Случайные события. Вероятность случайного события.

Представьте себе ситуации ( события ):

• прозвенел школьный звонок,
• выпал снег,
• тебя вызвали на уроке к доске,
• черный кот перебежал дорогу

Случайные события

Определение

Событие, которое в одних и тех же условиях может произойти, а может и не произойти, называют случайным.

Например:

• Подбрасываем монету. Появился герб. А ведь могла

появиться и цифра. То что появился Герб – случайное событие.

• Стрелок поражает цель. Но мог и не попасть.

Попадание в цель– случайное событие.

Вы участвуете в лотерее, в которой выпущено 1 000 000 билетов и разыгрывается только один автомобиль .

Выиграть можно, хотя это событие маловероятно .

А если разыгрывается 10 автомобилей?

Вероятность выигрыша увеличивается.

А если представить, что разыгрывается 999 999 автомобилей?

Вероятность выигрыша становиться очень большой.

Вероятности случайных событий – это величины, которые можно сравнивать.

Наука, которая занимается оценками вероятностей случайных событий, называется теорией вероятностей .

Если каждый лотерейный билет является призовым, то выигрыш гарантирован.

Если в лотерее нет ни одного призового билета, то выигрыш автомобиля невозможен.

Определение

События, которые при данных условиях обязательно происходят, называют достоверными

Например:

• после четверга наступила пятница;

• при бросании игрального кубика появилось число меньшее 7 .

Определение

События, которые в данных условиях никогда не происходят, называются невозможными.

Например:

• вода в реке замёрзла при температуре +25 градусах;
• при бросании игрального кубика появилось

7 очков

Событие называется достоверным , если его вероятность равна 1.

Событие называется невозможным , если вероятность равна 0.

Вероятность случайного события может быть любым числом от 0 до 1.

Покупка лотерейного билета, подбрасывание игрального кубика или монеты, вытягивание экзаменационного билета – это примеры экспериментов со случайными исходами (результатами).

Случайные события могут произойти в результате:

• опыта,
• Эксперимента ,
• Испытания,
• Наблюдения,

Результаты которых заранее предсказать нельзя.

Эксперимент: бросание игральной кости

Случайные события:

• При бросании игральной кости выпадет число меньшее 7.
• При бросании игральной кости выпадет число большее 6.

Эксперимент: бросание игральной кости

При бросании может получиться один из шести результатов: выпадет 1,2,3,4,5,6 очков.

Эти события равновероятные (равновозможные).

Вероятность выпадения 5 очков равна

Эксперимент: бросание игральной кости

Найти вероятность того, что при бросании игральной кости выпадет число, кратное 3.

Количество возможных событий 6.

Количество благоприятных событий 2 ( это выпадение числа 3 и числа 6)

Вероятность

Формула нахождения вероятности

Р – вероятность события

m – количество благоприятных событий,

n – количество возможных событий.

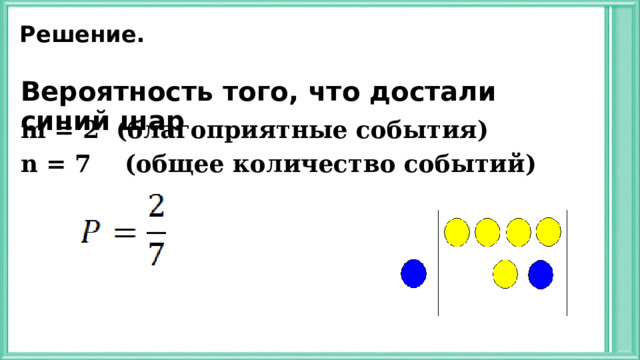
Задача

В коробке лежат два синих и пять жёлтых шаров. Наугад вынимают один шар. Какова вероятность того, что этот шар окажется:

1) синий,

2) красным?

Решение.

Вероятность того, что достали синий шар

m = 2 ( благоприятные события)

n = 7 (общее количество событий)

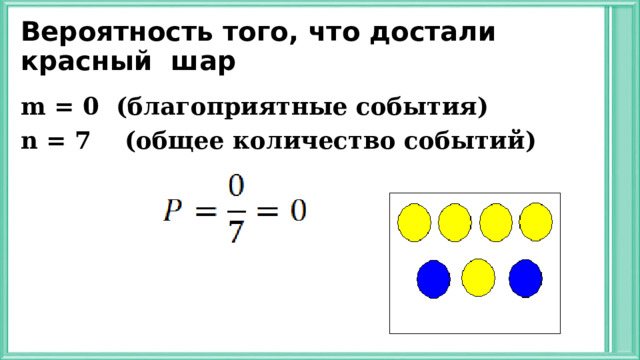
Вероятность того, что достали красный шар

m = 0 ( благоприятные события)

n = 7 (общее количество событий)

Запомним (для самоконтроля)

• Вероятность достоверного события всегда равна 1
• Вероятность невозможного события всегда равна 0
• Вероятность случайного события всегда 0 Р(А) 1

Определение

(классическое определение вероятности)

Вероятностью события А называется отношение

числа благоприятных для него исходов испытания к

числу всех равновозможных исходов.

где m – число исходов, благоприятствующих

осуществлению события,

n – число всех возможных исходов.

Задача

Женя, Лена, Маша, Аня и Коля бросили жребий – кому идти в магазин. Найдите вероятность того, что в магазин надо будет идти Лене .

Решение.

Задача

Бросают игральную кость. Найдите вероятность того, что выпадет число, меньшее 4 очков.

Решение.

Работаем по учебнику

стр.177

№ 802-804

№ 809, 811

Домашняя работа

§28 № 810, № 812.

Конспект
урока.

Тема
урока:  Случайные события.  Вероятность случайного
события.

Класс: 
6

Тип
урока: урок получения новых знаний

Цель: Создание условий для получения и осмысления
учениками новых знаний о  случайных событиях. Построение  алгоритма вычисления
вероятностей случайных событий и формирование  первичного умения его применять.

Задачи:

Образовательные:
 научиться использовать новые знания
при решении задач, оценивать события и сравнивать их, познакомиться с понятием «вероятность»,
“маловероятно”, “наиболее вероятно”.

 Развивающие:
развивать культуру речи через математически грамотные высказывания,   задавать вопросы о неизвестном.
Развивать практические умения учащихся при выполнении экспериментальных задач.

Воспитательные: 
формировать умение слушать и вступать в диалог, уважительное отношение к чужому
мнению, развивать у учащихся умение
работать индивидуально и в группах.

Планируемые результаты:

 Предметные:  знать
понятия – случайного события, достоверного события, невозможного события,
равновероятных событий. Уметь вычислить вероятности событий, находить число
благоприятных и равновозможных исходов, применять методы для решения задач практического характера и задач из
смежных дисциплин.

Личностные:
давать объективную оценку и самооценку учебной деятельности, адекватно
воспринимать оценку учителя и сверстников; учиться грамотно излагать свои
мысли.

 Метапредметные:
 уметь ставить и
формулировать для себя новые задачи, устанавливать причинно-следственные связи,
строить логические рассуждения, умозаключения и делать выводы.  Высказывать свою точку зрения, осваивать  правила работы индивидуально и
в группе.

Основные
понятия: Эксперимент, случайное событие,
вероятность случайного события, достоверное событие, невозможное событие,
равновероятные события, благоприятные исходы, равновозможные исходы.

Оборудование: 
мультимедийное оборудование (ПК, проектор),  монеты,  игральные кубики
(кости), коробка с цветными карандашами, словари.

Ход урока

1.    
Организационный этап. (1 мин)

Проверка готовности к
уроку

Учитель:
– Здравствуйте ребята, садитесь.

2.     Этап
мотивации к учебной деятельности (4 мин.)

Учитель:

Ребята,
вчера я услышала, как вы после уроков обсуждали, кто может победить в
спортивной эстафете «Золотая осень». В вашем классе два ученика – спортсмены. В
разговоре вы  не раз произносили: «Кирилл случайно может проиграть», «Ваня
обязательно победит», «Это возможно», «Это невозможно»,  «Это обязательно
случится». Мы не знаем правильного ответа, нам не хватает определенных знаний.

    
 В повседневной жизни мы часто употребляем эти слова.  Многое, несмотря на то,
что мы планируем заранее, зависит от случая. Мир случайностей постоянно нас
преследует. Наука математика обнаружила интересные закономерности, которые
позволяют человеку увереннее чувствовать себя при встрече со случайными
событиями.

Как
вы думаете, чем же мы будем сегодня заниматься на уроке?

Ответы
учащихся:

   
– Мы познакомимся с новыми правилами, которые нам помогут  решать задачи,
связанные со случайными событиями.

Учитель:

    
Сегодня я хочу познакомить вас с оценкой случайных событий, научить находить
вероятности событий в простейших случаях. А это очень важно для оценивания
вероятности случайного события в практических ситуациях, так как мир
случайностей начинается сразу же,  как только вы открываете утром глаза. 

Как вы думаете, какова тема урока? Какие
цели можно поставить перед собой?

Ответы
учащихся:

 
Случайные события. Вероятность случайного события.

3.    
Актуализация и фиксирование
индивидуального затруднения в пробном действии (5 мин.)

Учитель: Хочу с вами
поделиться: со мной сегодня произошло необычное событие – по дороге в школу я
нашла 500 рублей. Это что,  случайность или я каждый день буду находить
деньги?! (Ответы детей).

Учитель: – Ребята,
с какими случайностями  вы встречались? (Обсуждение)

Случай, случайность – с ними мы встречаемся повседневно: случайная
ошибка, случайный выигрыш, случайная поломка. Наука обнаружила интересные
закономерности, которые позволяют  человеку уверенно чувствовать себя при
встрече со случайными событиями.

4. Этап выявления места и причины
затруднений, построение проекта выхода из ситуации (10 мин.)

Учитель: Что
вы понимаете под словом событие? Случайное событие?  (Обсуждение)

Пока вы не можете четко
ответить на этот вопрос, потому что у вас не хватает знаний.

 Познакомимся с данным понятием в толковом
словаре (работают со словарями в группах по 4 человека).

Как вы думаете: в
русском языке и в математическом понятии «Событие» означает одно это же?
(Обсуждение).

Ученики:
Событие, которое может произойти, а может не произойти в процессе наблюдения
или эксперимента, называют случайным событием. 
Учитель: Закономерности случайных событий изучает
специальный раздел математики, который называется теорией вероятностей.

Примеры
событий:

1.     «При
подбрасывании игрального кубика выпадет 3 очка».

2.     «Покупая
лампочку она может оказаться рабочей, а может быть бракованной».

Ученики:
приводят свои примеры

Мы
уже поделились на  группы по 4 человека и сейчас проведем опыты.

Опыт
1: (учащиеся работают в группах). Подбросить монету
в 1 рубль 20 раз и подсчитать, сколько раз выпадет орел. Записать результаты в
тетради.

Опыт
2: (учащиеся работают в группах). Подбросить
игральный кубик 10 раз? Подсчитать сколько раз выпадет число меньше 4.

Опыт
3: (учащиеся работают в группах). В коробке
лежит 5 зеленых, 5 красных и 10 черных карандашей. Наугад выньте 1 карандаш (20
раз), и подсчитайте сколько раз достали красный карандаш.

Учитель:
Обсудим эти опыты, сделаем выводы.

5.    
Реализация  проекта(7 мин.)

Учитель: Давайте
познакомимся, какие бывают события:

Если
событие при рассматриваемых условиях происходит всегда, то оно называется достоверным.
Вероятность появления достоверного события равна 1.

Есть
события, которые при рассматриваемых условиях не происходят никогда. Вероятность
появления невозможного события равна 0.

Пример 
невозможного события:

«При подбрасывании
игрального кубика выпадет 8 очка».

Пример  достоверного
события:

«После субботы
наступит воскресенье».

        
Равновозможные или равновероятные события

         
Если все исходы эксперимента имеют равные шансы, то они называются равновозможными.

         
Не все события равновозможны. Может сломаться машина, не прозвенит звонок. В
обычных условиях такие события маловероятны. Более вероятно,
что машина не сломается, звонок прозвенит.

Определение
вероятности: вероятность события  равна отношению числа исходов,
благоприятствующих наступлению данного события, к числу всех равновозможных
исходов. Вероятность события обозначается буквой Р.

                 
  число благоприятных исходов

Р 
= ————————————————————————

                   
число всех возможных исходов

6.    
Этап первичного закрепления с
проговариванием во внешней речи(7 мин.)

Учитель: Попытаемся
применить  эти понятия и ответить на вопросы.

Какие из следующих событий – случайные;
достоверные; невозможные?

А) черепаха научится говорить;
(невозможное)

Б) ваш день рождения – 19 октября;
(случайное)

В) день рождения вашего друга – 30
февраля; (невозможное)

Г) вы выиграете, участвуя в лотерее;
(случайное)

Д) вы не выиграете, участвуя в
беспроигрышной лотерее; (невозможное)

Е) вы проиграете партию в шахматы;
(случайное)

Ж) вы завтра встретите инопланетянина;
(невозможное)

З) на следующей неделе испортится погода;
(случайное)

И) вы нажали звонок, а он не зазвонил;
(случайное)

К) сегодня – четверг; (случайное)

Л) после четверга будет пятница;
(достоверное)

М) Ель вечнозеленое дерево; (достоверное)

Н) Завтра я стану космонавтом; (случайное).

Тест (работают в парах)

В ящике имеются 4 белых и 7 черных шаров.
Из ящика наугад выбирают шар.

Соедините линиями верные ответы.

Всякое случайное событие является следствием многих причин. Невозможно
заранее предсказать, произойдет единичное событие или нет. Но при многократном
повторении опыта при одних и тех же условиях случайные события подчиняются
закономерностям, изучением которых и занимается теория вероятностей.
Когда и как возникла эта наука?
Теория вероятностей  сформировалась
на основе  азартных игр. Азартные игры так и создавались, чтобы исход был
случайным.

Попадали ли вы в такие ситуации, когда нужно выбирать среди двух (трех и
т.д.) вариантов какой-то один? Что мы обычно делаем? Обсуждение: бросаем
монету, загадываем и смотрим, какой стороной она упадет.

Теория
вероятности – это не только опыты, эксперименты, но и решение задач.

7.    
 Этап самостоятельной работы с
проверкой по эталону (8 мин.)

Учитель:
Мы записали формулу для нахождения вероятности в
тетрадь, а теперь  проверим нашу готовность решать задачи и
ответим на вопросы проводимых опытов.
Предлагаю решить задачи на  карточках.

1)    В
среднем из 80 карманных фонариков, поступивших в продажу, 
десять неисправных. Найдите вероятность того, что выбранный наудачу 
в магазине фонарик окажется исправен.

2)    В
лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов 
из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют,
определяется жребием. Найдите вероятность того, что первым будет стартовать
спортсмен из России.

3)    На
тарелке лежат одинаковые на вид пирожки: 1 с творогом, 12 с мясом 
и 3 с яблоками. Ваня наугад берёт один пирожок. Найдите вероятность того, что
пирожок окажется с мясом

4)    В
фирме такси в данный момент свободно 15 машин: 3 чёрных, 6 жёлтых 
и 6 зелёных. По вызову выехала одна из машин, случайно оказавшаяся 
ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое
такси.

5)    На
экзамене 40 билетов, Саша не выучил 2 из них. Найдите вероятность
того, что ему попадётся выученный билет.

Самопроверка
результатов своей работы осуществляется учащимися по критериям, записанными на
доске.

Критерий
оценивания:

«5» – 4-5 задач

«4» – 3 задачи

«3» – 1-2 задачи

Учитель:
Молодцы вы справились с задачами!

8.    
Этап рефлексии учебной деятельности на
уроке и  информации о домашнем задании (3 мин.)

Домашнее
задание:

 Решить
задачи на карточке, составить две задачи на нахождение вероятности случайного
события.

1)
Найти вероятность того, что число выпавших при броске игральной кости очков
четно/ нечетно.

2)
В коробке 25 шаров. Из них 7 белых, 9 черных, остальные цветов радуги. Какова
вероятность вытащить шар цвета радуги?

3)
В доме пустуют 33 квартиры, из которых 3 находятся на первом этаже, а 7 – на
последнем. Эти квартиры распределяются по жребию. Какова вероятность того, что
жильцу  достанется квартира, расположенная на последнем этаже?

Закончите
предложение:

·        Сегодня я узнал… ·        Было интересно… ·         Было трудно… ·        Я понял, что… ·        Теперь я могу… ·        Я почувствовал, что…

·        Я приобрёл… ·        Я научился… ·        У меня получилось… ·        Я смог… ·        Меня удивило… ·        Урок дал мне для жизни… ·        Мне захотелось…

Сегодня вы
научились  решать задачи на нахождение вероятности, познакомились с новыми понятиями.
В жизни часто приходиться поступать так, чтобы шансы на успех были наибольшими,
случайное событие нельзя предугадать, но можно найти его вероятность. Мне бы
хотелось, чтобы в незнакомых ситуациях, вы реально оценивали свои шансы и
возможности! Спасибо всем за урок!

Основная цель – на популярном
уровне познакомить школьников с разделом
дискретной математики, который приобрел сегодня
серьезное значение в связи с развитием теории
вероятностей, математической логики,
информационных технологий. Учащиеся должны
получить представление о том, что такое
комбинаторная задача, познакомиться с понятием
событие, равновозможные события, научить
определять вероятность того или иного события,
научить решать задачи по данной теме. Расширение
кругозора учащихся. Развитие интереса учащихся к
изучению нового раздела математики. Повышение
математической культуры, интеллектуального
уровня учащихся.

ХОД УРОКА

I. Актуализация задач урока.

II. Устный счет.

1. Какими вопросами занимается раздел
математики – комбинаторика?

(Комбинаторика – раздел
математики, в котором изучаются различные
вопросы, связанные с взаимным расположением
частей данного множества, состоящего обычно из
конечного числа элементов.)

2. Посчитайте: 2!; 3!; 4!; 5! .

(Ответ: 2; 6; 24; 120).

3. Всем известна знаменитая басня Ивана Крылова
“Квартет”:

Проказница Мартышка,
Осел, Козел
Да косолапый Мишка
Затеяли квартет…

Как помниться, герои басни никак не могли
усесться. Подсчитайте, сколькими способами герои
квартета могут пересаживаться?

(Решение Р_n = 4! = 24 способа).

4. В сборнике занимательных задач Я.
Перельмана “Живая математика” есть рассказ “Бесплатный
обед”. В нем описывается случай, происшедший с
десятью выпускниками, которые не могут
отпраздновать окончание школы, потому что никак
не решат: в каком порядке им сесть.

На выручку им пришел официант, который
предложил сегодня сесть, как придется, на другой
день придти и сесть по-другому и так каждый день,
пока не наступит такой день, когда они опять
сядут так, как сидят сегодня. И тогда официант
обещал угостить всех бесплатным обедом. Как вы
думаете, долго ли друзьям придется дожидаться
бесплатного обеда?

(РЕШЕНИЕ: Р_n = 10! =3 628 800 . Число
n! с ростом n растет очень быстро. Это означает, что
на самом деле официант ничем не рисковал, так как
обещанное событие произойдет почти через 10 000
лет.)

5. Встретились 5 друзей. Сколько было
рукопожатий?

Ответ: (4+3+2+1=10).

III. Объяснение нового материала.

Кое-что из прошлого теории вероятности.

(Прилагается к уроку презентация <Приложение 1>, выполненная в Power
Point, так как суммарный объем приложений не должен
превышать 200 Кб, то презентация сокращена до
минимума)

Еще первобытный вождь понимал, что у
десятка охотников вероятность поразить копьем
зубра гораздо больше, чем у одного. Поэтому и
охотились только коллективно.

Неосновательно было бы думать, что
такие древние полководцы, как Александр
Македонский или Дмитрий Донской, готовясь к
сражению, уповали только на доблесть и искусство
воинов.

Несомненно, они на основании
наблюдений и опыта военного руководства умели
как-то оценить вероятность своего возращения со
щитом или на щите, знали, когда принимать бой,
когда уклониться от него. Они не были рабами
случая, но вместе с тем они были еще очень далеки
от теории вероятностей.

Позднее, с опытом, человек все чаще
стал взвешивать случайные события,
классифицировать их исходы как невозможные,
возможные и достоверные. Он заметил, что
случайностями не так уж редко управляют
объективные закономерности. Вот простейший опыт
– подбрасывают монету. Выпадение орла или решки,
конечно, чисто случайное явление. Но при
многократном подбрасывании обычной монеты можно
заметить, что появление решки происходит
примерно в половине случаев.

Кто и когда впервые проделал опыт с
монетой, неизвестно. Французский
естествоиспытатель Ж.Л.Л.Бюффон (1707 – 1788) в 18
столетии 4040 раз подбрасывал монету – решка
выпала 2048 раз. Математик К.Пирсон в начале
двадцатого столетия подбрасывал ее 24 000 раз –
решка выпала 12 012 раз. Лет 40 назад американские
экспериментаторы повторили опыт. При 10 000
подбрасываний решка выпала 4 979 раз. Значит,
результаты бросаний монеты, хотя каждое из них и
является случайным событием, при неоднократном
повторении подвластны объективному закону.

Наиболее интересные задачи теории
вероятности возникли в области азартных игр.
Этому, по-видимому, способствовало наличие таких
“наглядных пособий”, как монета или игральная
кость.

К азартным играм относили бросание
шестигранных игральных костей. Слово “азар”
по-арабски означает “трудный”. Так, арабы
называли азартной игрой комбинацию очков,
которая при бросании нескольких костей могла
появиться лишь единственным способом. Например,
при бросании двух костей трудным (“азар”)
считалось появление в сумме двух или двенадцати
очков.

Впервые основы теории вероятностей
были изложены последовательно французским
математиком П.Лапласом (1749-1827) в книге
“Аналитическая теория вероятностей”.

В предисловии автор писал:
“Замечательно, что наука, которая началась с
рассмотрения азартных игр, обещает стать
наиболее важным объектом человеческого знания…
Ведь по большей части важнейшие жизненные
вопросы являются на самом деле лишь задачами
теории вероятностей”.

П.Лаплас не мог предусмотреть, что
пройдет несколько десятилетий и интерес к теории
вероятностей снизится. А так на деле и случилось.
Во второй половине XIX века и в начале XX века
некоторые математики перестали интересоваться
теорией вероятностей как математической
дисциплиной.

К счастью последние годы теория
вероятностей вернулась в школьную программу,
медленными, но уверенными шагами. Вот и наша
задача – научиться решать такие жизненные
задачи с помощью теории вероятностей.

Рассмотрим следующие примеры:

Пример 1. Пусть на стол бросают
монету. В результате обязательно произойдет одно
из двух событий (либо “выпала решка”, либо
“выпал орел”)

Событие А: “Выпала решка”

Событие В: “Выпал орел”

Так как предполагается, что монета не
изогнута, то события А и В в нашем примере равновозможные
и одно из них обязательно произойдет. Тогда
вероятность события определяется следующим
образом: Р(А) =,
где n – число всех равновозможных случаев, m –
число случаев, благоприятствующих событию А.
Тогда Р(А) = и
Р(В) = .

Пример 2. Пусть на стол бросают
игральный кубик.

Возможны 6 случаев: выпадение 1, 2, 3, 4, 5, 6
очков. Эти случаи равновозможные.

Событие А: “выпадение 3 очков”, тогда
Р(А) = .

Пример 3. Двое играют в эту игру. Они
бросают два кубика. Первый получает очко, если
выпадет сумма 8. Второй получает очко, если
выпадет сумма 9. Справедлива ли эта игра?

РЕШЕНИЕ:

Событие А: “при бросании двух кубиков
выпало 8 очков”

Событие В: “при бросании двух кубиков
выпало 9 очков”

При бросании двух кубиков могут
получиться следующие равновозможные результаты:

n = 36 – число всех равновозможных случаев;

m = 5 – число случаев благоприятствующих событию
А;

к = 4 – число случаев благоприятствующих
событию В.

тогда Р(А) =,
Р(В) = ,

, то Р(А) >
Р(В).

Так как 8 очков выпадает чаще, чем 9 очков, то
данная игра не справедлива.

Пример 4

Из пяти букв нарезной азбуки
составлено слово “книга”. Неграмотный мальчик
перемешал буквы, а потом наугад их собрал. Какова
вероятность того, что он опять составил слова
“книга”?

РЕШЕНИЕ:

Событие А: “составил слова “книга””

Общее число равновозможных случаев
равно 5! = 120, тогда Р(А) = .

IV. Тренировочные упражнения №№150, 151, 153, 155, 159, 162^*.

№ 150

Бросают игральный кубик. Подсчитайте
вероятность события:

1. А: “выпадает 5 очков”;
2. В: “выпадает четное число очков”;
3. С: “выпадает нечетное число очков”;
4. D: “выпадает число очков, кратное 3”.

РЕШЕНИЕ:

1. Р(А) = ;
2. Р(В) =
3. Р(С) =
4. Р(D) =

Ответ: , , ,.

№ 151

Из ящика, где находятся 2 черных и 5 белых шаров,
вынут наугад один шар.

Какова вероятность того, что вынут:

1. Черный шар;
2. Белый шар?

РЕШЕНИЕ:

Событие А: “вынут черный шар”

Событие В: “вынут белый шар”

Р(А) = Р(В) =

Ответ:

№ 153

На двух карточках написали буквы А и Д, положили
карточки на стол буквами вниз в произвольном
порядке. Какова вероятность того, что после
переворачивания карточек получится слово “ДА”?

РЕШЕНИЕ:

– всего 2
возможных случаев.

Событие А: “получилось слово “ДА””.

Р(А) = .

Ответ: .

№ 155

На четырех карточках написали буквы К, О, Л, Я и
положили карточки на стол буквами вниз в
произвольном порядке. Какова вероятность того,
что после переворачивания карточек получится
имя КОЛЯ?

РЕШЕНИЕ:

Событие А: “получилось имя КОЛЯ”.

1. 4! = –
   равновозможных случая;
2. Р(А) = .

Ответ: .

№ 159

Бросают два игральных кубика. Какова
вероятность события:

1. А: “сумма очков равна 2”;
2. В: “сумма очков равна 10”;
3. С: “сумма очков равна 12”;
4. D: “сумма очков равна 13”?

РЕШЕНИЕ:

Используя таблицу равновозможных случаев
бросания двух костей отвечаем на вопросы:

1. Р(А) = ;
2. Р(В) = ;
3. Р(С) = ;
4. Р(D) = 0.

Ответ: ; ; ; 0.

№162^*

Бросают два игральных кубика. Если сумма очков
11 – выиграл 1-й, если сумма очков 12 – выиграл 2 –й.
Справедлива ли эта игра?

РЕШЕНИЕ:

Событие А: “выпало 11 очков”.

Событие В: “выпало 12очков”

Р(А) = ;

Р(В) =;

, то Р(А) >
Р(В).

Так как 11 очков выпадает чаще, чем 12 очков, то
данная игра не справедлива.

Ответ: данная игра не справедлива.

V. Итог урока.

VI. Задание на дом: §1.10^* выучить;
решить №№ 154, 156.

Урок нового материала по теме «Случайные события. Вероятность случайного события» для 6 класса по учебнику Мерзляка.

Цели:

1. Познакомиться с такими понятиями, как событие, случайное событие, эксперимент, равновероятное событие, вероятность, благоприятный исход, равновозможное событие, невозможное событие, достоверное событие;

2. Узнать, как вычисляется вероятность события;

3. Научиться использовать новые знания при решении задач.

Ход урока

1. Организационный момент

2. Устный опрос

Знаете ли вы, что такое событие? И можете ли вы привести примеры событий? (Событие – это когда что-то происходит) А какими бывают события? (Приятные/неприятные) Сегодня мы с вами будем говорить о случайных событиях, а так же о вероятности таких случайных событий.

3. Объяснение нового материала

Все ваши примеры действительно являлись событиями, причём событиями случайными, то есть могли произойти, а могли бы и не произойти.

Представьте, что появилась новая лотерея: выпущен 1 миллион билетов, и разыгрывается 1 автомобиль. Покупка лотерейного билета – эксперимент со случайным исходом, так как нельзя заранее узнать, какой билет вам достанется. Исходы равновозможным, если заранее точно нельзя узнать, какой из билетов (выигрышный или нет) вам попадётся. Выиграть этот автомобиль маловероятно, но, тем не менее, возможно. Если же правила изменятся, и вместо 1 автомобиля будут разыгрывать 1000, тогда вероятность выиграть автомобиль становится ощутимее. Ну, а если правила поменяют снова и разыгрывать будут 999.999 автомобилей, то вероятность выиграть автомобиль становится очень большой.

Таким образом мы приходим к тому, что у любого случайного события есть вероятность – величина, которую можно сравнить, главное определиться – как количественно оценивать возможность появления того или иного события. Наука, которая занимается оценкой вероятности случайного события называется теорией вероятностей.

Исход, который удовлетворяет нас, называется благоприятным.

Чтобы выяснить вероятность выигрыша автомобиля в 1, 2 и 3 случае, мы должны разделить количество благоприятных для нас событий, то есть выигрыш автомобиля, на количество всех событий, то есть на количество лотерейных билетов, и тогда что мы получим? (В первом случае 1/1000 000, во втором 1000/1000 000=1/1000, в третьем – 999 999/1000 000). Значит, если эксперимент заканчивается одним из n равновозможных исходов, из которых m – благоприятны, то вероятность события m/n.

Если бы в лотерее был всего один билет, который являлся при этом призовым, то выигрыш автомобиля происходил бы стопроцентно. Такое событие называют достоверным, а его вероятность – 1.

Если бы билет в лотерее был один, но не призовой, то автомобиль выиграть было бы невозможно. Такие события называются невозможными, а вероятность их равна 0.

Таким образом, вероятность любого события может быть любым числом от 0 до 1.

Событие называют равновероятным, если количество благоприятных исходов составляет половину от всех возможных исходов.

4. Разбор примеров

В коробке лежат 2 синих и 5 жёлтых шаров. Наугад вынимают один шар.  Какова вероятность того, что шар окажется а) синим, б) красным.

Решение.

Сколько всего шаров в коробке? (2+5=7) Значит, сколько всего исходов? (7) А сколько благоприятных исходов, т.е. сколько синих шаров? (2) Как можно найти вероятность? (Нужно разделить количество благоприятных исходов на количество всех исходов, т.е. 2/7) Да, это искомая вероятность. А сколько красных шаров в коробке? (0) Значит, какое это событие? (Невозможное, вероятность равна 0)

5. Практическая часть (решение задач)

У доски дети решают номера 809, 811, 813, 815, 817.

6. Необязательная часть (если до конца урока больше 7 минут) – решение устных заданий 802-807

7. Подведение итогов

Какие события называют случайными? Какая наука называется оценкой вероятностей? Чему равна вероятность достоверного, невозможного события? Как вычислить вероятность случайного события в эксперименте с равновозможными исходами?

8. Домашнее задание

Дома решаются номера 810, 812, 814.