Как найти вероятность состояния графа

Уравнения Колмогорова.
Предельные вероятности состояний

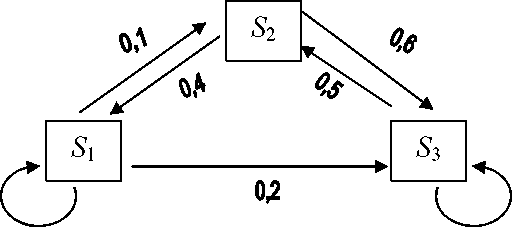
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока “окончаний ремонтов” первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .

Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:

Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.

1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.

Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:

2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .

Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).

Применяя теорему сложения вероятностей, получим

откуда

Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):

Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).

В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы в предельном стационарном режиме, т.е. при , которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:

Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом, согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.

---

Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или

(Здесь мы вместо одного “лишнего” уравнения системы (10) записали нормировочное условие (8)).

Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)

---

Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен

ден. ед.

Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока “окончаний ремонтов” каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:

Решив систему, получим .

Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:

ден.ед.

Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.

---

Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения. Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.

Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .

По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния

для состояния имеем , которое с учетом (12) приводится к виду

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

к которой добавляется нормировочное условие

При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние – при гибели одного члена популяции.

Решая систему (14), (15), можно получить

Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .

---

Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.

Решение. По формуле (16) найдем

по (17)

т.е. в установившемся, стационарном режиме в среднем 70,6% времени система будет находиться в состоянии , 17,6% — в состоянии и 11,8% — в состоянии .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Лекции по «Системы
массового обслуживания»

Пусть некоторая
система S
может находиться в одном из состояний
конечного (или счетного)
множества возможных состояний S₁,
S₂,…,
S_n,
а переход из одного состояния в другое
возможен только в определенные дискретные
моменты
времени t₁,
t₂,
t₃,
…, называемые шагами.

Если система
переходит из одного состояния в другое
случайно, то говорят, что имеет место
случайный
процесс с дискретным временем.

Случайный
процесс называется марковским,
если вероятность перехода из любого
состояния
S_i
в любое состояние S_j
не зависит от того, как и когда система
S
попала в
состояние S_i
(т.е. в системе S
отсутствует
последствие). В таком случае говорят,
что функционирование системы S
описывается
дискретной
цепью Маркова.

Переходы системы
S
в различные
состояния удобно изображать с помощью
графа состояний (рис.1).

0,7

Рис. 1

0,3

Вершины
графа S1,
S₂,
S₃
обозначают
возможные состояния системы. Стрелка,
направленная
из вершины S
_i
в
вершину S_j
обозначает
переход Si
→ Sj;
число,
стоящее
рядом со
стрелкой, обозначает величину вероятности
этого перехода. Стрелка, замыкающаяся
на i-той
вершине графа, обозначает, что система
остается в состоянии Si
с вероятностью,
стоящей у стрелки.

Графу системы,
содержащему n вершин, можно поставить
в соответствие матрицу nхn,
элементами
которой являются вероятности переходов
p
_ij
между
вершинами графа. Например, граф на рис.1
описывается матрицей P:

“0,7
0,1 0,2” P
=
0,4
0 0,6 0,2
0,5 0,3

называемой
матрицей
вероятностей переходов.
Элементы
матрицы p
_ij
удовлетворяют
условиям:

0<p_ij
<1; (1.1)

n

^Yjpij
=
1. (1.2)

Условие (1.1) –
обычное свойство вероятностей, а условие
(1.2) (сумма элементов любой
стрелки равна 1) означает, что система
S
обязательно
либо переходит их какого-то состояния
Si
в другое
состояние, либо остается в состоянии
Si.

6

Элементы матрицы
p_ij
дают
вероятности переходов в системе за один
шаг. Переход

Si
→ Sj
за два шага
можно рассматривать как происходящий
на первом шаге из S
_i
в некоторое промежуточное состояние
S_k
и на втором
шаге из S_k
в Si.
Таким образом,
для элементов матрицы вероятностей
переходов из Si
в S_j
за два шага
получим:

n

pi ⁽
j
²⁾
=∑pikpkj. (13)

k=1

В (m)

общем случае
перехода Si
→ Sj
за m
шагов для
элементов p
_i
j
матрицы

вероятностей
переходов справедлива формула:

pikpkj
, 1
≤ l ≤ m-1. (1.4)

k=1

Полагая в (1.4) l
= 1 и l
= m
– 1 получим
два эквивалентных выражения для p_i
j^m):

pi
(
jm)=∑
pik
pk (
mj
-1); (1.5)

k=1

n

(m) (m-1)

pij
=∑
pⁱ
k pkj . (1.6)

k=1

Пример 1.
Для графа
на рис.1 найти вероятность перехода
системы из состояния S1
в состояние
S₂
за 3 шага.

Решение.
Вероятность
перехода S1
→ S₂
за 1 шаг
равна p
₁₂
=
p
₁₂
=
0,1. Найдем

вначале
p₁⁽²₂⁾,
используя формулу (1.5), в которой полагаем
m = 2.

Получим:

3

p
₁⁽₂
=
∑
p
_1
kpk2
=р ₁₁
р ₁₂
+
р ₁₂
+
р ₂₂
+
р ₁₂
р
₃2
=
0,7⋅
0,1
+
0,1
⋅
0+0,2
⋅
0,5
=
0,17.

k=1

3

Аналогично
pп⁾
=
∑ p
1
k
p
k
⁽²2⁾
.

k=1

Как видно из этой
формулы, в дополнение к p
₁^(2
)
необходимо вычислить также

3

p⁽2²₂⁾
=
∑p2kpk2
=p21p12
+p₂₂p22
+
p₂₃p32
=
0,4
⋅0,1+0⋅0
+
0,6
⋅0,5
=
0,34
.

k=1

3

p
₃2
=
∑ p
_3
k
pk2 =
p
₃₁
p
₁2
+
p32p
₂₂
+
p
₃₃
p
₃2
=0⋅0,1+0,5⋅0
+
0,3⋅0,5=0,15.
k=1

p
₁₂
=
p
₁₁
p
₁⁽₂²⁾
+
p
₁₂p₂₂
+
p
₁₃
p
₃₂
=
0,7
⋅
0,17
+
0,1
⋅
0,34
+
0,2
⋅
0,15
=
0,183.
Ответ:
Вероятность перехода S1
→ S₂
после
третьего шага равна 0,183. Пусть система
S
описывается
матрицей вероятностей переходов Р

Таким образом

7

p ₁₁
p ₁₂
….. p _{1 n}

P
=

p
₂₁
p
₂₂
….. p2n

.

_p_n
1
p_n2 p_nn

(m)

Если обозначить
через P ^(m)
матрицу,
элементами которой являются p
вероятности
переходов из Si
в
S
_j
за m шагов, то справедлива формула

где
матрица ^P
m
получается
умножением матрицы P
саму
на себя m
раз.

O(1)

Исходное состояние
системы характеризуется вектором
состояния системы Q
(называемым
также стохастическим
вектором).

Q
= (q
₁,
q2,…,q
_n
),

где qj-вероятность
того, что исходным состоянием системы
является S_j
состояние.
Аналогично (1.1) и (1.2) справедливы
соотношения

n

0 ≤ q_i
≤1;

_Хqi
=
1.

i=1

Обозначим через

(m)

(m)

вектор состояния
системы после m
шагов, где
q_j
– вероятность
того, что после m
шагов
система находится в Si
состоянии.
Тогда справедлива формула

Q⁽m)=Q–Pm. (1.8)

Пример 2.
Найти вектор
состояния системы, изображенный на
рис.1 после двух шагов.

Решение.
Исходное
состояние системы характеризуется
вектором Q=(0,7;
0; 0,3).

После
первого шага (m
= 1)
система перейдет в состояние Q
⁽¹⁾

Q⁽¹⁾
=Q–P
=
(0,7;
0; 0,3)-

“0,7 0,1 0,2

=
(0,7
•
0,7
+
0
•
0,4
+
0,3
•
0,2;
0,7 •
0,1
+

0,4 0 0,6 0,2 0,5
0,3 +
0
•
0
+
0,3
•
0,5;
0,7 •
0,2
+
0
•
0,6
+
0,3
•
0,3)
=
(0,55;
0,22; 0,23).

r
После
второго шага система окажется в состоянии
Q⁽²⁾

0,7 0,1 0,2

(1)

Q

=
Q–P
=
(0,7;0;0,3)-

=
(0,519; 0,17;
0,311).

0,4 0 0,6 0,2 0,5
0,3

Ответ: Состояние
системы S
после двух
шагов характеризуется вектором (0,519;
0,17; 0,311).

При решении задач
в примерах 1, 2 предполагалось, что
вероятности переходов P_ij
остаются
постоянными. Такие марковские цепи
называются стационарными.
В противном
случае марковская цепь называется
нестационарной.

8

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ФИНАЛЬНЫЕ ВЕРОЯТНОСТИ ОДНОРОДНОЙ МАРКОВСКОЙ ЦЕПИ

Цель настоящего параграфа — описать понятия финального стационарного режима протекания случайного процесса в однородной марковской цепи и финальных вероятностей состояний, сформулировать достаточные условия их существования и вывести векторно-матричное уравнение, из которого можно определить финальные вероятности.

В приложении марковских процессов к финансово-экономическим ситуациям одним из важных факторов является довольно длительное протекание процесса, т.е. протекание процесса после окончания воздействия на него начальных условий. При некоторых условиях в конце концов устанавливается финальный стационарный режим процесса, при котором вероятности состояний системы уже не зависят ни от времени, ни от начального распределения вероятностей.

Определение 9.1. Вероятности состояний системы в финальном стационарном режиме называются финальными (или предельными, или стационарными) вероятностями и обозначаются через р_<, . р_п, а вектор (р_р . р_п), координатами которого служат финальные вероятности, называется финальным (или предельным, или стационарным) вектором.

Здесь мы рассмотрим случай однородной марковской цепи (см. § 2), т.е. систему S с дискретными состояниями s_p . s_n и с дискретным временем. Таким образом, система S может переходить (скачком) из состояния в состояние только в определенные моменты времени /_р . t_k. называемые шагами (см. определение 2.1).

вектор начального распределения вероятностей (см. определение 2.9) и

матрица переходных вероятностей /ь (из состояния s_f в состояние sj), не зависящих в силу однородности цепи от шагов /_р . t_k.

Теорема 9.1. Если существует финальный стационарный режим и, следовательно, существуют финальные вероятности, то для того, чтобы p_v —,р_п были финальными вероятностями, необходимо и достаточно, чтобы существовал т-й шаг, такой, что

Доказательство: Достаточность. Пусть существуют финальные вероятности. Пусть существует натуральное число т, для которого выполняется равенство (9.1). Из (2.4) при к = т + 2 и (9.1) имеем:

т.е. вектор (р_<, . р_п) не зависит от шагов, а это и означает, что p_v . р_п — финальные вероятности.

Необходимость. Пустьp_v . р_п — финальные вероятности. Тогда из их определения следует, что найдется m-й шаг, начиная с которого вероятности состояний не будут меняться и будут равны финальным. А это означает выполнение равенства (9.1). ?

Следствие 9.1. Если существуют финальные вероятности, то для того, чтобыр_<. р_п были финальными вероятностями, необходимо и достаточно, чтобы существовал т-й шаг, такой, что

Из (9.1) и (2.1) следует, что финальные вероятности удовлетворяют нормировочному условию

Теорема 9.2. Если существуют финальные вероятности, то финальные вектор (рj. ,р_п) можно найти из уравнения

где Р — матрица переходных вероятностей.

Доказательство: Так как финальные вероятности существуют, то найдется натуральное число т, такое, что выполняется равенство (9.1). Тогда из (2.4) при k = т + 1 имеем:

т.е. равенство (9.3) доказано. ?

Уравнение (9.3), решив которое можно найти финальные вероятности, было выведено только при условии существования последних. Сформулируем некоторые достаточные условия существования финальных вероятностей. Предварительно введем понятие регулярности марковской цепи.

Определение 9.2. Марковская цепь называется регулярной, если существует натуральное число т, такое, что любой элемент матрицы Р т положителен, за исключением, быть может, элементов, стоящих в столбцах, номера которых совпадают с номерами неустойчивых состояний системы S, т.е. состояний без входов (см. определение 1.9).

Пример 9.1 (нерегулярной цепи). Рассмотрим однородную марковскую цепь, размеченный граф состояний которой указан на рис. 9.1.

В данном случае у системы S нет неустойчивых состояний. Матрица переходных вероятностей имеет вид:

Отсюда понятно, что Р 4 = Р, Р 5 = Р 2 , Р в = Р 3 , Р 1 = Р, . . Таким образом, у системы S нет неустойчивых состояний и любая т-я степень Р т матрицы Р ее переходных вероятностей содержит нулевые элементы, а потому рассматриваемая марковская цепь не является регулярной. ?

Пример 9.2 (регулярной цепи). Рассмотрим однородную марковскую цепь с размеченным графом на рис. 9.2.

Состояние s₃ неустойчиво. Матрица переходных вероятностей

Мы видим, что при т = 2 каждый элемент матрицы Р т = Р 2 , кроме элементов третьего столбца, номер которого совпадает с номером неустойчивого состояния s₃, положителен. Следовательно, по определению регулярности, данная марковская цепь регулярна. ?

Приведем (без доказательства) следующую теорему, в которой сформулированы достаточные условия существования предельных вероятностей.

Теорема 9.3. Если однородная марковская цепь с конечным числом (п) состояний регулярна, то существуют финальные вероятности р_<, . р_п, причем

Таким образом, для нахождения финальных вероятностей целесообразно поступить следующим образом: сначала проверить марковскую цепь на регулярность и, если она таковой окажется, финальный стационарный вектор вероятностей можно найти из уравнения (9.3).

Пример 9.3. Марковская цепь, рассмотренная в примере 9.2, оказалась регулярной. Следовательно, по теореме 9.3, существуют финальные вероятности p_vp₂,p₃. Найдем их из уравнения (9.3) при п = 3 и матрице Р, задаваемой равенством (9.4):

Произведя умножение в правой части этого равенства, получим

Из первого уравнения

Итак, (р_< = (1/3)р₂; р₂; р_г = 0) — общее решение уравнения (9.5), зависящее от одного произвольного параметра р₂. Подберем этот параметр из нормировочного условия р^ +р₂+р^ = Отсюда

Подставив (9.7) в (9.6), найдем: р_< = 1/4. Но тогда из (9.7): р₂ = 3/4.

Итак, финальный вектор вероятностей состояний системы S имеет вид: (p_vp₂,p₃) = ( 1/4, 3/4, 0). ?

Обратим внимание на то, что в приведенном примере предельная вероятность неустойчивого состояния s₃ равна р₃ = 0. Это, очевидно, справедливо в общем случае любой системы.

Отметим, что у нерегулярной марковской цепи все же могут существовать предельные вероятности. Приведем подтверждающий пример.

Пример 9.4. Система S, граф состояний которой приведен на рис. 9.3, имеет поглощающее состояние s₃; поэтому рано или поздно она перейдет в это состояние и останется в нем навсегда; следовательно, для данной системы S финальные вероятности существуют и равны р j = /?₂ = 0, /?₃ = 1. Тем не менее рассматриваемая система не

является регулярной, ибо состояния s_l и s₂ не являются неустойчивыми, но элементы, стоящие на пересечениях третьей строки и первых двух столбцов любой степени Р т матрицы переходных вероятностей

очевидно равны нулю. ?

Приведем содержательный пример на вычисление предельных вероятностей.

Пример 9.5. (ср. [6, Упражнение 5, с. 220]).

Поведение рынка ценных бумаг обнаруживает следующую тенденцию: сделки, в которых цены возрастают, сменяются сделками, в которых цены падают. Наблюдения показали, что условная вероятность возрастания цен после предшествовавшего периода их падения равна 0,65, а условная вероятность падения цен после предшествовавшего периода их возрастания равна 0,6.

Определим соответствующие состояния, построим их размеченный граф, выпишем матрицу переходных вероятностей и найдем финальные вероятности состояний.

В качестве системы S будем рассматривать рынок ценных бумаг. Тогда система S может находиться только в двух состояниях: s _<— падение цен, И5₂– возрастание цен, и, следовательно, протекающий в системе S процесс является дискретным.

Предстоящее состояние, в которое перейдет система S, зависит (в существенном) от состояния, в котором она находится в настоящий момент времени; поэтому этот процесс является марковским.

Будем предполагать, что моменты времени /₂, /₃, . настолько близки друг к другу, что между ними система S не изменяет своего состояния и, следовательно, процесс, протекающий в системе S, с определенной погрешностью можно считать процессом с дискретным временем.

Условные вероятности 0,65 и 0,6, данные в условии примера, являются очевидно (см. определения 9.5) вероятностямир_п ир_2у

Тогда, используя нормировочное условие (2.2), при п = 2 для / = 1 и / = 2, получим:

Размеченный граф состояний системы S будет иметь следующий вид (рис. 9.4):

Матрица переходных вероятностей

Поскольку все элементы матрицы Р положительны, то система S регулярна и потому существуют предельные вероятности /), и р₂ соответственно состояний s, и s₂. Из уравнения (9.3) при п = 2 с матрицей Р, определяемой формулой (9.8), получаем:

Уравнения полученной системы пропорциональны (например, второе уравнение получается из первого умножением на -1), а потому одно из них, например второе, можно отбросить. Заменив второе уравнение нормировочным условием, получим систему

решив которую, найдем:

Таким образом, при достаточно длительном функционировании рынка ценных бумаг финальные вероятности падения и роста цен равны соответственно 0,48 и 0,52. При этом они не зависят от начального состояния рынка. ?

• • В финансово-экономической области случайные процессы в некоторых системах длятся довольно долго и при некоторых условиях переходят в финальный стационарный режим, при котором вероятности состояний системы уже не зависят ни от времени, ни от начального распределения вероятностей.
• • Характеристическим признаком финальных вероятностейр_<. р_п является существование шага т, такого, что выполняется равенство (9.1).
• • Финальные вероятности состояний, существующие при финальном стационарном режиме протекания случайного процесса, можно подсчитать по формуле (9.3).
• • Регулярность однородной марковской цепи гарантирует существование финальных вероятностей.
• • Однородная марковская цепь может не быть регулярной, но тем не менее финальные вероятности могут существовать.

КЛЮЧЕВЫЕ СЛОВА И ВЫРАЖЕНИЯ

Однородная марковская цепь; финальный стационарный режим случайного процесса; финальные вероятности состояний однородной марковской цепи; регулярная марковская цепь.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

• 1. Чем характеризуется финальный стационарный режим протекания случайного процесса в системе?
• 2. Дайте определение финальным вероятностям состояний системы.
• 3. Каковы необходимые и достаточные условия финальных вероятностей?
• 4. Какой вид имеет векторно-матричное уравнение, из которого можно определить финальные вероятности?
• 5. Каково определение регулярности марковской цепи?

• 6. Сформулируйте достаточные условия существования финальных вероятностей.
• 7. Является ли регулярность однородной марковской цепи необходимым условием существования финальных вероятностей?

Компания по прокату автомобилей выдает автомобили напрокат в трех аэропортах: А, В и С. Клиенты возвращают автомобили в эти аэропорты в соответствии с вероятностями, указанными в табл. 9.1.

Краткое введение в цепи Маркова

В 1998 году Лоуренс Пейдж, Сергей Брин, Раджив Мотвани и Терри Виноград опубликовали статью «The PageRank Citation Ranking: Bringing Order to the Web», в которой описали знаменитый теперь алгоритм PageRank, ставший фундаментом Google. Спустя чуть менее двух десятков лет Google стал гигантом, и даже несмотря на то, что его алгоритм сильно эволюционировал, PageRank по-прежнему является «символом» алгоритмов ранжирования Google (хотя только немногие люди могут действительно сказать, какой вес он сегодня занимает в алгоритме).

С теоретической точки зрения интересно заметить, что одна из стандартных интерпретаций алгоритма PageRank основывается на простом, но фундаментальном понятии цепей Маркова. Из статьи мы увидим, что цепи Маркова — это мощные инструменты стохастического моделирования, которые могут быть полезны любому эксперту по аналитическим данным (data scientist). В частности, мы ответим на такие базовые вопросы: что такое цепи Маркова, какими хорошими свойствами они обладают, и что с их помощью можно делать?

Краткий обзор

В первом разделе мы приведём базовые определения, необходимые для понимания цепей Маркова. Во втором разделе мы рассмотрим особый случай цепей Маркова в конечном пространстве состояний. В третьем разделе мы рассмотрим некоторые из элементарных свойств цепей Маркова и проиллюстрируем эти свойства на множестве мелких примеров. Наконец, в четвёртом разделе мы свяжем цепи Маркова с алгоритмом PageRank и увидим на искусственном примере, как цепи Маркова можно применять для ранжирования узлов графа.

Примечание. Для понимания этого поста необходимы знания основ вероятностей и линейной алгебры. В частности, будут использованы следующие понятия: условная вероятность, собственный вектор и формула полной вероятности.

Что такое цепи Маркова?

Случайные переменные и случайные процессы

Прежде чем вводить понятие цепей Маркова, давайте вкратце вспомним базовые, но важные понятия теории вероятностей.

Во-первых, вне языка математики случайной величиной X считается величина, которая определяется результатом случайного явления. Его результатом может быть число (или «подобие числа», например, векторы) или что-то иное. Например, мы можем определить случайную величину как результат броска кубика (число) или же как результат бросания монетки (не число, если только мы не обозначим, например, «орёл» как 0, а «решку» как 1). Также упомянем, что пространство возможных результатов случайной величины может быть дискретным или непрерывным: например, нормальная случайная величина непрерывна, а пуассоновская случайная величина дискретна.

Далее мы можем определить случайный процесс (также называемый стохастическим) как набор случайных величин, проиндексированных множеством T, которое часто обозначает разные моменты времени (в дальнейшем мы будем считать так). Два самых распространённых случая: T может быть или множеством натуральных чисел (случайный процесс с дискретным временем), или множеством вещественных чисел (случайный процесс с непрерывным временем). Например, если мы будем бросать монетку каждый день, то зададим случайный процесс с дискретным временем, а постоянно меняющаяся стоимость опциона на бирже задаёт случайный процесс с непрерывным временем. Случайные величины в разные моменты времени могут быть независимыми друг от друга (пример с подбрасыванием монетки), или иметь некую зависимость (пример со стоимостью опциона); кроме того, они могут иметь непрерывное или дискретное пространство состояний (пространство возможных результатов в каждый момент времени).

Разные виды случайных процессов (дискретные/непрерывные в пространстве/времени).

Марковское свойство и цепь Маркова

Существуют хорошо известные семейства случайных процессов: гауссовы процессы, пуассоновские процессы, авторегрессивные модели, модели скользящего среднего, цепи Маркова и другие. Каждое из этих отдельных случаев имеет определённые свойства, позволяющие нам лучше исследовать и понимать их.

Одно из свойств, сильно упрощающее исследование случайного процесса — это «марковское свойство». Если объяснять очень неформальным языком, то марковское свойство сообщает нам, что если мы знаем значение, полученное каким-то случайным процессом в заданный момент времени, то не получим никакой дополнительной информации о будущем поведении процесса, собирая другие сведения о его прошлом. Более математическим языком: в любой момент времени условное распределение будущих состояний процесса с заданными текущим и прошлыми состояниями зависит только от текущего состояния, но не от прошлых состояний (свойство отсутствия памяти). Случайный процесс с марковским свойством называется марковским процессом.

Марковское свойство обозначает, что если мы знаем текущее состояние в заданный момент времени, то нам не нужна никакая дополнительная информация о будущем, собираемая из прошлого.

На основании этого определения мы можем сформулировать определение «однородных цепей Маркова с дискретным временем» (в дальнейшем для простоты мы их будем называть «цепями Маркова»). Цепь Маркова — это марковский процесс с дискретным временем и дискретным пространством состояний. Итак, цепь Маркова — это дискретная последовательность состояний, каждое из которых берётся из дискретного пространства состояний (конечного или бесконечного), удовлетворяющее марковскому свойству.

Математически мы можем обозначить цепь Маркова так:

где в каждый момент времени процесс берёт свои значения из дискретного множества E, такого, что

Тогда марковское свойство подразумевает, что у нас есть

Снова обратите внимание, что эта последняя формула отражает тот факт, что для хронологии (где я нахожусь сейчас и где я был раньше) распределение вероятностей следующего состояния (где я буду дальше) зависит от текущего состояния, но не от прошлых состояний.

Примечание. В этом ознакомительном посте мы решили рассказать только о простых однородных цепях Маркова с дискретным временем. Однако существуют также неоднородные (зависящие от времени) цепи Маркова и/или цепи с непрерывным временем. В этой статье мы не будем рассматривать такие вариации модели. Стоит также заметить, что данное выше определение марковского свойства чрезвычайно упрощено: в истинном математическом определении используется понятие фильтрации, которое выходит далеко за пределы нашего вводного знакомства с моделью.

Характеризуем динамику случайности цепи Маркова

В предыдущем подразделе мы познакомились с общей структурой, соответствующей любой цепи Маркова. Давайте посмотрим, что нам нужно, чтобы задать конкретный «экземпляр» такого случайного процесса.

Сначала заметим, что полное определение характеристик случайного процесса с дискретным временем, не удовлетворяющего марковскому свойству, может быть сложным занятием: распределение вероятностей в заданный момент времени может зависеть от одного или нескольких моментов в прошлом и/или будущем. Все эти возможные временные зависимости потенциально могут усложнить создание определения процесса.

Однако благодаря марковскому свойству динамику цепи Маркова определить довольно просто. И в самом деле. нам нужно определить только два аспекта: исходное распределение вероятностей (то есть распределение вероятностей в момент времени n=0), обозначаемое

и матрицу переходных вероятностей (которая даёт нам вероятности того, что состояние в момент времени n+1 является последующим для другого состояния в момент n для любой пары состояний), обозначаемую

Если два этих аспекта известны, то полная (вероятностная) динамика процесса чётко определена. И в самом деле, вероятность любого результата процесса тогда можно вычислить циклически.

Пример: допустим, мы хотим знать вероятность того, что первые 3 состояния процесса будут иметь значения (s0, s1, s2). То есть мы хотим вычислить вероятность

Здесь мы применяем формулу полной вероятности, гласящую, что вероятность получения (s0, s1, s2) равна вероятности получения первого s0, умноженного на вероятность получения s1 с учётом того, что ранее мы получили s0, умноженного на вероятность получения s2 с учётом того, что мы получили ранее по порядку s0 и s1. Математически это можно записать как

И затем проявляется упрощение, определяемое марковским допущением. И в самом деле, в случае длинных цепей мы получим для последних состояний сильно условные вероятности. Однако в случае цепей Маркова мы можем упростить это выражение, воспользовавшись тем, что

получив таким образом

Так как они полностью характеризуют вероятностную динамику процесса, многие сложные события можно вычислить только на основании исходного распределения вероятностей q0 и матрицы переходной вероятности p. Стоит также привести ещё одну базовую связь: выражение распределения вероятностей во время n+1, выраженное относительно распределения вероятностей во время n

Цепи Маркова в конечных пространствах состояний

Представление в виде матриц и графов

Здесь мы допустим, что во множестве E есть конечное количество возможных состояний N:

Тогда исходное распределение вероятностей можно описать как вектор-строку q0 размером N, а переходные вероятности можно описать как матрицу p размером N на N, такую что

Преимущество такой записи заключается в том, что если мы обозначим распределение вероятностей на шаге n вектором-строкой qn, таким что его компоненты задаются

тогда простые матричные связи при этом сохраняются

(здесь мы не будем рассматривать доказательство, но воспроизвести его очень просто).

Если умножить справа вектор-строку, описывающий распределение вероятностей на заданном этапе времени, на матрицу переходных вероятностей, то мы получим распределение вероятностей на следующем этапе времени.

Итак, как мы видим, переход распределения вероятностей из заданного этапа в последующий определяется просто как умножение справа вектора-строки вероятностей исходного шага на матрицу p. Кроме того, это подразумевает, что у нас есть

Динамику случайности цепи Маркова в конечном пространстве состояний можно с лёгкостью представить как нормированный ориентированный граф, такой что каждый узел графа является состоянием, а для каждой пары состояний (ei, ej) существует ребро, идущее от ei к ej, если p(ei,ej)>0. Тогда значение ребра будет той же вероятностью p(ei,ej).

Пример: читатель нашего сайта

Давайте проиллюстрируем всё это простым примером. Рассмотрим повседневное поведение вымышленного посетителя сайта. В каждый день у него есть 3 возможных состояния: читатель не посещает сайт в этот день (N), читатель посещает сайт, но не читает пост целиком (V) и читатель посещает сайт и читает один пост целиком (R ). Итак, у нас есть следующее пространство состояний:

Допустим, в первый день этот читатель имеет вероятность 50% только зайти на сайт и вероятность 50% посетить сайт и прочитать хотя бы одну статью. Вектор, описывающий исходное распределение вероятностей (n=0) тогда выглядит так:

Также представим, что наблюдаются следующие вероятности:

• когда читатель не посещает один день, то имеет вероятность 25% не посетить его и на следующий день, вероятность 50% только посетить его и 25% — посетить и прочитать статью
• когда читатель посещает сайт один день, но не читает, то имеет вероятность 50% снова посетить его на следующий день и не прочитать статью, и вероятность 50% посетить и прочитать
• когда читатель посещает и читает статью в один день, то имеет вероятность 33% не зайти на следующий день (надеюсь, этот пост не даст такого эффекта!), вероятность 33% только зайти на сайт и 34% — посетить и снова прочитать статью

Тогда у нас есть следующая переходная матрица:

Из предыдущего подраздела мы знаем как вычислить для этого читателя вероятность каждого состояния на следующий день (n=1)

Вероятностную динамику этой цепи Маркова можно графически представить так:

Представление в виде графа цепи Маркова, моделирующей поведение нашего придуманного посетителя сайта.

Свойства цепей Маркова

В этом разделе мы расскажем только о некоторых самых базовых свойствах или характеристиках цепей Маркова. Мы не будем вдаваться в математические подробности, а представим краткий обзор интересных моментов, которые необходимо изучить для использования цепей Маркова. Как мы видели, в случае конечного пространства состояний цепь Маркова можно представить в виде графа. В дальнейшем мы будем использовать графическое представление для объяснения некоторых свойств. Однако не стоит забывать, что эти свойства необязательно ограничены случаем конечного пространства состояний.

Разложимость, периодичность, невозвратность и возвратность

В этом подразделе давайте начнём с нескольких классических способов характеризации состояния или целой цепи Маркова.

Во-первых, мы упомянем, что цепь Маркова неразложима, если можно достичь любого состояния из любого другого состояния (необязательно, что за один шаг времени). Если пространство состояний конечно и цепь можно представить в виде графа, то мы можем сказать, что граф неразложимой цепи Маркова сильно связный (теория графов).

Иллюстрация свойства неразложимости (несокращаемости). Цепь слева нельзя сократить: из 3 или 4 мы не можем попасть в 1 или 2. Цепь справа (добавлено одно ребро) можно сократить: каждого состояния можно достичь из любого другого.

Состояние имеет период k, если при уходе из него для любого возврата в это состояние нужно количество этапов времени, кратное k (k — наибольший общий делитель всех возможных длин путей возврата). Если k = 1, то говорят, что состояние является апериодическим, а вся цепь Маркова является апериодической, если апериодичны все её состояния. В случае неприводимой цепи Маркова можно также упомянуть, что если одно состояние апериодическое, то и все другие тоже являются апериодическими.

Иллюстрация свойства периодичности. Цепь слева периодична с k=2: при уходе из любого состояния для возврата в него всегда требуется количество шагов, кратное 2. Цепь справа имеет период 3.

Состояние является невозвратным, если при уходе из состояния существует ненулевая вероятность того, что мы никогда в него не вернёмся. И наоборот, состояние считается возвратным, если мы знаем, что после ухода из состояния можем в будущем вернуться в него с вероятностью 1 (если оно не является невозвратным).

Иллюстрация свойства возвратности/невозвратности. Цепь слева имеет такие свойства: 1, 2 и 3 невозвратны (при уходе из этих точек мы не можем быть абсолютно уверены, что вернёмся в них) и имеют период 3, а 4 и 5 возвратны (при уходе из этих точек мы абсолютно уверены, что когда-нибудь к ним вернёмся) и имеют период 2. Цепь справа имеет ещё одно ребро, делающее всю цепь возвратной и апериодической.

Для возвратного состояния мы можем вычислить среднее время возвратности, которое является ожидаемым временем возврата при покидании состояния. Заметьте, что даже вероятность возврата равна 1, то это не значит, что ожидаемое время возврата конечно. Поэтому среди всех возвратных состояний мы можем различать положительные возвратные состояния (с конечным ожидаемым временем возврата) и нулевые возвратные состояния (с бесконечным ожидаемым временем возврата).

Стационарное распределение, предельное поведение и эргодичность

В этом подразделе мы рассмотрим свойства, характеризующие некоторые аспекты (случайной) динамики, описываемой цепью Маркова.

Распределение вероятностей π по пространству состояний E называют стационарным распределением, если оно удовлетворяет выражению

Так как у нас есть

Тогда стационарное распределение удовлетворяет выражению

По определению, стационарное распределение вероятностей со временем не изменяется. То есть если исходное распределение q является стационарным, тогда оно будет одинаковых на всех последующих этапах времени. Если пространство состояний конечно, то p можно представить в виде матрицы, а π — в виде вектора-строки, и тогда мы получим

Это снова выражает тот факт, что стационарное распределение вероятностей со временем не меняется (как мы видим, умножение справа распределения вероятностей на p позволяет вычислить распределение вероятностей на следующем этапе времени). Учтите, что неразложимая цепь Маркова имеет стационарное распределение вероятностей тогда и только тогда, когда одно из её состояний является положительным возвратным.

Ещё одно интересное свойство, связанное с стационарным распределением вероятностей, заключается в следующем. Если цепь является положительной возвратной (то есть в ней существует стационарное распределение) и апериодической, тогда, какими бы ни были исходные вероятности, распределение вероятностей цепи сходится при стремлении интервалов времени к бесконечности: говорят, что цепь имеет предельное распределение, что является ничем иным, как стационарным распределением. В общем случае его можно записать так:

Ещё раз подчеркнём тот факт, что мы не делаем никаких допущений об исходном распределении вероятностей: распределение вероятностей цепи сводится к стационарному распределению (равновесному распределению цепи) вне зависимости от исходных параметров.

Наконец, эргодичность — это ещё одно интересное свойство, связанное с поведением цепи Маркова. Если цепь Маркова неразложима, то также говорится, что она «эргодическая», потому что удовлетворяет следующей эргодической теореме. Допустим, у нас есть функция f(.), идущая от пространства состояний E к оси (это может быть, например, цена нахождения в каждом состоянии). Мы можем определить среднее значение, перемещающее эту функцию вдоль заданной траектории (временное среднее). Для n-ных первых членов это обозначается как

Также мы можем вычислить среднее значение функции f на множестве E, взвешенное по стационарному распределению (пространственное среднее), которое обозначается

Тогда эргодическая теорема говорит нам, что когда траектория становится бесконечно длинной, временное среднее равно пространственному среднему (взвешенному по стационарному распределению). Свойство эргодичности можно записать так:

Иными словами, оно обозначает, что в пределе ранее поведение траектории становится несущественным и при вычислении временного среднего важно только долговременное стационарное поведение.

Вернёмся к примеру с читателем сайта

Снова рассмотрим пример с читателем сайта. В этом простом примере очевидно, что цепь неразложима, апериодична и все её состояния положительно возвратны.

Чтобы показать, какие интересные результаты можно вычислить с помощью цепей Маркова, мы рассмотрим среднее время возвратности в состояние R (состояние «посещает сайт и читает статью»). Другими словами, мы хотим ответить на следующий вопрос: если наш читатель в один день заходит на сайт и читает статью, то сколько дней нам придётся ждать в среднем того, что он снова зайдёт и прочитает статью? Давайте попробуем получить интуитивное понятие о том, как вычисляется это значение.

Сначала мы обозначим

Итак, мы хотим вычислить m(R,R). Рассуждая о первом интервале, достигнутом после выхода из R, мы получим

Однако это выражение требует, чтобы для вычисления m(R,R) мы знали m(N,R) и m(V,R). Эти две величины можно выразить аналогичным образом:

Итак, у нас получилось 3 уравнения с 3 неизвестными и после их решения мы получим m(N,R) = 2.67, m(V,R) = 2.00 и m(R,R) = 2.54. Значение среднего времени возвращения в состояние R тогда равно 2.54. То есть с помощью линейной алгебры нам удалось вычислить среднее время возвращения в состояние R (а также среднее время перехода из N в R и среднее время перехода из V в R).

Чтобы закончить с этим примером, давайте посмотрим, каким будет стационарное распределение цепи Маркова. Чтобы определить стационарное распределение, нам нужно решить следующее уравнение линейной алгебры:

То есть нам нужно найти левый собственный вектор p, связанный с собственным вектором 1. Решая эту задачу, мы получаем следующее стационарное распределение:

Стационарное распределение в примере с читателем сайта.

Можно также заметить, что π( R ) = 1/m(R,R), и если немного поразмыслить, то это тождество довольно логично (но подробно об этом мы говорить не будем).

Поскольку цепь неразложима и апериодична, это означает, что в длительной перспективе распределение вероятностей сойдётся к стационарному распределению (для любых исходных параметров). Иными словами, каким бы ни было исходное состояние читателя сайта, если мы подождём достаточно долго и случайным образом выберем день, то получим вероятность π(N) того, что читатель не зайдёт на сайт в этот день, вероятность π(V) того, что читатель зайдёт, но не прочитает статью, и вероятность π® того, что читатель зайдёт и прочитает статью. Чтобы лучше уяснить свойство сходимости, давайте взглянем на следующий график, показывающий эволюцию распределений вероятностей, начинающихся с разных исходных точек и (быстро) сходящихся к стационарному распределению:

Визуализация сходимости 3 распределений вероятностей с разными исходными параметрами (синяя, оранжевая и зелёная) к стационарному распределению (красная).

Классический пример: алгоритм PageRank

Настало время вернуться к PageRank! Но прежде чем двигаться дальше, стоит упомянуть, что интерпретация PageRank, данная в этой статье, не единственно возможная, и авторы оригинальной статьи при разработке методики не обязательно рассчитывали на применение цепей Маркова. Однако наша интерпретация хороша тем, что очень понятна.

Произвольный веб-пользователь

PageRank пытается решить следующую задачу: как нам ранжировать имеющееся множество (мы можем допустить, что это множество уже отфильтровано, например, по какому-то запросу) с помощью уже существующих между страницами ссылок?

Чтобы решить эту задачу и иметь возможность отранжировать страницы, PageRank приблизительно выполняет следующий процесс. Мы считаем, что произвольный пользователь Интернета в исходный момент времени находится на одной из страниц. Затем этот пользователь начинает случайным образом начинает перемещаться, щёлкая на каждой странице по одной из ссылок, которые ведут на другую страницу рассматриваемого множества (предполагается, что все ссылки, ведущие вне этих страниц, запрещены). На любой странице все допустимые ссылки имеют одинаковую вероятность нажатия.

Так мы задаём цепь Маркова: страницы — это возможные состояния, переходные вероятности задаются ссылками со страницы на страницу (взвешенными таким образом, что на каждой странице все связанные страницы имеют одинаковую вероятность выбора), а свойства отсутствия памяти чётко определяются поведением пользователя. Если также предположить, что заданная цепь положительно возвратная и апериодичная (для удовлетворения этим требованиям применяются небольшие хитрости), тогда в длительной перспективе распределение вероятностей «текущей страницы» сходится к стационарному распределению. То есть какой бы ни была начальная страница, спустя длительное время каждая страница имеет вероятность (почти фиксированную) стать текущей, если мы выбираем случайный момент времени.

В основе PageRank лежит такая гипотеза: наиболее вероятные страницы в стационарном распределении должны быть также и самыми важными (мы посещаем эти страницы часто, потому что они получают ссылки со страниц, которые в процессе переходов тоже часто посещаются). Тогда стационарное распределение вероятностей определяет для каждого состояния значение PageRank.

Искусственный пример

Чтобы это стало намного понятнее, давайте рассмотрим искусственный пример. Предположим, что у нас есть крошечный веб-сайт с 7 страницами, помеченными от 1 до 7, а ссылки между этими страницами соответствуют следующему графу.

Ради понятности вероятности каждого перехода в показанной выше анимации не показаны. Однако поскольку подразумевается, что «навигация» должна быть исключительно случайной (это называют «случайным блужданием»), то значения можно легко воспроизвести из следующего простого правила: для узла с K исходящими ссылками (странице с K ссылками на другие страницы) вероятность каждой исходящей ссылки равна 1/K. То есть переходная матрица вероятностей имеет вид:

где значения 0.0 заменены для удобства на “.”. Прежде чем выполнять дальнейшие вычисления, мы можем заметить, что эта цепь Маркова является неразложимой и апериодической, то есть в длительной перспективе система сходится к стационарному распределению. Как мы видели, можно вычислить это стационарное распределение, решив следующую левую задачу собственного вектора

Сделав так, мы получим следующие значения PageRank (значения стационарного распределения) для каждой страницы

Значения PageRank, вычисленные для нашего искусственного примера из 7 страниц.

Тогда ранжирование PageRank этого крошечного веб-сайта имеет вид 1 > 7 > 4 > 2 > 5 = 6 > 3.

Выводы

Основные выводы из этой статьи:

• случайные процессы — это наборы случайных величин, часто индексируемые по времени (индексы часто обозначают дискретное или непрерывное время)
• для случайного процесса марковское свойство означает, что при заданном текущем вероятность будущего не зависит от прошлого (это свойство также называется «отсутствием памяти»)
• цепь Маркова с дискретным временем — это случайные процессы с индексами дискретного времени, удовлетворяющие марковскому свойству
• марковское свойство цепей Маркова сильно облегчает изучение этих процессов и позволяет вывести различные интересные явные результаты (среднее время возвратности, стационарное распределение…)
• одна из возможных интерпретаций PageRank (не единственная) заключается в имитации веб-пользователя, случайным образом перемещающегося от страницы к странице; при этом показателем ранжирования становится индуцированное стационарное распределение страниц (грубо говоря, на самые посещаемые страницы в устоявшемся состоянии должны ссылаться другие часто посещаемые страницы, а значит, самые посещаемые должны быть наиболее релевантными)

В заключение ещё раз подчеркнём, насколько мощным инструментом являются цепи Маркова при моделировании задач, связанных со случайной динамикой. Благодаря их хорошим свойствам они используются в различных областях, например, в теории очередей (оптимизации производительности телекоммуникационных сетей, в которых сообщения часто должны конкурировать за ограниченные ресурсы и ставятся в очередь, когда все ресурсы уже заняты), в статистике (хорошо известные методы Монте-Карло по схеме цепи Маркова для генерации случайных переменных основаны на цепях Маркова), в биологии (моделирование эволюции биологических популяций), в информатике (скрытые марковские модели являются важными инструментами в теории информации и распознавании речи), а также в других сферах.

Разумеется, огромные возможности, предоставляемые цепями Маркова с точки зрения моделирования и вычислений, намного шире, чем рассмотренные в этом скромном обзоре. Поэтому мы надеемся, что нам удалось пробудить у читателя интерес к дальнейшему изучению этих инструментов, которые занимают важное место в арсенале учёного и эксперта по данным.

Теория массового обслуживания

Теория массового обслуживания

§1. Марковские цепи с конечным числом состояний и дискретным временем.

Пусть некоторая система S может находиться в одном из состояний конечного (или счетного) множества возможных состояний S1, S2,…, Sn, а переход из одного состояния в другое возможен только в определенные дискретные моменты времени t1, t2, t3, …, называемые шагами.

Если система переходит из одного состояния в другое случайно, то говорят, что имеет место случайный процесс с дискретным временем.

Случайный процесс называется марковским, если вероятность перехода из любого состояния Si в любое состояние Sj не зависит от того, как и когда система S попала в состояние Si (т. е. в системе S отсутствует последствие). В таком случае говорят, что функционирование системы S описывается дискретной цепью Маркова.

Переходы системы S в различные состояния удобно изображать с помощью графа состояний (рис.1).

Рис. 1

Вершины графа S1, S2, S3 обозначают возможные состояния системы. Стрелка, направленная из вершины Si в вершину Sj обозначает переход Si → Sj; число, стоящее рядом со стрелкой, обозначает величину вероятности этого перехода. Стрелка, замыкающаяся на i-той вершине графа, обозначает, что система остается в состоянии Si с вероятностью, стоящей у стрелки.

Графу системы, содержащему n вершин, можно поставить в соответствие матрицу n´n, элементами которой являются вероятности переходов pij между вершинами графа. Например, граф на рис.1 описывается матрицей P:

,

называемой матрицей вероятностей переходов. Элементы матрицы pij удовлетворяют условиям:

(1.1)

(1.2)

Условие (1.1) – обычное свойство вероятностей, а условие (1.2) (сумма элементов любой стрелки равна 1) означает, что система S обязательно либо переходит их какого-то состояния Si в другое состояние, либо остается в состоянии Si.

Элементы матрицы дают вероятности переходов в системе за один шаг. Переход Si → Sj за два шага можно рассматривать как происходящий на первом шаге из Si в некоторое промежуточное состояние Sk и на втором шаге из Sk в Si. Таким образом, для элементов матрицы вероятностей переходов из Si в Sj за два шага получим:

(1.3)

В общем случае перехода Si → Sj за m шагов для элементов матрицы вероятностей переходов справедлива формула:

, 1 ≤ l ≤ m

Полагая в (1.4) l = 1 и l = m – 1 получим два эквивалентных выражения для :

(1.5)

. (1.6)

Пример 1. Для графа на рис.1 найти вероятность перехода системы из состояния S1 в состояние S2 за 3 шага.

Решение. Вероятность перехода S1 → S2 за 1 шаг равна . Найдем вначале , используя формулу (1.5), в которой полагаем m = 2.

Аналогично .

Как видно из этой формулы, в дополнение к необходимо вычислить также и :

.

Ответ: Вероятность перехода S1 → S2 после третьего шага равна 0,183.

Пусть система S описывается матрицей вероятностей переходов Р

.

Если обозначить через P(m) матрицу, элементами которой являются – вероятности переходов из Si в Sj за m шагов, то справедлива формула

где матрица Pm получается умножением матрицы P саму на себя m раз.

Исходное состояние системы характеризуется вектором состояния системы (называемым также стохастическим вектором).

где qj-вероятность того, что исходным состоянием системы является Sj состояние. Аналогично (1.1) и (1.2) справедливы соотношения

0 ≤ qi ≤1;

Обозначим через

вектор состояния системы после m шагов, где – вероятность того, что после m шагов система находится в Si состоянии. Тогда справедлива формула

(1.8)

Пример 2. Найти вектор состояния системы, изображенный на рис.1 после двух шагов.

Решение. Исходное состояние системы характеризуется вектором =(0,7; 0; 0,3). После первого шага (m = 1) система перейдет в состояние

После второго шага система окажется в состоянии

Ответ: Состояние системы S после двух шагов характеризуется вектором (0,519; 0,17; 0,311).

При решении задач в примерах 1, 2 предполагалось, что вероятности переходов Pij остаются постоянными. Такие марковские цепи называются стационарными. В противном случае марковская цепь называется нестационарной.

§2. Марковские цепи с конечным числом состояний и непрерывным временем.

Если система S может переходить в другое состояние случайным образом в произвольный момент времени, то говорят о случайном процессе с непрерывным временем. В отсутствии последействия такой процесс называется непрерывной марковской цепью. При этом вероятности переходов Si → Sj для любых i и j в любой момент времени равны нулю (в силу непрерывности времени). По этой причине вместо вероятности перехода Pij вводится величина λij – плотность вероятности перехода из состояния Si в состояние Sj, определяемая как предел

; (i ≠ j). (2.1)

Если величины λij не зависят от t, то марковский процесс называется однородным. Если за время Δt система может изменить свое состояние не более чем один раз, то говорят, что случайный процесс является ординарным. Величину λij называют интенсивностью перехода системы из Si в Sj. На графе состояний системы численные значения λij ставят рядом со стрелками, показывающими переходы в вершины графа (рис. 2).

λ12=1

Рис. 2

Зная интенсивности переходов можно найти величины p1(t), p2(t),…, pn(t) – вероятности нахождения системы S в состояниях S1, S2,…, Sn соответственно. При этом выполняется условие

(2.2)

Распределение вероятностей состояний системы, которое можно характеризовать вектором называется стационарным, если оно не зависит от времени, т. е. все компоненты вектора являются константами.

Состояния Si и Sj называются сообщающимися, если возможны переходы Si ↔ Sj (на рис. 2 сообщающимися являются состояния S1 и S2, а S1, S3 и S2, S3 такими не являются).

Состояние Si называется существенным, если всякое Sj, достижимое из Si, является сообщающимся с Si. Состояние Si называется несущественным, если оно не является существенным (на рис. 2 существенными являются состояния S1 и S2).

Если существуют предельные вероятности состояний системы

(2.3)

не зависящие от начального состояния системы, то говорят, что при t → ∞ в системе устанавливается стационарный режим.

Система, в которой существуют предельные (финальные) вероятности состояний системы, называется эргодической, а протекающий в ней случайный процесс эргодическим.

Теорема 1. Если Si – несущественное состояние, то

(2.4)

т. е. при t → ∞ система выходит из любого несущественного состояния (для системы на рис. 2 т. к. S3 – несущественное состояние).

Теорема 2. Чтобы система с конечным числом состояний имела единственное предельное распределение вероятностей состояний, необходимо и достаточно, чтобы все ее существенные состояния сообщались между собой (система на рис.2 удовлетворяет этому условию, т. к. существенные состояния S1 и S2 сообщаются между собой).

Если случайный процесс, происходящий в системе с дискретными состояниями является непрерывной марковской цепью, то для вероятностей p1(t), p2(t),…, pn(t) можно составить систему линейных дифференциальных уравнений, называемых уравнениями Колмогорова. При составлении уравнений удобно пользоваться графом состояний системы. Рассмотрим получение уравнений Колмогорова на конкретном примере.

Пример 3. Записать уравнения Колмогорова для системы, изображенной на рис.2. Найти финальные вероятности для состояний системы.

Решение. Рассмотрим вначале вершину графа S1. Вероятность p1(t + Δt) того, что система в момент времени (t + Δt) будет находиться в состоянии S1 достигается двумя способами:

а) система в момент времени t с вероятностью p1(t) находилась в состоянии S1 и за малое время Δt не перешла в состояние S2. Из состояния S1 система может быть выведена потоком интенсивностью λ12; вероятность выхода системы из состояния S1 за время Δt при этом равна (с точностью до величин более высокого порядка малости по Δt) λ12 Δt, а вероятность невыхода из состояния S1 будет равна (1 – λ12 Δt). При этом вероятность того, что система останется в состоянии S1, согласно теореме об умножении вероятностей будет равна p1(t) (1 – λ12 Δt).

б) система в момент времени t находилась в состоянии S2 и за время Δt под воздействием потока λ21 перешла в состояние S1 с вероятностью λ21 Δt. Вероятность того, что система будет находиться в состоянии S1 равна p2(t)∙λ21Δt.

в) система в момент времени t находилась в состоянии S3 и за время Δt под воздействием потока λ31 перешла в состояние S1 с вероятностью λ31 Δt. Вероятность того, что система будет находиться в состоянии S1 равна p3(t)∙λ31Δt.

По теореме сложения вероятностей получим:

p1(t + Δt) = p1(t) (1 – λ12 Δt) + p2(t) (1 – λ21 Δt) + p3(t) (1 – λ31 Δt);

p1(t + Δt) – p1(t) = (-p1(t)·λ12 + p2(t) λ21 + p3(t) λ31) Δt

Переходя к пределу Δt → 0, получим

(2.5)

Аналогично, рассматривая вершины графа S2 и S3 , получим уравнения

, (2.6)

(2.7)

К уравнениям (2.5) – (2.7) следует добавить уравнение (2.2), имеющее в данном случае вид

Уравнение (2.8) выполняет роль нормировочного условия, накладываемого на вероятности pj.

Решение системы уравнений (2.5) – (2.8) в зависимости от времени можно найти либо аналитически, либо численно с учетом начальных условий. Мы найдем лишь финальные вероятности pj, которые по определению при t → ∞ не зависят от времени. При этом в (2.5) – (2.7) dpi/dt = 0 (j = 1, 2, 3). Получившиеся при этом три алгебраических уравнения являются однородными, поэтому одно из них можно отбросить. Отбросим, например, уравнение, получающееся из (2.6), а вместо него запишем уравнение (2.8). В результате система уравнений для финальных вероятностей примет вид

Из последнего уравнения следует, что p3 = 0. Решая оставшиеся уравнения, получим p1= 2/3, p2 = 1/3.

Ответ: вектор состояния системы в стационарном режиме равен

С учетом рассмотренного примера сформулируем общее правило составления уравнений Колмогорова:

В левой части каждого из них стоит производная вероятности какого-то (j-го) состояния. В правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков, минус суммарная интенсивность всех потоков, выводящих систему из данного (j-го) состояния, умноженная на вероятность данного (j-го) состояния.

§3. Процессы рождения и гибели.

Так называется широкий класс случайных процессов, происходящих в системе, размеченный граф состояний которой изображен на рис. 3.

λ0 λ1 λ2 λg-2 λ g-1

μ0 μ1 μ2 μg-2 μg-1

Здесь величины λ0, λ1,…, λg-1 – интенсивности переходов системы из состояния в состояние слева направо, можно интерпретировать как интенсивности рождения (возникновения заявок) в системе. Аналогично, величины μ0, μ 1,…, μ g-1 – интенсивности переходов системы из состояния в состояние справа налево, можно интерпретировать как интенсивности гибели (выполнения заявок) в системе.

Поскольку все состояния являются сообщающимися и существенными, существует (в силу теоремы 2) предельное (финальное) распределение вероятностей состояний. Получим формулы для финальных вероятностей состояний системы.

В стационарных условиях для каждого состояния поток, втекающий в данное состояние должен равняться потоку, вытекающему из данного состояния. Таким образом, имеем:

для состояния S0 :

p0∙λ0Δt = p1∙μ 0Δt;λ0 p0 = μ 0 p1;

для состояния S1:

р1·(λ1 + μ 0)Δt = p0∙λ0Δt + p2∙μ1·Δt;(λ1 + μ 0) p1 = λ0 p0 + μ1p2.

Последнее уравнение с учётом предыдущего можно привести к виду λ1 p1 = μ1p2. Аналогично можно получить уравнения для остальных состояний системы. В результате получится система уравнений:

(3.1)

Последнее уравнение в (3.1) является очевидным условием (2.2). Решение системы уравнений (3.1) имеет вид:

(3.2)

(3.3)

§4. Основные понятия и классификация систем массового обслуживания. Простейший поток заявок.

Заявкой (или требованием) называется спрос на удовлетворение какой-либо потребности (далее потребности предполагаются однотипными). Выполнение заявки называется обслуживанием заявки.

Системой массового обслуживания (СМО) называется любая система для выполнения заявок, поступающих в неё в случайные моменты времени.

Поступление заявки в СМО называется событием. Последовательность событий, заключающихся в поступлении заявок в СМО, называется входящим потоком заявок. Последовательность событий, заключающихся в выполнении заявок в СМО, называется выходящим потоком заявок.

Поток заявок называется простейшим, если он удовлетворяет следующим условиям:

1)отсутствие последействия, т. е. заявки поступают независимо друг от друга;

2)стационарность, т. е. вероятность поступления данного числа заявок на любом временнóм отрезке [t1, t2] зависит лишь от величины этого отрезка и не зависит от значения t1, что позволяет говорить о среднем числе заявок за единицу времени, l, называемом интенсивностью потока заявок;

3)ординарность, т. е. в любой момент времени в СМО поступает лишь одна заявка, а поступление одновременно двух и более заявок пренебрежимо мало.

Для простейшего потока вероятность pi(t) поступления в СМО ровно i заявок за время t вычисляется по формуле

(4.1)

т. е. вероятности распределены по закону Пуассона с параметром lt. По этой причине простейший поток называется также пуассоновским потоком.

Функция распределения F(t) случайного интервала времени T между двумя последовательными заявками по определению равна F(t) = P(T 0),

а математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины T равны соответственно

(4.4)

Пример 4. В справочное бюро обращается в среднем 2 человека за 10 минут. Найти вероятность того, что за 30 минут за справкой обратится:

а) 4 человека, б) не менее 3-х человек.

Решение. Интенсивность потока заявок равна λ = 2/10 мин = 0,2[мин-1]. Для решения используем формулу (4.1), где полагаем t = T = 30 минут; для пункта (а) i = 4, для пункта (б) i = 3, 4, 5,… .

а) ;

б) при решении этого пункта целесообразно использовать противоположную вероятность:

.

Пример 5. В приборе имеются два блока, работающих независимо друг от друга. Время безотказной работы определяется показательным законом. Среднее время безотказной работы 1-го блока – t1 = 2 года, 2-го – t2 = 1 год. Найти вероятность того, что за 1,5 года: а) не откажет ни один из блоков; б) откажет только 2-й блок; в) откажут оба блока.

Решение: В качестве события выступает неисправность какого-то блока. Вероятность p(i) (t) исправности i-го блока в течение времени t определяется формулой (4.2), т. е.

где λ1 = 1/t1 = 0,5[год-1], λ2 = 1/t2 = 1[год-1].

Вероятности исправности блоков по истечении времени t = T = 1,5 года будут равны соответственно

Вероятность того, что за время T i-й блок выйдет из строя, является противоположной вероятностью

Обозначим через А, В, С события, фигурирующие в пунктах (а), (б), (в) соответственно и учитывая, что блоки работают независимо друг от друга, найдём:

а)

б)

в)

Каналом обслуживания называется устройство в СМО, обслуживающее заявку. СМО, содержащее один канал обслуживания, называется одноканальной, а содержащее более одного канала обслуживания – многоканальной (например, 3 кассы на вокзале).

Если заявка, поступающая в СМО, может получить отказ в обслуживании (в силу занятости всех каналов обслуживания) и в случае отказа вынуждена покинуть СМО, то такая СМО называется СМО с отказами (примером такой СМО может служить АТС).

Если в случае отказа в обслуживании заявки могут вставать в очередь, то такие СМО называются СМО с очередью (или с ожиданием). При этом различают СМО с ограниченной и неограниченной очередью. Примером первых СМО может служить мойка для автомашин с маленькой стоянкой для ожидающих машин, а примером вторых СМО может служить билетная касса или метрополитен.

Возможны также СМО смешанного типа, когда, например, заявка может вставать в очередь, если она не очень велика, и может находиться в очереди ограниченное время и уйти из СМО не обслуженной.

Различают СМО открытого и замкнутого типа. В СМО открытого типа поток заявок не зависит от СМО (билетные кассы, очередь в булочной). В СМО замкнутого типа обслуживается ограниченный круг клиентов, а число заявок может существенно зависеть от состояния СМО (например, бригада слесарей – наладчиков, обслуживающих станки на заводе).

СМО могут также различаться по дисциплине обслуживания: обслуживаются ли заявки в порядке поступления, случайным образом или вне очереди (с приоритетом).

СМО описываются некоторыми параметрами, которые характеризуют эффективность работы системы.

λ – интенсивность поступления в СМО заявок;

μ– интенсивность обслуживания заявок;

ротк – вероятность отказа в обслуживании поступившей в СМО заявки;

Q ≡ pобс – вероятность обслуживания поступившей в СМО заявки (относительная пропускная способность СМО); при этом

А – среднее число заявок, обслуживаемых в СМО в единицу времени (абсолютная пропускная способность СМО)

Lсмо – среднее число заявок, находящихся в СМО;

– среднее число каналов в СМО, занятых обслуживанием заявок. В то же время это Lобс – среднее число заявок, обслуживаемых СМО за единицу времени. Величина определяется как математическое ожидание случайного числа занятых обслуживанием n каналов:

, (4.7)

где рk- вероятность системы находиться в Sk состоянии;

– коэффициент занятости каналов;

tож – среднее время ожидания (обслуживания) заявки в очереди,

v = 1/tож – интенсивность потока ухода заявок из очереди.

Lоч– среднее число заявок в очереди (если очередь есть); определяется как математическое ожидание случайной величины m – числа заявок, состоящих в очереди

(4.8)

– среднее время пребывания заявки в СМО;

– среднее время пребывания заявки в очереди (если есть очередь);

Для открытых СМО справедливы соотношения

(4.9)

, (4.10)

называемые формулами Литтла и применимые только для стационарных потоков заявок и обслуживания.

Рассмотрим некоторые конкретные типы СМО. При этом будет предполагаться, что плотность распределения промежутка времени между двумя последовательными событиями в СМО имеет показательное распределение (4.3), а все потоки являются простейшими.

§ 5. Одноканальная СМО с отказами.

Размеченный граф состояний одноканальной СМО представлен на рис.4.

Здесь λ и μ – интенсивность потока заявок и выполнения заявок соответственно. Состояние системы S0 обозначает, что канал свободен, а S1 – что канал занят обслуживанием заявки.

Система дифференциальных уравнений Колмогорова для такой СМО имеет вид (см. пример 3)

где p0(t) и p1(t) – вероятности нахождения СМО в состояниях S0 и S1 соответственно. Уравнения для финальных вероятностей p0 и p1 получим, приравнивая нулю производные в первых двух уравнениях системы. В результате получим:

, (5.1)

. (5.2)

Вероятность p0 по своему смыслу есть вероятность обслуживания заявки pобс, т. к. канал является свободным, а вероятность р1 по своему смыслу является вероятностью отказа в обслуживании поступающей в СМО заявки ротк, т. к. канал занят обслуживанием предыдущей заявки. Остальные характеристики СМО найдём, рассмотрев конкретный пример.

Пример 6. Секретарю директора завода поступает в среднем 1,2 телефонных вызовов в минуту. Средняя продолжительность разговора составляет 2 минуты. Найти основные характеристики СМО и оценить эффективность её работы.

Решение: По условию λ = 1,2 (мин)-1, μ = 2(мин)-1, откуда ρ = λ/μ = 0,6. По формулам (5.1) и (5.2) находим робс и ротк:

; .

Таким образом, обслуживается лишь 62,5% звонков, что нельзя считать удовлетворительным. Абсолютная пропускная способность СМО

т. е. в среднем обслуживается 0,75 звонка в минуту.

§ 6. Многоканальная СМО с отказами.

Пусть СМО содержит n каналов, интенсивность входящего потока заявок равна λ, а интенсивность обслуживания заявки каждым каналом равна μ. Размеченный граф состояний системы изображён на рис. 5.

λ λ λ λ λ λ λ

Рис. 5

Состояние S0 означает, что все каналы свободны, состояние означает, что обслуживанием заявок заняты k каналов. Переход из одного состояния в другое соседнее правое происходит скачкообразно под воздействием входящего потока заявок интенсивностью λ независимо от числа работающих каналов (верхние стрелки). Для перехода системы из одного состояния в соседнее левое неважно, какой именно канал освободится. Величина kμ характеризует интенсивность обслуживания заявок при работе в СМО k каналов (нижние стрелки).

Сравнивая графы на рис. 3 и на рис. 5 легко увидеть, что многоканальная СМО с отказами является частным случаем системы рождения и гибели, если в последней принять g = n и

(6.1)

При этом для нахождения финальных вероятностей можно воспользоваться формулами (3.2) и (3.3). С учётом (6.1) получим из них:

(6.2)

(6.3)

Формулы (6.2) и (6.3) называются формулами Эрланга – основателя теории массового обслуживания.

Вероятность отказа в обслуживании заявки ротк равна вероятности того, что все каналы заняты, т. е. система находится в состоянии Sn. Таким образом,

(6.4)

Относительную пропускную способность СМО найдём из (4.5) и (6.4):

(6.5)

Абсолютную пропускную способность найдём из (4.6) и (6.5):

(6.6)

Среднее число занятых обслуживанием каналов можно найти по формуле (4.7), однако сделаем это проще. Так как каждый занятый канал в единицу времени обслуживает в среднем μ заявок, то можно найти по формуле:

(6.7)

Пример 7. Найти оптимальное число телефонных номеров на предприятии, если заявки на переговоры поступают с интенсивностью 1,2 заявки в минуту, а средняя продолжительность разговора по телефону составляет минуты. Найти также вероятность того, что в СМО за 3 минуты поступит: а) точно 2 заявки, б) не более 2-х заявок.

Решение. Имеем: λ = 1,2 мин-1, μ = 1/t = 0,5 мин-1, ρ = λ/μ = 2,4. Оптимальное число каналов n неизвестно. Используя формулы (6.2) – (6.7) найдём характеристики СМО при различных значениях n и заполним таблицу 1.

[spoiler title=”источники:”]

http://habr.com/ru/post/455762/

http://pandia.ru/text/78/171/24200.php

[/spoiler]