Продолжение статьи «Теория вероятности. Классическое определение».
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Итак, теория.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет 
, потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом: 
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).
Вероятность первого события «кофе закончится в первом автомате» также как и вероятность второго события «кофе закончится во втором автомате» по условию равна 0,3. События являются совместными.
Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – 
. Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле: 
.
Подборку задач на отработку темы смотрите здесь.
Теорема.
Вероятность
суммы двух совместимых событий А и В
равна сумме вероятностей этих событий
минус вероятность их произведения:
Р(А
+ В)
= Р(А)
+ Р(В)
Р(АВ).
(6)
Замечание.
Если события А
и
В несовместимы,
то их произведение АВ
есть
невозможное событие и, следовательно,
Р(АВ)
= 0,
т.е. формула (1) является частным случаем
формулы (6).
Пример
8.
В посевах пшеницы на делянке имеется
95% здоровых растений. Выбирают два
растения. Определить вероятность того,
что среди них хотя бы одно окажется
здоровым.
Решение.
Введем
обозначения для событий: А1
первое растение здоровое; А2
второе растение здоровое; A1
+ А2
хотя
бы одно растение здоровое.
Так
как события А1
и
А2
совместимые,
то согласно формуле (6)
4. Формула полной вероятности.
Теорема.
Вероятность
события А, которое может наступить лишь
при условии появления одного из п попарно
несовместимых событий В1,
В2,
… ,
Вn,
образующих полную группу, равна сумме
произведений вероятностей каждого из
этих событий на соответствующую условную
вероятность события А:
(7)
(формула полной
вероятности).
Пример
9.
Для приема зачета преподаватель заготовил
50 задач: 20 задач по дифференциальному
исчислению, 30 по интегральному исчислению.
Для сдачи зачета студент должен решить
первую же доставшуюся наугад задачу.
Какова вероятность для студента сдать
зачет, если он умеет решить 18 задач по
дифференциальному исчислению и 15 задач
по интегральному исчислению?
Решение.
Вероятность
получить задачу по дифференциальному
исчислению (событие В1)
равна
Р(В1)
= 0,4,
по интегральному исчислению (событие
В2)
Р(В2)
=
0,6. Если событие А
означает,
что задача решена, то
(А)
= 0,9,
(А)
=
0,5. Теперь по формуле (7) имеем Р(А)
=
Пример
10.
Имеются три одинаковых по виду ящика.
В первом находятся две белые мыши и одна
серая, во втором
три белые и одна серая, в третьем
две белые и две серые мыши. Какова
вероятность того, что из наугад выбранного
ящика будет извлечена белая мышь?
Решение.
Обозначим
В1
выбор
первого ящика, В2
выбор
второго ящика, В3
выбор
третьего ящика, А
извлечение
белой мыши.
Так
как все ящики одинаковы, то P(B1)=Р(В2)=Р(В3)
Если
выбран первый ящик, то
.
Аналогично
,
.
Наконец,
по формуле (7) получаем
5.
Формула Бейеса. Пусть
в условиях рассуждения, относящегося
к формуле полной вероятности, произведено
одно испытание, в результате которого
произошло событие А.
Спрашивается:
как изменились (в связи с тем, что событие
А
уже
произошло) величины P(Bk),
k
= 1,…
,
п.
Найдем
условную вероятность РА(Вk).
По
теореме умножения вероятностей и формуле
(4) (см. п. 2) имеем
Отсюда
Наконец, используя
формулу полной вероятности, находим
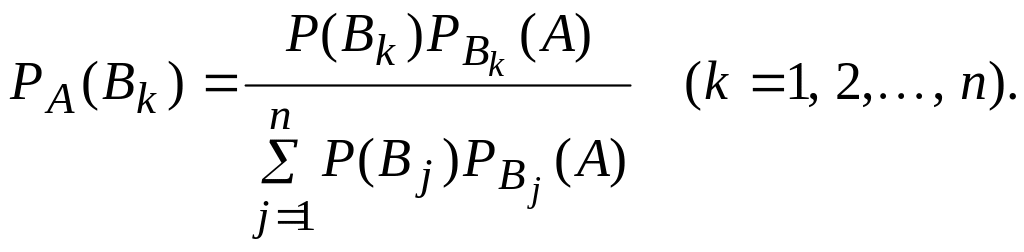
(8)
Формулы
(8) называют формулами
Бейеса (или
Байеса).
Пример
11.
Большая популяция людей разбита на две
группы одинаковой численности. Диета
одной группы отличалась высоким
содержанием ненасыщенных жиров, а диета
контрольной группы была богата насыщенными
жирами. После 10 лет пребывания на этих
диетах возникновение сердечно-сосудистых
заболеваний составило в этих группах
соответственно 31% и 48%. Случайно выбранный
из популяции человек имеет сердечно-сосудистое
заболевание. Какова вероятность того,
что этот человек принадлежит к контрольной
группе?
Решение.
Введем
обозначения для событий: А
случайно
выбранный из популяции человек имеет
сердечно-сосудистое заболевание; В1
человек
придерживался специальной диеты; В2
человек принадлежал к контрольной
группе. Имеем
Согласно формуле
полной вероятности
и, наконец, в силу
формулы (8) искомая вероятность
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
01.05.2022204.8 Кб0Учебники 6027.doc
- #
Полная вероятность и формула Байеса
- Зависимые события и условные вероятности
- Вероятность совместного появления событий
- Формула полной вероятности
- Формула Байеса
- Примеры
п.1. Зависимые события и условные вероятности
Чтобы вспомнить о сложении и умножении вероятностей и независимых событиях – см. §39 справочника для 9 класса.
Напомним, что два случайных события A и B называют независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Например: при бросании монеты несколько раз каждый следующий бросок совершенно не зависит от предыдущих.
Два случайных события A и B называют зависимыми, если вероятность одного из них зависит от того, произошло или нет другое событие.
Вероятность события B, определенная при условии, что событие A произошло, называется условной вероятностью и обозначается (P(B|A)) или (P_A(B)).
Для условных вероятностей справедливы формулы: $$ P(A|B)=frac{P(Awedge B)}{P(B)}, P(B|A)=frac{P(Awedge B)}{P(A)} $$ где (P(Awedge B)) – вероятность совместного появления событий A и B.
Например:
Рассмотрим урну, в которой находится 3 белых и 3 черных шара.
Мы достаем шары, смотрим на их цвет и не возвращаем их на место. События в последовательности становятся зависимыми.
Пусть событие A=”в 1й раз достаем черный шар”,
Событие B=”во 2й раз достаем белый шар”
Событие C=”во 2й раз достаем черный шар”
После того, как произошло событие A, в урне остается 3 белых и 2 черных шара.
Тогда условная вероятность для события B при условии, что событие A произошло:
(P(B|A)=frac35)
Аналогично, условная вероятность для события C:
(P(B|A)=frac25)
п.2. Вероятность совместного появления событий
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло: $$ P(Awedge B)=P(B)cdot P(A|B)=P(A)cdot P(B|A) $$ Это утверждение также называют теоремой умножения вероятностей.
Например:
Продолжая предыдущий пример, вероятность события ((Awedge B)) – 1й раз достали черный шар и 2й раз белый – равна: $$ P(Awedge B)=P(A)cdot P(B|A)=frac12cdot frac35=0,3 $$ Также, напомним:
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: $$ P(Awedge B)=P(A)cdot P(B) $$
Например:
Пусть в урне 3 белых и 3 черных шара. Мы достаем шары, смотрим на их цвет и возвращаем их на место. В последовательности наших действий все события будут независимыми. Каждый раз, вероятность достать белый или черный шар будет равна 1/2. Поэтому, в этом случае вероятность события ((Awedge B)) – 1й раз достали черный шар, а 2й раз белый – равна: $$ P(Awedge B)=P(A)cdot P(B)=frac12cdotfrac12=0,25 $$
п.3. Формула полной вероятности
Чтобы вспомнить о несовместных событиях и полной группе событий – см. §39 справочника для 9 класса.
Например:
При подбрасывании монеты события A=«получить орла» и B=«получить решку» – несовместные, т.к. одновременно произойти не могут.
В то же время, эти несовместные события A и B образуют пространство элементарных событий или полную группу (Omega=left{B;Bright}), т.к. ничего другого, кроме орла или решки, получить нельзя. Сумма вероятностей (P(A)+P(B)=frac12+frac12=1), как и положено для полной группы.
Если событие A может произойти только при выполнении одного из событий (B_1,B_2,…,B_k), которые образуют полную группу событий, то вероятность события A определяется по формуле полной вероятности: $$ P(A)=P(B_1)P(A|B_1)+P(B_2)P(A|B_2)+…+P(B_k)P(A|B_k)=sum_{i=1}^k P(B_i)P(A|B_i) $$
Например:
В 11А и 11Б учится по 35 человек, а в 11В – 30 человек. Будем считать тех, у кого 4 и 5 баллов по алгебре и геометрии, «знатоками математики». Таких учеников в 11А – 10 человек, в 11Б – 7 человек, и в 11В – 3 человека.
Какова вероятность, что произвольно выбранный 11-классник окажется знатоком математики?
Пусть события A=«знаток математики», Bi=«ученик i-го класса», (i=overline{1,3})
Составим таблицу:
| i | Класс | К-во учеников |
(P(B_i)) | К-во знатоков |
(P(A|B_i)) | (P(B_i)cdot P(A|B_i)) |
| 1 | 11A | 35 | 35/100=0,35 | 10 | 10/35=2/7 | 0,1 |
| 2 | 11Б | 35 | 35/100=0,35 | 7 | 7/35=1/5 | 0,07 |
| 3 | 11В | 30 | 30/100=0,3 | 10 | 3/30=1/10 | 0,03 |
| Всего | 100 | 1 | 20 | × | 0,2 |
Получаем полную вероятность (P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=0,2)
В данном случае ответ можно получить и проще: 20 знатоков на 100 человек дает (P(A)=0,2).
п.4. Формула Байеса
По данному выше определению полной вероятности событие A случается, если происходит одно из событий полной группы (left{B_iright}).
Допустим, что событие A случилось. А какова вероятность, что при этом произошло конкретное событие (B_1inleft{B_iright})? Т.е., нас интересует условная вероятность (P(B_1|A)).
По теореме об умножении вероятностей: $$ P(Awedge B_1)=P(B_1)cdot P(A|B_1)=P(A)cdot P(B_1|A) $$ Откуда: $$ P(B_1|A)=frac{P(B_1)cdot P(A|B_1)}{P(A)} $$ То же самое справедливо для любого события (B_pinleft{B_iright}). Предположение о том, что случилось событие (B_p), называют гипотезой.
Если событие A может произойти только при выполнении одного из событий полной группы (left{B_iright}) и событие A случилось, то вероятность гипотезы, что при этом случилось событие (B_pinleft{B_iright}), определяется формулой Байеса: $$ P(B_p|A)=frac{P(B_p)cdot P(A|B_p)}{P(A)}=frac{P(B_p)cdot P(A|B_p)}{sum_{i=1}^k P(B_i)P(A|B_i)} $$ Вероятность (P(B_p)) называют априорной вероятностью.
Вероятность (P(B_p|A)) называют апостериорной вероятностью. Случившееся событие A может поменять априорную (предварительную) оценку вероятности события (B_p).
Например:
Продолжим задачу с 11-классниками. Какова вероятность того, что произвольно взятый знаток математики учится в 11Б?
Наши события: A=«знаток математики», B2=«ученик 11Б класса».
Событие A «случилось» – у нас имеется знаток, а событие B2 – это гипотеза про 11Б.
И ответом на поставленный вопрос является вероятность (P(B_2|A)).
Из нашей таблицы: $$ P(B_2)cdot P(A|B_2)=0,07; P(A)=0,2 $$ Получаем: $$ P(B_2|A)=frac{P(B_2)cdot P(A|B_2)}{P(A)}=frac{0,07}{0,2}=0,35 $$ Т.е. 11Б дает 35% всех знатоков математики в этой школе.
Если сравнить апостериорную вероятность (P(B_2|A)=0,35) с априорной вероятностью (P(B_2)=0,35), они равны. Событие A не повлияло на оценку вклада 11Б в интеллектуальный багаж школы, он находится на среднем уровне.
Теперь найдем вероятность того, что произвольно взятый знаток математики учится в 11А: begin{gather*} P(B_1|A)=frac{P(B_1)cdot P(A|B_1)}{P(A)}=frac{0,1}{0,2}=0,5\ P(B_1|A)gt P(B_1) end{gather*} Вклад 11А по факту (апостериорная вероятность 0,5) оказывается большим, чем ожидалось по количеству учеников (априорная вероятность 0,35). 50% знатоков всей школы – из этого класса.
Наконец, найдем вероятность того, что произвольно взятый знаток математики учится в 11В: begin{gather*} P(B_3|A)=frac{P(B_3)cdot P(A|B_3)}{P(A)}=frac{0,03}{0,2}=0,15\ P(B_3|A)lt P(B_3) end{gather*} Вклад 11В по факту (апостериорная вероятность 0,15) оказывается меньшим, чем ожидалось по количеству учеников (априорная вероятность 0,3). Только 15% знатоков всей школы – из этого класса.
п.5. Примеры
Пример 1. Двигатель работает в трех режимах: нормальном (65% времени), форсированном (25% времени) и холостом. Вероятность поломки в каждом из режимов соответственно равна (p_1=0,1; p_2=0,8; p_3=0,05).
а) найдите вероятность поломки двигателя во время работы;
б) двигатель сломался. Какова вероятность, что он в этот момент работал в форсированном режиме?
а) Пусть событие A=«поломка двигателя», Bi – «работа в i-м режиме», (i=overline{1,3})
Необходимо найти полную вероятность (P(A)).
Составим таблицу:
| i | Режим | Часть времени (P(B_i)) |
Вероятность поломки (P(A|B_i)) |
(P(B_i)cdot P(A|B_i)) |
| 1 | Нормальный | 0,65 | 0,1 | 0,065 |
| 2 | Форсированный | 0,25 | 0,8 | 0,2 |
| 3 | Холостой | 0,1 | 0,05 | 0,005 |
| Всего | 1 | × | 0,27 |
Вероятность поломки (полная вероятность): $$ P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=0,27 $$
б) Событие A=«поломка двигателя» произошло. Гипотеза B2 – «работа в форсированном режиме» при фактической поломке имеет вероятность: $$ P(B_2|A)=frac{P(B_2)cdot P(A|B_2)}{P(A)}=frac{0,2}{0,27}=frac{20}{27}approx 0,741 $$ Апостериорная вероятность (P(B_2|A)approx 0,741) больше априорной вероятности (P(B_2)=0,25).
Ответ: a) 0,27; б) (frac{20}{27}approx 0,741)
Пример 2. В состязании лучников участвуют три стрелка. Вероятность попадания в мишень для каждого из них равна 0,3; 0,5 и 0,7. Один из стрелков стреляет и не попадает. Какова вероятность, что это был:
а) первый стрелок;
б) второй стрелок;
в) третий стрелок;
Пусть событие A=«промах», Bi – «выстрел i-го стрелка», (i=overline{1,3})
Т.к. стрелять мог любой из стрелков (P(B_i)=frac13) для каждого из них.
Чтобы найти вероятность промаха, нужно от 1 отнять вероятность попадания.
Составим таблицу:
| i | (P(B_i)) | Вероятность промаха (P(A|B_i)) |
(P(B_i)cdot P(A|B_i)) |
| 1 | (frac13) | 1-0,3=0,7 | (frac13cdot 0,7=frac{7}{30}) |
| 2 | (frac13) | 1-0,5=0,5 | (frac13cdot 0,5=frac{1}{6}) |
| 3 | (frac13) | 1-0,7=0,3 | (frac13cdot 0,3=frac{1}{10}) |
| ∑ | 1 | × | 0,5 |
Полная вероятность: $$ P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=frac{7}{30}+frac16+frac{1}{10}=0,5 $$ Промах произошел. Находим апостериорные вероятности для каждого стрелка: begin{gather*} P(B_1|A)=frac{P(B_1)cdot P(A|B_1)}{P(A)}=frac{7/30}{0,5}=frac{7}{15}approx 0,467\ P(B_2|A)=frac{P(B_2)cdot P(A|B_2)}{P(A)}=frac{1/6}{0,5}=frac{2}{3}approx 0,333\ P(B_3|A)=frac{P(B_3)cdot P(A|B_3)}{P(A)}=frac{1/10}{0,5}=frac{1}{5}=0,2\ end{gather*} С точки зрения практической, можно сказать, что «вероятнее всего», это был первый стрелок.
Ответ: a) (frac{7}{15}); б) (frac{1}{3}); в) (frac{1}{5})
Пример 3. Три фрилансера на площадке выполняют заказы в отношении по количеству 3:4:3. Доля успешно выполненных заказов для каждого из них составляет 98%, 95% и 90%.
а) найдите вероятность успешного выполнения заказа на площадке;
б) найдите вероятность неуспеха на площадке;
в) кто из фрилансеров, вероятнее всего, виноват в неуспешной работе?
Пусть событие A=«успех», Bi – «работа i-го фрилансера», (i=overline{1,3})
Составим таблицу успешной деятельности:
| i | (P(B_i)) | Вероятность успеха (P(A|B_i)) |
(P(B_i)cdot P(A|B_i)) |
| 1 | 0,3 | 0,98 | 0,294 |
| 2 | 0,4 | 0,95 | 0,38 |
| 3 | 0,3 | 0,9 | 0,27 |
| ∑ | 1 | × | 0,944 |
Вероятность успешного выполнения (полная вероятность): $$ P(A)=sum_{i=1}^3 P(B_i)cdot P(A|B_i)=0,944 $$ б) Вероятность неуспеха (противоположное событие): $$ P(overline{A})=1-P(A)=1-0,944=0,056 $$ в) Составим таблицу неуспешной деятельности:
| i | (P(B_i)) | Вероятность неуспеха (P(overline{A}|B_i)) |
(P(B_i)cdot P(overline{A}|B_i)) |
| 1 | 0,3 | 1-0,98=0,02 | 0,006 |
| 2 | 0,4 | 1-0,95=0,05 | 0,02 |
| 3 | 0,3 | 1-0,9=0,1 | 0,03 |
| ∑ | 1 | × | 0,056 |
Апостериорные вероятности для каждого из фрилансеров: begin{gather*} P(B_1|overline{A})=frac{P(B_1)cdot P(overline{A}|B_1)}{P(overline{A})}=frac{0,006}{0,056}=frac{3}{28}approx 0,107\ P(B_2|overline{A})=frac{P(B_2)cdot P(overline{A}|B_2)}{P(overline{A})}=frac{0,02}{0,056}=frac{5}{14}approx 0,357\ P(B_3|overline{A})=frac{P(B_3)cdot P(overline{A}|B_3)}{P(overline{A})}=frac{0,03}{0,056}=frac{15}{28}approx 0,536 end{gather*} Наибольшая вероятность неуспеха – у третьего фрилансера.
Ответ: а) 0,944; б) 0,056; в) третий фрилансер.
Пример 4. Докажите, что если полная вероятность события A равна $$ P(A)=sum_{i=1}^k P(B_i)cdot P(A|B_i) $$ то вероятность противоположного события равна (P(overline{A})=1-P(A)).
По условию событие A происходит только при выполнении одного из событий полной группы (left{B_iright}. i=overline{i,k}). Соответственно, противоположное событие (overline{A}) также происходит при выполнении одного из событий (B_i). При этом условная вероятность для противоположного события: $$ P(overline{A}|B_i)=1-P(A|B_i) $$ Заметим также, что для полной группы сумма вероятностей равна 1: begin{gather*} sum_{i=1}^k P(B_i)=1 end{gather*} Получаем: begin{gather*} P(overline{A})=sum_{i=1}^k P(B_i)cdot P(overline{A}|B_i)=sum_{i=1}^k P(B_i)cdot (1-P(A|B_i))=\ =sum_{i=1}^k P(B_i)-sum_{i=1}^k P(B_i)cdot P(A|B_i)=1-P(A) end{gather*} Что и требовалось доказать.
Содержание:
- Операции над вероятностями
- Вероятность объединения несовместимых событии
- Вероятность объединения совместимых событии
- Условные вероятности
- Независимость случайных событии и правило произведения вероятностей
- Независимость в совокупности
- Формула полной вероятности
Операции над вероятностями
Вероятность объединения несовместимых событии
Пусть m — число равновозможных элементарных событий, благоприятствующих событию A, k — число равновозможных элементарных событий, благоприятствующих событию B, несовместимому по отношению к событию А. Пусть n — общее число равновозможных элементарных событий, образующих пространство Е всех элементарных событий.
В силу формулы (4.1)
Согласно определению объединения несовместимых событий 
означает: «имеет место или А, или В». Но число событий, благоприятствующих такому событию, равно m+k, поэтому согласно формуле (4.1)
(5.1)
На рисунке 20 дана геометрическая интерпретация формулы (5.1), если m, k и n здесь величины площадей нарисованных фигур.
Последнее равенство выражает следующее правило, которое последовательным применением формулы (5.1) может быть распространено на любое конечное число событий:
Вероятность объединения попарно несовместимых событий равна сумме вероятностей этих событий.
С помощью этого правила мы можем справиться со многими задачами.
Примеры с решением:
Пример 1.
В лотерее выпущено 10 ООО билетов и установлено: 10 выигрышей по 200 р., 100 — по 100 р., 500 — по 25 р. и 1000 выигрышей по 5 р. Гражданин купил один билет. Какова вероятность того, что он выиграет не меньше 25 р.?
Обозначим события:
А — «выигрыш не менее 25 р.»,
— «выигрыш равен 25 р.»,
— «выигрыш равен 100 р.»,
— «выигрыш равен 200 р.».
Поскольку куплен только один билет, то 
где события 
попарно несовместимы, поэтому
Р (А) = 0,05 + 0,01 + 0,001 = 0,061.
Пример 2.
На военных учениях летчик получил задание «уничтожить» 3 рядом расположенных склада боеприпасов противника. На борту самолета одна бомба. Вероятность попадания в первый склад примерно равна 0,01, во второй — 0,008, в третий — 0,025.
Любое попадание в результате детонации вызывает взрыв и остальных складов. Какова вероятность того, что склады противника будут уничтожены?
Обозначим события:
А — «склады уничтожены»,
— «попадание в первый склад»,
— «попадание во второй склад»,
— «попадание в третий склад».
Для уничтожения складов достаточно попадания в один из упомянутых трех складов. Поэтому
Пример 3.
Бросают две монеты. Чему равна вероятность появления хотя бы одного герба? Обозначим события:
А — «появление герба при подбрасывании первой монеты», В — «появление герба при подбрасывании второй монеты». Снова предстоит найти вероятность события 
. Но в этом случае 
ибо события А и В совместимы. Поэтому формула (5.1) не применима. Приходится избрать другой путь решения.
Пусть событие 
— «выпадение герба не состоялось». Ясно, что 
, ибо при бросании двух монет могут произойти только следующие события:
Событие 
представляет собой достоверное событие, поэтому 
отсюда
Вероятность объединения совместимых событии
Пусть m — число равновозможных элементарных событий, благоприятствующих событию A, k — число равновозможных элементарных событий, благоприятствующих событию В. Допустим, что среди упомянутых m + k событий содержится 
таких, которые благоприятствуют и событию А, и событию В. Если n — общее число равновозможных элементарных событий, образующих пространство Е всех элементарных событий, то согласно формуле (4.1)
Запись 
означает: «произойдет или событие А, или событие Ву или то и другое вместе». Но такому событию благоприятствуют (m + k — ) элементарных событий. Поэтому по формуле (4.1) находим:
Подставляя значение, получим:
(5.2)
Ясно, что эта формула представляет собой обобщение формулы (5.1). На основании равенства (5.2) формулируем правило:
Вероятность объединения двух совместимых событий равна сумме вероятностей этих событий без вероятности их совместного осуществления.
Геометрическая интерпретация формулы (5.2) дается на рисунке 21, где m, k, , n представляют величины площадей изображенных фигур.
Примеры с решением:
Пример 1.
Подбрасываем две монеты. Какова вероятность выпадения хотя бы одного герба?
Обозначим события:
А — «появление герба при подбрасывании первой монеты»,
В — «появление герба при подбрасывании второй монеты».
Нам надо определить вероятность события 
Так как А и В — совместимые события, то
Ясно, что 
Отсюда
Пример 2.
А, В, С — совместимые события. Доказать:
Условные вероятности
Из ящика, в котором 
белых и b черных шаров, наугад вынимают последовательно один за другим два шара. Рассмотрим события:
А — «первый шар белый», В — «второй шар белый». Понятно, что 
. Какова же вероятность события В?
Если событие А произошло, то среди оставшихся + b — 1 шаров только — 1 белых, поэтому вероятность того, что второй шар белый, 
. Если же А не произошло, то среди оставшихся шаров белых , поэтому вероятность того, что второй шар белый, 
. Мы столкнулись с ситуацией, когда вероятность появления события В зависит от того, произошло или не произошло событие А. В таком случае говорим, что событие В зависит от события А, а вероятность появления события В условная.
Найдем способ вычисления таких вероятностей. Условную вероятность появления события В, если событие А произошло, будем обозначать Р (В/А).
Пусть из n равновозможных событий 
составляющих пространство Е всех элементарных событий,
событию А благоприятствуют m событий,
событию В благоприятствуют k событий,
событию 
благоприятствуют r событий (понятно, что 
).
Если событие А произошло, то это означает, что наступило одно из событий 
благоприятствующих событию А. При этом условии событию В благоприятствуют r и только r событий 
благоприятствующих 
(рис. 22). Таким образом,
(5.3)
Точно так же
На основании этих формул находим:
т. е.
(5.З’)
На основании (5.3) формулируем правило умножения вероятностей :
Вероятность пересечения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое произошло.
Замечание. Формулы (5.3) имеют смысл в том случае, если имеют смысл события А/В и В/А. А они имеют смысл тогда, когда события А и В совместимы.
Примеры с решением:
Пример 1.
В ящике 
белых и Ь черных шаров. Последовательно вынимаем два шара. Какова вероятность того, что оба они белые?
Обозначим события:
А — «первый шар белый»,
В — «второй шар белый».
Нам надлежит найти 
Имеем:
Согласно формуле (5.3) находим:
Пример 2.
Из колоды в 32 карты наугад одну за другой вынимают две карты. Найти вероятность того, что:
а) вынуты два валета;
б) вынуты две карты пиковой масти;
в) вынуты валет и дама. Обозначим события:
А — «первая карта — валет», В — «вторая карта — валет», С — «первая карта пиковой масти», D — «вторая карта пиковой масти», Е — «вторая карта — дама».
Нам следует найти 
По формуле (5.3)
Пример 3.
Доказать:
Независимость случайных событии и правило произведения вероятностей
К понятию независимости случайных событий есть несколько подходов.
Событие В называется независимым от А, если его вероятность не зависит от того, произошло или не произошло событие А, т. е.
Р(В/А) = Р(В) = Р(В/А).
В случае независимости события В от события А из формулы (5.3) получим:
(5.4)
Сопоставляя формулы (5.3) и (5.4), убеждаемся, что свойство независимости взаимно. Если событие В не зависит от осуществления А, то и А не зависит от осуществления В. На основании (5.4) формулируем правило: Вероятность пересечения двух независимых событий равна произведению вероятностей этих событий.
На практике, как мы убедимся при рассмотрении примеров, для установления независимости событий обычно пользуются соображениями, основанными на опыте обращения с данными объектами, а не анализом формул.
Доказательство правила (5.4) проводилось на основе соотношений
(5.5)
т. е. у нас получилось так: если имеет место (5.5), то имеет место и (5.4). Но читателя может интересовать и обратное: следует ли (5.5) из (5.4)? Пусть
Тогда на основании формул
и (5.4) получаем:
т. е. из (5.4) следует (5.5). Таким образом, исходной точкой определения независимости А и В может быть и формула (5.4), т. е. мы можем сказать и так:
События А и В называются независимыми тогда и только тогда, когда имеет место условие
(5.6)
Однако определение независимости событий на основе (5.5) более близкое к интуитивному воображению.
Важно запомнить: независимые события с положительными вероятностями не являются несовместимыми. Пусть
(5.7)
Как известно, пересечение несовместимых событий 
V — невозможное событие. Следовательно, для несовместимых событий
Но тогда в силу (5.6) по крайней мере одно из вероятностей Р (А) или Р (В) должно быть равно нулю. Это противоречит (5.7), а значит, подтверждает факт, что независимые события могут быть совместимы.
Приведем любопытный пример, когда интуитивное понимание независимости событий тоже приводит к формальному соотношению (5.4).
Пусть точка М наудачу бросается в прямоугольник с размерами X и Y, стороны которого параллельны координатным осям. Какова вероятность того, что М попадет в прямоугольник с размерами х и у, стороны которого тоже параллельны координатным осям (рис. 23)? Пусть события:
А — «М попала в полосу шириной х». Разумеется, Р(А) 
,
В— «М попала в полосу шириной у». Разумеется, Р(В) 
По формуле (4.3) Р («М попала в маленький прямоугольник») 
но Р(«М попала в маленький прямоугольник») 
Следовательно,
что и требовалось доказать.
Независимость в совокупности
Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных. Для независимости событий в их совокупности недостаточно, чтобы они были попарно независимы. Приведем такой пример.
Пусть в ящике 4 шара: черный, красный, белый и один пестрый — окрашенный в полоску всеми этими тремя цветами. Обозначим события: после изъятия одного шара видим
А — «черный цвет»,
В — «красный цвет»,
С — «белый цвет»,
тогда
Отсюда
Это значит, что А, В, С попарно независимы. Тем не менее 
Значит, в совокупности А, В и С не являются независимыми.
Для независимых в совокупности имеет место
(5.8)
Примеры с решением:
Пример 1.
Бросают две игральные кости. Какова вероятность появления на первой кости нечетного числа очков и на второй пяти очков?
Обозначим события:
А — «появление нечетного числа очков при бросании первой кости»,
В — «появление пяти очков при бросании второй кости». Нам нужно найти 
Так как события А и В совместимы и независимы, то 
поэтому 
Пример 2.
А, В и С — совместимые и независимые в совокупности события. Доказать, что 
Допустим, что 
Тогда 
Пример 3.
Зашедший в магазин мужчина что-нибудь покупает с вероятностыо 0,1, зашедшая женщина — с вероятностью 0,6. У прилавка один мужчина и две женщины. Какова вероятность того, что по крайней мере одно лицо что-нибудь купит?
Обозначим события:
А — «покупку сделает мужчина»,
— «покупку сделает первая женщина»,
— «покупку сделает вторая женщина».
Если событие С — «по крайней мере одно лицо что-нибудь купит», то 
По формуле, построенной в примере 2 параграфа 2,
Допуская, что покупатели между собой незнакомы, можем принимать, что 
— события независимы. Тогда в силу (5.6) 
Р (С) = 0,1 + 0,6 + 0,6 – 0,1*0,6 – 0,1*0,6 – 0,6*0,6 + 0,1*0,6*0,6 =0,856.
Пример 4.
Если события А и В независимы, то события А и 
также независимы.
Действительно, поскольку А и В независимы, то Р(В/А) = Р(В) и 
Аналогично убеждаемся, что в случае независимости событий А и В независимыми будут события В и 
Предлагаем вам самостоятельно установить, что в этом случае независимыми будут также события 
Формула полной вероятности
Пусть требуется найти вероятность события А, которое происходит вместе с одним из независимых событий 
(рис. 24).
Если А произошло вместе с одним из событий 
значит, произошло одно из несовместимых событий
Таким образом, событие А представляет или событие 
или 
а это означает, что
Поскольку события взаимно несовместимы, то и события
обладают тем же свойством. Поэтому
По формуле (5.3′)
Поэтому
(5.9)
Равенство (5.9) носит название формулы полной вероятности. С помощью этой формулы легко находим так называемую формулу Бейеса:
(5.10)
при i = 1, 2, …, n.
Особенно широко она применяется при решении задач, связанных с вероятностной оценкой гипотез. Докажем справедливость формулы Бейеса. По формуле (5.3′)
Из последнего равенства находим:
Подставляя значение Р (А) из формулы полной вероятности (5.9), получаем формулу Бейеса.
Примеры с решением:
Пример 1.
Охотник сделал три выстрела по кабану. Вероятность попадания первым выстрелом примерно равна 0,4, вторым — 0,5, третьим — 0,7. Одним попаданием кабана можно убить с вероятностью, примерно равной 0,2, двумя попаданиями — с вероятностью 0,6, а тремя наверняка. Найти вероятность того, что кабан будет убит.
Рассмотрим несовместимые события 
— «промах»,
— «одно попадание»,
— «два попадания»,
— «три попадания».
Пусть
— «попадание с первого выстрела»,
— «попадание со второго выстрела»,
— «попадание с третьего выстрела»,
А — «кабан убит».
Согласно формуле полной вероятности
Вспомнив, что события, противополоясные событиям 
обозначаются соответственно 
имеем:
Поскольку независимы в совокупности и независимы, то
Из условия задачи известно, что 
отсюда находим 
Поэтому
Из условия следует:
Подставляя эти результаты в формулу полной вероятности, получим:
Пример 2.
Строительная бригада получает железобетонные перекрытия от трех домостроительных комбинатов (ДСК): от I ДСК — 30%, от II ДСК — 55% и от III ДСК — 15% перекрытий. Известно, что брак продукции I ДСК составляет 5%, II ДСК — 6%, а III ДСК — 10%. Полученные перекрытия хранятся в общем складе. Наугад для контроля проверенное перекрытие оказалось браком. Какова вероятность того, что бракованное перекрытие изготовлено на I ДСК?
Обозначим события:
А — «наугад проверенное перекрытие — брак»,
— «наугад проверенное перекрытие изготовлено на I ДСК»,
— «наугад проверенное перекрытие изготовлено на II ДСК»,
— «наугад проверенное перекрытие изготовлено на III ДСК».
Нам следует найти 
по формуле (5.10):
Но по условию задачи
поэтому
Пример 3.
Из 10 учеников, которые пришли на экзамен по математике, трое подготовились отлично, четверо — хорошо, двое — удовлетворительно, а один совсем не готовился — понадеялся на то, что все помнит. В билетах 20 вопросов. Отлично подготовившиеся ученики могут ответить на все 20 вопросов, хорошо — на 16 вопросов, удовлетворительно — на 10, и непод-готовившийся — на 5 вопросов. Каждый ученик получает наугад 3 вопроса из 20. Приглашенный первым ученик ответил на все 3 вопроса. Какова вероятность того, что он отличник?
Обозначим события:
— «приглашен ученик, подготовившийся отлично»,
— «приглашен ученик, подготовившийся хорошо»,
— «приглашен ученик, подготовившийся удовлетворительно»,
— «приглашенный ученик к экзаменам не готов»,
А — «приглашенный ученик ответил на 3 вопроса».
Согласно условию задачи
Следует найти 
По формуле Бейеса (5.10)
Как видно, искомая вероятность сравнительно невелика. Поэтому учителю придется предложить ученику еще несколько дополнительных вопросов.
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Возможно вам будут полезны данные страницы:
Лекции:
- Независимые повторные испытания
- Дискретные случайные величины и их характеристики
- Непрерывные случайные величины и их характеристики
- Дискретные и непрерывные случайные величины
- Закон распределении дискретной случайной величины
- Действии над событиями
- Теоремы сложения и умножения вероятностей
- Формула полной вероятности. Формула Байеса
- Схема с повторением испытаний (схема Бернулли)
- Вероятность случайного события
Алгебра и начала математического анализа, 11 класс
Урок №34. Условная вероятность. Независимость событий.
Перечень вопросов, рассматриваемых в теме:
– Условная вероятность
– Совместные и несовместные события
– Схема решения задач на вычисление условной вероятности события;
– Задачи на определение независимости событий.
Глоссарий по теме
Совместные события – события, одновременное появление которых возможно.
Несовместные события – события, одновременное появление которых невозможно.
События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.
Событие В называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события В, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается PA(B).
Условная вероятность – вероятность наступления одного события при условии, что другое событие уже произошло.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. с. 186-194.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Иногда нам требуется выяснить вероятность совместного появления зависимых событий. Самый простой пример – найти вероятность получить выигрышную комбинацию в азартной карточной игре, где вероятность выпадения каждой новой карты зависит от того, какие карты уже лежат на столе.
Рассмотрим примерную задачу:
Из колоды карт извлекают четыре карты. Первые две оказались семёрками. Какова вероятность, что одна или обе оставшиеся карты окажутся семёрками? (колода содержит 36 карт)
1. 1/561
2. 65/561
3. 1/105
4. 17/518
Теоретическая часть
События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Пример совместных событий: выпадение чётного числа и выпадение числа, кратного трём, при броске игрального кубика. Когда выпадает шесть, реализуются сразу оба события.
События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.
Пример несовместных событий: выпадение чётного числа и выпадение нечётного числа при броске игрального кубика.
Теорема о сумме двух событий:
Вероятность суммы любых двух событий А и В равна сумме вероятностей этих событий без вероятности их совместного осуществления: Р(А+В) = Р(А)+Р(В)-Р(АВ)
Рассмотрим пример.
В лотерее выпущено 10 000 билетов, из них: 10 выигрышей по 200 рублей, 100 выигрышей по 100 рублей, 500 выигрышей по 50 рублей и 1000 выигрышей по 10 рублей. Какова вероятность того, что человек, купивший билет, выиграет не менее 50 рублей?
Решение: Введем для удобства обозначение событий А – «человек выиграл 50 рублей», В – «человек выиграл 100 рублей», С – «человек выиграл 200 рублей», D – «человек выиграл не менее 50 рублей». Событие D означает, что выигрыш может составлять 50 и более рублей, то есть 50, 100 или 200 рублей: М=А+В+С. События А, В, С – попарно несовместны.
Воспользуемся теоремой: Р(М)=Р(А)+Р(В)+Р(С)=0,061.
Задача.
Дана вероятность исходного события. Чему равна вероятность противоположного события?
Вероятность исходного события А обозначим Р(А). Вероятность противоположного события Р(Ᾱ).
Решение:
События А и Ᾱ образуют полную группу событий, вероятность которой равна 1.
Тогда вероятность противоположного события находится по формуле:
P(Ᾱ)=1-P(A)
- События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.
Например, монета брошена два раза.
A – выпала «Решка»
B – выпал «Орёл»
Вероятность появления «Орла» во втором испытании не зависит от результата первого испытания.
Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий A и B равна произведению вероятностей этих событий:
Р(АВ)=Р(А)·Р(В)
Рассмотрим пример.
Задача.
Подбрасываются две монеты. Найдите вероятность выпадения двух орлов.
Решение:
Введем обозначение событий:
A1– на 1-й монете выпадет орёл;
A2– на 2-й монете выпадет орёл.
Событие “выпадение двух орлов” заключается в том, что на 1-й монете появится орёл и на 2-й монете появится орёл, следовательно, это произведение событий A1A2. Вероятность выпадения орла на одной монете не зависит от результата броска другой монеты, следовательно, события A1 и A2 независимы. По теореме умножения вероятностей независимых событий получим:
P(A1A2) = P(A1)· P(A2) = 1/2 · 1/2 = 1/4.
- Событие B называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события B, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается PA(B).
Отыскать вероятность совместного появления зависимых событий помогает теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло: P(AB) = P(A)·PA(B).
Связь теории вероятностей с теорией множеств.
В математике принято устанавливать связи между различными разделами. Связь между теорией вероятностей и теорией множеств устанавливается следующим образом: события отождествляются с множествами. В таком случае понятию исход будет эквивалентно понятие элемент множества. При таком подходе выберите из списка, какому понятию из теории множеств соответствует данное понятие из теории вероятностей:
– Невозможное событие (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
– Сумма событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
– Произведение событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
Примеры и разбор решения заданий тренировочного модуля
1. В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара без возврата. Найдите вероятность того, что первый шар окажется черным, второй – красным и третий – белым.
Решение.
А – первый шар окажется черным
В – второй шар красный
С – третий шар белый
.
Ответ: 4/91.
2. Колю отпускают гулять при условии сделанных уроков с вероятностью 0,8. Папа выдает ему деньги на мороженое с вероятностью 0,6. С какой вероятностью Коля пойдет гулять без мороженого?
Решение.
A – папа выдал Коле денег на мороженое
B – Колю отпустили гулять
Вероятность того, что Коля пойдёт гулять, есть в условии задачи P(B) = 0,8. Вероятность, что папа не выдаст ему деньги на мороженое, равна P(Ᾱ) = 1 – P(A) = 1 – 0,6 = 0,4. Вероятность одновременного осуществления двух независимых событий – произведение их вероятностей P(ᾹB) = P(Ᾱ)·P(B) = 0,8·0,4 = 0,32.
Ответ: 0,32.
