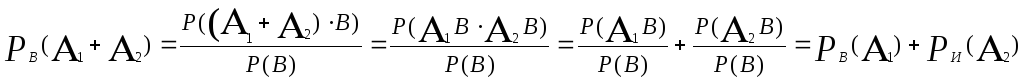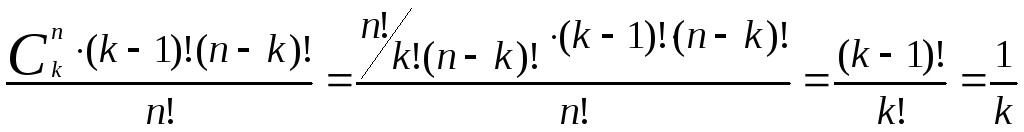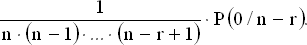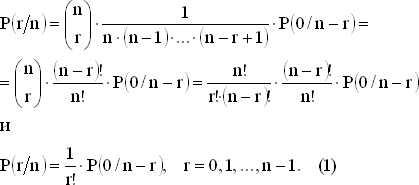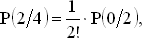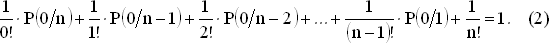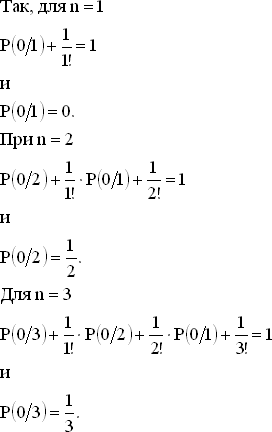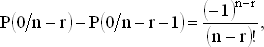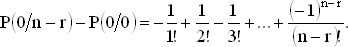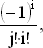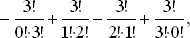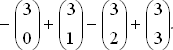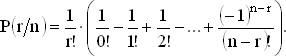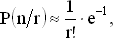Задача о совпадениях.
Идёт экзамен по теории вероятности. Все
студенты складывают свои зачетки на
стол. Преподаватель наугад берет зачетку
и выставляет оценку и вручает студенту.
Какова вероятность, что хотя бы один
студент получит свою зачетку.
события попарно не совместны
i–й студент получил свою
зачетку.
–
?
=
-
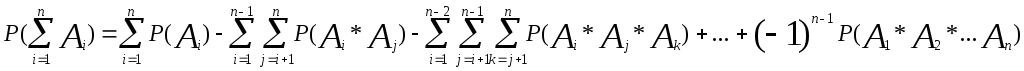
Р(
)
=
= Р(
)
=
-
)
= Р(
)
3)
4)
При
Условная вероятность. Правило умножения вероятностей.
Опр. 1: Условной вероятностью события
А при условии В называется вероятность
события А в предположении, что событие
В состоялось.
Р(А|В);
вероятность события А при условии В.
Опр. 2: Условной вероятностью события
А при условии В называется отношение
вероятности произведений этих событий
к вероятности события В.
(если эта вероятность не равна 0)
Р(А∙В) = Р(А|B) ∙P(B)
=P(B|A)
∙P(A) правило
умножения вероятностей
Следствие:
Замечание № 1:в рамках классического
подхода условная вероятность выводится
Ω
B
k
l
A m P(A|B)=
n
P(B|A) =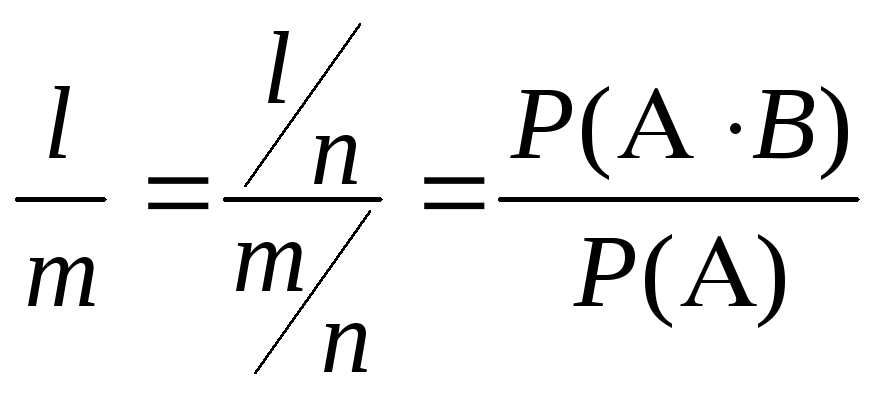
Замечание № 2:Условное вероятность
определяет новое вероятностное
пространство (Ω,
А,
)
Все свойства
вероятности сохраняются
1)
2)
3)
Если
то
4)
Независимость событий.
Опр. 1: Два события называются
независимыми если информация о том
произошло или нет одно из них не влияет
на вероятность другого.
Р(А)=
Р(В) =
Опр. 2: Несколько событий называются
попарно независимыми, если каждые два
из них независимы.
Опр.3:Несколько событий называются
независимыми в совокупности, если они
попарно независимы и каждое событие не
зависит от всевозможных произведений
остальных событий.
Пример:А,В,С – попарно независимы.
Тогда независимы А и В, В и С,А и С. Если
в совокупности, то А и В,В и С,А и С,А и
ВС,В и АС,С и АВ.
Теорема 1:Если событие А и В независимы,
то вероятность Р(АВ)=Р(А)∙Р(В)
Теорема 2:Если события
,
независимы в совокупности, то Р(
)
=
Пример 1:Есть 4 числа: 2,3,5,30
– вытащенное число делится на 2,3,5
1)Р(
)=Р(
)=Р(
)=
попарно независимы
2)Р(
)=
=
3)
в совокупности зависимы
Пример 2:
2
6
8
6
8
1
В
В
А
А
24 24
Р(А) =
Р(А) =
Р(В)=
Р(В)=
Р(АВ)=
Р(АВ)=
Р(АВ)=Р(А)∙Р(В)
Р(АВ)≠Р(А)∙Р(В)
Это означает, что А и В независимы
Это означает, что А и В
зависимы
P(A)=P(A|B)
P(A)≠P(A|B)
Пример 3: 1)Имеется колода карт из 36
карт
А – вытянули пику
В – вытянули даму
Р
(А)
Р(АВ)
= Р(А)∙Р(В) события независимы
Р
(В)
Р(АВ)
2)В колоду добавили джокера
Р
(А)
Р(АВ)
≠ Р(А)∙Р(В) события зависимы
Р
(В)
Р(АВ)
Замечание:при установлении
независимости А и В часто используют
следующий принцип: события А и В, реальные
прообразы которых причинно независимы
считаются независимыми и в
теоретико-вероятностном смысле.
Задача о наилучшем выборе.
Имеется nпредметов разного
качества. Задача заключается в том чтобы
выбрать предмет наилучшего качества.
Случайным образом извлекают первый
предмет. На этом опыт может закончится.
Если эксперимент продолжается, то
остановится можно лишь в тот момент,
когда вытащенный предмет лучше всех
предыдущих, предположим, что предмет,
извлечённый на шаге к лучше всех
предыдущих. Какова вероятность, что он
при этом окажется абсолютно лучшим.
А – предмет, вытащенный на шаге к
наилучший
В – предмет, вытащенный на шаге к- лучший
среди вытащенных
P(A|B)
– ?
P(A|B)
=
т.к А подмножество В
-
Р(А)=
-
Р(В)=
-
Р(А|B)=
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Эта задача родственна задаче 28, в которой мы впервые встретились с законом Пуассона. Однако в задаче о фальшивомонетчике в силу независимости испытаний появление фальшивой монеты было равновероятно на каждом шагу, в настоящей же задаче совпадения для каждой пары не являются независимыми. Например, если n ? 1 пар совпали, то необходимо совпадет и n-я пара, так что эти события действительно зависимы. Тем не менее при больших значениях n степень зависимости невелика, так что, казалось бы, вероятность r совпадений в этой задаче должна быть близка к вероятности обнаружения фальшивых монет, задаваемой распределением Пуассона. В конце мы сравним решение такой задачи с ответом, получаемым из закона Пуассона со средним 1.
При решении таких задач оказывается полезным рассмотрение частных случаев, отвечающих небольшим значениям n. При n = 1 совпадение неизбежно. При n = 2 вероятность отсутствия совпадения равна 1/2, вероятность двух совпадений также равняется 1/2. При n = 3 занумеруем карты цифрами 1, 2 и 3 и запишем в таблицу 6 возможных перестановок для верхней колоды при фиксированном порядке (1, 2 ,3) нижней.
Перестановки и совпадения, n = 3
Нижняя колода
1
2
3
Число совпадений
Перестановки верхней колоды
1
2
3
3
1
3
2
1
2
1
3
1
2
3
1
0
3
1
2
0
3
2
1
1
Отсюда получаем
Распределение числа совпадений, n = 3
Число совпадений
0
1
2
3
Вероятность
2/6
3/6
0/6
1/6
Приведем также соответствующую таблицу для n = 4. Легко заметить, что вероятность того, что произойдет n совпадений, равна 1/n!, поскольку только одной из n! перестановок отвечает n совпадений.
Число совпадений
0
1
2
3
4
n = 1, вероятность
0
1
n = 2, вероятность
1/2
0
1/2
n = 3, вероятность
2/6
3/6
0
1/6
n = 4, вероятность
9/24
8/24
6/24
0
1/24
Отметим, что математическое ожидание каждого распределения равно 1, как указано в предыдущей задаче.
Пусть P(r/n) обозначает вероятность ровно r совпадений при распределении n объектов. Эти r совпадений могут быть получены за счет совпадения r фиксированных объектов и несовпадения остальных. Так, например, вероятность того, что совпадают именно r первых объектов, равна
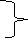
Число различных выборов r объектов из n равно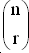 
так что
При r = n, как мы знаем, P(n/n) = 1/n!, и мы можем положить P(0/0) = 1.
Проверим справедливость соотношения (1) при n = 4, г = 2. Согласно (1)
а из нашей таблицы видно, что
P(2/4) = 6/24,
P(0/2) = 1/2
и 6/24 = 1/4, что подтверждает (1) в этом частном случае.
Мы знаем также, что сумма вероятностей по всем возможным числам совпадений при заданном значении n равна 1, т. е.
P(0/n) + P(1/n) + … + P(n ? 1/n) + P(n/n) = 1.
Используя (1), запишем это соотношение как
Так как P(n/n) = 1/n!, то отсюда можно последовательно находить значения P(0/n).
Итак, мы можем найти в принципе значение P(0/n) при любом n, но не располагаем общей формулой для вычисления P(0/n). Как и в некоторых других задачах, здесь помогает вычисление последовательных разностей. Подсчитаем P(0/n) ? P(0/n ? 1) для различных значений n. Имеем
P(0/1) ? P(0/0) = 0 ? 1 = ?1 = ?1/1!,
P(0/2) ? P(0/1) = 1/2 ? 0 = 1/2 = 1/2!,
P(0/3) ? P(0/2) = 2/6 ? 1/2 = ?1/6 = ?1/3!,
P(0/4) ? P(0/3) = 9/24 ? 2/6 = 1/24 = 1/4!.
Эти выкладки наводят на мысль о том, что искомые разности имеют вид (-l)r/r!, т. е.
Суммируя эти разности, получаем
Записывая P(0/0) в виде 1/0!, получаем
(3)
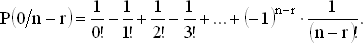
Осталось проверить теперь справедливость нашей догадки. Нам надо вычислить
(4)
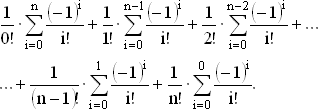
Не следует терять хладнокровия. при виде этого зловещего выражения. Ведь сумма в (4) образована слагаемыми вида
где индекс j отвечает множителю, стоящему перед знаком суммы, а индекс i соответствует отдельным членам этой суммы. Переставим местами слагаемые так, чтобы сумма i + j была постоянной. Так, для i + j = 3 получим
Умножая на 3!, получаем более знакомое выражение
которое с помощью биномиальных коэффициентов может быть записано в виде
Но эта сумма есть разложение (x + y)? при х = ?1, y = 1 и, значит, равна нулю, так как (-1 + 1)? = 0? = 0. Этот факт имеет место при каждом значении i + j = r, r = 1, 2, …., n, так что соответствующие суммы равны нулю. Лишь при r = 0 получаем единственный член (-1)0/(0!·0!) = 1. Следовательно, решение (3) удовлетворяет уравнению (2).
Ясно, что других решений у (2) нет. Это может быть доказано методом индукции, так как P(0/n) выражается через P(0/1), P(0/2), …, P(0/n ? 1).
Из (1) и (3), наконец, выводим
Если n ? r велико, то выражение в скобках близко к e?1 и
если только n ? r достаточно велико. Итак, действительно, вероятности r совпадений в нашей задаче близки к пуассоновским со средним 1. Однако для этой близости необходимо, чтобы разность n ? r была велика, а не только само n, как казалось в начале.
Вероятность того, что нет ни одного совпадения, при больших n стремится к e?1 ? 0.368.
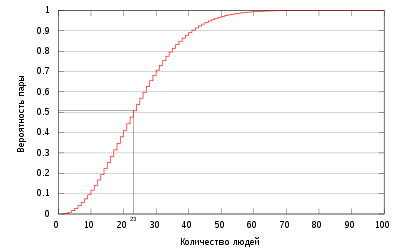
Парадо́кс дней рожде́ния — утверждение, состоящее в том, что в группе, состоящей из 23 или более человек, вероятность совпадения дней рождения (число и месяц) хотя бы у двух людей превышает 50 %. Например, если в классе 23 ученика или более, то более вероятно то, что у какой-то пары одноклассников дни рождения придутся на один день, чем то, что у каждого будет свой неповторимый день рождения[1]. Впервые эта задача была рассмотрена Рихардом Мизесом в 1939 году[2][3].
Для 57 и более человек вероятность такого совпадения превышает 99 %, хотя 100 % она достигает, согласно принципу Дирихле (здравому смыслу), только тогда, когда в группе не менее 367 человек (ровно на 1 больше, чем число дней в високосном году; с учётом високосных лет).
Такое утверждение может показаться неочевидным, так как вероятность совпадения дней рождения двух человек с любым днём в году 
, умноженная на число человек в группе (23), даёт лишь 
. Это рассуждение неверно, так как число возможных пар 
значительно превышает число человек в группе (253 > 23). Таким образом, утверждение не является парадоксом в строгом научном смысле: логического противоречия в нём нет, а парадокс заключается лишь в различиях между интуитивным восприятием ситуации человеком и результатами математического расчёта.
График зависимости вероятности совпадения дней рождения хотя бы у двух человек от количества людей
Интуитивное восприятие[править | править код]
В группе из 23 человек вероятность совпадения дней рождения у двух человек столь высока, потому что рассматривается вероятность совпадения дней рождения у любых двух человек в группе. Эта вероятность определяется количеством пар людей, которые можно составить из 23 человек. Так как порядок людей в парах не имеет значения, общее число таких пар равно числу сочетаний из 23 по 2, то есть (23 × 22) / 2 = 253 пары.
В формулировке парадокса речь идёт именно о совпадении дней рождения у каких-либо двух членов группы. Одно из распространённых заблуждений состоит в том, что этот случай путают с другим случаем, на первый взгляд похожим, когда из группы выбирается один человек и оценивается вероятность того, что день рождения каких-либо других членов группы совпадёт с днём рождения выбранного человека. В последнем случае вероятность совпадения значительно ниже.
Расчёт вероятности[править | править код]
Требуется определить вероятность того, что в группе из n человек как минимум у двух из них дни рождения совпадут.
Пусть дни рождения распределены равномерно, то есть примем, что:
- в году 365 дней (нет високосных лет);
- в группе нет людей, заведомо родившихся в один день (например, близнецов);
- рождаемость не зависит от дня недели, времени года и других факторов.
В действительности это не совсем так — в частности, в некоторых странах из-за особенностей работы больниц больше детей рождается в определённые дни недели. Однако неравномерность распределения может лишь увеличить вероятность совпадения дней рождения, но не уменьшить: если бы все люди рождались только в 3 дня из 365, то вероятность совпадения дней рождения была бы очень высокой.
Рассчитаем сначала 
— вероятность того, что в группе из 
человек дни рождения всех людей будут различными. Если 
, то в силу принципа Дирихле вероятность равна нулю. Если же 
, то будем рассуждать следующим образом. Возьмём наугад одного человека из группы и запомним его день рождения. Затем возьмём наугад второго человека, при этом вероятность того, что у него день рождения не совпадёт с днем рождения первого человека, равна 
. Затем возьмём третьего человека; при этом вероятность того, что его день рождения не совпадёт с днем рождения одного из первых двух, равна 
. Рассуждая по аналогии, мы дойдём до последнего человека, для которого вероятность несовпадения его дня рождения со всеми предыдущими будет равна 
. Перемножая все эти вероятности, получаем вероятность того, что все дни рождения в группе будут различными:
Тогда вероятность того, что хотя бы у двух человек из n дни рождения совпадут, равна
Значение этой функции превосходит 1/2 при 
, при этом вероятность совпадения равна примерно 50,73 %, а 
. Список значений n и соответствующих им вероятностей приведён в следующей таблице.
| n | p(n) |
|---|---|
| 10 | 12 % |
| 20 | 41 % |
| 30 | 70 % |
| 50 | 97 % |
| 100 | 99,99996 % |
| 200 | 99,9999999999999999999999999998 % |
| 300 | (1 − 7×10−73) × 100 % |
| 350 | (1 − 3×10−131) × 100 % |
| 367 | 100 % |
Данную задачу можно переформулировать в терминах классической «задачи о совпадениях». Пусть:
Требуется посчитать вероятность события, заключающегося в отсутствии повторений в выборке. Все расчёты аналогичны приведённым выше.
Альтернативный метод[править | править код]
Вероятность совпадения дней рождения у двух человек, входящих в группу из n людей, можно также рассчитать с использованием формул комбинаторики[4]. Представим, что каждый день года — это одна буква в алфавите, и алфавит состоит из 365 букв. Дни рождения n человек могут быть представлены строкой, состоящей из n букв такого алфавита. По формуле Хартли, количество возможных строк равно
Количество возможных строк, в которых буквы не повторяются (размещение из 365 по n), составит
Если строки выбираются случайно (с равномерным распределением), вероятность выбора строки, в которой хотя бы две буквы совпадут, равна
при и- при .
Таким образом,
а это выражение эквивалентно представленному выше.
Также общее количество возможных строк можно рассчитать по формуле комбинаторики количества размещений с повторениями А(повт) n/365 = 365n.
Аппроксимации[править | править код]
Экспоненциальная функция[править | править код]
Используя разложение экспоненциальной функции в ряд Тейлора
приведённое выше выражение для можно аппроксимировать следующим образом:
Следовательно:
Графики функции p(n) и близкой к ней функции аппроксимации
Заметим, что и упрощенная аппроксимация
как видно по графику, всё ещё даёт достаточную точность.
Приведём ещё одну аппроксимацию.
Вероятность того, что у двух людей дни рождения не совпадают, равна 364/365. В группе из человек 
пар. Поэтому вероятность при условии независимости этих событий может быть приближена числом
Следовательно, получаем приближение для искомой вероятности p(n):
Пуассоновское приближение[править | править код]
Используя приближение Пуассона для бинома, исходя из предыдущего приближения для 
, получим чуть больше 50 %:
Расчёт количества человек, при котором вероятность составляет 50 %[править | править код]
Из приведённой ранее формулы 
выразим n. Затем вместо p(n) подставим 50 % (0,5). В результате получим:
Существует ещё один способ оценки n при вероятности 50 %.
Согласно доказанному выше:
Найдём наименьшее n, при котором
или, что то же самое,
Воспользуемся приведённой выше аппроксимацией функции экспоненциальной функцией:
Подставив 
вместо в выражение 
, получим
Решая относительно n, получим
Отсюда найдём n и округлим до целого:
- n = 23.
Родившиеся в один день с заданным человеком[править | править код]
Сравним вероятность p(n) с вероятностью того, что в группе из n человек день рождения какого-либо человека из группы совпадёт с днём рождения некоторого заранее выбранного человека, не принадлежащего группе. Эта вероятность равна
Сравнение графиков функций p(n) и q(n).
Ось абсцисс: количество человек n.
Ось ординат: вероятность.
p(n) — вероятность того, что в группе из n человек как минимум у двух из них дни рождения совпадут.
q(n) — вероятностью того, что в группе из n человек день рождения какого‑либо человека из группы совпадёт с днём рождения некоторого заранее выбранного человека, не принадлежащего группе.
Подставляя n = 23, получаем q(n) ≈ 6,12 %. Для того, чтобы вероятность q(n) превысила 50 %, число людей в группе должно быть не менее 253 (q(252) ≈ 49,91 %; q(253) ≈ 50,05 %). Это число больше, чем половина дней в году (365/2 = 182,5); так происходит из-за того, что у остальных членов группы дни рождения могут совпадать между собой, и это уменьшает вероятность q(n). Если выразиться точнее, то это происходит из-за того, что при сложении вероятностей совпадений мы каждый раз вычитаем вероятность совместного появления этих событий, так как события являются совместными и вероятность их совместного появления при сложении учтена дважды. P(A + B) = P(A) + P(B) − P(AB) и т. д с каждым добавлением нового слагаемого.
Обобщения[править | править код]
Совпадение дискретных случайных величин[править | править код]
Описанная задача может быть сформулирована в общем виде:
- даны случайные числа;
- случайные числа распределены равномерно в диапазоне от 1 до d;
- n — количество случайных чисел;
- определить p( n ; d ) — вероятность того, что совпадут хотя бы два числа из заданных.
Если рассуждать таким же образом, как описано выше, можно получить общие решения:
Обратная задача:
- дана p — вероятность того, что совпадают хотя бы два случайных числа;
- известно, что случайные числа распределены равномерно в диапазоне от 1 до d;
- найти n(p;d) — количество случайных чисел.
Решение:
Несколько типов людей[править | править код]
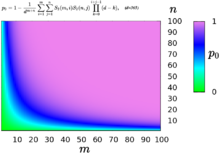
Вероятность совпадения дня рождения хотя бы у одного мужчины и у одной женщины
Выше парадокс дней рождения был представлен для одного «типа» людей. Можно обобщить задачу, введя несколько «типов», например, разделив людей на мужчин (m) и женщин (n). Подсчитаем вероятность того, что хотя бы у одной женщины и у одного мужчины совпадают дни рождения (совпадение дней рождения у двух женщин или у двух мужчин не учитываются):
где d = 365 и S2() — числа Стирлинга второго рода. Интересно, что нет однозначного ответа на вопрос о величине n+m для заданной вероятности. Например, вероятность 0,5 даёт как набор из 16 мужчин и 16 женщин, так и набор из 43 мужчин и 6 женщин.
Близкие дни рождения[править | править код]
Другое обобщение парадокса дней рождения состоит в постановке задачи о том, сколько требуется человек для того, чтобы вероятность наличия в группе людей, дни рождения которых различаются не более чем на один день (или на два, три дня и так далее), превысила 50 %. При решении этой задачи используется принцип включения-исключения. Результат (опять-таки в предположении, что дни рождения распределены равномерно) получается следующим:
| Максимальное различие дней рождения, количество дней | Необходимое количество людей |
|---|---|
| 1 | 23 |
| 2 | 14 |
| 3 | 11 |
| 4 | 9 |
| 5 | 8 |
| 6 | 8 |
| 7 | 7 |
| 8 | 7 |
Таким образом, вероятность того, что даже в группе из 7 человек дни рождения хотя бы у двух из них будут различаться не более чем на неделю, превышает 50 %.
Применение[править | править код]
Парадокс дней рождения в общем виде применим к хеш-функциям: если хеш-функция генерирует N‑битное значение, то число случайных входных данных, для которых хеш-коды с большой вероятностью дадут коллизию (то есть найдутся равные хеш-коды, полученные на разных входных данных), равно не 2N, а только около 2N/2. Это наблюдение используется в атаке на криптографические хеш‑функции, получившей название «атака „дней рождения“».
| N | Количество различных выходных цепочек (2N) | Вероятность хотя бы одной коллизии (p) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10−18 | 10−15 | 10−12 | 10−9 | 10−6 | 0,1 % | 1 % | 25 % | 50 % | 75 % | ||
| 32 | 4,3 × 109 | 2 | 2 | 2 | 2,9 | 93 | 2,9 × 10³ | 9,3 × 10³ | 5,0 × 10⁴ | 7,7 × 10⁴ | 1,1 × 10⁵ |
| 64 | 1,8 × 1019 | 6,1 | 1,9 × 10² | 6,1 × 10³ | 1,9 × 10⁵ | 6,1 × 10⁶ | 1,9 × 10⁸ | 6,1 × 10⁸ | 3,3 × 10⁹ | 5,1 × 10⁹ | 7,2 × 10⁹ |
| 128 | 3,4 × 1038 | 2,6 × 1010 | 8,2 × 1011 | 2,6 × 1013 | 8,2 × 1014 | 2,6 × 1016 | 8,3 × 1017 | 2,6 × 1018 | 1,4 × 1019 | 2,2 × 1019 | 3,1 × 1019 |
| 256 | 1,2 × 1077 | 4,8 × 1029 | 1,5 × 1031 | 4,8 × 1032 | 1,5 × 1034 | 4,8 × 1035 | 1,5 × 1037 | 4,8 × 1037 | 2,6 × 1038 | 4,0 × 1038 | 5,7 × 1038 |
| 384 | 3,9 × 10115 | 8,9 × 1048 | 2,8 × 1050 | 8,9 × 1051 | 2,8 × 1053 | 8,9 × 1054 | 2,8 × 1056 | 8,9 × 1056 | 4,8 × 1057 | 7,4 × 1057 | 1,0 × 1058 |
| 512 | 1,3 × 10154 | 1,6 × 1068 | 5,2 × 1069 | 1,6 × 1071 | 5,2 × 1072 | 1,6 × 1074 | 5,2 × 1075 | 1,6 × 1076 | 8,8 × 1076 | 1,4 × 1077 | 1,9 × 1077 |
В белых ячейках указано количество человек в группе, при котором коллизия произойдёт с заданной вероятностью (по аналогии с парадоксом количество выходных цепочек равно 365).
Сходный математический аппарат используется для оценки размера популяции рыб, обитающих в озёрах. Метод называется «capture-recapture» («поймать — поймать снова»). Действительно, если каждую пойманную рыбу помечать и отпускать, то вероятность поймать помеченную рыбу будет расти нелинейно (в соответствии с приведённым выше графиком) с ростом количества попыток. Размер популяции грубо может быть оценён как квадрат числа попыток, совершаемых до вылавливания первой помеченной рыбы.
Решение задачи в общем виде находит применение во многих разделах математики, например, в недетерминированных алгоритмах факторизации. Так, одно из самых простых объяснений ρ-метода Полларда аналогично объяснению парадокса дней рождения: достаточно иметь примерно 
случайных чисел от 0 до 
, где 
— простые, чтобы хотя бы для одной из пар чисел с высокой вероятностью нашёлся 
, который и будет делителем числа n.
Обратные задачи[править | править код]
- Поиск наименьшего числа n, при котором вероятность p(n) больше заданного числа p.
- Поиск наибольшего числа n, при котором вероятность p(n) меньше заданного числа p.
Пользуясь формулой, приведённой выше, получаем:
| p | n | n↓ | p(n↓) | n↑ | p(n↑) |
|---|---|---|---|---|---|
| 0,01 | 0,14178√365 = 2,70864 | 2 | 0,00274 | 3 | 0,00820 |
| 0,05 | 0,32029√365 = 6,11916 | 6 | 0,04046 | 7 | 0,05624 |
| 0,1 | 0,45904√365 = 8,77002 | 8 | 0,07434 | 9 | 0,09462 |
| 0,2 | 0,66805√365 = 12,76302 | 12 | 0,16702 | 13 | 0,19441 |
| 0,3 | 0,84460√365 = 16,13607 | 16 | 0,28360 | 17 | 0,31501 |
| 0,5 | 1,17741√365 = 22,49439 | 22 | 0,47570 | 23 | 0,50730 |
| 0,7 | 1,55176√365 = 29,64625 | 29 | 0,68097 | 30 | 0,70632 |
| 0,8 | 1,79412√365 = 34,27666 | 34 | 0,79532 | 35 | 0,81438 |
| 0,9 | 2,14597√365 = 40,99862 | 40 | 0,89123 | 41 | 0,90315 |
| 0,95 | 2,44775√365 = 46,76414 | 46 | 0,94825 | 47 | 0,95477 |
| 0,99 | 3,03485√365 = 57,98081 | 57 | 0,99012 | 58 | 0,99166 |
Наилучшая позиция[править | править код]
Пусть в комнате находятся n – 1 человек, и их дни рождения различны. Пусть g(n) — вероятность того, что день рождения вошедшего человека совпадает с днём рождения кого‑либо из присутствующих в комнате. Требуется найти значение n, при котором значение функции g(n) максимально.
Решение сводится к нахождению максимального значения выражения
- p(n) – p(n-1).
Используя приведённую выше формулу для p(n), получим n = 20.
Среднее число людей[править | править код]
Рассмотрим другую задачу. Сколько в среднем нужно людей для того, чтобы хотя бы у двух из них совпали дни рождения?
Эта проблема имела отношение к алгоритмам хеширования и была исследована Дональдом Кнутом.
Оказывается, что интересующая нас случайная величина имеет математическое ожидание, равное
где
Функция
была исследована Рамануджаном. Он же получил для этой функции следующее асимптотическое разложение:
При M = 365 среднее число людей равно
Это число немного больше, чем число людей, обеспечивающих вероятность 50 %. Как ни удивительно, необходимое число людей равно M + 1 = 366 (у 365 людей дни рождения могут распределиться по каждому из 365 дней года без совпадений), хотя в среднем нужно лишь 25.
См. также[править | править код]
- Задача о письмах
- Закон больших чисел
Примечания[править | править код]
- ↑ Мазур, 2017, с. 116.
- ↑ Мазур, 2017, с. 119.
- ↑ Миронкин В. О., Чухно А. Б. Об одном обобщении парадокса «дней рождения». Дата обращения: 30 марта 2020. Архивировано 9 июля 2020 года.
- ↑ Мазур, 2017, с. 117.
Литература[править | править код]
- Кемени Дж., Снелл Дж., Томпсон Дж. Введение в конечную математику = Introduction to Finite Mathematics. — Издательство иностранной литературы, 1963. — 488 с.
- Козлов М. В. Элементы теории вероятностей в примерах и задачах. — МГУ, 1990 год. — ISBN 5-211-00312-8.
- Мазур, Джозеф. Задача о дне рождения // Игра случая. Математика и мифология совпадения. — Альпина нон-фикшн, 2017. — С. 116—123. — 292 с. — ISBN 978-5-91671-636-8.
- Секей Г. Парадоксы в теории вероятностей и математической статистике. — РХД, 2003 год. — ISBN 5-93972-150-8.
- Ширяев А. Н. Вероятность-1. — МЦНМО, 2007 год. — ISBN 978-5-94057-036-3.
- Goldberg S. A Direct Attack on a Birthday Problem (англ.) // Mathematical Mathematics Magazine. — Май 1976 года. — Iss. 49. — P. 130—132.
- Mosteller F. Understanding the Birthday Problem (англ.) // The Mathematics Teacher. — Май 1962 года. — P. 322—325.
Ссылки[править | править код]
- Парадоксы теории вероятностей.
- Сравнительный обзор алгоритмов PGP. Парадокс «дней рождения» и стойкость криптографии.
- Eurobirthdays 2012 года (англ.). Практический пример.
Вероятность того, что у двух людей совпадет день рождения равна 1/365 – по числу дней в году (если год невисокосный). Например, ваш день рождения 5 ноября. Вероятность того, что у любого другого человека из какой-либо группы людей день рождения тоже будет 5 ноября равна 1/365.
Но когда речь идет о совпадении дня рождения не двух конкретных людей в группе, в которой, например, 23 человека, то здесь число совпадений надо рассматривать исходя из числа возможных пар. А число возможных пар – это сочетание из 23 по 2. Которое будет равно 23 х 22/2 = 253 пары.
Как видим, число пар из группы в 23 человека равно 253, а это значительно больше чем половина дней в году.
Формула, по которой рассчитывается вероятность того, что все дни рождения в группе будут различными:
где п – количество людей в группе. В нашем случае п=23.
А вероятность того, что хотя бы у 2-х человек из п дни рождения совпадут, равна
Решив это уравнение для п=23, получаем вероятность, равную 50,7 %.
Чтобы вероятность приближалась к 99 % количество людей в группе должно быть равно примерно 57 человек.
На чтение 16 мин Просмотров 125к. Опубликовано 25 мая, 2018
Вероятность — очень лёгкая тема, если концентрироваться на смысле задач, а не на формулах. Найти вероятность того что — не просто. И как решать задачи на вероятность?. Во-первых, что такое вероятность? Это шанс, что какое-то событие произойдёт. Если мы говорим, что вероятность некоторого события 50%, что это значит? Что оно либо произойдет, либо не произойдет — одно из двух. Таким образом подсчитать значение вероятности очень просто — нужно взять количество подходящих нам вариантов и разделить на количество всех возможных вариантов. Например, шанс получить решку при подбрасывании монеты это ½. Как мы получаем ½? Всего у нас два возможных варианта (орёл и решка), из них нам подходит один (решка), так мы и получаем вероятность ½.
Как мы уже с вами увидели, вероятность может быть выражена как в процентах, так и в обычных числах. Важно: на ЕГЭ вам нужно будет записать ответ в числах, не в процентах. Принято, что вероятность изменяется от 0 (никогда не произойдет) до 1 (абсолютно точно произойдет). Также можно сказать, что всегда
Вероятность подходящих событий + вероятность неподходящих событий = 1
Теперь мы точно понимаем, как считать вероятность отдельного события, и даже такие задачи есть в банке ФИПИ, но понятно, что на этом всё не заканчивается. Чтобы жизнь была веселее, в задачах на вероятность обычно происходят как минимум два события, и надо посчитать вероятность с учетом каждого из них.
Содержание
- Вероятность нескольких событий
- Задачи и решения задач на вероятность
- Вероятность нескольких событий
- Дополняющая вероятность
Вероятность нескольких событий
Подсчитываем вероятность каждого события в отдельности, затем между дробями ставим знаки:
1. Если нужно первое И второе событие, то умножаем.
2. Если нужно первое ИЛИ второе событие, то складываем.
Задачи и решения задач на вероятность
Задача 1. Среди натуральных чисел от 23 до 37 случайно выбирают одно число. Найдите вероятность того, что оно не делится на 5.
Решение:
Вероятность, это отношение благоприятных вариантов к общему их количеству.
Всего в этом промежутке 15 чисел. Из них на 5 делится всего 3, значит не делится 12.
Вероятность тогда: 
Ответ: 0,8.
Задача 2. Для дежурства в столовой случайно выбирают двух учащихся класса. Какова вероятность того, что дежурить будут два мальчика, если в классе обучается 7 мальчиков и 8 девочек?
Решение: Вероятность, это отношение благоприятных вариантов к общему их количеству. В классе 7 мальчиков, это благоприятные варианты. А всего 15 учеников.
Вероятность что первый дежурный мальчик:
Вероятность что второй дежурный мальчик:
Раз оба должны быть мальчики, вероятности перемножим:
Ответ: 0,2.
Задача 3. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Решение: Пассажиру В. удобны 30 мест (12 + 18 = 30), а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30/300, т. е. 0,1.
Задача 4. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
Решение: Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна 15/25, т. е. 0,6.
Задача 5. В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам.
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам.
Решение: Из 35 билетов 28 не содержат вопроса по кислотам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по кислотам, равна 28/35, т. е. 0,8.
Задача 6. В среднем из 500 садовых насосов, поступивших в продажу, 2 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение: Если из 500 насосов 2 подтекают, то 498 не подтекают. Следовательно, вероятность выбора хорошего насоса — 498/500, т. е. 0,996.
Задача 7. Вероятность того, что новый пылесос в течение года поступит в гарантийный ремонт, равна 0,065. В некотором городе из 1000 проданных пылесосов в течение года в гарантийную мастерскую поступило 70 штук.
На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение: Частота события «гарантийный ремонт» равна 70/1000, т. е. 0,07. Она отличается от предсказанной вероятности на 0,005 (0,07 – 0,065 = 0,005).
Задача 8. В чемпионате по гимнастике участвуют 50 спортсменок: 18 из России, 14 из Украины, остальные — из Белоруссии. Порядок, в котором выступают гимнастки, определяется жребием.
Найдите вероятность того, что спортсменка, выступающая первой, окажется из Белоруссии.
Решение: Всего участниц на чемпионате 50, а спортсменок из Белоруссии — 18 (50 – 18 – 14 = 18).
Вероятность того, что первой будет выступать спортсменка из Белоруссии — 18 из 50, т. е. 18/50, или 0,36.
Задача 9. Научная конференция проводится в 5 дней. Всего запланировано 80 докладов — первые три дня по 12 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой.
Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение: За первые три дня будут прочитаны 36 докладов (12 ∙ 3 = 36), на последние два дня планируется 44 доклада. Поэтому на последний день запланировано 22 докладов (44 : 2 = 22). Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 22/80, т. е. 0,275.
Задача 10.
Перед началом первого тура чемпионата по шахматам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шахматистов, среди которых 14 участников из России, в том числе Егор Косов.
Найдите вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России?
Решение: В первом туре Егор Косов может сыграть с 25 шахматистами (26 – 1 = 25), из которых 13 ― из России. Значит, вероятность того, что в первом туре Егор Косов будет играть с каким-либо шахматистом из России, равна 13/25, или 0,52.
Задача 11.
В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение: Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек, т. е. 4/16, или 0,25.
Задача 12. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
Решение: Выбирают двоих туристов из пяти. Следовательно, вероятность быть выбранным равна 2/5, т. е. 0,4.
Задача 13. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение: На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист полетит первым рейсом вертолёта, равна 6/30, или 0,2.
Задача 14. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
Решение: Натуральных чисел от 10 до 19 десять, из них на 3 делятся три числа: 12, 15 и 18. Следовательно, искомая вероятность равна 3/10, т. е. 0,3.
Вероятность нескольких событий
Задача 1. Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Ротор», «Мотор» и «Стратор». Найдите вероятность того, что «Стартер» будет начинать только вторую игру.
Решение:
Тип вопроса: совмещение событий.
Нас устроит следующий вариант: «Статор» не начинает первую игру, начинает вторую игру, не начинает третью игру. Вероятность такого развития событий равна произведению вероятностей каждого из этих событий. Вероятность каждого из них равна 0,5, следовательно: 0,5 · 0,5 · 0,5 = 0,125.
Задача 2. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей ― 1 очко, если проигрывает ― 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.
Решение:
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
| Игра №1 | Игра №2 | Вероятность данного варианта |
| 3 | 1 | 0,4 · 0,2 = 0,08 |
| 1 | 3 | 0,2 · 0,4 = 0,08 |
| 3 | 3 | 0,4 · 0,4 = 0,16 |
Вероятность происхождения какого-либо их этих 3-х вариантов равна сумме вероятностей каждого из вариантов: 0,08 + 0,08 + 0,16 = 0,32.
Задача 3. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того что Аня и Нина окажутся в одной группе.
Решение:
Тип вопроса: уменьшение групп.
Вероятность попадания Ани в одну из групп равна 1. Вероятность попадания Нины в ту же группу равна 2 из 20 (2 оставшихся места в группе, а человек осталось 20). 2/20 = 1/10 = 0,1.
Задача 4. В кармане у Пети было 4 монеты по рублю и 2 монеты по два рубля. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе двухрублёвые монеты лежат в одном кармане.
Решение:
Способ №1
Тип задачи: уменьшение групп.
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая однорублевая монета попадет в один из карманов (групп) = 1.
Вероятность, что две двухрублевые монеты попадут в этот же карман = количество оставшихся мест в этом кармане/на количество оставшихся мест в обоих карманах = 2/5 = 0,4.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют в несколько вариантов:
Если Петя переложил в другой карман три из четырех рублевых монет (а двухрублевые не перекладывал), или если переложил в другой карман обе двухрублевые монеты и одну рублевую одним из трех способов: 1, 2, 2; 2, 1, 2; 2, 2, 1. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 
Задача 5. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Решение:
Тип задачи: уменьшение групп.
Способ №1
Представим, что шесть монет делят на две группы по три монеты. Вероятность, что первая двухрублевая монета попадет в один из карманов (групп) = 1. Вероятность, что вторая монета попадет в другой карман = количество оставшихся мест в другом/ на количество оставшихся мест в обоих карманах = 3/5 = 0,6.
Способ №2
Тип вопроса: совмещение событий.
Задачу выполняют несколько вариантов:
Чтобы пятирублевые монеты оказались в разных карманах, Петя должен взять из кармана одну пятирублевую и две десятирублевые монеты. Это можно сделать тремя способами: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Можно изобразить это на схеме (перекладывает Петя в карман 2, поэтому будем высчитывать вероятности в колонке «карман 2»):
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 
Задача 6. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно два раза.
Решение: Тип вопроса: нахождение желаемого и действительного совмещение событий Нас устраивают три варианта:
Орёл ― решка ― орёл;
Орёл ― орёл ― решка;
Решка ― орёл ― орёл;
Вероятность каждого случая ― 1/2, а каждого варианта ― 1/8 (1/2 ∙ 1/2 ∙ 1/2 = 1/8)
Нас устроит либо первый, либо второй, либо третий вариант. Следовательно, складываем их вероятности и получаем 3/8 (1/8 + 1/8 + 1/8 = 3/8), т. е. 0,375.
Задача 7. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение:
Тип вопроса: совмещение событий.
В любом случае А. будет играть как белыми, так и черными, поэтому нас устроит вариант, когда гроссмейстер А. выиграет, играя белыми (вероятность ― 0,5), а также играя чёрными (вероятность ― 0,34). Поэтому надо перемножить вероятности этих двух событий: 0,5 ∙ 0,34 = 0,17.
Задача 8. Вероятность того, что батарейка бракованная, равна 0,02. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Решение:
Тип вопроса: совмещение событий.
Вероятность того, что батарейка исправна, равна 0,98. Покупателю надо, чтобы и первая, и вторая батарейка были исправны: 0,98 · 0,98 = 0,9604.
Задача 9. На рок-фестивале выступают группы ― по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из США будет выступать после группы из Канады и после группы из Китая? Результат округлите до сотых.
Решение:
Тип вопроса: совмещение событий.
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (КИТ — Китай, КАН = Канада):
… США, КАН, КИТ …
… США, КИТ, КАН …
… КИТ, США, КАН …
… КАН, США, КИТ …
… КАН, КИТ, США …
… КИТ, КАН, США …
США находится после Китая и Канады в двух последних случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна:
≈ 0,33.
Дополняющая вероятность
Задача 1.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05.
Найдите вероятность того, что случайно выбранная батарейка будет забракована.
Решение:
Существуют 2 варианта, которые нам подходят:
Вариант А: батарейка забракована, она неисправна;
Вариант Б: батарейка забракована, она исправна.
Вероятность варианта А: 0,02 ∙ 0,97 = 0,0194;
Вероятность варианта Б: 0,05 ∙ 0,98 = 0,049;
Нас устроит либо первый, либо второй вариант: 0,0194 + 0,049 = 0,0684.
Задача 2. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая — 40%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 5%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Вероятность того, что стекло куплено на первой фабрике и оно бракованное: 0,6 · 0,03 = 0,018.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное: 0,4 · 0,05 = 0,02.
Вероятность того, что случайно купленное в магазине стекло окажется бракованным, равна 0,018 + 0,02 = 0,038.
Задача 3. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до тысячных.
Решение:
Предположим, у нас х тарелок изначально (ведь мы постоянно имеем дело с процентами, поэтому нам ничего не мешает оперировать конкретными величинами).
Тогда 0,1х — дефектные тарелки, а 0,9х — нормальные, которые поступят в магазин сразу. Из дефектных убирается 80%, то есть 0,08х, и остаётся 0,02х, которые тоже пойдут в магазин. Таким образом, общее количество тарелок на полках в магазине окажется: 0,9х + 0,02х = 0,92х. Из них нормальными будет 0,9х. Соответственно, по формуле вероятность будет 0,9х/0,92х ≈ 0,978.
Задача 4. По отзывам покупателей Игорь Игоревич оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,91. Вероятность того, что этот товар доставят из магазина Б, равна 0,89. Игорь Игоревич заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.
Решение. Вероятность того, что первый магазин не доставит товар, равна 1 − 0,91 = 0,09. Вероятность того, что второй магазин не доставит товар, равна 1 − 0,89 = 0,11. Вероятность происхождения двух этих событий одновременно равна произведению вероятностей каждого из них: 0,09 · 0,11 = 0,0099.
Задача 5. При изготовлении подшипников диаметром 70 мм вероятность того, что диаметр будет отличаться от заданного меньше чем на 0,01 мм, равна 0,961. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 69,99 мм или больше чем 70,01 мм.
Решение: Нам дана вероятность события, при котором диаметр будет в пределах между 69,99 мм и 70,01 мм, и она равна 0,961. Вероятность всех остальных вариантов мы можем найти по принципу дополняющей вероятности: 1 − 0,961 = 0,039.
Задача 6. Вероятность того, что на тесте по истории учащийся верно решит больше 9 задач, равна 0,68. Вероятность того, что верно решит больше 8 задач, равна 0,78. Найдите вероятность того, что верно решит ровно 9 задач.
Решение: Вероятность того, что Т. верно решит более 8 задач, включает в себя вероятность решения ровно 9 задач. При этом, события, при которых О. решит больше 9 задач, нам не подходят. Следовательно, отняв от вероятности решения более 9 задач вероятность решения более 8 задач, мы и найдём вероятность решения только 9 задач: 0,78 – 0,68 = 0,1.
Задача 7. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,88. Вероятность того, что окажется меньше 12 пассажиров, равна 0,66. Найдите вероятность того, что число пассажиров будет от 12 до 20.
Решение. Вероятность того, что в автобусе окажется меньше 21 пассажира, включает в себя вероятность, что в нём окажутся от 12 до 20 пассажиров. При этом события, при которых пассажиров будет меньше 12, нам не подходят. Следовательно, отняв от первой вероятности (менее 21) вторую вероятность (менее 12), мы и найдём вероятность того, что пассажиров будет от 12 до 20 : 0,88 – 0,66 = 0,22.
Задача 8. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,9 погода завтра будет такой же, как и сегодня. 10 апреля погода в Волшебной стране хорошая. Найдите вероятность того, что 13 апреля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» — хорошая погода, «О» — отличная погода):
| 11 апреля | 12 апреля | 13 апреля | Вероятность данного варианта |
| X – 0,9 | X – 0,9 | O – 0,1 | 0,9 ·0,9 ·0,1 = 0,081 |
| X – 0,9 | O – 0,1 | O – 0,9 | 0,9 ·0,1 ·0,9 = 0,081 |
| O – 0,1 | O – 0,9 | O – 0,9 | 0,1 ·0,9 ·0,9 = 0,081 |
| O – 0,1 | X – 0,1 | O – 0,1 | 0,1 ·0,1 ·0,1 = 0,001 |
Вероятность происхождения какого-либо их этих 4-х вариантов равна сумме вероятностей каждого из вариантов: 0,081 + 0,081 + 0,081 + 0,001 = 0,244.
Задача 9. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
Решение:
Задачу выполняют несколько вариантов («Х» ― хорошая погода, «О» ― отличная погода):
| 4 июля | 5 июля | 6 июля | Вероятность данного варианта |
| X – 0,8 | X – 0,8 | O – 0,2 | 0,8 · 0,8 · 0,2 = 0,128 |
| X – 0,8 | O – 0,2 | O – 0,8 | 0,8 · 0,2 · 0,8 = 0,128 |
| O – 0,2 | O − 0,8 | O − 0,8 | 0,2 · 0,8 · 0,8 = 0,128 |
| O – 0,2 | X – 0,2 | O – 0,2 | 0,2 · 0,2 · 0,2 = 0,008 |
Вероятность происхождения какого-либо их этих 4 ― х вариантов равна сумме вероятностей каждого из вариантов: 0,128 + 0,128 + 0,128 + 0,008 = 0,392.
