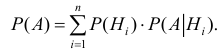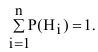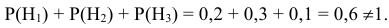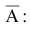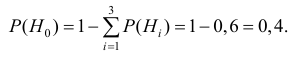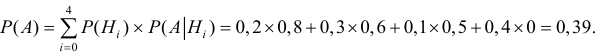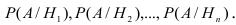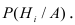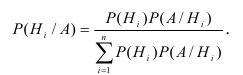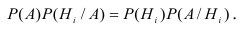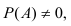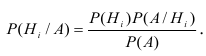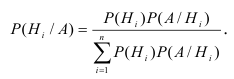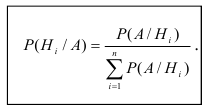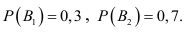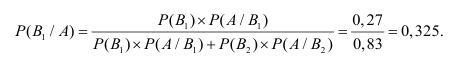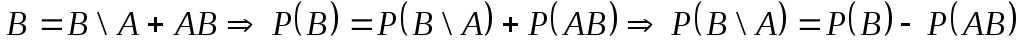Зависимые и независимые случайные события.
Основные формулы сложения и умножения вероятностей
Понятия зависимости и независимости случайных событий. Условная вероятность. Формулы сложения и умножения вероятностей для зависимых и независимых случайных событий. Формула полной вероятности и формула Байеса.
Теоремы сложения вероятностей
Найдем вероятность суммы событий и
(в предположении их совместности либо несовместности).
Теорема 2.1. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей:
Пример 1. Вероятность того, что в магазине будет продана пара мужской обуви 44-го размера, равна 0,12; 45-го — 0,04; 46-го и большего — 0,01. Найти вероятность того, что будет продана пара мужской обуви не меньше 44-го размера.
Решение. Искомое событие произойдет, если будет продана пара обуви 44-го размера (событие
) или 45-го (событие
), или не меньше 46-го (событие
), т. е. событие
есть сумма событий
. События
,
и
несовместны. Поэтому согласно теореме о сумме вероятностей получаем
Пример 2. При условиях примера 1 найти вероятность того, что очередной будет продана пара обуви меньше 44-го размера.
Решение. События “очередной будет продана пара обуви меньше 44-го размера” и “будет продана пара обуви размера не меньше 44-го” противоположные. Поэтому по формуле (1.2) вероятность наступления искомого события
поскольку , как это было найдено в примере 1.
Теорема 2.1 сложения вероятностей справедлива только для несовместных событий. Использование ее для нахождения вероятности совместных событий может привести к неправильным, а иногда и абсурдным выводам, что наглядно видно на следующем примере. Пусть выполнение заказа в срок фирмой “Electra Ltd” оценивается вероятностью 0,7. Какова вероятность того, что из трех заказов фирма выполнит в срок хотя бы какой-нибудь один? События, состоящие в том, что фирма выполнит в срок первый, второй, третий заказы обозначим соответственно . Если для отыскания искомой вероятности применить теорему 2.1 сложения вероятностей, то получим
. Вероятность события оказалась больше единицы, что невозможно. Это объясняется тем, что события
являются совместными. Действительно, выполнение в срок первого заказа не исключает выполнения в срок двух других.
Сформулируем теорему сложения вероятностей в случае двух совместных событий (будет учитываться вероятность их совместного появления).
Теорема 2.2. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:
Зависимые и независимые события. Условная вероятность
Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.
Пример 3. Монета брошена два раза. Вероятность появления “герба” в первом испытании (событие ) не зависит от появления или не появления “герба” во втором испытании (событие
). В свою очередь, вероятность появления “герба” во втором испытании не зависит от результата первого испытания. Таким образом, события
и
независимые.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
События называются зависимыми, если одно из них влияет на вероятность появления другого. Например, две производственные установки связаны единым технологическим циклом. Тогда вероятность выхода из строя одной из них зависит от того, в каком состоянии находится другая. Вероятность одного события , вычисленная в предположении осуществления другого события
, называется условной вероятностью события
и обозначается
.
Условие независимости события от события
записывают в виде
, а условие его зависимости — в виде
. Рассмотрим пример вычисления условной вероятности события.
Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение. Обозначим извлечение изношенного резца в первом случае, а
— извлечение нового. Тогда
. Поскольку извлеченный резец в ящик не возвращается, то изменяется соотношение между количествами изношенных и новых резцов. Следовательно, вероятность извлечения изношенного резца во втором случае зависит от того, какое событие осуществилось перед этим.
Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
Следовательно, вероятность события зависит от того, произошло или нет событие
.
Формулы умножения вероятностей
Пусть события и
независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий
и
.
Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Пример 5. Три ящика содержат по 10 деталей. В первом ящике — 8 стандартных деталей, во втором — 7, в третьем — 9. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что все три вынутые детали окажутся стандартными.
Решение. Вероятность того, что из первого ящика взята стандартная деталь (событие ),
. Вероятность того, что из второго ящика взята стандартная деталь (событие
),
. Вероятность того, что из третьего ящика взята стандартная деталь (событие
),
. Так как события
,
и
независимые в совокупности, то искомая вероятность (по теореме умножения)
Пусть события и
зависимые, причем вероятности
и
известны. Найдем вероятность произведения этих событий, т. е. вероятность того, что появится и событие
, и событие
.
Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
Пример 6. В урне находятся 5 белых шаров, 4 черных и 3 синих. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его в урну. Найти вероятность того, что при первом испытании появится белый шар (событие ), при втором — черный (событие
) и при третьем — синий (событие
).
Решение. Вероятность появления белого шара при первом испытании . Вероятность появления черного шара при втором испытании, вычисленная в предположении, что при первом испытании появился белый шар, т. е. условная вероятность
. Вероятность появления синего шара при третьем испытании, вычисленная в предположении, что при первом испытании появился белый шар, а при втором — черный,
. Искомая вероятность
Формула полной вероятности
Теорема 2.5. Если событие наступает только при условии появления одного из событий
, образующих полную группу несовместных событий, то вероятность события
равна сумме произведений вероятностей каждого из событий
на соответствующую условную вероятность события
:
(2.1)
При этом события называются гипотезами, а вероятности
— априорными. Эта формула называется формулой полной вероятности.
Пример 7. На сборочный конвейер поступают детали с трех станков. Производительность станков не одинакова. На первом станке изготовляют 50% всех деталей, на втором — 30%, на третьем — 20%. Вероятность качественной сборки при использовании детали, изготовленной на первом, втором и третьем станке, соответственно 0,98, 0,95 и 0,8, Определить вероятность того, что узел, сходящий с конвейера, качественный.
Решение. Обозначим событие, означающее годность собранного узла;
,
и
— события, означающие, что детали сделаны соответственно на первом, втором и третьем станке. Тогда
Искомая вероятность
Формула Байеса
Эта формула применяется при решении практических задач, когда событие , появляющееся совместно с каким-либо из событий
, образующих полную группу событий, произошло и требуется провести количественную переоценку вероятностей гипотез
. Априорные (до опыта) вероятности
известны. Требуется вычислить апостериорные (после опыта) вероятности, т. е., по существу, нужно найти условные вероятности
. Для гипотезы
формула Байеса выглядит так:
Раскрывая в этом равенстве по формуле полной вероятности (2.1), получаем
Пример 8. При условиях примера 7 рассчитать вероятности того, что в сборку попала деталь, изготовленная соответственно на первом, втором и третьем станке, если узел, сходящий с конвейера, качественный.
Решение. Рассчитаем условные вероятности по формуле Байеса:
для первого станка
для второго станка
для третьего станка
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Содержание:
Основные теоремы теории вероятностей:
Теоремы сложения вероятностей
Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Доказательство.
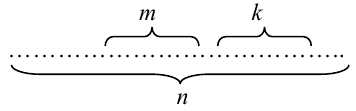
Докажем теорему для схемы случаев. Пусть всевозможные исходы опыта сводятся к совокупности случаев, которые можно наглядно изобразить в виде
Теорема 1 (Обобщенная теорема сложения несовместных событий) Вероятность суммы 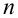
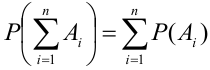
Доказательство (методом математической индукции).
Предположим, что теорема справедлива для 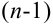
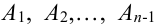
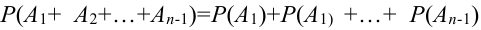
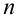
Обозначим 
Имеем 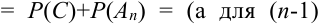
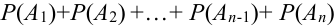
Следствие 1. Если события 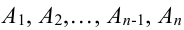
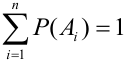
Доказательство.
Т.к. события 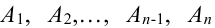
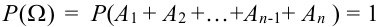
Т.к. события несовместные, то к ним применима обобщенная теорема сложения:
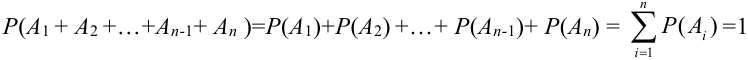
Следствие 2. Сумма вероятностей противоположных событий равна единице:
Доказательство.
События А, 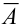
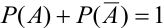
Замечание. Следствие 2 – частный случай следствия 1. На практике весьма часто оказывается легче вычислить вероятность противоположного события, чем прямого.
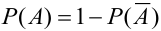
В формулировке таких задач встречаются слова «хотя бы», «не менее», «по крайней мере» и др.
Пример:
Из колоды карт (36) наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.
Решение.
1 способ (по теореме 1′).
Событие А = {из 3 карт окажется хотя бы один туз}.
Хотя бы один – это либо один, либо два, либо три, т.е. событие А может быть представлено в виде суммы трех событий: 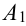
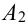
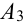
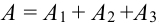
Т.к. события несовместны, то по теореме 1′: 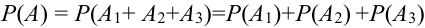
Найдем отдельно вероятности событий.
2 способ (по следствию 2).
Событие 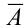
Теорема 2. Вероятность суммы двух совместных событий равна сумме вероятностей этих
событий без вероятности их произведения (совместного осуществления):
Доказательство (геометрическое)
События отождествляют с множествами. Два раза накладываем «лепесток» друг на друга, поэтому и отнимаем его. (что и треб. доказать)
Теорема 2 ( Обобщенная теорема сложения совместных событий).
Вероятность суммы 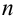
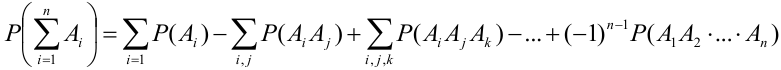
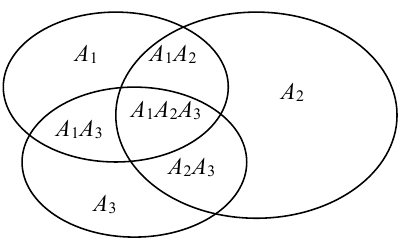
Для трех совместных событий теорема запишется в виде:
Доказательство для трех событий (геометрическое):
События отождествляют с множествами (см. рис.). (что и треб. доказать)
Замечание. Аналогичную формулу можно написать для произведения совместных событий:
Пример:
Для поражения самолета необходимо, чтобы были поражены оба двигателя (события 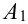
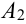
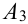
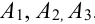
Решение.
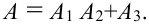
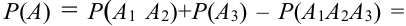
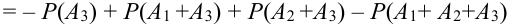
Теоремы умножения вероятностей
Определение 21. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Определение 22. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Примеры:
1) А = {появление решки на первой монете}, В = {появление решки на второй монете}. А и В – независимы.
2) А = {рождение мальчика у Тани}, В = {рождение мальчика у Лены}. А и В – независимы.
3) В урне 2 белых и 1 черный шар. Двое Таня и Ваня вынимают из урны по одному шару. Зависимы или независимы события: А = {появление белого шара у Тани}, В = {появление белого шара у Вани}?
Решение.
Найдем вероятности событий. 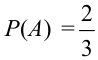
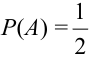
Определение 23. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Определение 24. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.
Определение 25. Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается 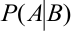
В Примере 3): 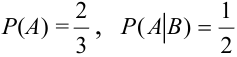
Условие независимости события А от события В:
Условие зависимости события А от события В:
Теорема 3. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
Доказательство.
Докажем для схемы урн истинность тождества формулы.
Пусть всевозможные исходы опыта сводятся к 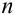
Пусть событию А благоприятствует 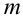
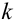
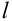
Тогда, вероятности данных событий равны: 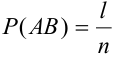
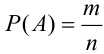
Вычислим условную вероятность 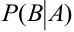
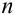
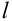
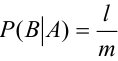
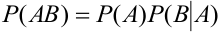
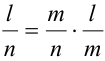
Замечание 1. При применении теоремы вполне безразлично, какое из событий А или В считать первым, а какое вторым, т.е. теорему можно записать в виде:
Замечание 2. В общем случае при 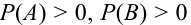
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.
Замечание 3. Зависимость и независимость событий всегда взаимны.
Замечание 4. Условные вероятности обладают всеми свойствами, присущими обычным вероятностям:
1. 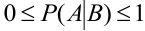
2. если наступление события В исключает возможность осуществления А, т.е. 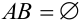
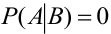
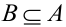
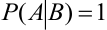
3. Если 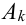
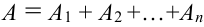
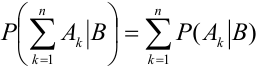
4. 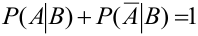
Замечание 5. Если А и В независимы, то независимы также события 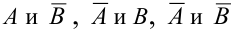
Теорема 3. ( Обобщенная теорема умножения зависимых событий).
Вероятность произведения нескольких зависимых событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что всс предыдущие имели место:
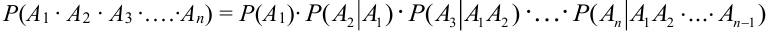
Теорема 4. {теорема умножения независимых событий).
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: 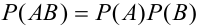
Теорема 4. ( Обобщенная теорема умножения независимых событий).
Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий:
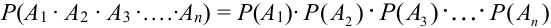
Пример:
Из колоды карт последовательно вынуты две карты. Найти: а) вероятность того, что вторая карта окажется тузом (неизвестно, какая карта была вынута вначале), б) вероятность того, что вторая карта будет тузом, если первоначально тоже был вынут туз.
Решение.
Обозначим А = {появление туза вторым}, В = {появление туза первым}.
а) 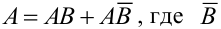
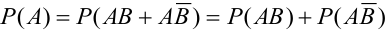
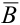
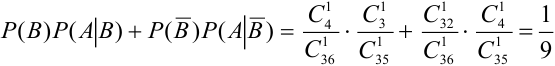
б) Если вынутая первая карта – туз , то в колоде осталось 35 карт и среди них только три туза, следовательно, 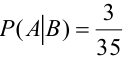
Или можно было найти эту вероятность, используя формулу условной вероятности:
Пример:
В урне 2 белых и 3 черных шара. Из урны вынимают подряд 2 шара. Найти вероятность того, что а) оба белые, б) оба белые, если после первого вынимания шар возвращают обратно в урну, и шары перемешиваются.
Решение.
Обозначим: А = {появление двух белых шаров}, В = {появление белого шара при первом вынимании}, С = {появление белого шара при втором вынимании}.
а) 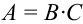
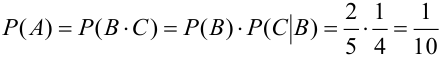
б) 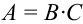
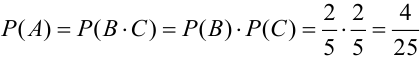
Теорема 5. Вероятность наступления события А, состоящего в появлении хотя бы одного из событий 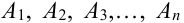
Если все 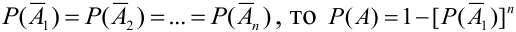
Пример:
Производится три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно 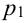
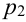
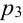
Решение.
Обозначим А = {хотя бы одно попадание в цель}.
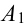
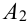
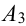
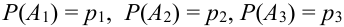
Можно расписать в алгебре событий данное событие в виде суммы произведений: 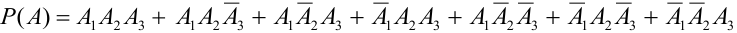
Перейдем от прямого события к противоположному: 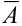
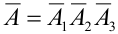
где 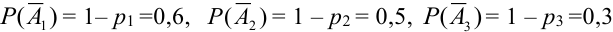
Тогда по теореме 5:
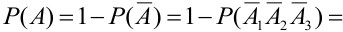
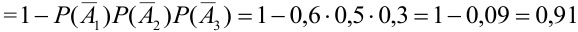
Основные формулы для вычисления вероятностей
Ограниченность классического и статистического способов определения вероятности событий, приемлемых, главным образом, для определения вероятности простых событий, приводит к тому, что в подавляющем большинстве случаев ни один из этих способов в чистом виде для решения задачи определения наступления событий применить не удаётся.
Например, требуется определить вероятность поражения движущегося танка. Определить эту вероятность по частоте наступления события на практике невозможно – необходимо провести большое число стрельб. При этом надо не только определить вероятность попадания в движущийся танк (что сделать не сложно), но и определить вероятность поражения его экипажа, если будет иметь место попадание в танк (а это выполнить на практике невозможно).
Факт сложности или невозможности определения вероятности сложных событий явился стимулом разработки аппарата теории вероятностей, с помощью которого вероятность определяется не прямым, а косвенным методом через вероятность более простых событий.
Сущность косвенного метода определения вероятности сложного события заключается в следующем: вначале анализируют условия испытания и устанавливают события 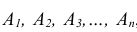
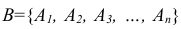
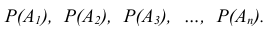
Однако определению вероятности наступления сложного события как комбинации более простых событий должны предшествовать твёрдые знания правил применения рассмотренных в лекции теорем сложения (объединения) и умножения (пересечения) событий.
Этому вопросу и будет посвящён вопрос нашего занятия.
Пример:
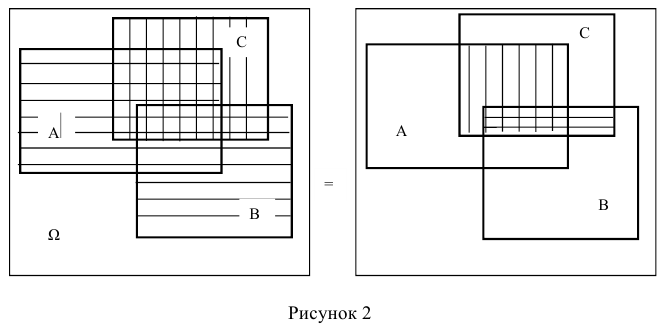
Для того что бы вывести из строя артиллерийскую батарею необходимо поразить либо два взвода с орудиями либо центр управления огнём. Используя операции сложения (объединения) и умножения (пересечения) событий представим сложное событие D={ поражение артиллерийской батареи} как комбинацию простых событий. Результат проиллюстрируем диаграммой Эйлера-Венна.
Решение:
Обозначим через событие А = {поражение первого взвода орудий}, через событие В = {поражение второго взвода орудий}, С = {поражение центра управления огнём}. Тогда событие D = {поражение артиллерийской батареи} определится как поражение либо центра управления огнём (событие С) либо одновременно первого взвода орудий (событие А) и второго взвода орудий (событие В), т.е. будет иметь место следующая комбинация событий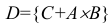
Для решения такого типа задач необходимо усвоить ряд основных свойств, которыми обладают действия над событиями.
Операции сложения (объединения) и умножения (пересечения) событий обладают рядом свойств, аналогичным свойствам сложения и умножения чисел.
1. Переместительное свойство:
А + В = В + А;
2. Сочетательное свойство:
3. Распределительное свойство:
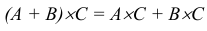
4. Операции прибавления пустого множества и умножения на пустое множество аналогичны операциям над числами, если считать пустое множество за ноль.
Ряд операций над событиями уже не обладают свойствами по аналогии с арифметическими действиями, например:
5. 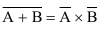
6. 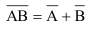
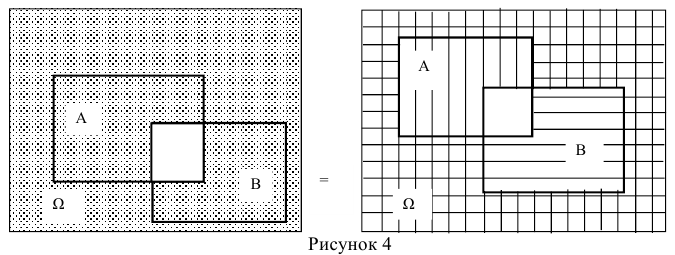
7. 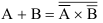
Основные теоремы теории вероятностей: сложение, умножение, формула полной вероятности
На предыдущей лекции мы говорили о том, что достаточно часто определить вероятность сложного события трудно или вообще невозможно. Для чего научились представлять события, как комбинацию других более простых событий используя понятия суммы (объединения) или произведения (пересечения) событий.
Вспомним пример, рассматриваемый нами на предыдущей лекции:
Для того что бы вывести из строя артиллерийскую батарею необходимо поразить либо два взвода с орудиями либо центр управления огнём. Используя для решения задачи правила сложения и умножения событий сложное событие – поражение артиллерийской батареи, заключающееся в поражении либо двух взводов орудий либо центра управления огнём, было представлено как следующая комбинация событий
На сегодняшнем занятии мы ответим на следующий вопрос: как определить вероятность сложного события представляющего собой функцию известных или заданных вероятностей
При определении вероятностей сложных событий пользуются теоремами сложения и умножения вероятностей. Эти теоремы теоретически могут быть доказаны только для таких событий, вероятность появления которых может быть определена классическим способом. Для других событий эти теоремы принимаются как аксиомы. Поэтому мы не будем показывать доказательство этих теорем, а ограничимся только понятием «правила», понимая при этом ряд теорем и следствий из них, с помощью которых определяется вероятность комбинации событий.
Правила сложения вероятностей
Аксиома: Вероятность суммы или наступления хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий (аддитивность Р):
Данную аксиому иногда называют «теоремой сложения», так как для опытов, сводящихся к «схеме случаев», она может быть доказана.
Эта аксиома легко обращается на любое число несовместных событий: вероятность суммы несовместных событий равна сумме вероятностей этих событий:
Пример №1
Вероятность попадания в башню танка при одном выстреле- 0,2, в его корпус – 0,1, в ходовую часть – 0,025. Найти вероятность попадания в танк при одном выстреле.
Решение:
Обозначим интересующее нас событие через А = {попадание в танк}, тогда 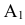
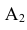
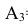
Очевидно, что попадание в танк наступит тогда, когда снаряд попадёт либо в башню, либо в корпус, либо в ходовую часть танка. Таким образом, интересующее нас событие А будет являться суммой событий
А так как события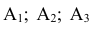
Вывод: полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 325 случаях из 1000 будет получено попадание в танк.
Из данной аксиомы вытекают два важных следствия.
Следствие 1. Если события 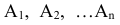
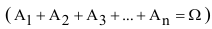
Следствие 2. Сумма вероятностей противоположных событий равна 1.
Для совместных событий аксиома примет следующий вид:
Вероятность суммы, или наступление хотя бы одного из двух совместных событий, равна сумме вероятности этих событий без вероятности произведения этих событий:
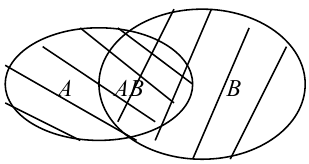
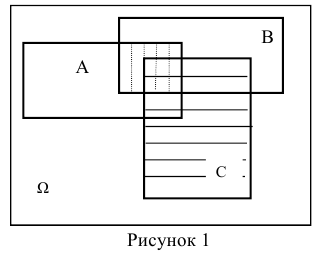
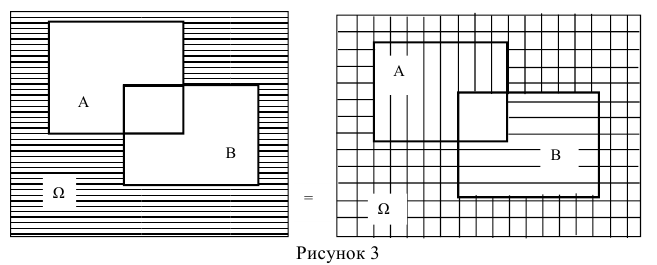
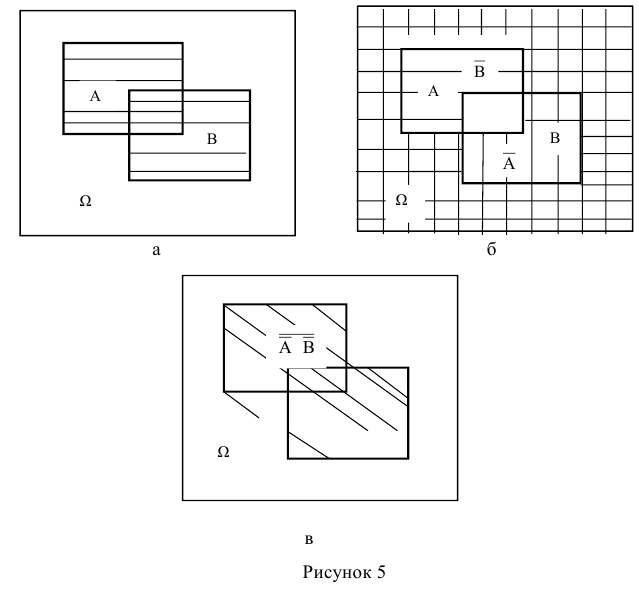
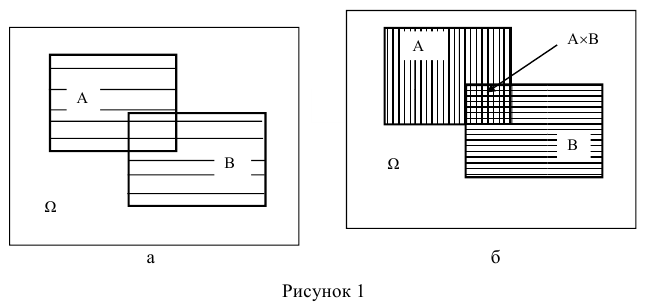
Справедливость этого тождества наглядно следует из его геометрической интерпретации (рисунок 1).
На диаграмме Эйлера-Венна вероятность наступления событий А (или
В) по существу есть площадь области, при попадании случайной точки в которую, наступает событие А (или В). Тогда вероятность комбинации А + В будет соответствовать площади заштрихованной области (рисунок 1 .а). Чтобы получить такую же по площади область, необходимо из площади областей наступления событий А и В вычесть площадь их совместного появления АхВ (рисунок 1.6).
Пример №2
Вероятность подавления батареи противника из-за потерь только в личном составе составляет 0,15; вследствие повреждения материальной части – 0,45; а из-за потерь одновременно в личном составе и материальной части – 0,25. Какова вероятность подавления артиллерийской батареи?
Решение: Пусть событие А = {подавление личного состава батареи}, а событие В= {повреждения материальной части}. Тогда одновременное подавление личного состава и повреждение материальной части будут являться совместным наступлением событий А и В или
Вероятность наступления события А по условию задачи равна 0,15 (Р(А)=0,15), вероятность наступления события В равна 0,45 (Р(В)=0,45), вероятность совместного наступления события А и В равна 0,25 (Р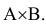
Требуется найти вероятность события С ={подавления батареи противника}, которое будет заключаться либо в подавлении личного состава батареи, либо в повреждении материальной части либо того и другого, или Р(А+В).
Применив теорему сложения вероятностей, получим:
Р(С) = Р(А + В) = Р(А) + Р(В) – Р(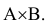
Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 35 случаях из 100 батарея противника будет подавлена, т.е. поражён либо личный состав, либо повреждена техника, либо и то и другое.
Правила умножения вероятностей
Перед рассмотрением правил умножения вероятностей введём ряд новых понятий, которые необходимы для логического понимания производимых над событиями действий.
Событие А называется независимым от события В, если вероятность наступления события А не зависит от того, произошло ли событие В.
Событие А называется зависимым от события В, если вероятность наступления события А меняется в зависимости от того, произошло событие В или нет.
Факт зависимости или независимости события устанавливают из анализа условий испытания. В теории вероятностей под зависимостью случайных событий понимают не причинную зависимость, при которой два события выступают по отношению друг к другу как причина и следствие, а вероятностную или стохастическую зависимость (стохастическая зависимость [stochastic dependence] – зависимость между случайными величинами, проявляющаяся в том, что изменение закона распределения одной из них происходит под влиянием изменения закона распределения другой). Смысл вероятностной или стохастической зависимости двух событий состоит в том, что при наступлении одного из них другое наступает чаще или реже, чем наступает вообще при реализации данного комплекса условий.
В качестве примеров зависимых событий можно привести следующие:
Пример №3
Реализация комплекса условий: выстрел по танку; событие А= {попадание в танк}; реализация комплекса условий – попадание в танк; событие В = {поражение экипажа танка}.
Для появления интересующего события В = {поражение экипажа танка} при реализации комплекса условий – выстрел по танку необходимо появления события А = {попадание в танк}, в то же время при реализации комплекса условий события А = {попадание в танк} не всегда может наступить событие В = {поражение экипажа танка}.
Раз нам требуется определить вероятность совместного наступления двух зависимых событий, одно из которых может наступить только при том условии, что имело место другое из них, введём понятие условной вероятности события.
Вероятность события В, вычисленная при условии, что имело место другое событие А называется условной вероятностью события В по отношению к событию А (обозначается 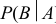
Теорема: Вероятность произведения или совместного наступления двух любых случайных событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
Пример №4
Вероятность попадания в танк при одном выстреле равна 0,8; вероятность поражения экипажа танка при попадании в танк равна 0,7. Определить вероятность поражения экипажа танка при одном выстреле.
Решение:
Пусть событие А = {попадание в танк при одном выстреле}, а событие В = {поражение экипажа танка}. Интересующее нас событие С = {поражение экипажа танка при одном выстреле} будет иметь место только в том случае, если наступит событие А, при этом наступление события С возможно только тогда, когда одновременно наступят события А и В.
Вероятность наступления события А по условию задачи равна 0,8 (Р(А)=0,8); вероятность наступления события В равна 0,7 (Р(В)=0,7).
Требуется найти вероятность поражения экипажа танка при одном выстреле, которая будет являться произведением вероятностей попадания в танк при одном выстреле и поражении экипажа танка при условии что имело место попадание в него, т.е. Р(С)=Р(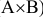
Применив теорему умножения вероятностей, получим:
Вывод: полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях по одному выстрелу в каждом в среднем в 56 случаях из 100 экипаж танка будет поражён.
Правило умножения вероятностей легко обращается на случай произвольного числа событий:
Из данной теоремы вытекает ряд важных следствий.
Следствие 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Пример №5
По цели в тире производят по одному выстрелу два студента. Вероятность попадания в цель первого студента равна 0,7, второго – 0,4. Найти вероятность того, что в цель попадут оба студента.
Решение:
Пусть событие А={попадание в цель первым студентом}, а событие В={попадание в цель вторым студентом}, тогда интересующее нас событие С={попадание в цель и первым и вторым студентом}.
Вероятность наступления события А по условию задачи равна 0,7 (Р(А)=0,7), вероятность наступления события В равна 0,4 (Р(В)=0,4).
Попадание в цель вторым студентом не зависит от того, попадёт ли в цель первый студент и наоборот, а следовательно события А и В -независимы. Применив следствие из теоремы умножения для независимых событий, получим:
Вывод: полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях в среднем в 28 случаях из 100 в цель попадут оба студента.
Зависимость и независимость событий всегда взаимны. Если событие А не зависит от события В, то и событие В не зависит от события А. Таким образом, можно уточнить данное ранее определение независимых событий. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Из рассмотренных выше правил сложения и умножения вероятностей вытекает ещё одно очень важное следствие: если противоположное событие распадается на меньшее число вариантов, чем прямое событие, то имеет смысл при вычислении вероятностей переходить к противоположному событию:
Пример №6
Два орудия, начиная с первого, ведут последовательно огонь по цели до получения первого попадания. При этом первое орудие может произвести два выстрела, а второе – только один. Вероятность попадания в цель при первом выстреле первого орудия – 0,4; вторым выстрелом – 0,8; вероятность попадания в цель вторым орудием – 0,6. Чему равна вероятность поражения цели?
Решение:
Обозначим за событие 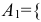
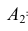
Так как события 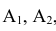
Вывод: полученный результат означает, что при проведении достаточно большого числа испытаний в аналогичных условиях в среднем в 95 случаях из 100, танк будет поражён.
Формула полной вероятности
При изложении третьего вопроса лекции преподаватель на примере поражения движущегося танка обозначает проблему определения вероятности сложного события (давая при этом понятие гипотезы).
После чего преподаватель доводит условие задачи (Пример 7), формулу для вычисления полной вероятности события (без её вывода) и условия её применения.
При постановке задачи и пояснения физической сущности вопроса преподаватель использует оверхэд-проектор и подготовленные слайды.
Решение задачи преподаватель проводит на доске, особое внимание при этом обращая на методику её решения и порядок записи. В заключении решения задачи преподаватель под запись доводит вывод, отражающий физическую сущность полученного результата.
При решении ряда практических задач вычисление вероятности некоторого сложного события можно существенно облегчить, если связать наступление этого события с наступлением единственно возможных и несовместных событий, под которыми понимаются гипотезы о всех возможных исходах испытаний.
Пусть, например, производится выстрел по танку (рисунок 2).
Известно, что башня танка, его корпус или ходовая часть имеют не только различные размеры, форму и т.д., что усложняет попадание, но и различную степень уязвимости. Первое приводит к тому, что вероятность попадания в различные отсеки танка будет различной, а второе – к тому, что различной будет и вероятность поражения танка при попадании в его башню, корпус или ходовую часть, а, следовательно, и вероятность поражения танка в целом. Поэтому для облегчения вычисления вероятности поражения танка Р(А) представляется целесообразным ввести гипотезы о возможном исходе стрельбы.
Дадим определение:
Под гипотезами понимают полную группу единственно возможных несовместных событий, которые могут наступить в результате проведения испытаний.
В условиях нашей задачи гипотезы о возможном исходе стрельбы будут следующие:
- •
={попадание в башню танка};
- •
={попадание в корпус танка};
- •
= {попадание в ходовую часть танка};
- •
={ промах}.
Вероятности этих гипотез 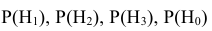
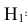
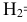
- •
– вероятность поражения танка при попадании в башню;
- •
– вероятность поражение танка при попадании в корпус;
- •
– вероятность поражение танка при попадании в ходовую часть.
Указанные условные вероятности возможно определить опытным путём, проводя полигонные стрельбы по танку.
Пример №7
Ведётся стрельба из орудия по танку. Известно, что при попадании снаряда в башню вероятность поражения танка равна 0,8; при попадании в корпус – 0,6; при попадании в ходовую часть – 0,5.
Известны также вероятности попадания снаряда в каждый из отсеков танка. Вероятность попадания в башню танка равна 0,2. Вероятность попадания в корпус равна 0,3; вероятность попадания в ходовую часть равна 0,1.
Требуется определить вероятность поражения танка при одном выстреле.
Вычислить вероятность наступления интересующего нас события позволяет формула, получившая особое название формулы полной вероятности.
Полная вероятность события равна сумме парных произведений вероятностей каждой из гипотез на отвечающие им условные вероятности наступления этого события.
Данная формула является следствием из обеих теорем – теорем сложения и умножения вероятностей.
При определении полной вероятности необходимо следить, чтобы были учтены все гипотезы о возможном исходе испытания, при которых может наступить интересующее нас событие, т.е. гипотезы должны составлять полную группу несовместных событий. Свидетельством полного учёта всех гипотез является выполнение равенства
Если данное равенство не выполняется, то это означает, что учтены не все гипотезы о возможных исходах испытания.
Таким образом оказывается, что знания вероятностей гипотез 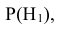
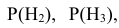
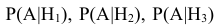
Вернёмся к решению примера.
Решение:
Таким образом, возможные гипотезы об исходах стрельбы:
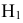
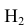
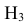
По условию задачи вероятности гипотез будут равны:
гипотеза 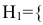
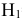
гипотеза 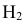
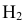
гипотеза Нз ={попадание в ходовую часть} – равна 0,1 (Р(Нз) = 0,1).
Интересующее нас событие А = {поражение танка}. По условию задачи вероятность поражения танка при реализации гипотез:
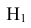
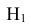
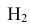
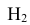
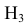
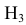
Проверим, все ли гипотезы об исходах стрельбы учтены:
Следовательно, имеющиеся гипотезы не составляют полной группы событий и не учтено событие 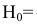
Таким образом, вероятность гипотезы 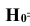
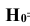
Вероятность поражения танка при реализации гипотезы 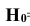
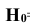
Применяя формулу полной вероятности для решения задачи получим:
Следовательно, полная вероятность поражения танка при одном выстреле равна
Р(А) = 0,39 = 39%.
Вывод: Полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях в среднем в 39 случаях из 100 танк окажется поражённым.
Формула Байеса, вероятность появления хотя бы одного события
Пусть имеется полная группа несовместных гипотез 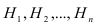
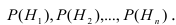
Требуется определить какие вероятности имеют гипотезы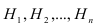
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, делённому на полную вероятность этого события.
Эта формула называется формулой Байеса.
Доказательство.
По Теореме умножения вероятностей получаем:
Тогда если
Для нахождения вероятности Р(А) используем формулу полной вероятности.
Если до испытания все гипотезы равновероятны с вероятностью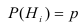
Пример №8
Известно, что 30% приборов собирает специалист высшей квалификации, 70% приборов – специалист средней квалификации. Вероятность того, что прибор, собранный специалистом высшей квалификации, надёжен, равна 0,9. Для специалиста средней квалификации эта вероятность равна 0,8. Взятый наудачу прибор оказался надёжным. Найти вероятность того, что этот прибор собран специалистом высшей квалификации.
Решение: пусть событие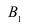
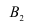
Пусть событие А означает появление надёжного прибора. По условию примера вероятность события А при условии, что появится прибор, собранный специалистом высшей квалификации,
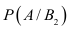
Искомая вероятность появления прибора, собранного специалистом высшей квалификации, т.е. события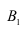
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Генеральная и выборочная совокупности
- Ковариация в теории вероятности
- Функциональные преобразования двухмерных случайных величин
- Правило «трех сигм» в теории вероятности
- Производящие функции
Сложение и умножение вероятностей
- Сложение вероятностей несовместных событий
- Вероятность противоположного события
- Умножение вероятностей независимых событий
- Вероятность появления хотя бы одного события
- Примеры
п.1. Сложение вероятностей несовместных событий
События называют несовместными, если они не могут произойти одновременно в результате одного опыта.
Например:
1) Нельзя одновременно A = «получить 5» и B = «получить 2» на экзамене. События A и B – несовместны.
2) Нельзя одновременно C = «достать туз» и D = «достать шестерку» из колоды карт. События C и D – несовместны.
Вероятность появления одного из двух несовместных событий A или B равна сумме вероятностей этих событий: $$ mathrm{ P(Avee B)=P(A) + P(B) } $$
Если обобщить на любое количество событий:
Вероятность появления нескольких несовместных событий A1 или A2 или …Ak равна сумме вероятностей этих событий: $$ mathrm{ P(A_1vee A_2vee … vee A_k)=P(A_1) + P(A_2) + … + P(A_k) } $$
Например:
Стрелок может попасть в «10» с вероятностью P(10) = 0,3, в «9» – с вероятностью P(9) = 0,2. Значит, попасть в «10 или 9» он может с вероятностью:
P(«10 или 9») = 0,3 + 0,2 = 0,5
п.2. Вероятность противоположного события
Пространство элементарных событий образует полную группу событий.
Сумма вероятностей всех событий, образующих полную группу, равна единице. $$ mathrm{ Omega={A_1, A_2, …, A_k}, P(A_1) + P(A_2) + … + P(A_k) = 1 } $$
Например:
При бросании кубика Ω = {1; 2; … ; 6} – полная группа событий.
Вероятности выпадения каждой грани: (mathrm{p_1=p_2=…=p_6=frac16})
Сумма всех вероятностей: (mathrm{p_1+p_2+…+p_6=6cdot frac16=1})
Два случайных события A и B называют противоположными, если они несовместны и образуют полную группу событий: $$ mathrm{ Omega=left{A;Bright}, B=overline{A}, } $$ Сумма вероятностей противоположных событий равна единице. $$ mathrm{ P(A) + P(B) = P(A) + P(overline{A}) = 1 } $$
Например:
Вероятность попадания стрелка в мишень p = 0,8.
Противоположное событие: стрелок не попадёт в мишень. Его вероятность:
q = 1 – p = 0,2.
п.3. Умножение вероятностей независимых событий
Два случайных события A и B называют независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Вероятность совместного появления двух независимых событий A и B равна произведению вероятностей этих событий: $$ mathrm{ P(A wedge B) = P(A) cdot P(B) } $$
Если обобщить на любое количество событий:
Вероятность совместного появления нескольких независимых событий A1 и A2 и … Ak равна произведению вероятностей этих событий: $$ mathrm{ P(A_1wedge A_2wedge …wedge A_k)=P(A_1)cdot P(A_2)cdot … cdot P(A_k) } $$
Например:
Вероятность попадания стрелка в мишень p = 0,8.
Стрелок делает три выстрела подряд.
1) Какова вероятность, что он попал все три раза?
Каждый выстрел является независимым событием, поэтому вероятность трёх удачных выстрелов подряд:
P3 = P(+, +, +) = p · p · p = 0,83 = 0,512
2) Какова вероятность, что он не попал ни разу?
Вероятность промаха равна q = 1 – p = 0,2.
Вероятность трёх промахов подряд:
P0 = P(–, –, –) = q · q · q = 0,23 = 0,008
3) Какова вероятность, что он попал только один раз?
Стрелок мог попасть при первом выстреле, а затем два раза промахнуться, или при втором выстреле (промахнуться на первом и третьем), или при третьем (промахнувшись два раза поначалу). Сложение и умножение вероятностей даёт итоговую вероятность одного попадания:
P1 = P(+,–,–) + P(–,+,–) + P(–,–,+) =
p · q · q + q · p · q + q · q · p = 3pq2 = 3 · 0,8 · 0,22 = 0,096
4) Какова вероятность, что он промахнулся один раз?
Аналогичные предыдущему пункту рассуждения приводят к такому выражению для вероятности двух попаданий (одного промаха):
P2 = P(–,+,+) + P(+,–,+) + P(+,+,–) =
q · p · p + p · q · p + p · p · q = 3p2q = 3 · 0,82 · 0,2 = 0,384
Мы получили следующий закон распределения для возможного количества попаданий из трёх выстрелов:
Количество попаданий, X
0
1
2
3
Вероятность, Px
0,008
0,096
0,384
0,512
X = {0; 1; 2; 3} образует полную группу событий. Сумма всех вероятностей:
P0 +P1 + P2 + P3 = 0,008 + 0,096 + 0,384 + 0,512 = 1
п.4. Вероятность появления хотя бы одного события
Вероятность появления хотя бы одного из событий A1, A2, …, Ak, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий: $$ mathrm{ P(A)=1-q_1cdot q_2cdot … cdot q_{k}, q_{i}=1-p_{i} } $$
Например:
Студент сдаёт два экзамена.
Вероятность сдать первый экзамен равна p1 = 0,7 второй – p2 = 0,6.
Тогда вероятность сдать хотя бы один экзамен: P = 1 – q1q2 = 1 – 0,3 · 0,4 = 0,88.
п.5. Примеры
Пример 1. Подбрасывают четыре игральных кубика. Какова вероятность, что на каждом из них выпадет нечётное число очков?
Для кубика Ω = {1; 2; 3; 4; 5; 6} – пространство элементарных событий.
Выпадение нечётного числа A = {1; 3; 5}. Вероятность выпадения нечётного числа для одного кубика: (mathrm{p=frac{k}{n}=frac36=frac12}).
Результаты подбрасывания 4-х кубиков являются независимыми. Вероятность, что на каждом выпадет нечётное число: $$ mathrm{ P=pcdot pcdot pcdot p=p^4=frac{1}{2^4}=frac{1}{16} } $$ Ответ: (frac{1}{16}).
Пример 2. На полигоне испытываются три ракеты.
Вероятность успешного испытания для каждой из ракет: p1 = 0,8, p2 = 0,75, p3 = 0,6.
Какова вероятность, что хотя бы одна ракета пройдёт испытания успешно?
Найдём вероятность того, что ни одна из ракет не пройдёт испытаний:
q1 = 1 – p1 = 0,2, q2 = 1 – p2 = 0,25, q3 = 1 – p3 = 0,4
q1 · q2 · q3 = 0,2 · 0,25 · 0,4 = 0,02
Тогда, искомая вероятность (противоположное событие):
P = 1 – q1 · q2 · q3 = 1 – 0,02 = 0,98
Ответ: 0,98.
Мораль: инвестору нужно показывать сразу несколько сырых проектов.
Пример 3. В системе пожарной сигнализации установлены два независимых датчика. Вероятность срабатывания каждого из датчиков при пожаре: p1 = 0,6; p2 = 0,7. Найдите вероятность того, что при пожаре:
1) сработает ровно один датчик;
2) сработает хотя бы один датчик.
Вероятности отказов: q1 = 1 – p1 = 0,4; q2 = 1 – p2 = 0,3.
1) Событие «сработает ровно один датчик» является суммой двух событий «первый сработал, второй – отказал» или «первый отказал, второй – сработал». Вероятность:
P1 = p1q2 + q1p2 = 0,6 · 0,3 + 0,4 · 0,7 = 0,46
2) Найдем вероятность отказа обоих датчиков:
P0 = q1q2 = 0,4 · 0,3 = 0,12
Событие «сработает хотя бы один датчик» является противоположным отказу обоих датчиков. Вероятность:
P1 ∨ 2 = 1 – P0 = 1 – 0,12 = 0,88
Ответ: 1) 0,46; 2) 0,88.
Пример 4. У админа в ящике 11 плат, из которых 3 – бракованные.
Наугад берётся 2 платы. Какова вероятность того, что хотя бы одна из них – рабочая?
Найдём вероятность того, что обе выбранные платы – бракованные.
Выбрать 2 платы из 3 бракованных можно (mathrm{C_3^2=C_3^1=3}) способами.
Выбрать 2 платы из общей совокупности можно (mathrm{C_{11}^2=frac{11cdot 10}{1cdot 2}=55}) способами.
Вероятность взять обе бракованные платы из ящика: (mathrm{P_{2 text{бр}}=frac{C_3^2}{C_2^{11}}=frac{3}{55}})
Значит, вероятность того, что хотя бы одна плата не будет бракованной (противоположное событие):
(mathrm{P=1-P_{2 text{бр}}=1-frac{3}{55}=frac{52}{55}}).
Ответ: (mathrm{frac{52}{55}}).
Пример 5*. Парадокс дней рождения
В классе учится k человек. Исследуйте вероятность того, что хотя бы у двух одноклассников дни рождения совпадают.
Считаем, что в году n = 365 дней.
Пусть день рождения одного из учеников известен (один день в году – «занят»).
Тогда вероятность того, что день рождения второго ученика не совпадает с днём рождения первого: (mathrm{q_2=1-frac{1}{365}}) («заняты» два дня).
Вероятность того, что день рождения третьего ученика не совпадает с днями рождения первых двух: (mathrm{q_3=1-frac{2}{365}}) («заняты» три дня). И т. д.
Для всех k учеников вероятность того, что все дни рождения разные: begin{gather*} mathrm{ widetilde{p}(k)=q_2cdot q_3cdot … cdot q_{k}=left(1-frac{1}{365}right)left(1-frac{2}{365}right)…left(1-frac{k-1}{365}right)= }\ mathrm{ =frac{364cdot 363cdot … cdot(365-k+1)}{365^{k-1}}= frac{365cdot 364cdot 363cdot … cdot(365-k+1)}{365^{k}}= frac{365!}{365^{k}(365-k)!} } end{gather*} Значит, вероятность того, что хотя бы у двух одноклассников дни рождения совпадают: begin{gather*} mathrm{ p(k)=1-widetilde{p}(k)=1-frac{365!}{365^{k}(365-k)!} } end{gather*}
Таким образом, в классе из 30 человек вероятность совпадения дней рождения равна 70,63%. А в группе из 50 человек она достигает 97,04%.
Формула вероятности суммы совместных событий (теорема сложения вероятностей)
В соответствии
со свойством 3) классической вероятности
вероятность суммы несовместных событий
равна сумме вероятностей этих событий.
А если события совместны?
Пусть мы имеем
два совместных события АиВ.
Преобразуем их сумму в сумму несовместных
событий (см. диаграмму Венна).
Подставляя
второе выражение в первое, получим
. (2.10)
Пример. По
мишени один раз стреляют два стрелка.
Вероятность попадания первого стрелка
в мишеньр1 = 0,7, второго
–р2 = 0,8. Какова
вероятность того, что кто-нибудь из
них попадет в мишень?
А = А1
+ А2, где А попадание в мишень;
А1 –
попал первый стрелок;
А2–
попал второй стрелок.
Р(А) = Р(А1
+ А2) = Р(А1) +
Р(А2) – Р(А1А2)=
= Р(А1)
+ Р(А2) – Р(А1 )Р(А2)=
= 0.7 + 0,8
– 0,7· 0,8 = 0,94.
Получим вероятность
суммы трех совместных событий.
Получена
формула
Р(А + В + С) = Р(А) + Р(В) + Р(С) –
Р(АВ) – Р(АС) – Р(ВС) + Р(АВС) (2.11)
Обобщая полученный
результат на сумму nсовместных событий, получим формулу
(2.12)
Формула полной вероятности
Пусть требуется
определить вероятность события А,
которое может произойти в сочетании с
одним из событийН1, Н2,…,
Н n,
образующих полную группу несовместных
событий (Ø,
).
Эти события будем называть гипотезами.
Н1 Н2 Н3
АН1 АН2 АН3
АНn-2 АНn-1 АНn
Hn-2 Hn-1 Hn
В соответствии со свойством
3) вероятности и теоремой умножения
вероятностей
(2.13)
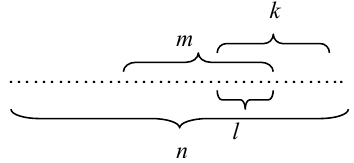
Пример. Изn экзаменационных
билетов студент знаетm
(«хорошие билеты»).
Что лучше: брать на экзамене билет первым
или вторым?
Решение. Введем
событие А – студент взял «хороший»
билет.
Студент берет
билет первым. В этом случае
-
Студент берет билет вторым.
Введем две гипотезы:
Н1
– первый студент взял «хороший»
билет,Н2 =.
Вывод: безразлично,
брать билет первым или вторым.
Формула Байеса (теорема гипотез)
В соответствии
с теоремой умножения вероятностей
Р(АНi)
= Р(Hi)·Р(А/Hi)
= Р(A)·Р(Hi/А).
В это равенство
подставим значение Р(А),вычисленное
по формуле полной вероятности (2.13) и
найдемР(Hi/А).
Р(Нi/A)
=

Это следствие
из теоремы умножения и формулы полной
вероятности называется формулой
Байесаили теоремой гипотез.
В формуле полной
вероятности определяется вероятность
события до его появления, т.е. до того,
как произведен опыт, в котором оно могло
появиться. Вероятности гипотез Р(Нi),
входящие в формулу полной вероятности,
называютаприорными, т.е. «до
опытными».
Пусть опыт
произведен и его результат известен,
т.е. мы знаем, произошло или не произошло
событие А.Получившийся результат
мог произойти при осуществлении какой-то
одной гипотезыНi.Дополнительная информация об исходе
опыта перераспределяет вероятности
гипотез. Эти перераспределенные
вероятности гипотезР(Нi/A)называютапостериорными, т.е.
«после опытными».
ПримерВ
одной из корзин 1 камешек и 4 кусочка
хлеба, во второй – 4 камешка и 1 кусочек
хлеба. Мышка наугад выбирает корзину,
бежит к ней и вытаскивает кусочек хлеба
– событие А (предполагается, что он затем
вновь возвращается в корзину). Какова
вероятность события А? Каковы вероятности
того, что второй раз мышка побежит к
первой корзине, ко второй корзине? Какова
вероятность того, что она второй раз
вытащит кусочек хлеба?
Рассмотрим
гипотезы
Н1– мышка бежит к первой корзине,
Н2– мышка бежит ко второй корзине.
Р(Н1)=1/2 =Р(Н2)(априорные
вероятности)
.
Р(Н1/A)

Р(Н2/A)

вероятности).
При втором подходе
Мышка обучилась, второй раз
она выберет первую корзину с большей
вероятностью и добьется большего успеха.
Заметим, что
это – один из основных принципов обучения
кибернетических систем.
Продолжение статьи «Теория вероятности. Классическое определение».
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Итак, теория.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
.
Подборку задач на отработку темы смотрите здесь.
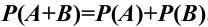
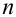
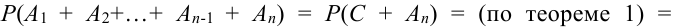
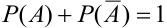
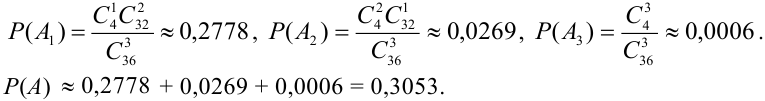
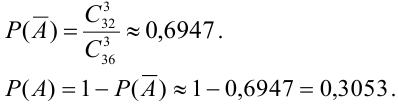
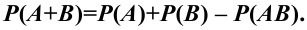
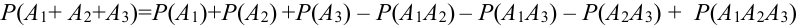
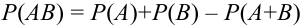
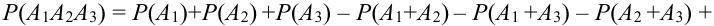
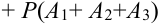
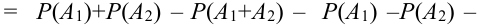
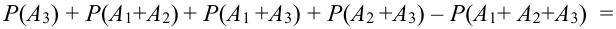
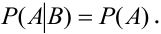
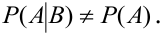
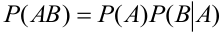
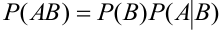
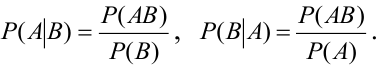
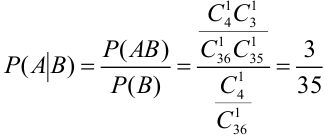
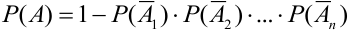
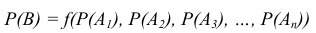
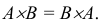
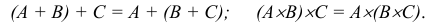

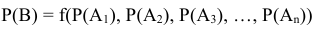
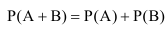
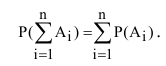
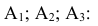
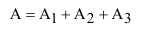
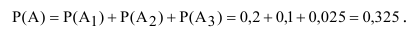
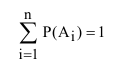
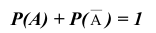
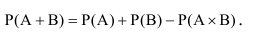
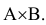
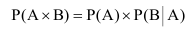
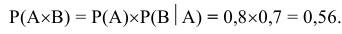
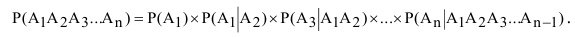
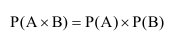
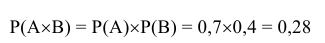
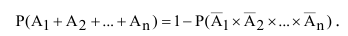
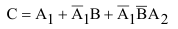
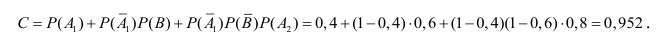
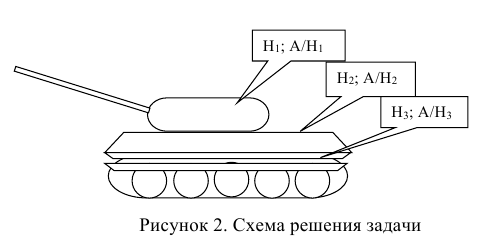
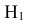 ={попадание в башню танка};
={попадание в башню танка};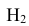 ={попадание в корпус танка};
={попадание в корпус танка};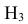 = {попадание в ходовую часть танка};
= {попадание в ходовую часть танка};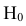 ={ промах}.
={ промах}.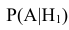 – вероятность поражения танка при попадании в башню;
– вероятность поражения танка при попадании в башню;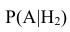 – вероятность поражение танка при попадании в корпус;
– вероятность поражение танка при попадании в корпус;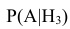 – вероятность поражение танка при попадании в ходовую часть.
– вероятность поражение танка при попадании в ходовую часть.