Как найти вероятность того что при бросании

Решение задач о бросании игральных костей

Еще одна популярная задача теории вероятностей (наравне с задачей о подбрасывании монет) – задача о подбрасывании игральных костей.

Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.

Основной метод решения подобных задач – использование формулы классической вероятности, который мы и разберем на примерах ниже.

Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).

Одна игральная кость

С одной игральной костью дело обстоит до неприличия просто. Напомню, что вероятность находится по формуле $P=m/n$, где $n$ – число всех равновозможных элементарных исходов эксперимента с подбрасыванием кубика или кости, а $m$ – число тех исходов, которые благоприятствуют событию.

Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?

Так как игральная кость представляет собой кубик (еще говорят, правильная игральная кость, то есть кубик сбалансированный, так что выпадает на все грани с одинаковой вероятностью), граней у кубика 6 (с числом очков от 1 до 6, обычно обозначаемых точкам), то и общее число исходов в задаче $n=6$. Благоприятствуют событию только такие исходы, когда выпадет грань с 2, 4 или 6 очками (только четные), таких граней $m=3$. Тогда искомая вероятность равна $P=3/6=1/2=0.5$.

Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.

Рассуждаем также, как и в предыдущем примере. Общее число равновозможных исходов при бросании игрального кубика $n=6$, а условию “выпало не менее 5 очков”, то есть “выпало или 5, или 6 очков” удовлетворяют 2 исхода, $m=2$. Нужная вероятность равна $P=2/6=1/3=0.333$.

Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.

Две игральные кости

Когда речь идет о задачах с бросанием 2 костей, очень удобно использовать таблицу выпадения очков. По горизонтали отложим число очков, которое выпало на первой кости, по вертикали – число очков, выпавшее на второй кости. Получим такую заготовку (обычно я делаю ее в Excel, файл вы сможете скачать ниже):

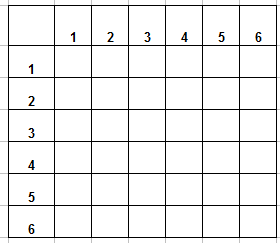
А что же в ячейках таблицы, спросите вы? А это зависит от того, какую задачу мы будем решать. Будет задача про сумму очков – запишем туда сумму, про разность – запишем разность и так далее. Приступаем?

Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.

Сначала разберемся с общим числом исходов эксперимента. когда мы бросали одну кость, все было очевидно, 6 граней – 6 исходов. Здесь костей уже две, поэтому исходы можно представлять как упорядоченные пары чисел вида $(x,y)$, где $x$ – сколько очков выпало на первой кости (от 1 до 6), $y$ – сколько очков выпало на второй кости (от 1 до 6). Очевидно, что всего таких пар чисел будет $n=6cdot 6=36$ (и им соответствуют как раз 36 ячеек в таблице исходов).

Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:

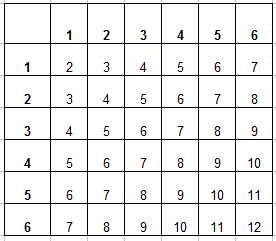
Теперь эта таблица поможем нам найти число благоприятствующих событию “в сумме выпадет менее 5 очков” исходов. Для этого подсчитаем число ячеек, в которых значение суммы будет меньше 5 (то есть 2, 3 или 4). Для наглядности закрасим эти ячейки, их будет $m=6$:

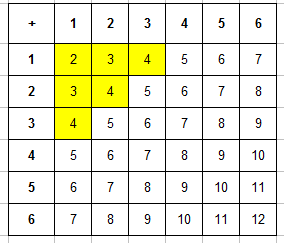
Тогда вероятность равна: $P=6/36=1/6$.

Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.

Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:

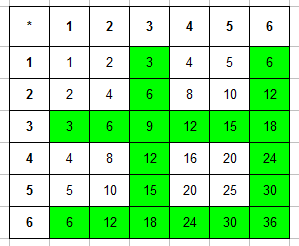
Остается только записать, что общее число исходов $n=36$ (см. предыдущий пример, рассуждения такие же), а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) $m=20$. Тогда вероятность события будет равной $P=20/36=5/9$.

Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).

Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.

Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:

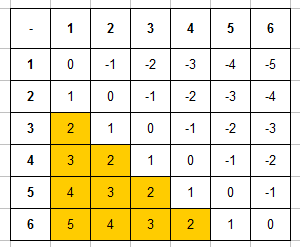
Итак, что общее число равновозможных элементарных исходов $n=36$, а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) $m=10$. Тогда вероятность события будет равной $P=10/36=5/18$.

Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).

Другие задачи про кости и кубики

Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.

Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.

В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.

Найдем общее число исходов эксперимента. Исходы можно представлять как упорядоченные тройки чисел вида $(x,y,z)$, где $x$ – сколько очков выпало на первой кости (от 1 до 6), $y$ – сколько очков выпало на второй кости (от 1 до 6), $z$ – сколько очков выпало на третьей кости (от 1 до 6). Очевидно, что всего таких троек чисел будет $n=6cdot 6cdot 6=216$ .

Теперь подберем такие исходы, которые дают в сумме 15 очков.

$$
(3,6,6), (6,3,6), (6,6,3),\
(4,5,6), (4,6,5), (5,4,6), (6,5,4), (5,6,4), (6,4,5),\
(5,5,5).
$$

Получили $m=3+6+1=10$ исходов. Искомая вероятность $P=10/216=0.046$.

Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.

Наиболее простой способ решения этой задачи – снова воспользоваться таблицей (все будет наглядно), как и ранее. Выписываем таблицу сумм очков и выделяем только ячейки с четными значениями:

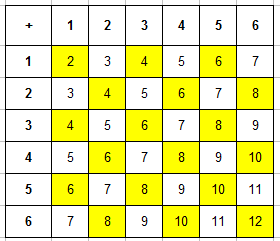
Получаем, что согласно условию эксперимента, всего есть не 36, а $n=18$ исходов (когда сумма очков четная).

Теперь из этих ячееек выберем только те, которые соответствуют событию “на первой кости выпало не более 4 очков” – то есть фактически ячейки в первых 4 строках таблицы (выделены оранжевым), их будет $m=12$.

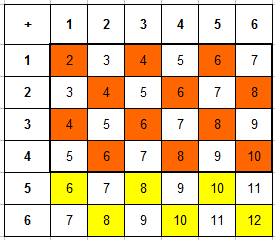
Искомая вероятность $P=12/18=2/3.$

Эту же задачу можно решить по-другому, используя формулу условной вероятности. Введем события:
А = Сумма числа очков четная
В = На первой кости выпало не более 4 очков
АВ = Сумма числа очков четная и на первой кости выпало не более 4 очков
Тогда формула для искомой вероятности имеет вид:
$$
P(B|A)=frac{P(AB)}{P(A)}.
$$
Находим вероятности. Общее число исходов $n=36$, для события А число благоприятствующих исходов (см. таблицы выше) $m(A)=18$, а для события АВ – $m(AB)=12$. Получаем:
$$
P(A)=frac{m(A)}{n}=frac{18}{36}=frac{1}{2}; quad P(AB)=frac{m(AB)}{n}=frac{12}{36}=frac{1}{3};\
P(B|A)=frac{P(AB)}{P(A)}=frac{1/3}{1/2}=frac{2}{3}.
$$
Ответы совпали.

Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.

В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.

Итак, имеем $n=4$ независимых испытания (броски кубика), вероятность выпадения четного числа очков в одном испытании (при одном броске кубика) равна $p=3/6=1/2=0.5$ (см. выше задачи для одной игральной кости).

Тогда по формуле Бернулли $P=P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k}$, подставляя $k=3$, найдем вероятность того, что четное число очков появится 3 раза:
$$
P_4(3)=C_4^3 cdot left(1/2right)^3 cdot left(1-1/2right)^1=4 cdot left(1/2right)^4=1/4=0,25.
$$

Приведем еще пример, решаемый аналогичным образом.

Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.

Подставляем в формулу Бернулли следующие значения: $n=8$ (число бросков), $p=1/6$ (вероятность появления 6 при одном броске), $kge 1$ (хотя бы один раз появится шестерка). Прежде чем вычислять эту вероятность, напомню, что практически все задачи с формулировкой “хотя бы один…” удобно решать, переходя к противоположному событию “ни одного…”. В нашем примере сначала стоит найти вероятность события “Шестёрка не появится ни разу”, то есть $k=0$:
$$
P_8(0)=C_8^0 cdot left(1/6right)^0 cdot left(1-1/6right)^8=left(5/6right)^8.
$$
Тогда искомая вероятность будет равна
$$
P_8(kge 1)=1-P_8(0)=1-left(5/6right)^8=0.767.
$$

А еще у нас есть онлайн калькулятор для формулы Бернулли

Полезные ссылки

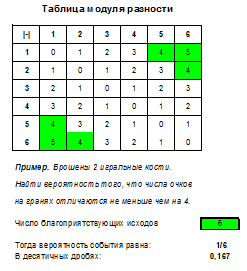
Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.

В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.

Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.

Еще по теории вероятностей:

В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):

Я уже разбирала один из типов специфичных заданий по теории вероятностей (ссылки в конце статьи). Сейчас же я предлагаю вам ознакомиться с самым простым и удобным способом вычисления задач с игральными кубиками. Условие задачи следующее.

Найдите вероятность того что при одновременном бросании двух игральных костей сумма выпавших очков окажется равной 8 или 9.

Первым делом смотрим на то, что в задаче бросают 2 кубика. Далее нас просят вычислить вероятность выпадения определенной суммы. Для подобных используется следующая таблица.

В фиолетовых областях таблицы мы пишем возможные исходы каждого отдельного броска (от 1 до 6). А на угловой ячейке указываем действие, которое необходимо выполнить.

Идём по ячейкам по порядку. 1+1=2, 1+2=3, 1+3=4 и так далее заполняем всю таблицу.

Так как просят найти вероятность выпадения суммы в 8 или 9 очков, то именно эти ячейки мы отмечаем в таблице.

Считаем количество закрашенных ячеек. Их получилось 9. А теперь по правилу вычисления вероятности количество наших закрашенных ячеек делим на общее количество всех ячеек:

9/36=1/4=0,25

Вот и получили ответ равный 0,25.

А как вы обычно решаете подобные задачи? Другие статьи по теории вероятностей, которые вам полезно будет прочитать:

Задача на вероятность (ОГЭ и ЕГЭ), которое кажется сложным, но решается с помощью простой схемы.

Понимание вероятности в математике – это то, что может изменить вашу жизнь.

Время на прочтение
10 мин

Количество просмотров 14K

Введение

На одном из собеседований по приёму на работу попросили за 30 минут написать программу, которая бы решал следующую задачу:

Есть n стандартных игральных костей (6-ти гранных кубиков) со стандартным обозначением всех граней от 1 до 6. Бросаем все n кубики разом. Нужно найти вероятность выпадения числа k, а именно суммы всех значений, выпавших на этих кубиках.

Решение

Не буду томить ожиданием и сразу выложу код алгоритма, который получился и впоследствии был немного обработан напильником.

Python

# -*- coding: utf-8 -*-
# import numpy  # <можно_использовать_numpy>

def main():
    c_int_side_dice: int = 6  # сколько граней у кубика
    c_int_dice_number: int = 6  # кол-во кубиков
    c_int_number_to_find: int = 18  # число, вероятность выпадения которого хотим найти
    probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
    print(probability)


# собственно поиск вероятности определённого значения
def dice_probability(int_dice_number: int, int_number_to_find: int, c_int_side_dice: int) -> float:
    list_values, list_interm_probability = list_values_and_interm_probabilities(int_dice_number, c_int_side_dice)
    if int_number_to_find < list_values[0] or int_number_to_find > list_values[-1]:
        # задаваемое число выходит за рамки реально возможного диапазона значений
        result_out: float = 0.0
    else:
        for i in range(len(list_values)):
            if list_values[i] == int_number_to_find:
                result_out: float = list_interm_probability[i] / (c_int_side_dice ** int_dice_number)
                break
    return result_out


# возвращает списки/массивы: значения (сумма выпавших всех значений кубиков), сколько раз встречается значение
def list_values_and_interm_probabilities(int_dice_number: int, c_int_side_dice: int) -> tuple[list[int], list[int]]:  # [кол-во кубиков], [сколько граней у кубика]
    list_values = [i for i in range(int_dice_number, c_int_side_dice * int_dice_number + 1)]  # <длина_списков_совпадает!>
    list_interm_probability = [1] * c_int_side_dice  # [1, 1, 1, 1, 1, 1]
    for i in range(int_dice_number - 1):
        list_interm_probability = multiply_by_ones(list_interm_probability, c_int_side_dice) # <длина_списков_совпадает!>
        # list_interm_probability = numpy.convolve(list_interm_probability, [1] * c_int_side_dice)  # <можно_использовать_numpy> и не использовать multiply_by_ones()

    return list_values, list_interm_probability


# "умножение" на единицы
def multiply_by_ones(list_in: list[int], c_int_side_dice: int) -> list[int]:  # [1, 1, 1, 1, 1, 1], 6
    list_dummy: list[list[int]] = []
    for i in range(c_int_side_dice):
        list_dummy.append([0] * i)  # [], [0], [0, 0], [0, 0, 0] ...

    list_for_sum: list[list[int]] = []
    for i in range(c_int_side_dice):
        list_for_sum.append(list_dummy[i] + list_in + list_dummy[c_int_side_dice - i - 1])

    """
    [list_in, 0, 0, 0, 0, 0]
    [0, list_in, 0, 0, 0, 0]
    [0, 0, list_in, 0, 0, 0]
    [0, 0, 0, list_in, 0, 0]
    [0, 0, 0, 0, list_in, 0]
    [0, 0, 0, 0, 0, list_in]
    """

    list_out: list[int] = []
    for i in range(len(list_for_sum[0])):
        sum_out: int = 0
        for j in range(c_int_side_dice):
            sum_out += list_for_sum[j][i]
        list_out.append(sum_out)

    """
    [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
    """
    return list_out

if __name__ == "__main__":
    main()

JavaScript

function main(){
    const c_int_side_dice = 6;  // сколько граней у кубика
    const c_int_dice_number = 6; // кол-во кубиков
    const c_int_number_to_find = 18; // число, вероятность выпадения которого хотим найти
    let probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice);
    console.log(probability);
}

// собственно поиск вероятности определённого значения
function dice_probability(int_dice_number, int_number_to_find, c_int_side_dice){
    let lists_val_and_prob = list_values_and_interm_probabilities(int_dice_number, c_int_side_dice);
    let result_out;
    if (int_number_to_find < lists_val_and_prob[0][0] || int_number_to_find > lists_val_and_prob[0][lists_val_and_prob[0].length - 1]){
        // задаваемое число выходит за рамки реально возможного диапазона значений
        result_out = 0.0;
    } else {
        for (let i = 0; i < lists_val_and_prob[0].length; i++){
            if (lists_val_and_prob[0][i] == int_number_to_find){
                result_out = lists_val_and_prob[1][i] / Math.pow(c_int_side_dice, int_dice_number);
                break;
            }
        }
    }
    return result_out;
}

// возвращает списки/массивы: значения (сумма выпавших всех значений кубиков), сколько раз встречается значение
function list_values_and_interm_probabilities(int_dice_number, c_int_side_dice){  // [кол-во кубиков], [сколько граней у кубика]
    let list_values = new Array();
    let i = 0;
    for (let j = int_dice_number; j <= c_int_side_dice * int_dice_number; j++){
        list_values[i] = j;
        i++;
    }
    console.log(list_values);
    let list_interm_probability = Array(c_int_side_dice).fill(1);  // [1, 1, 1, 1, 1, 1]
    for (let i = 0; i < int_dice_number - 1; i++){
        list_interm_probability = multiply_by_ones(list_interm_probability, c_int_side_dice);
    }
    console.log(list_interm_probability);
    return [list_values, list_interm_probability];
}

// "умножение" на единицы
function multiply_by_ones(list_in, c_int_side_dice){
    let list_dummy = new Array(c_int_side_dice);
    for (let j = 0; j < c_int_side_dice; j++){
        list_dummy[j] = Array(j).fill(0);
    }
    let list_for_sum = new Array(c_int_side_dice);
    for (let j = 0; j < c_int_side_dice; j++){
        list_for_sum[j] = list_dummy[j].concat(list_in, list_dummy[c_int_side_dice - j - 1]);
    }
    // [list_in, 0, 0, 0, 0, 0]
    // [0, list_in, 0, 0, 0, 0]
    // [0, 0, list_in, 0, 0, 0]
    // [0, 0, 0, list_in, 0, 0]
    // [0, 0, 0, 0, list_in, 0]
    // [0, 0, 0, 0, 0, list_in]
    
    let list_out = new Array();
    for (let i = 0; i < list_for_sum[0].length; i++){
        let sum_out = 0;
        for (let j = 0; j < c_int_side_dice; j++){
            sum_out += list_for_sum[j][i];
        }
        list_out[i] = sum_out;
    }
    // [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
    return list_out;
}

main();

VBScript

Option Explicit

Sub main()
    Const c_int_side_dice = 6  'сколько граней у кубика
    Const c_int_dice_number = 3  'кол-во кубиков
    Const c_int_number_to_find = 10  'число, вероятность выпадения которого хотим найти
    Dim probability
    probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
    MsgBox probability
End Sub


'собственно поиск вероятности определённого значения
Function dice_probability(int_dice_number, int_number_to_find, c_int_side_dice)
    Dim list_values()
    Dim list_interm_probability()
    list_values_and_interm_probabilities int_dice_number, c_int_side_dice, list_values, list_interm_probability
    Dim result_out
    Dim i
    If int_number_to_find < list_values(0) Or int_number_to_find > list_values(UBound(list_values)) Then
        'задаваемое число выходит за рамки реально возможного диапазона значений
        result_out = 0.0
    Else
        For i = 0 To UBound(list_values)
            If list_values(i) = int_number_to_find Then
                result_out = list_interm_probability(i) / (c_int_side_dice ^ int_dice_number)
            End If
        Next
    End If
    dice_probability = result_out
End Function

'возвращает списки/массивы: значения (сумма выпавших всех значений кубиков), сколько раз встречается значение
Sub list_values_and_interm_probabilities(int_dice_number, c_int_side_dice, list_values, list_interm_probability)  '[кол-во кубиков], [сколько граней у кубика]
    ReDim list_values(int_dice_number * (c_int_side_dice - 1))
    Dim i, j
    i = 0
    For j = int_dice_number To c_int_side_dice * int_dice_number
        list_values(i) = j
        i = i + 1
    Next
    ReDim list_interm_probability(c_int_side_dice - 1)
    For j = 0 To c_int_side_dice - 1
        list_interm_probability(j) = 1
    Next
    For j = 0 To int_dice_number - 2
        multiply_by_ones list_interm_probability, c_int_side_dice
    Next
End Sub

'"умножение" на единицы
Sub multiply_by_ones(list_in, c_int_side_dice)
    Dim list_in_length
    list_in_length = UBound(list_in)
    Dim list_for_sum()
    ReDim list_for_sum(c_int_side_dice - 1, list_in_length + c_int_side_dice - 1)
    Dim i, j, k, n
    For i = 0 To c_int_side_dice - 1
        j = 0
        For n = 0 To c_int_side_dice - 1
            If i = n Then
                For k = 0 To list_in_length
                    list_for_sum(i, j) = list_in(k)
                    j = j + 1
                Next
            Else
                list_for_sum(i, j) = 0
                j = j + 1
            End If
        Next
    Next
    ' [list_in, 0, 0, 0, 0, 0]
    ' [0, list_in, 0, 0, 0, 0]
    ' [0, 0, list_in, 0, 0, 0]
    ' [0, 0, 0, list_in, 0, 0]
    ' [0, 0, 0, 0, list_in, 0]
    ' [0, 0, 0, 0, 0, list_in]
    ' ArrOut_2 list_for_sum
    Erase list_in
    ReDim list_in(list_in_length + c_int_side_dice - 1)
    Dim sum_out
    For j = 0 To list_in_length + c_int_side_dice - 1
        sum_out = 0
        For i = 0 To c_int_side_dice - 1
            sum_out = sum_out + list_for_sum(i, j)
        Next
        list_in(j) = sum_out
    Next
    ' [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
    ' ArrOut_1 list_in
End Sub

'==================================================
'<Additional_MsgBox_For_Arrays>
Sub ArrOut_1(arr_in)
    Dim str_out
    Dim i
    For i = 0 To UBound(arr_in)
        If i = 0 Then
            str_out = arr_in(i)
        Else
            str_out = str_out & " " & arr_in(i)
        End If
    Next
    MsgBox str_out
End Sub

Sub ArrOut_2(arr_in)
    Dim str_out
    Dim i, j
    For i = 0 To UBound(arr_in, 1)
        For j = 0 To UBound(arr_in, 2)
            If i = 0 And j = 0 Then
                str_out = arr_in(i, j)
            ElseIf j = 0 Then
                str_out = str_out & vbNewLine & arr_in(i, j)
            Else
                str_out = str_out & " " & arr_in(i, j)
            End If
        Next
    Next
    MsgBox str_out
End Sub
'</Additional_MsgBox_For_Arrays>
'==================================================

main

Пояснение

Понятно, что копание в чужом коде — дело не благодарное, опишу работу алгоритма для одного конкретного примера.

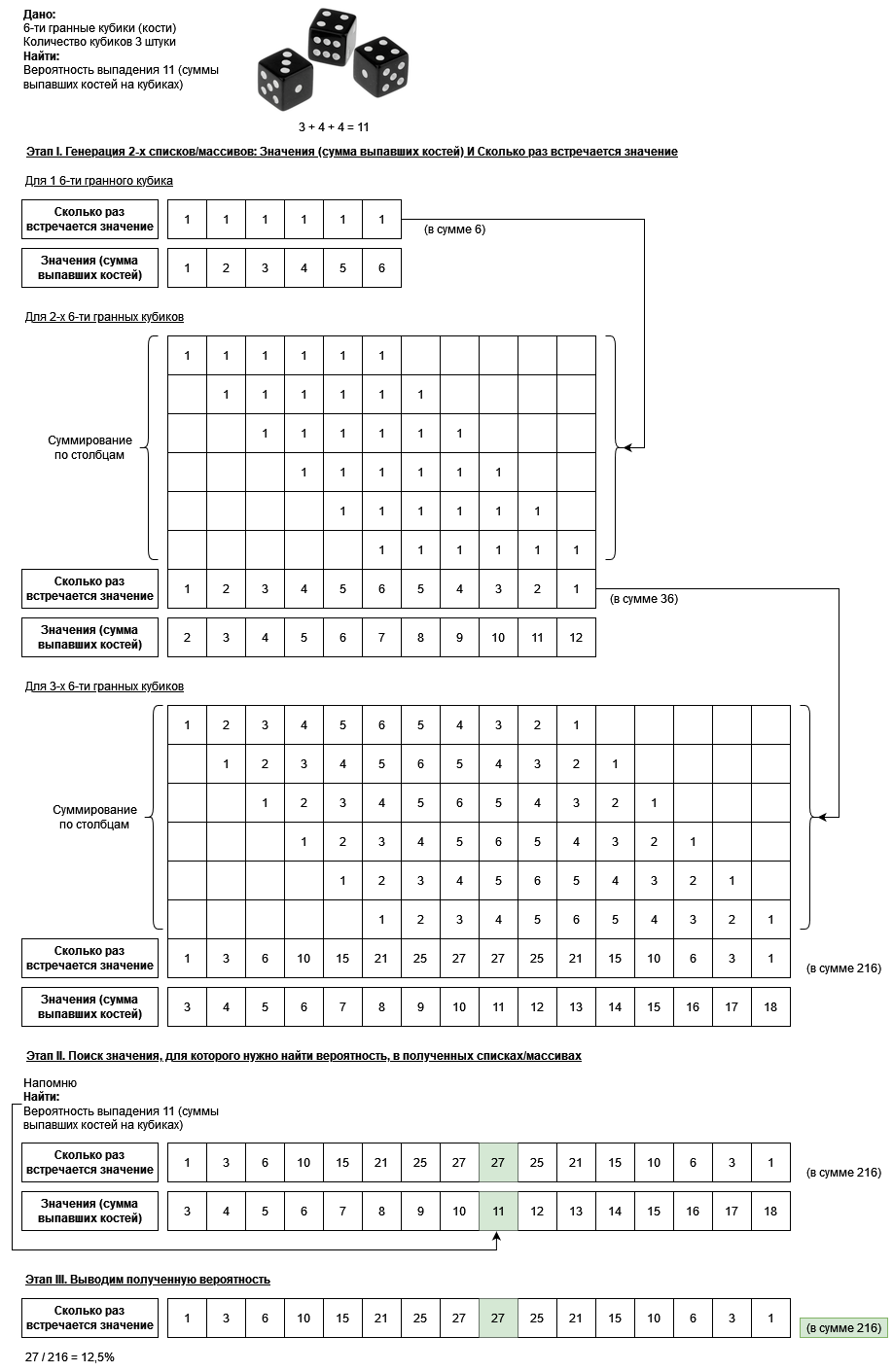
Картинку можно описать словами как: нахождение делимого вероятности выпадения при помощи многократной свёртки последовательности [1 1 1 1 1 1] на саму себя. Количество операций свёртки совпадает с количеством кубиков минус 1.

Смею предположить, что дочитав до этого момента у многих читателей уже зародятся скептические настроения, однако в свою очередь предложу поверить самостоятельно и в помощь приложу SQL запрос, который считает «в лоб», т.е. генерирует все возможные комбинации выпадения для 3-х кубиков, а потом пересчитывает все выпавшие суммы. В результате отработки скрипта мы получим 2 столбца из самого конца пункта “Этап I. Генерация 2-х списков/массивов: Значения (сумма выпавших костей) И Сколько раз встречается значение”.

SQL запрос – генератор решения “в лоб”

-- заводим значения сторон кубика
WITH step_01_insert (dice) AS (
    SELECT 1 AS dice UNION ALL
    SELECT 2 AS dice UNION ALL
    SELECT 3 AS dice UNION ALL
    SELECT 4 AS dice UNION ALL
    SELECT 5 AS dice UNION ALL
    SELECT 6 AS dice
)
-- генерируем все возможные ситуации для 3-х кубиков
, step_02_spawn (dice_1, dice_2, dice_3, dice_sum) AS (
    SELECT T1.dice AS dice_1
    , T2.dice AS dice_2
    , T3.dice AS dice_3
	, T1.dice + T2.dice + T3.dice AS dice_sum -- Значения (сумма выпавших костей)
    FROM step_01_insert AS T1
    , step_01_insert AS T2
    , step_01_insert AS T3
)
-- считаем в лоб, сколько раз встречается значение
SELECT dice_sum  -- Значения (сумма выпавших костей)
, COUNT(1) AS num  -- Сколько раз встречается значение
FROM step_02_spawn
GROUP BY dice_sum
ORDER BY dice_sum;

Конечно это не достаточно для полноценного доказательства, о котором я расскажу чуть позже, но хоть накал скепсиса, надеюсь, мне удалось сбавить.

Отмечу, что я не претендую на какую-то оригинальность, т.к. подобный алгоритм упоминается в данных статьях: “How to Calculate Multiple Dice Probabilities” Method 2 Recursion, “Как посчитать вероятность определенной комбинации при игре в кости” Метод 2 Рекурсия (перевод).

Пусть вас не смущает хитрое смещение суммирования в формуле Excel – суть от этого никак не меняется. Явно именно раздел «Метод 2» затачивался под Excel реализацию, но запрограммировать данный алгоритм в лоб без изменений именно на каком-либо языке программирования — задача не тривиальная.

Но всё-таки, почему этот алгоритм работает?

Для начала вспомним треугольник Паскаля:

Из всего множества его замечательных свойств я бы хотел заострить внимание на следующем: до строки:

цифры в треугольнике Паскаля повторяют степени числа 11 в степени 1<=k<=4 (натуральное). Но это утверждение верно для десятичной системы счисления, однако, если считать степень числа 11 в шестнадцатеричной системе счисления, то можно продлить совпадения до 1<=k<=5.

Можно задаться вопросом: а на каком калькуляторе можно 11 возводить в степень 5 в шестнадцатеричной системе счисления? Ответ: воспользуемся свойством

Иначе говоря идём итерационно:
121=11 * 11
1331=121 * 11
14641=1331 * 11
15AA51=14641 * 11

Давайте чуть здесь остановимся и вспомним школьную программу, а именно умножение в столбик, с одной лишь оговоркой, что перенос числа из одного разряда в другой (при переполнении разряда) буду делать отдельной операцией, а так же визуально для каждого разряда выделю отдельный столбец.
Пример 1.
14641 * 11 в десятеричной системе счисления.

1. Заполняем условия.

2. Записываем результаты умножения каждой единицы разряда.

3. Суммируем.

4. Переводим из переполнившихся разрядов в разряды выше.

Проделаем ту же операцию в шестнадцатеричной системе счисления (Шестнадцатеричная система счисления)
Пример 2.

1. Заполняем условия.

2. Записываем результаты умножения каждой единицы разряда.

3. Суммируем.

4. Записываем полученные числа правильно в шестнадцатеричной системе счисления.

И для закрепления ещё один.
Пример 3.
15AA51 * 11 в шестнадцатеричной системе счисления.

1. Заполняем условия в шестнадцатеричной системе счисления.

2. Переводим запись из шестнадцатеричной в десятичную систему счисления для улучшения восприятия (благо мы можем себе это позволить, т.к. визуально отделяем каждый разряд друг от друга).

3. Записываем результаты умножения каждой единицы разряда.

4. Суммируем.

5. Переводим поэтапно из переполнившихся разрядов в разряды выше.

6. Записываем полученные числа правильно в шестнадцатеричной системе счисления.

Во всех приведённых примерах я бы акцентировал внимание на пунктах «Суммируем» (Пример 1 – п3., Пример 2 – п3., Пример 3 – п4.), которые «цитируют» одну из строк треугольника Паскаля. Если продолжить мысль, то манипуляции с разрядами мешают нормальному воспроизведению всего треугольника. А давайте от них избавимся? Т.е. условно говоря будем считать (да простят меня математики) в «условно бесконечной системе счисления» (вероятно есть и более адекватный термин, но увы, беглый запрос по интернету ничего не дал, что больше доказывает мою лень, а не на отсутствие информации как таковой), т.е. когда перехода из одного разряда в другой при операции сложения не происходит. И это работает:

Тут я не претендую опять же на оригинальность, данный метод есть и им пользуются: как вывести треугольник Паскаля на Python? (см. «Простейшая реализация»)

Аналогия с умножением в столбик двух чисел в очень большой системой счисления, в принципе, имеет право на существование и даёт представление об операции, однако стоит грамотнее назвать её свёрткой последовательности. В данном посте приводится как раз выведение “строк” треугольника Паскаля сверткой: дискретная свёртка или полиномиальное умножение

Вернёмся к кубикам.

Посчитаем в лоб сколько раз встречается сумма костей для всех возможных случаев.

1 кубик (тут всё просто).

2 кубика (идём по классике жанра).

Тут конечно можно посчитать вручную, т.е. просуммировать все единицы в правой таблице, соответствующие полученным значениям в левой таблице (лучше визуализировать):

Однако, заметим смещение “Полученных значений” в левой таблице и преобразуем обе таблицы следующим образом:

После этого в правой таблице нам останется лишь просуммировать строки. Опять же тут немного остановимся на правой табличке, и заметим, что она напоминает уже упомянутое выше умножение столбик в десятичной системе счисления (или свёртку последовательностей).

В итоге получим:

Проделаем аналогичные шаги для 3-х кубиков:

Смещаем:

Акцентируем внимание, что опять же правая таблица напоминает умножение в столбик в «условно бесконечной системе счисления» (или свёртку последовательностей):

Выводим результат:

Описанные операции итерационно можно продолжать сколь угодно долго.

Данный алгоритм походит для любого числа одинаковых игровых кубиков с любым количеством граней, у которых числа на гранях входят в арифметическую последовательность. И его при некотором желании можно даже модифицировать и для решения задач, когда речь идёт не об однотипных кубиках а с разным количеством граней (правда я ума не приложу кому это может понадобиться).

Итого, выводы

1. Задачи на поиск вероятности выпадения числа k у n игральных кубиков попадаются на собеседованиях.

2. В данной статье рассмотрен довольно элегантный алгоритм по решению подобных задач, указанных выше. В принципе можно решать подобные задачи просто на листе бумаге.

О чём стоит упомянуть
Представленный алгоритм не является самым оптимальным. Например для 1000 кубиков (не знаю кому это будет нужно, но вдруг) придётся просчитать для всех элементов последовательности 1000 раз. Но можно ещё поиграться с умножением в столбик в «условно …» и снизить вычислительную сложность алгоритма с O(n^2) (“Оценка сложности алгоритмов, или Что такое О(log n)”).

Updated: 23.08.2022

Была ли эта статья полезной?

❓ Что такое теория вероятностей?

Теория вероятностей использует случайные величины и распределения вероятностей для математической оценки неопределенных ситуаций. Понятие вероятности используется для присвоения числового описания вероятности наступления события. Вероятность можно определить как число благоприятных исходов, деленное на общее число возможных исходов события.

Определение теории вероятностей

Теория вероятностей – это область математики и статистики, которая занимается определением вероятностей, связанных со случайными событиями. Существует два основных подхода к изучению теории вероятностей: теоретический и экспериментальный. Теоретическая вероятность определяется на основе логических рассуждений без проведения экспериментов. В отличие от нее, экспериментальная вероятность определяется на основе исторических данных путем проведения повторных экспериментов.

Пример теории вероятностей

Предположим, нам необходимо определить вероятность выпадения числа 4 при бросании игральной кости. Число благоприятных исходов равно 1. Возможные исходы игральной кости – {1, 2, 3, 4, 5, 6}. Из этого следует, что всего существует 6 исходов. Таким образом, вероятность выпадения 4 при бросании игральной кости, используя теорию вероятности, можно вычислить как 1 / 6 ≈ 0,167.

🎲 Основы теории вероятностей

Мы можем понять эту область математики с помощью нескольких основных терминов, напрямую связанных с теорией вероятностей.

Случайный эксперимент

Случайный эксперимент в теории вероятностей – это испытание, которое повторяется несколько раз для получения четко определенного набора возможных результатов. Подбрасывание монеты является примером случайного эксперимента.

Пространство выборки

Пространство выборки можно определить как множество всех возможных исходов, полученных в результате проведения случайного эксперимента. Например, пространство выборки при подбрасывании симметричной монеты (fair coin), стороны которой – это орел и решка.

Событие

Теория вероятностей определяет событие как набор исходов эксперимента, который образует подмножество пространства выборки.

Примеры событий:

1. Независимые – те, на которые не влияют другие события, являются независимыми.
2. Зависимые – те, на которые влияют другие события.
3. Взаимоисключающие – события, которые не могут произойти в одно и то же время.
4. Равновероятные – два или более события, которые имеют одинаковые шансы произойти.
5. Исчерпывающие – это события, которые равны выборочному пространству эксперимента.

Случайная величина

В теории вероятностей случайную переменную можно определить как величину, которая принимает значение при всех возможных исходах эксперимента.

Существует два типа случайных величин:

1. Дискретная случайная величина – принимает точные значения, такие как 0, 1, 2…. Описывается кумулятивной функцией распределения и функцией массы вероятности.
2. Непрерывная случайная величина – переменная, которая может принимать бесконечное число значений. Для определения характеристик этой переменной используются кумулятивная функция распределения и функция плотности вероятности.

Вероятность

Вероятность мы можем определить как численную вероятность наступления события. Вероятность того, что событие произойдет, всегда лежит между 0 и 1. Это связано с тем, что число желаемых исходов никогда не может превысить общее число исходов события. Теоретическая вероятность и эмпирическая вероятность используются в теории вероятностей для измерения шанса наступления события.

Условная вероятность

Ситуация, когда необходимо определить вероятность наступления события, притом что другое событие уже произошло.

Обозначается как P(A | B).

Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», на котором ты:

• Усвоишь специальную терминологию и сможешь читать статьи по Data Science без постоянных обращений к поисковику.
• Подготовишься к успешной сдачи вступительных экзаменов в Школу анализа данных Яндекс.
• Овладеешь математическим аппаратом, который необходим, чтобы стать специалистом в Data Science.

Ожидание

Ожидание случайной величины X можно определить как среднее значение результатов эксперимента, проводимого многократно. Ожидание обозначается как E[X]. Также известно как среднее значение случайной величины.

Дисперсия

Дисперсия – это мера, которая показывает, как распределение случайной величины изменяется относительно среднего значения. Дисперсия определяется как среднее квадратичное отклонение от среднего значения случайной величины. Обозначается как Var[X].

Функция распределения теории вероятностей

Распределение вероятностей или кумулятивная функция распределения – это функция, которая моделирует все возможные значения эксперимента, используя случайную переменную. Распределение Бернулли и биномиальное распределение – это примеры дискретных распределений вероятностей. Например, нормальное распределение представляет собой пример непрерывного распределения.

Массовая функция вероятности

Массовая функция вероятности определяется как вероятность того, что дискретная случайная величина будет в точности равна определенному значению.

Функция плотности вероятности

Функция плотности вероятности – это вероятность того, что непрерывная случайная величина принимает множество возможных значений.

Формулы теории вероятностей

В теории вероятностей существует множество формул, которые помогают рассчитать различные вероятности, связанные с событиями.

Наиболее важные формулы:

1. Теоретическая вероятность: Число благоприятных исходов / Число возможных исходов.
2. Эмпирическая вероятность: Число случаев, когда событие происходит / Общее число испытаний.
3. Правило сложения: P(A ∪ B) = P(A) + P(B) – P(A∩B), где A и B – события.
4. Правило комплементарности: P(A’) = 1 – P(A). P(A’) означает вероятность того, что событие не произойдет.
5. Независимые события: P(A∩B) = P(A) ⋅ P(B).
6. Условная вероятность: P(A | B) = P(A∩B) / P(B).
7. Теорема Байеса: P(A | B) = P(B | A) ⋅ P(A) / P(B).
8. Массовая функция вероятности: f(x) = P(X = x).
9. Функция плотности вероятности: p(x) = p(x) = dF(x) / dx, где F(x) – кумулятивная функция распределения.
10. Ожидание непрерывной случайной величины: ∫xf(x)dx, где f(x) является МФВ (Массовой функцией вероятности).
11. Ожидание дискретной случайной величины: ∑xp(x), где p(x) – это ФПВ (Функцией плотности вероятности).
12. Дисперсия: Var(X) = E[X2] – (E[X])2.

Применение теории вероятностей

Теория вероятностей используется во многих областях и помогает оценить риски, которые связаны с теми или иными решениями. Некоторые из направлений, где применяют теорию вероятностей:

• В финансовой отрасли теория вероятностей используется для создания математических моделей фондового рынка с целью прогнозирования будущих тенденций. Это помогает инвесторам вкладывать средства в наименее рискованные активы, которые дают наилучший доход.

• В потребительской индустрии теория вероятностей используется для снижения вероятности неудачи при разработке продукта.

• Казино использует теорию вероятностей для разработки азартных игр с максимизацией своей прибыли.

🏋️ Практические задания

Задача 1: При бросании двух игральных костей, какова вероятность того, что выпадет комбинация, сумма которой будет равна 8?

Задача 2: Какова вероятность вытащить карту королеву из колоды?

Задача 3: Из 10 человек 3 купили карандаши, 5 купили тетради, а 2 купили и карандаши, и тетради. Если покупатель купил тетрадь, какова вероятность того, что он также купил карандаш?

В заключение

Подведем итоги:

• Теория вероятностей – это раздел математики, в котором рассматриваются вероятности случайных событий.
• Понятие вероятности объясняет возможность наступления того или иного события.
• Значение вероятности всегда лежит между 0 и 1.
• В теории вероятностей все возможные исходы случайного эксперимента составляют пространство выборки.
• Теория вероятностей использует такие важные понятия, как случайные величины и кумулятивные функции распределения для моделирования случайного события. Сюда же относится определение различных вероятностей, связанных с этим.

Если хочешь подтянуть свои знания по математике, загляни на наш курс «Математика для Data Science», который включает в себя:

• 47 видеолекций и 150 практических заданий.
• Консультации с преподавателями курса.