ФИЗИКА
Модуль 1.10
1 Вероятность. Средние значения
Статистическая
физика – это раздел физики, в котором
изучают свойства макроскопических
систем – систем, образованных огромным
числом микрочастиц (молекул, атомов,
ионов, электронов). В дальнейшем такие
системы мы будем называть макросистемами.
Свойства макросистем изучают, исходя
из индивидуальных свойств микрочастиц
и взаимодействий между ними. Описание
движения каждой частицы макросистемы
(а их порядка 1022÷1023)
– задача совершенно немыслимая. Вместо
этого статистическая физика оперирует
со средними значениями параметров очень
большого числа частиц. Колоссальное
число частиц в макросистеме приводит,
несмотря на очевидный хаос (беспорядок),
к появлению новых, статистических
закономерностей.
Их изучение и делает возможным описание
макросистем на основе сведений о
свойствах отдельных частиц.
О вероятности
Основу статистической физики оставляет
теория вероятностей. Исходные понятия
этой теории – событие
и вероятность.
Событие – это,
например, выпадение одного из шести (6)
номеров при бросании игрального кубика.
Или при измерении скорости молекул
газа: разбив возможные значения скоростей
на отдельные интервалы
![]() (
(![]() )
)
и, обнаружив, что скорость молекулы
попала в![]() -й
-й
интервал, мы говорим об![]() -ом
-ом
событии.
В дальнейшем нас
будут интересовать лишь такие события,
которые являются:
1) случайными,
т.е. события, которые нельзя заранее с
уверенностью предсказать;
2) равновероятными
– для которых нет никаких оснований
ожидать, что при испытаниях они будут
вести себя по-разному (например, при
бросании игрального кубика или монеты).
Вероятность данного
случайного события характеризуется
кратностью его повторения.
Если в
![]() случаях
случаях![]() -е
-е
событие происходит![]() раз, то вероятностью
раз, то вероятностью![]() этого события называют величину
этого события называют величину
![]() (3.1)
(3.1)
Так как на практике
![]() всегда конечно, то для вычисления
всегда конечно, то для вычисления
вероятности стараются, чтобы![]() и
и![]() были достаточно большими. Тогда можно
были достаточно большими. Тогда можно
считать, что
![]() (3.2)
(3.2)
Ясно, что сумма
вероятностей всех возможных результатов
измерений равна единице
![]() . (3.3)
. (3.3)
Теперь обратимся
к вычислению вероятностей сложных
событий. Рассмотрим две основные теоремы:
о сложении и умножении вероятностей на
примере игрального кубика.
1 Теорема
сложения вероятностей
Если в результате
![]() бросаний кубика в
бросаний кубика в![]() случаях выпадет число
случаях выпадет число![]() ,
,
а![]() случаях –
случаях –![]() ,
,
что вероятность выпадения![]() и
и![]() равна
равна
![]() (
(![]() или
или![]() )
)
=![]() (3.4)
(3.4)
Это значит, что
при бросании кубика вероятность
выпадения, скажем, 2 или 5 равна
![]() .
.
В общем случае эта
теорема утверждает: вероятности
несовместимых событий складываются.
Пример
При бросании игрального кубика
вероятность:
1) выпадения четной
цифры (2, 4, 6), равна
![]()
2) того, что не
выпадет 2, равна
![]() .
.
2 Теорема
умножения вероятностей
Найдем вероятность
того, что при двух бросаниях кубика
выпадет последовательно
![]() и
и![]() .
.
Рассмотрим![]() двойных бросаний. Пусть первый из каждой
двойных бросаний. Пусть первый из каждой
пары бросков дал![]() в
в![]() случаях (так что
случаях (так что![]() ).
).
Теперь выделим из этих![]() случаев те
случаев те![]() событий, когда второй бросок кубика
событий, когда второй бросок кубика
давал![]() (так что
(так что![]() ).
).
Тогда искомая вероятность
![]() (
(![]() ,
,
затем![]() )
)
=![]() (3.5)
(3.5)
Значит, вероятность
того, что при двух бросаниях кубика
выпадут, допустим, сначала 2, а затем,
5, равна
 .
.
В общем случае
теорема умножения вероятностей
утверждает: вероятность одновременного
появления (совмещения) двух или нескольких
независимых событий равна произведению
вероятностей каждого из них в отдельности.
Пример
Вероятность того, что при двух бросаниях
кубика:
а) выпадут две 5,
равна
![]() .
.
б) не выпадет ни
одной 5 равна
![]() .
.
в) выпадет одна 5,
равна
![]() .
.
Заметим, что
![]() ,
,
как и должно быть.
Средние значения
случайных величин
Зная вероятности появления различных
результатов измерения дискретной
величины
![]() ,
,
можно найти их среднее значение![]() .
.
По определению среднего
![]() (3.6)
(3.6)
Функция
распределения
Рассмотрим случай, когда случайная
величина
![]() имеетнепрерывный
имеетнепрерывный
характер, например, скорости молекул.
В этом случае число возможных значений
![]() бесконечно велико, а количество молекул
бесконечно велико, а количество молекул![]() хотя и велико, но конечно.
хотя и велико, но конечно.
Возникает вопрос,
какова вероятность
![]() того, что величина
того, что величина![]() имеет значения, заключенные в пределах
имеет значения, заключенные в пределах
малого интервала![]() ,
,
расположенного в окрестности значения![]() .
.
При малом![]() эта вероятность будет пропорциональной
эта вероятность будет пропорциональной![]() .
.
Кроме того, она зависит от того, в каком
месте оси![]() расположен интервал
расположен интервал![]() ,
,
т.е. является функцией![]() :
:![]() .
.
Таким образом
![]() (3.7)
(3.7)
(индекс
![]() при
при![]() указывает значение
указывает значение![]() ,
,
в окрестности которого расположен![]() ).
).
Функцию
![]() ,
,
равную
![]() , (3.8)
, (3.8)
называют функцией
распределения случайной величины
![]() .
.
Из (3.8) видно, функции
распределения
![]() можно приписать смыслплотности
можно приписать смыслплотности
вероятности,
т.е. вероятности величины
![]() оказаться в единичном интервале вблизи
оказаться в единичном интервале вблизи
значения![]() .
.
В разных случаях
![]() имеет совершенно различный вид, один
имеет совершенно различный вид, один
из которых приведен на рис. 1. В соответствии
с (3.7) площадь полоски шириной![]() равна вероятности
равна вероятности![]() того, что случайная величина
того, что случайная величина![]() окажется в пределах интервала
окажется в пределах интервала![]()

Рис. 1
Вероятность того,
что величина
![]() попадет
попадет
в интервал![]() :
:
![]() . (3.9)
. (3.9)
Ясно, что вероятность
того, что величина
![]() может принять хотя бы какое-нибудь
может принять хотя бы какое-нибудь
значение (достоверное событие), равна
единице. Это называютусловием
нормировки:
![]() , (3.10)
, (3.10)
где интегрирование
производится по всему интервалу возможных
значений
величины
![]() .
.
Из этого следует, что вся площадь под
кривой![]() равна единице (см. рис. 1).
равна единице (см. рис. 1).
Средние значения
Средние значения величины
![]() можно найти, зная ее нормированную на
можно найти, зная ее нормированную на
единицу функцию распределения![]() .
.
Обратимся к формуле (3.6). Она справедлива
и для случая, когда интервал изменения
величины![]() будет разбит на небольшие участки.
будет разбит на небольшие участки.
Уменьшая участки, мы должны, в конце
концов, заменить![]() на
на![]() и
и![]() – на интеграл
– на интеграл![]() .
.
Тогда
![]() (3.11)
(3.11)
Аналогичные формулы
справедливы для любой функции
![]() ,
,
например,
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Файлы
- Литература
Хаустов П.А.
1
1 Ставропольский государственный аграрный университет
1. Трофимова Т.И., Курс физики: учебное пособие для вузов. – М.: Издательский центр «Академия», 2008. – 560 с.
2. Рабочая тетрадь «Математическая логика и теория алгоритмов» (учебное пособие) / Т.А. Гулай, С.В. Мелешко, И.А. Невидомская, А.А. Яновский. // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 8-2. – С. 169.
3. Яновский А.А., Симоновский А.Я., Савченко П.И. моделирование гидрогазодинамических процессов в кипящей магнитной жидкости // Информационные системы и технологии как фактор развития экономики региона: сб. науч. трудов. – Ставрополь, 2013. – С. 159-163.
4. Яновский А.А. Управление теплообменными процессами при кипении магнитной жидкости на неограниченной поверхности при помощи магнитного поля/ Яновский А.А., Симоновский А.Я. // Физическое образование в вузах. – 2012. – Т.18, №1. – С. 35-36.
5. Яновский А.А., Симоновский А.Я. Математическое моделирование формы пузырька пара в кипящей магнитной жидкости // Научно-практическая конференция «Финансово-экономические и учетно-аналитические проблемы развития региона». – Ставрополь, 2013. – С. 490-493
6. Яновский А.А. Тепло- и массоперенос поле в кипящей магнитной жидкости в однородном магнитном поле / Яновский А.А., Симоновский А.Я., Чуенкова И.Ю. // Труды XI Международной конференции «Перспективные технологии, оборудование и аналитические системы для материаловедения и наноматериалов». 2014. Ч.1. Курск. – С. 252-257.
7. Яновский А.А. К вопросу о теплообмене в кипящей магнитной жидкости / Яновский А.А., Симоновский А.Я., Холопов В.Л. // В сборнике: ХI Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики сборник докладов. Составители: Д.Ю. Ахметов, А.Н. Герасимов, Ш.М. Хайдаров. 2015. – С. 4336-4338.
8. Яновский А.А., Спасибов А.С. Математическое моделирование процессов в кипящих намагничивающихся средах // Современные наукоемкие технологии. – 2014. – № 5-2. – С. 183-186.
Теория вероятности представляет собой раздел математики, изучающей закономерности массовых случайных явлений. Однако, область ее применения не ограничивается одной только математикой, а активно используется в различных областях науки, например в различных разделах физике, о чем пойдет речь в данной статье. На рубеже девятнадцатого и двадцатого веков многие ученые пытались, с точки зрения классической физики, объяснить принцип поведения электронов и других элементарных частиц, однако их попытки потерпели неудачу, ввиду того, что фотоны и электроны проявляли то свойства волн (интерференция), то свойства частиц (отражение, преломление), то есть имели некий дуализм, который впоследствии был назван корпускулярно-волновым. Только в 1926 году получилось устранить, казавшуюся невозможность сочетания этих свойств, а наука, изучающая поведение таких частиц, получила название квантовой, однако из-за несовершенных приборов было невозможно полностью описать их поведение, и тут на помощь пришла теория вероятности. То есть надо было только вычислить вероятность, того что мы получим определенный результат. Однако позже выяснилось, что обычное сложение вероятностей по законам теории Лапласа не подходит, ввиду очень малых размеров исследуемых объектов. Но, не подчиняясь законам, само понятие вероятности не претерпевает изменений, то есть вероятность p наступления события A будет равно отношению благоприятных исходов опыта m к общему числу проведенных опытов:
 .
.
Следовательно, нам стоит лишь изменить способ вычисления вероятности в квантовой механики. Для нахождения такой формулы проводилось множество экспериментов, в основном мысленных, в данной статье я опишу один из них. Предположим, что у нас есть схема, которая состоит из слабого источника электронов (S), расположенного в некой области точки А, экран B с двумя отверстиями и за линией C детектор электронов, фиксирующий пролет частиц.

Рис. 1. Схема опыта
В результате электрон, выпущенный из источника, пролетает через одно из отверстий и регистрируется детектором, который может быть расположен на расстоянии х от C. В итоге мы имеем функцию x от вероятности p, то есть возможность попадания электрона в точку х. Данный график будет представлять собой сложную кривую и должен подчиняться функции плотности распределения вероятности, имеющей вид:
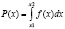 .
.
По теории вероятности, частица, летящая из источника в некоторую точку x, должна проходить через одно из открытых отверстий. Применяя формулу сложения вероятностей 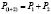 , мы должны получить кривую d, однако результат опыта представляет собой график а, который совпадает с картиной интерференции волн – явления наложения двух колебаний, при которых появляются точки максимума и минимума. Чтобы найти эту вероятность воспользуемся введением новой величин – амплитуды волны. Данную величину назовем амплитудой вероятности, квадрат которой будет равен нашей вероятности. Тогда общая формула принимает вид:
, мы должны получить кривую d, однако результат опыта представляет собой график а, который совпадает с картиной интерференции волн – явления наложения двух колебаний, при которых появляются точки максимума и минимума. Чтобы найти эту вероятность воспользуемся введением новой величин – амплитуды волны. Данную величину назовем амплитудой вероятности, квадрат которой будет равен нашей вероятности. Тогда общая формула принимает вид: 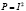 , с учетом
, с учетом  . Получим в итоге:
. Получим в итоге: 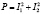 .
.
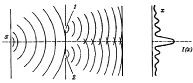
Рис. 2. Явление интерференции
И тут возникает парадокс, прослеживая пролеты частиц и регистрируя через какое отверстие он пролетает и проверив экспериментально правильность построение кривых b и с, в итоге получим кривую d, которая будет равна формуле сложения вероятностей:
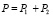 . (3)
. (3)
Таким образом, теория вероятности сыграла очень важную роль в становлении квантовой физики, ввиду отсутствия нужного оборудования, только она помогла в понимании поведения элементарных частиц.
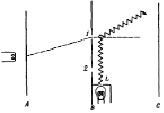
Рис. 3. Схема опыта с осветителем
Библиографическая ссылка
Хаустов П.А. ТЕОРИЯ ВЕРОЯТНОСТИ В КВАНТОВОЙ ФИЗИКЕ // Международный студенческий научный вестник. – 2016. – № 3-3.
;
URL: https://eduherald.ru/ru/article/view?id=15033 (дата обращения: 16.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Вероятность в квантовой механике. Откуда она взялась и как это упростить для понимания
Время на прочтение
15 мин
Количество просмотров 30K
Введение
Эта статья рассчитана на людей, имеющих начальные знания по квантовой механике, обычно входящей в вузовский курс теоретической физики, а также живой интерес к ней. Квантовая механика, как матанализ, требует определенных начальных знаний, и без этого любое чтение будет либо беллетристикой, либо приведет к неправильным представлениям. Все обещания квантовой механики для всех и даром сродни социалистическим предвыборным лозунгам. Тем не менее эти необходимые знания не так велики, как может показаться, особенно для знающих математику. В начале изучения у многих возникает проблема — вероятностный смысл волновой функции и связанные с этим вещи: процесс измерения и гипотеза редукции волновой функции, трудны для понимания. Тем более, что в дальнейшем при решении задач этот вероятностный смысл или интерпретация, как правило, не требуются, поэтому многие даже не задумываются над этим. Тем не менее хотелось бы разобраться, откуда это взялось и зачем вообще нужно, и нужно ли вообще. Оказывается, что соображения, которые, вероятно, легли в основу столь сложных и противоречивых постулатов, утратили силу по мере прогресса квантовой электродинамики. Глубоких знаний для понимания не потребуется — можно просто поверить хорошо известным результатам из учебников, но начальный уровень все же необходим.
По проблеме интерпретации волновой функции споры велись с самого начала разработки квантовой механики. Наиболее известный – дискуссия Бора и Эйнштейна, длившаяся много лет. Интерпретация волновой функции, как амплитуды вероятности, разработана, в-основном, Борном [1] и дополнена Бором и Гейзенбергом [2] — физиками «Копенгагенской школы». В дальнейшем в литературе было принято название «Копенгагенская интерпретация», далее КИ. Я использую стандартные обозначения, принятые в «Курсе теоретической физики» Л.Д.Ландау и Е.М.Лифшица [3] и в большинстве других аналогичных учебников. Во второй части статьи предлагаются критические эксперименты, которые могли бы опровергнуть или подтвердить КИ. К сожалению, они неосуществимы технически в наше время.
Вероятностная интерпретация
В КИ постулируется, что волновая функция  есть амплитуда плотности вероятности координат частицы. Это означает, что
есть амплитуда плотности вероятности координат частицы. Это означает, что  есть распределение плотности вероятности ее обнаружения в точке x. При этом вводится понятие измерения и постулат редукции волновой функции, не вытекающий из уравнения Шредингера. Если во всех предыдущих разделах физики процесс измерения был конкретным, описывался теми же уравнениями и подчинялся тем же законам, что и любой другой физический процесс, то в квантовой механике он не определен четко и понятными уравнениями не описывается. Например, в классическом учебнике Ландау и Лифшица [3] приговариваются абсолютно непонятные слова о том, что квантовая механика нуждается в классическом (неквантовом) приборе и т.п. Самое интересное то, что в дальнейшем никакой классический прибор не требуется. Совершенно непонятно при дальнейшем изучении, почему эволюция волновой функции электрона при взаимодействии с вполне классичным (с большой точностью, если отвлечься от спина) объектом — атомным ядром, рассчитывается с помощью уравнения Шредингера и хорошо исследована, а взаимодействие с измерительным прибором вызывает загадочную редукцию волновой функции, никак с помощью уравнения Шредингера не доказываемую. Редукция волновой функции — еще один постулат КИ, вызывающий довольно много возражений.
есть распределение плотности вероятности ее обнаружения в точке x. При этом вводится понятие измерения и постулат редукции волновой функции, не вытекающий из уравнения Шредингера. Если во всех предыдущих разделах физики процесс измерения был конкретным, описывался теми же уравнениями и подчинялся тем же законам, что и любой другой физический процесс, то в квантовой механике он не определен четко и понятными уравнениями не описывается. Например, в классическом учебнике Ландау и Лифшица [3] приговариваются абсолютно непонятные слова о том, что квантовая механика нуждается в классическом (неквантовом) приборе и т.п. Самое интересное то, что в дальнейшем никакой классический прибор не требуется. Совершенно непонятно при дальнейшем изучении, почему эволюция волновой функции электрона при взаимодействии с вполне классичным (с большой точностью, если отвлечься от спина) объектом — атомным ядром, рассчитывается с помощью уравнения Шредингера и хорошо исследована, а взаимодействие с измерительным прибором вызывает загадочную редукцию волновой функции, никак с помощью уравнения Шредингера не доказываемую. Редукция волновой функции — еще один постулат КИ, вызывающий довольно много возражений.
В настоящее время классическая борновская интерпретация претерпела изрядную ревизию, так многих не устраивает ни понятие измерения, ни загадочная редукция. Появилось довольно много работ на эту тему. Однако, следование борновской или какой-то другой интерпретации не влияет на методы решения задач в теории и на получаемые математические результаты. Поэтому эти работы больше похожи на философские или популяризаторские, к серьезной теоретической физике их трудно отнести. Например, многомировая интерпретация, предложенная в 1957 г. Эвереттом [4], обсуждаемая в [5], вводит множество вариантов реальностей, из которых неведомо как делается выбор. Вводятся новые категории, которые более нигде не используются. Такое количество различных версий позволяет предположить, что ни одна не является хорошо обоснованной. Вместе с тем именно непонятная интерпретация сильно затрудняет изучение квантовой механики на начальном этапе. Существует аксиоматическое изложение квантовой теории [6], где вообще отсутствует физическая интерпретация вектора состояния. Это удобно для математика, но для начинающего физика не годится.
Все имеющиеся работы не дают ответа на простой вопрос: «Что заставило в 20е годы XX века множество первоклассных талантов придти к такой спорной трактовке и вводить понятия, не определенные хотя бы на физическом уровне строгости — измерение, классический прибор, и гипотезу редукции волновой функции, не подкрепленную весомыми аргументами». Чтобы разобраться, надо вспомнить, что в эти годы в квантовой механике был только один тип взаимодействия — электромагнитное поле, а основной тип объектов — электроны.
В классической теории поля тоже есть вспомогательные понятия — пробный заряд или рамка с током. Но они нужны, чтобы пояснить физический смысл вводимых напряженностей поля и потенциалов. Последовательная и логичная теория строится и без них, на основе лагранжиана поля и зарядов. Так как к квантовой механике приступают, уже освоив теорию поля, у новичка возникает вопрос — а нужна ли вообще эта вероятностная интерпретация? Чем плоха точка зрения Эйнштейна, который считал частицы просто состояниями полей? Давайте забудем о классических частицах и будем просто рассматривать поле  , для которого есть уравнение Шредингера. Тем более, что с вероятностной интерпретацией (КИ) не соглашались немало авторитетов, как в прошлом (Эйнштейн, де Бройль), так и теперь (например, Хокинг). Также, как векторный потенциал в электродинамике,
, для которого есть уравнение Шредингера. Тем более, что с вероятностной интерпретацией (КИ) не соглашались немало авторитетов, как в прошлом (Эйнштейн, де Бройль), так и теперь (например, Хокинг). Также, как векторный потенциал в электродинамике,  не имеет непосредственного физического смысла. Имеют физический смысл некие квадратичные выражения. Для электрона плотность заряда есть –e
не имеет непосредственного физического смысла. Имеют физический смысл некие квадратичные выражения. Для электрона плотность заряда есть –e  , а плотность тока есть
, а плотность тока есть  e, m — заряд и масса электрона,
e, m — заряд и масса электрона,  — постоянная Планка. Опыты с дифракцией электрона на кристаллах и двух щелях интерпретируются в этом случае крайне просто — электрон, как и световая волна, проходит сразу через ОБЕ щели. Из уравнения Шредингера, также, как из волнового уравнения для света, определяется
— постоянная Планка. Опыты с дифракцией электрона на кристаллах и двух щелях интерпретируются в этом случае крайне просто — электрон, как и световая волна, проходит сразу через ОБЕ щели. Из уравнения Шредингера, также, как из волнового уравнения для света, определяется  на фотопластинке. Далее предполагаем, что степень почернения пропорциональна по аналогии со светом, где степень почернения пропорциональна среднему
на фотопластинке. Далее предполагаем, что степень почернения пропорциональна по аналогии со светом, где степень почернения пропорциональна среднему  (E — напряженность электрического поля). Это предположение вполне правдоподобно. В таком случае и принцип неопределенности Гейзенберга — просто известное математическое соотношение между среднеквадратичной дисперсией функции и ее Фурье-образа.
(E — напряженность электрического поля). Это предположение вполне правдоподобно. В таком случае и принцип неопределенности Гейзенберга — просто известное математическое соотношение между среднеквадратичной дисперсией функции и ее Фурье-образа.
Какие аргументы были у копенгагенской школы в пользу КИ?
КИ тоже позволяет интерпретировать ряд экспериментов, например, по дифракции электронов. Но эксперименты чисто качественные — рассматривалось [7] почернение фотопластинки. В принципе можно рассмотреть простейшую модель детектора, состоящую из  (x)-образной ямы в большом ящике. Электрон отдает энергию фотону и переходит на связанный уровень в яме. Для корректности эксперимента радиус локализации в
(x)-образной ямы в большом ящике. Электрон отдает энергию фотону и переходит на связанный уровень в яме. Для корректности эксперимента радиус локализации в  -яме должен быть много меньше длины волны электрона. Однако такой детектор, как нетрудно показать, заметно меняет стационарную волновую функцию электрона в ящике, так что эксперимент теряет смысл.
-яме должен быть много меньше длины волны электрона. Однако такой детектор, как нетрудно показать, заметно меняет стационарную волновую функцию электрона в ящике, так что эксперимент теряет смысл.
Один из основных аргументов Борна состоял в том, что, согласно уравнению Шредингера, волновой пакет микроскопической частицы неограниченно размывается со временем. Это казалось ему абсурдным. Однако в конденсате Бозе — Эйнштейна каждая частица размазана по всему макроскопическому образцу, так что аргумент Борна некорректен. Должны быть другие аргументы против простейшей полевой интерпретации  , близкой к точке зрения Эйнштейна.
, близкой к точке зрения Эйнштейна.
Действительно, можно просто ввести комплексное поле  , постулировав написанные выше выражения для плотности заряда и тока, основанные на уравнении непрерывности. Уравнение Шредингера выводится обычным путем, и оператор гамильтониана есть обобщение классического выражения для заряженной частицы. Но следом возникает неразрешимая при тогдашнем уровне теории проблема. При таком подходе в гамильтониан атома водорода, пришлось бы, помимо взаимодействия с электростатическим полем ядра, включить взаимодействие электронного облака с его собственным электростатическим полем, т.е. в энергии возникло бы слагаемое вида
, постулировав написанные выше выражения для плотности заряда и тока, основанные на уравнении непрерывности. Уравнение Шредингера выводится обычным путем, и оператор гамильтониана есть обобщение классического выражения для заряженной частицы. Но следом возникает неразрешимая при тогдашнем уровне теории проблема. При таком подходе в гамильтониан атома водорода, пришлось бы, помимо взаимодействия с электростатическим полем ядра, включить взаимодействие электронного облака с его собственным электростатическим полем, т.е. в энергии возникло бы слагаемое вида
 (1)
(1)
Это слагаемое можно вывести также, как энергию электромагнитного поля электронного облака в пренебрежении токами. Для атома водорода такое слагаемое того же порядка, что и взаимодействие с ядром, то есть хорошо известный и проверенный экспериментально спектр изменился бы кардинально. Мало того, даже для свободного электрона возникают абсурдные следствия — кулоновское отталкивание приводит к разлету волнового пакета и размазыванию электронного облака по всему доступному пространству. Ничего подобного в эксперименте не наблюдается. Наверное, именно это и привело копенгагенскую школу к КИ, так как все вышеизложенные простые соображения, вероятно, приходили им в голову. Действительно, для точечной частицы такое слагаемое отсутствует, точнее, сводится к постоянной. Далее, для атома гелия учет кулоновского взаимодействия двух электронов между собой дает вполне правдоподобные результаты, что опять-таки соответствует концепции точечных частиц. То есть КИ появилась за неимением лучшего. Но в нерелятивистской квантовой механике частицы не возникают и не исчезают. Тогда утверждение о том, что электрон находится в одной точке, противоречит экспериментам с дифракцией одного электрона на 2 щелях. Кроме того, в упоминавшемся [7] эксперименте наблюдали интерференцию на кристалле одного электрона. Так что просто и логично объяснить на основе КИ и уравнение Шредингера, и известные эксперименты не представляется возможным. В результате был придуман некий алгоритм, который в одних случаях предписывает считать электрон частицей, а в других — волной, и назван КИ с добавкой «корпускулярно-волновой дуализм». В то же время и обычная полевая интерпретация  кажется невозможной ввиду отсутствия в энергии членов типа (1), т.е. «самодействия» одного электрона.
кажется невозможной ввиду отсутствия в энергии членов типа (1), т.е. «самодействия» одного электрона.
На самом деле при написании (1) было неявно сделано одно недоказанное допущение – электроны взаимодействуют с классическим электромагнитным полем. Можно ли считать электромагнитное поле электрона классическим? Чтобы разобраться, надо использовать квантовую электродинамику. Ведь на самом деле нет никакого кулоновского потенциала, а есть электромагнитное поле, взаимодействующее с электронами. При этом электромагнитное поле, входящее в уравнение Шредингера или Дирака для атома водорода, принципиально иное, нежели то, которое вызывает взаимодействие между электронами. Оно классическое, то есть имеет определенное значение в каждой точке, и порождается классическим объектом — ядром.
Чтобы корректно исследовать задачу, надо перейти к релятивистской квантовой теории, тогда волновая функция становится оператором. Здесь нет необходимости (а также места) писать соответствующие формулы и вычисления, желающие найдут их в учебнике (см., например [8]). Я ограничусь изложением известных результатов. Рассмотрим для начала свободный электрон. Чтобы понять, что случится с его волновым пакетом (или облаком), надо выяснить, как меняется его гриновская функция или пропагатор из-за взаимодействия с электромагнитным полем. Поправки к гриновской функции свободного электрона, возникающие при учете взаимодействия с электромагнитным полем, написанные формально по теории возмущений, как известно, сводятся к расходящимся интегралам. Однако эта проблема была решена. Было показано, что учет взаимодействия с квантованным электромагнитным полем для свободного электрона приводит просто к замене в соответствующих формулах заряда и массы на перенормированные (наблюдаемые) величины [8]. Таким образом, в нерелятивистском случае малых импульсов учет взаимодействия одного электрона с электромагнитным полем приводит просто к обычному линейному уравнению Шредингера с перенормированными зарядом и массой вместо слагаемого (1), то есть предположение о классичности электромагнитного поля дает в этом случае принципиально неверный результат. Аналогичное решение с перенормировкой существует и для электрона во внешнем поле — оно рассматривается в теории лэмбовского сдвига для атома водорода [8,9].
Рассмотрим теперь два электрона. Для случая малых, нерелятивистских импульсов можно ввести некое эффективное взаимодействие между ними в уравнение Шредингера. Определить его вид можно по амплитуде взаимного рассеивания — она однозначно связана с взаимодействием. В диаграммной технике Фейнмана ей соответствуют диаграммы с 4-мя внешними электронными линиями. В случае малых импульсов соответствующая амплитуда рассеяния переходит в классическую формулу Резерфорда с учетом обмена [8], то есть взаимодействие между электронами в атоме действительно можно рассматривать, используя кулоновский потенциал.
Таким образом, от неприятных противоречий, вытекающих из интерпретации волновой функции, как обычного поля, без всяких корпускулярных свойств, можно избавиться, если привлечь релятивистскую квантовую теорию. Впрочем, постольку, поскольку рассматривается электромагнитное поле, это вполне логично. Во всяком случае, это намного понятнее, чем пресловутый дуализм и КИ, и близко к точке зрения Эйнштейна. В релятивистской теории  становится уже квантованным полем, то есть при заданном x является уже не числом, а оператором. Но все эти результаты были получены примерно через 30 лет после теоретического вычисления спектра атома водорода в рамках нерелятивистской квантовой механики и замечательного совпадения с экспериментом. За эти годы КИ укоренилась в головах и учебниках.
становится уже квантованным полем, то есть при заданном x является уже не числом, а оператором. Но все эти результаты были получены примерно через 30 лет после теоретического вычисления спектра атома водорода в рамках нерелятивистской квантовой механики и замечательного совпадения с экспериментом. За эти годы КИ укоренилась в головах и учебниках.
Может возникнуть вопрос: почему же КИ не исчезла из учебников, если без нее так легко сейчас обойтись? Я показал эту статью нескольким знакомым профессорам из разных университетов и обнаружил, что этот предмет их практически не интересует. Для людей, уже глубоко освоивших теоретическую физику он неактуален. Неактуален он и для математиков, работающих в теоретической физике. Крупные ученые вообще перестали интересоваться обучением и распространением знаний в той мере, как это было лет 50 назад. Ландау был последним из великих физиков-теоретиков, кто ставил преподавание и работу с учениками наравне или выше личных результатов, но он не успел освоить новые методы квантовой электродинамики — попал в роковую аварию.
Процесс измерения, значения физической величины и стационарные состояния. Другие проблемы в понимании
Из вероятностной интерпретации (КИ) и процесса измерения, который никак не конкретизируется, вытекает еще одна путаница с вероятностями состояний и значениями какой-либо физической величины F у квантовой частицы. Утверждается, что коэффициенты разложения  по собственным функциям есть амплитуды вероятности обнаружения соответствующего собственного значения или, что то же самое, амплитуды вероятности нахождения частицы в соответствующем собственном состоянии. После определения
по собственным функциям есть амплитуды вероятности обнаружения соответствующего собственного значения или, что то же самое, амплитуды вероятности нахождения частицы в соответствующем собственном состоянии. После определения  , как функции, дающей полное описание свойств частицы или системы, такой постулат воспринимается с трудом. Примерно, как утверждение, что в бутылке водки с вероятностью 0,4 находится чистый спирт, а с вероятностью 0,6 — чистая вода. Далее, постулируется, что величина
, как функции, дающей полное описание свойств частицы или системы, такой постулат воспринимается с трудом. Примерно, как утверждение, что в бутылке водки с вероятностью 0,4 находится чистый спирт, а с вероятностью 0,6 — чистая вода. Далее, постулируется, что величина  — среднее значение F в вероятностном смысле,
— среднее значение F в вероятностном смысле,  — оператор, соответствующий F. Отсюда студент делает совершенно неверный вывод, что величина F может принимать только значения из своего спектра, а законы сохранения имеют вероятностный характер. Это совершенно неправильно как с формальной точки зрения, так и с физической. Законы сохранения основных физических величин — энергии, импульса, момента импульса и т.п., имеют куда более фундаментальный характер, чем уравнение Шредингера, так как вытекают из общих свойств пространства-времени. С формальной точки зрения, величина
— оператор, соответствующий F. Отсюда студент делает совершенно неверный вывод, что величина F может принимать только значения из своего спектра, а законы сохранения имеют вероятностный характер. Это совершенно неправильно как с формальной точки зрения, так и с физической. Законы сохранения основных физических величин — энергии, импульса, момента импульса и т.п., имеют куда более фундаментальный характер, чем уравнение Шредингера, так как вытекают из общих свойств пространства-времени. С формальной точки зрения, величина  сохраняется (не зависит от времени), если оператор
сохраняется (не зависит от времени), если оператор  коммутирует с гамильтонианом, т.е. если F — интеграл движения. В таком случае логично считать именно
коммутирует с гамильтонианом, т.е. если F — интеграл движения. В таком случае логично считать именно  значением величины F в состоянии
значением величины F в состоянии  , иначе придется считать, что, например, энергия сохраняется только в среднем. Тогда значение физической величины F (энергии, импульса, момента импульса) у частицы может быть любым, то есть не обязательно собственным значением оператора
, иначе придется считать, что, например, энергия сохраняется только в среднем. Тогда значение физической величины F (энергии, импульса, момента импульса) у частицы может быть любым, то есть не обязательно собственным значением оператора  .
.
Существенную путаницу в этой области создает рассмотрение исключительно стационарных состояний, то есть собственных векторов гамильтониана. У студентов часто складывается убеждение, что других состояний вообще не бывает, а энергия принимает значения только из спектра гамильтониана. Между тем стационарные состояния — идеализация, в чистом виде редко существующая. Гораздо ближе к реальности (например, для свободных частиц) когерентные состояния, минимизирующие соотношение неопределенностей. Ограничение рассмотрения исключительно стационарными состояниями приводит к утверждению, кочующему из учебника в учебник, о том, что энергия моды электромагнитного поля с частотой  всегда меняется на кратное
всегда меняется на кратное  , то есть на целое число фотонов. Но это верно лишь в том случае, если начальное и конечное состояния — стационарные, что совершенно необязательно. Вообще говорится почти повсеместно в учебной литературе, что электромагнитное поле есть совокупность фотонов, то есть опять игнорируются нестационарные состояния. Это совершенно некорректно, и приводит к проблемам при решении простых задач. Рассмотрим, например, электрон в потенциальной яме с двумя уровнями
, то есть на целое число фотонов. Но это верно лишь в том случае, если начальное и конечное состояния — стационарные, что совершенно необязательно. Вообще говорится почти повсеместно в учебной литературе, что электромагнитное поле есть совокупность фотонов, то есть опять игнорируются нестационарные состояния. Это совершенно некорректно, и приводит к проблемам при решении простых задач. Рассмотрим, например, электрон в потенциальной яме с двумя уровнями  . Каким-то образом, например, в результате кратковременного возмущения, он переходит в состояние
. Каким-то образом, например, в результате кратковременного возмущения, он переходит в состояние  и
и  — волновые функции, соответствующие
— волновые функции, соответствующие  и
и  . Это состояние обладает большей энергией, чем основное, и со временем электрон должен вернуться на нижний уровень, отдав избыток энергии электромагнитному полю (полагаем, что переход
. Это состояние обладает большей энергией, чем основное, и со временем электрон должен вернуться на нижний уровень, отдав избыток энергии электромагнитному полю (полагаем, что переход  не запрещен в силу каких-то симметрий). Нетрудно видеть, что, если ограничиться первым порядком теории возмущений, то переход может произойти только в результате взаимодействия с модой электромагнитного поля частоты
не запрещен в силу каких-то симметрий). Нетрудно видеть, что, если ограничиться первым порядком теории возмущений, то переход может произойти только в результате взаимодействия с модой электромагнитного поля частоты  . Это следует из зависимости от времени начальной и конечной волновых функций в представлении Шредингера. Но переход с испусканием фотона с энергией невозможен в силу закона сохранения энергии — разность энергий начального и конечного состояний
. Это следует из зависимости от времени начальной и конечной волновых функций в представлении Шредингера. Но переход с испусканием фотона с энергией невозможен в силу закона сохранения энергии — разность энергий начального и конечного состояний  меньше
меньше  . После этого студент делает вывод, что переход запрещен. Однако, если отказаться от необоснованного предположения о стационарности конечного состояния, то ответ получается легко. Пусть для определенности исходное состояние электромагнитной моды с
. После этого студент делает вывод, что переход запрещен. Однако, если отказаться от необоснованного предположения о стационарности конечного состояния, то ответ получается легко. Пусть для определенности исходное состояние электромагнитной моды с  было основным, тогда ее конечное состояние
было основным, тогда ее конечное состояние  удовлетворяет закону сохранения энергии и имеет нужную частоту, чтобы был возможен переход электрона на основной уровень. Но говорить при этом о рождении фотона некорректно. Из этого примера, кстати, видно, что для качественного (упрощенного) объяснения спектров излучения и поглощения в нерелятивистском случае, а также фотоэффекта, привлекать «корпускулярные» свойства электромагнитных волн не обязательно.
удовлетворяет закону сохранения энергии и имеет нужную частоту, чтобы был возможен переход электрона на основной уровень. Но говорить при этом о рождении фотона некорректно. Из этого примера, кстати, видно, что для качественного (упрощенного) объяснения спектров излучения и поглощения в нерелятивистском случае, а также фотоэффекта, привлекать «корпускулярные» свойства электромагнитных волн не обязательно.
Наибольший интерес разобранная двухуровневая задача представляет применительно к спину электрона. Пусть имеется электрон в связанном состоянии со спином вдоль оси x. Прикладываем магнитное поле вдоль оси z. Тогда волновая функция электрона может быть записана в виде  , где
, где  , а
, а  и
и  — волновые функции со спином по и против оси z, являющиеся собственными функциями гамильтониана. Если придерживаться КИ, то с вероятностью ½ электрон испустит фотон с энергией
— волновые функции со спином по и против оси z, являющиеся собственными функциями гамильтониана. Если придерживаться КИ, то с вероятностью ½ электрон испустит фотон с энергией  . Если отказаться от КИ, в результате испускания получим описанное выше нестационарное состояние моды электромагнитного поля с частотой
. Если отказаться от КИ, в результате испускания получим описанное выше нестационарное состояние моды электромагнитного поля с частотой  . Так как всегда предполагается, что частоте
. Так как всегда предполагается, что частоте  соответствует энергия
соответствует энергия  , то по суммарной энергии излучения делается вывод о том, что число испущенных фотонов вдвое меньше числа электронов, то есть половина электронов находилась в состоянии
, то по суммарной энергии излучения делается вывод о том, что число испущенных фотонов вдвое меньше числа электронов, то есть половина электронов находилась в состоянии  . Если бы в процессе эксперимента можно было отличить нестационарное состояние с половинной энергией от стандартного фотона, то можно было бы дать экспериментальное подтверждение или опровержение КИ. Но, во всяком случае, уравнение Шредингера, написанное для электрона и фотонной моды
. Если бы в процессе эксперимента можно было отличить нестационарное состояние с половинной энергией от стандартного фотона, то можно было бы дать экспериментальное подтверждение или опровержение КИ. Но, во всяком случае, уравнение Шредингера, написанное для электрона и фотонной моды  , к излучению фотона с энергией
, к излучению фотона с энергией  привести не может — это следует из закона сохранения величины
привести не может — это следует из закона сохранения величины  , где оператор
, где оператор  — гамильтониан. Для этого необходима загадочная редукция волновой функции.
— гамильтониан. Для этого необходима загадочная редукция волновой функции.
Отличить нестационарное состояние от стационарного можно было бы по импульсу отдачи электрона. Во втором случае (если отбросить КИ) он в 2 раза меньше. Для локализованного состояния электрона с энергией связи E порядка 10-1 электрон-вольта вероятность ионизации будет в обоих случаях различной, и порог ионизации по магнитному полю будет отличаться в 2 раза. К сожалению, оценка показывает, что для ионизации нужны слишком сильные магнитные поля 1011 гс. Такие поля в настоящее время недостижимы.
Можно было бы использовать для экспериментальной проверки свободные электроны, ориентация спина которых задана магнитным полем. Рассмотрим установку, состоящую из камеры со свободными электронами в сильном магнитном поле вдоль оси z. Электроны вылетают из отверстия в камере с магнитным полем, имея спин вдоль оси z, в камеру, где на вращающейся оси расположены 2 одинаковых диска с отверстиями, смещенными на угол φ. Такая установка позволяет получить на выходе параллельный оси x пучок электронов одинаковой энергии. Попадая в область магнитного поля, направленного вдоль оси x, электроны со спинами, ориентированными вдоль оси z, должны начать излучать фотоны частоты  либо вышеописанные нестационарные моды той же частоты. При этом импульс отдачи может уменьшить или увеличить скорость электрона. Если скорость электронов в пучке достаточно малая, то появятся электроны, летящие назад, что может быть обнаружено. Это позволило бы провести критическую экспериментальную проверку КИ. К сожалению, при наибольших достижимых сейчас магнитных полях ~ 106 Гс импульс отдачи соответствует энергии 3*10-11эв или скорости порядка 3 м/с. Достаточно сложно обеспечить такую малую скорость электрона, так как она гораздо меньше тепловой.
либо вышеописанные нестационарные моды той же частоты. При этом импульс отдачи может уменьшить или увеличить скорость электрона. Если скорость электронов в пучке достаточно малая, то появятся электроны, летящие назад, что может быть обнаружено. Это позволило бы провести критическую экспериментальную проверку КИ. К сожалению, при наибольших достижимых сейчас магнитных полях ~ 106 Гс импульс отдачи соответствует энергии 3*10-11эв или скорости порядка 3 м/с. Достаточно сложно обеспечить такую малую скорость электрона, так как она гораздо меньше тепловой.
Заключение
Полевая интерпретация  позволяет вернуть квантовую механику в рамки систематического изложения, принятого в остальных разделах курса теоретической физики. Действительно, все тома курса теоретической физики Ландау и Лифшица построены по единой схеме, с четкой системой понятий и постулатов, и только том 3 опирается на какие-то внешние понятия вроде процесса измерения, классического прибора и т.п., причем сами эти понятия четко не определяются.
позволяет вернуть квантовую механику в рамки систематического изложения, принятого в остальных разделах курса теоретической физики. Действительно, все тома курса теоретической физики Ландау и Лифшица построены по единой схеме, с четкой системой понятий и постулатов, и только том 3 опирается на какие-то внешние понятия вроде процесса измерения, классического прибора и т.п., причем сами эти понятия четко не определяются.
Поэтому неудивительно, что есть свидетельство племянницы Л.Д. Ландау [10], что он сам, поместивший в своем знаменитом «Курсе теоретической физики» подробное изложение КИ [3], относился к ней совершенно равнодушно:
«Моему брату, тогда студенту, Лёне Кардашинскому, по его дословным воспоминаниям, в ответ на вопрос: что такое электрон, Дау, в свойственной ему решительной манере, ответил: «Электрон не корпускула и не волна. С моей точки зрения — он уравнение, в том смысле, что лучше всего его свойства описываются уравнением квантовой механики, и прибегать к другим моделям — корпускулярной или волновой, нет никакой необходимости». ». Выводы этой статьи, в-общем, в русле мнения Ландау — не нужно никаких дополнительных концепций, постулатов и т.п. для объяснения физического смысла квантовой механики. Традиционного понятия поля  вполне достаточно.
вполне достаточно.
Как я уже писал выше, для специалистов этот вопрос, как правило, неактуален. Но для студентов-физиков, осваивающих материал и пытающихся понять физический смысл формул, он очень важен. Особенно сейчас, когда общий интерес к физике упал ниже плинтуса.
Если статья вызовет интерес, я могу написать продолжение, посвященное так называемой «квантовой запутанности». На самом деле это название в русскоязычных материалах происходит от безграмотности — в учебниках, например, [3] §14, эти состояния всегда называются смешанными, но авторы статей, похоже, учебников не читали. Из простых рассуждений будет понятно, почему никакой квантовой телепортации информации не существует, и почему эффектные опыты с этими состояниями малоинтересны для науки. Это эффекты «на публику», а не для специалистов.
Литература:
1. Борн М. Статистическая интерпретация волновой механики // Атомная физика — М.: Мир, 1965
2. Гейзенберг В. Развитие интерпретации квантовой теории // Нильс Бор и развитие физики / сб. под ред.Паули В. — М: ИЛ, 1958. — С. 23—45.
3. Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 3-е, переработанное и дополненное. — М.: Наука, 1974. — 752 с. — («Теоретическая физика», том III).
4. Hugh Everett. “Relative State” Formulation of Quantum Mechanics. Rev. Mod. Phys., vol. 29, N 3, July 1957.
5. Менский М. Б. Человек и квантовый мир. Фрязино: «Век2», 2005. — 320 с. — (Наука для всех). ISBN 5-85099-161-1 УДК 530.1 ББК 22.31 М50
6. Боголюбов Н. Н., Логунов А. А., Тодоров И.Т. Основы аксиоматического подхода в квантовой теории поля.,«Наука», Главная редакция физико-математической литературы, 1969 г. Е30.1 Б 74 УДК Б30.14Б
7. Дифракция одиночных поочерёдно летящих электронов. Из текущей литературы. УФН, 1949 г. Август, XXXVIII, вып. 4
ufn.ru/ufn49/ufn49_8/Russian/r498e.pdf
8. Ахиезер А. И., Берестецкий В. Б. Квантовая электродинамика. — Издание 3-е, переработанное. — М.: Наука, 1969. — 623 с.
9. П.А.М. Дирак. Лекции по квантовой теории поля. Перевод с английского Б. А. Лысова. Под редакцией А. А. Соколова. Издательство «Мир», Москва 1971
10. Элла РЫНДИНА. Лев Ландау: штрихи к портрету // Вестник, №5, 6, 7 (№342‐344). Март 2004 г. www.vestnik.com/issues/2004/0303/win/ryndina.htm
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Плотность вероятности
В квантовой механике состояние микрочастиц описывают при помощи волновой функции $Psi(overrightarrow{r},t)$. Она является основным носителем информации о свойствах частиц. Вероятность ($dP$) нахождения частицы в элементе, который имеет объем $dV=dxdydz$ около точки с координатами $(x,y,z)$:
где величина равная:
называется плотностью вероятности. Она определяет вероятность того, что частица находится в единичном объеме в окрестности точки ($x,y,z$). Физический смысл имеет не сама волновая функция, квадрат ее модуля (${left|Psiright|}^2$).
Вероятность найти частицу в момент времени t в конечном объеме V по теореме о сложении вероятности равна:
Так как величина ${left|Psiright|}^2dV$ определена как вероятность, волновую функцию следует нормировать. Вероятность достоверного события должна быть равна единице, если в качестве объема ($V=infty )$ принимать все пространство. Это означает, что при данном условии частица находится в пространстве, где — либо. Условие нормировки вероятности записывается как:
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Интеграл в выражении (1) вычисляется по всему пространству. Условие (4) отражает факт объективного существования частицы во времени и пространстве.
Так, например, величина ${left|Psi(x)right|}^2$ определяет плотность вероятности нахождения частицы в точке $x$ для одномерного движения. Следовательно, среднее значение координаты частицы можно найти как:
Плотность потока вероятности
Найдем производную по времени ($frac{d}{dt}$) от вероятности нахождения частицы в объеме $V$, то есть:
В классической физике функцией Гамильтона ($Hleft(overrightarrow{r},overrightarrow{p}right)$) называют полную энергию, которая выражена через импульсы и координаты частицы. Для одной частицы полная энергия равна:
В квантовой механике функции Гамильтона соответствует оператор. Он получится, если в выражение (7) вместо вектора импульса подставить оператор $hat{p}$, равный:
То есть имеем:
Используя выражение (9), запишем:
Получаем, применяя (10):
Применим тождество:
Получаем:
где вектор $overrightarrow{j}$ равен выражению:
«Плотность вероятности и плотность потока вероятности» 👇
По теореме Гаусса имеем:
Из выражения (15) видно, что вектор $overrightarrow{j}$ может быть назван вектором плотности потока вероятности (плотность потока). Интеграл от данного вектора по поверхности $S$ – вероятность того, что частица за единицу времени пересечет выделенную поверхность. Вектор плотности потока вероятности и плотность вероятности удовлетворяют уравнению:
Уравнение (16) можно назвать аналогом уравнения непрерывности в классической физике.
Пример 1
Задание: Собственная волновая функция частицы, которая находится в бесконечно глубоком одномерном потенциальном ящике, равна: $Psileft(xright)=sqrt{frac{2}{l}}{sin left(frac{pi nx}{l}right) }left(n=1,2,3,dots right),$ где $l$ — длина ящика, $x$ — координата ($0
Решение:
Вероятность ($dP$) нахождения частицы в интервале $dx$ определим, используя плотность вероятности ${left|Psiright|}^2$ и выражение (для одномерного случая):
[dP={left|Psiright|}^2dxleft(1.1right).]
Следовательно, сама вероятность будет найдена как:
[P=intlimits^{frac{l}{3}}_0{{left|Psiright|}^2dxleft(1.2right)}.]
Если частица находится в основном состоянии, то для нее $n=1$. Используем волновую функцию, заданную в условиях, подставим ее в интеграл (1.2), получим:
[P=intlimits^{frac{l}{3}}_0{{left(sqrt{frac{2}{l}}{sin left(frac{pi x}{l}right) }right)}^2dx=frac{2}{l}intlimits^{frac{l}{3}}_0{{left({sin left(frac{pi x}{l}right) }right)}^2dx}left(1.3right).}]
Применим тригонометрическую формулу:
[{sin}^2alpha =frac{1-{cos left(2alpha right) }}{2}left(1.4right).]
Вычислим интеграл (1.3), получаем:
[P=frac{1}{l}left[intlimits^{frac{l}{3}}_0{dx}-intlimits^{frac{l}{3}}_0{{rm cos}Psi(frac{2pi x}{l})dx}right]=frac{1}{l}left[frac{l}{3}-frac{l}{2pi }{rm sin}Psi(frac{2pi x}{l})right]=frac{1}{3}-frac{sqrt{3}}{4pi }approx 0,195.]
Ответ: $P=0,195.$
Пример 2
Задание: Частица находится в сферически симметричном потенциальном поле. Волновая функция некоторой частицы имеет вид: $Psileft(rright)=frac{1}{sqrt{2pi a}}frac{e^{-frac{r}{a}}}{r}$, где $r$ — расстояние от частицы до силового центра, $a=const$. Каково среднее расстояние ($leftlangle rrightrangle $) от частицы до силового центра.
Решение:
Используем формулу, для вычисления среднего значения величины, через плотность вероятности:
[leftlangle rrightrangle =int{{left|Psileft(rright)right|}^2rdVleft(2.1right),}]
где $dV=4pi r^2dr- $сферический слой с радиусами $r$ и $r+dr$.
В интеграл (2.1) подставим ${left|Psileft(rright)right|}^2$, возьмем интеграл по частям, имеем:
[leftlangle rrightrangle =frac{1}{2pi a}intlimits^{infty }_0{frac{e^{-2frac{r}{a}}}{r^2}r4pi r^2dr=frac{2}{a}intlimits^{infty }_0{e^{-2frac{r}{a}}cdot rdr=frac{a}{2}}(2.2)}.]
Ответ: $leftlangle rrightrangle =frac{a}{2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Понятие вероятности появилось в физике в связи с развитием кинетической теории газов. Когда было установлено, что газ состоит из большого числа движущихся частиц, то возник вопрос о том, с какими скоростями движутся частицы газа — его молекулы.
Английский физик Дж. Максвелл построил первую теорию идеального газа, в которой состояние газа задавалось не положением и скоростью каждой частицы, а функцией распределения — вероятностью найти молекулу с заданной скоростью в заданном месте сосуда. Для того чтобы упростить изложение, предположим, что сосуд разбит на маленькие кубические ячейки с ребром, например, в 1 мм и что нас интересуют не точные координаты молекулы, а лишь то, в какой ячейке она находится. Скорости мы тоже будем задавать не точно, а считая, например, все скорости молекулы, двигающейся здесь вдоль оси ОХ, отличающиеся не более чем на 1 мм/с, одинаковыми. Тогда и скорости представляется возможным задавать ячейками, на которые можно разбить трехмерную диаграмму; по осям ее отложены компоненты скоростей vx, v3y, vz, а точка изображает скорость частицы. Если на молекулы газа не действуют никакие силы, например сила тяжести или электрическое поле, то молекула будет одинаково часто бывать в любом месте сосуда. Мы говорим, что вероятность найти молекулу в любой ячейке одна и та же. Обозначим эту вероятность через wi. Очевидно, что сумма wi, взятая по всем ячейкам, равна 1, так как вероятность найти молекулу в какой-либо ячейке равна 1. Если в сосуде находится N молекул, то в одной ячейке будет находиться в среднем wiN молекул. wi не зависит от номера ячейки; i — плотность газа, постоянная вдоль сосуда.
Совсем иначе выглядит вероятность найти молекулу с заданной скоростью или вероятность найти точку в заданной ячейке на диаграмме скоростей.
Так как энергия газа — Е Джоулей — определена, то, грубо говоря, на каждую молекулу приходится примерно E/N Джоулей, и в газе должно быть мало молекул, энергия которых сильно отличается от этой величины. Клетки на диаграмме скоростей не равноправны, и распределение по скоростям не равновероятно. Такое распределение вероятностей и нашел Максвелл.
Из теории Максвелла следовало, что большая часть молекул газа имеет скорость
v* = (m/(2πkT))1/2 где k — постоянная Больцмана, Т — абсолютная температура, m — масса молекул. Это значение называют наиболее вероятной скоростью.
Понятие вероятности оказалось очень плодотворным. С ее помощью можно рассчитывать различные процессы, в которых участвуют много частиц и в которых роль отдельных частиц становится незаметной. Это такие процессы, как теплопроводность, перемешивание — диффузия, химические реакции и многие другие. Их изучает статистическая физика.
До создания квантовой механики считалось, что появление вероятностей связано обычно с большим числом частиц, координаты и скорости которых практически нельзя измерить.
Оказалось, однако, что даже для одной определенной частицы нельзя точно измерить координату и импульс одновременно и что результат опыта можно предсказать только в вероятностной форме.
Так как нет возможности точно измерить траекторию частицы, значит, нельзя и дать точный ответ на вопрос о том, на какой угол отклонится летящий протон в поле атомного ядра. Можно лишь указать вероятность его отклонения на тот или иной угол. Нельзя сказать также, когда распадается определенный радиоактивный атом, можно лишь указать вероятность того, что он распадается через t секунд. Известно, что число атомов уменьшается по закону Nt = N0e-λt, если при t=0 было N0 атомов. Постоянная λ в этой формуле называется постоянной распада (см. Радиоактивность) . Таким образом, хотя и нельзя установить, какие именно атомы распадутся, утверждение о законе распада большого числа атомов оказывается вполне определенным.
Вероятности появляются еще в одном разделе физики — в теории измерений. Никакое измерение не дает абсолютно точного значения измеряемой величины. Точное значение отличается от измеренного, и теория может лишь оценить вероятность того или иного отклонения. Оценка вероятности ошибки из анализа совокупности повторных измерений — важная задача экспериментальной физики.
В таблицах пишут, например, что скорость света равна 2,997924580 (1,2)•108 м/с; величина в скобках называется стандартным отклонением.
В данном случае из теории вероятности следует, что истинная скорость света не может отличаться от написанной более чем на 1,2 единицы в последнем знаке с вероятностью 68,3%.
Дело в том, что в любом опыте существует большое количество неучтенных факторов. В случае скорости света такими факторами могут быть непостоянство температуры, неточность в измерении длины волны и т. д., но они могут сказываться лишь в восьмом знаке после запятой. Степень достоверности этого утверждения и оценивается вероятностью.
Теория вероятности очень важна при вычислении достоверных значений основных физических величин.

