Как найти вероятность в паскале

Конспект урока по информатике в 11 классе

Тема: Задачи на вероятность: поможет
программа.

Любакова Мария Васильевна, учитель математики
и информатики МБОУ «Средняя общеобразовательна школа №34»

Тип урока: комплексного применения знаний, умений и навыков;

Цели:

Образовательные

1.             
Продолжить формирование
представлений о компьютерном моделировании и навыков создания компьютерной
модели.

2.             
Повторить и углубить
понятия комбинаторики и вероятности; рассмотреть статистическое определение
вероятности.

3.             
Закрепить навыки по
составлению программ.

Развивающие:

1.             
Развивать способности
учащихся к самостоятельной и исследовательской деятельности

2.             
Обучить способам
представления объектов окружающей действительности с помощью информационных
объектов;

Воспитательные:

1.             
Воспитание целостного
представления о естественно-математических дисциплинах, установление
межпредметных связей;

2.             
Развитие навыков обобщения
и анализа.

Оборудование: презентация PowerPoint, система
программирования PascalABC.

Ход урока.

1.
Организационный момент. Постановка цели урока.

Теория
вероятностей давно тесно связана с повседневной жизнью человека и стала в
настоящее время неотъемлемой частью школьного курса и ЕГЭ по математики. Сегодня
на уроке мы узнаем, как программирование может помочь нам в решении
математических задач, а именно задач по теме «Вероятность», которые входят в
программу государственного экзамена по математике. Составив программу для
решения сложной вероятностной задачи, мы можем убедиться в правильности её
решения.

2.
Подготовительный этап.

Вопрос
учащимя: Что такое вероятность случайного события?

Вероятность
случайного события равна отношению числа благоприятных исходов и числу
возможных исходов.

Каким образом найти
число исходов? В этом нам может помочь или перебор вариантов или формулы
комбинаторики.

Какие виды
комбинаций вам известны? – Перестановки, размещения и сочетания.

Записываем на доске
и в тетради формулы для нахождения перестановок, размещений и сочетаний: Р _n =n!, .

3. Решение
задач.

Рассмотрим решение
одной старой задачи.

Задача 1. Одна из классических знаменитых задач теории
вероятностей – задача кавалера Де Мере.

«Если бросить
одновременно три игральных кости, то какая сумма очков будет выпадать чаще—11
или 12?»

Сумма 11 может
получиться следующими шестью различными способами: 1+4+6, 1+5+5, 2+3+6, 2+4+5,
3+3+5. 3+4+4.

Также шестью
различными способами образуется сумма 12: 1+5+6, 2+4+6, 2+5+5,

3+3+6, 3+4+5, 4+4+4.
Это обстоятельство наводит на мысль, будто обе суммы

должны появляться
одинаково часто. Однако это неверно. Уже на практике было

замечено, что сумма
11 появляется чаще суммы 12. Дело а том,  что

вышеуказанные по три
числа сами по себе неодинаково часто выпадают. Так,

если каждую из трех
костей окрасить по-разному, скажем в белый, красный и

зелёный  цвет, то становится
ясным, что сочетание, а котором имеются три

различных слагаемых,
например (1+4+6), может получаться шестью различными

способами:

Двое бросают
игральные кости. Кто чаще выигрывает: у кого выпадет 6 очков в сумме или 7?

Найдём вероятность
каждого события по определению вероятности. С помощью перебора установим,
сколько вариантов благоприятствует событию «В сумме 6 очков»: (5 и 1), (4 и 2),
(3 и 3), (2 и 4), (1 и 5). Таких вариантов 5. Тогда вероятность этого события
равна . Для события «В сумме 7 очков»
благоприятными будут 6 вариантов: (6 и 1), (5 и 2), (4 и 3), (3 и 4), (2 и 5),
(1 и 6), вероятность равна .

Чтобы
удостовериться в этом на практике воспользуемся частотным определением вероятности.
За вероятность случайного события можно принять его относительную частоту,
полученную в серии экспериментов. Чем больше число проведённых экспериментов,
тем точнее можно оценить вероятность события по его частоте. Но мы не будем
бросать кости, а используем моделирование случайного эксперимента. Инструментом
такого моделирования будет служить генератор случайных чисел в программе на
языке Паскаль. Бросание монеты будет аналогично выбору компьютером случайного
числа в диапазоне 1..6. Это можно сделать с помощью команды random(6)+1.

Составим программу
(текст программы на слайде и распечатан на каждого ученика:

program costy;

 var k,n,s,i,m1,m2:integer;

begin

 randomize;

 writeln(‘Введите количество
испытаний’);

 readln(n);

 for i:=1 to n do

 begin

  k:=random(6)+1; {бросание первой
кости}

  s:=random(6)+1; {бросание второй
кости}

  if k+s=7 then m1:=m1+1;

  if k+s=6 then m2:=m2+1;

 end;

 writeln(‘частота выпадения в сумме 6 равна ‘, m1/n:2:2);

 writeln(‘частота выпадения в сумме
7 равна ‘, m2/n:2:2);

end.

Проведем компьютерный эксперимент для
различных значений n и результаты занесем в таблицу (распечатана
на каждого ученика). Сравните результаты, полученные программой с точным
значением вероятности и сделайте вывод: на сколько точно можно доверять данным,
полученным в результате компиютерного эксперимента.

Задача 2 была
задана учащимся в качестве домашнего задания.

В кармане у Пети было 2 монеты по 5 рублей и 4
монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой
карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных
карманах.

Проверим ваше решение (к доске выходит ученик
и объясняет решение задачи). Например так: (возможны также другие способы
решения)

Чтобы пятирублевые монеты лежали в разных
карманах, надо переложить только одну из них. Количество способов это сделать
равно числу сочетаний из 2 по 1: C₂¹.

Поскольку всего Петя переложил 3 монеты,
придется переложить еще 2 монеты по 10 рублей. Таких монет у Пети 4, поэтому
количество способов равно числу сочетаний из 4 по 2: C₄².

Осталось найти, сколько всего вариантов
переложить 3 монеты из 6 имеющихся. Это количество равно числу сочетаний из 6
по 3: C₆³.

Находим вероятность: .

Подтверди правильность решения, рассчитав
статистическую вероятность. Стоимость монет будем хранить в массиве а, а
выбор монеты будем задаваться генерированием случайного числа в диапазоне 1..6
(т.е. выбирать будем номер элемента массива).

program petia;

 var a:array[1..10] of
integer;

 k,n,s,z,i,m:integer;

begin

 a[1]:=5; a[2]:=5;a[3]:=10;a[4]:=10;a[5]:=10;a[6]:=10;

 randomize;

 writeln(‘Введите количество испытаний‘);readln(n);

 for i:=1 to n do

 begin

  repeat

k:=random(6)+1; {выбор первой монеты}

s:=random(6)+1; {выбор второй монеты}

z:=random(6)+1; {выбор третьей монеты}

  until not((k=s)or(s=z)or(k=z)); {каждую монету можно
выбрать только один раз, поэтому выбирать числа, до тех пор, пока все три не
будут различны}

  if a[k]*a[s]*a[z]=500 then m:=m+1;{проверка условия, что
выбраны две десятки и одна пятёрка}

 end;

 writeln(‘вероятность равна ‘,m/n)

end.

Снова проведём серию экспериментов для разного
количества испытаний. (Учащиеся вводят и тестируют программу, занося результаты
в таблицу).

Сделайте вывод. Как видим, при достаточно
большом значении n cтатистическая вероятность достаточно близка по
значению к теоретической.

4. Подведение итогов.

Вопрос учащимся: в чем же преимущества
компьютерного эксперимента?

Как видим, компьютер даёт возможность почти
мгновенно провести 100000экспериментов, что невозможно было бы произвести
вручную. Ещё одно достоинство – мы можем моделировать и более общую ситуацию с
любым количеством монет разного достоинства, любым количеством костей и
суммами, выпадающими на них.

Это и будет ваше домашнее задание: найти с
помощью компьютерного эксперимента вероятность выпадения в сумме S
очков при бросании n монет. При этом значение суммы должно быть
реальным (в зависимости от n), предусмотреть защиту от неправильного ввода
данных.

Время на прочтение
10 мин

Количество просмотров 14K

Введение

На одном из собеседований по приёму на работу попросили за 30 минут написать программу, которая бы решал следующую задачу:

Есть n стандартных игральных костей (6-ти гранных кубиков) со стандартным обозначением всех граней от 1 до 6. Бросаем все n кубики разом. Нужно найти вероятность выпадения числа k, а именно суммы всех значений, выпавших на этих кубиках.

Решение

Не буду томить ожиданием и сразу выложу код алгоритма, который получился и впоследствии был немного обработан напильником.

Python

# -*- coding: utf-8 -*-
# import numpy  # <можно_использовать_numpy>

def main():
    c_int_side_dice: int = 6  # сколько граней у кубика
    c_int_dice_number: int = 6  # кол-во кубиков
    c_int_number_to_find: int = 18  # число, вероятность выпадения которого хотим найти
    probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
    print(probability)


# собственно поиск вероятности определённого значения
def dice_probability(int_dice_number: int, int_number_to_find: int, c_int_side_dice: int) -> float:
    list_values, list_interm_probability = list_values_and_interm_probabilities(int_dice_number, c_int_side_dice)
    if int_number_to_find < list_values[0] or int_number_to_find > list_values[-1]:
        # задаваемое число выходит за рамки реально возможного диапазона значений
        result_out: float = 0.0
    else:
        for i in range(len(list_values)):
            if list_values[i] == int_number_to_find:
                result_out: float = list_interm_probability[i] / (c_int_side_dice ** int_dice_number)
                break
    return result_out


# возвращает списки/массивы: значения (сумма выпавших всех значений кубиков), сколько раз встречается значение
def list_values_and_interm_probabilities(int_dice_number: int, c_int_side_dice: int) -> tuple[list[int], list[int]]:  # [кол-во кубиков], [сколько граней у кубика]
    list_values = [i for i in range(int_dice_number, c_int_side_dice * int_dice_number + 1)]  # <длина_списков_совпадает!>
    list_interm_probability = [1] * c_int_side_dice  # [1, 1, 1, 1, 1, 1]
    for i in range(int_dice_number - 1):
        list_interm_probability = multiply_by_ones(list_interm_probability, c_int_side_dice) # <длина_списков_совпадает!>
        # list_interm_probability = numpy.convolve(list_interm_probability, [1] * c_int_side_dice)  # <можно_использовать_numpy> и не использовать multiply_by_ones()

    return list_values, list_interm_probability


# "умножение" на единицы
def multiply_by_ones(list_in: list[int], c_int_side_dice: int) -> list[int]:  # [1, 1, 1, 1, 1, 1], 6
    list_dummy: list[list[int]] = []
    for i in range(c_int_side_dice):
        list_dummy.append([0] * i)  # [], [0], [0, 0], [0, 0, 0] ...

    list_for_sum: list[list[int]] = []
    for i in range(c_int_side_dice):
        list_for_sum.append(list_dummy[i] + list_in + list_dummy[c_int_side_dice - i - 1])

    """
    [list_in, 0, 0, 0, 0, 0]
    [0, list_in, 0, 0, 0, 0]
    [0, 0, list_in, 0, 0, 0]
    [0, 0, 0, list_in, 0, 0]
    [0, 0, 0, 0, list_in, 0]
    [0, 0, 0, 0, 0, list_in]
    """

    list_out: list[int] = []
    for i in range(len(list_for_sum[0])):
        sum_out: int = 0
        for j in range(c_int_side_dice):
            sum_out += list_for_sum[j][i]
        list_out.append(sum_out)

    """
    [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
    """
    return list_out

if __name__ == "__main__":
    main()

JavaScript

function main(){
    const c_int_side_dice = 6;  // сколько граней у кубика
    const c_int_dice_number = 6; // кол-во кубиков
    const c_int_number_to_find = 18; // число, вероятность выпадения которого хотим найти
    let probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice);
    console.log(probability);
}

// собственно поиск вероятности определённого значения
function dice_probability(int_dice_number, int_number_to_find, c_int_side_dice){
    let lists_val_and_prob = list_values_and_interm_probabilities(int_dice_number, c_int_side_dice);
    let result_out;
    if (int_number_to_find < lists_val_and_prob[0][0] || int_number_to_find > lists_val_and_prob[0][lists_val_and_prob[0].length - 1]){
        // задаваемое число выходит за рамки реально возможного диапазона значений
        result_out = 0.0;
    } else {
        for (let i = 0; i < lists_val_and_prob[0].length; i++){
            if (lists_val_and_prob[0][i] == int_number_to_find){
                result_out = lists_val_and_prob[1][i] / Math.pow(c_int_side_dice, int_dice_number);
                break;
            }
        }
    }
    return result_out;
}

// возвращает списки/массивы: значения (сумма выпавших всех значений кубиков), сколько раз встречается значение
function list_values_and_interm_probabilities(int_dice_number, c_int_side_dice){  // [кол-во кубиков], [сколько граней у кубика]
    let list_values = new Array();
    let i = 0;
    for (let j = int_dice_number; j <= c_int_side_dice * int_dice_number; j++){
        list_values[i] = j;
        i++;
    }
    console.log(list_values);
    let list_interm_probability = Array(c_int_side_dice).fill(1);  // [1, 1, 1, 1, 1, 1]
    for (let i = 0; i < int_dice_number - 1; i++){
        list_interm_probability = multiply_by_ones(list_interm_probability, c_int_side_dice);
    }
    console.log(list_interm_probability);
    return [list_values, list_interm_probability];
}

// "умножение" на единицы
function multiply_by_ones(list_in, c_int_side_dice){
    let list_dummy = new Array(c_int_side_dice);
    for (let j = 0; j < c_int_side_dice; j++){
        list_dummy[j] = Array(j).fill(0);
    }
    let list_for_sum = new Array(c_int_side_dice);
    for (let j = 0; j < c_int_side_dice; j++){
        list_for_sum[j] = list_dummy[j].concat(list_in, list_dummy[c_int_side_dice - j - 1]);
    }
    // [list_in, 0, 0, 0, 0, 0]
    // [0, list_in, 0, 0, 0, 0]
    // [0, 0, list_in, 0, 0, 0]
    // [0, 0, 0, list_in, 0, 0]
    // [0, 0, 0, 0, list_in, 0]
    // [0, 0, 0, 0, 0, list_in]
    
    let list_out = new Array();
    for (let i = 0; i < list_for_sum[0].length; i++){
        let sum_out = 0;
        for (let j = 0; j < c_int_side_dice; j++){
            sum_out += list_for_sum[j][i];
        }
        list_out[i] = sum_out;
    }
    // [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
    return list_out;
}

main();

VBScript

Option Explicit

Sub main()
    Const c_int_side_dice = 6  'сколько граней у кубика
    Const c_int_dice_number = 3  'кол-во кубиков
    Const c_int_number_to_find = 10  'число, вероятность выпадения которого хотим найти
    Dim probability
    probability = dice_probability(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
    MsgBox probability
End Sub


'собственно поиск вероятности определённого значения
Function dice_probability(int_dice_number, int_number_to_find, c_int_side_dice)
    Dim list_values()
    Dim list_interm_probability()
    list_values_and_interm_probabilities int_dice_number, c_int_side_dice, list_values, list_interm_probability
    Dim result_out
    Dim i
    If int_number_to_find < list_values(0) Or int_number_to_find > list_values(UBound(list_values)) Then
        'задаваемое число выходит за рамки реально возможного диапазона значений
        result_out = 0.0
    Else
        For i = 0 To UBound(list_values)
            If list_values(i) = int_number_to_find Then
                result_out = list_interm_probability(i) / (c_int_side_dice ^ int_dice_number)
            End If
        Next
    End If
    dice_probability = result_out
End Function

'возвращает списки/массивы: значения (сумма выпавших всех значений кубиков), сколько раз встречается значение
Sub list_values_and_interm_probabilities(int_dice_number, c_int_side_dice, list_values, list_interm_probability)  '[кол-во кубиков], [сколько граней у кубика]
    ReDim list_values(int_dice_number * (c_int_side_dice - 1))
    Dim i, j
    i = 0
    For j = int_dice_number To c_int_side_dice * int_dice_number
        list_values(i) = j
        i = i + 1
    Next
    ReDim list_interm_probability(c_int_side_dice - 1)
    For j = 0 To c_int_side_dice - 1
        list_interm_probability(j) = 1
    Next
    For j = 0 To int_dice_number - 2
        multiply_by_ones list_interm_probability, c_int_side_dice
    Next
End Sub

'"умножение" на единицы
Sub multiply_by_ones(list_in, c_int_side_dice)
    Dim list_in_length
    list_in_length = UBound(list_in)
    Dim list_for_sum()
    ReDim list_for_sum(c_int_side_dice - 1, list_in_length + c_int_side_dice - 1)
    Dim i, j, k, n
    For i = 0 To c_int_side_dice - 1
        j = 0
        For n = 0 To c_int_side_dice - 1
            If i = n Then
                For k = 0 To list_in_length
                    list_for_sum(i, j) = list_in(k)
                    j = j + 1
                Next
            Else
                list_for_sum(i, j) = 0
                j = j + 1
            End If
        Next
    Next
    ' [list_in, 0, 0, 0, 0, 0]
    ' [0, list_in, 0, 0, 0, 0]
    ' [0, 0, list_in, 0, 0, 0]
    ' [0, 0, 0, list_in, 0, 0]
    ' [0, 0, 0, 0, list_in, 0]
    ' [0, 0, 0, 0, 0, list_in]
    ' ArrOut_2 list_for_sum
    Erase list_in
    ReDim list_in(list_in_length + c_int_side_dice - 1)
    Dim sum_out
    For j = 0 To list_in_length + c_int_side_dice - 1
        sum_out = 0
        For i = 0 To c_int_side_dice - 1
            sum_out = sum_out + list_for_sum(i, j)
        Next
        list_in(j) = sum_out
    Next
    ' [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
    ' ArrOut_1 list_in
End Sub

'==================================================
'<Additional_MsgBox_For_Arrays>
Sub ArrOut_1(arr_in)
    Dim str_out
    Dim i
    For i = 0 To UBound(arr_in)
        If i = 0 Then
            str_out = arr_in(i)
        Else
            str_out = str_out & " " & arr_in(i)
        End If
    Next
    MsgBox str_out
End Sub

Sub ArrOut_2(arr_in)
    Dim str_out
    Dim i, j
    For i = 0 To UBound(arr_in, 1)
        For j = 0 To UBound(arr_in, 2)
            If i = 0 And j = 0 Then
                str_out = arr_in(i, j)
            ElseIf j = 0 Then
                str_out = str_out & vbNewLine & arr_in(i, j)
            Else
                str_out = str_out & " " & arr_in(i, j)
            End If
        Next
    Next
    MsgBox str_out
End Sub
'</Additional_MsgBox_For_Arrays>
'==================================================

main

Пояснение

Понятно, что копание в чужом коде — дело не благодарное, опишу работу алгоритма для одного конкретного примера.

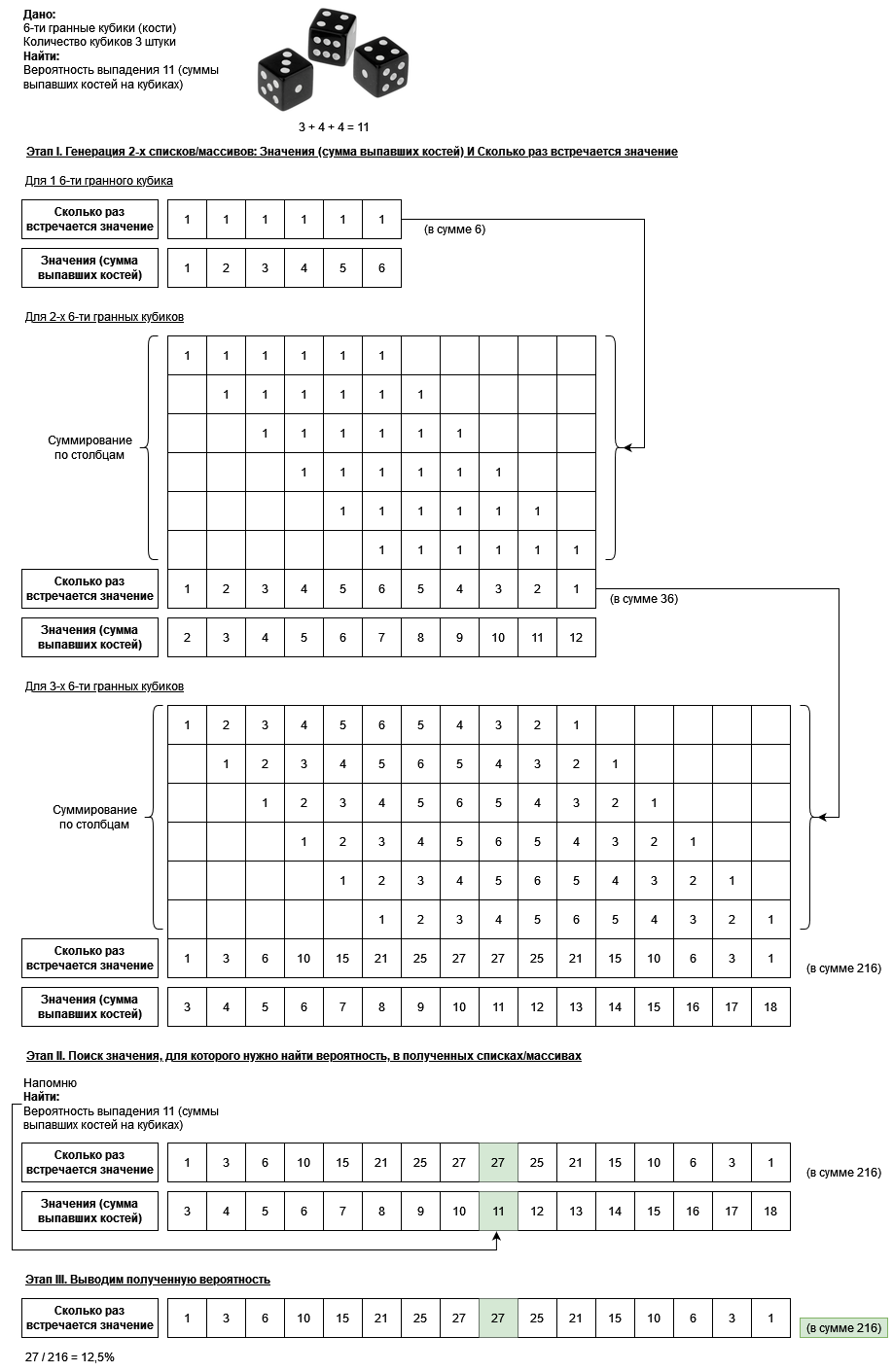
Картинку можно описать словами как: нахождение делимого вероятности выпадения при помощи многократной свёртки последовательности [1 1 1 1 1 1] на саму себя. Количество операций свёртки совпадает с количеством кубиков минус 1.

Смею предположить, что дочитав до этого момента у многих читателей уже зародятся скептические настроения, однако в свою очередь предложу поверить самостоятельно и в помощь приложу SQL запрос, который считает «в лоб», т.е. генерирует все возможные комбинации выпадения для 3-х кубиков, а потом пересчитывает все выпавшие суммы. В результате отработки скрипта мы получим 2 столбца из самого конца пункта “Этап I. Генерация 2-х списков/массивов: Значения (сумма выпавших костей) И Сколько раз встречается значение”.

SQL запрос – генератор решения “в лоб”

-- заводим значения сторон кубика
WITH step_01_insert (dice) AS (
    SELECT 1 AS dice UNION ALL
    SELECT 2 AS dice UNION ALL
    SELECT 3 AS dice UNION ALL
    SELECT 4 AS dice UNION ALL
    SELECT 5 AS dice UNION ALL
    SELECT 6 AS dice
)
-- генерируем все возможные ситуации для 3-х кубиков
, step_02_spawn (dice_1, dice_2, dice_3, dice_sum) AS (
    SELECT T1.dice AS dice_1
    , T2.dice AS dice_2
    , T3.dice AS dice_3
	, T1.dice + T2.dice + T3.dice AS dice_sum -- Значения (сумма выпавших костей)
    FROM step_01_insert AS T1
    , step_01_insert AS T2
    , step_01_insert AS T3
)
-- считаем в лоб, сколько раз встречается значение
SELECT dice_sum  -- Значения (сумма выпавших костей)
, COUNT(1) AS num  -- Сколько раз встречается значение
FROM step_02_spawn
GROUP BY dice_sum
ORDER BY dice_sum;

Конечно это не достаточно для полноценного доказательства, о котором я расскажу чуть позже, но хоть накал скепсиса, надеюсь, мне удалось сбавить.

Отмечу, что я не претендую на какую-то оригинальность, т.к. подобный алгоритм упоминается в данных статьях: “How to Calculate Multiple Dice Probabilities” Method 2 Recursion, “Как посчитать вероятность определенной комбинации при игре в кости” Метод 2 Рекурсия (перевод).

Пусть вас не смущает хитрое смещение суммирования в формуле Excel – суть от этого никак не меняется. Явно именно раздел «Метод 2» затачивался под Excel реализацию, но запрограммировать данный алгоритм в лоб без изменений именно на каком-либо языке программирования — задача не тривиальная.

Но всё-таки, почему этот алгоритм работает?

Для начала вспомним треугольник Паскаля:

Из всего множества его замечательных свойств я бы хотел заострить внимание на следующем: до строки:

цифры в треугольнике Паскаля повторяют степени числа 11 в степени 1<=k<=4 (натуральное). Но это утверждение верно для десятичной системы счисления, однако, если считать степень числа 11 в шестнадцатеричной системе счисления, то можно продлить совпадения до 1<=k<=5.

Можно задаться вопросом: а на каком калькуляторе можно 11 возводить в степень 5 в шестнадцатеричной системе счисления? Ответ: воспользуемся свойством

Иначе говоря идём итерационно:
121=11 * 11
1331=121 * 11
14641=1331 * 11
15AA51=14641 * 11

Давайте чуть здесь остановимся и вспомним школьную программу, а именно умножение в столбик, с одной лишь оговоркой, что перенос числа из одного разряда в другой (при переполнении разряда) буду делать отдельной операцией, а так же визуально для каждого разряда выделю отдельный столбец.
Пример 1.
14641 * 11 в десятеричной системе счисления.

1. Заполняем условия.

2. Записываем результаты умножения каждой единицы разряда.

3. Суммируем.

4. Переводим из переполнившихся разрядов в разряды выше.

Проделаем ту же операцию в шестнадцатеричной системе счисления (Шестнадцатеричная система счисления)
Пример 2.

1. Заполняем условия.

2. Записываем результаты умножения каждой единицы разряда.

3. Суммируем.

4. Записываем полученные числа правильно в шестнадцатеричной системе счисления.

И для закрепления ещё один.
Пример 3.
15AA51 * 11 в шестнадцатеричной системе счисления.

1. Заполняем условия в шестнадцатеричной системе счисления.

2. Переводим запись из шестнадцатеричной в десятичную систему счисления для улучшения восприятия (благо мы можем себе это позволить, т.к. визуально отделяем каждый разряд друг от друга).

3. Записываем результаты умножения каждой единицы разряда.

4. Суммируем.

5. Переводим поэтапно из переполнившихся разрядов в разряды выше.

6. Записываем полученные числа правильно в шестнадцатеричной системе счисления.

Во всех приведённых примерах я бы акцентировал внимание на пунктах «Суммируем» (Пример 1 – п3., Пример 2 – п3., Пример 3 – п4.), которые «цитируют» одну из строк треугольника Паскаля. Если продолжить мысль, то манипуляции с разрядами мешают нормальному воспроизведению всего треугольника. А давайте от них избавимся? Т.е. условно говоря будем считать (да простят меня математики) в «условно бесконечной системе счисления» (вероятно есть и более адекватный термин, но увы, беглый запрос по интернету ничего не дал, что больше доказывает мою лень, а не на отсутствие информации как таковой), т.е. когда перехода из одного разряда в другой при операции сложения не происходит. И это работает:

Тут я не претендую опять же на оригинальность, данный метод есть и им пользуются: как вывести треугольник Паскаля на Python? (см. «Простейшая реализация»)

Аналогия с умножением в столбик двух чисел в очень большой системой счисления, в принципе, имеет право на существование и даёт представление об операции, однако стоит грамотнее назвать её свёрткой последовательности. В данном посте приводится как раз выведение “строк” треугольника Паскаля сверткой: дискретная свёртка или полиномиальное умножение

Вернёмся к кубикам.

Посчитаем в лоб сколько раз встречается сумма костей для всех возможных случаев.

1 кубик (тут всё просто).

2 кубика (идём по классике жанра).

Тут конечно можно посчитать вручную, т.е. просуммировать все единицы в правой таблице, соответствующие полученным значениям в левой таблице (лучше визуализировать):

Однако, заметим смещение “Полученных значений” в левой таблице и преобразуем обе таблицы следующим образом:

После этого в правой таблице нам останется лишь просуммировать строки. Опять же тут немного остановимся на правой табличке, и заметим, что она напоминает уже упомянутое выше умножение столбик в десятичной системе счисления (или свёртку последовательностей).

В итоге получим:

Проделаем аналогичные шаги для 3-х кубиков:

Смещаем:

Акцентируем внимание, что опять же правая таблица напоминает умножение в столбик в «условно бесконечной системе счисления» (или свёртку последовательностей):

Выводим результат:

Описанные операции итерационно можно продолжать сколь угодно долго.

Данный алгоритм походит для любого числа одинаковых игровых кубиков с любым количеством граней, у которых числа на гранях входят в арифметическую последовательность. И его при некотором желании можно даже модифицировать и для решения задач, когда речь идёт не об однотипных кубиках а с разным количеством граней (правда я ума не приложу кому это может понадобиться).

Итого, выводы

1. Задачи на поиск вероятности выпадения числа k у n игральных кубиков попадаются на собеседованиях.

2. В данной статье рассмотрен довольно элегантный алгоритм по решению подобных задач, указанных выше. В принципе можно решать подобные задачи просто на листе бумаге.

О чём стоит упомянуть
Представленный алгоритм не является самым оптимальным. Например для 1000 кубиков (не знаю кому это будет нужно, но вдруг) придётся просчитать для всех элементов последовательности 1000 раз. Но можно ещё поиграться с умножением в столбик в «условно …» и снизить вычислительную сложность алгоритма с O(n^2) (“Оценка сложности алгоритмов, или Что такое О(log n)”).

Updated: 23.08.2022