Содержание:
- § 1 Основные понятия и формулы теории вероятности
- § 2 Примеры решения задач на вероятность
§ 1 Основные понятия и формулы теории вероятности
На этом занятии мы рассмотрим основные понятия и формулы теории вероятности, позволяющие решать текстовые задачи на вероятность. А также рассмотрим методику решения текстовых задач на вероятность. Окружающий нас мир состоит из различных действий и явлений. Например, ежедневно мы можем видеть солнце на небе в ясную погоду или не видеть его в пасмурный день. Действие ежедневного наблюдения солнца на небе называют испытанием. А результат этого действия, солнечно или пасмурно, называют событием. Таким образом, всякое действие, явление или наблюдение с несколькими различными исходами, реализуемое при данных условиях, называется испытанием. Результат этого действия или наблюдения называется событием.
Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. Например, на уроке математики ученик может успешно решить текстовую задачу, а может и не решить, значит, событие “успешно решить текстовую задачу на уроке математики” является случайным. В том случае, когда событие должно непременно произойти, его называют достоверным. Например, событие “в сентябре дети России идут в школу учиться” является достоверным событием, так как выполняется при любых условиях. В том случае, когда событие заведомо не может произойти, его называют невозможным. Например, событие “в полночь над Москвой светит солнце” никогда не может произойти, значит, оно является невозможным событием.
События принято обозначать заглавными буквами латинского алфавита A, B, C, D… Каждое событие имеет числовую характеристику, которую называют вероятностью. Итак, вероятностью события А называется число, которое показывает объективную возможность его свершения. Вероятность обозначают латинской заглавной буквой Р или прописной р и вычисляют по формуле Р от А равно m делённое на n, где m – число благоприятных исходов, n –
Все достоверные события имеют вероятность Р(А) = 1, так как у достоверных событий число благоприятных исходов m и число всевозможных исходов n равны между собой.
Все невозможные события имеют вероятность Р(А) = 0, так как у невозможных событий изменяется в пределах от 0 до 1. События, у которых вероятности всех возможных исходов равны, называются равновозможными. Например, при подбрасывании монеты вероятности выпадения решки или орла равны, значит, исходы выпадения решки или орла будут равновозможными.
События называются несовместными, если каждый раз возможно появление только одного из них. Например, не может быть небо одновременно безоблачным и в дождливых тучах, значит, эти два события несовместны. События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании. Например, события “яблоко красное” и “яблоко сладкое” могут происходить одновременно, значит, эти события будут совместными.
События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны. Например, при подбрасывании монеты события “выпал орёл” и “выпала решка” являются противоположными. Противоположные события обозначаются одноименной буквой события с чертой над ней.
§ 2 Примеры решения задач на вероятность
Рассмотрим текстовые задачи на вычисление вероятности.
Задача 1.
На 1200 электрических лампочек в среднем приходится 9 бракованных лампочек. Какова вероятность, что наугад взятая лампочка окажется исправной?
Решение:
Пусть событие А – взятая лампочка исправна. Тогда вероятность изъятия исправной лампочки будет именно количество исправных лампочек, равное 1200 минус 9. Получаем m равно 1191. n – количество всех возможных исходов, а значит количество всех лампочек в партии, то есть n равно 1200. Подставив числовые значения переменных в формулу, имеем – вероятность наугад
вопрос задачи.
Ответ: 0,9925.
Задача 2.
Юля дважды бросила игральный кубик. В сумме у неё выпало 8 очков. Найти вероятность того, что при первом броске выпало 5 очков.
Решение:
Пусть событие А – при первом броске выпало 5 очков. Для вычисления вероятности вновь 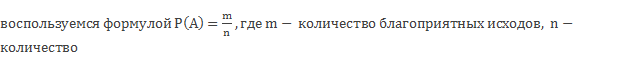
первом броске выпадет 5 очков, равна 0,2. Ответ: 0,2.
Таким образом, на этом занятии мы рассмотрели основные понятия и формулы вычисления вероятности, а также рассмотрели методику решения текстовых задач на вероятность.
Список использованной литературы:
- Г.Н. Тимофеев Математика для поступающих в вузы. Учебное пособие. Текстовые задачи.– Йошкар-Ола: Мар. гос. ун-т, 2006г.
- В. Булынин Применение графических методов при решении текстовых задач. – Еженедельная учебно-методическая газета «Математика», №14, 2005г.
- Н.И. Попов, А.Н. Марасанов Задачи на составление уравнений. Учебное пособие. Йошкар-Ола: Мар. гос. ун-т, 2003г.
- http://festival.1september.ru/articles/310281/ Н.А. Зарипова Программа элективного курса “Текстовые задачи”.
- http://festival.1september.ru/articles/415044/ Н.А. Зарипова Методика решения задач группы vts. Материалы к проведению элективного курса “Решение текстовых задач”
Видеоуроки по теории вероятности
На этой странице вы найдете каталог видеуроков по теории вероятностей. Переходите в нужный раздел, подписывайтесь на наш канал, чтобы не пропускать новые видео, учитесь с удовольствием.
Страницы с полными плейлистами
- Видеоуроки по комбинаторике
- Видеоуроки по задачам классической вероятности
- Видеоуроки по задачам по схеме Бернулли
Каталог по темам и разделам
Комбинаторика
Вы можете перейти на страницу, где собраны все ролики по теме, или открывать уроки прямо в YouTube по ссылкам ниже
- Что изучает комбинаторика. Знаменитые задачи
- Факториал: формула, свойства, примеры
- Формула числа перестановок и решение задач
- Формула числа сочетаний и решение задач
- Формула размещений и решение задач
- Перестановки с повторениями: примеры задач в Excel и калькулятор
- Размещения с повторениями: примеры задач в Excel и калькулятор
- Сочетания с повторениями: примеры задач в Excel и калькулятор
- Правило суммы и произведения. Примеры решений
- Формула включений и исключений. Примеры решений
- Задача о беспорядках. Примеры решений
Классическая вероятность
Вы можете перейти на страницу, где собраны все ролики о классической вероятности, или открывать уроки прямо в YouTube по ссылкам ниже
- Решение задач про цветные шары
- Решение задач про бракованные детали
- Решение задач про лотерейные билеты
Формула Бернулли
Вы можете перейти на страницу, где собраны все ролики по схеме Бернулли, или открывать уроки прямо в YouTube по ссылкам ниже
- Как решать задачи о шахматных партиях
- Как решать задачи о вероятности рождения мальчиков
- Как решать задачи о попадании в цель (схема Бернулли)
- Как решать задачи о лотерейных билетах (схема Бернулли)
- Как решать задачи на наивероятнейшее число успехов
- Приближенная формула Пуассона: примеры задач и расчеты в Excel
Решение нужно прямо сейчас? Используй решебник!
Более 10000 задач с полными и подробными решениями по теории вероятностей и математической статистике.
Изучаем теорию вероятностей
- Тервер для чайников – онлайн учебник
- Онлайн-калькуляторы для вычисления вероятностей
- Формулы и таблицы по теории вероятности
- Решенные контрольные по теории вероятности
- Как найти вероятность в задачах про подбрасывания монеты?
- Как найти вероятность в задачах про подбрасывание игральных костей?
Представим
себе такую историю…
Саша
и Паша встретились по дороге в школу, и между ними завязался такой разговор.
–
Вероятно, меня сегодня вызовут к доске на уроке математики, – сказал Саша.
–
Вполне вероятно, что и меня тоже сегодня вызовут к доске на уроке математики, –
продолжил Паша.
–
Тебя недавно спрашивали, – возразил Саша, – а меня давно не спрашивали. Значит,
маловероятно, что тебя вызовут к доске сегодня, а вот меня вызовут с большей
вероятностью.
–
Согласен, – произнёс Паша, – но вероятность всё же есть, что меня тоже могут
вызвать к доске.
–
А давай спросим у Мудряша, кого же из нас скорее всего вызовут к доске, –
предложил Саша.
–
Давай – согласился Паша.
–
Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним
устные задания, – предложил Мудряш.
–
Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было
получиться!
–
Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – В вашем разговоре
прозвучали такие слова, как «вероятно», «вполне вероятно», «маловероятно»,
«с большей вероятностью». Все эти слова связаны со словом «вероятность».
Давайте разберёмся, что же такое вероятность.
–
Итак, – продолжил Мудряш, – многое в нашей жизни, несмотря на то, что мы
планируем заранее, зависит от случая. Купив лотерейный билет, мы можем
выиграть, а можем не выиграть. Сегодня на уроке математики учитель может
вызвать вас к доске, а может и не вызвать. Снег может выпасть, а может и не
выпасть, чёрный кот может перебежать дорогу перед вами, а может и передумать.
Всё это события. И каждое из этих событий в одних и тех же условиях могло
произойти, а могло и не произойти.
Запомните! Событие,
которое при данных условиях может наступить, а может и не наступить, называют
случайным.
–
Разве в нашей жизни всегда происходят только случайные события? – спросил Паша.
–
Вообще, событие бывает трёх видов: достоверное, невозможное и случайное,
– продолжил Мудряш. – Событие, которое при данных условиях обязательно
наступит, называют достоверным. Например, вы знаете, что
после понедельника всегда наступает вторник. Это достоверное событие. Событие,
которое при данных условиях никогда не наступит, называют невозможным.
Например, вода на озере замёрзнет при + 20о. Данное событие никогда
не произойдёт при таком условии, значит, это событие невозможное.
А
вы можете привести примеры достоверных и невозможных событий? – спросил у ребят
Мудряш.
–
Достоверными будут такие события: вода на озере замёрзнет при – 20о,
так как вода замерзает при минусовой температуре; дата рождения моего друга –
число меньшее, чем 32, так как в каждом месяце не более 31 дня, – привёл
примеры Паша.
–
А невозможными будут такие события: среди ночи выглянуло солнце, при бросании
игрального кубика выпадет 7 очков, – сказал Саша.
–
Молодцы! – похвалил ребят Мудряш. – Но всё же в жизни всё не так чётко и ясно.
Чаще всего мы сталкиваемся именно со случайными событиями, одни из которых
более вероятны, другие — менее вероятны.
–
А эти случайные события нельзя заранее предугадать? – спросил Паша.
–
Хороший вопрос! – сказал Мудряш. – Очень часто нам важно знать, на сколько или
во сколько раз одно случайное событие вероятнее другого. Существует специальная
наука, которая занимается оценками вероятностей случайных событий. Называется
эта наука теорией вероятностей.
Итак,
вероятность наступления достоверного события можно охарактеризовать как
стопроцентную, а вероятность наступления невозможного события — как нулевую.
Так как 100 % – это величины
(в свою очередь, ),
то договорились о следующем: вероятность достоверного события считается
равной 1, вероятность невозможного события считается равной 0. Тогда вероятность
случайного события может быть любым числом от 0 до 1.
–
Давайте проведём небольшой эксперимент, – предложил Мудряш. – Будем
подбрасывать монету, например рубль. Скажите, в результате этого эксперимента
какие события могут произойти?
–
Монета может упасть решкой вверх, – предположил Саша.
–
Или монета может упасть орлом вверх, – сказал Паша.
–
Правильно! – согласился Мудряш. – Случай «монета встала на ребро» считаем
невероятным и не учитываем. Эксперимент с монетой – это достоверное событие:
монета обязательно упадёт орлом или решкой вверх, третьего варианта не дано. Но
оба исхода – выпадение орла или выпадение решки – равновозможны,
или ещё можно сказать равновероятны. В результате эксперимента
может произойти как первое событие, так и второе. Тогда вероятность каждого
из этих событий будет равна отношению числа благоприятных случаев к числу
равновозможных случаев.
Допустим,
нас интересует исход выпадение орла – это благоприятный для нас случай. Тогда вероятность
этого события будет равна отношению благоприятных случаев (таких случаев – 1) к
числу всех равновозможных случаев (их 2), то есть равна .
То же самое мы можем сказать и о вероятности события выпадение решки. Она тоже
равна .
–
Давайте проведём ещё один эксперимент, – предложил Мудряш. – Будем подбрасывать
игральный кубик. Скажите, какие события могут произойти в результате этого
эксперимента?
–
В результате эксперимента с игральным кубиком можно получить один из 6 исходов:
выпадет 1, 2, 3, 4, 5 или 6 очков, – сказал Паша.
–
Хорошо! – согласился Мудряш. – Все эти 6 исходов равновозможны, и один из них
обязательно произойдёт. Если нас интересует событие, например выпадение 2
очков, то вероятность данного события будет равна .
–
А теперь представьте, что нас интересуют следующие события: первое — выпадение
чётного числа очков; второе — выпадение числа очков, кратного числу 3.
Определите вероятность этих событий.
–
Событию выпадение чётного числа очков благоприятствуют 3 случая: выпадение 2, 4
или 6 очков, – начал Саша. – Тогда вероятность этого события равна отношению
числа случаев, благоприятствующих этому событию (их 3), к числу всех
равновозможных случаев (их 6). Значит, вероятность выпадения чётного числа
очков равна или
.
–
Событию выпадение числа очков, кратного числу 3, благоприятствуют только 2
случая: выпадение 3 или 6 очков, – сказал Паша. – Тогда вероятность этого
события равна отношению числа случаев, благоприятствующих этому событию (их 2),
к числу всех равновозможных случаев (их 6). Следовательно, вероятность
выпадения числа очков, кратного числу 3, равна или
.
–
Молодцы! – похвалил ребят Мудряш. – Приведённые примеры иллюстрируют следующее.
Если эксперимент заканчивается одним из равновозможных
исходов, из которых являются
благоприятными для наступления данного события, то вероятность этого события
равна .
–
А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько
заданий.
Задание
первое: в коробке лежит 3 красных и 7 синих шаров. Наугад
вынимают 1 шар. Какова вероятность того, что этот шар окажется: красным; синим?
Решение: представим
себе, что шары пронумерованы числами от 1 до 10, так как всего у нас 7 + 3 = 10
шаров в коробке. Тогда при вынимании шара может произойти 10 равновозможных
исходов: вынули шар с номером один, вынули шар с номером 2 и так далее. В
первом случае благоприятных исходов будет только 3 (ведь в коробке только 3 красных
шара). Поэтому искомая вероятность равна .
Во
втором случае благоприятных исходов будет 7, так как в коробке лежит 7 синих
шаров. Поэтому искомая вероятность равна .
Задание
второе: в коробке лежит 10 карточек, пронумерованных числами
от 1 до 10. Какова вероятность того, что наугад будет вытянута карточка с
чётным числом?
Решение: при
вынимании карточек может произойти десять равновозможных исходов: вынули карточку
с номером 1, вынули карточку с номером 2 и так далее. Но благоприятных исходов
будет только 5: вынули карточку с номером 2, вынули карточку с номером 4,
вынули карточку с номером 6, вынули карточку с номером 8 или вынули карточку с
номером 10. Значит, искомая вероятность равна или
.
Как поступить
в Онлайн-школу и получить аттестат?
Подробно расскажем о том, как перевестись на дистанционный формат обучения, как устроены онлайн-уроки и учебный процесс, как улучшить успеваемость и повысить мотивацию!
Нажимая на кнопку, я соглашаюсь на обработку
персональных данных
- Все предметы
- 11 класс
- Алгебра
-
Вероятность события
-
Элементы комбинаторики и теории вероятностей
- Видеоурок
- Учебник
- Тест
Видеоурок: Вероятность события
Элементы комбинаторики и теории вероятностей
-
Видеоурок 24. Вероятность события. Алгебра 11 класс
Предыдущий урок
Сочетания и их свойства
Элементы комбинаторики и теории вероятностей
Следующий урок
Размещения
Элементы комбинаторики и теории вероятностей
-
Великобритания во второй половине ХХ – начале ХХI в.
История
-
Экономический рост и развитие
Обществознание
-
А.А. Блок. Лирика. Темы и образы ранней лирики. «Стихи о Прекрасной Даме»
Литература
Зарегистрируйся, чтобы присоединиться к обсуждению урока
Добавьте свой отзыв об уроке, войдя на платфому или зарегистрировавшись.
Отзывы об уроке:
Пока никто не оставил отзыв об этом уроке




