Решение задач про шахматные партии
Лучшее спасибо – порекомендовать эту страницу

Чаще всего в задаче про партии следует вычислить две вероятности и сравнить:
Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть 2 партии из 4 или 3 партии из 6 (ничьи во внимание не принимаются).
Пример подробного решения этой и подобных задач будет ниже, а формулу мы запишем для упрощенной задачи (когда нужно просто найти вероятность того, что будет выиграно $k$ партий):
Два равносильных шахматиста играют в шахматы $n$ партий. Какова вероятность первому шахматисту выиграть в точности $k$ партий (ничьи не учитываются).
Так как шахматисты по условию равносильные, а ничьи не учитываются, считаем, что выигрыш и проигрыш может наступить с равной вероятностью. Поэтому $p=q=1/2=0,5$, $q=1-p=1/2=0,5$. Применяем формулу Бернулли и получаем:
$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot 0,5^{n}. qquad (1)
$$
Далее:
- Онлайн решение задачи о шахматных партиях (калькулятор)
- Видеоурок и шаблон Excel
- Примеры решенных задач о партиях
- Полезная информация
Видеоурок и шаблон Excel
Посмотрите наш ролик о решении задач об играх и партиях: как использовать Excel для решения типовых задач с игроками и партиями (как для малого, так и для большого числа партий).
Расчетный файл Эксель из видео можно бесплатно скачать и использовать для решения своих задач.
Примеры решений задач о шахматных партиях
Рассмотрим несколько типовых примеров.
Пример 1. Два равносильных шахматиста играют в шахматы. Что вероятнее выиграть 2 партии из 4 или 3 партии из 6 (ничьи во внимание не принимаются).
Нужно вычислить две вероятности, для каждой из которых применяем формулу (1). В первом случае $n=4, k=2$, во втором – $n=6, k=3$. Получаем:
$$
P_1=P_4(2)=C_{4}^2 cdot 0,5^4 = 6cdot 0,5^4= 0,375.
$$
$$
P_2=P_6(3)=C_{6}^3 cdot 0,5^6 = 20cdot 0,5^6= 0,313.
$$
Число 0,375 больше, чем 0,313. Поэтому вероятнее выиграть 2 партии из 4.
Пример 2. Играет два равных по силе игрока, какая вероятность выше: выиграть одну партию из трех, или три из пяти.
Нужно вычислить две вероятности, для каждой из которых применяем формулу (1). В первом случае $n=3, k=1$, во втором – $n=5, k=3$. Получаем:
$$
P_1=P_3(1)=C_{3}^1 cdot 0,5^3 = 3cdot 0,5^3= 0,375.
$$
$$
P_2=P_5(3)=C_{5}^3 cdot 0,5^5 = 10cdot 0,5^5= 0,313.
$$
Так как 0,375 больше, чем 0,313, вероятнее выиграть 1 партию из 3.
Пример 3. Играют равносильные противники. Что вероятнее: выиграть не менее трех партий из четырех или не менее шести из восьми? (Ничьи не учитываются)
В отличие от предыдущих задач, здесь нужно найти вероятность того, что число выигрышных партий будет находится в некотором интервале (а не равно в точности какому-то числу). Но формула используется по-прежнему таже самая.
Найдем вероятность выиграть не менее трех партий из четырех, то есть вероятность выиграть или три партии, или четыре партии. Данные вероятности равны по формуле (1):
$$
P_4(3)=C_{4}^3 cdot 0,5^4 = 4cdot 0,5^4= 0,25.
$$
$$
P_4(4)=C_{4}^4 cdot 0,5^4 = 1cdot 0,5^4= 0,0625.
$$
Так как события (выиграть 3 партии из 4) и (выиграть 4 партии из 4) несовместные, искомая вероятность может быть найдена по формуле сложения вероятностей: $P_1=P_4(3)+P_4(4)=0,3125.$
Аналогично находим вторую вероятность выиграть не менее 6 партий из 8 (то есть выиграть или 6, или 7, или 8 партий). В этот раз все вычисления запишем сразу в одну формулу:
$$
P_2=P_8(6)+P_8(7)+P_8(8)=C_{8}^6 cdot 0,5^8+C_{8}^7 cdot 0,5^8+C_{8}^8 cdot 0,5^8 =
$$
$$
=28 cdot 0,5^8+8 cdot 0,5^8+1 cdot 0,5^8 =0,145.
$$
Итак, вероятнее выиграть не менее 3 партий из 4 (так как 0,3125 больше чем 0,145).
Пример 4. Какова вероятность, что игрок, который слабее своего оппонента в два раза выиграет две партии из трех
Для полноты изложения приведу решение этой задачи, с первого взгляда она похожа на предыдущие (и так и есть, конечно), но есть некоторое отличие. А именно, противники тут не равносильные, а один слабее другого. С точки зрения формализации задачи, это будет означать, что вероятность выигрыша для игрока равна не 0,5, а другому числу. Какому?
Пусть вероятность выигрыша для игрока равна $p$, тогда для второго игрока (который по условию в 2 раза его сильнее), она равна $2p$. При этом, раз ничьи не учитываются (это стандартное предположение), должно выполняться равенство: $p+2p=1$, откуда находим $p=1/3$.
А дальше остается только применить формулу Бернулли для $n=3$, $k=2$, $p=1/3$. Получаем
$$
P_3(2)=C_{3}^2 cdot (1/3)^2 cdot (2/3)^1= 3cdot (1/3)^2 cdot (2/3) = 2/9= 0,222.
$$
Ответ: 0,222.
Полезная страница? Сохрани или расскажи друзьям
Полезные ссылки
- Учебник по теории вероятностей
- Выполненные контрольные по теории вероятностей
- Заказать работу по теории вероятностей
Найдите готовые задачи в решебнике:
Если в n испытаниях событие А случается (происходит) k раз и не случается (не происходит) (n-k) раз, то данную вероятность Рn(k) можно найти по формуле Бернулли:
![]()
где
p — вероятность успеха испытания (опыта);
q=1-p — вероятность неудачи испытания (вероятность противоположного события);
$C_n^k$ — число сочетаний, вычисляется по формуле комбинаторики — сочетание без повторения
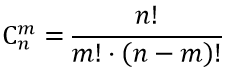
Пример 1
Монету бросают шесть раз. Найти вероятность того, что герб выпадет не менее двух раз.
Решение
По условию, n=6, k=2
Вероятность выпадения орла и герба одинаковая, значит p=1/2=0.5, a q=1-p=0.5
применим формулу Бернулли
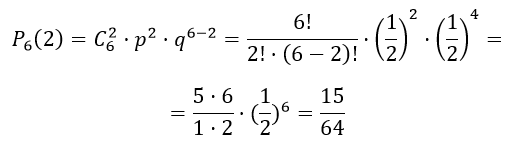
Пример 2
Каждый день акции компании X поднимаются в цене или падают в цене на один пункт с вероятностями 0,75 и 0,25. Найти вероятность того, что акции после 6 дней вернутся к своей первоначальной цене, то есть чтобы акции за это время 3 раза поднялись в цене и три раза опустились в цене. При этом изменения цены акции вверх и вниз – независимые события.
Решение
${P_6}left( 3 right) = C_6^3{left( {frac{3}{4}} right)^3}{left( {frac{1}{4}} right)^3} = 0,13$
Пример 3
По каналу связи передаётся 10 сообщений, каждое из которых независимо от других с вероятностью р = 0,2 искажается помехами. Найти вероятность того, что:
a) из 10 сообщений ровно 3 будет искажено помехами;
б) все сообщения будут приняты без искажений;
в) не менее двух сообщений будет искажено.
Решение
a)
Вероятность искажения равна $р ={frac{1}{5}}$
, а не неискажения $q=1–p={frac{4}{5}}$
n = 10, k = 3
Тогда вероятность того, что из 10 сообщений ровно 3 будет искажено помехами равна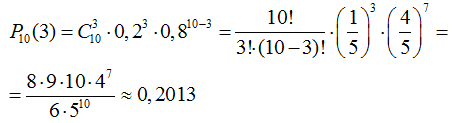
б)
Тогда вероятность того, что все сообщения будут приняты без искажений равна
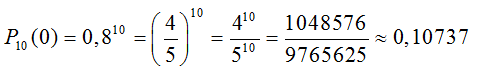
в)
Тогда вероятность того, что не менее двух сообщений будет искажено равна
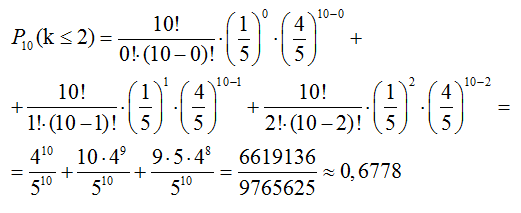
Пример 4
Два равносильных противника играют в шахматы.
Что вероятнее:
а) выиграть одну партию из двух или две партии из четырех?
б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи во внимание не принимаются.
Решение
Вероятность выигрыша шахматиста равна р=1/2, а вероятность проигрыша шахматиста
q=1-p=0.5
а) По формуле Бернулли найдём вероятность P2(1) «выиграть одну партию из двух» и вероятность P4(2) «выиграть две партии из четырех»
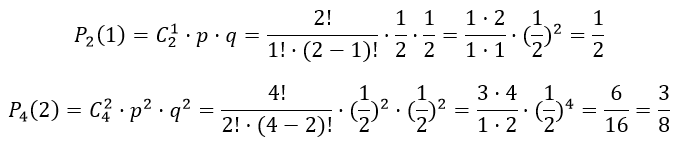
Имеем P2(1)>Р4(2) следовательно, вероятнее в шахматы выиграть одну партию из двух, чем две партии из четырех.
б) Сначала рассмотрим событие A — «выиграть не менее двух партий из четырех», которое соответствует сумме независимых событий Р4(2), Р4(3), Р4(3), то есть «выиграть две или три или четыре партии из четырех»
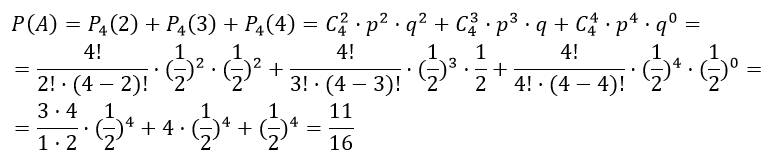
Теперь рассмотрим событие В — «выигрыш не менее трех партий из пяти», которое соответствует сумме независимых событий Р5(3), Р5(4), Р5(5), то есть «выиграть три или четыре или пять партий из трех»
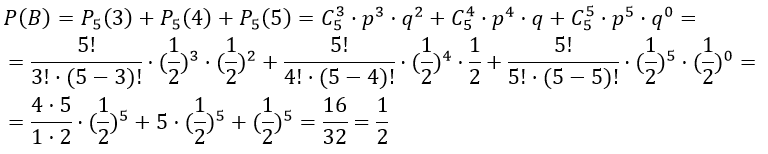
Здесь Р(А)>P(B), следовательно, вероятнее выиграть не менее двух партий из четырех, чем не менее трех партий из пяти.
![]() 16176
16176
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №19 г. Новоалтайска»
МАТЕМАТИЧЕСКИЕ
МЕТОДЫ В ШАХМАТАХ
Выполнила: Ревина Маргарита
ученица 8 г класса
Руководитель: С.В. Куличенко
учитель математики,
высшей квалификационной категории
2021
Оглавление
Введение
История
возникновения
Основная
часть
Треугольник
Паскаля
Теория
вероятности в шахматах
ALPHAZERO
Заключение
Список
использованной литературы
ВВЕДЕНИЕ
Эпиграф
Великий математик А. Пуанкаре считал,
что шахматы – вид математического творчества. По его мнению, шахматы являются
удобной моделью для изучения особенностей мышления.
Позже с мнением Пуанкаре согласился и
Р. Харди. Он заметил, что решение проблем шахматной игры есть не что иное, как
математическое упражнение, а игра в шахматы – это как бы насвистывание
математических мелодий. Формы мышления математика и шахматиста довольно близки,
и не случайно математики часто бывают способными шахматистами.
Сопоставление математики и шахмат,
как сфер человеческой деятельности, очень интересно и заслуживает специального
изучения. Поэтому мне и захотелось разобрать следующий вопрос:
«В чем же заключается связь между
шахматами и математикой и существует ли она вообще?»
Актуальность:
С давних времен и по настоящее время огромной популярностью
пользуется такая игра, как шахматы, но мало кто знает, что эта игра тесно
связана с математикой. Для любого начинающего игрока в шахматы будет полезно
узнать тонкости соединяющие с такой наукой, как математика.
Цель: Найти и доказать связь
между математикой и шахматами.
Задачи исследования:
1.
Узнать, как возникла игра в шахматы.
2.
Выявить математику на шахматной доске.
3.
Есть ли вероятность при игре в шахматы.
4.
На каком принципе устроены шахматные
движки.
5.
Подвести итоги.
Гипотеза:
В чем же заключается связь между шахматами и математикой и существует ли она
вообще?
Методы
исследования:
1.
Работа с литературой и интернет ресурсами.
2.
Анализ собранной информации и переработка.
3.
Обобщение полученной информации.
ИСТОРИЯ ВОЗНИКНОВЕНИЯ
Существует несколько древних легенд
возникновения шахмат. Рассмотрим одну из них:
Легенда гласит, что как-то в Индии,
когда она была очень сильной страной, ею правил один правитель. А вся мощь
армии была в особо обученных боевых слонах. С их помощью он уже разбил все
армии его противников, и множество лет не знал чем заняться. Как-то раз он
объявил, что тот, кто сумеет придумать что-то, что ему понравится получит всё
что пожелает. И к нему приходило безумно много мудрецов со всех стран, и
приносило ему все очень красивое и сделанное только из золота или драгоценностей.
Но все что приносили эти мудрецы было не по душе правителю. И как-то раз к нему
пришел один небогатый Шах. Он пришел с небольшой дощечкой и фигурками, но вся
игра была сделана из дерева, и как только правитель увидел это, то ужасно
разозлился: «Что это еще такое? Все изделия, которые мне показывают, сделаны из
золота или драгоценностей, а ты мне тут с какими-то деревяшками пришел», на то
Шах ответил так: «Не в золоте интерес игр, а в мудрости», и в этот момент
правитель увидел, что фигурки на вид, как и его армия. Правитель
заинтересовался и согласился посмотреть. А когда Шах показал правителю, как
играть в игру со словами “Твоя армия величественная и непобедимая, но
сможешь ли ты выиграть здесь на маленькой дощечке со своим войском и с
противником с такой же армией”. Когда правитель начал играть ему
понравилась эта игра, и он был уверен, что выиграет Шаха с легкостью, однако в
первой партии Шах победил правителя, и правитель попробовал снова, но, уже
обдумывая каждый ход, и во второй партии он выиграл. После этого ему безумно
понравилась эта игра. И каждый раз, когда он нападал на вражеского короля, он
произносил «шах» (ей шах), предупреждая, что королю грозит опасность, а когда
он побеждал, он говорил «Шаху мат», что означало король умер. Но как вы помните
правитель обещал всего, что пожелает тому, кто сделает то изделие, которое ему
понравится, и король решил исполнить свое обещание, и он спросил чего Шах
желает, и Шах ответил на первый взгляд небольшую награду «если на первую клетку
шахматный доски положить одно зерно на вторую два на третью четыре и так далее,
но оказалось что такого количества нет во всём королевстве. Ведь это 92 233 720
000 019 зёрен. Истории так и не сказано как правитель рассчитался с Шахом.
ТРЕУГОЛЬНИК
ПАСКАЛЯ
Треугольник Паскаля — бесконечная
таблица биномиальных коэффициентов, имеющая треугольную форму. В этом
треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух
расположенных над ним чисел. Строки треугольника симметричны относительно
вертикальной оси. Назван в честь Блеза Паскаля. Числа, составляющие треугольник
Паскаля, возникают естественным образом в алгебре, комбинаторике, теории
вероятностей, математическом анализе, теории чисел. Но есть ли связь между
треугольником Паскаля и шахматами?
В книге Евгения Гика “Шахматы и
математика” в главе, посвященной геометрии шахматной доски) автор приводит
удивительные примеры, когда знание вариантов маршрута короля позволило мастерам
спасать совершенно проигрышные позиции. (Приведен знаменитый этюд Рети, в
котором король удивительным образом успевает повоевать в двух противоположных
участках доски). А связь с этой темой в том, что количество вариантов маршрутов
короля для достижения каждого поля подчиняется закономерности треугольника
Паскаля!
И самый последний вопрос, связанный
одновременно с треугольником Паскаля и с шахматами. Чему равна сумма всех
чисел, стоящих выше какого-либо ряда? Эти суммы дают значения 1, 3, 7, 15,
31,… Не надо обладать большой фантазией, чтобы увидеть простую закономерность:
сумма всех чисел для n рядов равна 2n-1. И как эта закономерность связана с
шахматами? По общеизвестной легенде, которая была рассказана мною, делаем
вывод, что на каждой клетке доски лежало (бы) количество зерен, равное сумме
чисел в соответствующей строке треугольника Паскаля, а сумма всех зернышек на
первых n клетках равнялась (бы) сумме чисел на этих n строках этого волшебного
треугольника. Вот такая необычная связь.

ТЕОРИЯ ВЕРОЯТНОСТИ В ШАХМАТАХ
Теория вероятности – это один из
разделов высшей математики, изучающий случайные события, величины и их
свойства.
Сама вероятность представляет из себя
степень(оценка) возможности наступления некоторого события. Теория вероятности
– это попытка превратить случайность(хаос) в заранее известный порядок
математических алгоритмов.
Возьмём для примера игральную кость с
6 гранями.
Шанс выпадения нужной стороны кубика
приблизительно 16,6%. Соответственно возникает вопрос: «Бросив игральную кость
100 раз мы получим желаемый результат 16 раз?» На самом деле нет, нужная цифра
на кубике может выпасть нам и 10 раз, и 20, и 30. А может и не выпасть от слова
совсем.
В этом и заключается вся сложность в
100% предсказании результата броска игральной кости.
Но в теории, при должных физических и
математических данных можно абсолютно точно предсказывать результат броска
кубика. Для этого нужно всего лишь знать:
– Вес, плотность, эластичность кубика
– Плотность, жесткость поверхности о
которую кубик ударяется
– Высота, сила и изначальное
ускорение кубика при броске
– Сила ветра, плотность воздуха
То есть руками человека такие
действия практически невозможны, при этом вполне реальны для техники и
вычислительных машин.
Но сейчас речь пошла об играх, где
присутствует фактор случайности, где не мало зависит от фортуны, и насколько
она к тебе благосклонна.
Что же касаемо шахмат, в которых нет
игральных костей, колоды карт и прочих тонкостей азартных игр. В них только ты,
твой противник и абсолютно равное количество фигур отзеркалено установленных
друг к другу. Для чего же тогда здесь может понадобиться теория вероятности?
Случайности то нет, только бесчисленный набор различных комбинаций. В этом и
кроется весь ответ.
Бесчисленные комбинации! – Означает,
что есть миллиарды вариантов исхода и какими ходами этот исход будет получен.
Представим обычное начало шахматной
партии.
Вариантов партий практически
бесконечно. Ведь только на первый ход приходится 129.960 различных комбинаций.
Допустим, что оно ограничено, тогда в сумме всего лишь 1 миллиард. С каждым
новым ходом в игре, это количество будет уменьшаться и со временем сойдется на
ноль. Зная все эти миллиарды комбинаций, можно составить идеальную «формулу»
победы. В шахматах, зная все возможные комбинации партий, можно анализировать,
сравнивать и выбирать максимально преимущественные тактики после каждого хода.
Проблема заключается в том, что такое огромное количество данных анализировать
и выбирать наилучший ход невозможно для человека.
Но сейчас время техники, есть машины (компьютеры),
которые могут без проблем запомнить абсолютно каждую возможную партию в
шахматах. И с каждым ходом перестраивать алгоритм игры, путем отсеивания худших
вариантов, приходя, таким образом, к лучшему ходу.
В 2017 году была анонсирована и
представлена программа AlfaZero. Совершен гигантский шаг: компьютер может
освоить шахматную игру на высоком уровне, полагаясь на обучение, присущее
людям, а не на привычный для компьютеров счет методом полного перебора. Это
способно поколебать наше представление о человеческом превосходстве и неизбежно
повлияет на развитие шахматных движков в будущем, поскольку нам придется
неохотно согласиться, что машины не только лучше считают варианты, но и лучше
понимают шахматы.
ALPHAZERO
Давайте
перейдем к самой сути: AlphaZero обучается с использованием нейросети, которую
можно изобразить следующим образом:

Нейросеть – попытка
сделать компьютерную систему более похожей на человеческий мозг, а не, сами
понимаете, кремниевый. Данные на входе, то есть, позиция на доске, приходят
слева. Их обрабатывает первый слой нейронов, каждый из которых передает данные
на выходе нейронам следующего слоя, и так далее, пока мы не получим конечные
данные от самого правого слоя нейронов. В AlphaZero конечные данные состоят из
двух частей:
1. Оценка данной
шахматной позиции.
2. Оценка каждого
возможного хода в этой позиции.
То есть это можно считать
официальным проигрышем человека в шахматах компьютеру.
Факты
И так, мы выяснили для
чего нужны познания теории вероятности в шахматах. И что Теория Вероятности
является основой для создания непобедимого игрока в шахматах – Компьютера. В
основе создания, которого лежит число Шеннона.
Число́ Ше́ннона —
оценочное минимальное количество неповторяющихся шахматных партий, вычисленное
в 1950 году американским математиком Клодом Шенноном. Составляет приблизительно
10¹²⁰.
Вычисление описано в
работе «Программирование компьютера для игры в шахматы», опубликованной в марте
1950 года в журнале Philosophical Magazine и ставшей одним из фундаментальных
трудов в развитии компьютерных шахмат как дисциплины. В основу вычислений легло
предположение о том, что каждая игра длится в среднем 40 ходов и на каждом ходе
игрок делает выбор в среднем из 30 вариантов. Для сравнения — количество атомов
в наблюдаемой Вселенной составляет по разным оценкам от 4⋅10⁷⁹ до 10⁸¹, то есть в 10⁴⁰
раз меньше числа Шеннона.
Кроме этого, Шеннон
высчитал и количество возможных позиций, равняющееся примерно

Это число, однако,
включает также ситуации, исключаемые правилами игры и поэтому недосягаемые в
дереве возможных ходов.
Статья состоит из двух серий, разделенных годами. Разумеется, со временем на многие вещи начинаешь смотреть иначе, а также иначе писать. Кто-то из классиков даже сказал, что нет людей более разных, чем один и тот же человек в разные моменты жизни. Но в данном случае я во многом согласен с молодым собой.
Оценка позиции в шахматах.
Статистическая или абсолютная оценка – что важнее?
В процессе написания книги про одного маленького лесного зверька меня посещали одинокие, блуждающие мысли, которыми я и хочу поделиться с читателями. Во время работы и игрок, и комментатор все время оперируют понятием «оценка позиции». Каждый раз в конце варианта в комментариях принято оценивать позицию словами или загадочными значками, и на основе этой оценки делается вывод о пригодности варианта для той или иной стороны. Иначе комментарии теряют смысл! Во время партии шахматист также должен все время иметь представление о текущей оценке позиции, чтобы иметь возможность планировать свои дальнейшие действия. Если положение лучше, то надо искать возможность развить наступление и реализовать перевес. Если хуже, то надо искать способ нейтрализовать активность соперника, например, путем упрощений позиции, или созданием собственной контригры. Также, при выборе хода надо считать варианты, и сравнивая конечные оценки делать конкретный выбор. Непонимание реальной оценки позиции чревато серьезными последствиями и для комментатора, и для практика. У комментатора в этом случае из-под пера выйдет полнейшая чушь, лишенная, при ближайшем рассмотрении, логической связи. А практик, действуя несообразно особенностям и возможностям позиции, наверняка получит полновесный ноль в турнирной таблице. Все это – прописные истины, известные каждому. Гораздо интереснее другое. Зададим себе несложный на вид вопрос – что такое оценка позиции? На простой вопрос хочется дать простой логичный ответ – оценкой позиции определяется вероятность выигрыша каждой из сторон или мирного результата. Например, оценка “+ -” говорит о том, что выигрыш белых наиболее вероятен, а ничья и, уж тем более, выигрыш черных маловероятны. Оценка “+/-” означает, что выигрыш белых и ничья примерно равновероятны, а победа черных вряд ли возможна. Оценка “+/=” означает то, что перевес белых, скорее всего, недостаточен для победы, вероятность ничьей велика, а вероятность победы черных несколько меньше вероятности противоположного исхода. Все правильно, но из данного ответа возникает следующий вопрос – а как определить это понятие вероятности? Думаю, логично напрямую воспользоваться тем, что написано в учебниках по теории вероятностей. Математика тут очень простая. Допустим, есть какая-то позиция, которую требуется оценить. Проведем большое количество практических проверок этой позиции. Случайным образом наберем N (этой буквой математики означают не просто большое, а очень большое число) пар шахматистов, которые с равным временем на обдумывание разыграют данную незнакомую для них позицию до финального результата. В результате у W пар победят белые, у D – будет ничья, и в B случаях выигрыш окажется на стороне черных. Сумма этих чисел и даст общее количество пар. Т. е. W + D + B = N . Тогда вероятность выигрыша белых будет составлять W / N , вероятность ничьей – D / N , и вероятность победы черных, соответственно, – B / N. В сумме эти числа, понятное дело, дадут единицу, и это будет означать, что партия непременно завершится с одним из этих трех результатов. Это обычная процедура и есть определение вероятности. Чем больше число испытаний N , тем точнее полученные результаты. Можно также провести несколько серий испытаний, варьируя условия игры и временной контроль, а затем усреднить результаты, что также позволит повысить точность. Благодаря большому количеству испытаний становится совершенно неважным, какие шахматисты разыгрывали данную позицию, если, конечно, мы действительно случайно их выбираем! Скажем, для получения «нужного» результата можно все время за черных сажать гроссмейстеров, а за белых – новичков, и тогда даже очень хорошая позиция белых в результате такого «статистического» исследования будет объявлена плохой. 🙂 Итак, полученные вероятности будут вполне адекватной – статистической оценкой позиции. И когда она возникнет в какой-нибудь партии, он-лайн букмекеры будут знать, на каких условиях надо принимать ставки на исход поединка. Через несколько лет, надеюсь, таким букмекером в Интернете станет bazar-wokzal, а мне останется пойти к нему на работу в качестве скромного консультанта. 🙂 Есть и другой подход, другой способ определить оценку позиции! Можно посадить Каспарова, Крамника и других сильных шахматистов-аналитиков за мощные компьютеры. Где-то на месяц! Пусть поработают с хорошими программами и подумают. Многие позиции они сумеют проанализировать до жесткого конечного результата (одного из трех), а по остальным смогут дать более или менее надежное заключение, какой исход борьбы при лучшей игре с обеих сторон наиболее вероятен. Я не случайно выделил эти слова! Данный способ оценки позиции принципиально отличается от обычного статистического способа именно этим условием. Речь идет о точной, объективной, и если хотите, абсолютной оценке позиции! Так вот, очень часто абсолютная и статистическая оценка позиции не совпадают! В этом я совершенно убежден, хотя подобные эксперименты и сравнения, насколько мне известно, еще не проводились. При определении статистической оценки результат партии получается при средней игре с обеих сторон. Причем, играют люди – живые люди с их страхами, сомнениями, и недостатками. Играть наилучшим образом они не способны в принципе. От характера позиции очень сильно зависит не только качество, но и манера игры, которые демонстрирует обычный (средний) игрок. Так, например, ясно, что в сложных, подвешенных позициях с множеством фигур на доске люди больше ошибаются, не могут просчитать варианты до конца. И в большинстве своем живые люди сознательно ищут возможность стабилизировать позицию, почувствовать позиционную опору в буре осложнений, даже ценой конкретных упущений, которые в принципе неизбежны. С другой стороны, компьютерный анализ позволяет, ничего не боясь и никого не таясь, идти к объективной, абсолютной оценке позиции сквозь все бури осложнений. Вот и получается, что одни и те же позиции могут дать довольно разные оценки в статистическом и абсолютном варианте. Про них обычно говорят «неясно», «с обоюдными шансами», «у белых есть некоторая компенсация за ладью», а также «оценить данную позицию комментатор не в состоянии»! Так, например, в моем любимом Еже такие позиции возникают регулярно! Другой весьма характерный пример – вариант защиты Грюнфельда: 1.d4 Nf6 2.c4 g6 3.Nc3 d5 4.Nf3 Bg7 5.Bg5 c5 !? (хулиганский ход, конечно) 6.dxc5 Qa5 7.cxd5 Nxd5 8.Qxd5 Bxc3+ 9.Bd2 Be6 10.Qxb7 Bxd2 11.Nxd2 0-0.
У белых здесь уже две лишние пешки, можно съесть и больше. А у черных – некоторое преимущество в развитии, помноженное на оптимизм! В борьбе против компьютера этого недостаточно для позитивного результата. А вот против людей вариант играть можно, даже против гроссмейстеров. Никто из них (кроме тех, кто с наушником) не может в процессе партии найти точный путь к победе, все непременно ошибутся в больших осложнениях. Очень важно, есть ли в позиции ясный план, ясные позиционные идеи, облегчающие выбор хода. В случае отсутствия оных даже очень хорошие в абсолютном смысле позиции могут привести к плачевному результату в исполнении белковых игроков. Итак, для человека, который собирается играть в шахматы с себе подобными, гораздо важнее первая оценка позиции – статистическая! Можно назвать эту оценку человеческой. Пусть позднее Гарри Кимович на пару с железным монстром докажет, что ваша позиция была на самом деле плохой. Ведь это будет уже потом, после выигранной вами партии. Выигранной вопреки объективной оценке позиции! Можно регулярно успешно играть объективно плохую позицию, и можно раз за разом проигрывать объективно хорошую. Так что не стоит бояться тех оценок, которые выдают комментаторы тем или иным вариантам. Помните – напротив вас за доской будет сидеть живой человек, который вполне может ошибиться! Он вам поможет. Главное, чтобы позиция была полна жизни, и чтобы играть ее было непросто за обе стороны. В этом случае объективно–абсолютная оценка не будет иметь особого значения. Особенно при дефиците времени! Играйте в шахматы с людьми! Сергей Шипов, 2002-й год.
А теперь позвольте мне дополнить статью соображениями нынешнего дня, которые возникли в процессе обсуждения на форуме КС… Они разъясняют, раскрывают и дополняют некоторые моменты. Мобуту написал: «Вывод статьи, как я его понял применительно к этому примеру: если ты не богатырь, то плевать тысячу раз на абсолютную оценку. Выбирай ту дубину, у которой лучше статистика.» Именно так! А также выбирай ту дубину, которая нравится. Ибо если играешь с настроением, с желанием, с азартом, то и плохие позиции регулярно выигрываешь. Например, некий игрок, уже сложившийся (это важно), играет с удовольствием кривые дебюты, гамбиты, и набирает там приличный процент очков. Потом появляется умный, строгий дядя и начинает наставлять игрока, мол, играй правильно – выбирай солидные дебюты, получай объективно хорошие позиции. И что происходит? Разумеется, настроение у игрока пропадает, напор исчезает и процент очков вполне может снизиться. Вот вам конкретный пример – международный мастер Николай Власов (он же bazar-wokzal, он же чемпион мира в Интернете, он же обладатель двух самоваров и т.д.). Отнимите у него его любимых коняшек (1.d4 Nf6 2.c4 Nc6!), фирменную скандинавку, атаку Гроба и прочую кривизну, вручите в руки ортодоксальные, правильные дебюты – и вместо яркого, оригинального бойца, который может обыграть буквально любого соперника, вы получите ничем не примечательного, бесперспективного игрока. Ему будет просто не интересно играть возникающие позиции. Не будет желания погружаться в нюансы. И как следствие – упадет практическая сила. Разумеется, очень важно учитывать свой стиль игры. Под него надо подбирать дебютный репертуар, не смущаясь теоретическими оценками строгих аналитиков. И он же диктует оптимальную стратегию борьбы в незнакомых позициях. Например, возьмем Таля, Широва и других талантливейших атакеров… Они стали теми, кто они есть, потому что сумели использовать свои лучшие качества, не подстраиваясь под стандарты и предписания. Наряду с вполне корректными комбинациями они часто блефовали, что также приносило им успех. Соперники порой знали и чувствовали, что жертвы кудесников некорректны, что опровержение должно где-то быть. И анализ после партии это подтверждал. А толку-то? За доской, под тиканье часов соперники в объективно лучших или даже выигранных положениях ошибались и проигрывали – в большинстве случаев! А вот в сухой позиционной, правильной борьбе у них было бы больше шансов. Таким образом, атакеры сознательным ухудшением позиции добиваются улучшения своих результатов. И это нормально. Абсолютная оценка позиции – не самоцель! И напротив, тонкие позиционные мастера – Петросян, Крамник и др. – порой чувствуют, что позиция объективно требует жертв, комбинаций и прочих спецэффектов. Но они, зная за собой недостатки, сознательно сушат игру, строго говоря, ухудшают свою позицию, но при этом повышают вероятность позитивного результата и практически исключают проигрыш. Исключают возможность грубой ошибки. И это опять же нормально. Статистика говорит в пользу этого метода. Итак, игроки регулярно избирают тот класс позиций, в которых вероятность их ошибки ниже, чем вероятность ошибки соперника – в сответствии с собственным стилем и иногда (это случается намного реже) в соответствии со стилем соперника. А абсолютные оценки возникающих позиций зачастую играют второстепенную роль – это самое главное! Усреднение здесь происходит не по всем играющим с обеих сторон, а лишь по соперникам с одной стороны – соперникам конкретного исполнителя. Это и есть один из способов реализации вероятностной стратегии в шахматах. Видимо, в контексте вышесказанного стоит ввести еще и третий термин – индивидуальная оценка позиции. (Можно сказать и «субъективная», и тогда единообразия ради придется заменить слово «абсолютная» на «объективная»). Одна и та же позиция для жесткого атакера и осторожного технаря может оцениваться по-разному. И никакого противоречия в этих оценках нет! Перед нами самая настоящая теория относительности в шахматах. Все зависит от точки зрения, от системы координат. Действительно, в сложной иррациональной позиции атакер будет иметь большие шансы на победу, а технарь – лишь некоторые шансы на спасение. И наоборот, легко придумать обратный пример. Несовпадение (разночтение, не полное соответствие) абсолютной и статистической оценки встречается сплошь и рядом. Но я приведу яркий пример. Представим себе миттельшпильную позицию, в которой белые атакуют и уже пожертвовали пару фигур. Допустим, у них есть единственный, нетривиальный, весьма сложный, многоходовый путь к победе, связанный с жертвой еще парочки фигур и с тихими ходами посреди жаркой битвы. Это может быть любая промежуточная позиция из сложной комбинации. Например,
Абсолютная оценка позиции: 1-0. Строго! Для ее понимания достаточно понять идею (жертва ферзя на е5 с последующей доминацией) и посмотреть ее с хорошим компьютером. Тем самым, который не в состоянии просчитать подавляющее большинство других позиций и будет в них выдавать лишь приблизительные оценки, которые можно в некотором приближении принять за абсолютные. А вот статистическая оценка нашей позиции будет совсем другой! Ну, не могут люди считать, как машины, особенно в условиях ограниченного времени. Да и ферзей отдавать за коней они не привыкли. Поэтому в позиции на диаграмме наверняка последует отступление белого ферзя, пешка е6 погибнет, черные раскрутятся. И чаще всего партия будет заканчиваться миром или поражением белых. То есть эту объективно проигранную для черных позицию в человеческих поединках объективно выгоднее играть черными! Подведем итог двухсерийного фильма! Оценка шахматной позиции бывает трех типов: абсолютная, статистическая и индивидуальная. Очень важно различать ситуации, когда на первый план выходит одна из них. Все по-своему важны, и зачастую они противоречат друг другу. А в целом никакого противоречия нет! Последний ёмкий пример – мой любимый зверек, которого можно видеть на логотипе сайта Crestbook. Я упорно продолжаю играть черными некоторые объективно тяжелые позиции системы Ёж, которые по статистике, однако, дают неплохие результаты. Абсолютная оценка позиции – черным плохо! Статистическая оценка – шансы сторон взаимны. А моя индивидуальная оценка такова – у черных перевес! Надеюсь, что так и будет в дальнейшем… Вот такой парадокс. У одной позиции – три разные оценки! Сергей Шипов, 16 ноября 2006г.
Consider one game between two opponents (I am actually thinking about chess but it doesn’t have to be that). The ELO rating system gives the expected score $E_A$ and $E_B$ for both players. That is
$$E_A=Pr(A wins)+frac12Pr(draw)+0Pr(A loses)=Pr(A wins)+frac12Pr(draw)$$
$$E_B=Pr(B wins)+frac12Pr(draw)+0Pr(B loses)=Pr(B wins)+frac12Pr(draw)$$
From Elo’s logistic formulas
$$E_A=frac{Q_A}{Q_A+Q_B}, E_B=frac{Q_B}{Q_A+Q_B}$$
where $Q_A=10^{R_A/alpha},Q_B=10^{R_B/alpha}$, $R_A,R_B$ are the ratings of the opponents and $alpha$ is a normalization constant. As expected
$$E_A+E_B=Pr(A wins)+Pr(draw)+Pr(B wins)=1$$
which agrees with the formula.
Prof. Elo originally made his system for two outcomes only, win and loss. However if we have three outcomes and want explicitly the probability of win lose or draw for the game we need more data, right? We need one more equation. Anybody have an idea how to remedy this?
Thanks in advance, I appreciate.
