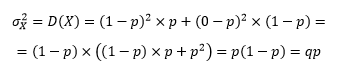Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 июля 2022 года; проверки требует 1 правка.
| Биномиальное распределение | |
|---|---|
 Функция вероятности |
|
 Функция распределения |
|
| Обозначение |
 |
| Параметры |
 — число «испытаний» — вероятность «успеха» |
| Носитель |
 |
| Функция вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 |
| Медиана |
одно из  |
| Мода |
 |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |
 |
| Производящая функция моментов |
 |
| Характеристическая функция |
 |
Биномиа́льное распределе́ние с параметрами 
и 
в теории вероятностей — распределение количества «успехов» в последовательности из независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна .
Определение[править | править код]
Пусть 
— конечная последовательность независимых случайных величин, имеющих одинаковое распределение Бернулли с параметром , то есть при каждом 
величина 
принимает значения 
(«успех») и 
(«неудача») с вероятностями и 
соответственно. Тогда случайная величина
имеет биномиальное распределение с параметрами и .
Это записывается в виде:
.
Случайную величину 
обычно интерпретируют как число успехов в серии из одинаковых независимых испытаний Бернулли с вероятностью успеха в каждом испытании.
Функция вероятности задаётся формулой:
где
- — биномиальный коэффициент.
Функция распределения[править | править код]
Функция распределения биномиального распределения может быть записана в виде суммы:
- ,
где 
обозначает наибольшее целое, не превосходящее число 
, или в виде неполной бета-функции:
- .
Моменты[править | править код]
Производящая функция моментов биномиального распределения имеет вид:
- ,
откуда
- ,
- ,
![{mathbb {E}}[Y]=np](https://wikimedia.org/api/rest_v1/media/math/render/svg/4449a990a54c49f0dea0dd10fe21507f002191cf)
![{mathbb {E}}left[Y^{2}right]=np(q+np)](https://wikimedia.org/api/rest_v1/media/math/render/svg/0487942f4eef0b21afe6b6fce2d94ff3a357e58a)
а дисперсия случайной величины.
- .
![{mathbb {D}}[Y]=npq](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4258ca89d2fbdbe66aa2fb66a65574cfbfe1e7)
Пример биноминального распределения
Свойства биномиального распределения[править | править код]
Связь с другими распределениями[править | править код]
См. также[править | править код]
- Треугольник Паскаля
- Локальная теорема Муавра — Лапласа
Задача 1
Прямоугольник
со сторонами l1 и l2 разделен на четыре равные
части, одна из которых заштрихована. На прямоугольник брошены три точки.
Попадание точки в любое место прямоугольника равновозможно. Дискретная случайная величина – число точек,
попавших на заштрихованную часть. Найти: закон распределения, числовые
характеристики, функцию распределения F(x). Построить график F(x).
Задача 2
Для
случайной величины X найти: а) закон распределения; б) функцию
распределения; в) математическое ожидание и дисперсию. При установившемся
технологическом процессе всей
производимой продукции станок-автомат выпускает 2/3 первым сортом и 1/3 – вторым. Случайным образом отбирается 5
изделий. X – число изделий первого сорта среди отобранных.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 3
Игральную
кость подбросили 3 раза. Найти математическое ожидание, дисперсию, среднее
квадратическое отклонение числа невыпадения единицы.
Задача 4
Монету
подбросили 4 раза. Найти математическое ожидание, дисперсию, среднее
квадратическое отклонение дискретной случайной величины X –
числа появлений герба.
Задача 5
В городе
имеется N=3 оптовых баз. Вероятность того, что требуемого сорта товар
отсутствует, на этих базах одинакова и равна p=0,2. Составить закон
распределения числа баз, на которых товар отсутствует в данный момент. Найти
математическое ожидание и среднее квадратическое отклонение.
Задача 6
Продавец
азартных игр объясняет, что в его лотерее 40% заклепок. Игрок покупает 5
билетов.
а) Какова
вероятность того, что он вытащит не более двух заклепок?
б)
Рассчитайте ожидаемое значение и интерпретируйте его
Задача 7
Случайные
величины ξ и η имеют биномиальные распределения с параметрами n=20 и p=0,2
для величины ξ и n=100 и p=0,1 для величины η.
Найти
математическое ожидание и дисперсию величины γ=10ξ-2η, если известен
коэффициент корреляции ρ(ξ,η)=-0,7.
Задача 8
Вероятность
изготовления бракованной детали на первом станке составляет 3%, на второй
станке – 5%. На первом станке изготовлено 20 деталей, на втором 40 деталей.
Найти математическое ожидание и дисперсию числа бракованных деталей.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 9
Производится
9 бомбометаний с вероятностью попадания при каждом 0,89. Какова вероятность при
более чем 4 бомбометаниях? Найти характеристики распределения случайной
величины.
Задача 10
Вероятность
того, что саженец абрикоса приживется в Новосибирской области, равна 0,6.
Посадили 5 саженцев. Записать закон распределения случайной величины X –
число прижившихся саженцев. Найти математическое ожидание и дисперсию
полученного распределения.
Задача 11
Из
курьерской службы отправились на объекты 5 курьеров. Каждый курьер с
вероятностью 0,3 независимо от других опаздывает на объект. Указать вид
распределения случайной величины X – числа опоздавших
курьеров. Построить ряд распределения случайной величины X.
Найти ее математическое ожидание и дисперсию. Найти вероятность того, что на
объекты опоздают не менее двух курьеров.
Задача 12
Проведено
5 независимых опытов. Вероятность взрыва в каждом опыте равна p=2/7.
Составить закон распределения числа взрывов, вычислить математическое ожидание,
дисперсию, среднеквадратическое отклонение и построить многоугольник
распределения.
Задача 13
На складе
производителя электрических гирлянд, которые планируется поставлять на продажу,
проводится выборочная проверка их работоспособности. Известно, что у примерно
5% производимых гирлянд бывают неисправности различного рода. Предположим, были
отобраны 3 гирлянды для проверки их работоспособности. Найдите закон
распределения случайной величины
– число гирлянд без неисправностей среди
отобранных. Определите вероятность того, что более чем одна гирлянда будет
исправлена.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Торговый
агент в среднем контактирует с 4 потенциальными покупателями в день. Из опыта
ему известно, что вероятность того, что потенциальный покупатель совершит
покупку, равна 0,023. Составить закон распределения ежедневного числа продаж
для агента. Найти числовые характеристики этого распределения. Чему равна
вероятность того, что у агента будет хотя бы 2 продажи в течение дня?
Задача 15
Случайная
величина имеет биноминальное распределение с математическим ожиданием M(X)=3 и
дисперсией D(X)=1,2. Найти P(X≥2).
Задача 16
По мишени
производится 4 независимых выстрела с вероятностью попадания при каждом
выстреле p=0,9. Найти закон распределения дискретной
случайной величины X, равной числу попадания в мишень. Написать функцию
распределения.
Задача 17
Производится
4 независимых выстрела по некоторой цели. Вероятность попадания при одном
выстреле равна 0,25. Выписать ряд распределения для числа попаданий в цель.
Задача 18
Вероятность
попадания в цель одним выстрелом равна 0,5. Производят пять выстрелов. Найти:
а) Распределение вероятностей числа попаданий; б) Наивероятнейшее число
попаданий; в) Вероятность, что попаданий будет не более двух.
Задача 19
Клиенты
банка не возвращают полученный кредит в 12% случаев.
а)
составить ряд распределения числа не отдавших кредит клиентов из взятых наудачу
3-х.
б) найти
среднее число не отдавших кредит клиентов и отклонение от него.
Задача 20
При
установившемся технологическом процессе происходит в среднем 10 обрывов нити на
100 веретен в час. Найти закон распределения и математическое ожидание
случайного числа обрывов нити в течение часа среди трех веретен, работающих
независимо друг от друга.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 21
Составить
закон распределения случайной величины Х и найти ее математическое ожидание,
дисперсию и среднее квадратическое отклонение:
Х – число
выигравших билетов лотереи, если куплено 3 билета, а выигрышные билеты
составляют в тираже 8%;
Задача 22
Производится
3 независимых опыта, в каждом из которых событие A появляется с вероятностью
0,4. Построить ряд распределения числа появлений события в 3-х опытах.
Найти F(X),M(X),D(X),σ(X),p(x≥1)
Задача 23
Построить
ряд распределения числа попаданий мячом в корзину при 4 бросках, если
вероятность попадания равна 0,7.
Задача 24
Производится
три независимых испытания, в каждом из которых вероятность появления события A равна
0,4. Составить закон распределения дискретной случайной величины X –
числа появления события A в указанных испытаниях.
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Задача 25
Запишите
таблицу для данного закона распределения случайной величины X,
постройте многоугольник распределения. Найдите числовые характеристики распределения
(M(X),D(X),σ(X)). Запишите функцию распределения и постройте ее график.
Ответьте на вопрос о вероятности описанного события.
Записи
страховой компании показали, что 30% держателей страховых полисов старше 50 лет
потребовали возмещения страховых сумм. Для проверки в случайном порядке было
отобрано 5 человек старше 50 лет, имеющих полисы. Случайная величина X –
количество требующих возмещения среди отобранных. Чему равна вероятность того,
что потребуют возмещения более трех человек?
Задача 26
На
некоторой остановке автобус останавливается только по требованию. Вероятность
остановки равна 0,2. За смену автобус проходит мимо этой остановки 5 раз.
Составить закон распределения числа остановки за смену, найти математическое
ожидание и дисперсию этой случайной величины.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 27
Устройство
состоит из пяти независимых элементов. Вероятность безотказной работы каждого
элемента в одном опыте равна 0,7. Для случайной величины X
элементов, безотказно работавших в одном опыте, построить закон распределения,
их графики, найти ее числовые характеристики.
Задача 28
В группе
студентов среднее число отличников составляет 20%. Составить закон распределения количества
отличников среди четырех студентов, отобранных случайным образом для участия в
деловой игре.
Задача 29
В урне 6
белых и 14 черных шара. Из урны извлекается один шар 4 раз подряд, причем
каждый раз вынутый шар возвращается в урну и шары перемешиваются. Приняв за
случайную величину Х число извлеченных белых шаров, составить закон
распределения этой случайной величины, найти ее математическое ожидание и
дисперсию.
Задача 30
Устройство состоит из трех
независимо работающих элементов. Вероятность отказа в одном опыте для каждого
элемента равна 0.1. Составить закон распределения случайного числа отказавших
элементов в одном опыте. Составить функцию распределения, построить ее график.
Задача 31
В
контрольной работе три задачи. Вероятность того, что задача будет решена, равна
0,9. Найти математическое ожидание случайной величины – числа решенных задач,
стандартное отклонение.
Задача 32
Известна
вероятность события A: p(A)=0,6. Дискретная случайная
величина ξ – число появлений A в трех опытах. Построить
ряд распределения случайной величины ξ. Найти математическое
ожидание mξ и дисперсию Dξ.
@import url(‘https://fonts.googleapis.com/css?family=Droid+Serif|Raleway’);
words {
color: black; font-family: Raleway; max-width: 550px; margin: 25px auto; line-height: 1.75; padding-left: 100px; }
words label, input {
display: inline-block; vertical-align: baseline; width: 350px; }
#button { border: 1px solid; border-radius: 10px; margin-top: 20px; padding: 10px 10px; cursor: pointer; outline: none; background-color: white; color: black; font-family: ‘Work Sans’, sans-serif; border: 1px solid grey; /* Green */ }
#button:hover { background-color: #f6f6f6; border: 1px solid black; }
p, li { color:#000000; font-size: 19px; font-family: ‘Helvetica’; }
p a { color: #9b59b6 !important; } Биномиальное распределение является одним из самых популярных распределений в статистике. Чтобы понять биномиальное распределение, сначала нужно понять биномиальные эксперименты .
Биномиальные эксперименты
Биномиальный эксперимент — это эксперимент, обладающий следующими свойствами:
- Эксперимент состоит из n повторных попыток.
- Каждое испытание имеет только два возможных исхода.
- Вероятность успеха, обозначаемая p , одинакова для каждого испытания.
- Каждое испытание является независимым.
Наиболее очевидным примером биномиального эксперимента является подбрасывание монеты. Например, предположим, что мы подбрасываем монету 10 раз. Это биномиальный эксперимент, поскольку он обладает следующими четырьмя свойствами:
- Эксперимент состоит из n повторных попыток – всего 10 попыток.
- В каждом испытании есть только два возможных исхода — орел или решка.
- Вероятность успеха, обозначаемая p , одинакова для каждого испытания. Если мы определим «успех» как приземление орлом, то вероятность успеха для каждого испытания равна ровно 0,5.
- Каждое испытание является независимым — результат одного подбрасывания монеты не влияет на результат любого другого подбрасывания монеты.
Биномиальное распределение
Биномиальное распределение описывает вероятность достижения k успехов в n биномиальных экспериментах.
Если случайная величина X подчиняется биномиальному распределению, то вероятность того, что X = k успехов, можно найти по следующей формуле:
P(X=k) = n C k * p k * (1-p) nk
куда:
- n: количество испытаний
- k: количество успехов
- p: вероятность успеха в данном испытании
- n C k : количество способов добиться k успехов в n испытаниях.
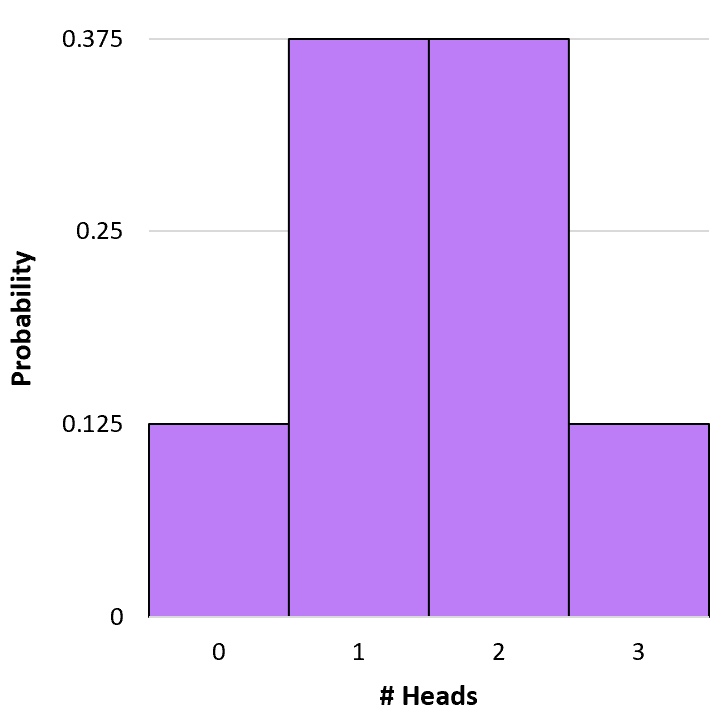
Например, предположим, что мы подбрасываем монету 3 раза. Мы можем использовать приведенную выше формулу, чтобы определить вероятность получения 0, 1, 2 и 3 решек во время этих 3 подбрасываний:
P(X=0) = 3 C 0 * 0,5 0 * (1-0,5) 3-0 = 1 * 1 * (0,5) 3 = 0,125
P(X=1) = 3 C 1 * 0,5 1 * (1-0,5) 3-1 = 3 * 0,5 * (0,5) 2 = 0,375
P(X=2) = 3 C 2 * 0,5 2 * (1-0,5) 3-2 = 3 * 0,25 * (0,5) 1 = 0,375
P(X=3) = 3 C 3 * 0,5 3 * (1-0,5) 3-3 = 1 * 0,125 * (0,5) 0 = 0,125
Примечание. Мы использовали этот Калькулятор комбинаций для расчета n C k для каждого примера.
Мы можем создать простую гистограмму, чтобы визуализировать это распределение вероятностей:
### Вычисление кумулятивных биномиальных вероятностей
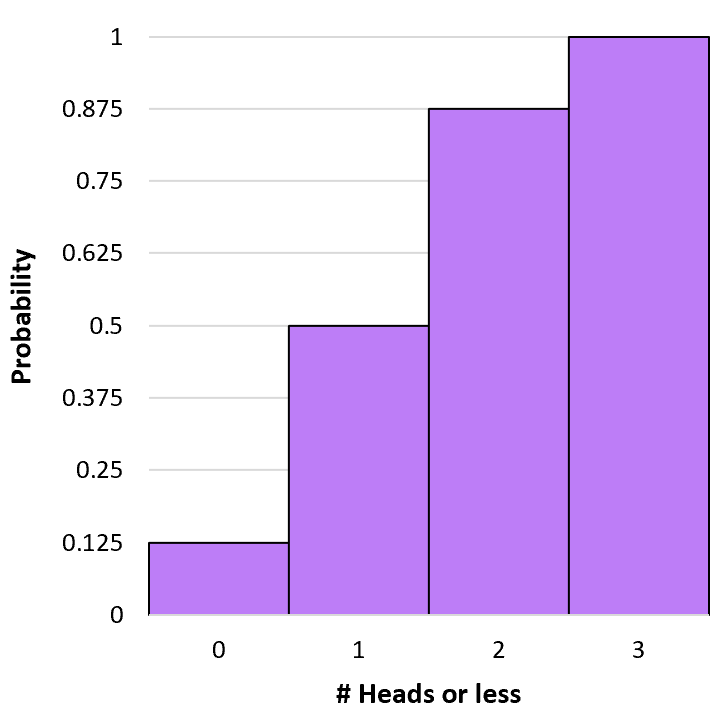
Несложно рассчитать одну биномиальную вероятность (например, вероятность того, что монета выпадет орлом 1 раз из 3 бросков), используя приведенную выше формулу, но для расчета кумулятивных биномиальных вероятностей нам нужно сложить отдельные вероятности.
Например, предположим, что мы хотим узнать вероятность того, что монета выпадет орлом 1 или менее раз из 3 бросков. Мы будем использовать следующую формулу для расчета этой вероятности:
P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .
Это известно как кумулятивная вероятность , потому что она включает в себя добавление более одной вероятности. Мы можем рассчитать кумулятивную вероятность выпадения k или меньше орлов для каждого исхода, используя аналогичную формулу:
Р(Х≤0) = Р(Х=0) = 0,125 .
P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .
P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .
P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .
Мы можем создать гистограмму, чтобы визуализировать это кумулятивное распределение вероятностей:
### Калькулятор биномиальной вероятности
Когда мы работаем с небольшими числами (например, 3 подбрасывания монеты), целесообразно рассчитать биномиальные вероятности вручную. Однако, когда мы работаем с большими числами (например, 100 бросков монеты), вычисление вероятностей вручную может оказаться затруднительным. В этих случаях может быть полезно использовать калькулятор биномиальной вероятности , подобный приведенному ниже.
Например, предположим, что мы подбрасываем монету n = 100 раз, вероятность того, что она выпадет орлом в данном испытании, равна p = 0,5, и мы хотим узнать вероятность того, что она выпадет орлом k = 43 раза или меньше:
p (вероятность успеха в данном испытании) n (количество испытаний) k (количество успехов) Р(Х= 43 ) = 0,03007
Р(Х< 43 ) = 0,06661
Р( Х≤43 ) = 0,09667
Р(Х > 43 ) = 0,90333
Р( Х≥43 ) = 0,93339
function pvalue() {
//get input values var p = document.getElementById(‘p’).value*1; var n = document.getElementById(‘n’).value*1; var k = document.getElementById(‘k’).value*1;
//assign probabilities to variable names var exactProb = jStat.binomial.pdf(k,n,p); var lessProb = jStat.binomial.cdf(k-1,n,p); var lessEProb = jStat.binomial.cdf(k,n,p); var greaterProb = 1-jStat.binomial.cdf(k,n,p); var greaterEProb = 1-jStat.binomial.cdf(k-1,n,p);
//output probabilities document.getElementById(‘k1’).innerHTML = k; document.getElementById(‘k2’).innerHTML = k; document.getElementById(‘k3’).innerHTML = k; document.getElementById(‘k4’).innerHTML = k; document.getElementById(‘k5’).innerHTML = k;
document.getElementById(‘exactProb’).innerHTML = exactProb.toFixed(5); document.getElementById(‘lessProb’).innerHTML = lessProb.toFixed(5); document.getElementById(‘lessEProb’).innerHTML = lessEProb.toFixed(5); document.getElementById(‘greaterProb’).innerHTML = greaterProb.toFixed(5); document.getElementById(‘greaterEProb’).innerHTML = greaterEProb.toFixed(5); } Вот как интерпретировать вывод:
- Вероятность того, что монета выпадет орлом ровно 43 раза, равна 0,03007 .
- Вероятность того, что монета выпадет орлом менее 43 раз, равна 0,06661 .
- Вероятность того, что монета выпадет орлом не более 43 раз, равна 0,09667 .
- Вероятность того, что монета выпадет орлом более 43 раз, равна 0,90333 .
- Вероятность того, что монета выпадет орлом 43 или более раз, равна 0,93339 .
Свойства биномиального распределения
Биномиальное распределение обладает следующими свойствами:
Среднее значение распределения равно µ = np
Дисперсия распределения равна σ 2 = np(1-p)
Стандартное отклонение распределения равно σ = √ np(1-p)
Например, предположим, что мы подбрасываем монету 3 раза. Пусть p = вероятность того, что монета выпадет орлом.
Среднее количество голов, которое мы ожидаем, равно μ = np = 3*.5 = 1.5 .
Ожидаемая дисперсия числа головок составляет σ 2 = np(1-p) = 3*,5*(1-,5) = 0,75 .
Проблемы практики биномиального распределения
Используйте следующие практические задачи, чтобы проверить свои знания о биномиальном распределении.
Проблема 1
Вопрос: Боб делает 60% своих штрафных бросков. Если он выполнит 12 штрафных бросков, какова вероятность того, что он сделает ровно 10?
Ответ: Используя приведенный выше калькулятор биномиального распределения с p = 0,6, n = 12 и k = 10, мы находим, что P(X=10) = 0,06385 .
Проблема 2
Вопрос: Джессика подбрасывает монету 5 раз. Какова вероятность того, что монета выпадет орлом 2 раза или меньше?
Ответ: Используя приведенный выше калькулятор биномиального распределения с p = 0,5, n = 5 и k = 2, мы находим, что P(X≤2) = 0,5 .
Проблема 3
Вопрос: Вероятность того, что данный студент будет принят в определенный колледж, равна 0,2. Если подали заявки 10 студентов, какова вероятность того, что будут приняты более 4?
Ответ: Используя приведенный выше калькулятор биномиального распределения с p = 0,2, n = 10 и k = 4, мы находим, что P(X>4) = 0,03279 .
Проблема 4
Вопрос: Вы подбрасываете монету 12 раз. Каково среднее ожидаемое количество выпавших орлов?
Ответ: Вспомните, что среднее биномиального распределения вычисляется как µ = np.Таким образом, µ = 12*0,5 = 6 голов .
Проблема 5
Вопрос: Марк совершает хоумран в 10% своих попыток. Если у него есть 5 попыток в данной игре, какова дисперсия количества хоум-ранов, которые он сделает?
Ответ: Напомним, что дисперсия биномиального распределения рассчитывается как σ 2 = np(1-p). Таким образом, σ 2 = 6*.1*(1-.1) = 0,54 .
Дополнительные ресурсы
Следующие статьи помогут вам научиться работать с биномиальным распределением в различных статистических программах:
- Как рассчитать биномиальные вероятности в Excel
- Как рассчитать биномиальные вероятности на калькуляторе ТИ-84
- Как рассчитать биномиальные вероятности в R
- Как построить биномиальное распределение в R
Биномиальный закон распределения
На этой странице мы собрали примеры решения учебных задач, в которых встречается биномиальное распределение дискретной случайной величины – наиболее распространённое в учебниках и сборниках. Давайте научимся его опознавать и решать соответствующие задачи.
Краткая теория
Биномиальным называют распределение количества «успехов» в последовательности из $n$ независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна $p$.
Иначе говоря, пусть происходит $n$ независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ – количество испытаний, в которых появилось событие, имеет биномиальное распределение вероятностей.
Она может принимать целые значения от 0 (событие не произошло ни разу) до $n$ (событие произошло во всех испытаниях). Формула для вычисления соответствующих вероятностей – уже известная нам формула Бернулли для схемы повторных независимых испытаний:
$$
P(X=k) = C_n^k cdot p^k cdot (1-p)^{n-k}, k=0,1,2,…,n.
$$
Для биномиального распределения известны готовые формулы для математического ожидания и дисперсии:
$$M(X)=np, quad D(X)=npq, quad sigma(X)=sqrt{npq}.$$
А теперь перейдем к примерам и разберем “на пальцах”, что за испытания и события имеются в виду, и как применять формулы, приведенные выше.
Лучшее спасибо – порекомендовать эту страницу
Примеры решенных задач
Задача 1. В городе 4 коммерческих банка. У каждого риск банкротства в течение года составляет 20%. Составьте ряд распределения числа банков, которые могут обанкротиться в течение следующего года.
Задача 2. Контрольная работа состоит из трех вопросов. На каждый вопрос приведено четыре варианта ответа, один из которых правильный. Составить закон распределения числа правильных ответов при простом угадывании. Найти M(X), D(X).
Задача 3. На контроль качества медицинских препаратов поступила партия из 8 штук. Вероятность того, что препарат окажется некачественным, равна 0,35.
А) найти вероятности $P_n(k)$ того, что число некачественных препаратов $k$ в партии составляет 0, 1, …, 8.
Б) построить ломаную линию с вершинами в точках $P_n(k)$.
В) найти наивероятнейшее число некачественных препаратов.
Задача 4. Наблюдение за районом осуществляется тремя радиолокационными станциями (РЛС). В район наблюдений попал объект, который обнаруживается любой радиолокационной станцией с вероятностью 0,2.
Построить ряд распределения, найти функцию распределения, математическое ожидание и среднее квадратичное отклонение числа РЛС, обнаруживших объект.
Найти вероятность того, что их будет не менее двух.
Задача 5. Составить закон распределения случайной величины $X$. Записать функцию распределения, построить её график. Вычислить числовые характеристики $М(Х), D(Х), sigma(X)$.
В партии 10% бракованных изделий. Наудачу отобрано 5 изделий. $X$ – число бракованных изделий среди отобранных. Дискретная случайная величина Х распределена по биномиальному закону.
Задача 6. Стрелок производит 4 выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0,3. За каждое попадание стрелку засчитывается 10 очков. Найти закон распределения числа засчитанных очков.
Задача 7. Опыт состоит из трех независимых подбрасываний одновременно трех монет, каждая из которых с одинаковой вероятностью падает гербом или цифрой вверх.
Построить ряд распределения, найти функцию распределения, математическое ожидание и среднее квадратичное отклонение числа одновременного выпадения двух гербов.
Найти вероятность того, что два герба одновременно выпадут хотя бы один раз.
Задача 8. ОТК проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,7. Проверено 20 изделий. Найти закон распределения случайной величины $X$ – числа стандартных изделий среди проверенных. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Задача 9. По многолетним статистическим данным известно, что вероятность рождения мальчика равна 0,515. Составить закон распределения случайной величины Х – числа мальчиков в семье с 4 детьми. Найти математическое ожидание и дисперсию этой случайной величины.
Задача 10. Производится три независимых опыта, в каждом из которых событие А появляется с вероятностью 0,6. Построить ряд распределения и функцию распределения случайной величины X числа появления события А в трех опытах. Найти числовые характеристики этой случайной величины X.
Мы отлично умеем решать задачи по теории вероятностей
Решебник по терверу
Нужны еще решения? Более 11000 подробно решенных и оформленных задач. Найди в решебнике сейчас:
Не все явления измеряются в количественной шкале типа 1, 2, 3 … 100500 … Не всегда явление может принимать бесконечное или большое количество различных состояний. Например, пол у человека может быть либо М, либо Ж. Стрелок либо попадает в цель, либо не попадает. Голосовать можно либо «За», либо «Против» и т.д. и т.п. Другими словами, такие данные отражают состояние альтернативного признака – либо «да» (событие наступило), либо «нет» (событие не наступило). Наступившее событие (положительный исход) еще называют «успехом».
Эксперименты с такими данными называются схемой Бернулли, в честь известного швейцарского математика, который установил, что при большом количестве испытаний соотношение положительных исходов и общего количества испытаний стремится к вероятности наступления этого события.
Переменная альтернативного признака
Для того, чтобы в анализе задействовать математический аппарат, результаты подобных наблюдений следует записать в числовом виде. Для этого положительному исходу присваивают число 1, отрицательному – 0. Другими словами, мы имеем дело с переменной, которая может принимать только два значения: 0 или 1.
Какую пользу отсюда можно извлечь? Вообще-то не меньшую, чем от обычных данных. Так, легко подсчитать количество положительных исходов – достаточно просуммировать все значения, т.е. все 1 (успехи). Можно пойти далее, но для этого потребуется ввести парочку обозначений.
Первым делом нужно отметить, что положительные исходы (которые равны 1) имеют некоторую вероятность появления. Например, выпадение орла при подбрасывании монеты равно ½ или 0,5. Такая вероятность традиционно обозначается латинской буквой p. Следовательно, вероятность наступления альтернативного события равна 1 — p, которую еще обозначают через q, то есть q = 1 – p. Указанные обозначения можно наглядно систематизировать в виде таблички распределения переменной X.
Мы получили перечень возможных значений и их вероятности. Можно рассчитать математическое ожидание и дисперсию. Матожидание – это сумма произведений всех возможных значений на соответствующие им вероятности:
Вычислим матожидание, используя обозначения в таблицы выше.
Получается, что математическое ожидание альтернативного признака равно вероятности этого события – p.
Теперь определим, что такое дисперсия альтернативного признака. Дисперсия – есть средний квадрат отклонений от математического ожидания. Общая формула (для дискретных данных) имеет вид:
Отсюда дисперсия альтернативного признака:
Нетрудно заметить, что эта дисперсия имеет максимум 0,25 (при p=0,5).
Стандартное отклонение – корень из дисперсии:
Максимальное значение не превышает 0,5.
Как видно, и математическое ожидание, и дисперсия альтернативного признака имеют очень компактный вид.
Биномиальное распределение случайной величины
Рассмотрим ситуацию под другим углом. Действительно, кому интересно, что среднее выпадение орлов при одном бросании равно 0,5? Это даже невозможно представить. Интересней поставить вопрос о числе выпадения орлов при заданном количестве бросков.
Другими словами, исследователя часто интересует вероятность наступления некоторого числа успешных событий. Это может быть количество бракованных изделий в проверяемой партии (1- бракованная, 0 — годная) или количество выздоровлений (1 – здоров, 0 – больной) и т.д. Количество таких «успехов» будет равно сумме всех значений переменной X, т.е. количеству единичных исходов.
Случайная величина B называется биномиальной и принимает значения от 0 до n (при B = 0 – все детали годные, при B = n – все детали бракованные). Предполагается, что все значения x независимы между собой. Рассмотрим основные характеристики биномиальной переменной, то есть установим ее математическое ожидание, дисперсию и распределение.
Матожидание биномиальной переменной получить очень легко. Математическое ожидание суммы величин есть сумма математических ожиданий каждой складываемой величины, а оно у всех одинаковое, поэтому:
Например, математическое ожидание количества выпавших орлов при 100 подбрасываниях равно 100 × 0,5 = 50.
Теперь выведем формулу дисперсии биномиальной переменной. Дисперсия суммы независимых случайных величин есть сумма дисперсий. Отсюда
Стандартное отклонение, соответственно
Для 100 подбрасываний монеты стандартное отклонение количества орлов равно
И, наконец, рассмотрим распределение биномиальной величины, т.е. вероятности того, что случайная величина B будет принимать различные значения k, где 0≤ k ≤n. Для монеты эта задача может звучать так: какова вероятность выпадения 40 орлов при 100 бросках?
Чтобы понять метод расчета, представим, что монета подбрасывается всего 4 раза. Каждый раз может выпасть любая из сторон. Мы задаемся вопросом: какова вероятность выпадения 2 орлов из 4 бросков. Каждый бросок независим друг от друга. Значит, вероятность выпадения какой-либо комбинации будет равна произведению вероятностей заданного исхода для каждого отдельного броска. Пусть О – это орел, Р – решка. Тогда, к примеру, одна из устраивающих нас комбинаций может выглядеть как ООРР, то есть:
Вероятность такой комбинации равняется произведению двух вероятностей выпадения орла и еще двух вероятностей не выпадения орла (обратное событие, рассчитываемое как 1 — p), т.е. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Такова вероятность одной из устраивающих нас комбинации. Но вопрос ведь стоял об общем количестве орлов, а не о каком-то определенном порядке. Тогда нужно сложить вероятности всех комбинаций, в которых присутствует ровно 2 орла. Ясно, все они одинаковы (от перемены мест множителей произведение не меняется). Поэтому нужно вычислить их количество, а затем умножить на вероятность любой такой комбинации. Подсчитаем все варианты сочетаний из 4 бросков по 2 орла: РРОО, РОРО, РООР, ОРРО, ОРОР, ООРР. Всего 6 вариантов.
Следовательно, искомая вероятность выпадения 2 орлов после 4 бросков равна 6×0,0625=0,375.
Однако подсчет подобным образом утомителен. Уже для 10 монет методом перебора получить общее количество вариантов будет очень трудно. Поэтому умные люди давно изобрели формулу, с помощью которой рассчитывают количество различных сочетаний из n элементов по k, где n – общее количество элементов, k – количество элементов, варианты расположения которых и подсчитываются. Формула сочетания из n элементов по k такова:
Подобные вещи проходят в разделе комбинаторики. Всех желающих подтянуть знания отправляю туда. Отсюда, кстати, и название биномиального распределения (формула выше является коэффициентом в разложении бинома Ньютона).
Формулу для определения вероятности легко обобщить на любое количество n и k. В итоге формула биномиального распределения имеет следующий вид.
Количество подходящих под условие комбинаций умножить на вероятность одной из них.
Для практического использования достаточно просто знать формулу биномиального распределения. А можно даже и не знать – ниже показано, как определить вероятность с помощью Excel. Но лучше все-таки знать.
Рассчитаем по этой формуле вероятность выпадения 40 орлов при 100 бросках:
Или всего 1,08%. Для сравнения вероятность наступления математического ожидания этого эксперимента, то есть 50 орлов, равна 7,96%. Максимальная вероятность биномиальной величины принадлежит значению, соответствующему математическому ожиданию.
Расчет вероятностей биномиального распределения в Excel
Если использовать только бумагу и калькулятор, то расчеты по формуле биномиального распределения, несмотря на отсутствие интегралов, даются довольно тяжело. К примеру значение 100! – имеет более 150 знаков. Раньше, да и сейчас тоже, для вычисления подобных величин использовали приближенные формулы. В настоящий момент целесообразно использовать специальное ПО, типа MS Excel. Таким образом, любой пользователь (даже гуманитарий по образованию) вполне может вычислить вероятность значения биномиально распределенной случайной величины.
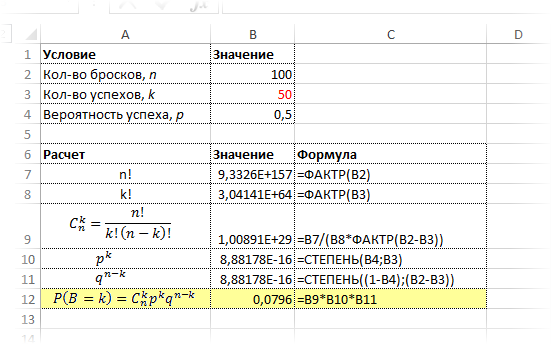
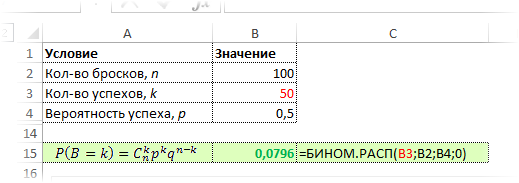
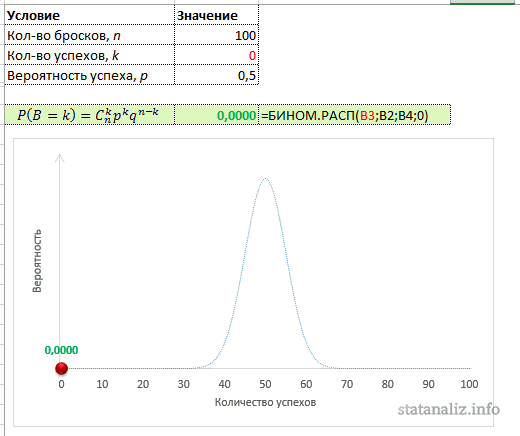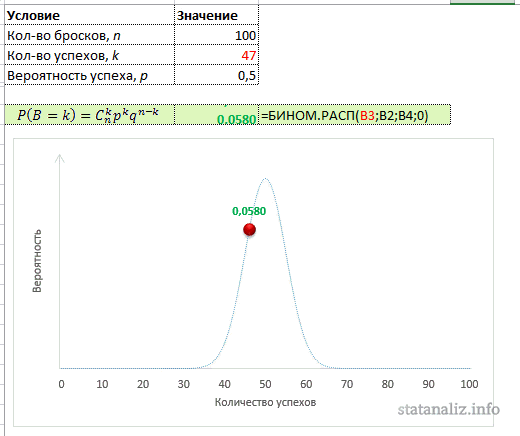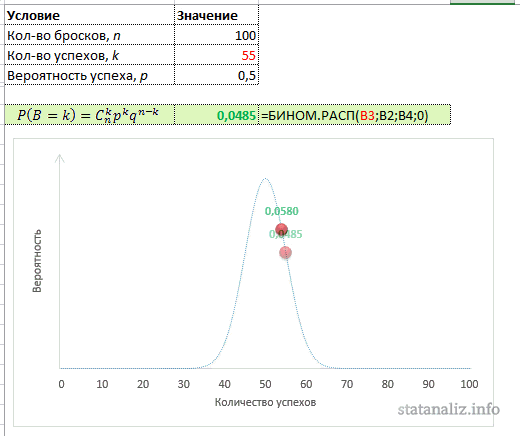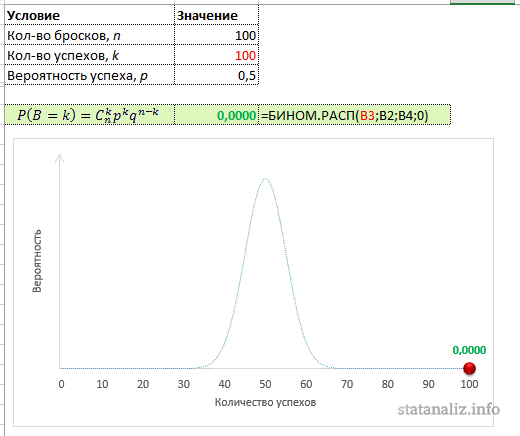
Для закрепления материала задействуем Excel пока в качестве обычного калькулятора, т.е. произведем поэтапное вычисление по формуле биномиального распределения. Рассчитаем, например, вероятность выпадения 50 орлов. Ниже приведена картинка с этапами вычислений и конечным результатом.
Как видно, промежуточные результаты имеют такой масштаб, что не помещаются в ячейку, хотя везде и используются простые функции типа: ФАКТР (вычисление факториала), СТЕПЕНЬ (возведение числа в степень), а также операторы умножения и деления. Более того, этот расчет довольно громоздок, во всяком случаен не является компактным, т.к. задействовано много ячеек. Да и разобраться с ходу трудновато.
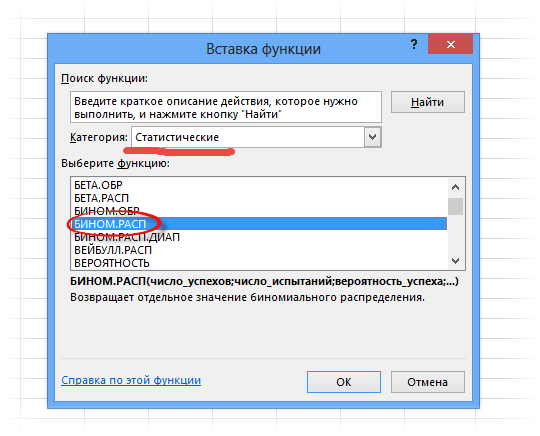
В общем в Excel предусмотрена готовая функция для вычисления вероятностей биномиального распределения. Функция называется БИНОМ.РАСП.
Синтаксис функции состоит из 4 аргументов:
Поля имеют следующие назначения:
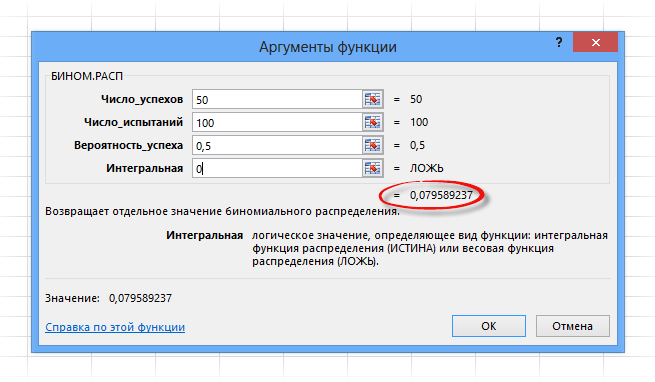
Число успехов – количество успешных испытаний. У нас их 50.
Число испытаний – количество бросков: 100 раз.
Вероятность успеха – вероятность выпадения орла при одном подбрасывании 0,5.
Интегральная – указывается либо 1, либо 0. Если 0, то рассчитается вероятность P(B=k); если 1, то рассчитается функция биномиального распределения, т.е. сумма всех вероятностей от B=0 до B=k включительно.
Нажимаем ОК и получаем тот же результат, что и выше, только все рассчиталось одной функцией.
Очень удобно. Эксперимента ради вместо последнего параметра 0 поставим 1. Получим 0,5398. Это значит, что при 100 подкидываниях монеты вероятность выпадения орлов в количестве от 0 до 50 равна почти 54%. А поначалу то казалось, что должно быть 50%. В общем, расчеты производятся легко и быстро.
Настоящий аналитик должен понимать, как ведет себя функция (каково ее распределение), поэтому произведем расчет вероятностей для всех значений от 0 до 100. То есть зададимся вопросом: какова вероятность, что не выпадет ни одного орла, что выпадет 1 орел, 2, 3, 50, 90 или 100. Расчет приведен в следующей картинке. Синяя линия – само биномиальное распределение, красная точка – вероятность для конкретного числа успехов k.
Кто-то может спросить, а не похоже ли биномиальное распределение на… Да, очень похоже. Еще Муавр (в 1733 г.) говорил, что биномиальное распределение при больших выборках приближается к нормальному закону (не знаю, как это тогда называлось), но его никто не слушал. Только Гаусс, а затем и Лаплас через 60-70 лет вновь открыли и тщательно изучили нормальной закон распределения. На графике выше отлично видно, что максимальная вероятность приходится на математическое ожидание, а по мере отклонения от него, резко снижается. Также, как и у нормального закона.
Биномиальное распределение имеет большое практическое значение, встречается довольно часто. С помощью Excel расчеты проводятся легко и быстро.
Поделиться в социальных сетях:
