Вероятность гипотез, формула Бейеса
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Пусть имеется полная группа несовместных событий — гипотез $Н_1, Н_2,dots , Н_n$. Вероятности этих гипотез до опыта известны и равны соответственно: $Pleft(H_{1} right),Pleft(H_{2} right),…,Pleft(H_{n} right)$.
Произведен опыт, в результате которого событие А появилось. Какие вероятности получат гипотезы в связи с появлением события А. По-другому будем искать условные вероятности $Pleft({raise0.7exhbox{$ H_{i} $} left/{vphantom{H_{i} A}}right.lower 0.7exhbox{$ A $}} right)$ для каждой гипотезы.
Теорема Байеса
Теорема
Вероятность гипотезы при условии, что событие А произошло, равна произведению вероятности этой гипотезы на соответствующую ей условную вероятность события А, которое произошло при испытании, деленному на полную вероятность события А.
[P(H_{i} /A)=frac{P(H_{i} )cdot P(A/H_{i} )}{sum limits _{i=1}^{n}P(H_{i} )cdot P(A/H_{i} )} ]

Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Доказательство
Согласно теореме умножения для двух событий
$$P(AH_i)=P(A) cdot P (H_i/A)=P(H_i) cdot P(A/H_i)$$
Откуда
[P(H_{i} /A)=frac{P(H_{i} )cdot P(A/H_{i} )}{P(A)} ]
Выразив $Р(А)$ получим формулу:
[P(H_{i} /A)=frac{P(H_{i} )cdot P(A/H_{i} )}{sum limits _{i=1}^{n}P(H_{i} )cdot P(A/H_{i} )} ]
которая носит название формулы Байеса. Теорема доказана.
Использование формулы Байеса при решении задач
Пример 1
Каждый из двух стрелков независимо друг от друга произвел выстрел по некоторому объекту. Вероятность попадания в цель первым стрелком равна 0,7; вторым — 0,6. Объект поражен одним попаданием. Определить вероятность того, что объект поражен первым стрелком.
Решение.
Обозначим событие А — поражение объекта одним попаданием. Для опыта виделим следующие гипотезы:
$Н_1$ — стрелки не попадают;
$Н_2$ — стрелки одновременно попадают;
$Н_3$ — первый стрелок попадет, второй — нет;
$Н_4$ — второй стрелок попадет, первый — нет.
Найдем вероятность этих гипотез:
$P(H_1)=0,3•0,4=0,12,$
$$P(H_2)=0,7•0,6=0,42,$$
$$P(H_3)=0,7•0,4=0,28,$$
$$P(H_4)=0,3•0,6=0,18.$$
Найдем условные вероятности события А при этих гипотезах:
$$P(A/H_1)=0$$
$$P(A/H_2)=0$$
$$P(A/H_3)=1$$
$$P(A/H_4)=1$$
После опыта гипотезы $Н_1$ и $Н_2$ становятся невозможными, а вероятности гипотез $Н_3$ и $Н_4$ будут соответственно равны.
[Pleft(H_{3} /A right)=frac{Pleft(H_{3} right)cdot Pleft(A/H_{3} right)}{Pleft(H_{3} right)cdot Pleft(A/H_{3} right)+Pleft(H_{4} right)cdot Pleft(A/H_{4} right)} =frac{0,28cdot 1}{0,28+0,18} approx 0,61;]
Следовательно, вероятность того, что объект поражен первым стрелком, равна 0,61.
«Вероятность гипотез, формула Бейеса» 👇
Пример 2
Экономист полагает, что в течение периода активного экономического роста американский доллар будет расти в цене с вероятностью 0,7, в период умеренного экономического роста доллар подорожает с вероятностью 0,4, и при низких темпах экономического роста доллар подорожает с вероятностью 0,2. В течение любого периода времени вероятность активного экономического роста равна 0,3, в периоды умеренного экономического роста — 0,5 и низкого роста — 0,2. Предположим, доллар дорожает в течение текущего периода, чему равна вероятность того, что анализируемый период совпал с периодом активного экономического роста?
Решение. Обозначим гипотезы: $Н_1$ — «активный экономический рост»; $H_2$ — «умеренный экономический рост»; $H_3$ — «низкий экономический рост».
Обозначим событие А — «доллар дорожает». Получим:
$Р(Н_1) = 0,3$;
$Р(Н_2) = 0,5$;
$Р(Н_3) = 0,2$;
$Р(А/Н_1) = 0,7$;
$Р(А/Н_2) = 0,4$;
$Р(A/Н_3) = 0,2$.
Необходимо найти: $Р(Н_1/А)$.
Пользуясь формулой Бейеса и подставив заданные значения вероятностей, получаем:
[P(H_{1} /A)=frac{P(H_{1} )cdot P(A/H_{1} )}{P(H_{1} )cdot P(A/H_{1} )+P(H_{2} )cdot P(A/H_{2} )+P(H_{3} )cdot P(A/H_{3} )} =]
[=frac{0,3cdot 0,7}{0,3cdot 0,7+0,5cdot 0,4+0,2cdot 0,2} =0,467.]
Пример 3
При разрыве бронебойного снаряда крупные осколки составляют 20% от общего числа осколков, средние — 30%, мелкие 50%. Вероятность того, что крупный осколок пробьет броню танка, равна 0,8. Для мелких и средних осколков эти вероятности соответственно равны 0,5 и 0,2.
- Найти вероятность того, что осколок пробьет броню.
- Броня танка оказалась пробитой. Найти вероятность того, что пробоина произошла от мелкого осколка.
Решение.
Обозначим события: $А$ — броня танка пробита; $H_1$ — осколок крупный; $H_2$ — осколок средний; $H_3$ — осколок мелкий.
События $H_1$, $H_2$, $H_3$ — это полная система гипотез. Найдем вероятности этих гипотез. По условию 20% осколков крупные, 30% — средние и 50% – мелкие. Найдем вероятности событий $H_1$, $H_2$, $H_3$:
$$P(H_1)=0,2;$$
$$P(H_2)=0,3;$$
$$P(H_3)=0,5.$$
Выполним проверку:
$$P(H_1)+P(H_2)+P(H_3)=0,2+0,3+0,5=1.$$
Найдем условные вероятности события А при наших гипотезах. Получим:
$$P(А /H_1)=0,8; P(А /H_2)=0,5; P(А /H_3)=0,2.$$
Вероятность события А посчитаем за формулой полной вероятности и получим:
[P(A)=sum limits _{k=1}^{3}P(H_{k} )cdot P(A/H_{k} )=0,2cdot 0,8+0,3cdot 0,5+0,5cdot 0,2=0,41.]
Для решения второй части задачи воспользуемся формулой Байеса. Найдем вероятность того, что пробоина в броне произошла от мелкого осколка (событие $H_3$), т.е. вероятность $P(H_3/А)$. По формуле Байеса найдем значение:
[P(H_{3} /A)=frac{P(H_{3} )cdot P(A/H_{3} )}{sum limits _{k=1}^{3}P(H_{k} )cdot P(A/H_{k} )} =frac{0,5cdot 0,2}{0,41} =frac{0,1}{0,41} approx 0,24. ]
Пример 4
Специализированая больница принимает в среднем 40% больных, которые имеют заболевание $H_1$, 35% – что имеют заболевание $H_2$ и 25% – $H_3$. Статистически известно, что лечение болезни $H_1$ равняется 0,9, для болезни $H_2$ и $H_3$ эти вероятности равняются 0,8 и 0,7. Какая вероятность того, что выписаный из больницы болел болезнью $H_2$?
Решение. Будем считать, что выписаный из больницы полностью здоров. По формуле полной вероятности найдем $P(A)$. По условию задачи:
$$Р(Н_1) = 0,4; $$
$$Р(Н_2) = 0,35;$$
$$Р(Н_3) = 0,25;$$
$$Р(А/Н_1) = 0,9;$$
$$Р(А/Н_2) = 0,8$$
$$Р(A/Н_3) = 0,7. $$
Тогда по формуле полной вероятности:
[P(A)=sum limits _{k=1}^{3}P(H_{k} )cdot P(A/H_{k} )=0,4cdot 0,9+0,35cdot 0,8+0,25cdot 0,7=0,815.]
По формуле Байеса найдем:
[P(H_{2} /A)=frac{P(H_{2} )cdot P(A/H_{2} )}{P(H_{1} )cdot P(A/H_{1} )+P(H_{2} )cdot P(A/H_{2} )+P(H_{3} )cdot P(A/H_{3} )} =]
[=frac{0,35cdot 0,8}{0,815} =0,344.]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 25.12.2022
Следствием
формулы (3.6) является формула Байеса или
теорема гипотез. Она позволяет переоценить
вероятности гипотез Hi,
принятых до опыта и называемых априорными
(«a
priory»,
доопытные, лат.) по результатам уже
проведенного опыта, то есть найти
условные вероятности P(Hi|A),
которые называются апостериорными
(«a
posteriori»,
послеопытные, лат.).
Пусть
событие А
может наступить при условии появления
одного из несовместных событий Н1,
Н2,…,
Нn,
образующих полную группу. Поскольку
заранее не известно, какое из этих
событий наступит, их называют гипотезами.
Вероятность появления события А
определяется по формуле полной вероятности
(3.6):
Р(А)
=
![]() .
.
Допустим,
что произведено испытание, в результате
которого появилось событие А.
Поставим своей задачей определить, как
изменились (в связи с тем, что событие
А
уже наступило) вероятности гипотез.
Другими словами, будем искать условные
вероятности
P(H1|A),
P(H2|A),…,
P(Hn|A).
Найдем
сначала условную вероятность P(H1|A).
По теореме умножения имеем
Р(AH1)
= Р(А)
P(H1|A)
= P(H1)
P(А/H1).
Отсюда
 .
.
Заменив
здесь Р(А)
по формуле (3.6), получим
 .
.
Аналогично
выводятся формулы, определяющие условные
вероятности остальных гипотез, т.е.
условная вероятность любой гипотезы
Hi
(i
= 1,2, …, n)
может быть вычислена по формуле
 (3.8)
(3.8)
Полученные
формулы называют формулами Бейеса (по
имени английского математика, который
их вывел; опубликованы в 1764 г.). Формулы
Бейеса позволяют переоценить вероятности
гипотез после того, как становится
известным результат испытания, в итоге
которого появилось событие А.
Теорема.
Вероятность гипотезы после испытания
равна произведению вероятности гипотезы
до испытания на соответствующую ей
условную вероятность события, которое
произошло при испытании, деленному на
полную вероятность этого события.
Замечание.
Вероятности
P(H1),
…, P(Hn)
часто называют априорными вероятностями
группы событий
H1,
…, Hn,
в то время как условные вероятности
P(H1|A),…,
P(Hn|A)
– апостериорными, полученными после
дополнительного эксперимента, в котором
произошло событие А.
В связи с этим формула Байеса называется
также формулой обновления
априорных вероятностей.
Приведем
несколько задач, решаемых с помощью
полученных формул условной вероятности.
Статистический
контроль качества.
Формула Байеса играет большую роль в
планировании процедур гарантийного
контроля качества выпускаемой продукции.
Производитель продукта должен выполнять
определенные договорные обязательства
перед потребителем, которые, так или
иначе, сводятся к ограничениям на долю
некондиционной продукции, поставляемой
потребителю, или, что то же, доля
кодндиционной продукции должна быть
достаточно высокой. Обеспечение этих
ограничений достигается с помощью
контроля (как правило, выборочног)
производимой продукции. Пусть Qin
– доля кондиционной продукции среди
изготавливаемой предариятием. Обычно
эта доля называется входным
уровнем качества,
и необходимость контроля продукции
обуславливается невысоким значеним
Qin,
которое не удовлетворяет потребителя.
Если контроль продукции производится
на основе обследования только ее части
(так называемый выборочный
или статистический
контроль качества), то возникает
вероятность принятия ошибочного решения
о качестве контролируемого продукта:
с некоторой вероятностью
процедура контроля может пропустить
некондиционный продукт или, наоборот,
с вероятностью
отклонить кондиционный. Вероятность
называется риском
потребителя,
а вероятность
– риском
изготовителя.
Существуют методы расчета этих рисков
на основе вероятностной модели
статистического контроля. Зная значения
Qin,
и ,
можно, используя формулу Байеса, вычислить
выходной уровень качества Qout
– долю кондиционной продукции, срели
отсылаемой потребителю после контроля.
Пусть
H1
– событие, состоящее в том, что поступивший
на контроль продукт кондиционен, а H2
– продукт «плохой». В наших обозначениях
Р(H1)
= Qin.
Пусть, далее, А
– утверждение о кондиционности продукта
после его контроля. Тогда Qout
= P(H1
/А)
– вероятность кондиционности продукта
при условии, что он проше контроль.
Наконец, P(А/H1)
= 1 –
и P(А/H2)
= .
По формуле Байеса
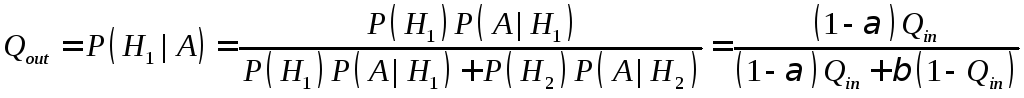 .
.
Проиллюстрируем
расчеты, производимые по этой формуле,
на основе конкретных числовых данных.
Пусть предприятие работает из рку вон
плохо: Qin
= 0,1 (90% выпускаемой продукции не
удовлетворяет нормам качества), но на
предприятии существует довольно жесткий
контроль, в котором риск потребителя
= 0,01, а риск изготовителя
= 0,1. Тогда выходной уровень качества
![]() ,
,
и это совсем неплохо
по сравнению с тем, что было до контроля.
Пример.
Детали, изготовляемые цехом завода,
попадают для проверки их на стандартность
к одному из двух контролеров. Вероятность
того, что деталь попадает к первому
контролеру, равна 0,6, а ко второму – 0,4.
Вероятность того, что годная деталь
будет признана стандартной первым
контролером, равна 0,94, а вторым – 0,98.
Годная деталь при проверке была признана
стандартной. Найти вероятность того,
что эту деталь проверил первый контролер.
Решение.
Обозначим через А
событие, состоящее в том, что годная
деталь признана стандартной. Можно
сделать два предположения:
1)
деталь проверил первый контролер
(гипотеза H1);
2)
деталь проверил второй контролер
(гипотеза H2).
Искомую
вероятность того, что деталь проверил
первый контролер, найдем по формуле
Бейеса:

По условию задачи
имеем:
Р(H1)
= 0,6 (вероятность того, что деталь попадает
к первому контролеру);
Р(H2)
= 0,4 (вероятность того, что деталь попадет
ко второму контролеру);
P(А/H1)
= 0,94 (вероятность того, что годная деталь
будет признана первым контролером
стандартной);
P(А/H2)
= 0,98 (вероятность того, что годная деталь
будет признана вторым контролером
стандартной).
Искомая вероятность
![]() .
.
Как
видно, до испытания вероятность гипотезы
H1
равнялась 0,6, а после того, как стал
известен результат испытания, вероятность
этой гипотезы (точнее, условная
вероятность) изменилась и стала равной
0,59. Таким образом, использование формулы
Бейеса позволило переоценить вероятность
рассматриваемой гипотезы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Составитель преподаватель кафедры высшей математики Ищанов Т.Р. Занятие №4. Формула полной вероятности. Вероятность гипотез. Формулы Байеса.
Теоретический материал
Доказательство. По условию, событие А может наступить, если наступит одно из несовместных событий ![]() .
.
Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий ![]() . Пользуясь для вычисления вероятности события А теоремой сложения, получим
. Пользуясь для вычисления вероятности события А теоремой сложения, получим
![]()
Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий имеем
![]()
![]()
Подставив правые части этих равенств в соотношение (*), получим формулу полной вероятности
![]()
Пример 1. Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго—0,9. Найти вероятность того, что взятая наудачу деталь (из наудачу взятого набора) — стандартная.
Решение. Обозначим через А событие «извлеченная деталь стандартна».
Деталь может быть извлечена либо из первого набора (событие B1), либо из второго (событие B2).
Вероятность того, что деталь вынута из первого набора, ![]() .
.
Вероятность того, что деталь вынута из второго набора, ![]() .
.
Условная вероятность того, что из первого набора будет извлечена стандартная деталь, ![]() .
.
Условная вероятность того, что из второго набора будет извлечена стандартная деталь ![]() .
.
Искомая вероятность того, что извлеченная наудачу деталь — стандартная, по формуле полной вероятности равна
![]()
Пример 2. В первой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке—10 ламп, из них 9 стандартных. Из второй коробки наудачу взята лампа и переложена в первую. Найти вероятность того, что лампа, наудачу извлеченная из первой коробки, будет стандартной.
Решение. Обозначим через А событие «из первой коробки извлечена стандартная лампа».
Из второй коробки могла быть извлечена либо стандартная лампа (событие B1), либо нестандартная (событие B2).
Вероятность того, что из второй коробки извлечена стандартная лампа, ![]()
Вероятность того, что из второй коробки извлечена нестандартная лампа, ![]()
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена стандартная лампа, равна ![]()
Условная вероятность того, что из первой коробки извлечена стандартная лампа, при условии, что из второй коробки в первую была переложена нестандартная лампа, равна ![]()
Искомая вероятность того, что из первой коробки будет извлечена стандартная лампа, по формуле полной вероятности равна
![]()
Вероятность гипотез. Формулы Байеса
Пусть событие A может наступить при условии появления одного из несовместных событий ![]() , образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события A определяется по формуле полной вероятности:
, образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события A определяется по формуле полной вероятности:
![]()
Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменились (в связи с тем, что событие А уже наступило) вероятности гипотез. Другими словами, будем искать условные вероятности
![]()
Найдем сначала условную вероятность ![]() . ПО теореме умножения имеем
. ПО теореме умножения имеем
![]()
Отсюда
![]()
Заменив здесь Р (А) по формуле (*), получим
![Rendered by QuickLaTeX.com [P_{A}(B_1)=frac{P(B_1)P_{B_1}(A)}{P(B_1)P_{B_1}(A)+P(B_2)P_{B_2}(A)+cdots+P(B_n)P_{B_n}(A)}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-414c0ad64a0dade48eaf03b7537ae016_l3.png)
.
Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т. е. условная вероятность любой гипотезы ![]() может быть вычислена по формуле
может быть вычислена по формуле
![]()
Полученные формулы называют формулами Байеса (по имени английского математика, который их вывел; опубликованы в 1764 г.). Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Пример. Детали, изготовляемые цехом завода, попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что деталь попадает к первому контролеру, равна 0,6, а ко второму — 0,4. Вероятность того, что годная деталь будет признана стандартной первым контролером, равна 0,94, а вторым—0,98. Годная деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.
Решение. Обозначим через А событие, состоящее в том, что годная деталь признана стандартной. Можно сделать два предположения:
1)деталь проверил первый контролер (гипотеза ![]() );
);
2)деталь проверил второй контролер (гипотеза ![]() ). Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Байеса:
). Искомую вероятность того, что деталь проверил первый контролер, найдем по формуле Байеса:
![]()
По условию задачи имеем:
![]() (вероятность того, что деталь попадает к первому контролеру);
(вероятность того, что деталь попадает к первому контролеру);
![]() (вероятность того, что деталь попадет ко второму контролеру);
(вероятность того, что деталь попадет ко второму контролеру);
![]() (вероятность того, что годная деталь будет признана первым контролером стандартной);
(вероятность того, что годная деталь будет признана первым контролером стандартной);
![]() (вероятность того, что годная деталь будет признана вторым контролером стандартной).
(вероятность того, что годная деталь будет признана вторым контролером стандартной).
Искомая вероятность
![]()
Как видно, до испытания вероятность гипотезы ![]() равнялась 0,6, после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равной 0,59. Таким образом, использование формулы Байеса позволило переоценить вероятность рассматриваемой гипотезы.
равнялась 0,6, после того, как стал известен результат испытания, вероятность этой гипотезы (точнее, условная вероятность) изменилась и стала равной 0,59. Таким образом, использование формулы Байеса позволило переоценить вероятность рассматриваемой гипотезы.
Практический материал.
1. (4) Сборщик получил 3 коробки деталей, изготовленных заводом № 1, и 2 коробки деталей, изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна, равна 0,8, а завода № 2 — 0,9, Сборщик наудачу извлек деталь из наудачу взятой коробки. Найти вероятность того, что извлечена стандартная деталь.
Отв. 0,84.
2. (5) В первом ящике содержится 20 деталей, из них 15 стандартных; во втором—30 деталей, из них 24 стандартных; в третьем — 10 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика—стандартная.
Отв. 43/60.
3. (6) В телевизионном ателье имеется 4 кинескопа. Вероятности того, что кинескоп выдержит гарантийный срок службы, соответственно равны 0,8; 0,85; 0,9; 0,95. Найти вероятность того, что взятый наудачу кинескоп выдержит гарантийный срок службы.
Отв. 0,875.
4. (3) В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника—0,9, для велосипедиста—0,8. и для бегуна—0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму.
Отв. 0,86.
5. © В белом ящике 12 красных и 6 синих шаров. В черном – 15 красных и 10 синих шаров. Бросают игральный кубик. Если выпадет количество очков, кратное 3, то наугад берут шар из белого ящика. Если выпадет любое другое количество очков, то наугад берут шар из черного ящика. Какова вероятность появления красного шара?
Показать решение
Решение:
Возможны две гипотезы:
![]() – при бросании кубика выпадет количество очков, кратное 3, т.е. или 3 или 6;
– при бросании кубика выпадет количество очков, кратное 3, т.е. или 3 или 6;
![]() – при бросании кубика выпадет другое количество очков, т.е. 1, 2, 4 или 5.
– при бросании кубика выпадет другое количество очков, т.е. 1, 2, 4 или 5.
По классическому определению вероятности гипотез равны:
![]()
Поскольку гипотезы составляют полную группу событий, то должно выполняться равенство
![]()
Пусть событие А состоит в появлении красного шара. Условные вероятности этого события зависят от того, какая именно гипотеза реализовалась, и составляют соответственно:
![Rendered by QuickLaTeX.com [P_{H_1}(A)=frac{12}{18}=frac23;qquad P_{H_2}(A)=frac{15}{25}=frac35]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-d2acaa8e470f760cbca1bc340a038923_l3.png)
Тогда по формуле полной вероятности вероятность события А будет равна:
![]()
6. (7) В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная; во втором 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной.
Отв. 13/132.
7. (89 Г) В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если равновозможны все возможные предположения о первоначальном составе шаров (по цвету).
Показать решение
Решение. Обозначим через А событие – извлечен белый шар. Возможны следующие предположения (гипотезы) о первоначальном составе шаров:
![]() — белых шаров нет,
— белых шаров нет,
![]() — один белый шар,
— один белый шар,
![]() — два белых шара.
— два белых шара.
Поскольку всего имеется три гипотезы, причем по условию они равновероятны, и сумма вероятностей гипотез равна единице (так как они образуют полную группу событий), то вероятность каждой из гипотез равна 1/3, т.е. ![]() .
.
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне не было белых шаров, ![]() .
.
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне был один белый шар, ![]() .
.
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне было два белых шара ![]() .
.
Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:
![]()
8. (10) В ящик, содержащий 3 одинаковых детали, брошена стандартная деталь, а затем наудачу извлечена одна деталь. Найти вероятность того, что извлечена стандартная деталь, если равновероятны все возможные предположения о числе стандартных деталей, первоначально находящихся в ящике.
Отв. 0,625.
9. (6.5.2Л) Для улучшения качества радиосвязи используются два радиоприемника. Вероятность приема сигнала каждым приемником равна 0,8, и эти события (прием сигнала приемником) независимы. Определить вероятность приема сигнала, если вероятность безотказной работы за время сеанса радиосвязи для каждого приемника равна 0,9.
Показать решение
Решение.
Пусть событие А={сигнал будет принят}. Рассмотрим четыре гипотезы:
![]() ={первый приемник работает, второй — нет};
={первый приемник работает, второй — нет};
![]() ={второй работает, первый — нет};
={второй работает, первый — нет};
![]() ={оба приемника работают};
={оба приемника работают};
![]() ={оба приемника не работают}.
={оба приемника не работают}.
Событие А может произойти только с одной из этих гипотез. Найдем вероятность этих гипотез, рассматривая следующие события:
![]() ={первый приемник работает},
={первый приемник работает},
![]() ={второй приемник работает}.
={второй приемник работает}.
Тогда:
![]()
![]()
![]()
![]()
Контроль:
![Rendered by QuickLaTeX.com [sum_{i=1}^4 P(H_i )=0,09+0,09+0,81+0,01=1.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-42f28b7e0bb0599dd26aa0e693d0f6e4_l3.png)
Условные вероятности ![]() соответственно равны:
соответственно равны:
![]()
![]()
![]()
![]()
Теперь по формуле полной вероятности находим искомую вероятность
![]()
10. (11) При отклонении от нормального режима работы автомата срабатывает сигнализатор С-1 с вероятностью 0,8, а сигнализатор С-11 срабатывает с вероятностью 1. Вероятности того, что автомат снабжен сигнализатором С-1 или С-11, соответственно равны 0,6 и 0,4. Получен сигнал о разделке автомата. Что вероятнее: автомат снабжен сигнализатором С-1 или С-11?
Отв. Вероятность того, что автомат снабжен сигнализатором С-1, равна 6/11, а С- 11— 5/11
11. (12) Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй — 6, из третьей группы — 5 студентов. Вероятности того, что студент первой, второй и третьей группы попадает в сборную института, соответственно равны 0,9; 0,7 и 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент?
Отв. Вероятности того, что выбран студент первой, второй, третьей групп, соответственно равны: 18/59, 21/59, 20/59.
12. (1.34К) В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го, 2-го и 3-го поставщиков, не потребуют ремонта в течении гарантийного срока соответственно в 98, 88 и 92% случаев.
1) Найти вероятность того, что поступивший в торговую фирму телевизор не потребует ремонта в течение гарантийного срока.
2) Проданный телевизор потребовал ремонта в течение гарантийного срока. От какого поставщика вероятнее всего поступил этот телевизор?
Показать решение
Решение.
Обозначим события: ![]() — телевизор поступил в торговую фирму от i-го поставщика (i=1,2,3);
— телевизор поступил в торговую фирму от i-го поставщика (i=1,2,3);
A – телевизор не потребует ремонта в течение гарантийного срока.
По условию
![]()
![]()
![]()
По формуле полной вероятности
![]()
Событие ![]() телевизор потребует ремонта в течение гарантийного срока:
телевизор потребует ремонта в течение гарантийного срока:
![]()
По условию
![]()
![]()
![]()
По формуле Байеса
![]()
![]()
Таким образом, после наступления события ![]() вероятность гипотезы H2 увеличилась с P (H2)=0,4 до максимальной
вероятность гипотезы H2 увеличилась с P (H2)=0,4 до максимальной
![]() ,
,
а гипотезы H3 — уменьшилась от максимальной P (H3)=0,5 до ![]() ; если ранее (до наступления события А) наиболее вероятной была гипотеза H3, то теперь, в свете новой информации (наступления события А), наиболее вероятна гипотеза H2 -поступление данного телевизора от 2-го поставщика.
; если ранее (до наступления события А) наиболее вероятной была гипотеза H3, то теперь, в свете новой информации (наступления события А), наиболее вероятна гипотеза H2 -поступление данного телевизора от 2-го поставщика.
13. (1.35К) Известно, что в среднем 95% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,98, если она стандартна, и с вероятностью 0,06, если она нестандартна. Определить вероятность того, что:
1) взятое наудачу изделие пройдет упрощенный контроль;
2) изделие стандартное, если оно: а) прошло упрощенный контроль; б) дважды прошло упрощенный контроль.
Показать решение
Решение.
1). Обозначим события:
![]() — взятое наудачу изделие соответственно стандартное или нестандартное;
— взятое наудачу изделие соответственно стандартное или нестандартное;
![]() — изделие прошло упрощенный контроль.
— изделие прошло упрощенный контроль.
По условию
![Rendered by QuickLaTeX.com [P(H_1)=0,95,qquad P(H_2)=0,05,qquad P_{H_1}(A)=0,98,qquad P_{H_2}(A)=0,06.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-2adac332ec23eb79c8ea2227c66be229_l3.png)
Вероятность того, что взятое наудачу изделие пройдет упрощенный контроль, по формуле полной вероятности:
![Rendered by QuickLaTeX.com [P(A)=0,95cdot 0,98+0,05cdot 0,06=0,934.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-995052df9771efa0f0993a2aedf2769c_l3.png)
2. а). Вероятность того, что изделие, прошедшее упрощенный контроль, стандартное, по формуле Байеса:
![Rendered by QuickLaTeX.com [P_{A}(H_1)=frac{0,95cdot 0,98}{0,934}=0,997.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-2f90a08c4245cec6eb881023bc98a312_l3.png)
2. б). Пусть событие ![]() — изделие дважды прошло упрощенный контроль. Тогда по теореме умножения вероятностей:
— изделие дважды прошло упрощенный контроль. Тогда по теореме умножения вероятностей:
![Rendered by QuickLaTeX.com [P_{H_1}(A^*)=0,98cdot 0,98=0,9604, qquad P_{H_2}(A^*)=0,06cdot 0,06=0,0036.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-9fad10e748c24a6f6ef888161d2262ba_l3.png)
По формуле Байеса
![Rendered by QuickLaTeX.com [P_{A^*}(H_1)=frac{0,95cdot 0,9604}{0,95cdot 0,9604+0,05cdot 0,0036}=0,9998.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-f7fa8f07d58a1ca7b6a6547f45088ff8_l3.png)
Так как
![Rendered by QuickLaTeX.com [P_{A^*}(H_2)=1-P_{A^*}(H_1)=1-0,9998=0,0002]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-44e0370a1466aab6f6b8b2e1a33748d4_l3.png)
очень мала, то гипотезу ![]() о том, что изделие, дважды прошедшее упрощенный контроль, нестандартное, следует отбросить как практически невозможное событие.
о том, что изделие, дважды прошедшее упрощенный контроль, нестандартное, следует отбросить как практически невозможное событие.
14. (1.36К) Два стрелка независимо друг от друга стреляют по мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0,8; для второго – 0,4. После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что она принадлежит:
а) 1-му стрелку;
б) 2-му стрелку?
Показать решение
Решение.
Обозначим события:
![]() — оба стрелка не попали в мишень;
— оба стрелка не попали в мишень;
![]() — оба стрелка попали в мишень;
— оба стрелка попали в мишень;
![]() — 1-й стрелок попал в мишень, 2-й нет;
— 1-й стрелок попал в мишень, 2-й нет;
![]() — 1-й стрелок не попал в мишень, 2-й попал;
— 1-й стрелок не попал в мишень, 2-й попал;
![]() — в мишени одна пробоина (одно попадание).
— в мишени одна пробоина (одно попадание).
Найдем вероятности гипотез и условные вероятности события ![]() для этих гипотез:
для этих гипотез:
![Rendered by QuickLaTeX.com [P(H_1)=0,2cdot 0,6=0,12,qquad P_{H_1}(A)=0;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-f5ea1fb3127c9a2a5d4aedf0131e7cda_l3.png)
![Rendered by QuickLaTeX.com [P(H_2)=0,8cdot 0,4=0,32,qquad P_{H_2}(A)=0;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-a89ee391a2b0e2d588e191dd964ccd9e_l3.png)
![Rendered by QuickLaTeX.com [P(H_3)=0,8cdot 0,6=0,48,qquad P_{H_3}(A)=1;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-54985f83008fa4483efee09d4f7b6fc7_l3.png)
![Rendered by QuickLaTeX.com [P(H_4)=0,2cdot 0,4=0,08,qquad P_{H_4}(A)=1.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-a280aea2aa24bade5f160606e1031bca_l3.png)
Теперь по формуле Байеса
![]()
![Rendered by QuickLaTeX.com [P_{A}(H_4)=frac{0,08cdot 1}{0,12cdot 0+0,32cdot 0+0,48cdot 1+0,08cdot 1}=frac{1}{7}=0,143,]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-3a5796e5d18187076c6197c45d9f22ad_l3.png)
т.е. вероятность того, что попал в цель 1-й стрелок при наличии одной пробоины, в 6 шесть раз выше, чем для второго стрелка.
15. (6.5.8Л) Техническое устройство выйдет из строя, если откажут не менее двух из трех независимо работающих элементов. Вероятности отказов 1-го, 2-го, 3-го элементов соответственно равны 0,2; 0,4; 0,3. Известно, что устройство отказало. Найти вероятность того, что отказали 1-й и 2-й элементы.
Показать решение
Решение.
Пусть событие А={устройство отказало}. До опыта, т.е. до отказа устройства, можно сделать следующие предположения-гипотезы:
![]() ={откажут все три элемента};
={откажут все три элемента};
![]() ={откажут два элемента: 1-й и 2-й, 3-й — не откажет};
={откажут два элемента: 1-й и 2-й, 3-й — не откажет};
![]() ={откажут два элемента: 1-й и 3-й, 2-й — не откажет};
={откажут два элемента: 1-й и 3-й, 2-й — не откажет};
![]() ={откажут два элемента: 2-й и 3-й, 1-й — не откажет};
={откажут два элемента: 2-й и 3-й, 1-й — не откажет};
![]() ={откажет один элемент: 1-й, не откажут 2-й и 3-й};
={откажет один элемент: 1-й, не откажут 2-й и 3-й};
![]() ={откажет один элемент: 2-й, не откажут 1-й и 3-й};
={откажет один элемент: 2-й, не откажут 1-й и 3-й};
![]() ={откажет один элемент: 3-й, не откажут 1-й и 2-й};
={откажет один элемент: 3-й, не откажут 1-й и 2-й};
![]() ={все элементы, будут работать}.
={все элементы, будут работать}.
Пользуясь правилом умножения вероятностей для независимых событий, найдем вероятности этих гипотез:
![Rendered by QuickLaTeX.com [P(H_0)=0,2cdot 0,4cdot 0,3=0,024;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c150b618b1a03475027e1fcddcd656ea_l3.png)
![Rendered by QuickLaTeX.com [P(H_1)=0,2cdot 0,4cdot 0,7=0,056;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-7a0ff50fcdd0530d1a08cc8c903dc631_l3.png)
![Rendered by QuickLaTeX.com [P(H_2)=0,2cdot 0,3cdot 0,6=0,036;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-f68aaae357b59f86391b2321090eae2e_l3.png)
![Rendered by QuickLaTeX.com [P(H_3)=0,4cdot 0,3cdot 0,8=0,096;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-93c899c03286331a768d9a0d8f38374e_l3.png)
![Rendered by QuickLaTeX.com [P(H_4)=0,2cdot 0,6cdot 0,7=0,084;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-908d20d239c45c75545035dc76b709b7_l3.png)
![Rendered by QuickLaTeX.com [P(H_5)=0,4cdot 0,8cdot 0,7=0,224;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c890e565babe2e62a029e36a556149c9_l3.png)
![Rendered by QuickLaTeX.com [P(H_6)=0,3cdot 0,8cdot 0,6=0,144;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-2ed2234cc67b53f9804c6f6c8b7e5838_l3.png)
![Rendered by QuickLaTeX.com [P(H_7)=0,8cdot 0,6cdot 0,7=0,336.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-ed607db639e529dfd9d7675d9463d9e0_l3.png)
Контроль:
![Rendered by QuickLaTeX.com [sum_{i=0}^7 P(H_i)=0,024+0,056+cdots+0,336=1.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6784a3f4ac0528d74d1d2a753ebe98d5_l3.png)
Учитывая, что в результате опыта произошло событие А, которое невозможно при гипотезах H4, H5, H6, H7 и достоверно при гипотезах H0, H1, H2, H3, найдем условные вероятности событий ![]() :
:
![]()
![]()
![]()
![]()
Найдем вероятность гипотезы ![]() при условии, что событие А произошло по формуле Байеса. Для этого предварительно найдем вероятность события А по формуле:
при условии, что событие А произошло по формуле Байеса. Для этого предварительно найдем вероятность события А по формуле:
![Rendered by QuickLaTeX.com [P(A)=sum_{i=0}^7 P(H_i)cdot P_{H_i}(A)=0,024cdot 1+0,056cdot 1+0,096cdot 1+0+0+0+0=0,212.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-e030566203f16ea9c5480b9d5320e782_l3.png)
Отсюда
![Rendered by QuickLaTeX.com [P_{A}(H_1)=frac{P(H_1)cdot P_{H_1}(A)}{P(A)}=frac{0,056cdot 1}{0,212}=frac{56}{212}=frac{14}{53}approx 0,264.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c8a3425e4be5d81f241b52f6c267fe39_l3.png)
16.(1.36аК) Компания по страхованию автомобилей разделяет водителей на три класса, которые включают 20%, 50% и 30% водителей соответственно. Вероятности того, что в течение года водитель попадет в аварию, равны 0,01, 0,03 и 0,1 соответственно для каждого класса. Наугад выбранный водитель два года подряд из пяти лет срока страховки попал в аварию. Какова вероятность того, что он относится:
а) к первому классу;
б) к третьему классу?
Показать решение
Решение.
Обозначим события:
![]() — водитель соответственно первого, второго и третьего класса;
— водитель соответственно первого, второго и третьего класса;
![]() — водитель два года подряд из пяти лет срока страховки попадал в аварию.
— водитель два года подряд из пяти лет срока страховки попадал в аварию.
По условию ![]()
Найдем условные вероятности события ![]() (учитываем, что из пяти лет водитель три года не попадал в аварию, два года — попадал, причем попадал два года подряд, что дает четыре варианта (по годам 1-2, 2-3, 3-4, 4-5)):
(учитываем, что из пяти лет водитель три года не попадал в аварию, два года — попадал, причем попадал два года подряд, что дает четыре варианта (по годам 1-2, 2-3, 3-4, 4-5)):
![Rendered by QuickLaTeX.com [P_{H_1}(A)=4cdot 0,01^2cdot 0,99^3=0,00039;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-585ce04e64c3f23510caa64df7b7af35_l3.png)
![Rendered by QuickLaTeX.com [P_{H_2}(A)=4cdot 0,03^2cdot 0,97^3=0,00329;]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-0e9e421e4012e73591ad829ecc000429_l3.png)
![Rendered by QuickLaTeX.com [P_{H_3}(A)=4cdot 0,1^2cdot 0,9^3=0,02916.]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-3e9fcebc7976a710fc3dfdc6c8ab173f_l3.png)
По формуле Байеса:
![]()
![Rendered by QuickLaTeX.com [P_{A}(H_3)=frac{0,3cdot 0,02916}{0,2cdot 0,00039+0,5cdot 0,00329+0,3cdot 0,02916}=0,835,]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-c384e73d499dbd38ef962c10d257ed6a_l3.png)
т.е. после наступления события A гипотеза ![]() практически невозможна и должна быть отвергнута.
практически невозможна и должна быть отвергнута.
Формула полной вероятности. Вероятность гипотез
Формула полной вероятности
Теорема Вероятность события $A$, которое может наступить лишь при появлении одного из несовместных событий $B_1 ,B_2 ,ldots B_n $, образующих полную группу равна сумме произведений вероятности каждого из событий на соответствующую условную вероятность. begin{equation} label { eq5 } P( A )=P( { B_1 } )cdot P_ { B_1 } ( A )+P( { B_2 } )cdot P_ { B_2 } ( A )+ldots +P( { B_n } )cdot P_ { B_n } ( A ) qquad (5) end{equation} Формула полной вероятности.
Вероятность полной группы несовместных событий $ P( { B_1 } )+P( { B_2 } )+ldots +P( { B_n } )=1 $
Пример. Имеется два набора ламп. Вероятность того, что лампа 1-го набора стандартна, равна 0,8, второго – 0,7. Найти вероятность того, что взятая наудачу лампа { из наудачу взятого набора } – стандартна.
Решение } : пусть событие $A=$ { извлеченная лампа стандартна }
$B_1 =$ { лампа извлечена из 1-го набора }
$B_2 =$ { лампа извлечена из 2-го набора }
эти события попарно – несовместны.
Вероятность того, что лампа вынута из 1-го набора $P( { B_1 } )=frac { 1 } { 2 } =0,5$.
Вероятность того, что лампа вынута из 2-го $P( { B_2 } )=frac { 1 } { 2 } =0,5$.
Вероятность полной группы несовместных событий $sumlimits_i { P( { B_i } )=0,5+0,5=1 } $.
Вероятность того, что вынутая из 1-го набора лампа является стандартной, есть условная вероятность $P_ { B_1 } ( A )=0,8$
Вероятность того, что вынутая из 2-го набора лампа является стандартной, есть условная вероятность $P_ { B_2 } ( A )=0,7$
Искомая вероятность того, что вынутая наудачу лампа является стандартной, есть $ P( A )=P( { B_1 } )cdot P_ { B_1 } ( A )+P( { B_2 } )cdot P_ { B_2 } ( A )=frac { 1 } { 2 } cdot 0,8+frac { 1 } { 2 } cdot 0,7=frac { 1 } { 2 } cdot 1,5=0,75 $
Вероятность гипотез. Формула Байеса
При рассмотрении формулы полной вероятности событие $A$наступает при условии появления одного из несовместных событий $B_i $, следовательно, события $A$ и $B_i$ – зависимы. Поскольку заранее неизвестно какое из событий наступит, то будем события $B_i$ называть гипотезами.
Допустим теперь, что событие $A$ – наступило. Этот факт изменит вероятность гипотез $P_A ( { B_1 } )ldots P_A ( { B_n } )$
Найдем условные вероятности в предположении, что событие $A$ наступило т.е. $P_A ( { B_1 } ),,,P_A ( { B_2 } )ldots $ { переоценка гипотезы }
Для этого используем теорему умножения.
$P(AB_1)=P(A)cdot P_A(B_1)=P(B_1)cdot P_ { B_ { 1 } } (A)$
$P_A ( { B_1 } )=frac { P( { B_1 } )cdot P_ { B_1 } ( A ) } { P( A ) } $, Формула Байеса
где $P( A )$ находится по формуле полной вероятности.
Формула Байеса позволяет переоценить вероятности гипотез после того, как событие $A$ произошло.
В формуле Байеса есть контроль $ sumlimits_i { P( { B_i } )=1 } $
Пример. Сверла попадают для проверки их на стандартность к одному из двух контролеров. Вероятность того, что сверло попало к первому контролеру, равна 0,6. Ко второму – 0,4. Вероятность того, что сверло будет признано стандартным 1-м контролером, равна 0,95 – вторым 0,97. Готовое сверло было признано стандартным. Найти вероятность того, что это сверло проверил 1-й контролер.
Решение. Через $A$, обозначим событие, которое произошло. $A=$ { готовое сверло признано стандартным }
Сделаем два предположения, две гипотезы:
$B_1 =$ { сверло проверил 1 -й контролер } , $P(B_1 )=0,6$,
$B_2 =$ { сверло проверил 2 -й контролер } , $P(B_2 )=0,4$,
Контроль $sumlimits_i { P( { B_i } )=0,6+0,4=1 } $
Вероятность того, что сверло будет признано стандартным 1-м контролером $P_ { B_1 } (A)=0,95$,
Вероятность того, что сверло будет признано стандартным 1-м контролером $P_ { B_2 } (A)=0,97$,
Искомую вероятность, т.е. вероятность того, что стандартное сверло проверил } 1-й контролер, $P_A ( { B_1 } )$ найдем по формуле Байеса, $P( A )$ – находится по формуле полной вероятности.
$ P_A ( { B_1 } )=frac { P( { B_1 } )cdot P_ { B_1 } ( A ) } { P( A ) } =frac { P( { B_1 } )cdot P_ { B_1 } ( A ) } { P( { B_1 } )cdot P_ { B_1 } ( A )+P( { B_2 } )cdot P_ { B_2 } ( A ) } =frac { 0,6cdot 0,95 } { 0,6cdot 0,95+0,4cdot 0,97 } =frac { 0,57 } { 0,57+0,388 } =frac { 0,57 } { 0,958 } approx 0,595$
До испытания вероятность гипотезы $B_1 $ равнялась 0,6, а после того, как стал известен результат испытания, вероятность этой гипотезы { т.е. условная вероятность } изменилась и стала 0,595.
Содержание:
Формула полной вероятности:
Пусть событие А может произойти в результате появления одного и только одного события 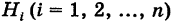
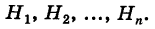
События этой группы обычно называются гипотезами.
Теорема: Вероятность события А равна сумме парных произведений вероятностей всех гипотез, образующих полную группу, на соответствующие условные вероятности данного события А, т. е.
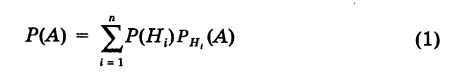
(формула полной вероятности), причем здесь

Доказательство. Так как
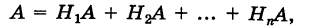
причем, ввиду несовместности событий 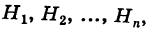 события
события 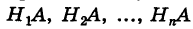 также несовместны, то на основании теорем сложения и умножения вероятностей имеем
также несовместны, то на основании теорем сложения и умножения вероятностей имеем
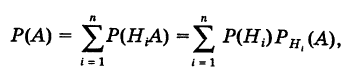
что и требовалось доказать.
Пример:
В магазин для продажи поступает продукция трех фабрик, относительные доли которых есть: I — 50%, II — 30%, III — 20%. Для продукции фабрик брак соответственно составляет: I — 2%, II — 3%, III — 5%. Какова вероятность того, что изделие этой продукции, случайно приобретенное в магазине, окажется доброкачественным (событие А)?
Решение:
Здесь возможны следующие три гипотезы: 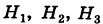 — приобретенная вещь выработана соответственно на I, II и III фабриках; очевидно, система этих гипотез полная, причем их вероятности
— приобретенная вещь выработана соответственно на I, II и III фабриках; очевидно, система этих гипотез полная, причем их вероятности
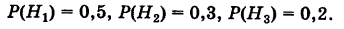
Соответствующие условные вероятности события А равны
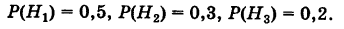
По формуле полной вероятности имеем
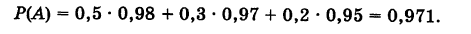
Формула Бейеса:
Пример:
Имеется полная группа несовместных гипотез
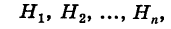
вероятности которых 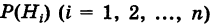 известны до опыта (вероятности априори). Производится опыт (испытание), в результате которого зарегистрировано появление события А, причем известно, что этому событию наши гипотезы приписывали определенные вероятности
известны до опыта (вероятности априори). Производится опыт (испытание), в результате которого зарегистрировано появление события А, причем известно, что этому событию наши гипотезы приписывали определенные вероятности 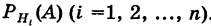 . Спрашивается, каковы будут вероятности этих гипотез после опыта (вероятности апостериори).
. Спрашивается, каковы будут вероятности этих гипотез после опыта (вероятности апостериори).
Например, очевидно, следует отбросить гипотезы, отрицающие появление события А. Вообще, проблема состоит в том, что, имея новую информацию, мы должны переоценить вероятности наших гипотез.
Иными словами, нам нужно определить условные вероятности
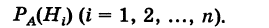
На основании теоремы умножения вероятностей имеем
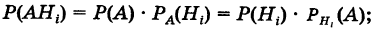
отсюда
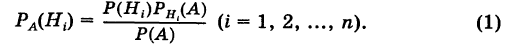
Для нахождения вероятности Р(А) можно использовать формулу полной вероятности
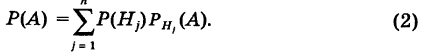
Отсюда имеем формулу вероятностей гипотез после опыта (<формулу Бейеса)
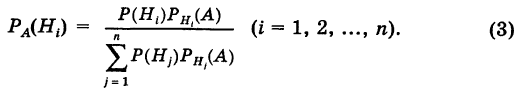
Пример:
Вероятность поражения самолета при одиночном выстреле для 1-го ракетного расчета (событие А) равна 0,2, а для 2-го (событие В) — 0,1. Каждое из орудий производит по одному выстрелу, причем зарегистрировано одно попадание в самолет (событие С). Какова вероятность, что удачный выстрел принадлежит первому расчету?
Решение:
До опыта возможны четыре гипотезы: 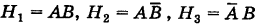
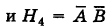 ; эти гипотезы образуют полную группу событий.
; эти гипотезы образуют полную группу событий.
Вероятности их, при независимом действии расчетов, соответственно равны
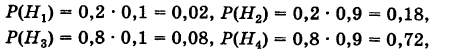
причем 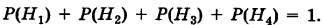
Условные вероятности для наблюдаемого события С при данных гипотезах будут
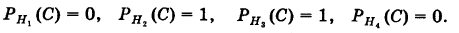
Следовательно, гипотезы 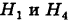 отпадают, а вероятности гипотез
отпадают, а вероятности гипотез 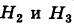 вычисляются по формуле Бейеса:
вычисляются по формуле Бейеса:
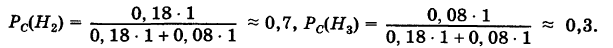
Таким образом, с вероятностью приблизительно 0,7 можно утверждать, что удачный выстрел принадлежит 1-му расчету,
Формула полной вероятности
Пусть событие А еще не произошло, но вскоре должно произойти. Событие А может протекать в различных условиях, относительно характера которых сделано 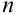 гипотез
гипотез 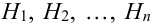 , образующих полную группу несовместных событий. Вероятности гипотез известны. Тогда вероятность события А равна сумме произведений вероятности каждой гипотезы на вероятность события при этой гипотезе:
, образующих полную группу несовместных событий. Вероятности гипотез известны. Тогда вероятность события А равна сумме произведений вероятности каждой гипотезы на вероятность события при этой гипотезе:
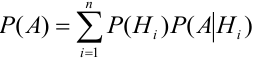 – формула полной вероятности.
– формула полной вероятности.
Доказательство.
По условию теоремы гипотезы 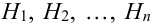 образуют полную группу несовместных событий, следовательно, событие А может произойти с одной и только с одной гипотезой:
образуют полную группу несовместных событий, следовательно, событие А может произойти с одной и только с одной гипотезой:
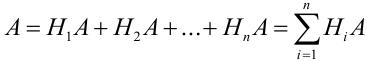 .
.
Т.к. гипотезы несовместны, то и комбинации 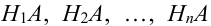 – несовместны. Применим теорему 1:
– несовместны. Применим теорему 1:
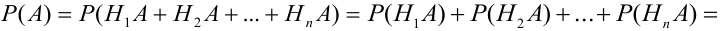
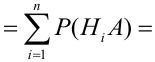 (события А и
(события А и 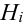 – зависимы, т.е. надо применить теорему 3) =
– зависимы, т.е. надо применить теорему 3) = 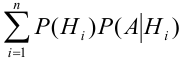 . (что и треб, доказать)
. (что и треб, доказать)
Пример:
Имеется пять урн:
2 урны состава  – по 2 белых шара и 1 черному,
– по 2 белых шара и 1 черному,
1 урна состава  – 10 черных шаров,
– 10 черных шаров,
2 урны состава  — по 3 белых и 1 черному шару.
— по 3 белых и 1 черному шару.
Наудачу выбирается урна, и из нее наудачу выбирается шар. Чему равна вероятность события А = {будет вынут белый шар}?
Решение.
Событие А еще не произошло. Шар может быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 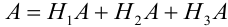 . Тогда по формуле полной вероятности:
. Тогда по формуле полной вероятности:
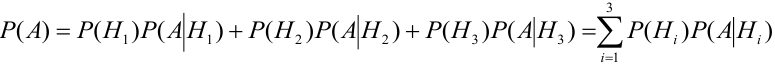 (*).
(*).
Найдем отдельно вероятности событий:
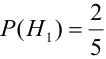 (две урны состава
(две урны состава 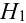 из пяти),
из пяти), 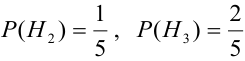 ,
,
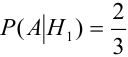 (в каждой урне состава
(в каждой урне состава  2 белых шара из трех),
2 белых шара из трех),
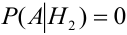 ( в урне состава
( в урне состава 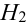 белых шаров нет),
белых шаров нет),
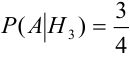 .
.
Подставим найденные вероятности в формулу (*): 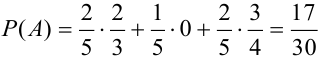 .
.
Формула полной вероятности и решение задач
Пример:
В двух одинаковых коробках имеется по 100 резисторов. В 1-й – 60 резисторов по 100 КОм, во 2-й 30 – резисторов по 100 КОм. Определить вероятность того, что взятый наугад из какой-либо коробки резистор будет 100 КОм.
Решение:
Пусть событие 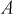 – достали резистор 100 КОм, гипотезы:
– достали резистор 100 КОм, гипотезы: 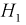 – выбрали 1-ю коробку,
– выбрали 1-ю коробку, 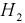 – выбрали 2-ю коробку. Так как коробки выбирали произвольно, то
– выбрали 2-ю коробку. Так как коробки выбирали произвольно, то 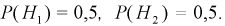 Условная вероятность того, что взяли резистор 100 КОм, при условии, что выбрана 1-я коробка –
Условная вероятность того, что взяли резистор 100 КОм, при условии, что выбрана 1-я коробка – 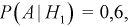 соответственно
соответственно 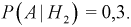 Тогда, применяя формулу (1.14) для
Тогда, применяя формулу (1.14) для 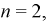 получаем
получаем 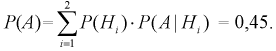
Пример №1
В первой коробке находится 20 деталей, из них 18 стандартных, во второй коробке – 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята одна деталь и переложена в первую коробку.
Какова вероятность того, что деталь, наудачу извлечённая после этого из первой коробки, окажется стандартной?
Решение. Обозначим события:
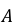 – из первой коробки извлечена стандартная деталь.
– из первой коробки извлечена стандартная деталь.
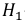 − из второй коробки в первую переложена стандартная деталь.
− из второй коробки в первую переложена стандартная деталь.
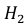 − из второй коробки в первую переложена нестандартная деталь.
− из второй коробки в первую переложена нестандартная деталь.
Событие А может наступить при условии наступления одного из событий 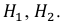 Эти события несовместны и образуют полную группу, т. е. являются гипотезами в формуле полной вероятности. Вероятность того, что из второй коробки извлечена стандартная деталь,
Эти события несовместны и образуют полную группу, т. е. являются гипотезами в формуле полной вероятности. Вероятность того, что из второй коробки извлечена стандартная деталь, 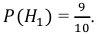
Вероятность того, что из второй коробки извлечена нестандартная деталь 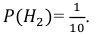
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена стандартная деталь, 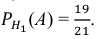
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена нестандартная деталь, 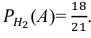
Искомая вероятность того, что из первой коробки будет извлечена стандартная деталь, по формуле полной вероятности равна:
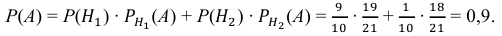 .
.
Ответ: 0,9.
Пример №2
Два станка производят одинаковые детали, которые поступают на общий конвейер. Производительность первого станка в два раза больше производительности второго станка. Первый производит 60 % деталей высшего сорта, а второй – 84 %. Наудачу взятая с конвейера деталь оказалась высшего сорта. Какова вероятность того, что эта деталь произведена на первом станке?
Решение. Обозначим события:
А – деталь, взятая с конвейера, оказалась высшего сорта.
Это событие наступит с одним из двух событий (гипотез):
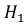 – эта деталь произведена на первом станке,
– эта деталь произведена на первом станке,
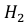 – эта деталь произведена на втором станке.
– эта деталь произведена на втором станке.
Поскольку производительность первого станка в два раза больше производительности второго станка, вероятности гипотез равны: 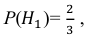
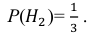
Условные вероятности события А даны: 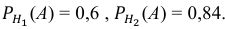
По формуле полной вероятности находим:
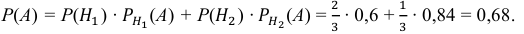
По формуле Байеса найдём условную вероятность того, что взятая наудачу деталь высшего сорта произведена на первом станке:
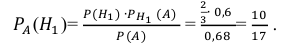
Ответ: 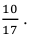
Пример №3
В ящике 20 белых и 10 чёрных шаров. Поочерёдно извлекают 4 шара, причём каждый извлечённый шар возвращают в ящик перед извлечением следующего. Какова вероятность того, что среди четырёх извлечённых шаров окажется два белых?
Решение. Вероятность извлечения белого шара одна и та же во всех четырёх испытаниях, так как каждый извлечённый шар возвращается в ящик: 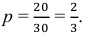
Тогда вероятность извлечения чёрного шара во всех четырёх испытаниях равна 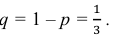
Используя формулу Бернулли, находим вероятность того, что из четырёх извлечённых шаров два шара будут белыми:
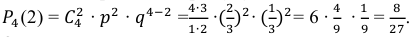
Ответ: 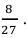
Пример №4
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена 75 раз?
Решение. По условию задачи 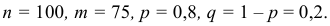
Так как n – достаточно большое число, воспользуемся локальной формулой Лапласа:
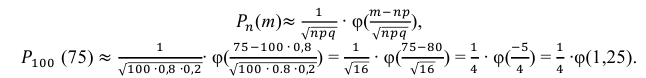
В таблице значений функции 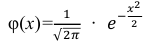 находим φ(1,25) =
находим φ(1,25) =
0,1826.
Следовательно, 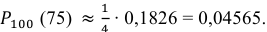
Ответ: 0,04565.
Пример №5
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена
а) не менее 75 раз и не более 90 раз?
б) не менее 75 раз?
в) не более 74 раз?
Решение.
Воспользуемся интегральной формулой Лапласа:
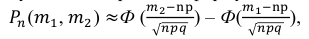
где 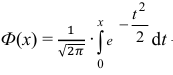 – функция Лапласа.
– функция Лапласа.
а) По условию задачи 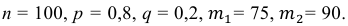 Тогда, воспользовавшись таблицей значений функции Ф(х), получаем:
Тогда, воспользовавшись таблицей значений функции Ф(х), получаем:
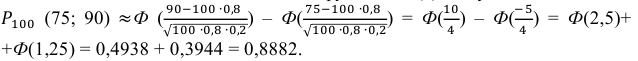
б) Требование того, чтобы событие наступило не менее 75 раз, означает следующее: число появлений события может быть равно либо 75, либо 76, … , либо 100.
Тогда следует принять 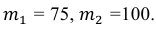 Воспользовавшись таблицей значений функции Лапласа Ф(х), получаем:
Воспользовавшись таблицей значений функции Лапласа Ф(х), получаем: 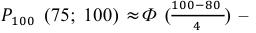
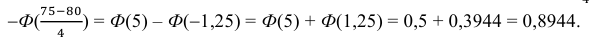
в) Событие “мишень поражена не более 74 раз” и событие “мишень поражена не менее 75 раз” являются противоположными. Поэтому сумма их вероятностей равна 1. Следовательно, искомая вероятность 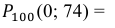
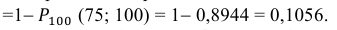
Ответ: а) 0,8882; б) 0,8944; в) 0,1056.
Пример №6
Учебник издан тиражом 100000 экземпляров.
Вероятность того, что один учебник сброшюрован неправильно, равна 0,0001. Какова вероятность того, что тираж содержит 5 бракованных книг?
Решение. По условию задачи n = 100000, p = 0,0001.
События “из n книг ровно m книг сброшюрованы неправильно”, где m = 0,1,2, … ,100000, являются независимыми. Так как число n велико, а вероятность p мала, вероятность 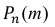 можно вычислить по формуле Пуассона:
можно вычислить по формуле Пуассона: 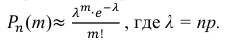
В рассматриваемой задаче 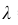 = 100000 ∙ 0,0001 = 10. Поэтому искомая вероятность
= 100000 ∙ 0,0001 = 10. Поэтому искомая вероятность 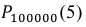 определяется равенством:
определяется равенством:
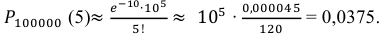
Ответ: 0,0375.
Формула Байеса (Бейеса)
Пусть событие А произошло, причем А могло протекать в различных условиях, относительно характера которых было сделано 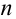 гипотез
гипотез 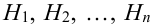 , образующих полную группу несовместных событий. Вероятности гипотез известны. Требуется узнать, как изменятся вероятности гипотез в связи с появлением события А. Т.е. надо найти условную вероятность
, образующих полную группу несовместных событий. Вероятности гипотез известны. Требуется узнать, как изменятся вероятности гипотез в связи с появлением события А. Т.е. надо найти условную вероятность 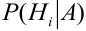 .
.
Решение:
По условию теоремы гипотезы 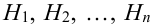 , образуют полную группу несовместных событий, следовательно событие .А произошло с одной и только с одной гипотезой:
, образуют полную группу несовместных событий, следовательно событие .А произошло с одной и только с одной гипотезой:
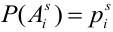 , причем события А и
, причем события А и 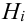 – зависимы, поэтому найдем вероятность произведения
– зависимы, поэтому найдем вероятность произведения 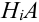 , воспользовавшись теоремой 3:
, воспользовавшись теоремой 3:
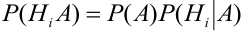 — (или, что то же самое) =
— (или, что то же самое) = 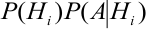 =
= 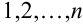 , отсюда
, отсюда
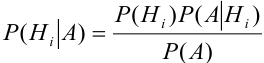 .
.
Выразим Р(А) с помощью формулы полной вероятности:
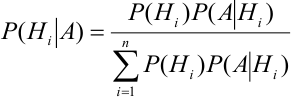 – формула Байеса.
– формула Байеса.
Пример №7
Имеется пять урн:
2 урны состава  – по 2 белых шара и 3 черных шара,
– по 2 белых шара и 3 черных шара,
2 урны состава 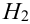 – по 1 белому и 4 черных шара,
– по 1 белому и 4 черных шара,
1 урна состава 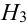 – 4 белых и 1 черный шар.
– 4 белых и 1 черный шар.
Из одной наудачу выбранной урны взят шар. Он оказался белым (событие А). Чему равна после опыта вероятность события, что шар вынут из урны третьего состава.
Решение.
Событие А произошло. Шар мог быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 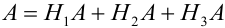 .
.
Найдем вероятности событий:
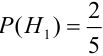 (две урны состава
(две урны состава 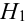 из пяти),
из пяти), 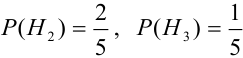 ,
,
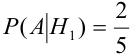 (в каждой урне состава
(в каждой урне состава  2 белых шара из пяти),
2 белых шара из пяти),
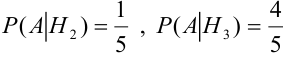 .
.
По формуле Байеса найдем условную вероятность 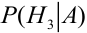 :
:
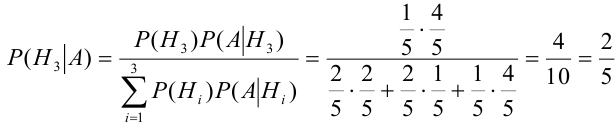 .
.
Пример №8
Вероятность дождливого дня в городе равна 0,2. Известно, что вероятность выиграть футбольный матч команде этого города в дождливый день равна 0,4, а в сухой – 0,7. Известно, что команда выиграла матч. Определить, что в этот день шел дождь.
Решение:
Событие  состоит в том, что команда выиграла матч. Гипотезы:
состоит в том, что команда выиграла матч. Гипотезы: 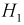 – шел дождь,
– шел дождь, 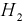 – дождя не было.
– дождя не было.
Чтобы ответить на вопрос, пересмотрим вероятность 1-й гипотезы с учетом результата опыта-появилось событие 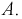 Определим апостериорную вероятность гипотезы
Определим апостериорную вероятность гипотезы 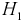 с учетом результата опыта (появилось событие
с учетом результата опыта (появилось событие 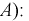
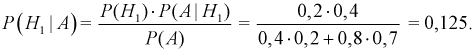
Из полученного результата видим, что с учетом события 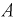 вероятность дождя в городе уменьшилась
вероятность дождя в городе уменьшилась 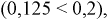 значит скорее всего дождя не было.
значит скорее всего дождя не было.
Независимые испытания
Под испытанием станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства 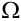 элементарных событий.
элементарных событий.
Определение 26. Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.
В каждом испытании вероятность появления события А одинакова.
Ряд задач связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Рассматривается последовательность п независимых испытаний, под которой будем понимать дискретное новое пространство 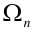 элементарных исходов, состоящее из точек
элементарных исходов, состоящее из точек 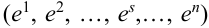 , где
, где 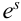 – произвольная точка пространства, отвечающая испытанию с номером s. В каждом испытании может произойти один из
– произвольная точка пространства, отвечающая испытанию с номером s. В каждом испытании может произойти один из  исходов:
исходов: 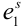 или
или 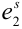 или ….
или …. 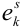 .
.
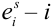 -тый исход в s-том испытании, где
-тый исход в s-том испытании, где  = 1, 2,…,
= 1, 2,…,  ; s = 1,2,…,
; s = 1,2,…,  .
.
Пример №9
Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных событий 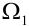 состоит из шести точек:
состоит из шести точек: 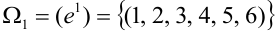 , т.е. шесть исходов. Если провести три испытания, то пространство
, т.е. шесть исходов. Если провести три испытания, то пространство  состоит из 216 точек.
состоит из 216 точек.
Обычно исходы обозначали большими заглавными буквами. Переобозначим! Пусть происходит  независимых испытаний: 1, 2,…, s,…,
независимых испытаний: 1, 2,…, s,…,  . В каждом испытании может произойти к исходов: 1-ый, 2, 3,…,
. В каждом испытании может произойти к исходов: 1-ый, 2, 3,…,  ,…,
,…,  -ый.
-ый.
Обозначим событие 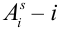 -тый исход в s-том испытании, где
-тый исход в s-том испытании, где  = 1,2,…,
= 1,2,…, ; s = 1,2,…,
; s = 1,2,…, . Эти к исходов – несовместные случайные события. Тогда для s-ого испытания можем записать:
. Эти к исходов – несовместные случайные события. Тогда для s-ого испытания можем записать:
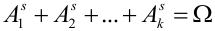 , причем
, причем 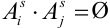 .
.
Обозначим вероятность  -ого исхода при s-том испытании через
-ого исхода при s-том испытании через 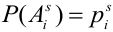 .
.
Пусть при первом испытании произошло событие под номером 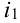 , при 2-ом – событие под номером
, при 2-ом – событие под номером 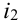 , …, при
, …, при  -ом – событие под номером
-ом – событие под номером 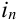 . Результат сразу
. Результат сразу  испытаний – событие, которое обозначим через произведение событий
испытаний – событие, которое обозначим через произведение событий 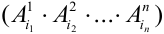 – цепочка результатов отдельных испытаний.
– цепочка результатов отдельных испытаний.
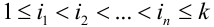 . Данное событие – цепочка состоит из всех точек
. Данное событие – цепочка состоит из всех точек 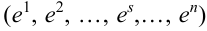 пространства
пространства 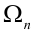 , для которых
, для которых 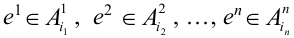 .
.
Испытания – независимые, следовательно, по теореме 4, имеет место равенство:
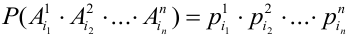
В случае, когда вероятности событий 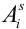 не зависят от номера испытаний,
не зависят от номера испытаний, 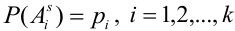 .
.
В силу несовместности и единственной возможности исходов, очевидно, что 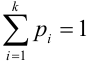 , так как
, так как 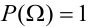 .
.
Теорема. Если данные 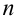 испытаний независимы, то любые
испытаний независимы, то любые 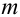 из них также независимы.
из них также независимы.
Теорема. Для того, чтобы 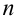 испытаний были независимы, необходимо и достаточно выполнения условия:
испытаний были независимы, необходимо и достаточно выполнения условия:
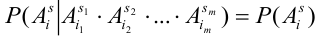 ,
,
для любой группы чисел 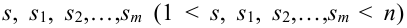 и
и 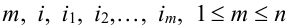 ,
, 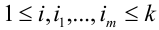 .
.
Формулы Бернулли
Пусть проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Схема независимых испытаний является математической моделью серии испытаний, повторяющихся при неизменных условиях. Такая схема называется полиномиальной.
Простейшим классом повторяющихся независимых испытаний является последовательность независимых испытаний с двумя исходами (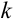 = 2): «успех», «неудача» и с неизменными вероятностями успеха – р и неудачи – q, где q = 1 – р, в каждом испытании. Такая схема называется биномиальной.
= 2): «успех», «неудача» и с неизменными вероятностями успеха – р и неудачи – q, где q = 1 – р, в каждом испытании. Такая схема называется биномиальной.
Определение 27. Независимые испытания при двух исходах называются испытаниями Бернулли.
Пример №10
Определить вероятность того, что в результате проведения 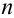 независимых испытаний некоторое событие А – успех (У) наступит ровно
независимых испытаний некоторое событие А – успех (У) наступит ровно  раз, если в каждом из этих испытаний данное событие наступает с постоянной вероятностью
раз, если в каждом из этих испытаний данное событие наступает с постоянной вероятностью 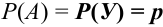 .
.
Решение.
Искомую вероятность обозначим 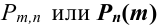 .
.
Событие А в данных испытаниях может появиться ровно  раз, причем, в разных последовательностях или комбинациях. Следовательно, остальные
раз, причем, в разных последовательностях или комбинациях. Следовательно, остальные 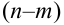 раз наступает противоположное событие
раз наступает противоположное событие 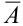 — неудача (Н), вероятность которого
— неудача (Н), вероятность которого 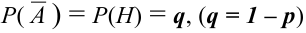 .
.
Сначала найдем вероятность того, что события У наступают при определенных  испытаниях. Элементарные события в этом случае естественно обозначать цепочками вида: УУУННУНН…УН (где У-
испытаниях. Элементарные события в этом случае естественно обозначать цепочками вида: УУУННУНН…УН (где У- штук, Н –
штук, Н –  штук).
штук).
По условию данные события – независимые, следовательно, по теореме 4 для произведения независимых событий можем записать, что
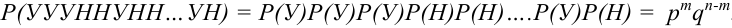 .
.
Число успехов и неудач задано. Можно менять только их расположения в цепочках, которое однозначно определяется выбором из  мест
мест  мест для успехов. Это можно сделать
мест для успехов. Это можно сделать 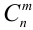 способами. Следовательно,
способами. Следовательно,
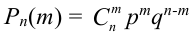 .
.
В данной задаче мы доказали теорему Бернулли.
Теорема Бернулли. Если  – число успехов в
– число успехов в  независимых испытаниях Бернулли, то вероятность того, что в результате проведения этих испытаний некоторое событие А наступит ровно
независимых испытаниях Бернулли, то вероятность того, что в результате проведения этих испытаний некоторое событие А наступит ровно  раз, находится по формуле:
раз, находится по формуле: 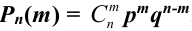 , которая называется формулой Бернулли.
, которая называется формулой Бернулли.
Следствие. 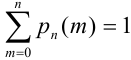 -так как события, состоящие в различном числе появления события А в серии
-так как события, состоящие в различном числе появления события А в серии  испытаний несовместны и образуют полную группу. Или можно было данное равенство объяснить так:
испытаний несовместны и образуют полную группу. Или можно было данное равенство объяснить так: 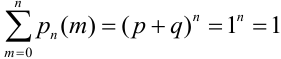 .
.
Пример №11
Пусть монета брошена 5 раз. Требуется найти вероятность того, что выпало ровно 3 орла.
Решение.
В каждом из 5 независимых испытаниях ( = 5) – бросании монеты – два исхода (
= 5) – бросании монеты – два исхода (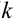 = 2: орел, решка), следовательно, это схема Бернулли с вероятностью успеха (выпал орел) и неудачи (выпала решка)
= 2: орел, решка), следовательно, это схема Бернулли с вероятностью успеха (выпал орел) и неудачи (выпала решка) 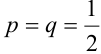 . Количество успехов:
. Количество успехов:  = 3.
= 3.
По формуле Бернулли 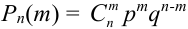 найдем искомую вероятность:
найдем искомую вероятность: 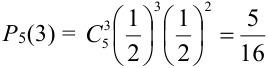 .
.
Замечания.
Замечание 1. Вероятность  равна коэффициенту при
равна коэффициенту при  в разложении бинома
в разложении бинома 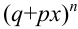 по степеням
по степеням 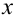 . В силу этого свойства совокупность вероятностей
. В силу этого свойства совокупность вероятностей 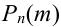 называют биномиальным законом распределения вероятностей, (будем изучать позднее)
называют биномиальным законом распределения вероятностей, (будем изучать позднее)
Замечание 2. Рассмотрим схему испытаний с произвольным количеством исходов. Пусть каждое из  независимых испытаний имеет
независимых испытаний имеет 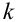 взаимно исключающих друг друга исходов, т.е. в каждом испытании может появиться одно из
взаимно исключающих друг друга исходов, т.е. в каждом испытании может появиться одно из 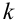 несовместных событий:
несовместных событий: 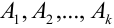 с вероятностями
с вероятностями 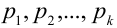 , не меняющимися от испытания к испытанию. Найдем вероятность появления в течении этих
, не меняющимися от испытания к испытанию. Найдем вероятность появления в течении этих  испытаний
испытаний 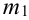 раз события
раз события 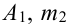 раза события
раза события 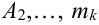 раз события
раз события 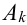 .
.  . Данная вероятность находится по формуле:
. Данная вероятность находится по формуле:
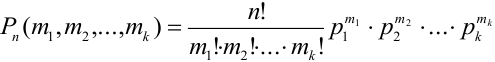 .
.
Эта совокупность вероятностей является коэффициентом при 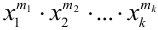 в разложении полинома
в разложении полинома 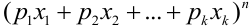 по степеням
по степеням 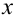 . Поэтому эту схему называют полиномиальной.
. Поэтому эту схему называют полиномиальной.
Например. При  подбрасываниях игральной кости получается полиномиальная схема с шестью исходами (
подбрасываниях игральной кости получается полиномиальная схема с шестью исходами (  = 6) и вероятностями
= 6) и вероятностями 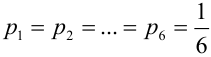 .
.
Если различать только «6» и «не 6», то получим схему Бернулли с двумя исходами ( = 2) и вероятностями успеха
= 2) и вероятностями успеха 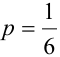 и неудачи
и неудачи 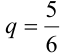 .
.
Замечание 3. При вычислении вероятности события, состоящего в том, что число успехов m лежит, например, между а и b, приходится находить числовые значения сумм вероятностей вида: 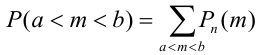 .
.
Например, вероятность того, что событие наступит а) менее  раз, b) более
раз, b) более  раз, с) не менее
раз, с) не менее  раз, d) не более
раз, d) не более  раз находятся соответственно по формулам:
раз находятся соответственно по формулам:
a) 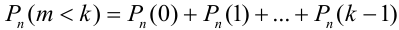 .
.
b) 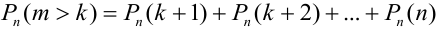 .
.
c) 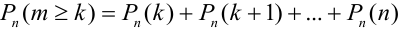 .
.
d) 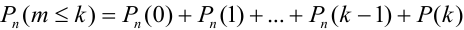 .
.
В некоторых случаях удобнее перейти к противоположному событию, например, 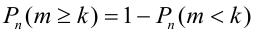 .
.
Пример №12
Пусть монета брошена 5 раз. Требуется найти вероятность того, что 1) менее двух раз выпал орел, 2) не менее двух раз выпал орел.
Решение.
Два исхода ( = 2: орел, решка) при 5 независимых испытаниях (n = 5) – схема Бернулли с вероятностью успеха и неудачи
= 2: орел, решка) при 5 независимых испытаниях (n = 5) – схема Бернулли с вероятностью успеха и неудачи 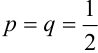 .
.
1) Орел выпал менее двух раз, значит, не выпал или выпал раз.
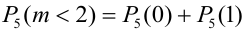 = (вероятности найдем по формуле Бернулли) =
= (вероятности найдем по формуле Бернулли) =
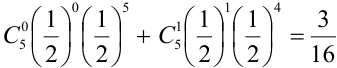
2) Орел выпал не менее двух раз, т.е. выпал два раза или три или четыре или пять:
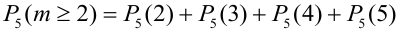 =(удобнее перейти к противоположному событию, т.е. «не менее двух», значит, противоположное событие: меньше двух, т.е. орел не выпал совсем или выпал один раз) =
=(удобнее перейти к противоположному событию, т.е. «не менее двух», значит, противоположное событие: меньше двух, т.е. орел не выпал совсем или выпал один раз) = 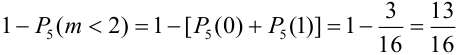 .
.
Замечание 4. В примере на формулу Бернулли вычисления проводятся очень легко, однако часто приходится вычислять вероятности при очень больших значениях n и m, например, при n = 1000, m = 500. Также затруднения при вычислении возникают при малых значениях р или q.
В этих случаях удается заменить формулу Бернулли какой-нибудь приближенной асимптотической формулой. Существуют три предельные теоремы, содержащие такие формулы.
Предельные теоремы в схеме Бернулли
Теорема Пуассона (асимптотическая формула для случая малых значений р)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, причем  при
при  так, что
так, что 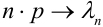 , где
, где 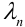 – среднее число появления события А в n испытаниях,
– среднее число появления события А в n испытаниях, 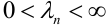 , то вероятность
, то вероятность 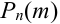 того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при
того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при  соотношению (или приближенно равна):
соотношению (или приближенно равна):
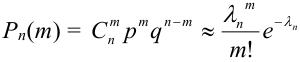
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при  :
:
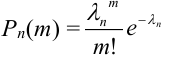 , при этом
, при этом 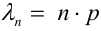 .
.
2. Формулой пользуются при больших n и малых р. Например, при n > 100, 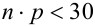 .
.
3. Теорема имеет место и в том случае, когда вероятность события А в каждом испытании равна нулю. В этом случае 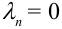 .
.
4. Существуют таблицы значений данной вероятности (стр. 410, 411 в задачнике Ефимова -Демидовича).
Пример №13
Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более пулями, если число выстрелов равно 5000.
Решение.
Считаем каждый выстрел за испытание и попадание в цель за событие. Количество испытаний n = 5000 (велико), р = 0,001 (мало). По формуле Бернулли считать сложно. Поэтому применим формулу Пуассона.
Найдем среднее число попаданий: 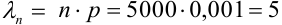 . Найдем заданную вероятность:
. Найдем заданную вероятность:
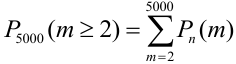 = (перейдем к противоположному событию: m < 2) =
= (перейдем к противоположному событию: m < 2) = 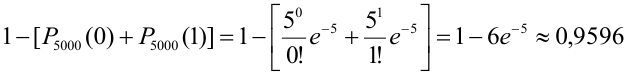 .
.
По точной формуле (формуле Бернулли) 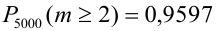 , т.е. ошибка невелика.
, т.е. ошибка невелика.
Локальная предельная теорема Муавра – Лапласа (асимптотическая формула для случая больших значений n и m)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, (0 < р < 1), то вероятность 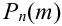 того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при
того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при  соотношению (или приближенно равна):
соотношению (или приближенно равна):
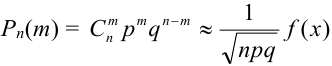 ,
,
где 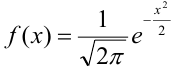 ,
, 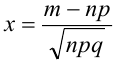 .
.
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при  :
:
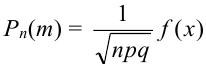
2. Формулой пользуются при больших n и m. Например, при п > 100, 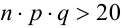 .
.
3. Из того, что  следует, что
следует, что 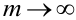 . Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение.
. Это означает, что n и m должны отличаться друг от друга не очень сильно. Например, для случая m = 0, теорема дает плохое приближение.
4. Существуют таблицы значений функции 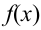 для положительных значений х (стр. 408 в задачнике Ефимова – Дсмидовича). Для отрицательных значений х используется та же таблица, так как
для положительных значений х (стр. 408 в задачнике Ефимова – Дсмидовича). Для отрицательных значений х используется та же таблица, так как 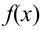 – четная функция:
– четная функция: 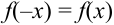 . Функцию
. Функцию 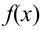 называют плотностью нормального распределения.
называют плотностью нормального распределения.
Пример №14
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
Количество испытаний n = 243, количество успехов m = 70, вероятность успеха р = 0,25, вероятность неудачи q = 1 – 0,25 = 0,75.
По формуле Бернулли считать сложно. Так как n и m велики, поэтому применим формулу Муавра – Лапласа.
Найдем сначала х и 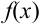 :
:
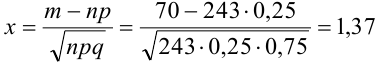 , тогда
, тогда 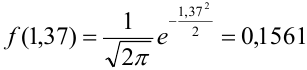 .
.
Можно было не считать значение 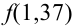 напрямую, а обратиться к таблице в учебнике.
напрямую, а обратиться к таблице в учебнике.
Подставим найденное значение 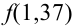 в формулу:
в формулу:
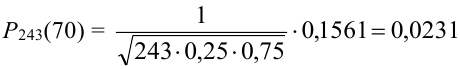 .
.
Предельная интегральная теорема Муавра – Лапласа (асимптотическая формула для случая, когда число успехов m лежит в некоторых пределах)
Теорема 1. Если m – число наступлений события А в n независимых испытаниях, в каждом из которых вероятность этого события равна р (0 < р < 1), то равномерно относительно а и b 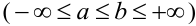 при
при 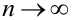 имеет место соотношение:
имеет место соотношение:
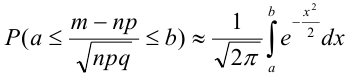 .
.
В некоторых источниках 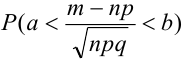 или
или 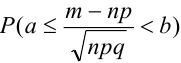 .
.
Ранее вывели, что 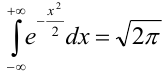 . Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф(х):
. Численное значение нашего интеграла можно найти с помощью таблиц (стр. 406 в задачнике Ефимова – Демидовича) для функции Лапласа Ф(х):
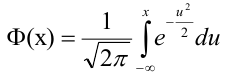 , где
, где 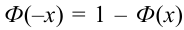 . Для тех значений х, которых нет в таблице, т.е для
. Для тех значений х, которых нет в таблице, т.е для 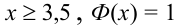
Либо, функция Лапласа может быть в виде: 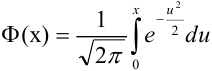 , где
, где 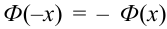 , для тех значений х, которых нет в таблице, т.е. для
, для тех значений х, которых нет в таблице, т.е. для 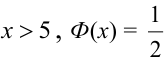 .
.
Теорема 2. (Теорема Муавра-Лапласа) Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие А наступит не менее  раза и не более
раза и не более 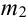 раз приближенно равна:
раз приближенно равна: 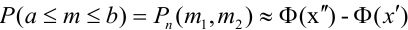 ,
,
где Ф(х) – функция Лапласа, значения 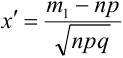 ,
, 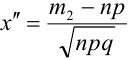 .
.
Теорема 3. (Закон больших чисел или теорема Бернулли).
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте.
Иначе, вероятность того, что отклонение относительной частоты наступления события 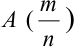 от постоянной вероятности события А (p) очень мало при
от постоянной вероятности события А (p) очень мало при  п —> оо стремится к 1.
п —> оо стремится к 1.
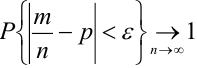
Доказательство.
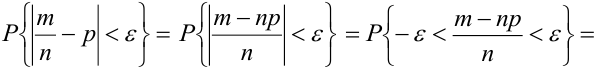
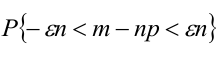 = (разделим все части неравенства на положительное число
= (разделим все части неравенства на положительное число 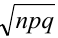 )
)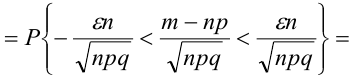
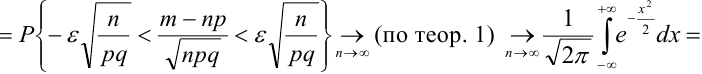
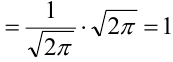 .
.
Пример №15
Вероятность появления события А в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появиться не менее 75 раз и не более 90 раз.
Решение.
Количество испытаний n = 100, вероятность успеха р = 0,8, вероятность неудачи q = 1 – 0,8 = 0,2 , 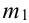 = 75,
= 75, 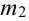 – 90.
– 90.
Найдем 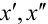 :
:
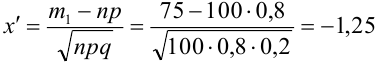 ,
, 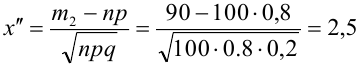 .
.
По теореме 2:
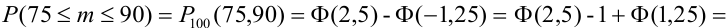 (по таблице для функции Лапласа) =
(по таблице для функции Лапласа) = 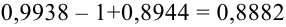 .
.
Наивероятнейшее число появления события в независимых испытаниях
Определение 28. Число 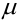 наступления события в независимых испытаниях, в каждом из которых вероятность появления события А равна р, называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях
наступления события в независимых испытаниях, в каждом из которых вероятность появления события А равна р, называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях 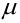 раз превышает или, по крайней мере, не меньше вероятности остальных возможных исходов испытаний.
раз превышает или, по крайней мере, не меньше вероятности остальных возможных исходов испытаний.
Наивероятнейшее число  определяется из двойного неравенства:
определяется из двойного неравенства:
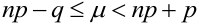 ,
,
причем 1) если (np – q) -дробное, то существует одно  , 2) если (nр- q) – целое, то существует два наивероятнейших числа, 3) если nр – целое, то
, 2) если (nр- q) – целое, то существует два наивероятнейших числа, 3) если nр – целое, то  = nр.
= nр.
Пример №16
Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание и вероятность этого числа.
Решение.
Количество испытаний n = 15, вероятность успеха р = 0,9, вероятность неудачи q = 0,1.
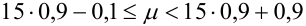 ,
, 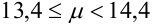 .
.
Т.к.  — целое число, то
— целое число, то  = 14— наивероятнейшее число элементов, выдержавших испытание. Вероятность этого числа найдем по формуле Бернулли:
= 14— наивероятнейшее число элементов, выдержавших испытание. Вероятность этого числа найдем по формуле Бернулли:
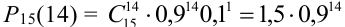 . (Удобнее было по локальной формуле Муавра – Лапласа).
. (Удобнее было по локальной формуле Муавра – Лапласа).
Всё о формуле полной вероятности
Пусть событие 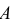 может произойти с одним и только с одним из несовместимых событий
может произойти с одним и только с одним из несовместимых событий 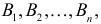 образующих полную группу. Иными словами, событие
образующих полную группу. Иными словами, событие 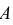 появится, если произойдет событие B1 и при этом появится событие
появится, если произойдет событие B1 и при этом появится событие 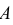 , или произойдет событие B2 и при этом появится событие
, или произойдет событие B2 и при этом появится событие 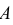 и т.д. Символическая запись этой фразы имеет вид
и т.д. Символическая запись этой фразы имеет вид
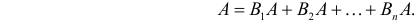
В силу несовместимости событий можно записать 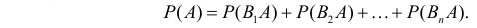
Используя теорему умножения вероятностей, получаем формулу 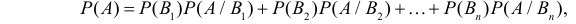
которая и называется формулой полной вероятности.
Обычно ее записывают кратко:
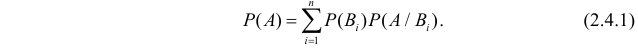
Пример №17
Имеется две коробки деталей, в каждой из которых по 10 деталей. В первой коробке среди деталей две низкого сорта, а во второй четыре низкосортных детали. Из первой коробки для нужд производства взяли наугад половину деталей, а оставшиеся высыпали во вторую коробку. Через некоторое время из второй коробки взяли наугад деталь. Какова вероятность того, что это деталь низкого сорта?
Решение. Обозначим через A событие, состоящее в выборе из второй коробки детали низкого сорта. Возможность этого выбора зависит от того, какие именно детали были добавлены во вторую коробку. На этот счет можно выдвинуть следующие предположения: B1 – во вторую коробку добавили пять годных деталей; B2 – добавили одну деталь низкого сорта и четыре доброкачественные; B3 – добавили две детали низкого сорта и три доброкачественные. Пять деталей во вторую коробку можно переложить 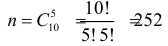 способами. Из них событию B1 благоприятствует
способами. Из них событию B1 благоприятствует 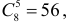 событию B2 —
событию B2 — 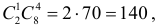 а событию B3 —
а событию B3 — 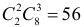 способов. Событие A произойдет, если появится событие B1 и после этого произойдет событие A или появится событие B2 и после этого произойдет событие A или появится B3 и после этого произойдет A. Символически:
способов. Событие A произойдет, если появится событие B1 и после этого произойдет событие A или появится событие B2 и после этого произойдет событие A или появится B3 и после этого произойдет A. Символически: 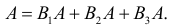 Учитывая несовместность событий
Учитывая несовместность событий  , имеем
, имеем 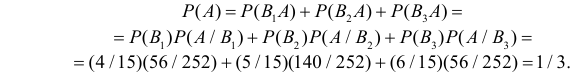
Ответ. 1/ 3.
Всё о Формуле Байеса
Пусть событие A может наступить только при появлении одного из несовместных событий 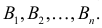 В этих условиях вероятность события A можно вычислить по формуле полной вероятности (2.4.1). События
В этих условиях вероятность события A можно вычислить по формуле полной вероятности (2.4.1). События  иногда называют «гипотезами», поскольку можно лишь предполагать какое именно из них произойдет. Предположим, что известны вероятности
иногда называют «гипотезами», поскольку можно лишь предполагать какое именно из них произойдет. Предположим, что известны вероятности 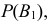
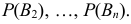
Проделан опыт, в результате которого событие A произошло. Тогда вероятности событий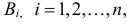 при условии появления события A определяются по формулам Байеса
при условии появления события A определяются по формулам Байеса
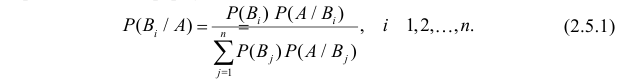
Формулы Байеса позволяют переоценивать вероятности гипотез (событий  ) с учетом информации, которую содержит в себе факт появления события A.
) с учетом информации, которую содержит в себе факт появления события A.
Пример №18
По каналу связи передается одна из последовательностей букв  с вероятностями соответственно 0,5; 0,4; 0,1. Каждая передаваемая буква принимается правильно с вероятностью 0,8 и с вероятностями 0,1 и 0,1 за любую из двух других букв. Предполагается, что искажаются буквы при передаче независимо друг от друга. Найти вероятность того, что передано
с вероятностями соответственно 0,5; 0,4; 0,1. Каждая передаваемая буква принимается правильно с вероятностью 0,8 и с вероятностями 0,1 и 0,1 за любую из двух других букв. Предполагается, что искажаются буквы при передаче независимо друг от друга. Найти вероятность того, что передано  если принято
если принято 
Решение. Для краткости записи формулы обозначим  через
через 
 через
через 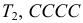 через
через 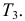 Тогда по формулам Байеса (2.5.1)
Тогда по формулам Байеса (2.5.1)

Ответ. 8/9.
Пример №19
Три стрелка производят по одному выстрелу в одну и ту же мишень. Вероятности попадания в мишень при одном выстреле для этих стрелков соответственно равны 0,8; 0,7; 0,6. Какова вероятность того, что третий стрелок промахнулся, если в мишени оказалось две пробоины?
Решение. Обозначим через А событие, состоящее в появлении двух пробоин в мишени. В отношении двух пробоин могут быть три предположения: В1 – попали первый и второй стрелки, а третий не попал, вероятность чего равна  В2 – попали первый и третий, а второй не попал, вероятность чего равна
В2 – попали первый и третий, а второй не попал, вероятность чего равна 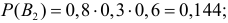 В3 – попали второй и третий, а первый не попал, вероятность чего равна
В3 – попали второй и третий, а первый не попал, вероятность чего равна 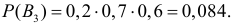
Заметим, что 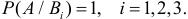 Тогда по формулам Байеса (2.5.1)
Тогда по формулам Байеса (2.5.1)
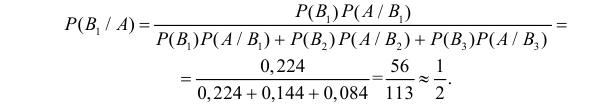
Ответ. 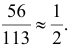
Пример №20
В партии из 10 изделий с равными шансами может оказаться от нуля до трех бракованных. Наугад взяли и проверили три изделия. Они оказались годными. Какова вероятность того, что остальные изделия в партии тоже годные?
Решение. Насчет содержания в партии бракованных изделий по условиям задачи может быть четыре предположения 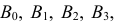 где
где 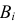 означает, что в партии
означает, что в партии 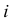 бракованных изделий. По условиям задачи все эти предположения равновозможны и поэтому имеют вероятности
бракованных изделий. По условиям задачи все эти предположения равновозможны и поэтому имеют вероятности 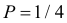 каждое. Обозначим через A факт проверки трех годных изделий. Требуется найти
каждое. Обозначим через A факт проверки трех годных изделий. Требуется найти 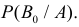
Заметим, что 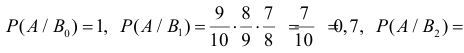
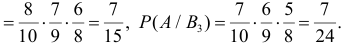 Поэтому по формулам Байеса (2.5.1)
Поэтому по формулам Байеса (2.5.1)
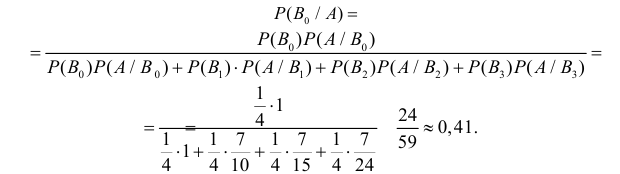
Ответ. 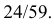
Пример №21
Вероятность того, событие B произойдет в течение часа, равна 0,9. Оказалось, что в течение первых 40 мин. событие B не произошло. Какова вероятность того, что это событие появится в оставшиеся 20 мин. времени?
Решение. В отношении события 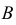 могут быть два предположения: либо оно появится
могут быть два предположения: либо оно появится 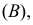 либо оно не появится
либо оно не появится 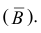 Обозначим через
Обозначим через 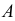 тот факт, что событие
тот факт, что событие 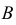 не появилось в течение первых 40 мин. Нас интересует вероятность
не появилось в течение первых 40 мин. Нас интересует вероятность 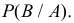 По формулам Байеса (2.5.1) получим
По формулам Байеса (2.5.1) получим
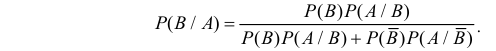
В задаче по умолчанию предполагается, что событие 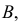 если оно происходит, то равновозможно его появление в любой момент данного часа. Поэтому по геометрическому определению вероятности
если оно происходит, то равновозможно его появление в любой момент данного часа. Поэтому по геометрическому определению вероятности 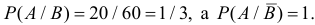 В итоге получаем, что
В итоге получаем, что
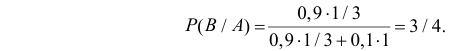
Ответ. 3/4.
Пример №22
В кошельке лежат четыре монеты. Три монеты обычных, а у четвертой на той и другой стороне изображен герб. Наугад взяли монету и подбросили три раза. Все три раза выпал герб. Какова вероятность того, что и при четвертом подбрасывании выпадет герб?
Решение. Обозначим через B1 – выбор монеты с одним гербом, через B2 – выбор монеты с двумя гербами. Априорные вероятности этих событий равны: 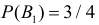 и
и 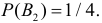
Обозначим через A – выпадение трех гербов подряд. Апостериорные вероятности по формулам Байеса равны: 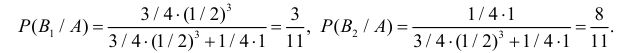
Тогда по формуле полной вероятности (2.4.1):
P(выпадения герба в четвертый раз)
Ответ. 
Подробное объяснение формулы полной вероятности
Постановка задачи: Пусть 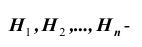 – полная система (группа) попарно несовместных событий (в дальнейшем эти события
– полная система (группа) попарно несовместных событий (в дальнейшем эти события 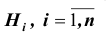 будем называть гипотезами) т. е.
будем называть гипотезами) т. е.  или что то же самое
или что то же самое  и пусть событие A может произойти лишь совместно с каким-либо одним из этих событий (гипотез).
и пусть событие A может произойти лишь совместно с каким-либо одним из этих событий (гипотез).
Требуется найти вероятность события A.
Выведем формулу решения этой задачи. Имеем
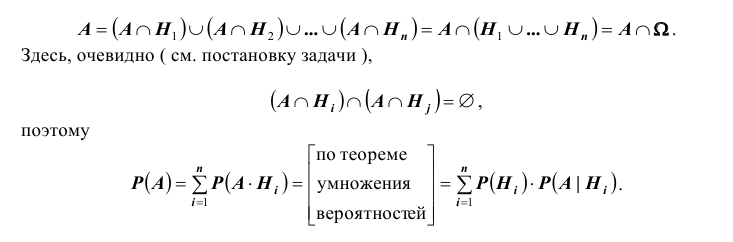
маршрутов (схема дорог). Какова вероятность того, что он попадет в пункт А ?
Решение. Как видим из схемы дорог, путь туриста обязательно проходит через один из пунктов 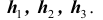 Тогда
Тогда – гипотеза (предположение) которая состоит в том, что турист попал в пункт
– гипотеза (предположение) которая состоит в том, что турист попал в пункт  .
.
Заметим, что события (гипотезы) попарно несовместны и равновероятны, т.е., очевидно, образуют полную группу событий: во-первых,
попарно несовместны и равновероятны, т.е., очевидно, образуют полную группу событий: во-первых,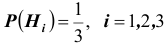 , во-вторых
, во-вторых 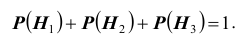 Событие A- турист попал в пункт А. Тогда, нетрудно
Событие A- турист попал в пункт А. Тогда, нетрудно
видеть (см. схему), что 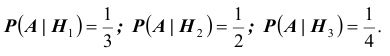 Значит, по формуле полной вероятности, получаем:
Значит, по формуле полной вероятности, получаем: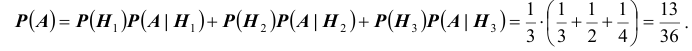

Пример №23 (о мудреце и властелине).
Властелин, разгневавшись на мудреца, приказал отрубить ему голову. Но затем, смягчившись, дал мудрецу возможность попытаться спастись. Итак, властелин взял 2 белых и 2 черных шара и предложил мудрецу распределить их по своему усмотрению по двум одинаковым урнам. После чего, палач сначала наугад выберет одну из урн, а затем также наугад, не глядя, вытащит из неё один шар. Мудрец будет помилован, если вытянутый шар оказался белым. Какую стратегию распределения шаров по урнам должен
выбрать мудрец, чтобы быть помилованным? Какова максимальная вероятность спастись мудрецу? Какая стратегия наименее выгодна для него?
Решение. Выдвинем гипотезы (предположения) 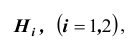 которые состоят в том, что палач вытащит шар из i – ой урны
которые состоят в том, что палач вытащит шар из i – ой урны 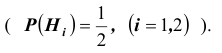 Очевидно, что эти события
Очевидно, что эти события  несовместны и их сумма является достоверным событием
несовместны и их сумма является достоверным событием 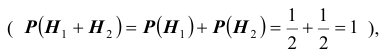 т.е. образуют полную группу (систему) событий. И пусть A- это событие состоящее в том, что
т.е. образуют полную группу (систему) событий. И пусть A- это событие состоящее в том, что
палачом вытянут белый шар. Далее, рассмотрим следующие варианты распределения мудрецом шаров по
урнам:
1). В первой урне 2 белых, а во второй 2 черных шара. Тогда 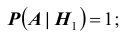
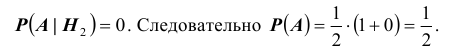
2 Хотим заметить, что далеко не всегда властелины были глупыми людьми, не знающими математики. Так, например, Наполеон был немного математиком, интересовался, в частности, геометрией. Он вёл дискуссии с Лагранжем и Лапласом, когда ещё не был правителем Франции.
Как-то в одной из таких дискуссий Лаплас резко оборвал Бонапарта: «Менее всего мы хотим от Вас, генерал, урока геометрии». В дальнейшем Лаплас стал его главным военным инженером. Наполеону приписывают теорему: «Если на сторонах произвольного треугольника во внешнюю сторону построены равносторонние треугольники, то их центры образуют равносторонний треугольник» – это так называемый вешний треугольник Наполеона.Так же ему приписывают один из знаменитых палиндромов (читается в обе стороны одинаково): «ABLE WAS I ERE I SAW ELBA» – я был силён, пока не увидел Эльбу.
2). В первой и во второй урнах по 1 белому и 1 черному шару. Тогда 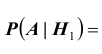
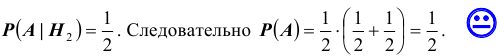
3). В первой урне 1 белый, а во второй 1 белый и 2 черных шара. Тогда 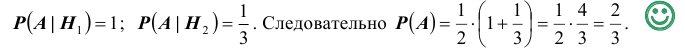
4). В первой урне 1 черный, а во второй 2 белых и 1 черный шары. Тогда 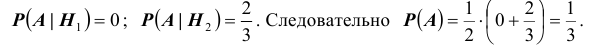
5). Первая урна оказалась пустой, т.е. все шары во второй урне. Тогда 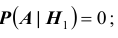
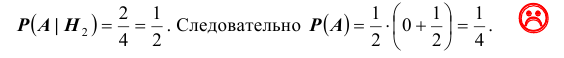
Как видим, наиболее предпочтительной является 3-я стратегия, ей соответствует вероятность быть помилованным равная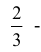 – действительно мудрое решение; наименее выгодна – последняя, 5 – я стратегия, где вероятность спастись равна
– действительно мудрое решение; наименее выгодна – последняя, 5 – я стратегия, где вероятность спастись равна 
Вероятность гипотез. Формула Байеса
Постановка задачи: Пусть 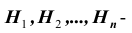 – полная система (группа) попарно несовместных событий (гипотез) т. е.
– полная система (группа) попарно несовместных событий (гипотез) т. е.
и пусть событие A может произойти лишь совместно с каким – либо одним из этих событий (гипотез) – ситуация аналогичная той, которая была ранее. И пусть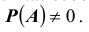 Требуется найти условную вероятность k – ой гипотезы при условии, что событие A произошло, т.е.
Требуется найти условную вероятность k – ой гипотезы при условии, что событие A произошло, т.е.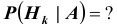 – переоценка гипотез.
– переоценка гипотез.
По теореме об умножении вероятностей
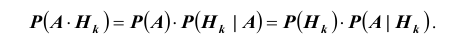 Следовательно
Следовательно 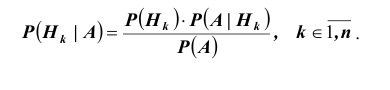
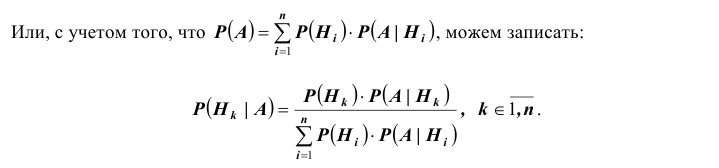
Полученная формула называется формулой Байеса (Бейеса) для переоценки гипотез. Другими словами: вероятность 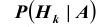 гипотезы после испытания равна произведению вероятности
гипотезы после испытания равна произведению вероятности 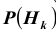 гипотезы до испытания на соответствующую ей условную вероятность
гипотезы до испытания на соответствующую ей условную вероятность 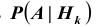 события, происшедшего при испытании, деленному на полную вероятность
события, происшедшего при испытании, деленному на полную вероятность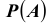 этого события.
этого события.
Пример №24
При обследовании больного имеется подозрение (т.е. делаются предположения или, что то же самое, выдвигаются гипотезы)
на одно из двух заболеваний 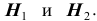 . Их вероятности в данных условиях равны
. Их вероятности в данных условиях равны 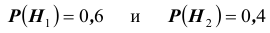 соответственно. Для уточнения диагноза назначается обследование, результатом которого будет отрицательная или положительная реакция. В случае болезни вероятность положительной реакции равна 0,9 , а в случае болезни
соответственно. Для уточнения диагноза назначается обследование, результатом которого будет отрицательная или положительная реакция. В случае болезни вероятность положительной реакции равна 0,9 , а в случае болезни эта вероятность равна 0,5. Обследования проведены дважды и оба раза реакция оказалась отрицательной. Найти вероятность каждого заболевания.
эта вероятность равна 0,5. Обследования проведены дважды и оба раза реакция оказалась отрицательной. Найти вероятность каждого заболевания.

Решение. Во – первых, очевидно, что события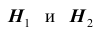 образуют полную группу событий. Действительно, эти события несовместны, так как у больного имеется подозрение только лишь на одно из двух заболеваний и сумма событий – есть достоверное событие (обследуемый болен):
образуют полную группу событий. Действительно, эти события несовместны, так как у больного имеется подозрение только лишь на одно из двух заболеваний и сумма событий – есть достоверное событие (обследуемый болен): 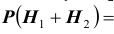 .
.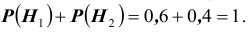 Во – вторых, если обозначить через A событие, которое состоит в том, что оба обследования дали отрицательный результат, то
Во – вторых, если обозначить через A событие, которое состоит в том, что оба обследования дали отрицательный результат, то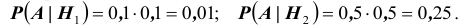 Таким образом, нетрудно видеть, что
Таким образом, нетрудно видеть, что
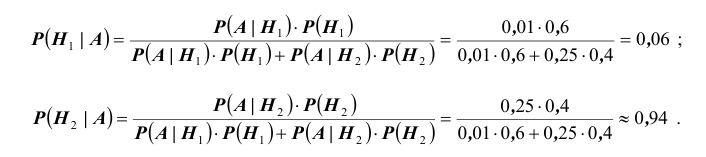
Как видим, при данных результатах обследования следует предполагать болезнь 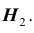
Повторение испытаний
Формула Бернулли (схема повторения опытов)
Опыты называются независимыми , если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Независимые опыты могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого – либо события A во всех опытах одна и та же, во втором случае – она меняется от опыта к опыту. Ниже мы воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми. Итак, пусть производится n независимых опытов в одинаковых условиях, в каждом из которых некоторое событие A может произойти с одной и той же вероятностью 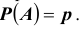 . Причём, каждый опыт (испытание) имеет лишь два исхода: событие A может появиться (произойти), либо не появиться. Условно, появление события A будем рассматривать как успех, а его не наступление (т.е. событие
. Причём, каждый опыт (испытание) имеет лишь два исхода: событие A может появиться (произойти), либо не появиться. Условно, появление события A будем рассматривать как успех, а его не наступление (т.е. событие 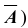 – как неудачу. Следовательно, вероятность не наступления события A в каждом испытании также постоянна и равна
– как неудачу. Следовательно, вероятность не наступления события A в каждом испытании также постоянна и равна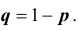 . Данная ситуация, или данная схема проведения опытов называется схемой Бернулли.
. Данная ситуация, или данная схема проведения опытов называется схемой Бернулли.
Итак, еще раз: схемой Бернулли называется последовательность n независимых испытаний, проводимых при одних и тех же условиях, в каждом из которых событие A либо происходит с постоянной вероятностью p , не зависящей от номера испытания, либо не происходит с вероятностью 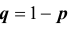
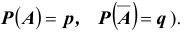
Ставятся задачи:
Задача №1. Найти вероятность  того, что в схеме Бернулли из n испытаний событие A произойдет ровно k раз
того, что в схеме Бернулли из n испытаний событие A произойдет ровно k раз и, следовательно, не осуществится
и, следовательно, не осуществится 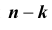 раз.
раз.
Задача № 2. Найти вероятность 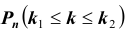 того, что в схеме Бернулли из n испытаний событие A произойдет не менее
того, что в схеме Бернулли из n испытаний событие A произойдет не менее 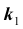 и не более
и не более 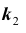 раз
раз
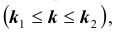 где
где заданы.
заданы.
Задача № 3. Найти наивероятнейшее число 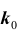 появления события A в схеме Бернулли из n испытаний, при котором
появления события A в схеме Бернулли из n испытаний, при котором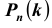 достигает наибольшего значения.
достигает наибольшего значения.
Решение №1.
Вероятность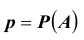 не зависит от номера испытания и, что также важно, не требуется чтобы событие A повторилось ровно k раз в определенной последовательности. Предположим, для определенности, что событие A произойдет подряд k раз, а в остальных
не зависит от номера испытания и, что также важно, не требуется чтобы событие A повторилось ровно k раз в определенной последовательности. Предположим, для определенности, что событие A произойдет подряд k раз, а в остальных 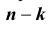 испытаниях – не произойдет. Используя теорему об умножении вероятностей, можем в этом случае записать:
испытаниях – не произойдет. Используя теорему об умножении вероятностей, можем в этом случае записать:
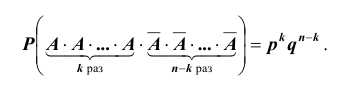
Таких несовместных событий столько, сколько сочетаний из n элементов по k элементов в каждом. Поэтому по теореме о вероятности суммы несовместных событий получим формулу, называемую формулой Бернулли:
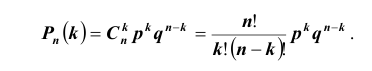
 Легко видеть, что вероятность
Легко видеть, что вероятность , вычисленная по формуле Бернулли, является коэффициентом при
, вычисленная по формуле Бернулли, является коэффициентом при  в разложении бинома
в разложении бинома  поэтому вероятность
поэтому вероятность 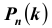 называется биномиальной, а функция
называется биномиальной, а функция 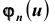 – производящей функцией для распределения вероятностей в схеме Бернулли из n испытаний. Разложение бинома Ньютона
– производящей функцией для распределения вероятностей в схеме Бернулли из n испытаний. Разложение бинома Ньютона  имеет вид:
имеет вид:

которую называют биномиальным законом распределения вероятностей события A в n испытаниях схемы Бернулли.
Заметим, что вероятность хотя бы одного появления события A в n испытаниях схемы Бернулли равна: 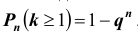 . Кстати, подумайте над
. Кстати, подумайте над
следующим вопросом: честное ли пари вам предлагают, если вы выиграете в том случае, когда при 24-х кратном бросании двух игральных костей хотя бы один раз одновременно появятся две шестёрки? Ответ дайте в конце пары.

(РЕШЕНИЕ. Вероятность одновременного выпадения двух шестерок при одном подбрасывании равна 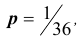 , следовательно – не выпадения равна
, следовательно – не выпадения равна 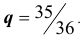 . Нетрудно видеть, что испытания, т.е. подбрасывания двух игральных костей 24 раза, удовлетворяют схеме Бернулли, следовательно вероятность одновременного появления двух шестерок хотя бы один раз равна
. Нетрудно видеть, что испытания, т.е. подбрасывания двух игральных костей 24 раза, удовлетворяют схеме Бернулли, следовательно вероятность одновременного появления двух шестерок хотя бы один раз равна 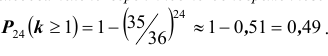 .То есть, пари нечестное.)
.То есть, пари нечестное.)
Другие примеры на применение формулы Бернулли, рассмотрим немного позднее, а именно после того, как решим задачи № 2 и № 3
Решение № 2.
Нетрудно показать, что вероятность  того, что в схеме Бернулли из n испытаний событие A произойдет не менее
того, что в схеме Бернулли из n испытаний событие A произойдет не менее 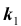 и не более
и не более 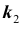 раз
раз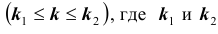 заданы, может быть вычислена по формуле:
заданы, может быть вычислена по формуле: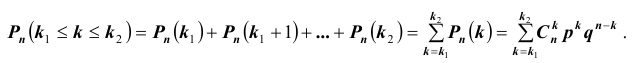
Решение № 3
Важной является задача № 3 о наивероятнейшем числе 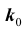 появления события A в схеме Бернулли из n испытаний.
появления события A в схеме Бернулли из n испытаний.
Рассмотрим отношение:
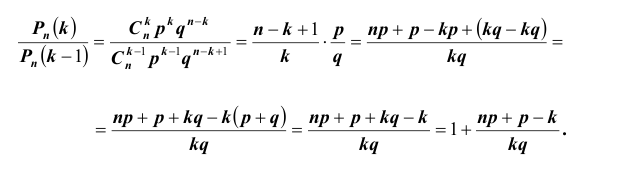
Из полученного следует, что:
1) если 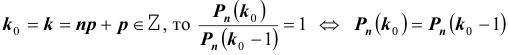 т.е. существует
т.е. существует
два максимума;
2) если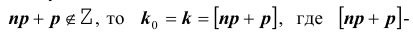 целая часть числа
целая часть числа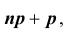 тогда
тогда 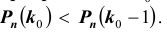

Пример №25
При некоторых условиях стрельбы вероятность p попадания в цель при одном выстреле равна
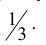 Произведено
Произведено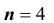 выстрела.
выстрела.
- а). Каково наивероятнейшее число попаданий в цель?
- б). Какова его вероятность?
- в). Какова вероятность двух попаданий?
- г). Какова вероятность хотя бы одного попадания?
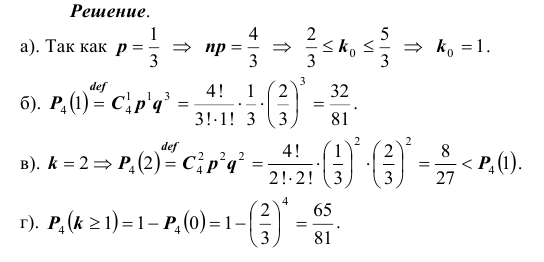
Пример №26
Некто Сэмюэль Пепайс обратился к Исааку Ньютону с вопросом: какое из событий наиболее вероятно –
- появление по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей;
- хотя бы двух «шестерок» при подбрасывании 12-ти;
- хотя бы трех «шестерок» при подбрасывании 18-ти?
Решение.
Вероятность q непоявления «шестерки» при одном подбрасывании, как известно, равна 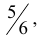 , следовательно, при шести подбрасываниях равна
, следовательно, при шести подбрасываниях равна 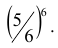
5 . Таким образом, вероятность появления по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей может быть найдена по формуле:
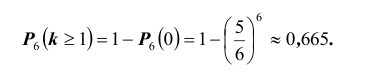
Событие «хотя бы две» противоположно событию «либо ни разу, либо один раз», т.е. 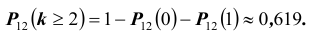
Событие «хотя бы три» противоположно событию «либо ни разу, либо один раз, либо два раза», т.е.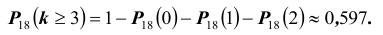
Таким образом, как видим, предпочтительнее первая стратегия – таким и был ответ Ньютона.
Замечу, что при больших значениях числа n испытаний в схеме Бернулли формула для подсчета становится громоздкой для вычислений. В этих случаях пользуются асимптотическими формулами. Рассмотрим асимптотическую формулу Пуассона, которая справедлива при малых p и больших n (распределение редких событий в схеме Бернулли). Другими словами
становится громоздкой для вычислений. В этих случаях пользуются асимптотическими формулами. Рассмотрим асимптотическую формулу Пуассона, которая справедлива при малых p и больших n (распределение редких событий в схеме Бернулли). Другими словами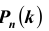 рассматривается как функция трех переменных n,k , p , при условии, что k – фиксировано, а n и p меняются
рассматривается как функция трех переменных n,k , p , при условии, что k – фиксировано, а n и p меняются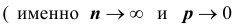
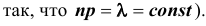
ТЕОРЕМА Пуассона 3. Пусть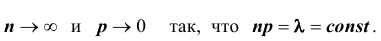 Тогда в схеме Бернулли
Тогда в схеме Бернулли 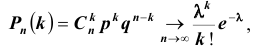 или то же самое
или то же самое 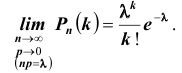
Доказательство

Что и требовалось доказать.
При доказательстве можно воспользоваться приближенной формулой Стирлинга.
Следствие: при указанных выше условиях, т.е. при  и
и 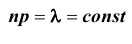 справедлива приближенная формула Пуассона:
справедлива приближенная формула Пуассона:
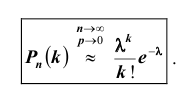
Пример №27
Телефонная станция обслуживает 800 абонентов. Для каждого абонента вероятность того, что в течении часа он позвонит на станцию равна p =0,01. Найти вероятность того, что четыре абонента позвонят на станцию в течении часа.
Решение 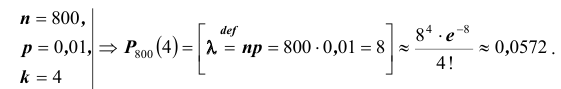
Теорема Муавра – Лапласа (локальная)
Остановлюсь еще на двух предельных теоремах в схеме Бернулли – локальной теореме Муавра – Лапласа (её доказательство получим как частный случай закона больших чисел – предельной теоремы Ляпунова, доказательство которой нам ещё предстоит провести) и интегральной теореме Муавра – Лапласа. Итак:

причем, во-первых, погрешность этой формулы есть величина порядка во-вторых, для функции
во-вторых, для функции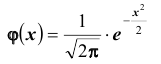 составлена таблица её значений. Для отрицательных значений аргумента пользуются той же таблицей, так как, очевидно,
составлена таблица её значений. Для отрицательных значений аргумента пользуются той же таблицей, так как, очевидно, 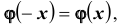 , то есть функция
, то есть функция 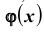 четная. Заметим также, что график функции
четная. Заметим также, что график функции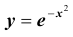 называется кривой Гаусса (см. рис.).
называется кривой Гаусса (см. рис.).
интегральная приближенная формула Лапласа ( при больших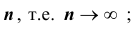
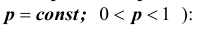

Для функции также есть табличные значения, когда
также есть табличные значения, когда  справедливо неравенство
справедливо неравенство 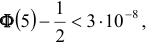
равносильно условию 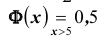 (график функции
(график функции  см. на рис.). Отметим, что точность растет с ростом произведения npq, и, обычно, пользуются этими формулами в случае, когда
см. на рис.). Отметим, что точность растет с ростом произведения npq, и, обычно, пользуются этими формулами в случае, когда 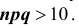
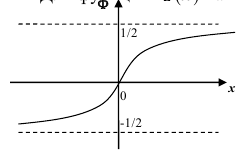
Замечание: если функция Лапласа записана в виде 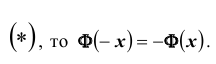 Иногда функция Лапласа может быть записана в виде
Иногда функция Лапласа может быть записана в виде
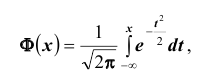
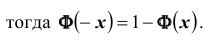 Отметим, что в схеме Бернулли рассматривались независимые испытания. Если же вероятность наступления события в k -ом опыте зависит от результата только предыдущего,
Отметим, что в схеме Бернулли рассматривались независимые испытания. Если же вероятность наступления события в k -ом опыте зависит от результата только предыдущего, 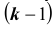 – ого опыта, то такая схема называется цепью Маркова.
– ого опыта, то такая схема называется цепью Маркова.
Формула полной вероятности и сложные задачи
В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события.
Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) 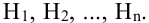 Пусть также имеется некоторое событие А и известны
Пусть также имеется некоторое событие А и известны 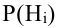 – вероятность гипотезы,
– вероятность гипотезы, 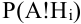 – условная вероятность события А при этой гипотезе). Тогда вероятность события А вычисляется по формуле полной вероятности:
– условная вероятность события А при этой гипотезе). Тогда вероятность события А вычисляется по формуле полной вероятности: 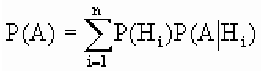
Пример №28
Из 40 деталей 10 изготовлены в первом цехе, 25 – во втором, а остальные – в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех – с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?
Решение:
Обозначим событие А = {выбрана деталь отличного качества}, Hi= {выбранная деталь изготовлена в i цехе}, i = 1, 2, 3. Тогда 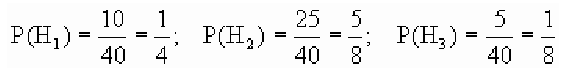
По условию задачи 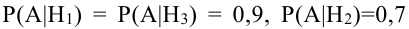 . По формуле полной вероятности находим искомую вероятность:
. По формуле полной вероятности находим искомую вероятность: 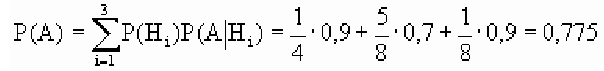
Пример №29
На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной).
Решение:
Обозначим Нi = {приход туриста в пункт Hi}, i = 1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то 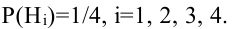
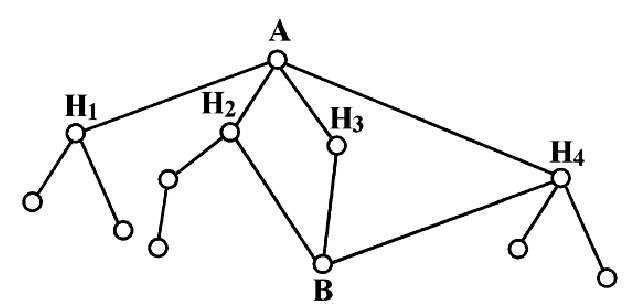
Исходя из схемы дорог, определяем, что 
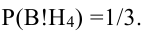
Таким образом, по формуле полной вероятности 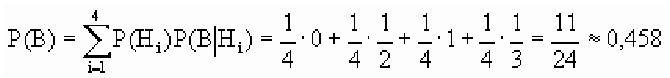
Пример №30
Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет?
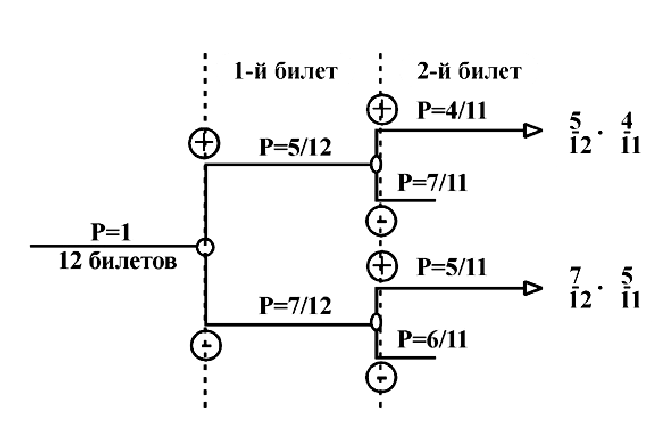
Решение:
Как обычно, вдоль каждой ветви “дерева вероятностей” значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ: 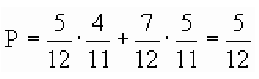
Случайные события независимые в совокупности
Следует различать попарно независимые случайные события и случайные события независимые в совокупности.
Определение: События называются попарно независимыми событиями, если любые два из них независимы.
Определение: События 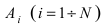 называются независимыми в совокупности, если каждое из них независимо от произведения любого числа остальных событий.
называются независимыми в совокупности, если каждое из них независимо от произведения любого числа остальных событий.
Замечание: Из определений видно, что из попарной независимости еще не следует, что эти события независимы в совокупности. Это означает, что условие независимости в совокупности является более сильным, чем условие попарной независимости случайных событий.
Теорема: Вероятность наступления хотя бы одного из событий 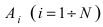 независимых в совокупности выражается формулой:
независимых в совокупности выражается формулой:
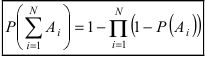 .
.
Доказательство: Обозначим через А событие, состоящее в том, что наступит хотя бы одно из событий 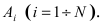 Очевидно, что противоположные события
Очевидно, что противоположные события 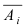 к событиям
к событиям 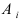 также будут независимы в совокупности. При этом событие
также будут независимы в совокупности. При этом событие 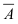 состоит в том, что в результате опыта не наступает ни одно из случайных событий
состоит в том, что в результате опыта не наступает ни одно из случайных событий 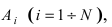 следовательно,
следовательно, 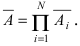 Так как события
Так как события 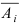 независимы в совокупности, то
независимы в совокупности, то 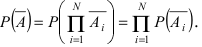 В силу того, что
В силу того, что 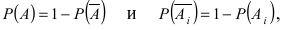 то
то 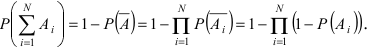
Пример №31
Пусть прибор содержит N последовательно соединенных блоков. Определить вероятность того, что цепь будет разорвана, если вероятность работы каждого блока равна р и она не зависит от работы других блоков.
Решение:
Пусть А – событие, которое состоит в том, что данная цепь разорвана. Это событие происходит, если выходит из строя хотя бы один из блоков, так как блоки включены последовательно. Противоположное событие состоит в том, что все блоки работают, т.е. 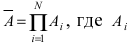 – событие, заключающееся в работе блока i. По условию задачи
– событие, заключающееся в работе блока i. По условию задачи 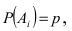 следовательно,
следовательно, 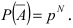 Таким образом, вероятность того, что цепь будет разорвана, равна
Таким образом, вероятность того, что цепь будет разорвана, равна 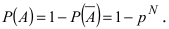
Теорема сложения вероятностей для совместных событий
Если случайные события одновременно появляются в условиях опыта, то имеет место следующая теорема.
Теорема: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их произведения:
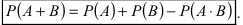
Доказательство: Пусть в результате опыта возможно n равно возможных, несовместных, элементарных исходов. При этом в 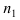 случаях наступает событие А, в
случаях наступает событие А, в 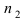 случаях – событие В, а в m случаях наступает и событие А, и событие B, т.е. событие
случаях – событие В, а в m случаях наступает и событие А, и событие B, т.е. событие 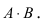 Таким образом, число исходов, в которых наступает или событие А , или событие В (т.е. событие А + В), равно
Таким образом, число исходов, в которых наступает или событие А , или событие В (т.е. событие А + В), равно 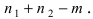 Согласно классическому определению вероятности вероятность суммы случайных, совместных событий А и В равна
Согласно классическому определению вероятности вероятность суммы случайных, совместных событий А и В равна
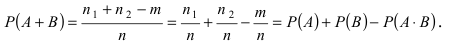
Замечание: Методом математической индукции вышеприведенная теорема может быть обобщена на любое число совместных событий, например, в случае 3 совместных событий А, В и С теорема принимает вид:
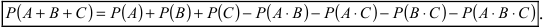
Пример №32
Найти вероятность того, что взятое наугад число из чисел от 10 до 20 делится или на 2, или на 3.
Решение:
Всего равновозможных, элементарных исходов 11 (числа от 10 включительно до 20 включительно). В 6 случаях (10, 12, 14, 16, 18, 20) число кратно 2; в 3 случаях (12, 15, 18) число кратно 3; в 2 случаях (12, 18) число кратно и 2, и 3. Пусть событие А состоит в том, что наугад взятое число кратно 2, а событие В состоит в том, что наугад взятое число кратно 3. Сложное событие С состоит в том, что наугад взятое число делится или на 2, или на 3, т.е. С = А + В. Следовательно, вероятность этого события равна:
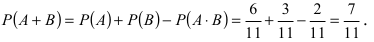
Все вышерассмотренные теоремы объединяются в теории вероятностей общим названием “основные теоремы теории вероятностей”.
Формула полной вероятности и события
Формула полной вероятности является следствием основных теорем теории вероятностей: теорем сложения и умножения вероятностей событий.
Пусть некоторое случайное событие А наступает с одним и только с одним из несовместных событий 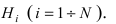
Определение: События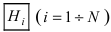 называются гипотезами, так как заранее неизвестно, какое из этих событий произойдет.
называются гипотезами, так как заранее неизвестно, какое из этих событий произойдет.
Теорема: Формула полной вероятности определяет вероятность случайного
события л, как сумму произведений вероятности каждой гипотезы 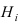 на условную вероятность события А при условии реализации гипотезы
на условную вероятность события А при условии реализации гипотезы 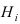 , т.е.
, т.е. 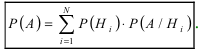
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 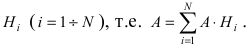 В силу того, что события
В силу того, что события 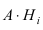 несовместны, то по теореме сложения вероятностей для несовместных событий имеем:
несовместны, то по теореме сложения вероятностей для несовместных событий имеем: 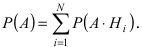 Используя теорему об умножении вероятностей зависимых событий, получаем искомую формулу:
Используя теорему об умножении вероятностей зависимых событий, получаем искомую формулу: 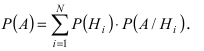
Пример №33
Пусть на сборку поступают детали с двух автоматических станков. Первый станок дает в среднем 0.3 % брака, а второй – 0.15 % брака. Производительность второго станка в два раза выше, чем первого станка. Найти вероятность того, что наугад взятая деталь окажется бракованной.
Решение:
Пусть событие А состоит в том, что наугад взятая деталь окажется бракованной. Тогда гипотеза 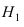 заключается в том, что эта деталь изготовлена на первом станке, а гипотеза
заключается в том, что эта деталь изготовлена на первом станке, а гипотеза 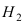 заключается в том, что эта деталь изготовлена на втором станке. Очевидно, что эти гипотезы являются несовместными событиями. В виду различной производительности станков обозначим через х количество деталей, изготовленных на первом станке, тогда на втором станке изготавливается 2х деталей. Общее число деталей, которые были изготовлены на обоих станках равна Зх. Следовательно, вероятности гипотез равны:
заключается в том, что эта деталь изготовлена на втором станке. Очевидно, что эти гипотезы являются несовместными событиями. В виду различной производительности станков обозначим через х количество деталей, изготовленных на первом станке, тогда на втором станке изготавливается 2х деталей. Общее число деталей, которые были изготовлены на обоих станках равна Зх. Следовательно, вероятности гипотез равны: 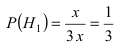 — для первой гипотезы и
— для первой гипотезы и 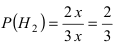 – для второй гипотезы.
– для второй гипотезы.
Вероятности события А при условии реализации первой и второй гипотез равны: 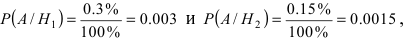 соответственно. Согласно формуле полной вероятности вероятность того, что наугад взятая деталь окажется бракованной, равна:
соответственно. Согласно формуле полной вероятности вероятность того, что наугад взятая деталь окажется бракованной, равна:
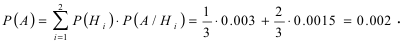
Формула вероятностей гипотез (формула Байеса)
Ниже будет получена формула, которая является следствием основных теорем теории вероятностей и формулы полной вероятности. Эта формула применяется для решения задач следующего типа. Пусть проводится эксперимент, в результате которого может появиться или не появиться событие л, которое наступает с одним и только с одним из несовместных событий  (
(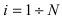 ). Предположим, что события
). Предположим, что события 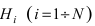 образуют полную группу и вероятности их появления
образуют полную группу и вероятности их появления 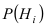 известны до проведения опыта. В результате проведения эксперимента событие А произошло. Используя этот факт, необходимо определить, какая из гипотез была ближе к истине, т.е. определить вероятность каждой гипотезы при условии реализации события А. Ответ на поставленный вопрос дает следующая теорема.
известны до проведения опыта. В результате проведения эксперимента событие А произошло. Используя этот факт, необходимо определить, какая из гипотез была ближе к истине, т.е. определить вероятность каждой гипотезы при условии реализации события А. Ответ на поставленный вопрос дает следующая теорема.
Теорема: Вероятность гипотезы 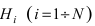 при условии реализации события А равна отношению произведения вероятности гипотезы на условную вероятность события А к паз ной вероятности события А:
при условии реализации события А равна отношению произведения вероятности гипотезы на условную вероятность события А к паз ной вероятности события А:
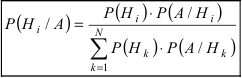
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 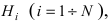 т.е. в каждом опыте происходит событие
т.е. в каждом опыте происходит событие  По теореме умножения вероятностей для зависимых событий:
По теореме умножения вероятностей для зависимых событий: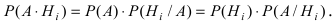
Следовательно, 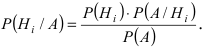 Воспользовавшись формулой полной вероятности, получим формулу Байеса:
Воспользовавшись формулой полной вероятности, получим формулу Байеса: 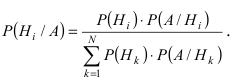
Пример №34
Однотипные пластмассовые детали изготавливаются на 3 прессах. Первый пресс выпускает 50 % всех деталей, второй – 40 %, третий – 10 % . При этом с первого пресса сходит в среднем 0.025 нестандартных деталей, со второго – 0.02 и с третьего – 0.015. Все детали поступают на сборку. Взятая наудачу деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на первом прессе.
Решение:
Событие А состоит в том, что наудачу взятая деталь изготовлена на первом прессе. Гипотеза  заключается в том, что эта деталь изготовлена на первом прессе, гипотеза
заключается в том, что эта деталь изготовлена на первом прессе, гипотеза  – на втором прессе, а гипотеза
– на втором прессе, а гипотеза 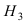 – на третьем прессе.
– на третьем прессе.
По условию задачи 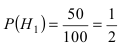 – для первой гипотезы,
– для первой гипотезы, 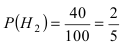 – для второй гипотезы и
– для второй гипотезы и 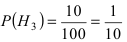 – для третьей гипотезы. Вероятности события А при условии реализации первой, второй и третьей гипотез, соответственно, равны:
– для третьей гипотезы. Вероятности события А при условии реализации первой, второй и третьей гипотез, соответственно, равны: 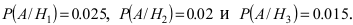 Согласно фор- муле пал ной вероятности вероятность того, что наугад взятая деталь окажется нестандартной, равна:
Согласно фор- муле пал ной вероятности вероятность того, что наугад взятая деталь окажется нестандартной, равна: 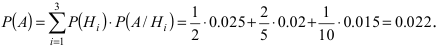
Используя формулу Байеса, получим 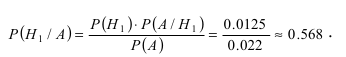
Независимые испытания и формула Бернулли
Пусть испытания повторяются n раз, причем событие А появляется в каждом опыте с одной и той же вероятностью р или не появляется с одной и той же вероятностью 
Определение: Испытания называются независимыми, если вероятность события А не зависит от того, какие события появились в предыдущих опытах, или появятся в последующих экспериментах.
Пример:
Независимы ли следующие испытания: а) многократное бросание кубика; б) извлечение карты из колоды без ее возвращения в колоду (выяснить самостоятельно).
Формула Бернулли
Теорема: Пусть проводится серия из n независимых испытаний, в каждом из которых событие А появляется с постоянной вероятностью 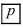 или не появляется с постоянной вероятностью
или не появляется с постоянной вероятностью 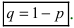 Тогда вероятность появления со- бытия А ровно m раз в серии из n независимых испытаний равна:
Тогда вероятность появления со- бытия А ровно m раз в серии из n независимых испытаний равна: 
Доказательство: Пусть 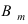 событие, состоящее в том, что в серии из n независимых испытаний событие А появится ровно m раз. Пусть
событие, состоящее в том, что в серии из n независимых испытаний событие А появится ровно m раз. Пусть 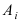 событие, описывающее появление события А в опыте i, а ему противоположное событие обозначим через
событие, описывающее появление события А в опыте i, а ему противоположное событие обозначим через 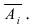 Так как вероятность появления события А в опыте i равна
Так как вероятность появления события А в опыте i равна 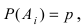 то вероятность появления противоположного события
то вероятность появления противоположного события 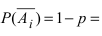
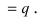 Для наступления события
Для наступления события 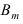 безразлично, в каких опытах произойдет событие A, а в каких – событие
безразлично, в каких опытах произойдет событие A, а в каких – событие 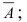 важно, чтобы число появлений события A в данной серии равнялось числу m. В качестве одного из вариантов чередования событий
важно, чтобы число появлений события A в данной серии равнялось числу m. В качестве одного из вариантов чередования событий 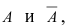 благоприятствующих появлению события
благоприятствующих появлению события 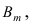 рассмотрим такое событие
рассмотрим такое событие 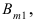 для которого событие А появится в m первых опытах и не появится в (n-m) последующих экспериментах, т.е.
для которого событие А появится в m первых опытах и не появится в (n-m) последующих экспериментах, т.е.
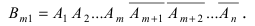
Воспользуемся теоремой умножения вероятностей для независимых событий, получим: 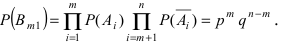 Аналогичные к
Аналогичные к 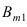 события отличаются от него только чередованием событий
события отличаются от него только чередованием событий 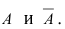 Все эти события равновероятны и их число равно количеству сочетаний из n элементов по m элементов, т.е.
Все эти события равновероятны и их число равно количеству сочетаний из n элементов по m элементов, т.е. 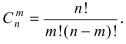 Таким образом, интересующее нас событие можно записать в виде
Таким образом, интересующее нас событие можно записать в виде 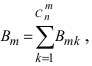 причем события
причем события  несовместны. По теореме сложения вероятностей несовместных событий вероятность изучаемого события равна
несовместны. По теореме сложения вероятностей несовместных событий вероятность изучаемого события равна 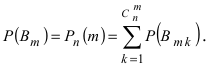 В правой части равенства суммируется
В правой части равенства суммируется 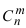 одинаковых слагаемых, следовательно,
одинаковых слагаемых, следовательно, 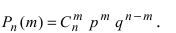 O5. Формула
O5. Формула  называется биномиальной или формулой Бернулли.
называется биномиальной или формулой Бернулли.
Пример №35
Монета подбрасывается 6 раз. Определить вероятность того, что герб выпадет а) 5 раз; б) от 2 до 4 раз.
Решение:
Вероятность выпадения герба не изменяется от опыта к опыту и равна 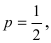 а, следовательно, вероятность выпадения решки равна
а, следовательно, вероятность выпадения решки равна 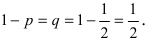 Для определения вероятности выпадения герба 5 раз в серии из 6 испытаний воспользуемся формулой Бернулли:
Для определения вероятности выпадения герба 5 раз в серии из 6 испытаний воспользуемся формулой Бернулли: 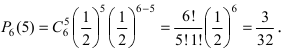 Событие, состоящее в том, что герб выпадет от 2 до 4 раз, соответствует события, которое состоит в том, что герб выпадет или 2 раза, или 3 раза, или 4 раза. Следовательно, вероятность
Событие, состоящее в том, что герб выпадет от 2 до 4 раз, соответствует события, которое состоит в том, что герб выпадет или 2 раза, или 3 раза, или 4 раза. Следовательно, вероятность 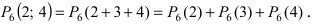 Вычислим соответствующие вероятности:
Вычислим соответствующие вероятности: 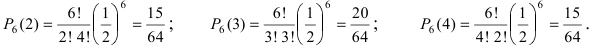 Таким образом, искомая вероятность равна
Таким образом, искомая вероятность равна 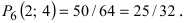
При больших значениях чисел m и n применение формулы Бернулли затруднительно, так как вычисление коэффициентов 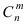 становится достаточно сложным. Поэтому при фиксированном значении т и в случае, когда вероятность появления события р<0.1, применяется формула Пуассона, а при р>0.1 – дифференциальная формула Муавра-Лапласа. Если
становится достаточно сложным. Поэтому при фиксированном значении т и в случае, когда вероятность появления события р<0.1, применяется формула Пуассона, а при р>0.1 – дифференциальная формула Муавра-Лапласа. Если 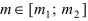 , то применяют интегральную формулу Муавра-Лапласа.
, то применяют интегральную формулу Муавра-Лапласа.
Формула Пуассона
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А мала (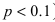 ), то при больших значениях чисел m и n применяют приближенную формулу Пуассона:
), то при больших значениях чисел m и n применяют приближенную формулу Пуассона: 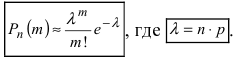
Формулы Муавра-Лапласа
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А р>0.1, то при больших значениях чисел m и n применяют дифференциальную формулу Муавра-Лапласа: 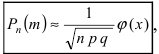 дифференциальная функция Муавра-Лапласа
дифференциальная функция Муавра-Лапласа 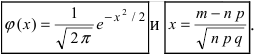
Замечание: В общем случае дифференциальная формула Муавра-Лапласа применяется при выполнении неравенств 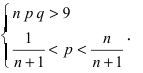
Если при проведении серии испытаний по схеме Бернулли числа m и n принимают большие значения, причем число m принимает значения от 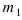 до
до 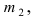 то применяют интегральную формулу Муавра-Лапласа:
то применяют интегральную формулу Муавра-Лапласа:
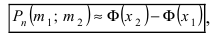 где
где 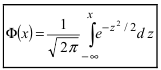 – интегральная функция Муавра-Лапласа и
– интегральная функция Муавра-Лапласа и 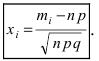
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Комбинаторика – правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей
