Как найти вершину додекаэдра - Сайт, где вы сможете решить свои вопросы

Правильный додекаэдр

(вращающаяся модель, 3D-модель)

Тип

правильный многогранник

Свойства

выпуклый

Комбинаторика

Элементы

12 граней
30 рёбер
20 вершин

Χ = 2

Грани

правильные пятиугольники

Конфигурация вершины

5³

Двойственный многогранник

правильный икосаэдр

Вершинная фигура

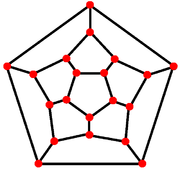
Развёртка

Классификация

Обозначения

U₂₃, C₂₆, W₅

Символ Шлефли

{5,3}

Символ Витхоффа^[en]

3 | 2 5

Диаграмма Дынкина

Группа симметрии

I_h, H₃, [5,3], (*532)

Группа вращения

I, [5,3]⁺, (532)

Количественные данные

Длина ребра

Площадь поверхности

${displaystyle 3{sqrt {25+10{sqrt {5}}}}a^{2}}$

Объём

${displaystyle {tfrac {15+7{sqrt {5}}}{4}}a^{3}}$

Двугранный угол

${displaystyle arccos(-1/5^{1/2})approx 116.565}$

Телесный угол при вершине

${displaystyle pi -tan ^{-1}left({frac {2}{11}}right)quad approx 2.96}$

Медиафайлы на Викискладе

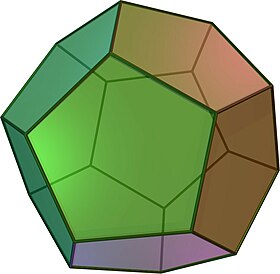
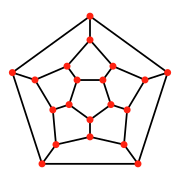
Пра́вильный додека́эдр (др.-греч. δωδεκάεδρον, от δώδεκα — «двенадцать» и ἕδρα — «грань») — один из пяти возможных правильных многогранников. Додекаэдр составлен из двенадцати правильных пятиугольников^[1], являющихся его гранями. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).

Додекаэдр и его описанная сфера

История[править | править код]

Пожалуй, самый древний предмет в форме додекаэдра был найден в северной Италии, около Падуи, в конце XIX века, он датируется 500 г. до н. э. и предположительно использовался этрусками в качестве игральной кости^[2]^[3].

Додекаэдр рассматривали в своих сочинениях древнегреческие учёные. Платон сопоставлял с правильными многогранниками различные классические стихии. О додекаэдре Платон писал, что «…его бог определил для Вселенной и прибегнул к нему в качестве образца»^[4]. Евклид в предложении 17 книги XIII «Начал» строит додекаэдр на рёбрах куба^[5]^[6]^:132-136. Папп Александрийский в «Математическом собрании» занимается построением додекаэдра, вписанного в данную сферу, попутно доказывая, что вершины додекаэдра лежат в параллельных плоскостях^[7]^[6]^:318-319^[8].

На территории нескольких европейских стран найдено множество предметов, называемых римскими додекаэдрами, относящихся ко II—III вв. н. э., назначение которых не совсем понятно.

Вскоре после появления кубика Рубика, в 1981 году была запатентована подобная головоломка в форме правильного додекаэдра — мегаминкс. Как и у классического кубика Рубика, к каждому ребру у неё прилегает по три детали^[9]. Позднее, как и для кубика Рубика появились такие додекаэдрические головоломки с четырьмя деталями при ребре (гигаминкс), пятью (тераминкс) и т.д. Сложность и время сборки их, как и для кубика Рубика возрастает по мере увеличения числа деталей при ребре.

Основные формулы[править | править код]

Если за длину ребра принять , то площадь поверхности додекаэдра равна

${displaystyle S=3a^{2}{sqrt {5(5+2{sqrt {5}})}}approx 20{,}65a^{2}.}$

Объём додекаэдра

${displaystyle V={frac {a^{3}}{4}}(15+7{sqrt {5}})approx 7{,}66a^{3}.}$

Радиус описанной сферы^[10]

${displaystyle R={frac {a}{4}}(1+{sqrt {5}}){sqrt {3}}approx 1{,}4012a.}$

Радиус полувписанной сферы равен ${displaystyle {frac {3+{sqrt {5}}}{4}}aapprox 1{,}309a.}$ ^[10]

Радиус вписанной сферы^[10]

${displaystyle r={frac {a}{4}}{sqrt {10+{frac {22}{sqrt {5}}}}}approx 1{,}1135a.}$

Свойства[править | править код]

Все двадцать вершин додекаэдра лежат по пять в четырёх параллельных плоскостях, образуя в каждой из них правильный пятиугольник.
Двугранный угол между любыми двумя смежными гранями додекаэдра равен arccos(−1/√5) ≈ 116,565°^[10].
Сумма плоских углов при каждой из 20 вершин равна 324°, телесный (трёхгранный) угол равен arccos(−11/5√5) ≈ 2,9617 стерадиана.
В додекаэдр можно вписать куб так, что стороны куба будут диагоналями додекаэдра.
Додекаэдр имеет три звёздчатые формы.
В додекаэдр можно вписать пять кубов. Если заменить пятиугольные грани додекаэдра плоскими пятиугольными звездами так, что исчезнут все рёбра додекаэдра, то получим пространство пяти пересекающихся кубов. Додекаэдр как таковой исчезнет. Вместо замкнутого многогранника появится открытая геометрическая система пяти ортогональностей. Или симметричное пересечение пяти трёхмерных пространств.
Ближайшая параллельная к произвольно выбранной грани плоскость, в которой лежат пять вершин, не принадлежащих выбранной грани, отстоит от этой грани на расстояние радиуса описанной вокруг данной грани окружности. А радиус описанной вокруг этих пяти вершин окружности равен диаметру вписанной в любую из граней окружности. Эти две величины равны, соответственно, ${displaystyle {sqrt {frac {5+{sqrt {5}}}{10}}}a}$ и ${displaystyle {frac {{sqrt {5}}+1}{2}}cdot {sqrt {frac {5+{sqrt {5}}}{10}}}a}$ , где — длина ребра додекаэдра.

Элементы симметрии додекаэдра[править | править код]

Связь со сферическим замощением[править | править код]

Правильный додэкаэдр также индуцирует замощение сферы правильными пятиугольниками.

Ортографическая проекция^[en]	Стереографическая проекция

Интересные факты[править | править код]

В 1887 году Эрнст Геккель описал радиолярию Circorrhegma dodecahedra, имеющую форму, близкую к додекаэдру^[11].
в 1982 году был синтезирован додекаэдран, химическое соединение (C₂₀H₂₀) в форме додекаэдра.
В 2003 году при анализе данных космического аппарата WMAP, была выдвинута гипотеза, что Вселенная представляет собой додекаэдрическое пространство Пуанкаре^[12]^[13]^[14].

В культуре[править | править код]

Додекаэдр применяется как генератор случайных чисел (вместе с другими костями) в настольных ролевых играх^[15], и обозначается при этом d12 (dice — кости).
Изготавливаются настольные календари в форме додекаэдра из бумаги, где каждый из двенадцати месяцев расположен на одной из граней^[15].
В игре Пентакор мир представлен в виде этой геометрической фигуры^{[источник не указан 2659 дней]}.
В играх «Sonic the Hedgehog 3» и «Sonic & Knuckles» серии Sonic the Hedgehog вид додекаэдра имеют Изумруды Хаоса^{[источник не указан 2659 дней]}.
В игре «Destiny» форму додекаэдра имеют энграммы^{[источник не указан 2659 дней]}.
В игре «Overwatch» персонаж Сигма при основной атаке выпускает по 2 додекаэдра^{[источник не указан 1136 дней]}.
Пульт управления системой освещения Nanoleaf Smart Remote Control ^[16].

См. также[править | править код]

Пентагондодекаэдр — неправильный додекаэдр
Ромбододекаэдр
Ромбоикосододекаэдр
Двенадцатигранники

Примечания[править | править код]

↑ Селиванов Д. Ф.,. Тело геометрическое // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
↑ Stefano De’ Stefani. Intorno un dodecaedro quasi regolare di pietra a facce pentagonali scolpite con cifre, scoperto nelle antichissime capanne di pietra del Monte Loffa (итал.) // Atti del Reale Istituto veneto di scienze, lettere ed arti : diario. — 1885-86. — P. 1437—1459. См. также изображение этого предмета в конце тома, стр. 709 файла со сканом
↑ Amelia Carolina Sparavigna. An Etruscan Dodecahedron. — arXiv:1205.0706.
↑ Платон. «Тимей»
↑ Euclid’s Elements. Book XIII. Proposition 17. Дата обращения: 1 июня 2014. Архивировано 19 мая 2014 года.
↑ ¹ ² Начала Евклида. Книги XI—XV. — М.—Л.: Государственное издательство технико-теоретической литературы, 1950. — Помимо перевода на русский язык сочинения Евклида это издание в комментариях содержит перевод предложений Паппа о правильных многогранниках.
↑ Оригинальный текст на древнегреческом языке с параллельным переводом на латинский язык: Liber III. Propos. 58 // Pappi Alexandrini Collectionis. — 1876. — Т. I. — С. 156—163.
↑ Roger Herz-Fischler. A Mathematical History of the Golden Number (англ.). — Courier Dover Publications, 2013. — P. 117—118.
↑ Хорт В. Отчаянные головоломки. Мегаминкс — каверзный додекаэдр // Наука и жизнь. — 2018. — № 1. — С. 104—109. В этой статье, помимо прочего, приведён алгоритм сборки мегаминкса.
↑ ¹ ² ³ ⁴ Доказательство приведено в: Cobb, John W. The Dodecahedron (англ.) (2005—2007). Дата обращения: 1 июня 2014. Архивировано 4 марта 2016 года.
↑ http://www.biodiversitylibrary.org/page/10685137#page/111/mode/1up таблице XVII] Архивная копия от 7 июня 2014 на Wayback Machine четвёртого тома его монографии о радиоляриях она обозначена номером 2
↑ The optimal phase of the generalised Poincare dodecahedral space hypothesis implied by the spatial cross-correlation function of the WMAP sky maps (англ.). Дата обращения: 31 октября 2012. Архивировано 7 декабря 2013 года.
↑ Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background (англ.). Дата обращения: 31 октября 2012. Архивировано 7 декабря 2013 года.
↑ Jeffrey Weeks. The Poincare Dodecahedral Space and the Mystery of the Missing Fluctuations (англ.). Архивировано 4 ноября 2012 года.
↑ ¹ ² A. T. White. Graphs of Groups on Surfaces: Interactions and Models. — Elsevier, 2001. — P. 45. — 378 p. — ISBN 0-080-50758-1, 978-0-080-50758-3.
↑ Products » Nanoleaf Remote | USA » Consumer IoT & LED Smart Lighting Products (амер. англ.). Nanoleaf | USA. Дата обращения: 25 ноября 2021. Архивировано 25 ноября 2021 года.

Ссылки[править | править код]

На Викискладе есть медиафайлы по теме Правильный додекаэдр

Источник

Правильный додекаэдр
. (Щелкните здесь для вращения модели)
Тип	Платоново твердое тело
Элементы	F = 12, E = 30. V = 20 (χ = 2)
Грани по сторонам	12 {5}
Обозначение Конвея	D
символы Шлефли	{5, 3}
Конфигурация лица	V3.3.3.3.3
Символ Wythoff	3 \| 2 5
Диаграмма Кокстера
Симметрия	Ih, H 3, [5,3], (* 532)
Группа вращения	I, [5,3], ( 532)
Ссылки	U 23, C 26, W 5
Свойства	обычный, выпуклый
Двугранный угол	116,56505 ° = arccos (- ⁄ √5)
. 5.5.5. (Вершинная фигура )	. Правильный икосаэдр. (двойной многогранник )
. Сеть

Анимация складывающейся сети правильного (пятиугольного) додекаэдра 3D-модель правильного додекаэдра

A Правильный додекаэдр или пятиугольный додекаэдр – это додекаэдр, который является правильным, который состоит из 12 правильных пятиугольных граней, трех встречаются в каждой вершине . Это одно из пяти Платоновых тел. У него 12 граней, 20 вершин, 30 ребер и 160 диагоналей (60 диагоналей граней, 100 диагонали пространства ). Он представлен символом Шлефли {5,3}.

Содержание

1 Размеры
2 Площадь и объем
3 Двумерные проекции симметрии
4 Сферические t iling
5 Декартовы координаты
- 5.1 Уравнения, определяющие грань
6 Свойства
7 Геометрические отношения
- 7.1 Связь с правильным икосаэдром
- 7.2 Связь с вложенным кубом
- 7.3 Связь с золотой прямоугольник
- 7.4 Связь с 6-кубом и ромбическим триаконтаэдром
8 История и использование
- 8.1 В природе
- 8.2 Форма вселенной
9 Заполнение пространства кубом и двунабиротондами
10 Связанные многогранники и мозаики
11 Расположение вершин
12 Звездчатость
13 Додекаэдрический граф
14 См. Также
15 Ссылки
16 Внешние ссылки

Размеры

Если длина ребра правильного додекаэдра равна «a { displaystyle a}», радиус описанной сферы (той, которая касается правильной додекаэдр во всех вершинах) равно

ru = a 3 4 (1 + 5) ≈ 1,401 258 538 ⋅ a { displaystyle r_ {u} = a { frac { sqrt {3}} {4}} left (1 + { sqrt {5}} right) приблизительно 1.401 , 258 , 538 cdot a} ${ displaystyle r_ {u} = a { frac { sqrt {3}} {4}} left ( 1 + { sqrt {5}} right) приблизительно 1.401 , 258 , 538 cdot a}$

OEIS : A179296

an d радиус вписанной сферы (касательная к каждой из граней правильного додекаэдра) равен

ri = a 1 2 5 2 + 11 10 5 ≈ 1,113 516 364 ⋅ a { displaystyle r_ {i } = a { frac {1} {2}} { sqrt {{ frac {5} {2}} + { frac {11} {10}} { sqrt {5}}}} приблизительно 1,113 , 516 , 364 cdot a} ${ displaystyle r_ {i} = a { frac {1} {2}} { sqrt {{ frac {5} {2}} + { frac {11} {10}} { sqrt {5}}}} приблизительно 1.113 , 516 , 364 cdot a}$

, а средний радиус, который касается середины каждого края, равен

rm = a 1 4 (3 + 5) ≈ 1,309 016 994 ⋅ a { displaystyle r_ { m} = a { frac {1} {4}} left (3 + { sqrt {5}} right) приблизительно 1,309 , 016 , 994 cdot a} ${ displaystyle r_ {m} = a { frac {1} {4}} left (3 + { sqrt {5}} right) приблизительно 1.309 , 016 , 994 cdot a}$

Эти величины также могут быть выражается как

ru = a 3 2 ϕ { displaystyle r_ {u} = a , { frac { sqrt {3}} {2}} phi} $r_ {u} = a , { frac { sqrt {3}} {2}} phi$

ri = a ϕ 2 2 3 – ϕ { displaystyle r_ {i} = a , { frac { phi ^ {2}} {2 { sqrt {3- phi}}}}} $r_ {i} = a , { frac { phi ^ {2}} {2 { sqrt {3 - phi}}}}$

rm = a ϕ 2 2 { displaystyle r_ {m} = a , { frac { phi ^ {2}} {2}}} $r_ {m} = a , { frac { phi ^ {2 }} {2}}$

где ϕ – золотое сечение.

Обратите внимание, что для правильного додекаэдра с длиной ребра один, r u – радиус описывающей сферы вокруг куба с длиной ребра ϕ, а r i – апофема ar правильный пятиугольник с длиной ребра ϕ.

Площадь поверхности и объем

Площадь поверхности A и объем V правильного додекаэдра с длиной ребра a равны:

A Знак равно 3 25 + 10 5 a 2 ≈ 20,645 728 807 a 2 { displaystyle { displaystyle A = 3 { sqrt {25 + 10 { sqrt {5}}}} a ^ {2} приблизительно 20,645 , 728 , 807a ^ {2}}} ${ displaystyle { displaystyle A = 3 { sqrt {25 + 10 { sqrt {5}}}} a ^ {2} приблизительно 20.645 , 728 , 807a ^ {2}}}$

V = 1 4 (15 + 7 5) a 3 ≈ 7,663 118 9606 a 3 { displaystyle V = { frac {1} {4}} (15 + 7 { sqrt {5}}) a ^ {3} приблизительно 7.663 , 118 , 9606a ^ {3}} ${ displaystyle V = { frac {1} {4}} (15 + 7 { sqrt {5}}) a ^ {3} приблизительно 7.663 , 118 , 9606a ^ {3} }$

Кроме того, площадь поверхности и объем правильного додекаэдра связаны с золотым сечением. Додекаэдр с длиной ребра в одну единицу имеет следующие свойства:

A = 15 φ 3 – φ { displaystyle { displaystyle A = { frac {15 varphi} { sqrt {3- varphi}}} }} ${ displaystyle { displaystyle A = { frac {15 varphi) } { sqrt {3- varphi}}}}}$

V = 5 φ 3 6 – 2 φ { displaystyle { displaystyle V = { frac {5 varphi ^ {3}} {6-2 varphi}}}} ${ displaystyle { displaystyle V = { frac {5 varphi ^ {3}} { 6-2 varphi}}}}$

Двумерный проекции симметрии

Правильный додекаэдр имеет две специальные ортогональные проекции с центром на вершинах и пятиугольные грани, соответствующие A 2 и H 2Плоскости Кокстера.

Ортогональные проекции

Центрированы по	Вершина	Край	Грань
Изображение
Проективная. симметрия	[[3]] = [6]	[2]	[[5]] = [10]

В перспективной проекции, Если смотреть на вершину пятиугольной грани, правильный додекаэдр можно рассматривать как линейную диаграмму Шлегеля или стереографическую проекцию как сферический многогранник. Эти проекции также используются для отображения четырехмерного 120-элементного, правильного 4-мерного многогранника, построенного из 120 додекаэдров, проецируя его вниз до 3-х измерений.

Проекция	Ортогональная проекция	Перспективная проекция
Диаграмма Шлегеля	Стереографическая проекция
Правильный додекаэдр
Додекаплекс. (120-ячеечная )

Сферическая мозаика

Правильный додекаэдр также можно представить в виде сферической мозаики.

Ортографическая проекция	Стереографическая проекция

Декартовы координаты

Координаты вершин:
	Оранжевые вершины лежат в точках (± 1, ± 1, ± 1) и образуют куб (пунктирные линии).
	Зеленые вершины лежат в точках (0, ± ϕ, ± 1 / ϕ) и образуют прямоугольник на плоскости yz.
	Синие вершины лежат в точках (± 1 / ϕ, 0, ± ϕ) и образуют прямоугольник на плоскости xz.
	Розовые вершины лежат в точках (± ϕ, ± 1 / ϕ, 0) и образуют прямоугольник на плоскости xy.
расстояние между соседними вершинами равно 2 / ϕ, а расстояние от начала координат в любую вершину √3.. ϕ = 1 + √5 / 2 – золотое сечение.

Следующие декартовы координаты определяют 20 вершин правильного додекаэдра с центром в начале координат, соответствующим масштабом и ориентацией:

(± 1, ± 1, ± 1)

(0, ± ϕ, ± 1 / ϕ)

(± 1 / ϕ, 0, ± ϕ)

(± ϕ, ± 1 / ϕ, 0)

где ϕ = 1 + √5 / 2 – это золотое сечение (также пишется τ) ≈ 1,618. Длина ребра равна 2 / ϕ = √5 – 1. Радиус описанной окружности равен √3.

Уравнения, определяющие грань

Подобно симметрии координат вершины, уравнения двенадцати граней правильного додекаэдра также демонстрируют симметрию в своих коэффициентах:

x ± ϕy = ± ϕ

y ± ϕz = ± ϕ

z ± ϕx = ± ϕ

Свойства

двугранный угол правильного додекаэдра равен 2 arctan (ϕ) или приблизительно 116,565 ° (где снова ϕ = 1 + √5 / 2, золотое сечение ). OEIS : A137218 Обратите внимание, что тангенс двугранного угла равен -2.
Если исходный правильный додекаэдр имеет длину ребра 1, его двойной икосаэдр имеет длину ребра ϕ.
Если пять Платоновых тел имеют одинаковый объем, у правильного додекаэдра самые короткие ребра.
Он имеет 43 380 цепей.
число раскраски карты граней правильного додекаэдра равно 4.
Расстояние между вершинами одной и той же грани, не соединенными ребром, равно ϕ, умноженному на длину ребра.
Если два ребра имеют общую общей вершине, то середины этих ребер образуют треугольник 36-72-72 с центром тела.

Геометрические соотношения

Правильный додекаэдр является третьим в бесконечном наборе усеченных трапецоэдров, который может быть построен путем усечения двух осевых вершин пятиугольного трапеции .

Звёздчатые формы правильного додекаэдра составляют три из четырех многогранников Кеплера – Пуансо.

A выпрямленный правильный додекаэдр образует икосододекаэдр.

Правильный додекаэдр имеет икосаэдрическую симметрию Ih, группу Кокстера [5,3], порядок 120, с абстрактной групповой структурой A5 × Z2.

Отношение к правильному икосаэдру

Когда правильный додекаэдр вписан в сферу , он занимает больше объема сферы (66,49%), чем икосаэдр, вписанный в ту же сферу (60,55). %).

Правильный додекаэдр с длиной ребра 1 имеет более чем в три с половиной раза объем икосаэдра с такой же длиной ребер (7,663… по сравнению с 2,181…), что составляет примерно 3,51246117975, или в точных терминах: 3/5 (3ϕ + 1) или (1.8ϕ + 0.6).

У правильного додекаэдра 12 граней и 20 вершин, а у правильного икосаэдра 20 граней и 12 вершин. У обоих по 30 ребер.

Связь с вложенным кубом

Куб может быть встроен в правильный додекаэдр, прикрепленный к восьми из его равноотстоящих вершин в пяти различных положениях. Фактически, пять кубов могут перекрываться и сцепляться внутри правильного додекаэдра, что приводит к соединению пяти кубов.

Отношение края правильного додекаэдра к краю куба, заключенного внутри такого правильного додекаэдра, равно 1 : ϕ, или (ϕ – 1): 1.

Отношение объема правильного додекаэдра к объему куба, заключенного внутри такого правильного додекаэдра, равно 1: 2/2 + ϕ, или 1 + ϕ / 2: 1 или (5 + √5): 4.

Например, вложенный куб с объемом 64 (и длиной ребра 4) будет вложен в правильный додекаэдр объемом 64+. 32ϕ (и длина кромки 4ϕ – 4).

Таким образом, разница в объеме между окружающим правильным додекаэдром и замкнутым кубом всегда равна половине объема куба, умноженного на ϕ.

Из этих соотношений выводятся простые формулы для объема правильного додекаэдра с длиной ребра a в терминах золотой середины:

V = (aϕ) · 1/4 (5 + √5)

V = 1/4 (14ϕ + 8) a

Отношение к золотому прямоугольнику

Золотые прямоугольники отношения (ϕ + 1): 1 и ϕ: 1 также идеально вписываются в правильный додекаэдр. Пропорционально этому золотому прямоугольнику край замкнутого куба равен ϕ, когда длинная длина прямоугольника равна ϕ + 1 (или ϕ), а короткая длина равна 1 (ребро, общее с правильным додекаэдром).

Кроме того, центр каждой грани правильного додекаэдра образует три пересекающихся золотых прямоугольника.

Отношение к 6-кубу и ромбическому триаконтаэдру

Проекция 6-полукуба в правильный додекаэдр конверт

Его можно спроецировать в 3D из 6-мерного 6-полукуба с использованием тех же базисных векторов, которые образуют оболочку ромбического триаконтаэдра из 6- куб. Показанные здесь 12 внутренних вершин, которые не соединены внешними ребрами корпуса с 6D нормальной длиной √2, образуют правильный икосаэдр.

. Используемые базисные векторы трехмерной проекции [u, v, w]:

u = (1, φ, 0, -1, φ, 0)

v = (φ, 0, 1, φ, 0, -1)

w = (0, 1, φ, 0, -1, φ)

История и использование

Римский додекаэдр Всенаправленный источник звука

Обычные додекаэдрические объекты нашли практическое применение, а также сыграли свою роль в визуальном восприятии. искусства и философии.

Ямвлих заявляет, что Гиппас, пифагорейец, погиб в море, потому что он хвастался, что впервые раскрыл «сферу с двенадцатью пятиугольниками». В Теэтете, диалоге Платона, Платон смог доказать, что существует только пять однородных правильных тел; позже они стали известны как платоновы тела. Тимей (ок. 360 г. до н.э.), как персонаж диалога Платона, связывает другие четыре платоновых тела с четырьмя классическими элементами, добавляя, что существует пятый твердый образец, который, хотя обычно ассоциируется с правильным додекаэдром, но никогда прямо не упоминается как таковой; «этот Бог использовал в очерчивании вселенной». Аристотель также постулировал, что небеса состоят из пятого элемента, который он назвал aithêr (эфир на латыни, эфир на американском английском)).

Обычные додекаэдры использовались как игральные кости и, вероятно, также как гадательные приспособления. В течение эллинистической эры были изготовлены небольшие полые бронзовые римские додекаэдры, которые были найдены в различных римских руинах в Европе. Их цель не ясна.

В искусстве ХХ века додекаэдры появляются в творчестве М. К. Эшер, например его литографии Рептилии (1943) и Гравитация (1952). На картине Сальвадора Дали Таинство Тайной вечери (1955) комната представляет собой полый правильный додекаэдр. Джерард Карис основал все свое творчество на правильном додекаэдре и пятиугольнике, которые представлены как новое направление в искусстве, получившее название пентагонизма.

Стена для лазания, состоящая из трех додекаэдрических частей

В современных ролевых играх правильный додекаэдр часто используется как двенадцатигранный кубик, один из наиболее распространенных многогранных кубиков.

Immersive Media, компания-производитель камер, создала камеру Dodeca 2360, первую в мире камеру с полным движением 360 °, которая снимает видео высокого разрешения со всех сторон одновременно со скоростью более 100 миллионов пикселей в секунду или 30 кадров в секунду. Он основан на правильном додекаэдре.

Извилистая головоломка Megaminx, наряду со своими аналогами большего и меньшего порядка, имеет форму правильного додекаэдра.

В детском романе Призрачная будка правильный додекаэдр появляется как персонаж в стране математики. У каждого из его лиц разное выражение – например, счастливый, сердитый, грустный – который он поворачивает вперед, чтобы соответствовать своему настроению.

В природе

Ископаемое кокколитофора Ho-Mg-Zn квазикристалл

Ископаемое кокколитофора Braarudosphaera bigelowii (см. рисунок), одноклеточная прибрежная фитопланктонная водоросль, имеет раковину из карбоната кальция с правильной додекаэдрической структурой около 10 микрометров в поперечнике.

Некоторые квазикристаллы имеют додекаэдрическую форму (см. Рисунок). Некоторые регулярные кристаллы, такие как гранат и алмаз, также имеют «додекаэдрический» вид, но это утверждение фактически относится к ромбическому додекаэдру форма.

Форма вселенной

Были предложены различные модели для глобальной геометрии вселенной. В дополнение к этим предложениям, эти предложения включают додекаэдрическое пространство Пуанкаре, пространство с положительной кривизной, состоящее из правильного додекаэдра, противоположные грани которого совпадают (с небольшим поворотом). Это было предложено Жан-Пьером Люмине и его коллегами в 2003 году, а оптимальная ориентация модели на небе была оценена в 2008 году.

В Бертран Рассел ‘ В рассказе 1954 года «Кошмар математика: видение профессора Скверпунта» цифра 5 гласила: «Я – количество пальцев на руке. Я делаю пятиугольники и пентаграммы. И без меня додекаэдров не могло бы существовать; и, поскольку всем известно, что вселенная – это додекаэдр. Итак, но для меня не могло быть никакой вселенной ».

Заполнение пространства кубом и двунабиротондами

Обычные додекаэдры заполняют пространство кубами и двунабиротондами (Johnson solid 91), в соотношении 1: 1: 3. Только додекаэдры образуют решетку из граней пиритоэдров. Двунабиротонды заполняют ромбические промежутки. Каждый куб встречается с шестью билунабиротондами в трех ориентациях.

Связанные многогранники и мозаики

Правильный додекаэдр топологически связан с серией мозаик фигурой вершины п.

* n32 изменение симметрии правильных мозаик: {n, 3} [ v ]
Сферическое	Евклидово	Компактная гиперболика.	Парако.	Некомпактный гиперболический

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞, 3}	{12i, 3}	{9i, 3}	{6i, 3}	{3i, 3}

* n32 изменение симметрии правильных мозаик: {n, 3} [

]

Сферическое

Евклидово

Компактная гиперболика.

Парако.

Некомпактный гиперболический

{2,3}

{3,3}

{4,3}

{5,3}

{6,3}

{7,3}

{8,3}

{∞, 3}

{12i, 3}

{9i, 3}

{6i, 3}

{3i, 3}

Обычный додекаэдр может быть преобразован с помощью усечения последовательности в его двойственный, икосаэдр:

Семейство однородные икосаэдрические многогранники
Симметрия : [5,3], (* 532)	[5,3], (532)


{5,3}	t {5,3}	r {5,3}	t {3,5}	{3,5}	rr {5,3}	tr {5, 3}	sr {5,3}
Двойник к однородным многогранникам

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3. 3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Однородные октаэдрические многогранники
Симметрия : [4,3], (* 432)	[4,3]. (432)	[1,4,3] = [3,3]. (* 332)	[3, 4]. (3 * 2)
{4,3}	t {4,3}	r {4,3}. r {3}	t{3,4}. t {3}	{3,4}. {3}	rr {4,3}. s2{3, 4}	tr{4,3}	sr{4,3}	h{4,3}. {3,3}	h2{4, 3}. t {3,3}	s{3,4}. s {3}

		. =	. =	. =				=. или	=. или	=.
		.	.	.	.					.
Двойники к однородным многогранникам
V4	V3.8	V (3.4)	V4.6	V3	V3.4	V4.6.8	V3.4	V3	V3.6	V3

Правильный додекаэдр – это член последовательности, в остальном неоднородных многогранников и мозаик, состоящей из пятиугольников с конфигурацией граней (V3.3.3.3.n). (Для n>6 последовательность состоит из мозаик гиперболической плоскости.) Эти гранно-транзитивные фигуры имеют (n32) вращательную симметрию.

n32 мутаций симметрии плоскостных мозаик: 3.3.3.3.n v
Симметрия. n32	Сферическая	Евклидова	Компактная гиперболическая	Паракомп.
232	332	432	532	632	732	832	∞32
Snub. цифры
Конфиг.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Гироскоп. цифры
Конфиг.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3. 3.3.3.8	V3.3.3.3.∞

Расположение вершин

Правильный додекаэдр разделяет его расположение вершин с четырьмя невыпуклыми однородными многогранниками и три однородных многогранных соединения.

Пять кубов вписываются внутрь, их края являются диагоналями граней правильного додекаэдра, и вместе они составляют правильное многогранное соединение пять кубиков. Поскольку два тетраэдра могут поместиться на чередующихся вершинах куба, пять и десять тетраэдров также могут поместиться в правильный додекаэдр.

. Большой звездчатый додекаэдр

Маленький двутригональный icosidodecahedron.png

. Малый дитригональный икосододекаэдр

. Дитригональный додекадодекаэдр

Большой дитригональный icosidodecahedron.png

. Большой дитригональный икосододекаэдр

. Соединение пяти кубов

. Соединение пяти тетраэдров

. Соединение десяти тетраэдров <9202>>

Три звёздчатой формы правильного додекаэдра – все правильные (невыпуклые ) многогранники: (Многогранники Кеплера – Пуансо )

	0	1	2	3
Звездчатость	. Правильный додекаэдр	. Малый звездчатый додекаэдр	. Большой додекаэдр	. Большой звездчатый додекаэдр
Фасеточная диаграмма

Додекаэдр

Правильный додекаэдр
A Гамильтонов цикл в додекаэдре.
Вершины	20
Ребра	30
Радиус	5
Диаметр	5
Обхват	5
Автоморфизмы	120 (A5 × Z2)
Хроматическое число	3
Свойства	Гамильтониан, правильный, симметричный, дистанционно-регулярный, дистанционно-транзитивный, 3-вершинно-связанный, планарный граф
Таблица графиков и параметров

Скелет додекаэдра (вершины и ребра) образуют граф. Это один из 5 платоновых графов, каждый из которых является скелетом своего платонового тела.

Этот граф также может быть построен как обобщенный граф Петерсена G (10,2). Высокая степень симметрии многоугольника воспроизводится в свойствах этого графа, который является дистанционно-транзитивным, дистанционно-регулярным и симметричным. Группа автоморфизмов имеет порядок 120. Вершины могут быть окрашены в 3 цвета, как и ребра, а диаметр равен 5.

Додекаэдрический граф – это гамильтониан – есть цикл, содержащий все вершины. Действительно, это название происходит от математической игры, изобретенной в 1857 году Уильямом Роуэном Гамильтоном, икозианской игры. Целью игры было найти гамильтонов цикл по краям додекаэдра.

Ортогональная проекция

См. Также

120-элементный, правильный полихорон (четырехмерный многогранник, поверхность которого состоит из 120 додекаэдрических ячеек)
Додекаэдран (молекула)
Додекаэдр Пентакиса
Плоский додекаэдр
Усеченный додекаэдр

Ссылки

Внешние ссылки

На Викискладе есть материалы, связанные с Додекаэдром .

Weisstein, Eric W. “Правильный додекаэдр”. MathWorld.
Клитцинг, Ричард. “3D выпуклые однородные многогранники o3o5x – doe”.
Редактируемая печатная сетка додекаэдра с интерактивным трехмерным изображением
Однородные многогранники
Многогранники оригами – Модели, созданные с помощью модульного оригами
Додекаэдр – трехмерная модель, которая работает в вашем браузере
Многогранники виртуальной реальности Энциклопедия многогранников
- VRML # Правильный додекаэдр
KJM Маклин, Геометрический анализ пяти платоновых тел и других полурегулярных многогранников
Трехмерная визуализация додекаэдра
Стелла: Навигатор по многогранникам : Программное обеспечение, используемое для создания некоторых изображений на этой странице.
Как сделать сделать додекаэдр из куба из пенополистирола
Греческие, индийские и китайские элементы – теория семи элементов

v t Фундаментальные выпуклые правильные и однородные многогранники в измерениях 2–10
An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Треугольник	Квадрат	p-угольник	Шестиугольник	Пентагон
Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
5-элементный	16-элементный • Тессеракт	Демитессеракт	24-элементный	120-элементный • 600 ячеек
5-симплекс	5-ортоплекс • 5-куб	5-полукуб
6-симплекс	6-ортоплекс • 6-куб	6-полукуб	122 • 221
7-симплекс	7-ортоплекс • 7-куб	7-полукуб	132 • 231 • 321
8-симплекс	8- ортоплекс • 8-кубик	8-полукуб	142 • 241 • 421
9-симплекс	9-орт хоплекс • 9-куб	9-полукуб
10-симплекс	10-ортоплекс • 10-куб	10-полукуб
n-симплекс	n-ортоплекс • n- куб	n-полукуб	1k2 • 2k1 • k21	n-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильные многогранники и составные части

Контакты: mail@wikibrief.org

Последняя правка сделана 2021-05-29 09:57:19

Содержание доступно по лицензии CC BY-SA 3.0 (если не указано иное).

Источник

Regular dodecahedron
(Click here for rotating model)
Type	Platonic solid
Elements	F = 12, E = 30 V = 20 (χ = 2)
Faces by sides	12{5}
Conway notation	D
Schläfli symbols	{5,3}
Face configuration	V3.3.3.3.3
Wythoff symbol	3 \| 2 5
Coxeter diagram
Symmetry	I_h, H₃, [5,3], (*532)
Rotation group	I, [5,3]⁺, (532)
References	U₂₃, C₂₆, W₅
Properties	regular, convex
Dihedral angle	116.56505° = arccos(−1⁄√5)
5.5.5 (Vertex figure)	Regular icosahedron (dual polyhedron)
Net

Animation of a net of a regular (pentagonal) dodecahedron being folded

3D model of a regular dodecahedron

Crystal structure of Co20L12 dodecahedron reported by Kai Wu, Jonathan Nitschke and co-workers at University of Cambridge in Nat. Synth. 2023, DOI:10.1038/s44160-023-00276-9^{^[1]}

A regular dodecahedron or pentagonal dodecahedron is a dodecahedron that is regular, which is composed of 12 regular pentagonal faces, three meeting at each vertex. It is one of the five Platonic solids. It has 12 faces, 20 vertices, 30 edges, and 160 diagonals (60 face diagonals, 100 space diagonals).^[2] It is represented by the Schläfli symbol {5,3}.

Dimensions[edit]

If the edge length of a regular dodecahedron is , the radius of a circumscribed sphere (one that touches the regular dodecahedron at all vertices) is

${displaystyle r_{u}=a{frac {sqrt {3}}{4}}left(1+{sqrt {5}}right)approx 1.401,258,538cdot a}$

(sequence A179296 in the OEIS)

and the radius of an inscribed sphere (tangent to each of the regular dodecahedron’s faces) is

${displaystyle r_{i}=a{frac {1}{2}}{sqrt {{frac {5}{2}}+{frac {11}{10}}{sqrt {5}}}}approx 1.113,516,364cdot a}$

while the midradius, which touches the middle of each edge, is

${displaystyle r_{m}=a{frac {1}{4}}left(3+{sqrt {5}}right)approx 1.309,016,994cdot a}$

These quantities may also be expressed as

$r_{u}=a,{frac {sqrt {3}}{2}}phi$

$r_{i}=a,{frac {phi ^{2}}{2{sqrt {3-phi }}}}$

$r_{m}=a,{frac {phi ^{2}}{2}}$

where ϕ is the golden ratio.

Note that, given a regular dodecahedron of edge length one, r_u is the radius of a circumscribing sphere about a cube of edge length ϕ, and r_i is the apothem of a regular pentagon of edge length ϕ.

Surface area and volume[edit]

The surface area A and the volume V of a regular dodecahedron of edge length a are:

${displaystyle {displaystyle A=3{sqrt {25+10{sqrt {5}}}}a^{2}approx 20.645,728,807a^{2}}}$

${displaystyle V={frac {1}{4}}(15+7{sqrt {5}})a^{3}approx 7.663,118,9606a^{3}}$

Additionally, the surface area and volume of a regular dodecahedron are related to the golden ratio. A dodecahedron with an edge length of one unit has the properties:^[3]

${displaystyle {displaystyle A={frac {15phi }{sqrt {3-phi }}}}}$

${displaystyle {displaystyle V={frac {5phi ^{3}}{6-2phi }}}}$

Two-dimensional symmetry projections[edit]

The regular dodecahedron has two high orthogonal projections, centered, on vertices and pentagonal faces, correspond to the A₂ and H₂ Coxeter planes. The edge-center projection has two orthogonal lines of reflection.

Orthogonal projections

Centered by	Vertex	Face	Edge
Image
Projective symmetry	[[3]] = [6]	[[5]] = [10]	[2]

In perspective projection, viewed on top of a pentagonal face, the regular dodecahedron can be seen as a linear-edged Schlegel diagram, or stereographic projection as a spherical polyhedron. These projections are also used in showing the four-dimensional 120-cell, a regular 4-dimensional polytope, constructed from 120 dodecahedra, projecting it down to 3-dimensions.

Projection	Orthogonal projection	Perspective projection
Schlegel diagram	Stereographic projection
Regular dodecahedron
Dodecaplex (120-cell)

Spherical tiling[edit]

The regular dodecahedron can also be represented as a spherical tiling.

Orthographic projection	Stereographic projection

Cartesian coordinates[edit]

Vertex coordinates:
	The orange vertices lie at (±1, ±1, ±1) and form a cube (dotted lines).
	The green vertices lie at (0, ±ϕ, ±1/ϕ) and form a rectangle on the yz-plane.
	The blue vertices lie at (±1/ϕ, 0, ±ϕ) and form a rectangle on the xz-plane.
	The pink vertices lie at (±ϕ, ±1/ϕ, 0) and form a rectangle on the xy-plane.
The distance between adjacent vertices is 2/ϕ, and the distance from the origin to any vertex is √3. ϕ = 1 + √5/2 is the golden ratio.

The following Cartesian coordinates define the 20 vertices of a regular dodecahedron centered at the origin and suitably scaled and oriented:^[4]

(±1, ±1, ±1)

(0, ±ϕ, ±1/ϕ)

(±1/ϕ, 0, ±ϕ)

(±ϕ, ±1/ϕ, 0)

where ϕ = 1 + √5/2 is the golden ratio (also written τ) ≈ 1.618. The edge length is 2/ϕ = √5 − 1. The circumradius is √3.

Facet-defining equations[edit]

Similar to the symmetry of the vertex coordinates, the equations of the twelve facets of the regular dodecahedron also display symmetry in their coefficients:

x ± ϕy = ±ϕ²

y ± ϕz = ±ϕ²

z ± ϕx = ±ϕ²

Properties[edit]

The dihedral angle of a regular dodecahedron is 2 arctan(ϕ) or approximately 116.565° (where again ϕ = 1 + √5/2, the golden ratio). OEIS: A137218 Note that the tangent of the dihedral angle is exactly −2.
If the original regular dodecahedron has edge length 1, its dual icosahedron has edge length ϕ.
If the five Platonic solids are built with same volume, the regular dodecahedron has the shortest edges.
It has 43,380 nets.
The map-coloring number of a regular dodecahedron’s faces is 4.
The distance between the vertices on the same face not connected by an edge is ϕ times the edge length.
If two edges share a common vertex, then the midpoints of those edges form a 36-72-72 golden triangle with the body center.

As a configuration[edit]

This configuration matrix represents the dodecahedron. The rows and columns correspond to vertices, edges, and faces. The diagonal numbers say how many of each element occur in the whole dodecahedron. The nondiagonal numbers say how many of the column’s element occur in or at the row’s element.^[5]^[6]

${displaystyle {begin{bmatrix}{begin{matrix}20&3&3\2&30&2\5&5&12end{matrix}}end{bmatrix}}}$

Here is the configuration expanded with k-face elements and k-figures. The diagonal element counts are the ratio of the full Coxeter group H₃, order 120, divided by the order of the subgroup with mirror removal.

H₃	k-face	f_k	f₀	f₁	f₂	k-fig	Notes
A₂	( )	f₀	20	3	3	{3}	H₃/A₂ = 120/6 = 20
A₁A₁	{ }	f₁	2	30	2	{ }	H₃/A₁A₁ = 120/4 = 30
H₂	{5}	f₂	5	5	12	( )	H₃/H₂ = 120/10 = 12

Geometric relations[edit]

The regular dodecahedron is the third in an infinite set of truncated trapezohedra which can be constructed by truncating the two axial vertices of a pentagonal trapezohedron.

The stellations of the regular dodecahedron make up three of the four Kepler–Poinsot polyhedra.

A rectified regular dodecahedron forms an icosidodecahedron.

The regular dodecahedron has icosahedral symmetry I_h, Coxeter group [5,3], order 120, with an abstract group structure of A₅ × Z₂.

Relation to the regular icosahedron[edit]

The dodecahedron and icosahedron are dual polyhedra. A regular dodecahedron has 12 faces and 20 vertices, whereas a regular icosahedron has 20 faces and 12 vertices. Both have 30 edges.

When a regular dodecahedron is inscribed in a sphere, it occupies more of the sphere’s volume (66.49%) than an icosahedron inscribed in the same sphere (60.55%).

A regular dodecahedron with edge length 1 has more than three and a half times the volume of an icosahedron with the same length edges (7.663… compared with 2.181…), which ratio is approximately 3.51246117975, or in exact terms: 3/5(3ϕ + 1) or (1.8ϕ + 0.6).

Relation to the nested cube[edit]

A cube can be embedded within a regular dodecahedron, affixed to eight of its equidistant vertices, in five different positions.^[7] In fact, five cubes may overlap and interlock inside the regular dodecahedron to result in the compound of five cubes.

The ratio of the edge of a regular dodecahedron to the edge of a cube embedded inside such a regular dodecahedron is 1 : ϕ, or (ϕ − 1) : 1.

The ratio of a regular dodecahedron’s volume to the volume of a cube embedded inside such a regular dodecahedron is 1 : 2/2 + ϕ, or 1 + ϕ/2 : 1, or (5 + √5) : 4.

For example, an embedded cube with a volume of 64 (and edge length of 4), will nest within a regular dodecahedron of volume 64 + 32ϕ (and edge length of 4ϕ − 4).

Thus, the difference in volume between the encompassing regular dodecahedron and the enclosed cube is always one half the volume of the cube times ϕ.

From these ratios are derived simple formulas for the volume of a regular dodecahedron with edge length a in terms of the golden mean:

V = (aϕ)³ · 1/4(5 + √5)

V = 1/4(14ϕ + 8)a³

Relation to the regular tetrahedron[edit]

Five tetrahedra inscribed in a dodecahedron. Five opposing tetrahedra (not shown) can also be inscribed.

As two opposing tetrahedra can be inscribed in a cube, and five cubes can be inscribed in a dodecahedron, ten tetrahedra in five cubes can be inscribed in a dodecahedron: two opposing sets of five, with each set covering all 20 vertices and each vertex in two tetrahedra (one from each set, but not the opposing pair).

Just as a tetrahedron can be inscribed in a cube, so a cube can be inscribed in a dodecahedron. By reciprocation, this leads to an octahedron circumscribed about an icosahedron. In fact, each of the twelve vertices of the icosahedron divides an edge of the octahedron according to the “golden section”. Given the icosahedron, the circumscribed octahedron can be chosen in five ways, giving a compound of five octahedra, which comes under our definition of stellated icosahedron. (The reciprocal compound, of five cubes whose vertices belong to a dodecahedron, is a stellated triacontahedron.) Another stellated icosahedron can at once be deduced, by stellating each octahedron into a stella octangula, thus forming a compound of ten tetrahedra. Further, we can choose one tetrahedron from each stella octangula, so as to derive a compound of five tetrahedra, which still has all the rotation symmetry of the icosahedron (i.e. the icosahedral group), although it has lost the reflections. By reflecting this figure in any plane of symmetry of the icosahedron, we obtain the complementary set of five tetrahedra. These two sets of five tetrahedra are enantiomorphous, i.e. not directly congruent, but related like a pair of shoes. [Such] a figure which possesses no plane of symmetry (so that it is enantiomorphous to its mirror-image) is said to be chiral.^[8]

Relation to the golden rectangle[edit]

Golden rectangles of ratio (ϕ + 1) : 1 and ϕ : 1 also fit perfectly within a regular dodecahedron.^[9] In proportion to this golden rectangle, an enclosed cube’s edge is ϕ, when the long length of the rectangle is ϕ + 1 (or ϕ²) and the short length is 1 (the edge shared with the regular dodecahedron).

In addition, the center of each face of the regular dodecahedron form three intersecting golden rectangles.^[10]

Relation to the 6-cube and rhombic triacontahedron[edit]

Projection of 6-demicube into regular dodecahedral envelope

It can be projected to 3D from the 6-dimensional 6-demicube using the same basis vectors that form the hull of the rhombic triacontahedron from the 6-cube. Shown here including the inner 12 vertices, which are not connected by the outer hull edges of 6D norm length √2, form a regular icosahedron.

The 3D projection basis vectors [u,v,w] used are:

u = (1, ϕ, 0, −1, ϕ, 0)

v = (ϕ, 0, 1, ϕ, 0, −1)

w = (0, 1, ϕ, 0, −1, ϕ)

History and uses[edit]

Omnidirectional sound source

Regular dodecahedral objects have found some practical applications, and have also played a role in the visual arts and in philosophy.

Iamblichus states that Hippasus, a Pythagorean, perished in the sea, because he boasted that he first divulged “the sphere with the twelve pentagons.”^[11] In Theaetetus, a dialogue of Plato, Plato hypothesized that the classical elements were made of the five uniform regular solids; these later became known as the platonic solids. Of the fifth Platonic solid, the dodecahedron, Plato obscurely remarked, “…the god used [it] for arranging the constellations on the whole heaven”. Timaeus (c. 360 BC), as a personage of Plato’s dialogue, associates the other four platonic solids with the four classical elements, adding that there is a fifth solid pattern which, though commonly associated with the regular dodecahedron, is never directly mentioned as such; “this God used in the delineation of the universe.”^[12] Aristotle also postulated that the heavens were made of a fifth element, which he called aithêr (aether in Latin, ether in American English).

Theaetetus gave a mathematical description of all five and may have been responsible for the first known proof that no other convex regular polyhedra exist.
Euclid completely mathematically described the Platonic solids in the Elements, the last book (Book XIII) of which is devoted to their properties. Propositions 13–17 in Book XIII describe the construction of the tetrahedron, octahedron, cube, icosahedron, and dodecahedron in that order. For each solid Euclid finds the ratio of the diameter of the circumscribed sphere to the edge length. In Proposition 18 he argues that there are no further convex regular polyhedra.

Regular dodecahedra have been used as dice and probably also as divinatory devices. During the Hellenistic era, small, hollow bronze Roman dodecahedra were made and have been found in various Roman ruins in Europe. Their purpose is not certain.

In 20th-century art, dodecahedra appear in the work of M. C. Escher, such as his lithographs Reptiles (1943) and Gravitation (1952). In Salvador Dalí’s painting The Sacrament of the Last Supper (1955), the room is a hollow regular dodecahedron. Gerard Caris based his entire artistic oeuvre on the regular dodecahedron and the pentagon, which is presented as a new art movement coined as Pentagonism.

A climbing wall consisting of three dodecahedral pieces

In modern role-playing games, the regular dodecahedron is often used as a twelve-sided die, one of the more common polyhedral dice.

Immersive Media Company, a former Canadian digital imaging company, made the Dodeca 2360 camera, the world’s first 360° full-motion camera which captures high-resolution video from every direction simultaneously at more than 100 million pixels per second or 30 frames per second.^[promotion?] It is based on regular dodecahedron.^{[citation needed]}

The Megaminx twisty puzzle, alongside its larger and smaller order analogues, is in the shape of a regular dodecahedron.

In the children’s novel The Phantom Tollbooth, the regular dodecahedron appears as a character in the land of Mathematics. Each of his faces wears a different expression – e.g. happy, angry, sad – which he swivels to the front as required to match his mood.

In nature and supramolecules[edit]

The fossil coccolithophore Braarudosphaera bigelowii (see figure), a unicellular coastal phytoplanktonic alga, has a calcium carbonate shell with a regular dodecahedral structure about 10 micrometers across.^[13]

Some quasicrystals and cages have dodecahedral shape (see figure). Some regular crystals such as garnet and diamond are also said to exhibit “dodecahedral” habit, but this statement actually refers to the rhombic dodecahedron shape.^[14] ^[1]

Shape of the universe[edit]

Various models have been proposed for the global geometry of the universe. In addition to the primitive geometries, these proposals include the Poincaré dodecahedral space, a positively curved space consisting of a regular dodecahedron whose opposite faces correspond (with a small twist). This was proposed by Jean-Pierre Luminet and colleagues in 2003,^[15]^[16] and an optimal orientation on the sky for the model was estimated in 2008.^[17]

In Bertrand Russell’s 1954 short story “The Mathematician’s Nightmare: The Vision of Professor Squarepunt,” the number 5 said: “I am the number of fingers on a hand. I make pentagons and pentagrams. And but for me dodecahedra could not exist; and, as everyone knows, the universe is a dodecahedron. So, but for me, there could be no universe.”

Space filling with cube and bilunabirotunda[edit]

Regular dodecahedra fill space with cubes and bilunabirotundas (Johnson solid 91), in the ratio of 1 to 1 to 3.^[18]^[19] The dodecahedra alone make a lattice of edge-to-edge pyritohedra. The bilunabirotundas fill the rhombic gaps. Each cube meets six bilunabirotundas in three orientations.

Related polyhedra and tilings[edit]

The regular dodecahedron is topologically related to a series of tilings by vertex figure n³.

*n32 symmetry mutation of regular tilings: {n,3} v t e
Spherical	Euclidean	Compact hyperb.	Paraco.	Noncompact hyperbolic

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

The regular dodecahedron can be transformed by a truncation sequence into its dual, the icosahedron:

Family of uniform icosahedral polyhedra
Symmetry: [5,3], (*532)	[5,3]⁺, (532)


{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duals to uniform polyhedra

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Uniform octahedral polyhedra
Symmetry: [4,3], (*432)	[4,3]⁺ (432)	[1⁺,4,3] = [3,3] (*332)	[3⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1,1}	t{3,4} t{3^1,1}	{3,4} {3^1,1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h₂{4,3} t{3,3}	s{3,4} s{3^1,1}

		=	=	=				= or	= or	=

Duals to uniform polyhedra
V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8	V3⁴.4	V3³	V3.6²	V3⁵

The regular dodecahedron is a member of a sequence of otherwise non-uniform polyhedra and tilings, composed of pentagons with face configurations (V3.3.3.3.n). (For n > 6, the sequence consists of tilings of the hyperbolic plane.) These face-transitive figures have (n32) rotational symmetry.

n32 symmetry mutations of snub tilings: 3.3.3.3.n v t e
Symmetry n32	Spherical	Euclidean	Compact hyperbolic	Paracomp.
232	332	432	532	632	732	832	∞32
Snub figures
Config.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
Gyro figures
Config.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.∞

Vertex arrangement[edit]

The regular dodecahedron shares its vertex arrangement with four nonconvex uniform polyhedra and three uniform polyhedron compounds.

Five cubes fit within, with their edges as diagonals of the regular dodecahedron’s faces, and together these make up the regular polyhedral compound of five cubes. Since two tetrahedra can fit on alternate cube vertices, five and ten tetrahedra can also fit in a regular dodecahedron.

Stellations[edit]

The 3 stellations of the regular dodecahedron are all regular (nonconvex) polyhedra: (Kepler–Poinsot polyhedra)

	0	1	2	3
Stellation	Regular dodecahedron	Small stellated dodecahedron	Great dodecahedron	Great stellated dodecahedron
Facet diagram

Dodecahedral graph[edit]

Regular dodecahedron graph
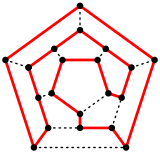
A Hamiltonian cycle in a dodecahedron.
Vertices	20
Edges	30
Radius	5
Diameter	5
Girth	5
Automorphisms	120 (A₅ × Z₂)^[20]
Chromatic number	3
Properties	Hamiltonian, regular, symmetric, distance-regular, distance-transitive, 3-vertex-connected, planar graph
Table of graphs and parameters

The skeleton of the dodecahedron (the vertices and edges) form a graph. It is one of 5 Platonic graphs, each a skeleton of its Platonic solid.

This graph can also be constructed as the generalized Petersen graph G(10,2). The high degree of symmetry of the polygon is replicated in the properties of this graph, which is distance-transitive, distance-regular, and symmetric. The automorphism group has order 120. The vertices can be colored with 3 colors, as can the edges, and the diameter is 5.^[21]

The dodecahedral graph is Hamiltonian – there is a cycle containing all the vertices. Indeed, this name derives from a mathematical game invented in 1857 by William Rowan Hamilton, the icosian game. The game’s object was to find a Hamiltonian cycle along the edges of a dodecahedron.

Orthogonal projection

References[edit]

^ ^a ^b Kai Wu, Jonathan Nitschke and co-workers “Systematic construction of progressively larger capsules from a fivefold linking pyrrole-based subcomponent”, Nature Synthesis, 2023, DOI: https://doi.org/10.1038/s44160-023-00276-9.
^ Sutton, Daud (2002), Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA, p. 55, ISBN 9780802713865.
^ Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number (First trade paperback ed.). New York City: Broadway Books. pp. 70–1. ISBN 0-7679-0816-3.
^ Weisstein, Eric W. “Icosahedral group”. MathWorld.
^ Coxeter, H.S.M. (1973) [1948]. “§1.8 Configurations”. Regular Polytopes (3rd ed.). New York: Dover.
^ Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge: Cambridge University Press. p. 117.
^ http://mathworld.wolfram.com/images/eps-gif/DodecahedronCube_700.gif^{[bare URL image file]}
^ Coxeter, H.S.M.; du Val, Patrick; Flather, H.T.; Petrie, J.F. (1938). The Fifty-Nine Icosahedra. Vol. 6. University of Toronto Studies (Mathematical Series). p. 4.
^ Knott, Ron (26 September 2016). “The Golden Geometry of Solids or Phi in 3 dimensions”. Ron Knott’s Mathematics Pages. Retrieved 2022-03-19.
^ http://www.toshen.com/images/dodecahedronwithgoldrectang.gif^{[bare URL image file]}
^ Florian Cajori, A History of Mathematics (1893)
^ Plato, Timaeus, Jowett translation [line 1317–8]; the Greek word translated as delineation is diazographein, painting in semblance of life.
^ Hagino, K., Onuma, R., Kawachi, M. and Horiguchi, T. (2013) “Discovery of an endosymbiotic nitrogen-fixing cyanobacterium UCYN-A in Braarudosphaera bigelowii (Prymnesiophyceae)”. PLoS One, 8(12): e81749. doi:10.1371/journal.pone.0081749.
^ Dodecahedral Crystal Habit Archived 12 April 2009 at the Wayback Machine
^ Dumé, Belle (Oct 8, 2003). “Is The Universe A Dodecahedron?”. PhysicsWorld. Archived from the original on 2012-04-25.
^ Luminet, Jean-Pierre; Jeff Weeks; Alain Riazuelo; Roland Lehoucq; Jean-Phillipe Uzan (2003-10-09). “Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background”. Nature. 425 (6958): 593–5. arXiv:astro-ph/0310253. Bibcode:2003Natur.425..593L. doi:10.1038/nature01944. PMID 14534579. S2CID 4380713.
^ Roukema, Boudewijn; Zbigniew Buliński; Agnieszka Szaniewska; Nicolas E. Gaudin (2008). “A test of the Poincaré dodecahedral space topology hypothesis with the WMAP CMB data”. Astronomy and Astrophysics. 482 (3): 747. arXiv:0801.0006. Bibcode:2008A&A…482..747L. doi:10.1051/0004-6361:20078777. S2CID 1616362.
^ “Dodecahedron and Bilunabirotunda – Wolfram Demonstrations Project”.
^ http://www.lcv.ne.jp/~hhase/memo/m09_08b.html
^ Frucht, Roberto (1936–1937), “Die gruppe des Petersen’schen Graphen und der Kantensysteme der regulären Polyeder”, Comment. Math. Helv., 9: 217–223, doi:10.1007/bf01258190, S2CID 121791222
^ Weisstein, Eric W. “Dodecahedral Graph”. MathWorld.

External links[edit]

Weisstein, Eric W. “Regular Dodecahedron”. MathWorld.
Klitzing, Richard. “3D convex uniform polyhedra o3o5x – doe”.
Editable printable net of a dodecahedron with interactive 3D view
The Uniform Polyhedra
Origami Polyhedra – Models made with Modular Origami
Dodecahedron – 3-d model that works in your browser
Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRML#Regular dodecahedron
K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
Dodecahedron 3D Visualization
Stella: Polyhedron Navigator: Software used to create some of the images on this page.
How to make a dodecahedron from a Styrofoam cube
The Greek, Indian, and Chinese Elements – Seven Element Theory

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	A_n	B_n	I₂(p) / D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds

Источник

Вы здесь:

Главная
Додекаэдр

Додекаэдр

Древние греки дали многограннику имя по числу граней. «Додека» означает двенадцать, «хедра» – означает грань (додекаэдр – двенадцатигранник).

Поэтому на вопрос – “что такое додекаэдр?”, можно дать следующее определение: “Додекаэдр это геометрическое тело из двенадцати граней, каждая их которых – правильный пятиугольник“.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел.
Додекаэдр имеет следующие характеристики:

Тип грани – правильный пятиугольник;
Число сторон у грани – 5;
Общее число граней – 12;
Число рёбер, примыкающих к вершине – 3;
Общее число вершин – 20;
Общее число рёбер – 30.

Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.
Додекаэдр имеет центр симметрии – центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.

Математические характеристики додекаэдра

Додекаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы додекаэдра

где a – длина стороны.

Сфера может быть вписана внутрь додекаэдра.

Радиус вписанной сферы додекаэдра

Площадь поверхности додекаэдра.

Для наглядности площадь поверхности додекаэдра можно представить в виде площади развёртки.

Площадь поверхности можно определить как площадь одной из сторон додекаэдра (это площадь правильного пятиугольника) умноженной на 12. Либо воспользоваться формулой:

Объем додекаэдра определяется по следующей формуле:

Понятие правильного многогранника

Ранее мы уже рассматривали такой выпуклый многогранник, как куб. Легко заметить, что каждая грань куба – это квадрат, то есть правильный многоугольник. Более того, все грани куба одинаковы, а из каждой вершины исходит одинаковое количество ребер (по три ребра).

Однако куб – не единственная фигура, обладающая такими свойствами. Так же нам знаком правильный тетраэдр. У него каждая грань – это равносторонний треугольник (а это правильный многоуг-к), а из каждой вершины также выходит по 3 ребра тетраэдра.

И куб, и правильный тетраэдр являются примерами так называемых правильных многогранников. Дадим определение понятию правильного многогранника:

Иногда правильные многогранники именуют иначе – платоновыми телами. Дело в том, что древнегреческий философ Платон использовал их в своей философии, однако огромный вклад в их исследование внес другой ученый – Теэтет Афинский.

Ясно, что все ребра правильных многогранников имеют одинаковую длину. Можно доказать, что и двугранные углы, образованные смежными гранями таких многогранников, также одинаковы.

Пять правильных многогранников

Вероятно, куб и правильный тетраэдр являются первыми правильными многогранниками, открытыми человечеством. Уже во времена Пифагора люди знали и о третьем правильном многограннике – октаэдре. Каждая его грань – это равносторонний треуг-к, но, в отличие от тетраэдра, из каждой его вершины исходит уже не три, а четыре ребра. Выглядит правильный октаэдр так:

Можно доказать, что октаэдр состоит из двух правильных пирамид, у которых общее основание, но вершины располагаются по разные стороны от плоскости основания. Название октаэдра происходит от греческого слова «окта», означающее число 8. Легко увидеть, что у октаэдра как раз 8 граней. Также видно, что он имеет 6 вершин и 12 ребер.

Следующие два правильных многогранника как раз и были открыты Теэтетем Афинским. Это икосаэдр и додекаэдр. Икосаэдр также состоит из равносторонних треуг-ков, но каждая его вершина принадлежит сразу 5 ребрам.Правильный икосаэдр довольно сложно нарисовать на плоскости, поэтому его внешний вид мы покажем с помощью анимации:

Гранями додекаэдра являются правильные пятиугольники, причем в каждой его вершине соприкасаются ровно 3 грани, и, соответственно, сходятся 3 ребра. Нарисовать правильный додекаэдр ещё тяжелее, поэтому снова посмотрим на него с помощью gif-анимации:

Для подсчета количества ребер, граней и вершин у додекаэдра и икосаэдра можно применить теорему Эйлера. Начнем с икосаэдра. Обозначим количество его граней буквой Г. Теперь подсчитаем ребра (Р), принадлежащие каждой грани. Так как эти грани являются треуг-ками, то получится 3Г ребер. Но при этом каждое ребро мы посчитали дважды, ведь ребра принадлежат строго двум граням. То есть у икосаэдра количество ребер равно 3Г/2 = 1,5Г.

Также подсчитаем и вершины (В), находящиеся вокруг граней. На каждую грань приходится 3 вершины, но при этом каждая вершины принадлежит уже 5 граням. Тогда общее количество вершин составит 3Г/5 = 0,6Г.

Записываем теорему Эйлера и подставляем в ней полученные значения:

Теперь проведем аналогичные расчеты для додекаэдра. Его грани – пятиугольники, поэтому количество его ребер составляет 5Г/2. В каждой вершине додекаэдра сходятся три грани, а потому количество вершин составит 5Г/3. Используем теорему Эйлера:

Теперь составим таблицу, в которой отразим основные сведения о пяти известным нам правильных многогранниках:

Возникает вопрос – существуют ли ещё какие-нибудь правильные многогранники? Оказывается, что нет. Действительно, каждая вершина правильного многогранника является одновременно и вершиной многогранного угла. Напомним, что сумма плоских углов в многогранном угле всегда меньше 360°. Легко подсчитать, что в правильном шестиугольнике каждый угол составляет 120°, а в многоуг-ках с большим количеством сторон (семиугольник, восьмиугольник…) этот угол ещё больше. Это значит, что если трехгранный угол образован тремя шестигранниками, то сумма его плоских углов составит ровно 120°•3 = 360°, что невозможно. Также невозможно, чтобы трехгранный угол и любой другой многогранный угол был образован правильными семиугольниками, восьмиугольниками и т. д. То есть грани правильного многогранника могут быть исключительно треуг-ками, четырехуг-ками или пятиугольниками.

Рассмотрим случай, когда грани – это треуг-ки. У равностороннего треуг-ка угол составляет 60°. У тетраэдра в вершине смыкаются 3 грани, у октаэдра – 4 грани, а у икосаэдра – 5 граней. А 6 треуг-ков уже не могут образовать многогранный угол, ведь сумма углов составит 6•60° = 360°.

Теперь рассмотрим случай с четырехуг-ком. Правильный четырехуг-к – это квадрат с углом 90°. Варианту с 3 смыкающимися квадратами соответствует куб, а 4 квадрата уже не образуют многогранный угол, ведь сумма углов снова составит 4•90° = 360°.

Остался случай с пятиугольником. У правильного пятиугольника угол равен 108°. Значит, 4 таких фигуры не смогут сомкнуться и образовать многогранный угол, а варианту с тремя пятиугольниками соответствует додекаэдр.

Итак, мы рассмотрели все возможные варианты, и оказалось, что никаких других правильных многогранников, кроме пяти описанных, существовать не может, ч. т. д. Отметим также, что этот факт можно доказать и без применения свойства многогранного угла, используя только теорему Эйлера.

Задачи на правильные многогранники

Задание. Центры смежных граней куба со стороной, равной единице, соединили отрезками. Докажите, что получившийся в результате этого многогранник – это октаэдр, и найдите длину его стороны.

Решение. Грани куба – это квадраты. Напомним, что у любого правильного многоуг-ка, в том числе и квадрата, можно опустить из центра перпендикуляры на стороны, которые будут радиусами вписанной окружности. Все эти радиусы будут иметь одну и ту же длину, при этом они будут падать на середины сторон многоуг-ка. При этом у квадрата радиус вписанной окружности будет вдвое меньше стороны квадрата. В частности, у рассматриваемого куба перпендикуляры, опущенные на середины ребер, будут иметь длину 1:2 = 0,5:

Теперь возьмем любые два центра смежных граней А и В и опустим из них перпендикуляры на ребро, по которому эти грани пересекаются. Перпендикуляры упадут в одну точку – середину ребра Н:

В результате мы получили прямоугольный ∆АВН. Найдем длину его гипотенузы АВ:

Так как мы выбрали центры смежных граней произвольно, то ясно, что расстояние между любыми двумя другими вершинами многогранника, вписанного в куб, будет иметь такую же длину. Тогда каждая его грань оказывается равносторонним треуг-ком. В каждой вершине смыкается 4 ребра, поэтому многогранник оказывается октаэдром.

Задание. Вычислите площадь поверхности икосаэдра, если его ребро имеет длину 1.

Решение. Найдем площадь одной грани икосаэдра. Она представляет собой равносторонний треуг-к со стороной 1. Удобно вычислить его площадь по формуле Герона. Сначала найдем полупериметр треуг-ка:

Задание. Найдите двугранный угол, который образуют грани правильного тетраэдра

Решение. Обозначим вершины тетраэдра буквами А, В, С и D. Далее соединим середину ребра АС, обозначенную как М, с вершинами B и D:

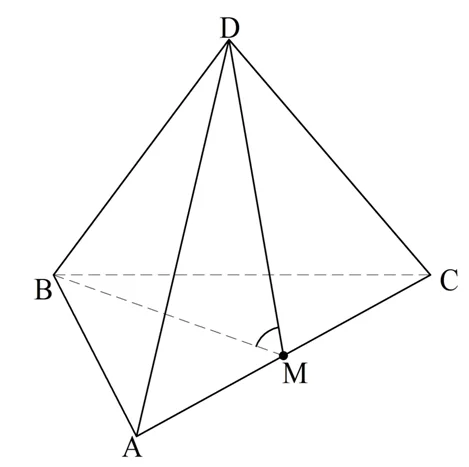
Так как М – середина АС, то ВМ и DM будут медианами ∆АВС и ∆ADC. Но эти треуг-ки равносторонние, поэтому ВМ и DM ещё и высоты. То есть ВМ⊥АС и DM⊥АС. Тогда по определению ∠DMB и будет плоским углом двугранного угла, то есть его как раз и надо вычислить. Предварительно обозначим длину грани тетраэдра буквой а.

∠ВАС составляет 60° как угол равностороннего ∆АВС. Тогда ВМ можно найти из прямоугольного ∆АВМ:

Аналогично из ∆DMC получаем, что и DM имеет такую же длину.

Теперь используем теорему косинусов для ∆BDM:

Задание. Вычислите двугранный угол, который образуют смежные грани октаэдра

Решение. Мы уже говорили, что октаэдр состоит из двух правильных четырехугольных пирамид с общим основанием. Поэтому нам надо просто найти двугранный угол между двумя боковыми гранями такой пирамиды:

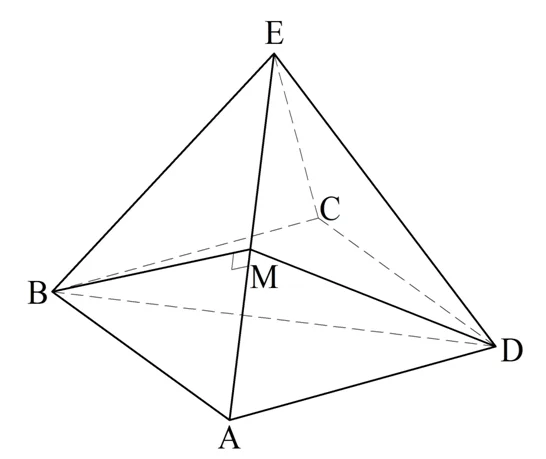
Для этого на ребре АЕ отметим середину М и соединим ее с вершинами B и D. Как и в предыдущей задаче с тетраэдром, ВМ и МD окажутся медианами и высотами в равносторонних ∆АЕВ и ∆АЕD, а потому ∠ВМD является искомым.

Обозначим сторону октаэдра буквой а. Тогда длина ВМ и МD, медиан в равносторонних треуг-ках будет такой же, как и в предыдущей задаче:

Задание. Вычислите двугранный угол, образованный смежными гранями додекаэдра

Решение. Нет необходимости строить весь додекаэдр для решения задачи. Построим только трехгранный угол, образованный ребрами, выходящими из одной вершины. То есть нам достаточно рассмотреть только область, выделенную на додекаэдре красным цветом:

Каждый плоский угол такого трехгранного угла будет равен углу правильного пятиугольника, который в свою очередь рассчитывается так:

Итак, надо найти двугранный угол между гранями ADC и ADB. Они пересекаются по прямой AD. Опустим из В и С перпендикуляры на AD. ∆ABD и ∆ADC равны, ведь у них есть одинаковый угол 108°, сторона AD– общая, а BD и DC одинаковы как ребра правильного многогранника. Это значит, что перпендикуляры на AD упадут в одну точку, которую мы обозначим как H. Нам надо вычислить ∠BНС.Обратите внимание, что так как ∆ABD и ∆ADC тупоугольные, то точка Н будет находиться не на отрезке AD, а на его продолжении.

Обозначим длину ребра додекаэдра буквой а. Мы можем найти ∠HDC:

Примечание. Здесь мы использовали одну из тригонометрических формул приведения.

Аналогично из ∆BHD получаем, что BH имеет такую же длину. Теперь из ∆BDC вычисляем величину ВС²:

Задание. Вычислите площадь поверхность додекаэдра, если его ребро имеет длину 1

Решение. Каждая грань додекаэдра – правильный пятиугольник. Для нахождения его площади используем уже известные нам формулы для правильных многоугольников:

Здесь n – число сторон у многоуг-ка, Р – его периметр, S – площадь, a_n – длина стороны, R и r – радиусы соответственно описанной и вписанной окружности. По условию

Теперь вспомним, что у додекаэдра 12 граней. Значит, площадь всей его поверхности будет в 12 раз больше:

Ответ: ≈ 20,646.

Сегодня мы познакомились с особыми телами – правильными многогранниками. Важно запомнить, что существует всего 5 типов правильных многогранников. Эти фигуры встречаются не только в геометрии, но и в других науках. Например, атомы в никеле и меди могут выстраиваться в форме октаэдра, а оболочки некоторых вирусов похожи на икосаэдр. Правильные многогранники могут использоваться в настольных играх в качестве игральных костей. Чаще всего применяются кости в виде куба, но встречаются кости в виде додекаэдра и икосаэдра.

Источник

История[править | править код]

Основные формулы[править | править код]

Свойства[править | править код]

Элементы симметрии додекаэдра[править | править код]

Связь со сферическим замощением[править | править код]

Интересные факты[править | править код]

В культуре[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Содержание

Размеры

Площадь поверхности и объем

Двумерный проекции симметрии

Сферическая мозаика

Декартовы координаты

Уравнения, определяющие грань

Свойства

Геометрические соотношения

Отношение к правильному икосаэдру

Связь с вложенным кубом

Отношение к золотому прямоугольнику

Отношение к 6-кубу и ромбическому триаконтаэдру

История и использование

В природе

Форма вселенной

Заполнение пространства кубом и двунабиротондами

Связанные многогранники и мозаики

Расположение вершин

Додекаэдр

См. Также

Ссылки

Внешние ссылки

Dimensions[edit]

Surface area and volume[edit]

Two-dimensional symmetry projections[edit]

Spherical tiling[edit]

Cartesian coordinates[edit]

Facet-defining equations[edit]

Properties[edit]

As a configuration[edit]

Geometric relations[edit]

Relation to the regular icosahedron[edit]

Relation to the nested cube[edit]

Relation to the regular tetrahedron[edit]

Relation to the golden rectangle[edit]

Relation to the 6-cube and rhombic triacontahedron[edit]

History and uses[edit]

In nature and supramolecules[edit]

Shape of the universe[edit]

Space filling with cube and bilunabirotunda[edit]

Related polyhedra and tilings[edit]

Vertex arrangement[edit]

Stellations[edit]

Dodecahedral graph[edit]

See also[edit]

References[edit]

External links[edit]

Додекаэдр

Математические характеристики додекаэдра

Популярное

Понятие правильного многогранника

Пять правильных многогранников

Задачи на правильные многогранники

Вам также может понравиться

Как найти стройки на карте

Как найти код к пульту приставки

Как найти фазмида disco elysium

Добавить комментарий Отменить ответ