Как найти вершину графика функции прямой

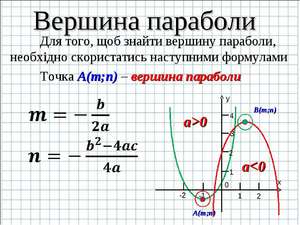
Как находить вершины функции

Для функций (точнее их графиков) используется понятие наибольшего значения, в том числе и локального максимума. Понятие же «вершина» скорее связано с геометрическими фигурами. Точки максимумов гладких функций (имеющих производную) легко определить с помощью нулей первой производной.

Инструкция

Для точек, в которых функция не дифференцируема, но непрерывна, наибольшее на промежутке значение может иметь вид острия (на пример y=-|x|). В таких точках к графику функции можно провести сколь угодно много касательных и производная для нее просто не существует. Сами функции такого типа обычно задаются на отрезках. Точки, в которых производная функции равна нулю или не существует, называются критическими.

Итак, для нахождения точек максимумов функции y=f(x) следует:- найти критические точки;- для того чтобы выбрать происходит чередование знака с «+» на «-», то имеет место максимум.

Пример. Найти наибольшие значения функции (см. рис.1).y=x+3 при x≤-1 и y=((x^2)^(1/3)) –х при x>-1.

Реение. y=x+3 при x≤-1 и y=((x^2)^(1/3)) –х при x>-1. Функция задана на отрезках умышленно, так как в данном случае преследуется цель отобразить все в одном примере. Легко проверить, что при х=-1 функция остается непрерывной.y’=1 при x≤-1 и y’=(2/3)(x^(-1/3))-1=(2-3(x^(1/3))/(x^(1/3)) при x>-1. y’=0 при x=8/27. y’ не существует при x=-1 и x=0.При этом y’>0 если x

Видео по теме

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Общие сведения

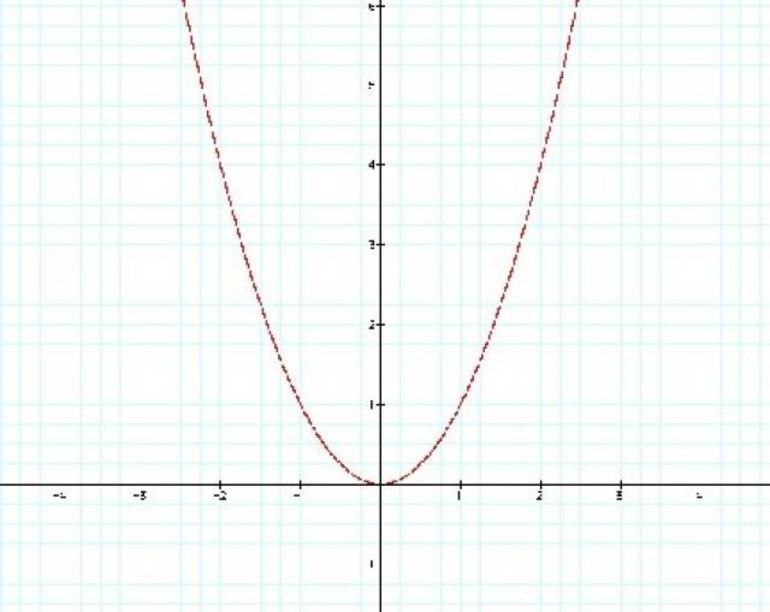
Парабола — кривая, состоящая из равноудаленных точек от заданной точки (вершина) и прямой. Последняя называется директрисой. График функции имеет ось симметрии, которая проходит по определенной траектории и зависит от функции кривой (рис. 1). Ее вершина находится в центре координат.

Рисунок 1. График квадратичной функции с вершиной в начале координат.

Однако существуют и другие случаи прохождения кривой. Она может пересекать оси абсцисс или ординат. В некоторых случаях ее ветви направлены вниз. При вращении вокруг оси симметрии получается поверхность, которая используется в различных устройствах. По этому принципу изготовлены фары автомобиля, зеркала в телескопах и т. д. Кроме того, парабола — это квадратичная зависимость переменных друг от друга. Парабола имеет некоторые свойства:

1. Парабола — кривая второго порядка.
2. Ось симметрии перпендикулярна директрисе и проходит через фокус и вершины.
3. Оптическое свойство отражения.
4. Отрезок, который соединяет середину любой хорды параболы и точку пересечения касательных прямых, является перпендикуляром относительно директрисы.
5. Подобность всех парабол.
6. Траектория фокуса, которая катится по произвольной прямой — цепная молния.

Следует отметить, что оптическое свойство — это способность отражать свет от источника. Если пучок лучей, которые являются параллельными ее оси, отражаются в параболе, то они собираются в фокусе кривой. При нахождении источника света в фокусе происходит отражение параллельного пучка лучей относительно ее оси.

Уравнения квадратичной функции

Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:

1. Каноническая.
2. Квадратичная.
3. Общая.

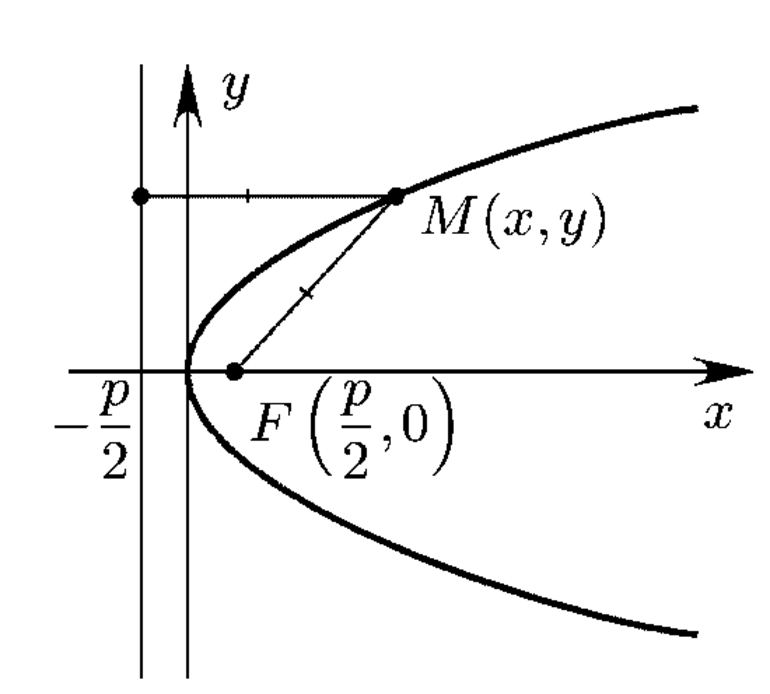
В первой форме она имеет следующий вид: y ² = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x ² = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).

Рисунок 2. Директриса и фокус.

Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y ² ]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y ² ]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y ² = 2px).

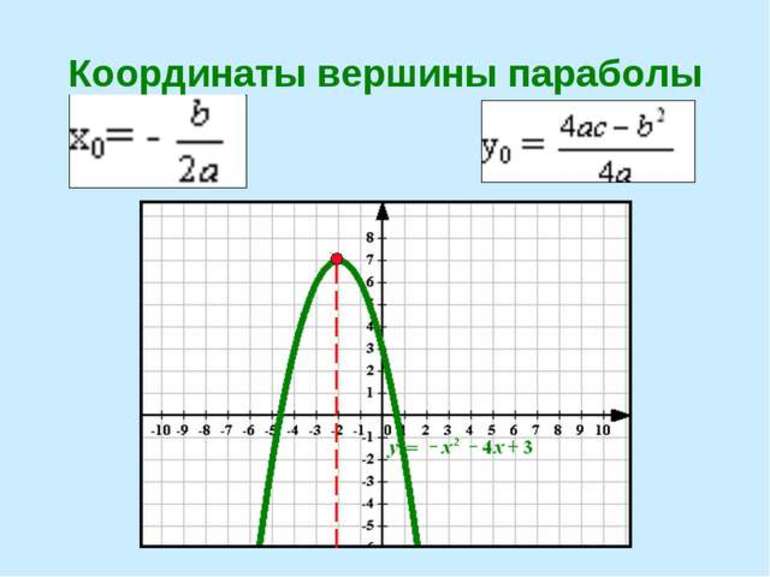
Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax ² + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax ² . В этом случае формула нахождения вершины параболы выглядит таким образом:

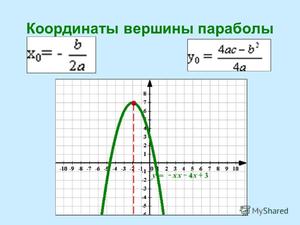
1. Абсцисса вершины параболы: xa = -b / 2a.
2. Координата «игрек» по оси ординат: yb = – D / 2a.

В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b ² — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а<0, то ось ее симметрии параллельна оси абсцисс. Расстояние до фокуса также равно ¼а. Уравнение y = a (x — xa)^2 + ya — функция, определяющая кривую II порядка, как параболу.

Поскольку искомую функцию можно назвать кривой второго порядка, то ее уравнение может быть записано в виде квадратного многочлена в декартовой системе координат. Вид его имеет такой вид: Ax ² + Bxy + Cy ² + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).

В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.

Методы нахождения вершины

В математике есть три способа нахождения координат точки вершины кривой: по формуле, выделением полного квадрата и нахождением производной. Следует отметить, что первый способ не подойдет в том случае, когда функция отличается от вида y = ax ² + bx + c. Первый способ — расчет по формуле вершины параболы квадратичной функции. Координата x0 вычисляется таким образом: x0 = -b / 2a. Для нахождения координаты y0 следует подставить в функцию найденное значение x0.

Когда функция представлена неполным квадратом, нужно прибавить или отнять одинаковое число к двум частям уравнения. Если воспользоваться этим методом, то можно вычислить сразу значения х и у. Алгоритм нахождения вершины для функции у = x ² + 4x + 2 имеет такой вид:

1. Приравнять многочлен к нулю, и перенести свободный член в правую сторону с противоположным знаком: x ² + 4x = -2.
2. Дополнить до полного квадрата. Необходимо вычислить свободный член по такому соотношению: с = (b/2)^2 = (4/2)^2 = 4.
3. Записать полный квадрат, отняв и прибавив свободный член: x ² + 4x + 4 — 4 = -2.
4. Выделить квадрат: (x ² + 2x + 4) — 4 = -2.
5. Перенести свободное число в правую сторону с противоположным знаком: (x ² + 2x + 4) = 4 — 2.
6. Уравнение принимает следующий вид: (x + 2)^2 = 2.
7. Для того чтобы вычислить x0, нужно решить уравнение (x + 2)^2 = 0. Следовательно, x = -2.
8. Ординату точки определить очень просто, поскольку ее значение соответствует числу (нужно брать с противоположным знаком), которое находится в правой части уравнения, т. е. у = -2.

При изображении графика вершину нужно сместить в точку (-2;2). Третий способ позволяет узнать координаты вершины с помощью определения производной. Находить ее следует от заданной функции. Для вычисления координат вершины нужно действовать по следующему алгоритму:

1. Найти производную и приравнять ее к нулю: f'(x) = (ax ² + bx + c)’ = 2ax + b.
2. Выразить х: х = -b / (2a).
3. Подставить в функцию для вычисления y.
4. Записать координаты точки.

Однако эти все три метода относятся к ручному вычислению. Автоматизация действий осуществляется с помощью специализированного программного обеспечения. Для этой цели подойдет онлайн-калькулятор, поддерживающий функцию нахождения точек вершины квадратичной кривой. Программы рекомендуется применять только для проверки решения, поскольку очень важно знать методы нахождения этой точки.

Алгоритм построения

В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:

1. Если вершина не задана, то нужно найти ее любым из методов.
2. Определить точки пересечения с осями декартовой системы координат.
3. Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
4. Выполнить построение, соединив точки.

Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x ² + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.

Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.

Примеры решений

В математике существует определенная классификация заданий на простые и сложные типы. Все они считаются однотипными, но отличаются только объемами вычислений и необходимостью построения графиков. Для решения нужно воспользоваться рекомендуемыми алгоритмами, которые существенно оптимизируют вычисления.

«Корень» трудностей при расчете — отсутствие систематизации вычислений. Не все ими пользуются. В результате простая задача становится очень сложной, поскольку в ней присутствует много ненужных вычислений. Кроме того, как отмечалось выше, рекомендуется «набить руку» на ручных вычислениях, ведь не всегда можно будет воспользоваться программами.

Упрощенная задача

Простым примером задания является следующий: необходимо вычислить координаты вершины точки параболы y = x ² + 3x — 18. Следует продемонстрировать решение тремя способами. Решение первым методом:

1. Координата по оси абсцисс: х0 = -3 / (2 * 1) = -1,5.
2. По ординате: (-1,5)^2 + 3 * (-1,5) — 18 — y= 0. Отсюда, y = -20,25.

Следовательно, вершина находится в точке (-1,5;20,25). Второй способ решения данной задачи имеет такой вид:

1. Составить уравнение и перенести свободный член: x ² + 3x = 18.
2. Вычислить свободный член: с = (b/2)^2 = 2,25.
3. Записать выражение: x ² + 3x + 2,25 — 2,25 = 18.
4. Выделить квадрат: (x ² + 3x + 2,25) = 20,25.
5. Определить координаты: (x + 1,5)^2 = 20,25.
6. Искомая точка: (-1,5;20,25).

Для решения третьим методом следует найти производную: y’ = (x ² + 3x — 18)’ = 2x + 3. Затем нужно приравнять ее к нулю: 2х + 3 = 0. Уравнение является простым, а его переменная легко находится: x = -3 / 2 = -1,5. После этого необходимо подставить абсциссу в функцию, приравняв ее к 0: y = 20,25.

Повышенная сложность

Задания повышенной сложности сводятся к вычислению нескольких значений. Кроме того, в некоторых случаях следует построить график параболы y = x ² — 7x +10. Необходимо выполнить такие действия:

1. Пересечение с осями.
2. Вычислить экстремум (вершину) всеми методами.
3. Выполнить графический эскиз (график).

Точек пересечения по ОУ нет. Они есть по оси абсцисс. Следует приравнять функцию к 0. Нахождение корней выполняется по теореме Виета: x1 = 2 и x2 = 5.

Для нахождения вершины необходимо воспользоваться тремя методами. При решении первым способом находится координата x0 = 7 / (2 * 1) = 3,5. Ордината определяется таким образом: y0 = (3,5)^2 — (7 * 3,5) + 10 = -2,25. Точка экстремума имеет координаты (3,5;-2,25). Находить вершину параболы необходимо по такому алгоритму:

1. Записать уравнение, и выполнить перенос свободного члена: x ² — 7x = -10.
2. Найти свободный член: с = (7/2)^2 = 12,25.
3. Составить уравнение: x ² — 7x + 12,25 — 12,25 = -10.
4. Выделить квадрат: (x — 3,5)^2 = 2,25.
5. Экстремум: (3,5;-2,25).

Для следующего метода нужно найти производную: y’ = (x ² — 7x +10)’ = 2x — 7. Далее нужно приравнять y’ к нулю: 2x — 7 = 0. Значение по оси абсцисс равно х0 = 3,5, а y0 = -2,25. Далее нужно заполнить таблицу зависимостей ординаты от переменной.

y	4	0	-2	-2,25	-2	0	4
x	1	2	3	3,5	4	5	6

Таблица 1. Зависимость y от x.

После заполнения таблицы следует построить график искомой функции (рис. 3). Таблица состоит из следующих элементов: вершины, точек пересечения с осью абсцисс и 4 произвольных значений.

Рисунок 3. График функции.

Математики рекомендуют использовать для построения графика полученные значения при расчетах, поскольку подстановка и вычисление произвольных х существенно снижает скорость вычислений.

Таким образом, нахождение координат вершины параболы является довольно простой задачей, поскольку существует несколько методов. Из них можно выбрать оптимальный, который подходит в конкретной ситуации.

Координаты вершины параболы онлайн

Парабола – это функция, заданная уравнением:

Её график имеет следующий вид:

Причем, в зависимости от знака коэффициента , ветви параболы направлены вверх (если ) или вниз (если ).

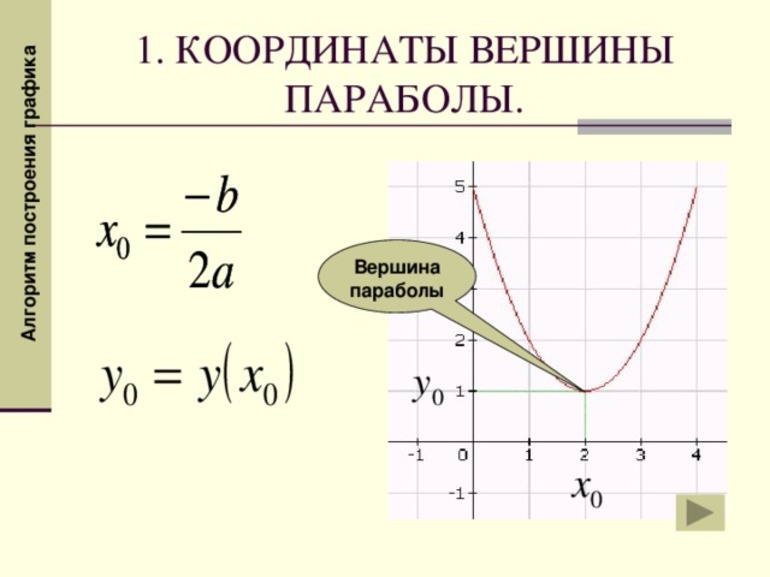
В школьном курсе алгебры возникает задача нахождения координат вершины параболы. Их можно найти по формулам:

Вершина параболы, отмечена оранжевой точкой на приведённом выше графике.

Наш онлайн калькулятор позволяет найти координаты вершины параболы с описанием подробного хода решения на русском языке. Для работы калькулятора, необходимо ввести уравнение параболы и указать её переменную. Уравнение параболы можно вводить в различных форматах, а коэффициентами могут быть не только числа или дроби, но и параметры. Нажмите на кнопку “Примеры”, расположенную на панели калькулятора, чтобы посмотреть различные форматы ввода.

Как найти вершину параболы: три формулы

Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.

Нахождение вершины параболы: способы, примеры, советы

График функции y = ax 2 + bx + c, где a — первый коэффициент, b – второй коэффициент, c – свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.

У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.

Первый способ

Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.

Например, y =x 2 –8 x +15;

находим первый, второй коэффициенты и свободный член;

подставляем значения a и b в формулу;

вычисляем значения y;

Значит, вершина находится в точке (4;-1).

Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n – корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.

Рассмотрим на примере y =x 2 –6x+5

1) Приравниваем к нулю:

2) Находим дискриминант, используя формулу: D = b 2 –4 ac:

3) Находим корни уравнения по формуле (-b±√ D)/2a:

• 1 – первый корень;
• 5 – второй корень.

Второй способ

Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.

1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.

2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.

У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:

3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.

4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).

Третий способ

Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:

1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.

2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.

Рассмотрим этот способ подробнее.

Дана функция y = 4x²+16x-17;

• Записываем производную и приравниваем к нулю.

f'(x) = (4x²+16x-17)’ = 8x+16 =0

Построение параболы

Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

2) Заполняем таблицу

Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Советы

Правильно находите коэффициенты.

Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.

Делайте всё поэтапно. Следуйте алгоритму.

Обратите ваше внимание на то, что:

• Нужно проверять правильно ли ваше решение.
• Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.

Видео

Это видео поможет вам научиться находить вершину параболы

Как построить параболу? Что такое парабола? Как решаются квадратные уравнения?

Урок: как построить параболу или квадратичную функцию?

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Парабола — это график функции описанный формулой ax 2 +bx+c=0.
Чтобы построить параболу нужно следовать простому алгоритму действий:

1 ) Формула параболы y=ax 2 +bx+c,
если а>0 то ветви параболы направленны вверх,
а 2 +bx+c=0;

a) Полное квадратное уравнение имеет вид ax 2 +bx+c=0 и решается по дискриминанту;
b) Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
ax 2 +bx=0,
х(ax+b)=0,
х=0 и ax+b=0;
c)Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x 2 +4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2) 2 +4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x 2 +4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b 2 -4ac=16-12=4
x=(-b±√(D))/2a
x₁=(-4+2)/2=-1
x₂=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x 2 +4x+3 значения
y=(-4) 2 +4*(-4)+3=16-16+3=3
y=(-3) 2 +4*(-3)+3=9-12+3=0
y=(-1) 2 +4*(-1)+3=1-4+3=0
y=(0) 2 +4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x 2 +4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1 2 +4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x 2 +4x=0
Неполное квадратное уравнение вида ax 2 +bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x 2 +4x значения
y=0 2 +4*0=0
y=-(1) 2 +4*1=-1+4=3
y=-(3) 2 +4*3=-9+13=3
y=-(4) 2 +4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x 2 -4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0) 2 -4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x 2 -4=0
Неполное квадратное уравнение вида ax 2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x 2 =4
x₁=2
x₂=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x 2 -4 значения
y=(-2) 2 -4=4-4=0
y=(-1) 2 -4=1-4=-3
y=1 2 -4=1-4=-3
y=2 2 -4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

Подписывайтесь на канал на YOUTUBE, чтобы быть в курсе всех новинок и готовится с нами к экзаменам.

[spoiler title=”источники:”]

http://liveposts.ru/articles/education-articles/matematika/kak-najti-vershinu-paraboly-tri-formuly

http://tutomath.ru/uroki/kak-postroit-parabolu.html

[/spoiler]

Определение

Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.

Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.

Число k называется угловым коэффициентом прямой.

Свойства линейной функции

1. Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
2. Областью значений также является множество всех действительных чисел.
3. Функция не имеет ни наибольших, ни наименьших значений.
4. При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
5. При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
6. При k=0 прямая параллельна оси х.
7. Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.

Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.

Пример №1

Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:

Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).

Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:

у=2х – 1=2×0 – 1= –1;

у=2х – 1=2×3 – 1= 5.

Вписываем в таблицу значения у:

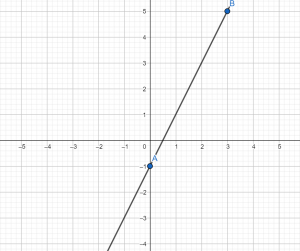
Теперь строим систему координат, отмечаем в ней точки с координатами      А(0; –1) и В(3;5), проводим через эти две точки прямую.

Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.

Пример №2.

Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.

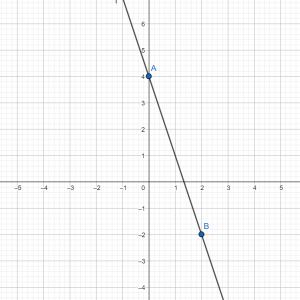
По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).

Пример №3

Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:

Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.

Задание OM1106o

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

ГРАФИКИ:

КОЭФФИЦИЕНТЫ:

1) k>0, b<0                   2) k>0, b>0                    3) k<0, b<0 

---

ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>90⁰) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.

У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<90⁰). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.

В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.

Ответ: 213

pазбирался: Даниил Романович | обсудить разбор

Задание OM1103o

Установите соответствие между функциями и их графиками.

Функции:

A) y = 3x

Б) y = -3x

В) y = (1/3)x

Графики:

---

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:

y = kx + b

График данной функции зависит от k и b.

• если k < 0,  то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
• если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
• коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если  b > 0, то выше ноля в точке y = b
• если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1

Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.

Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор

Даниил Романович | Просмотров: 6.1k