Как найти вершину квадрата 2 класс

Ответов на вопрос о том, что такое квадрат, может быть множество. Все зависит от того, кому вы этот вопрос адресовали. Музыкант скажет, что квадрат – это 4, 8, 16, 32 такта или джазовая импровизация. Ребенок – что это игра с мячом или детский журнал. Печатник отправит вас изучать кегли шрифта, а техник – разновидности металлопрокатного профиля.

Много и других значений у этого слова, но сегодня мы зададим вопрос математику. Итак…

Разбираться с этой фигурой мы будем постепенно, от простого к сложному, и начнем с истории квадрата. Как он появился, как его воспринимали люди, ученые разных стран и цивилизаций?

История изучения квадрата

Древний мир воспринимает квадрат, главным образом, как четыре стороны света. Вообще, несмотря на множество четырехугольников, именно у квадрата главное число – четыре. Для ассирийцев и перуанцев квадрат – весь мир, то есть он представляет четыре основных направления, стороны света.

Даже Вселенную представляли как квадрат, еще и разделенный на четыре части – это видение жителей Северной Америки. Для кельтов вселенная – это целых три квадрата, вложенных друг в друга, а из центра вытекают четыре (!) реки. А египтяне вообще обожествляли эту фигуру!

Впервые описали квадрат посредством математических формул греки. Но для них этот многоугольник обладал только отрицательными характеристиками. Пифагор вообще не любил четные числа, видя в них слабость и женственность.

Даже в религиях присутствует квадрат. В Исламе Кааба – пуп Земли – имеет не какую-нибудь сферическую, а именно кубическую форму.

В Индии главной графемой, изображающей Землю, или символом земли, был перекрещенный квадрат. И снова речь идет о четырех сторонах света, четырех областях земли.

В Китае квадрат – это мир, гармония и порядок. Хаос побеждается построением квадратной Вары. А квадрат, вписанный в круг, является основой видения мира, символизируя единство и связь Космоса и Земли.

Языческая Русь – Квадрат Сварога. Этот символ еще называют Звездой Сварога, или Звездой Руси. Он довольно сложный, так как составлен из пересекающихся и замкнутых линий. Сварог – бог-Кузнец, самый главный творец, создатель и само небо в представлении русичей. В этом символе есть ромб, что опять говорит о Земле и четырех ее направлениях. И звезда с четырьмя лучами – 4 стороны света, 4 лика Сварога – его всеведение. А пересечение лучей – очаг.

Интересное о квадрате

Самое популярное словосочетание, которое приходит в голову о нашем главном герое – “Черный Квадрат”.

Картина Малевича до сих пор очень популярна. Сам автор после ее создания долго мучился вопросом о том, что же это такое, и почему простой черный квадрат на белом фоне так притягивает внимание к себе.

Но если вы приглядитесь внимательно, то заметите, что плоскость квадрата не гладкая, а в трещинах черной краски есть множество разноцветных оттенков. Видимо, вначале была некая композиция, которая автору не понравилась, и он закрыл ее от наших глаз этой фигурой. Черный квадрат, как ничто – черная дыра, только магической квадратной формы. А пустота, как известно, притягивает…

Еще очень популярны “магические квадраты”. По сути это – таблица, естественно, квадратная, заполненная числами в каждой графе. Сумма этих чисел одинакова во всех строках, столбцах и диагоналях (по отдельности). Если диагонали исключаются из равенства, то квадрат – полумагический.

Альбрехт Дюрер в 1514 году создал картину “Меланхолия I”, на которой изобразил магический квадрат 4х4. В нем сумма чисел всех столбцов, строк, диагоналей и даже внутренних квадратов равна тридцати четырем.

На базе этих таблиц появились очень интересные и популярные головоломки – “Судоку”.

Египтяне первыми стали проводить линии взаимосвязи чисел (дата рождения) и качеств характера, способностей и талантов человека. Пифагор взял эти знания, несколько переработал и поместил в квадрат. Получился Квадрат Пифагора.

Это уже отдельное направление в нумерологии. Из даты рождения человека путем сложений высчитывают четыре основных числа, которые помещают в психоматрицу (квадрат). Так и раскладывают все тайные сведения о вашей энергии, здоровье, таланте, удаче, темпераменте и прочем по полочкам. В среднем, по опросам достоверность составляет 60%-80%.

Что такое квадрат?

Квадратом называют геометрическую фигуру. Форма квадрата – четырехугольник, который имеет равные стороны и углы. Еще точнее, этот четырехугольник называют правильным.

У квадрата есть свои признаки. Это:

• стороны, равные по длине;
• равные между собой углы – прямые (по 90 градусов).

В силу этих признаков и особенностей в квадрат можно вписать окружность и описать ее вокруг него. Описанная окружность будет касаться всех его вершин, вписанная – середины всех его сторон. Их центр будет совпадать с центром квадрата и разделит все его диагонали пополам. Последние, в свою очередь, равны между собой и делят углы квадрата на равные части.

Одна диагональ разделяет квадрат на два равнобедренных треугольника, обе – на четыре.

Таким образом, если длина стороны квадрата – t, длина радиуса описанной окружности – R, а вписанной – r, то

• площадь основания квадрата, или площадь квадрата (S) будет равна S=t²=2R²=4r²;

• периметр квадрата P следует вычислять по формуле P=4t=4√2R=8r;

• длину радиуса описанной окружности R=(√2/2)t;

• вписанной – r=t/2.

Площадь основания квадрата еще можно вычислить, зная его сторону (a) или длину его диагонали (c), тогда формулы будут выглядеть соответственно: S=a² и S=1/2c².

Что такое квадрат, мы с вами выяснили. Давайте подробнее рассмотрим детали, ведь фигура квадрат самый симметричный четырехугольник. У него пять осей симметрии, причем одна (четвертого порядка) проходит через центр и является перпендикуляром к плоскости самого квадрата, а четыре другие – оси симметрии второго порядка, две из них параллельны сторонам, а еще две проходят через диагонали квадрата.

Способы построения квадрата

Исходя из определений, кажется, что нет ничего проще, чем построить правильный квадрат. Это так, но при условии, что у вас есть все измерительные инструменты. А если чего-то нет в наличии?

Давайте рассмотрим существующие способы, которые помогут нам построить эту фигуру.

Измерительная линейка и угольник – это основные инструменты, при помощи которых наиболее просто можно построить квадрат.

Сначала отметьте точку, допустим А, от нее мы построим основание квадрата.

С помощью линейки отложите от нее вправо расстояние, равное длине стороны, допустим 30 мм, и поставьте точку Б.

Теперь от обеих точек, воспользовавшись угольником, проведите вверх перпендикуляры по 30 мм каждый. На концах перпендикуляров ставим точки В и Г, которые соединяем между собой, пользуясь линейкой – все, квадрат АБВГ со стороной 30 мм готов!

С помощью линейки и транспортира тоже довольно легко построить квадрат. Начните, как и в предыдущем случае с точки, допустим Н, от нее отложите горизонтальный отрезок, например 50 мм. Поставьте точку О.

Теперь центр транспортира соедините с точкой Н, поставьте отметку у величины угла 90⁰, через нее и точку Н постройте вертикальный отрезок 50 мм, на его конце поставьте точку П. Далее подобным образом постройте третий отрезок от точки О через угол 90⁰, равный 50 мм, пусть он заканчивается точкой Р. Соедините точки П и Р. У вас получился квадрат НОРП с длиной стороны 50 мм.

Можно построить квадрат, пользуясь только циркулем и линейкой. Если вам важен размер квадрата и известна длина стороны, то понадобится еще и калькулятор.

Итак, ставьте первую точку Е – это будет она из вершин квадрата. Далее укажите место, где будет находится противоположная вершина Ж, то есть постойте диагональ ЕЖ вашей фигуры. Если вы строите квадрат по размерам, то имея длину стороны, высчитайте длину диагонали по формуле:

d=√2*a, где a – длина стороны.

После того как вы узнаете длину диагонали, постройте отрезок ЕЖ этой величины. Из точки Е с помощью циркуля в направлении точки Ж проведите полукруг радиусом ЕЖ. И наоборот, из точки Ж – полукруг в сторону точки Е, радиусом ЖЕ. Через точки пересечения этих полукругов, пользуясь линейкой, постройте отрезок ЗИ. ЕЖ и ЗИ пересекаются под прямым углом и являются диагоналями будущего квадрата. Соединив точки ЕИ, ИЖ, ЖЗ и ЗЕ с помощью линейки, вы получите вписанный квадрат ЕИЖЗ.

Еще есть возможность построить квадрат с помощью одной линейки. Что такое квадрат? Это участок плоскости, ограниченный пересекающимися отрезками (линиями, лучами). Следовательно, мы можем построить квадрат по координатам его вершин. Сначала начертите оси координат. Стороны квадрата могут лежать на них, или центр пересечения диагоналей будет совпадать с точкой начала координат – это зависит от вашего желания или условий задачи. Возможно, ваша фигура будет отстоять от осей на некотором расстоянии. В любом случае, сначала отмечаете по числовым значениям (произвольно или условно) две точки, тогда вам будет известна длина стороны квадрата. Теперь можно вычислить координаты оставшихся двух вершин, помня, что стороны квадрата равны и между собой попарно параллельны. Последний шаг – соединить все точки последовательно между собой с помощью линейки.

Какие бывают квадраты?

Квадрат – фигура четко определенная и жестко ограниченная своими определениями, поэтому виды квадратов не отличаются многообразием.

В Неевклидовой геометрии квадрат воспринимается более широко – это четырехугольник с равными сторонами и углами, но градус углов не задан. Это значит, что углы могут быть и по 120 градусов (“выпуклый” квадрат) и, например, по 72 градуса (“вогнутый” квадрат).

Если вы спросите, что такое квадрат, у геометра или информатика, вам ответят, что – это полный или планарный граф (графы с К₁ по К₄). И это абсолютно справедливо. У графа есть вершины и ребра. Когда они встают в упорядоченную пару, образуется граф. Число вершин – это порядок графа, число ребер – его размер. Таким образом, квадрат – это планарный граф с четырьмя вершинами и шестью ребрами, или К₄:6.

Сторона квадрата

Одно из главных условий существования квадрата – наличие равных по длине сторон – делает сторону очень важной для различных вычислений. Но в то же время дает много способов, чтобы длина стороны квадрата была вычислена при наличии самых разных исходных данных.

Итак, как найти значение стороны квадрата?

• Если вам известна только длина диагонали квадрата d, то вычислить сторону можно по следующей формуле: a=d/√2.
• Диаметр вписанной окружности равен стороне квадрата и, следовательно, двум радиусам, то есть: a=D=2R.
• Радиус описанной окружности тоже может помочь вычислить, чему равна сторона квадрата. Мы можем по радиусу R узнать диаметр D, который, в свою очередь, равен диагонали квадрата d, а формулу для стороны квадрата через диагональ мы уже знаем: a=D/√2=d/√2=2R/√2.
• Из равенства сторон следует, что узнать сторону квадрата (a) можно при помощи его периметра P или площади S: a=√S=P/4.
• Если мы знаем длину линии, которая выходит из угла квадрата и пересекает середину его смежной стороны C, то нам также удастся узнать, какова же длина стороны квадрата: a=2C/√5.

Вот сколько способов существует, чтобы выяснить такой важный параметр, как длина стороны квадрата.

Объем квадрата

Сама фраза является абсурдом. Что такое квадрат? Это плоская фигура, имеющая всего два параметра – длину и ширину. А объем? Это количественная характеристика пространства, которое занимает объект, то есть ее можно вычислить только у объемных тел.

Объемное тело, всеми гранями которого являются квадраты, – куб. Несмотря на колоссальное и принципиальное различие, школьники довольно часто пытаются вычислить объем квадрата. Если это кому-то удастся, Нобелевская премия обеспечена.

А чтобы узнать объем куба V, достаточно перемножить все три его ребра – a, b, c: V=a*b*c. А так как они по определению равны, то формула может выглядеть иначе: V=a³.

Величины, части и характеристики

У квадрата, как и у любого многоугольника, есть вершины – это точки, в которых пересекаются его стороны. Вершины квадрата лежат на описанной вокруг него окружности. Через вершину в центр квадрата проходит диагональ, которая также является биссектрисой и радиусом описанной окружности.

Так как квадрат – это плоская фигура, то рассечь и построить сечение квадрата невозможно. Зато он может быть результатом пересечения многих объемных тел плоскостью. Например, цилиндра. Осевое сечение у цилиндра – прямоугольник или квадрат. Даже при пересечении тела плоскостью под произвольным углом может получиться квадрат!

Но у квадрата есть еще одно отношение к сечению, да не к какому-нибудь, а к Золотому сечению.

Все мы знаем, что Золотое сечение – это пропорция, в которой одна величина относится к другой так же, как их сумма к большей величине. В обобщенном процентном выражении это выглядит следующим образом: исходная величина (сумма) делится на 62 и 38 процентов.

Золотое сечение очень популярно. Оно используется в дизайне, архитектуре, да где угодно, даже в экономике. Но это далеко не единственная пропорция, выведенная Пифагором. Есть, например, еще выражение “√2”. На его основе проводится построение динамических прямоугольников, которые, в свою очередь, являются основоположниками форматов группы А (А6, А5, А4 и т.п.). Почему речь зашла о динамических прямоугольниках? Потому что их построение начинается с квадрата.

Да, для начала вам нужно построить квадрат. Его сторона будет равна меньшей стороне будущего прямоугольника. Затем необходимо провести диагональ этого квадрата и, воспользовавшись циркулем, длину этой диагонали отложить на продолжении стороны квадрата. Из полученной на пересечении точки выстраиваем прямоугольник, у которого снова строим диагональ и откладываем ее длину на продолжении стороны. Если продолжить работу по этой схеме, получатся те самые динамические прямоугольники.

Отношение длинной стороны первого прямоугольника к короткой будет 0,7. Это почти 0,68 в Золотом сечении.

Углы квадрата

Собственно, что-то свежее сказать об углах уже сложно. Все свойства, они же признаки квадрата, мы перечислили. Что касается углов, их четыре (как и во всяком четырехугольнике), каждый угол в квадрате – прямой, то есть имеет размер девяносто градусов. По определению, существует лишь прямоугольный квадрат. Если углы большего или меньшего размера – это уже другая фигура.

Диагонали квадрата делят его углы пополам, то есть являются биссектрисами.

Уравнение квадрата

При необходимости вычислить значение различных величин у квадрата (площади, периметра, длин сторон или диагоналей) используют различные уравнения, которые выводятся из свойств квадрата, основных законов и правил геометрии.

1. Уравнение площади квадрата

Из уравнений для вычисления площади четырехугольников мы знаем, что она (площадь) равна произведению длины и ширины. А так как стороны квадрата одинаковые по длине, то площадь его будет равна длине любой стороны, возведенной во вторую степень

S=a².

Используя теорему Пифагора, мы можем вычислить площадь квадрата, зная длину его диагонали.

S=d²/2.

2. Уравнение периметра квадрата

Периметр квадрата, как и всех четырехугольников, равен сумме длин его сторон, а так как они все одинаковые, то можно сказать, что периметр квадрата равен длине стороны, умноженной на четыре

P=a+a+a+a=4a.

Снова теорема Пифагора поможет нам найти периметр через диагональ. Нужно значение длины диагонали умножить на два корня из двух

P=2√2d

3. Уравнение диагонали квадрата

Диагонали квадрата равны, пересекаются под прямым углом и делятся точкой пересечения пополам.

Найти их можно, исходя из вышеприведенных уравнений площади и периметра квадрата

d=√2*a, d=√2S, d=P/2√2

Есть еще способы узнать, какова же длина диагонали квадрата. Радиус вписанной в квадрат окружности равен половине его диагонали, отсюда

d=√2D=2√2R, где D – диаметр, а R – радиус вписанной окружности.

Зная радиус описанной окружности, рассчитать диагональ еще проще, ведь она является диаметром, то есть d=D=2R.

Также есть возможность вычислить длину диагонали, зная длину линии, выходящей из угла к центру стороны квадрата C: d=√8/5*C.

Но не стоит забывать, что квадрат – это участок плоскости, ограниченный четырьмя пересекающимися линиями.

Для линий (и образованных ими фигур) существует достаточно уравнений, не нуждающихся в дополнительном описании, но линия бесконечна. А многоугольники ограничены пересечением линий. Для них можно использовать линейные уравнения, объединенные в систему, задающие прямые линии. Но необходимо указывать дополнительные параметры, условия.

Для определения многоугольников же необходимо составить такое уравнение, которое бы описывало не линию, а отдельный произвольный отрезок без вмешательства дополнительных условий и описаний.

[ x/x_i ]*[ x_i/x]*y_i – вот это специальное уравнение для многоугольников.

Квадратные скобки в нем указывают на условие исключения дробной части числа, то есть мы должны оставить только целое число. y_i – функция, которая выполнятся в диапазоне параметра от x до x_i.

Используя это уравнение, можно вывести новые уравнения для вычисления отрезков и линий, состоящих из нескольких отрезков. Оно является базовым, универсальным для многоугольников.

Помним, что квадрат – это часть плоскости, поэтому его описание типа y=f(x) можно представить, чаще всего, только как многозначную функцию, которую, в свою очередь, можно выразить через однозначные, если представлять их параметрически, то есть зависящими от какого-либо параметра t:

x=f(t), y=f(t).

Так вот, если использовать в совокупности универсальное уравнение и параметрическое представление, то действительно можно вывести уравнение для выражения многоугольников:

x=((A2+A3)*A5+A4*P)*Cos(L)

y=((A1+A4)*A5+A3*P)*Sin(L),

где

A1=[1/[T/P]]*[T/P]; A2=[2/[T/P]]*[[T/P]/2]; A3=[3/[T/P]]*[[T/P]/3]; A4=[4/[T/P]]*[[T/P]/4]; A5=T-P*[T/P],

где P – диагональ прямоугольника, L – угол наклона к горизонтали диагонали P, T – параметр изменяющийся в диапазоне от P до 5P.

Если L=3,14/4, то уравнение будет описывать квадраты разной величины, в зависимости от размера диагонали P.

Применение квадрата

В современном мире технологии позволяют придавать различным материалам квадратную форму, точнее квадратное сечение.

Это во многом выгоднее, дешевле, долговечнее и безопаснее. Так, сейчас делают квадратные трубы, сваи, проволоку (провода) и даже квадратные нити.

Основные преимущества очевидны, они выходят из элементарной геометрии. При одинаковом размере площадь вписанного круга меньше площади квадрата, в который он вписан, следовательно, пропускная способность квадратной трубы или энергоемкость квадратного провода будут выше, чем у круглых аналогов.

Зачастую расходные материалы квадратного сечения более эстетичны и удобны в использовании, монтаже, креплении.

При выборе этих материалов важно правильно рассчитать сечение квадрата, чтобы провод или труба выдержали необходимую нагрузку. В каждом отдельном случае, конечно, будут необходимы такие параметры, как сила тока или давление, но и без основных геометрических правил квадрата тут не обойтись. Хотя размеры квадратных сечений уже не столько вычисляют, сколько выбирают по заданным параметрам из таблиц, установленных ГОСТами для разных отраслей.

Найди на рисунках квадраты и прочитай их обозначения. Назови вершины и стороны квадратов.

Сколько всего треугольников на каждом из рисунков?

Общие сведения

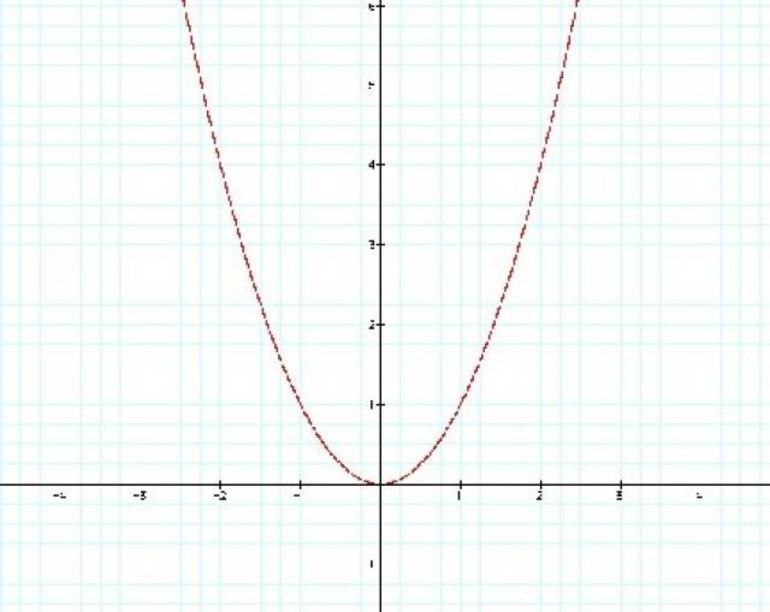
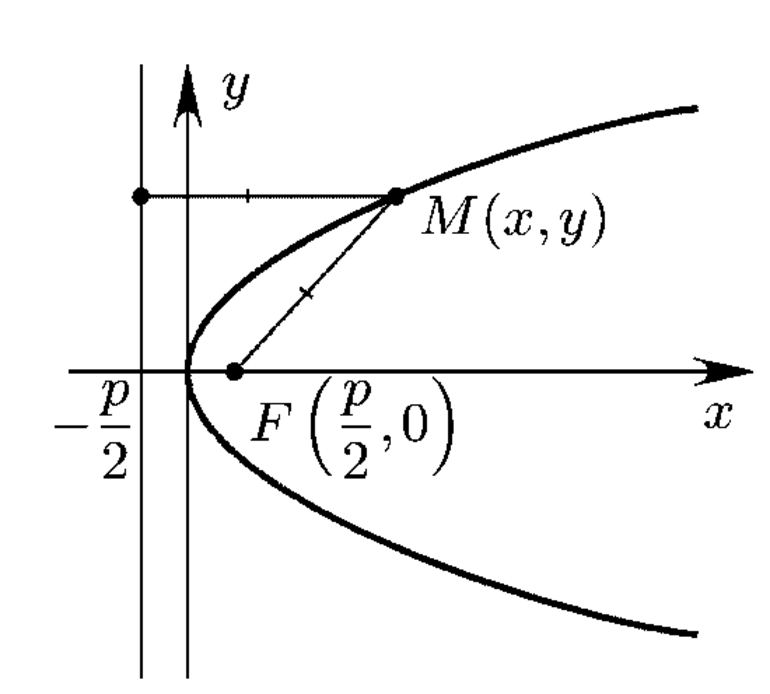
Парабола — кривая, состоящая из равноудаленных точек от заданной точки (вершина) и прямой. Последняя называется директрисой. График функции имеет ось симметрии, которая проходит по определенной траектории и зависит от функции кривой (рис. 1). Ее вершина находится в центре координат.

Рисунок 1. График квадратичной функции с вершиной в начале координат.

Однако существуют и другие случаи прохождения кривой. Она может пересекать оси абсцисс или ординат. В некоторых случаях ее ветви направлены вниз. При вращении вокруг оси симметрии получается поверхность, которая используется в различных устройствах. По этому принципу изготовлены фары автомобиля, зеркала в телескопах и т. д. Кроме того, парабола — это квадратичная зависимость переменных друг от друга. Парабола имеет некоторые свойства:

1. Парабола — кривая второго порядка.
2. Ось симметрии перпендикулярна директрисе и проходит через фокус и вершины.
3. Оптическое свойство отражения.
4. Отрезок, который соединяет середину любой хорды параболы и точку пересечения касательных прямых, является перпендикуляром относительно директрисы.
5. Подобность всех парабол.
6. Траектория фокуса, которая катится по произвольной прямой — цепная молния.

Следует отметить, что оптическое свойство — это способность отражать свет от источника. Если пучок лучей, которые являются параллельными ее оси, отражаются в параболе, то они собираются в фокусе кривой. При нахождении источника света в фокусе происходит отражение параллельного пучка лучей относительно ее оси.

Уравнения квадратичной функции

Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:

1. Каноническая.
2. Квадратичная.
3. Общая.

В первой форме она имеет следующий вид: y ² = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x ² = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).

Рисунок 2. Директриса и фокус.

Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y ² ]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y ² ]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y ² = 2px).

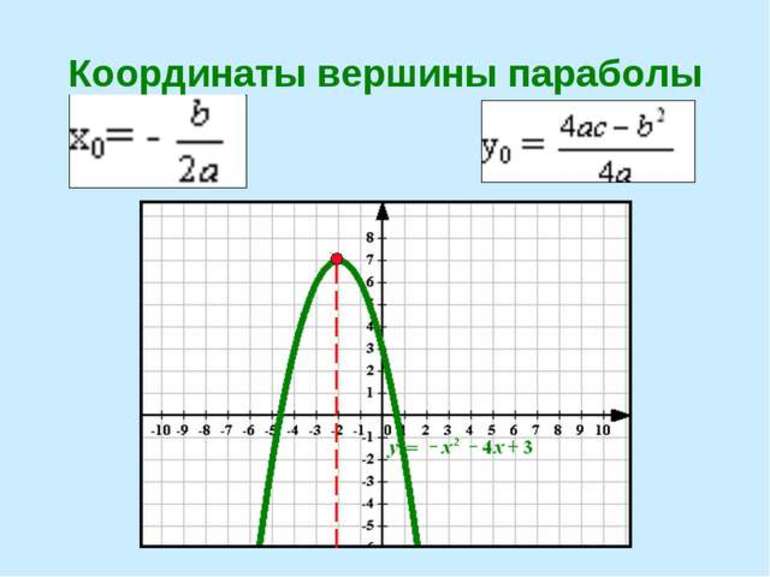
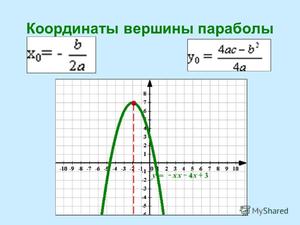
Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax ² + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax ² . В этом случае формула нахождения вершины параболы выглядит таким образом:

1. Абсцисса вершины параболы: xa = -b / 2a.
2. Координата «игрек» по оси ординат: yb = – D / 2a.

В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b ² — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а<0, то ось ее симметрии параллельна оси абсцисс. Расстояние до фокуса также равно ¼а. Уравнение y = a (x — xa)^2 + ya — функция, определяющая кривую II порядка, как параболу.

Поскольку искомую функцию можно назвать кривой второго порядка, то ее уравнение может быть записано в виде квадратного многочлена в декартовой системе координат. Вид его имеет такой вид: Ax ² + Bxy + Cy ² + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).

В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.

Методы нахождения вершины

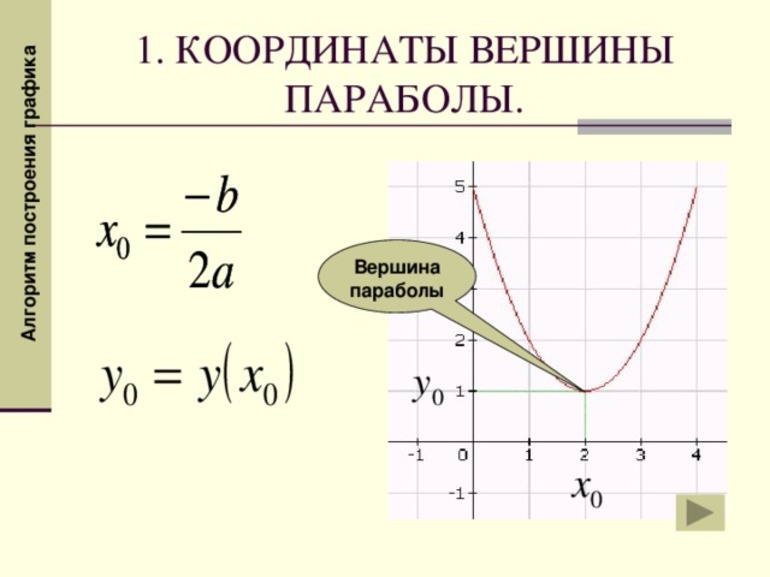
В математике есть три способа нахождения координат точки вершины кривой: по формуле, выделением полного квадрата и нахождением производной. Следует отметить, что первый способ не подойдет в том случае, когда функция отличается от вида y = ax ² + bx + c. Первый способ — расчет по формуле вершины параболы квадратичной функции. Координата x0 вычисляется таким образом: x0 = -b / 2a. Для нахождения координаты y0 следует подставить в функцию найденное значение x0.

Когда функция представлена неполным квадратом, нужно прибавить или отнять одинаковое число к двум частям уравнения. Если воспользоваться этим методом, то можно вычислить сразу значения х и у. Алгоритм нахождения вершины для функции у = x ² + 4x + 2 имеет такой вид:

1. Приравнять многочлен к нулю, и перенести свободный член в правую сторону с противоположным знаком: x ² + 4x = -2.
2. Дополнить до полного квадрата. Необходимо вычислить свободный член по такому соотношению: с = (b/2)^2 = (4/2)^2 = 4.
3. Записать полный квадрат, отняв и прибавив свободный член: x ² + 4x + 4 — 4 = -2.
4. Выделить квадрат: (x ² + 2x + 4) — 4 = -2.
5. Перенести свободное число в правую сторону с противоположным знаком: (x ² + 2x + 4) = 4 — 2.
6. Уравнение принимает следующий вид: (x + 2)^2 = 2.
7. Для того чтобы вычислить x0, нужно решить уравнение (x + 2)^2 = 0. Следовательно, x = -2.
8. Ординату точки определить очень просто, поскольку ее значение соответствует числу (нужно брать с противоположным знаком), которое находится в правой части уравнения, т. е. у = -2.

При изображении графика вершину нужно сместить в точку (-2;2). Третий способ позволяет узнать координаты вершины с помощью определения производной. Находить ее следует от заданной функции. Для вычисления координат вершины нужно действовать по следующему алгоритму:

1. Найти производную и приравнять ее к нулю: f'(x) = (ax ² + bx + c)’ = 2ax + b.
2. Выразить х: х = -b / (2a).
3. Подставить в функцию для вычисления y.
4. Записать координаты точки.

Однако эти все три метода относятся к ручному вычислению. Автоматизация действий осуществляется с помощью специализированного программного обеспечения. Для этой цели подойдет онлайн-калькулятор, поддерживающий функцию нахождения точек вершины квадратичной кривой. Программы рекомендуется применять только для проверки решения, поскольку очень важно знать методы нахождения этой точки.

Алгоритм построения

В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:

1. Если вершина не задана, то нужно найти ее любым из методов.
2. Определить точки пересечения с осями декартовой системы координат.
3. Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
4. Выполнить построение, соединив точки.

Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x ² + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.

Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.

Примеры решений

В математике существует определенная классификация заданий на простые и сложные типы. Все они считаются однотипными, но отличаются только объемами вычислений и необходимостью построения графиков. Для решения нужно воспользоваться рекомендуемыми алгоритмами, которые существенно оптимизируют вычисления.

«Корень» трудностей при расчете — отсутствие систематизации вычислений. Не все ими пользуются. В результате простая задача становится очень сложной, поскольку в ней присутствует много ненужных вычислений. Кроме того, как отмечалось выше, рекомендуется «набить руку» на ручных вычислениях, ведь не всегда можно будет воспользоваться программами.

Упрощенная задача

Простым примером задания является следующий: необходимо вычислить координаты вершины точки параболы y = x ² + 3x — 18. Следует продемонстрировать решение тремя способами. Решение первым методом:

1. Координата по оси абсцисс: х0 = -3 / (2 * 1) = -1,5.
2. По ординате: (-1,5)^2 + 3 * (-1,5) — 18 — y= 0. Отсюда, y = -20,25.

Следовательно, вершина находится в точке (-1,5;20,25). Второй способ решения данной задачи имеет такой вид:

1. Составить уравнение и перенести свободный член: x ² + 3x = 18.
2. Вычислить свободный член: с = (b/2)^2 = 2,25.
3. Записать выражение: x ² + 3x + 2,25 — 2,25 = 18.
4. Выделить квадрат: (x ² + 3x + 2,25) = 20,25.
5. Определить координаты: (x + 1,5)^2 = 20,25.
6. Искомая точка: (-1,5;20,25).

Для решения третьим методом следует найти производную: y’ = (x ² + 3x — 18)’ = 2x + 3. Затем нужно приравнять ее к нулю: 2х + 3 = 0. Уравнение является простым, а его переменная легко находится: x = -3 / 2 = -1,5. После этого необходимо подставить абсциссу в функцию, приравняв ее к 0: y = 20,25.

Повышенная сложность

Задания повышенной сложности сводятся к вычислению нескольких значений. Кроме того, в некоторых случаях следует построить график параболы y = x ² — 7x +10. Необходимо выполнить такие действия:

1. Пересечение с осями.
2. Вычислить экстремум (вершину) всеми методами.
3. Выполнить графический эскиз (график).

Точек пересечения по ОУ нет. Они есть по оси абсцисс. Следует приравнять функцию к 0. Нахождение корней выполняется по теореме Виета: x1 = 2 и x2 = 5.

Для нахождения вершины необходимо воспользоваться тремя методами. При решении первым способом находится координата x0 = 7 / (2 * 1) = 3,5. Ордината определяется таким образом: y0 = (3,5)^2 — (7 * 3,5) + 10 = -2,25. Точка экстремума имеет координаты (3,5;-2,25). Находить вершину параболы необходимо по такому алгоритму:

1. Записать уравнение, и выполнить перенос свободного члена: x ² — 7x = -10.
2. Найти свободный член: с = (7/2)^2 = 12,25.
3. Составить уравнение: x ² — 7x + 12,25 — 12,25 = -10.
4. Выделить квадрат: (x — 3,5)^2 = 2,25.
5. Экстремум: (3,5;-2,25).

Для следующего метода нужно найти производную: y’ = (x ² — 7x +10)’ = 2x — 7. Далее нужно приравнять y’ к нулю: 2x — 7 = 0. Значение по оси абсцисс равно х0 = 3,5, а y0 = -2,25. Далее нужно заполнить таблицу зависимостей ординаты от переменной.

y	4	0	-2	-2,25	-2	0	4
x	1	2	3	3,5	4	5	6

Таблица 1. Зависимость y от x.

После заполнения таблицы следует построить график искомой функции (рис. 3). Таблица состоит из следующих элементов: вершины, точек пересечения с осью абсцисс и 4 произвольных значений.

Рисунок 3. График функции.

Математики рекомендуют использовать для построения графика полученные значения при расчетах, поскольку подстановка и вычисление произвольных х существенно снижает скорость вычислений.

Таким образом, нахождение координат вершины параболы является довольно простой задачей, поскольку существует несколько методов. Из них можно выбрать оптимальный, который подходит в конкретной ситуации.

Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.

Нахождение вершины параболы: способы, примеры, советы

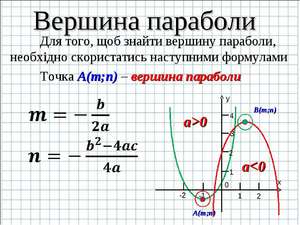
График функции y = ax²+ bx + c, где a — первый коэффициент, b – второй коэффициент, c – свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.

У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.

Первый способ

Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.

Например, y =x²–8 x +15;

находим первый, второй коэффициенты и свободный член;

• a =1, b =-8, c =15;

подставляем значения a и b в формулу;

• x0=8/2=4;

вычисляем значения y;

• y0 = 16–32+15 = -1;

Значит, вершина находится в точке (4;-1).

Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n – корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.

Рассмотрим на примере y =x²–6x+5

1) Приравниваем к нулю:

• x²–6x+5=0.

2) Находим дискриминант, используя формулу: D = b ²–4 ac:

• D =36–20=16.

3) Находим корни уравнения по формуле (-b±√ D)/2a:

• 1 – первый корень;
• 5 – второй корень.

4) Вычисляем:

• x0 =(5+1)/2=3

Второй способ

Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x ²+8 x +10.

1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x² + 8x = -10.

2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2)² и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.

У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:

x² + 8x +16= 6.

3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4)² = 6.

4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).

Третий способ

Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:

1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.

2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.

Рассмотрим этот способ подробнее.

Дана функция y = 4x²+16x-17;

• Записываем производную и приравниваем к нулю.

f'(x) = (4x²+16x-17)’ = 8x+16 =0

Построение параболы

Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x ²+11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

X			5,5
Y

2) Заполняем таблицу

Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Советы

Правильно находите коэффициенты.

Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.

Делайте всё поэтапно. Следуйте алгоритму.

Обратите ваше внимание на то, что:

• Нужно проверять правильно ли ваше решение.
• Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.

Видео

Это видео поможет вам научиться находить вершину параболы