Как найти вершину пирамиды на чертеже

Необходимо построить наклонную пирамиды по известному основанию и высоте.

Для решения задачи необходимо знать теоретический материал:

—  способы восстановления перпендикуляра к плоскости;

—  определение натуральных величин методом вращения;

—  определение видимости на чертеже с помощью конкурирующих точек (рассматривали в задаче 1).

Порядок решения задачи

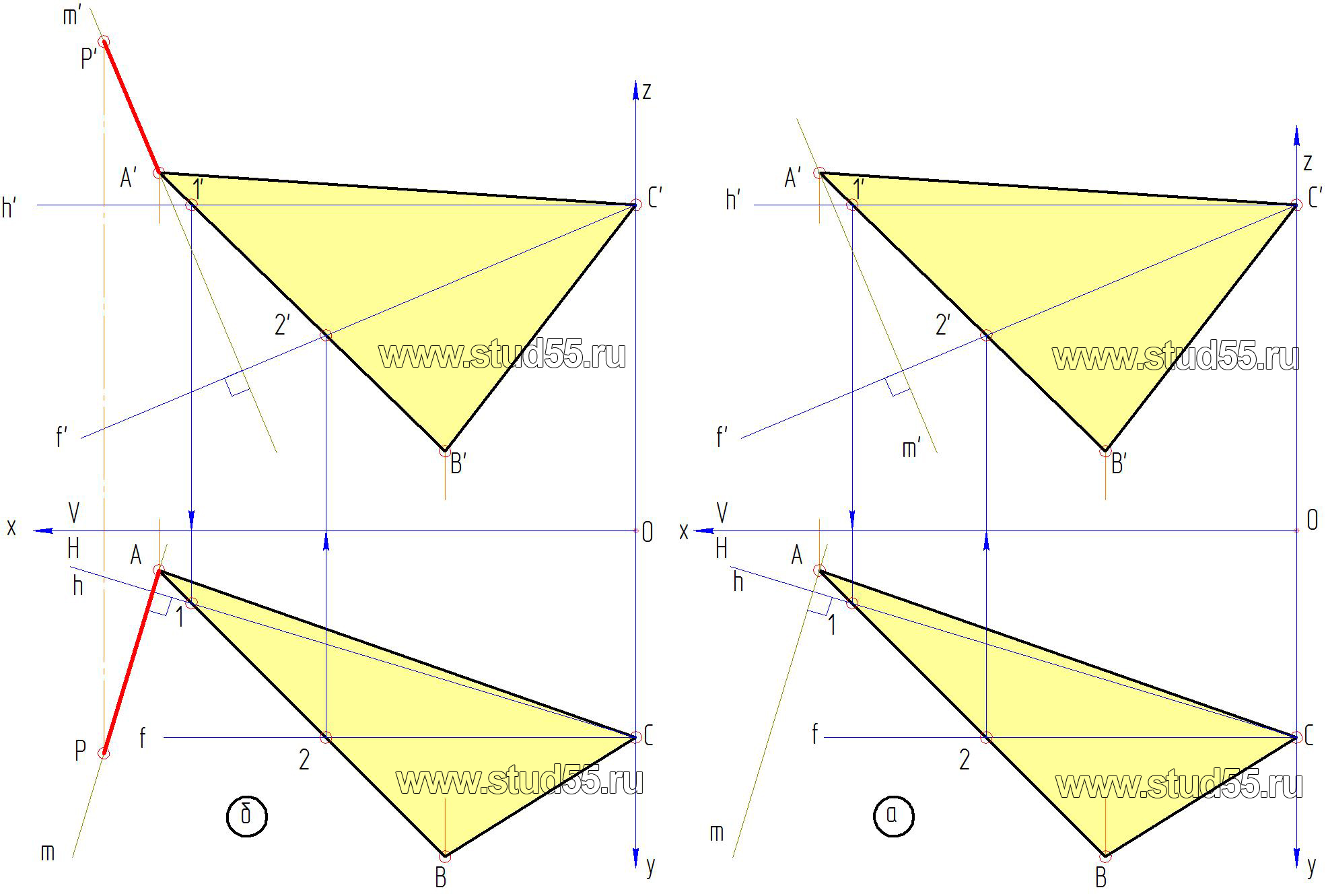
1. Согласно варианту задания наносим на комплексный чертеж координаты точек основания пирамиды, получаем плоскость в виде треугольника ABC(A’B’C’; ABC) (рис.2.1.a).

 

Рис. 2.1

2. Для нахождения вершины пирамиды по заданной высоте необходимо к указанной плоскости провести перпендикуляр через точку А (A’; A) т.к. величина высоты задана SA, для чего:

— в заданной плоскости треугольника основания пирамиды проводим горизонталь h’и h и фронталь – f’ и f  (рис.2.1.б).

— к проекциям горизонтали и фронтали, которые выражены в натуральной величине через точку А(A’; A) проводим перпендикуляр m (рис.2.2.а).

Рис.2.2

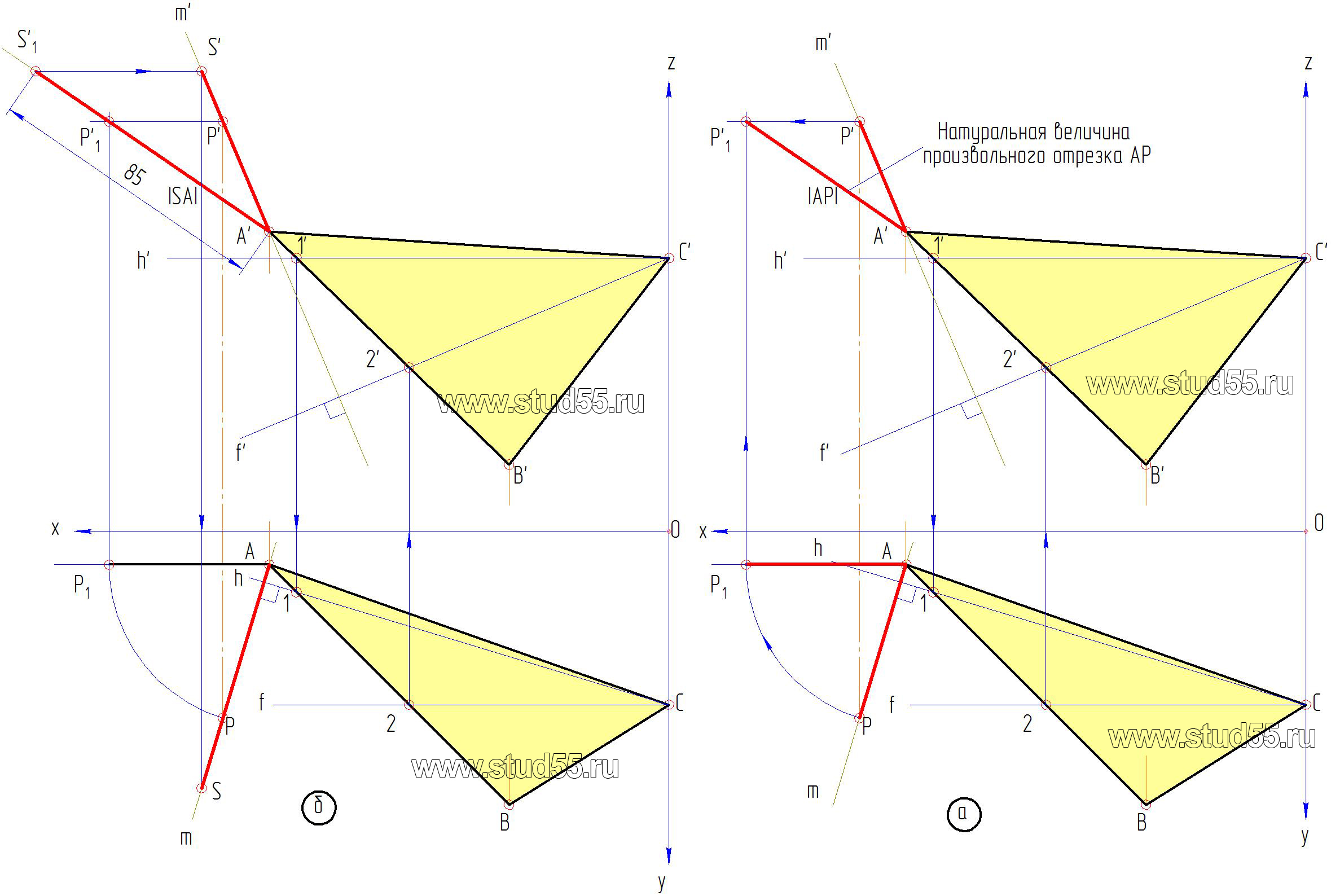
3. Так как высота пирамиды задана в натуральной величине, а проведенный перпендикуляр — в проекциях, необходимо получить линию натуральной величины произвольного отрезка на перпендикуляре. Для этого воспользуемся методом вращения:

-на проекциях перпендикуляра возьмем произвольную точку P (P’ и Р) (рис.2.2.б);

—  отрезок AР в горизонтальной проекции переведем в частное положение путем разворота его вокруг точки A, до параллельности оси х, получим точку P₁ (рис.2.3.а).

—   можно отметить, что при вращении точки в какой-то плоскости ее проекция на сопряженной плоскости движется по прямой параллельной оси х. Проведем ее из точки P’ и тогда по линиям связи на ней находим фронтальную проекцию точки P —P’₁

— соединив P’₁ и A’ получим линию натуральной величины отрезка перпендикуляра, на котором откладываем заданное расстояние SA (h=85мм), получая S’₁ — истинное положение вершины пирамиды.

4. Переведем истинную вершину пирамиды S’₁ на фронтальную проекцию перпендикуляра по линии параллельной оси х получаем S’ — фронтальную проекцию вершины пирамиды. По линии связи получаем ее горизонтальную проекцию – S (рис.2.3.б).

Рис.2.3

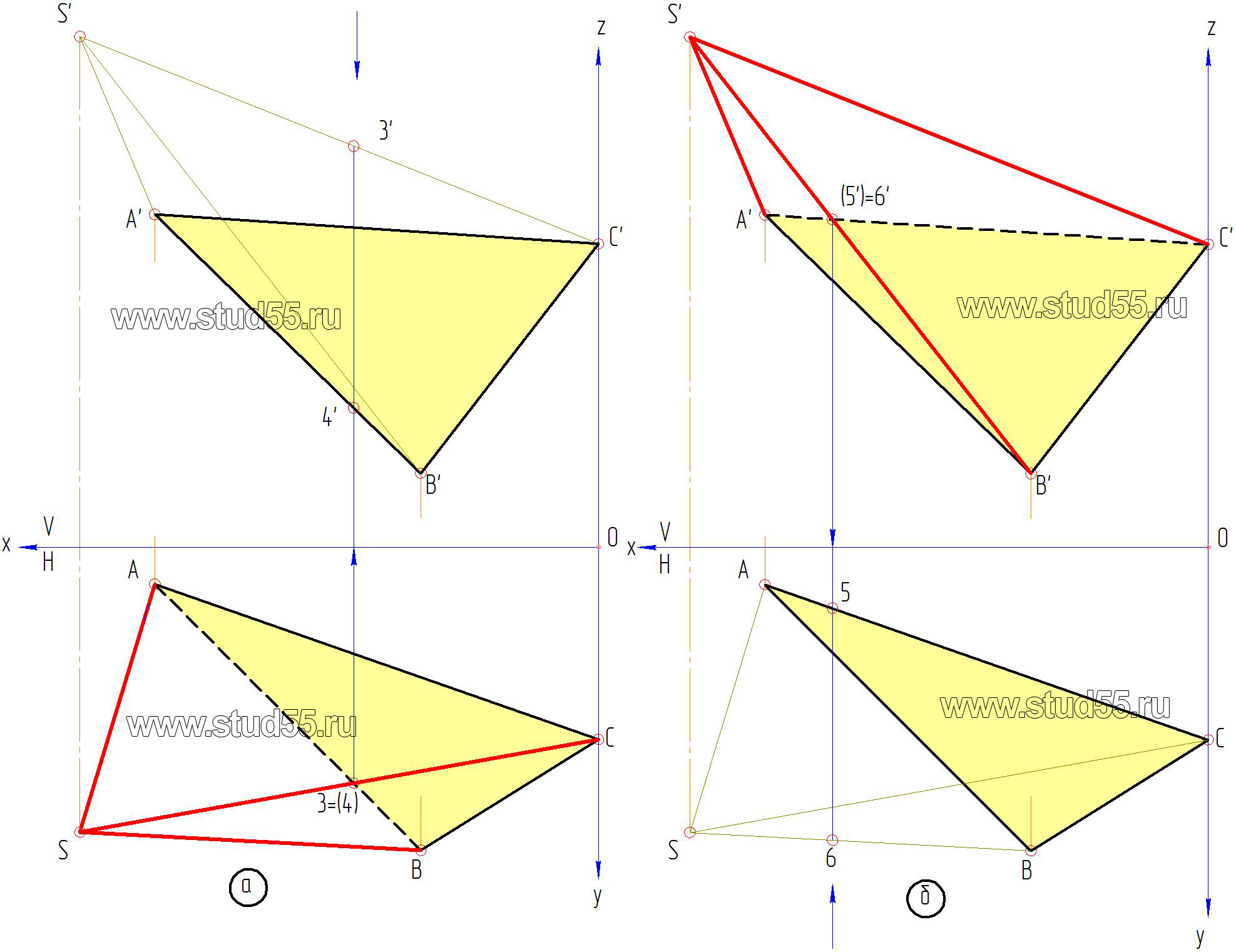
5. Таким образом, вершина пирамиды S (S’ и S) построена, соединяем ее с основанием и в заключение определяем видимость ребер пирамиды, для чего:

—  возьмем на горизонтальной проекции две конкурирующие точки 3 и 4, принадлежащие соответственно линиям SC и AB спроецируем данные точки на фронтальную плоскость, получим 3’ и 4’ на линиях S’C’ и A’B’;

—  по правилу определения видимости с помощью конкурирующих точек определяем, что прямая SC, в горизонтальной проекции будет видимой, т.к. ордината точки 3’, находящаяся на ней во фронтальной плоскости больше, чем ордината точки 4’, а линия AB будет невидимой (рис.2.4.а);

—  аналогично определяем видимость во фронтальной плоскости, беря пару конкурирующих точек 5’ и 6’, находящихся на прямых S’B’ и A’C’. По выше изложенному правилу S’B’ на фронтальной плоскости проекций будет видимой, а A’C’–невидимой (рис.2.4.б).

Рис.2.4

Рис.2.5

---

У меня есть все готовые решения задач с такими координатами, купить можно  >>здесь<<

Купленные чертежи по начертательной геометрии из книжки Фролова Вы легко можете скачать сразу после оплаты или я вышлю Вам на почту. Они находятся в ZIP архиве в различных форматах:
*.jpg – обычный цветной рисунок чертежа в масштабе 1 к 1 в хорошем разрешении 300 dpi;
*.cdw – формат программы Компас 12 и выше или версии LT;
*.dwg и .dxf — формат программы AUTOCAD, nanoCAD;

---

Раздел: Начертательная геометрия / 

Построение проекции прямоугольной пирамиды

Дано:
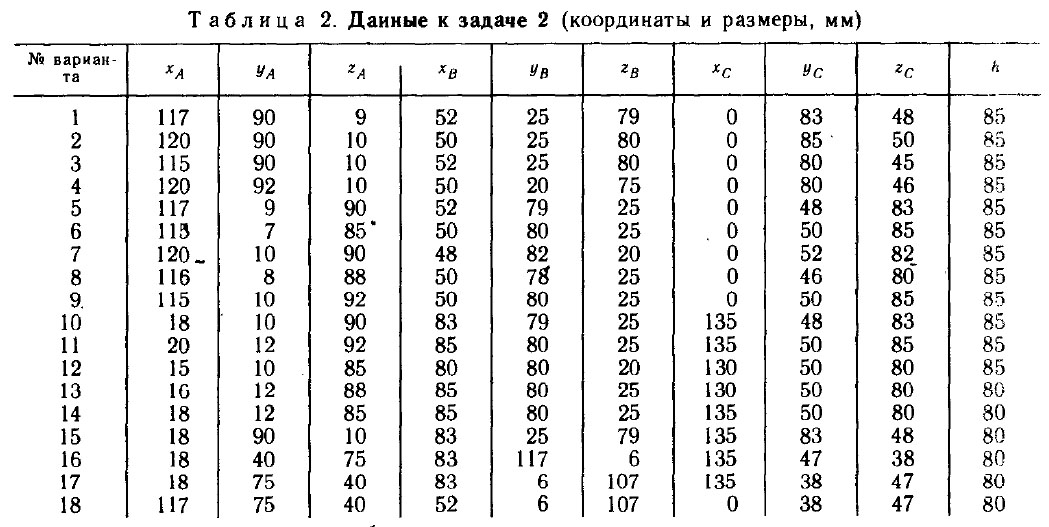
Таблица значения координат основания ABC прямоугольной пирамиды. Значение высоты h прямоугольной пирамиды SABC

Необходимо: Построить проекции пирамиды

Решение задачи на построение проекции пирамиды схоже с решением задачи на построение плоскости параллельной заданной.

Алгоритм решение задачи по начертательной геометрии на построение проекции пирамиды:

• При выполнении задачи по начертательной геометрии на пересечение двух плоскостей заданных треугольниками, мы построили проекции треугольника ABC. Значения координат точек A, B и C вершин треугольника ABC ничем не отличаются от значения координат точек A, B и C вершин треугольника основания пирамиды, по-этому скопируем из данного чертежа оси координат X, Y, Z и проекции треугольника ABC.
• Далее строим перпендикуляр к плоскости заданной треугольником ABC основания пирамиды.
• Определение натуральной величины перпендикуляра способом прямоугольного треугольника.
• Откладываем на перпендикуляре отрезок AS (высота пирамиды). Строим ребра прямоугольной пирамиды.
• Способом конкурирующих точек определяем видимость ребр пирамиды.

Подробнее в видеоуроке по начертательной геометрии в Автокад.

Построение проекции пирамиды

Онлайн решение Пирамиды по координатам вершин

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

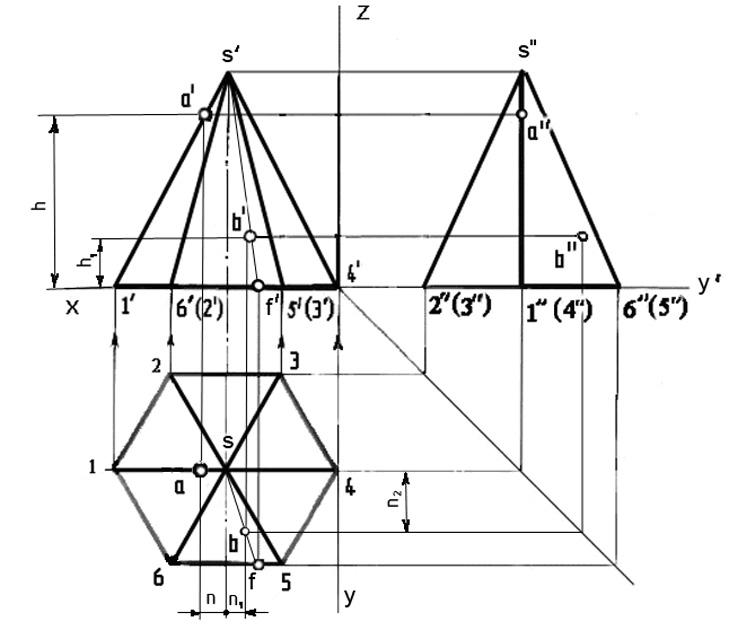
Построение
фронтальной проекции пирамиды:

1)
Из вершин шестиугольника – точек 1,
2, 3, 4,
5 и
6 (рис. 4.4,
а) –
проводим вверх вертикальные линии связи
и чертим фронтальную проекцию основания
пирамиды –
отрезок 1′–
4′.

2)
Из горизонтальной проекции вершины
пирамиды –
точки s
–
проводим вертикальную линию связи и
от отрезка
1′–
4′
откладываем высоту пирамиды, получаем
точку s‘
–
фронтальную проекцию вершины.

3)
Строим фронталь­ные проекции ребер
пирамиды –
соеди­няем
точку s‘
с точками 1′,
6′(2′), 5(3‘),
4′.

Построение
профильной проекции пирамиды;

1)
Координаты
y
точек 1, 2,
3, 4,
5, 6 (рис.
4.4, а) и вершины – точки
s
– переносим с помощью линий связи с
горизонтальной проекции на профильную
проекцию.

2)
Координаты z
основания и вершины пирамиды –
точки s’
– переносим
с помощью линии связи с фронтальной
проекции на профильную проекцию.

3)
Чертим профильные проекции основания
пирамиды отрезок 2”–
6”
и вершины – точку s”.

4)
Строим профильные
проекции ребер пирамиды –
соеди­няем
точку s”
с точками
2”(3”),
1′‘(4”),
6”(5”).

а)

б)

Рисунок
4.4 Комплексный чертеж и изометрия
шестигранной пирамиды

Построение
проекций точек на поверхности пирамиды:

На
рисунке 4.4, а фронтальная проекция
точки А
– точка
а‘–
находится на ребре
s’-1‘, поэтому
для построения горизонтальной проекции
– точки а
– надо опустить линию связи из точки
а‘
на
горизонтальную проекцию этого ребра –
отрезок s-1.
Чтобы
построить профильную проекцию – точку
а”
– надо из точки
а‘
провести
линию связи на профильную проекцию
ребра – отрезок
s‘‘-1‘‘.

Точка
В расположена
не на ребре, поэтому для построения ее
проекций надо сначала провести через
точку в‘
(она задана) отрезок, соединяющий вершину
с основанием (s’-f
‘).
Затем найти горизонтальную проекцию
этого отрезка (s-f
) и, опустив на него из точки а‘
линию
связи, построить точку а..
Профильная
проекция – точка
а”
– строится на пересечении линий связи,
проведенных из точек а
и
а‘.

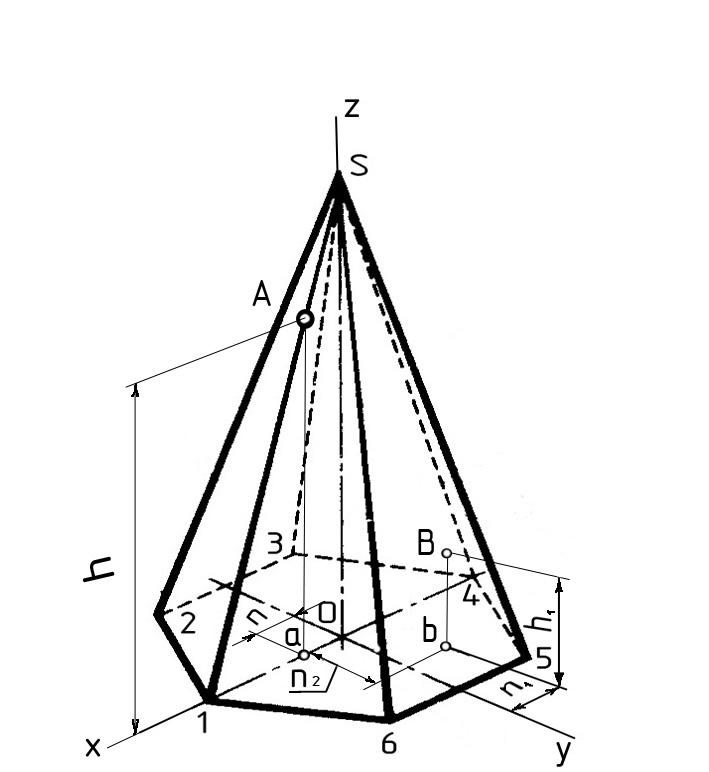
Построение
изометрии

В

А

пирамиды:

1)
На горизонтальной плоскости строим
изометрию многоугольника основания
пирамиды. На рисунке 4.4, б это шестиугольник.

2)
Из точки О
откладываем вверх высоту пирамиды и
по­лучаем точку s
–
вершину
пирамиды.

3)
Соединяем точку s
с точками 1,
2, 3, 4, 5, 6 и
получаем изометрическую проекцию
пирамиды.

Построение
изометрии точек на поверхности пирамиды:

Изометрию
точек А
и В
строим по их координатам, взятым из
комплексного
чертежа (рис. 4.4, б).

1)
От точки О
отложим на оси х
расстояние n
(координата
y
точки А,
взятая с комплексного чертежа, рис.
3.5), получим точку
а.

2)
От точки
а
отложим
вверх высоту h
(координата z
точки А,
взятая также с комплексного чертежа,
рис. 3.5) и получим
точку А.

3)
От точки О
отложим на оси х
расстояние n₁,
а на оси у
расстояние n₂,
взятые с комплексного чертежа, рис. 3.5,
получим точку
в.

4)
От точки
в
отложим вверх высоту h₁
и получим
точку В.

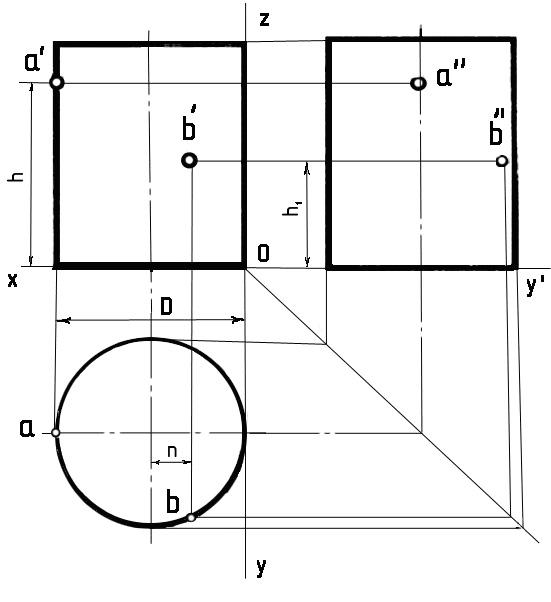
4.3 Цилиндр

Построение
фронтальной проекции цилиндра:

От
горизонтальной проекции проводим вверх
вертикальные линии связи и чертим
фронтальную проекцию нижнего основания
цилиндра –
горизонтальный отрезок, равный диаметру
D
(рис. 4.5).
От концов этого отрезка откладываем
вверх два вертикальных отрезка, равных
высоте цилиндра и чертим фронтальную
проекцию верхнего основания цилиндра
– еще один отрезок, равный диаметру
D.

Рис.
4.5 Проекции цилиндра Рис. 4.6 Изометрия
окружности Рис. 4.7 Изометрия цилиндра

Построение
профильной проекции цилиндра:

1)
Координаты
y
переносим на профильную проекцию с
помощью линий связи с горизонтальной
проекции.

2)
Координаты z
нижнего и верхнего оснований переносим
с помощью линий связи с фронтальной
проекции. Профильная проекция цилиндра
является повторением его фронтальной
проекции

Построение
проекций точек на поверхности цилиндра:

Горизонталь­ные
проекции точек А
и В
можно найти, проводя из данных точек
а’
и b‘
вертикальные
линии связи до их пересечения с окружностью
в точках а
и b.
Профильная
проекция точки А
– точка
а”
– строится на пересечении линий связи,
проведенных из точек а.
и
а‘.
Профильная проекция точки В
– точка
b”
– строится на пересечении линий связи,
проведенных из точек.
b
и
b‘.

Построение
изометрии

А

окружности:

Изометрическая
проекция окружности заменяется овалом.
У овала две оси – большая и малая. В
плоскости хОz
малой осью овала является ось Оу,
в плоскости
хОу
малой осью овала является ось Оz,
в плоскости
zОу
малой осью
овала является ось Ох.
Большие оси
овалов перпендикулярны малым осям.

1. Проводим
   малую ось овала (рис. 4.6).

2. Проводим
   перпендикулярно малой оси большую ось
   и обозначаем точку пересечения малой
   и большой оси – О₁
   – центр овала.

3. Через
   центр овала О₁
   проводим две осевые штрих-пунктирные
   линии, параллельные осям – Ох
   и Oz
   для плоскости хОz;
   Оz
   и Оу
   для плоскости
   zОу;
   Ох
   и Оу
   для плоскости хОу.

4. Из
   центра О₁
   проводим
   вспомогательную окружность радиусом,
   равным радиусу изображаемой окружности.

5. Из
   точек 1
   и 2 –
   проводим
   большие дуги овала радиусом 1А
   = 1В = 2С = 2D.
   

6. Из
   точек 1
   или 2
   проводим отрезки 1А
   и 1В
   или 2С
   и 2D
   и получаем на большой оси овала точки
   3 и 4. (рис. 4.4, плоскость z
   О у).

7. Из
   точек 3
   и 4
   проводим
   малые дуги радиусом 3А
   = 3C
   = 4В = 4D.

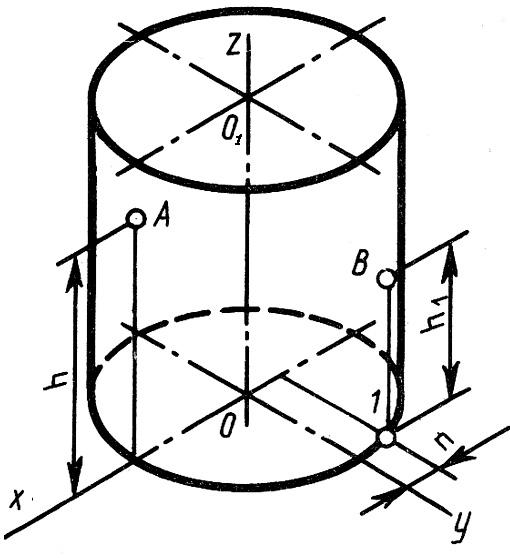
Построение
изометрии цилиндра:

1)
Строим овал – изометрию нижнего основания
в горизонтальной плоскости (рис 4.7).

2)
Из точки О
поднимаем высоту цилиндра и получаем
точку О₁,
относительно которой строим второй
такой же овал – изометрию верхнего
основания.

3)
Соединяем два основания образующими
вертикальными линиями.

Построение
изометрии точек на поверхности цилиндра:

Изометрию
точек А
и В
строим по их координатам, взятым из
комплексного
чертежа (рис. 4.7).

1)
От точки пересечения оси х
с овалом нижнего основания откладываем
вверх расстояние h
(координата z
точки А),
получаем точку А.

2)
Проводим прямую, параллельную оси у
на расстоянии n
от нее, получаем точку 1.

3)
От точки 1 откладываем вверх расстояние
h₁
(координата z
точки В)
получаем точку В.
(Расстояния
n,
h,
h₁
взяты
с комплексного чертежа).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра.
Ребра, пересекаясь, образуют вершины.
Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Упражнение

Дана пирамида, основание которой  параллельно π₁. Основание представляет собой некоторый треугольник.

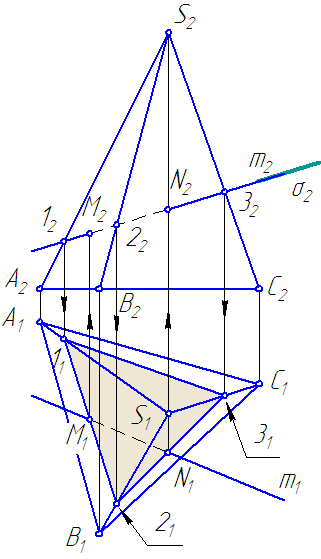
S – вершина пирамиды (Рисунок 6.1).

Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

Решение

1.  

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции  необходимо выполнять при помощи пропорционального деления отрезка.

1. В сечении находим точки M и N принадлежащие прямой m.
2. Определяем видимость прямой m.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

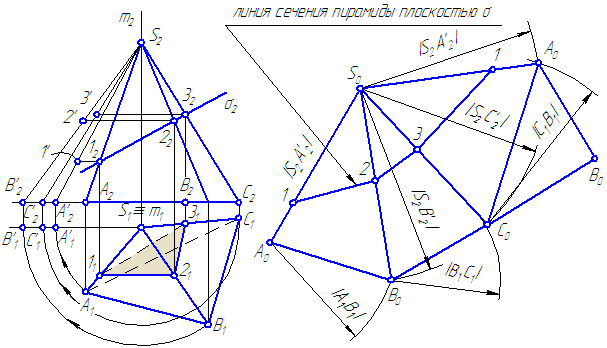
Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки overline{1},overline{2},overline{3}, проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Упражнение

Дана призма, основания которой параллельны плоскости проекций π₁.

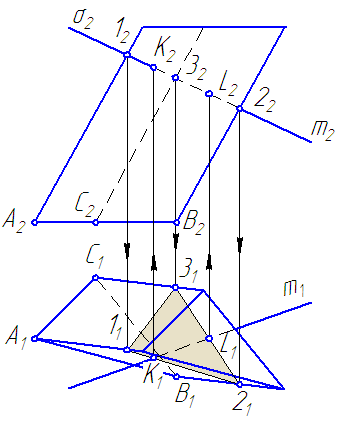
Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы

Порядок построения:

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
3. В сечении находим точки K и L принадлежащие прямой m.
4. Определяем видимость прямой m. Если грань АВ на π₂ видна, то точка К на π₂ видима, грань ВС невидима, следовательно, точка Lневидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно π₁, а ребра параллельны π₂.

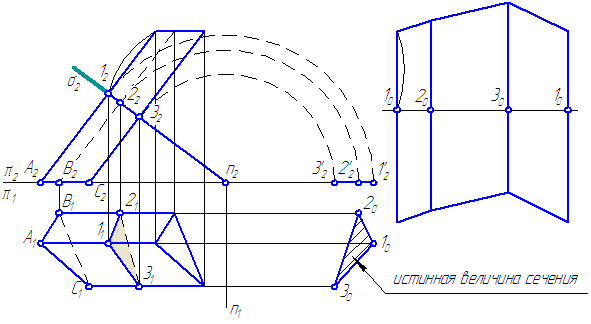
Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

Рисунок 6.4 – Построение развёртки призмы
Порядок построения:

1.  

1. Найдем истинную величину сечения – (1₀2₀3₀), для чего повернём сечение (123) вокруг оси n⊥π₂, (можно ввести ДПП π₃//σ).
2. Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
   /1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

1. Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на π₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

6.3. Взаимное пересечение многогранников

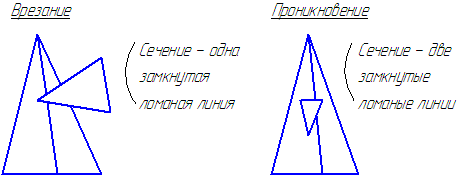
В результате пересечения многогранников получим ломаную линию.

Возможны два случая пересечения многогранников (Рисунок 6.5):

Рисунок 6.5 – Варианты пересечения многогранников

Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.

Звенья ломаной – линии пересечения граней.

Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.

Построенные точки соединить.

Упражнение

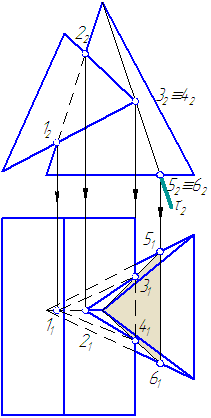
Построить линии пересечения призмы с пирамидой (Рисунок 6.6).

Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение

1.  

1. Находим на π₂ проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 1₂ и 2₂). Находим их горизонтальные проекции.
2. Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 3₂ и 4₂), для чего используем вспомогательную плоскость τ⊥π₂.
3. Полученные на π₁ точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 1₁-3₁, 1₁-2₁, 1₁-4₁ невидимы. Получили замкнутую линию пересечения пирамиды с призмой.

Упражнение

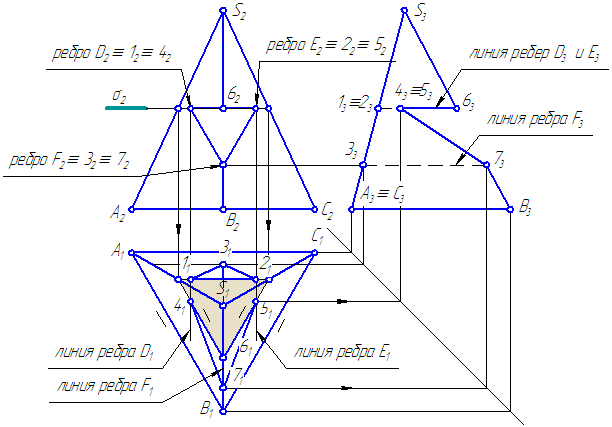
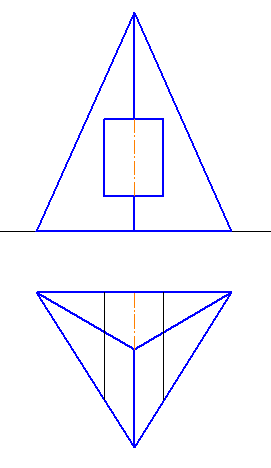
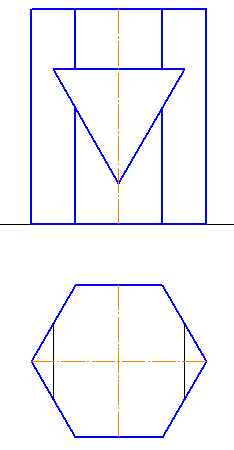
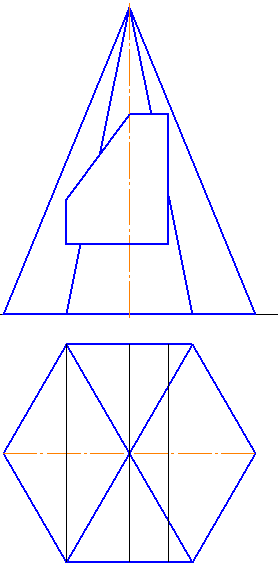
остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).

1. По двум проекциям построить третью;
2. На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
3. Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
4. Построить развёртку пирамиды с нанесением линии пересечения.

Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение:

1. Проводим линии рёбер призмы на всех проекциях.
2. Введём плоскость σ⊥π₂, σ//π₁:

• σ//АВС – основанию пирамиды;
• σ пересекает пирамиду ’ сечение подобно ΔА₁В₁С₁.

Это сечение пересекается:

— с ребром D в двух точках 1 и 4;

— с ребром Е в двух точках 2 и 5.

Грань D₂E₂∩S₂B₂ =6₂.

Ребро F₂∩S₂B₂ =7₂.

Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.

Построение развертки рассмотрено ранее.

6.4. Задачи для самостоятельной работы

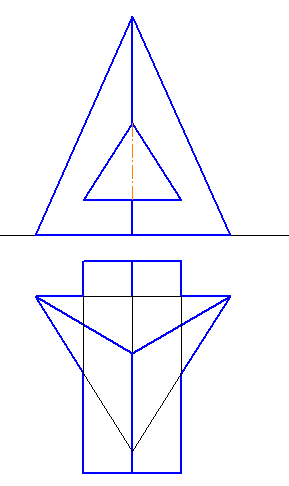
1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).

Рисунок 6.8

Рисунок 6.9

Рисунок 6.10

Рисунок 6.11

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.