Как найти вершину равнобедренного треугольника в пирамиде - Сайт, где вы сможете решить свои вопросы

Задача.
В основании пирамиды лежит равнобедренный треугольник с боковой стороной b и углом при основании β. все боковые грани образуют с основанием угол φ.

Решение.
Поскольку в основании пирамиды лежит равнобедренный треугольник, то для нахождения площади равнобедренного треугольника, воспользуемся приведенными в соответствующем уроке формулами.

При желании можно разбить треугольник ABC на два прямоугольных треугольника AKB и AKC. Но в результате формулы будут все равно тождественны. Действительно,

AK = AB sin ß = b sin β
BK = AB cos β = b cos β
S_ABK = AK * BK / 2 = b 2 sin β cos β / 2

откуда
S_ABС = 2S_ABK = b 2 sin β cos β
(примем за искомую площадь основания, далее справочно приведем к той же формуле, которая указана по ссылке выше)

Если воспользоваться основными тригонометрическими тождествами, то
b 2 sin β cos β = 1/2 b 2 sin 2β = 1/2 b 2 sin 2β
или как по основной формуле (площади равнобедренного треугольника)
1/2 b 2 sin 2β = 1/2 b 2 sin (180 – α) = 1/2 b 2 sin α

Теперь найдем площадь боковой поверхности пирамиды.
Сначала найдем высоту боковых граней, прилежащих к равным сторонам равнобедренного треугольника, лежащего в основании пирамиды. При этом учтем, что высота пирамиды проецируется в точку О основания, которая одновременно является центром вписанной окружности. Вместе с радиусом вписанной окружности, высота боковой грани образует прямоугольный треугольник. Откуда высота боковой грани пирамиды равна:
h = r / sin φ

Учитывая, что BC = 2BK, то BC = 2b cos β
откуда
p = ( b + b + 2b cos β ) / 2
p = ( 2b + 2b cos β ) / 2
p = 2b ( 1 + cos β ) / 2
p = b ( 1 + cos β )

Таким образом, радиус вписанной окружности в основание пирамиды будет равен
r = S / p
r = b 2 sin β cos β / b ( 1 + cos β ) = b sin β cos β / ( 1 + cos β )

Теперь определим высоту боковых граней пирамиды. Зная, что
l / r = cos φ, то
l = r cos φ

Тогда площадь грани пирамиды, прилегающей к равным сторонам основания (а в основании пирамиды у нас лежит равнобедренный треугольник) будет равна:
S1 = lb / 2
S1 = r cos φ * b / 2
S1 = b sin β cos β / ( 1 + cos β ) cos φ * b / 2
S1 = b 2 sin β cos β / ( 1 + cos β ) cos φ / 2
S1 = b 2 sin β cos β cos φ / ( 2 ( 1 + cos β ) )

Площадь боковой грани, прилегающей к основанию, равна:
S2 = BC * l / 2
S2 = 2b cos β * r cos φ / 2
S2 = b cos β * r cos φ
S2 = b cos β * b sin β cos β / ( 1 + cos β ) * cos φ
S2 = b 2 cos 2 β sin β cos φ / ( 1 + cos β )

Площадь боковой поверхности пирамиды равна:
Sбок = 2S1 + S2
Sбок = 2 * b 2 sin β cos β / ( 2 ( 1 + cos β ) cos φ ) + b 2 cos 2 β sin β cos φ / ( 1 + cos β )
Sбок = b 2 sin β cos β cos φ / ( 1 + cos β ) + b 2 cos 2 β sin β cos φ / ( 1 + cos β )
Sбок = ( b 2 sin β cos β cos φ + b 2 cos 2 β sin β cos φ ) / ( 1 + cos β )
Sбок = b 2 sin β cos β cos φ ( 1 + cos β ) / ( 1 + cos β )
Sбок = b 2 sin β cos β cos φ

Откуда площадь полной поверхности пирамиды с равнобедренным треугольником в основании составит:
S = Sбок + Sосн
S = b 2 sin β cos β cos φ + b 2 cos 2 β sin β cos φ / ( 1 + cos β )

Решение задач с использованием свойств различных видов пирамид

Разделы: Математика

Изучение пирамиды и ее элементов представляет широкие возможности для составления и решения задач на различных видах пирамид по следующим темам:

Пирамиды, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.
Пирамиды, в которых одна или две боковые грани перпендикулярны плоскости основания.
Пирамиды, в которых заданы расстояния между точками и элементами пирамиды.

Действующие учебники геометрии либо не содержат , либо содержат в недостаточном количестве задачи по этим темам.

Как показала практика, учащиеся с большим интересом принимают участие не только в решении данных задач, но и в их составлении. Они с удовольствием предлагают различные решения придуманных ими задач.

К этому учащихся необходимо подводить хорошо продуманной системой теоретических положений и практических упражнений.

Учебники Л.С. Атанасяна и др. “Геометрия 10–11” и А.В.Погорелова “Геометрия 10–11” содержат опорный теоретический материал по теме “Пирамида и ее элементы”.

В дополнение к нему можно рассмотреть следующие свойства часто встречающихся видов пирамид.

Теория.

Теоремы о пирамидах, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.

Если все боковые ребра пирамиды составляют с плоскостью основания равные углы, то:

а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды;

б) все боковые ребра пирамиды равны между собой.

Если основание высоты пирамиды совпадает с центром окружности, описанной около ее основания, то:

а) все боковые ребра пирамиды образуют с плоскостью основания равные углы;

в) все боковые ребра пирамиды равны между собой.

Если все боковые ребра пирамиды равны, то:

а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды;

б) все боковые ребра пирамиды составляют с плоскостью ее основания равные между собой углы.

Если высота пирамиды пересекает ее основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в ее основание.
Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.
Если у треугольной пирамиды все боковые ребра равны, а в основании лежит прямоугольный треугольник, то грань, содержащая его гипотенузу, перпендикулярна основанию. Основание высоты данной пирамиды является середина гипотенузы.

Теоремы о пирамидах, в которых одна или две боковые грани перпендикулярны плоскости основания.

Если пирамида содержит ровно одну боковую грань, которая перпендикулярна плоскости основания, то высота такой пирамиды лежит в этой боковой грани.
Если пирамида содержит две смежные боковые грани, перпендикулярные плоскости основания, то высотой такой пирамиды является боковое ребро, общее для этих граней.
Если в пирамиде две не смежные боковые грани перпендикулярны плоскости основания, то высота такой пирамиды лежит на прямой пересечения плоскостей этих граней.
Если боковое ребро пирамиды перпендикулярно основанию, то и боковые грани, содержащие это ребро, перпендикулярны основанию.
Если в четырехугольной пирамиде в основании ромб, и две смежные боковые грани перпендикулярны основанию, то боковые грани данной пирамиды – две пары равных треугольников.

Задачи для решения.

Задания из книги “Самостоятельные и контрольные работы по геометрии для 11-го класса” Ершовой А.П., Голобородько В.В.

Пирамиды, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.

Вариант А.

Основание пирамиды SABCD – прямоугольник АВСД со сторонами 6 и 8 см. Все боковые ребра пирамиды равны 13 см.

а) Опишите построение высоты пирамиды SO.

б) Докажите равенство отрезков АО, ВО, СО и ДО.

в) Обоснуйте положение точки О в прямоугольнике АВСД и найдите длину высоты SO.

Основание пирамиды – равнобедренный треугольник с основанием а и углом при вершине . Все двугранные углы при основании пирамиды равны .

а) Опишите построение высоты пирамиды, высот боковых граней и их проекций на плоскость основания. Обоснуйте двугранные углы при основании пирамиды.

б) обоснуйте положение основания высоты пирамиды в данном равнобедренном треугольнике.

в) Найдите высоту пирамиды.

Вариант Б.

Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при основании . Все боковые ребра пирамиды наклонены к плоскости основания под углом .

а) Обоснуйте положение основания высоты пирамиды в данном равнобедренном треугольнике.

б) Определите, при каких значениях ? высота пирамиды будет находиться вне пирамиды.

в) Найдите высоту пирамиды.

Основание пирамиды – ромб с большей диагональю d и острым углом . Все двугранные углы при основании пирамиды равны .

а) Обоснуйте данные двугранные углы и положение основания высоты пирамиды в ромбе.

б) Найдите высоту пирамиды.

в) Двумя способами – путем вычисления площадей боковых граней и с помощью теоремы об ортогональной проекции многоугольника – найдите боковую поверхность пирамиды. Сравните полученные результаты.

Вариант В.

Основание пирамиды – треугольник с углами и . Точка высоты пирамиды, удаленная от плоскости основания на расстояние d, равноудалена от концов бокового ребра. Все боковые ребра пирамиды наклонены к плоскости основания под углом .

а) Обоснуйте положение основания высоты пирамиды.

б) При каких условиях высота пирамиды лежит внутри пирамиды?

в) Найдите высоту пирамиды.

г) Найдите площадь основания пирамиды.

В основании пирамиды лежит равнобокая трапеция с острым углом . Высота пирамиды равна Н, а все двугранные углы при основании равны .

а) обоснуйте положение основания высоты пирамиды.

б) Найдите высоту трапеции, лежащей в основании пирамиды.

в) Не вычисляя площадей боковых граней, найдите боковую поверхность пирамиды.

Пирамиды, в которых одна или две боковые грани перпендикулярны плоскости основания.

Вариант А.

Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при вершине . Боковые грани пирамиды, содержащие стороны данного угла перпендикулярны плоскости основания, а третья боковая грань наклонена к ней под углом .

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте угол .

в) Найдите площадь третьей боковой грани.

г) Найдите боковую поверхность пирамиды.

Основание пирамиды – правильный треугольник со стороной а. Одна из боковых граней пирамиды перпендикулярна плоскости основания, а две другие – наклонены к ней под углом .

а) Из вершины пирамиды в плоскости грани, перпендикулярной основанию, проведите перпендикуляр к ребру основания и обоснуйте, почему он будет высотой пирамиды.

б) Обоснуйте углы наклона, равные .

в) Докажите, что основание высоты пирамиды равноудалено от двух сторон правильного треугольника, и обоснуйте положение основания высоты на стороне правильного треугольника.

г) Найдите боковую поверхность пирамиды.

Вариант Б.

Основание пирамиды – квадрат со стороной а, две смежные боковые грани пирамиды перпендикулярны плоскости основания, а две другие – наклонены к ней под углом .

а ) Обоснуйте положение высоты пирамиды.

б ) Обоснуйте углы, равные .

в ) Докажите, что боковые грани пирамиды попарно равны.

г ) Найдите боковую поверхность пирамиды.

Основание пирамиды – прямоугольный треугольник с гипотенузой с и острым углом . Боковая грань, содержащая катет, противолежащий данному углу , перпендикулярна плоскости основания, а две другие грани наклонены к ней под углом .

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты пирамиды.

в) Найдите высоту пирамиды.

г) Найдите боковую поверхность пирамиды.

Вариант В.

Основание пирамиды – ромб с тупым углом . Две боковые грани, содержащие стороны этого угла, перпендикулярны плоскости основания, а две другие – наклонены к ней под углом . Высота пирамиды равна Н.

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте углы, равные .

в) Найдите боковую поверхность пирамиды.

Основание пирамиды – прямоугольная трапеция с острым углом ? и прилежащей к нему боковой стороной . Боковая грань, содержащая большее основание трапеции, перпендикулярна плоскости основания, а три другие грани наклонены к ней под углом .

а ) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты пирамиды.

в) Найдите площадь основания пирамиды.

г) Найдите боковую поверхность пирамиды.

Пирамиды, в которых заданы расстояния между точками и элементами пирамиды.

Вариант А.

В правильной треугольной пирамиде боковое ребро наклонено к плоскости основания под углом . Расстояние от середины высоты пирамиды до середины бокового ребра равно d.

б ) Найдите площадь основания пирамиды.

В правильной четырехугольной пирамиде двугранный угол при основании равен . Расстояние от середины высоты пирамиды до ее апофемы равно l . Найдите боковую поверхность пирамиды.

Вариант Б.

В правильной четырехугольной пирамиде двугранный угол при основании равен . Расстояние от основания высоты пирамиды до середины апофемы равно l . Найдите полную поверхность пирамиды.
Основание пирамиды – равнобедренный треугольник с углом при вершине. Все боковые ребра пирамиды наклонены к плоскости основания под углом . Биссектриса этого угла пересекает высоту пирамиды в точке, удаленной от бокового ребра на расстояние d.

б ) Найдите площадь основания пирамиды.

Вариант В.

Основание пирамиды – равнобедренный треугольник с углом при основании . Все двугранные углы при основании пирамиды равны . Отрезок, соединяющий точки пересечения медиан боковых граней, содержащих боковые стороны треугольника, равен m. Найдите боковую поверхность пирамиды.
Основание пирамиды – прямоугольный треугольник с острым углом . Боковые грани пирамиды, содержащие катеты треугольника, перпендикулярны плоскости основания, а третья боковая грань наклонена к ней под углом . Расстояние от основания высоты пирамиды до этой грани равно l. Найдите боковую поверхность пирамиды.

Указанный в статье перечень задач может быть расширен Вами и вашими учениками.

[spoiler title=”источники:”]

http://profmeter.com.ua/communication/learning/course/course7/lesson408/

http://urok.1sept.ru/articles/526725

[/spoiler]

Источник

Как найти высоту в пирамиде: треугольной, четырехугольной, правильной

Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.

В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.

Содержание этой статьи:

Теория

Правильная пирамида

Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.

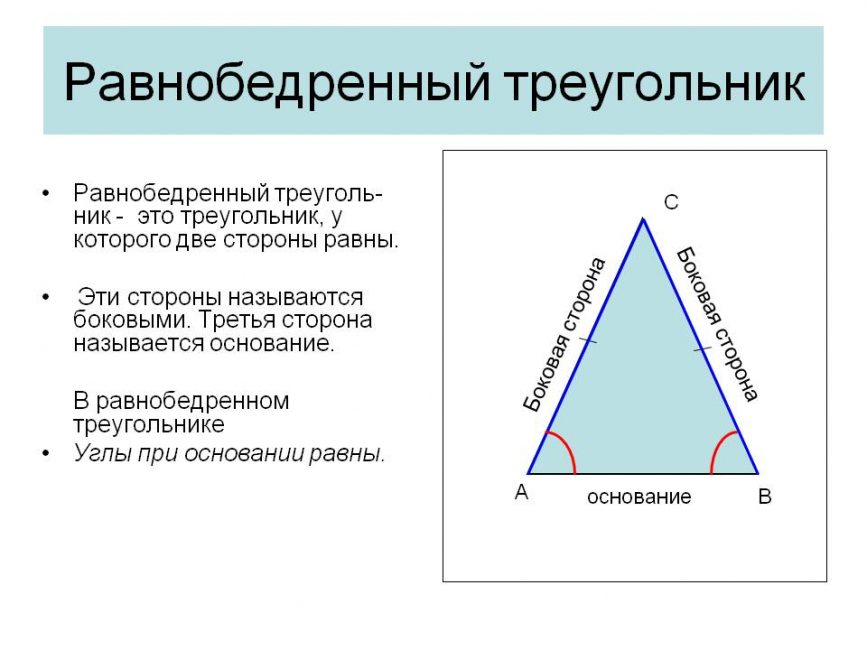
Для решения задач понадобится знать теоремы равнобедренного треугольника:

Основные свойства

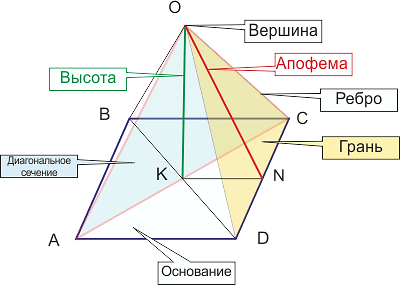
Четырехугольная пирамида

В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

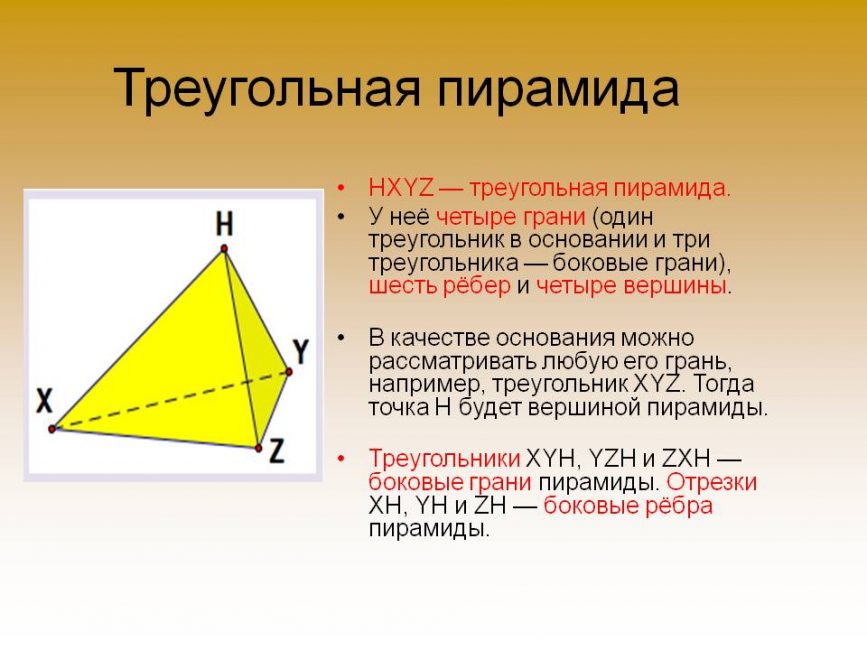
Треугольная пирамида

В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.

Необходимые знания для нахождения высоты

Когда теория закреплена, можно переходить к формулам.

Формулы для нахождения высоты

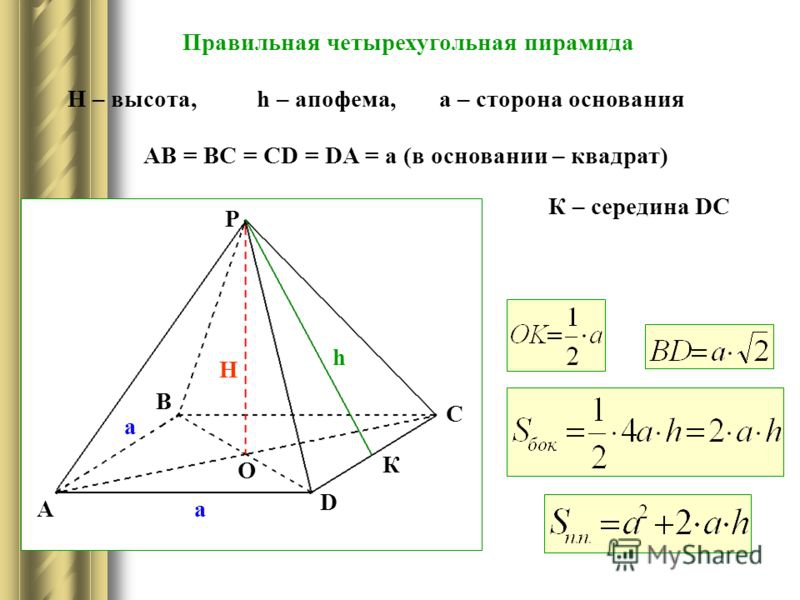
Запомните, что маленькая буква h – это апофема, а большая H – высота.

В некоторых задачах, высоту можно найти через объем:

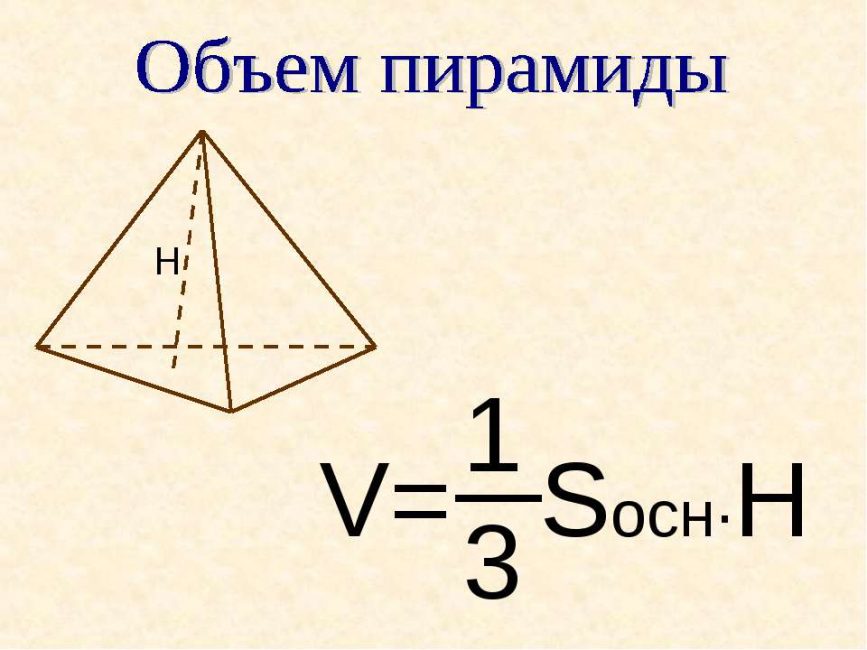
ВИДЕО: Примеры решения задач

Нахождение высоты в правильной пирамиде

Ниже будут представлены текстовые решения часто встречающихся задач.

Треугольная пирамида

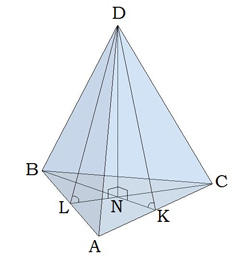
Задача 1

В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.

DN – высота, следовательно, объем фигуры можно выразить по формуле:

DN = 3V/S основания = 3*12/4 = 9

Задача 2

DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.

Пользуясь формулой объема, получается:

DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6

Четырехугольная пирамида

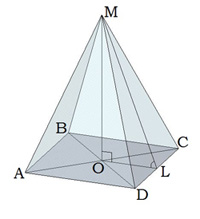
Задача 1

Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.

ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:

Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:

MO ² = √ML ² — √OL ² = √100- √36 = √64

Задача 2

Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.

Найдем OL

В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).

Пользуясь теоремой Пифагора, находим OL:

OL² = √OC² — √LC² = √100 – √36 = √64 = 8

Задача 3

Ищем MO

Пользуясь той же теоремой, находим высоту:

MO² = √ML² – √OL² = 100 – 64 = 36

Задача 4

Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.

Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.

Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема. Пользуясь формулами, найдем высоту.

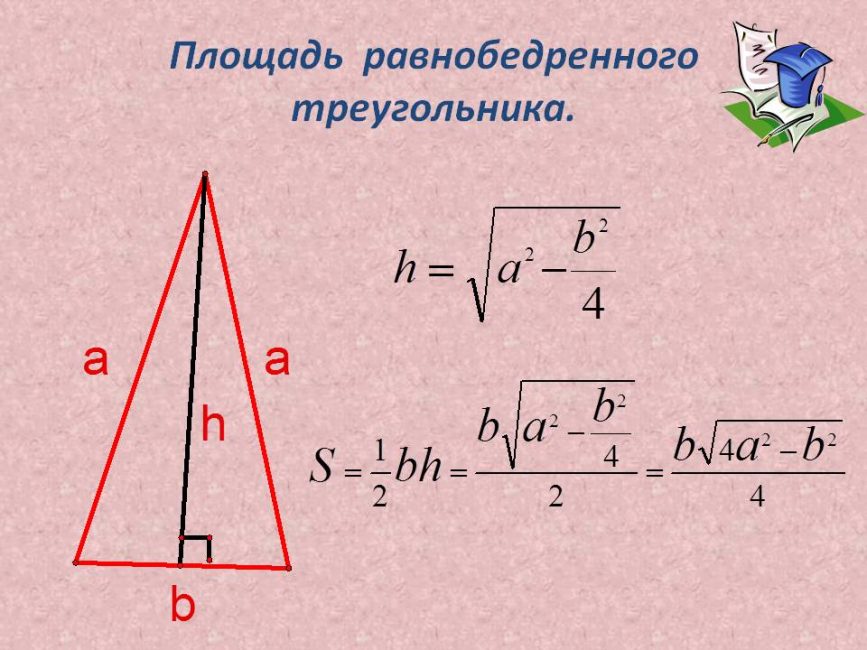
Площадь равнобедренного треугольника

Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.

MO = ML – OL = 18 – 6 = 12

Часто задаваемые вопросы

Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.

Зная определения и свойства, определить тип фигуры очень легко.

Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.

Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой. Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении.

Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.

Если выразить высоту через формулу объема, то получится следующее:

Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²

Типичные ошибки на ЕГЭ

Полезные советы

Если в задаче указан объем – ищите высоту через него.
Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.

Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи! Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!

Онлайн решение Пирамиды по координатам вершин

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Примечание: дробные числа записывайте
через точку, а не запятую.

источники:

http://mathhelpplanet.com/static.php?p=onlayn-resheniye-piramidy

http://dudom.ru/kompjutery/kak-najti-vysotu-piramidy-po-vektoram/

A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Как найти высоту пирамиды по векторам

Инструкция . Для решения подобных задач в онлайн режиме заполните координаты вершин, нажмите Далее . см. также по координатам треугольника найти.

Решение онлайн
Видеоинструкция
Оформление Word

Пример №1 . В пирамиде SABC : треугольник ABC – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S . Сделать чертеж.
Решение: Координаты векторов находим по формуле: X = x₂ – x₁; Y = y₂ – y₁; Z = z₂ – z₁
Так, для вектора AB, это будут координаты: X = 0-2; Y = 3-0; Z = 0-0, или AB(-2;3;0).
AC(-2;0;1); AD(-2;2;3); BC(0;-3;1); BD(0;-1;3); CD(0;2;2) .
Длину вектора находим по формуле:

Пример №2 . В тетраэдре ABCD вычислить:

объем тетраэдра ABCD;
высоту тетраэдра, опущенную из вершины D на грань ABC.

A(2, 3, -2), B(3, 1, 0), C(-2, 2, 1), D(6, 1, -1)

Ответ

Проверено экспертом

Даны вершины пирамиды A(3;-2;3)B(-1;0;2)C(-3;1;-1)D(-3;-3;1) .

Находим векторы АВ, АС и АД.

Вектор АВ = (-4; 2; -1 ), модуль равен √(16+4+1) = √21 ≈ 4,58258.

Определяем векторное произведение АВ х АС.

-6 3 -4 | -6 3 = -8i + 6j – 12k – 16j + 3i + 12k = -5i – 10j = (-5; -10; 0).

Далее находим смешанное произведение (АВ х АС) х АД.

(АВ х АС) = (-5; -10; 0),

(АВ х АС) х АД = 30 + 10 + 0 = 40.

Объем пирамиды равен (1/6) этого произведения:

V = (1/6)*40 = (20/3) куб.ед.

Высота h пирамиды ABCD, опущенная из вершины D на плоскость основания ABC, равна: h = 3V/S(ABC).

Площадь основания АВС равна половине модуля векторного произведения АВ х АС.

S(ABC) = (1/2)*√((-5)² + (-10)² + 0²) = (1/2)√(25 + 100) = (5/2)√5 кв.ед.

h = (3*20/3)/((5/2)√5) = 8/√5 = 8√5/5 ≈ 3,5777.

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )

Источник

Изучение пирамиды и ее элементов представляет
широкие возможности для составления и решения
задач на различных видах пирамид по следующим
темам:

Пирамиды, в которых основание высоты является
центром описанной или вписанной окружности
основания пирамиды.
Пирамиды, в которых одна или две боковые грани
перпендикулярны плоскости основания.
Пирамиды, в которых заданы расстояния между
точками и элементами пирамиды.

Действующие учебники геометрии либо не
содержат , либо содержат в недостаточном
количестве задачи по этим темам.

Как показала практика, учащиеся с большим
интересом принимают участие не только в решении
данных задач, но и в их составлении. Они с
удовольствием предлагают различные решения
придуманных ими задач.

К этому учащихся необходимо подводить хорошо
продуманной системой теоретических положений и
практических упражнений.

Учебники Л.С. Атанасяна и др. “Геометрия 10–11” и
А.В.Погорелова “Геометрия 10–11” содержат
опорный теоретический материал по теме
“Пирамида и ее элементы”.

В дополнение к нему можно рассмотреть
следующие свойства часто встречающихся видов
пирамид.

Справочный материал.

Теория.

Теоремы о пирамидах, в которых основание высоты
является центром описанной или вписанной
окружности основания пирамиды.

Если все боковые ребра пирамиды составляют с
плоскостью основания равные углы, то:

а) основание высоты пирамиды совпадает с
центром окружности, описанной около основания
пирамиды;

б) все боковые ребра пирамиды равны между собой.

Если основание высоты пирамиды совпадает с
центром окружности, описанной около ее
основания, то:

а) все боковые ребра пирамиды образуют с
плоскостью основания равные углы;

в) все боковые ребра пирамиды равны между собой.

Если все боковые ребра пирамиды равны, то:

а) основание высоты пирамиды совпадает с
центром окружности, описанной около основания
пирамиды;

б) все боковые ребра пирамиды составляют с
плоскостью ее основания равные между собой углы.

Если высота пирамиды пересекает ее основание и
все боковые грани пирамиды образуют с плоскостью
основания равные двугранные углы, то основание
высоты пирамиды совпадает с центром окружности,
вписанной в ее основание.
Если вершина пирамиды проектируется в центр
окружности, вписанной в основание пирамиды, то
боковые грани пирамиды образуют с плоскостью
основания равные двугранные углы.
Если у треугольной пирамиды все боковые ребра
равны, а в основании лежит прямоугольный
треугольник, то грань, содержащая его гипотенузу,
перпендикулярна основанию. Основание высоты
данной пирамиды является середина гипотенузы.

Теоремы о пирамидах, в которых одна или две
боковые грани перпендикулярны плоскости
основания.

Если пирамида содержит ровно одну боковую
грань, которая перпендикулярна плоскости
основания, то высота такой пирамиды лежит в этой
боковой грани.
Если пирамида содержит две смежные боковые
грани, перпендикулярные плоскости основания, то
высотой такой пирамиды является боковое ребро,
общее для этих граней.
Если в пирамиде две не смежные боковые грани
перпендикулярны плоскости основания, то высота
такой пирамиды лежит на прямой пересечения
плоскостей этих граней.
Если боковое ребро пирамиды перпендикулярно
основанию, то и боковые грани, содержащие это
ребро, перпендикулярны основанию.
Если в четырехугольной пирамиде в основании
ромб, и две смежные боковые грани
перпендикулярны основанию, то боковые грани
данной пирамиды – две пары равных треугольников.

Задачи для решения.

Задания из книги “Самостоятельные и
контрольные работы по геометрии для 11-го класса”
Ершовой А.П., Голобородько В.В.

Пирамиды, в которых основание высоты является
центром описанной или вписанной окружности
основания пирамиды.

Вариант А.

Основание пирамиды SABCD – прямоугольник АВСД со
сторонами 6 и 8 см. Все боковые ребра пирамиды
равны 13 см.

а) Опишите построение высоты пирамиды SO.

б) Докажите равенство отрезков АО, ВО, СО и ДО.

в) Обоснуйте положение точки О в прямоугольнике
АВСД и найдите длину высоты SO.

Основание пирамиды – равнобедренный
треугольник с основанием а и углом при вершине . Все
двугранные углы при основании пирамиды равны .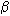

а) Опишите построение высоты пирамиды, высот
боковых граней и их проекций на плоскость
основания. Обоснуйте двугранные углы при
основании пирамиды.

б) обоснуйте положение основания высоты
пирамиды в данном равнобедренном треугольнике.

в) Найдите высоту пирамиды.

Вариант Б.

Основание пирамиды – равнобедренный
треугольник с боковой стороной b и углом при
основании .
Все боковые ребра пирамиды наклонены к плоскости
основания под углом .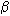

а) Обоснуйте положение основания высоты
пирамиды в данном равнобедренном треугольнике.

б) Определите, при каких значениях ? высота
пирамиды будет находиться вне пирамиды.

в) Найдите высоту пирамиды.

Основание пирамиды – ромб с большей диагональю
d и острым углом . Все двугранные углы при основании
пирамиды равны .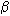

а) Обоснуйте данные двугранные углы и положение
основания высоты пирамиды в ромбе.

б) Найдите высоту пирамиды.

в) Двумя способами – путем вычисления площадей
боковых граней и с помощью теоремы об
ортогональной проекции многоугольника –
найдите боковую поверхность пирамиды. Сравните
полученные результаты.

Вариант В.

Основание пирамиды – треугольник с углами и 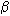. Точка высоты
пирамиды, удаленная от плоскости основания на
расстояние d, равноудалена от концов бокового
ребра. Все боковые ребра пирамиды наклонены к
плоскости основания под углом .

а) Обоснуйте положение основания высоты
пирамиды.

б) При каких условиях высота пирамиды лежит
внутри пирамиды?

в) Найдите высоту пирамиды.

г) Найдите площадь основания пирамиды.

В основании пирамиды лежит равнобокая трапеция
с острым углом . Высота пирамиды равна Н, а все
двугранные углы при основании равны .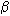

а) обоснуйте положение основания высоты
пирамиды.

б) Найдите высоту трапеции, лежащей в основании
пирамиды.

в) Не вычисляя площадей боковых граней, найдите
боковую поверхность пирамиды.

Пирамиды, в которых одна или две боковые грани
перпендикулярны плоскости основания.

Вариант А.

Основание пирамиды – равнобедренный
треугольник с боковой стороной b и углом при
вершине .
Боковые грани пирамиды, содержащие стороны
данного угла перпендикулярны плоскости
основания, а третья боковая грань наклонена к ней
под углом .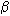

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте угол .

в) Найдите площадь третьей боковой грани.

г) Найдите боковую поверхность пирамиды.

Основание пирамиды – правильный треугольник со
стороной а. Одна из боковых граней пирамиды
перпендикулярна плоскости основания, а две
другие – наклонены к ней под углом .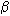

а) Из вершины пирамиды в плоскости грани,
перпендикулярной основанию, проведите
перпендикуляр к ребру основания и обоснуйте,
почему он будет высотой пирамиды.

б) Обоснуйте углы наклона, равные .

в) Докажите, что основание высоты пирамиды
равноудалено от двух сторон правильного
треугольника, и обоснуйте положение основания
высоты на стороне правильного треугольника.

г) Найдите боковую поверхность пирамиды.

Вариант Б.

Основание пирамиды – квадрат со стороной а, две
смежные боковые грани пирамиды перпендикулярны
плоскости основания, а две другие – наклонены к
ней под углом .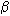

а ) Обоснуйте положение высоты пирамиды.

б ) Обоснуйте углы, равные .

в ) Докажите, что боковые грани пирамиды попарно
равны.

г ) Найдите боковую поверхность пирамиды.

Основание пирамиды – прямоугольный
треугольник с гипотенузой с и острым углом . Боковая грань,
содержащая катет, противолежащий данному углу ,
перпендикулярна плоскости основания, а две
другие грани наклонены к ней под углом .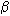

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты
пирамиды.

в) Найдите высоту пирамиды.

г) Найдите боковую поверхность пирамиды.

Вариант В.

Основание пирамиды – ромб с тупым углом . Две боковые
грани, содержащие стороны этого угла,
перпендикулярны плоскости основания, а две
другие – наклонены к ней под углом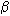 . Высота пирамиды равна Н.

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте углы, равные .

в) Найдите боковую поверхность пирамиды.

Основание пирамиды – прямоугольная трапеция с
острым углом ? и прилежащей к нему боковой
стороной .
Боковая грань, содержащая большее основание
трапеции, перпендикулярна плоскости основания, а
три другие грани наклонены к ней под углом .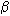

а ) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты
пирамиды.

в) Найдите площадь основания пирамиды.

г) Найдите боковую поверхность пирамиды.

Пирамиды, в которых заданы расстояния между
точками и элементами пирамиды.

Вариант А.

В правильной треугольной пирамиде боковое
ребро наклонено к плоскости основания под углом . Расстояние от
середины высоты пирамиды до середины бокового
ребра равно d.

а ) Найдите высоту пирамиды.

б ) Найдите площадь основания пирамиды.

В правильной четырехугольной пирамиде
двугранный угол при основании равен . Расстояние от
середины высоты пирамиды до ее апофемы равно l .
Найдите боковую поверхность пирамиды.

Вариант Б.

В правильной четырехугольной пирамиде
двугранный угол при основании равен . Расстояние от
основания высоты пирамиды до середины апофемы
равно l . Найдите полную поверхность пирамиды.
Основание пирамиды – равнобедренный
треугольник с углом при вершине. Все боковые ребра
пирамиды наклонены к плоскости основания под
углом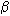 . Биссектриса этого
угла пересекает высоту пирамиды в точке,
удаленной от бокового ребра на расстояние d.

а ) Найдите высоту пирамиды.

б ) Найдите площадь основания пирамиды.

Вариант В.

Основание пирамиды – равнобедренный
треугольник с углом при основании . Все двугранные углы
при основании пирамиды равны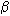 . Отрезок, соединяющий точки пересечения
медиан боковых граней, содержащих боковые
стороны треугольника, равен m. Найдите боковую
поверхность пирамиды.
Основание пирамиды – прямоугольный
треугольник с острым углом .
Боковые грани пирамиды, содержащие катеты
треугольника, перпендикулярны плоскости
основания, а третья боковая грань наклонена к ней
под углом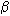 . Расстояние от
основания высоты пирамиды до этой грани равно l.
Найдите боковую поверхность пирамиды.

Указанный в статье перечень задач может быть
расширен Вами и вашими учениками.

Желаем успеха!

Источник

Высота правильной треугольной пирамиды.

Основание правильной пирамиды представляет собой правильный многоугольник. Так как мы имеем дело с треугольной пирамидой, то её основанием будет равносторонний треугольник.

Чтобы найти высоту пирамиды SO, достаточно вспомнить, что:

1) AO = BO = CO = R = a√3 / 3. (св-во равностороннего треугольника).

2) SB = AB. (боковое ребро равно длине стороны основания).

По теореме Пифагора высота SO равна:

SO = √(SB² – OB²) = √(a² – a²/3) = √(a²(1 – 1/3)) = √(a² * (2/3) = a√(2/3).

Итак, высота правильной треугольной пирамиды (H) равна произведению длины ребра (a) на корень из 2/3:

Высоту пирамиды также можно найти из формулы объёма:

V = 1 / 3 Sосн * H.

Так как основание пирамиды – это равносторонний треугольник, то Sосн = a² * √3 / 4.

Отсюда V = a² * √3 * H / 12 = a² * H / 4√3.

Остаётся выразить высоту:

V * 4√3 = a² * H.

H = V * (4√3 / a²).

Высота правильной треугольной пирамиды (H) равна дроби – в числителе произведение объёма пирамиды (V) на 4√3, в знаменателе – квадрат ребра (a).

Если же в условии задачи уже известна площадь основания, то высоту найти ещё проще:

H = 3 * V / Sосн.

Пример

Сторона основания правильной треугольной пирамиды равна 4 см, объём равен 10√3.

Нужно найти высоту пирамиды.

Воспользуемся вышеприведённой формулой:

H = V * (4√3 / a²) = 10√3 * 4√3 / 16 = 120 / 16 = 7,5 см.

Источник

Главная » Образование » Школа » Как найти высоту в пирамиде: треугольной, четырехугольной, правильной

Как найти высоту в пирамиде: треугольной, четырехугольной, правильной

35881 Просмотров 0

Высота основания в пирамиде – тема, на которую часто попадаются задачи на экзаменах и в старших классах. Решать такие задачи просто, если понимать принцип решения и знать формулы.

В нашей статье, вы без лишних формул и теории сможете понять, как решать задачи на нахождение высоты в пирамиде. Обратите внимание, что в разделе «формулы» отсутствуют все формулы правильной пирамиды, так как наша цель – научить решать задачи на нахождение высоты.

Содержание этой статьи:

Теория
Часто задаваемые вопросы
Типичные ошибки на ЕГЭ
Полезные советы

Теория

Это интересно: Как оформлять реферат в школе по ГОСТу + образец титульного листа 2019

Правильная пирамида

Правильная пирамида имеет в основании многоугольник, а высота проходит через центр основания. Боковые грани – равнобедренные треугольники. Напомним, что в равнобедренном треугольнике две стороны равны, следовательно, боковые ребра в правильной пирамиде тоже равны. Многоугольник в основании правильный, т.е. его стороны равны.

Для решения задач понадобится знать теоремы равнобедренного треугольника:

Равнобедренный треугольник

Основные свойства

1В правильную пирамиду можно вписать и описать сферу, так как при пересечении диагоналей, основание делится на равные части. Сферу нельзя вписать в любую фигуру.

2Площадь боковой поверхности – половина произведения периметра основания на апофему. Апофема есть на каждой грани, а не только на одной.

Пирамида

Четырехугольная пирамида

В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.

Четырехугольная пирамида

Треугольная пирамида

Читайте также: Как решать задачи по математике 5 класс

В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.

Треугольная пирамида

Необходимые знания для нахождения высоты

1Нужно понимать, что из себя представляют треугольники: свойства, формулы, определение. Большинство задач решается через треугольники (боковые грани).

2Понимать, что такое сечение и как оно влияет на геометрическую фигуру.

3Что такое правильные многоугольники: виды, свойства, формулы.

Когда теория закреплена, можно переходить к формулам.

Формулы для нахождения высоты

Формулы

Запомните, что маленькая буква h – это апофема, а большая H – высота.

В некоторых задачах, высоту можно найти через объем:

Объем пирамиды

ВИДЕО: Примеры решения задач

Нахождение высоты в правильной пирамиде

Ниже будут представлены текстовые решения часто встречающихся задач.

Треугольная пирамида

Задача 1

DN – высота, следовательно, объем фигуры можно выразить по формуле:

DN = 3V/S основания = 3*12/4 = 9

Ответ: 9

Задача 2

DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.

Пользуясь формулой объема, получается:

DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6

Ответ: 6

Четырехугольная пирамида

Задача 1

Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.

ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:

OL = ½*12 = 6

Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:

MO ² = √ML ² — √OL ² = √100- √36 = √64

MO = 8

Задача 2

Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.

Найдем OL

Пользуясь теоремой Пифагора, находим OL:

OL² = √OC² — √LC² = √100 – √36 = √64 = 8

Задача 3

Ищем MO

Пользуясь той же теоремой, находим высоту:

MO² = √ML² – √OL² = 100 – 64 = 36

Ответ: 36

Задача 4

Площадь равнобедренного треугольника

36 = ½ * 4 *h

36 = 2h

H = 18

MO = ML – OL = 18 – 6 = 12

Ответ: 12

Часто задаваемые вопросы

1Как понять, что пирамида правильная, если в условии это не указано?

Зная определения и свойства, определить тип фигуры очень легко.

2Могут ли быть указаны в задании лишние данные?

3Обязательно ли оформлять высоту большой буквой H? Нужно ли выделять апофему?

4Как можно быстро изучить стереометрию?

4Как искать высоту, если известен объем?

Если выразить высоту через формулу объема, то получится следующее:

H = (3*V)/ S;

Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²

H = 3*70/30 = 7см

Типичные ошибки на ЕГЭ

Незнание темы

Когда человек не знает, где находится апофема и что для нее есть определенные формулы, задачу может и можно решить, но тогда необходимо выполнить в 2 раза большей действий.То же обстоит с теорией – если человек не знает свойства многоугольников, то и решить задание он не сможет. Для того, чтобы понимать геометрию, не нужно обладать особенными способностями. Даже при отсутствии способностей к математике, зная теорию, вы будете понимать геометрию.

Отсутствие проверки

Хотите потерять балл на ЕГЭ? – не перепроверяйте решения. Часто, задания решаются хаотично и на листе бумаге разные решения намешаны в кучу. Когда приходит время написать ответ, человек по невнимательности либо забывает выполнить последнее действие, либо вписывает не тот ответ.Решайте задачи по действиям, проставляйте пункты и делайте проверку ответа, каким бы он ни был.

Задачи под копирку

Решая сотни аналогичных задач, человек настолько привыкает, что теряет бдительность, игнорируя многие исходные данные. Придя на экзамен, в задании может быть вопрос с подвохом и человек ошибается в теме, которую он знал идеально. Помните, к каждой задаче нужен индивидуальный подход, как бы хорошо вы в ней не разбирались.

Запись

Структурируйте решения, прописывая каждое действие и каждый полученный вывод. Это необходимо для того, чтобы не запутаться. Решая задания хаотично, можно легко записать неправильное число, не тот ответ, подставить не те числа, и задача уже решена неверно. Обидно получать низкий балл из-за невнимательности.

Подсчеты в уме

На экзамене все нервничают и переживают, а потому зарабатывают баллы ниже, чем планировалось изначально. Когда человек нервничает, уровень концентрации и внимания резко снижается. Он может упустить что-то важное, не поставить запятую или запутаться в ходе размышлений.Считая примеры в столбик, вы обезопасите себя от глупых ошибок.

Незнание структуры экзамена

Очень обидные ошибки допускают люди, пересдающие ЕГЭ через несколько лет, либо обучающиеся в экстернате. Как правило, они плохо знакомы с процедурой заполнения бланков и внесения ответов.Заполнение бланков для части А и С – различно. Внимательно посмотрите, как необходимо их заполнять, так как неправильное внесение ответа (например, запятая и число в одной клетке) будет приравниваться к ошибке и ответ будет не засчитан.Также, если вы самостоятельно готовитесь к экзамену, учитесь рассчитывать время на каждое задание.

Поспешные решения

В случае, если ответ был записан с ошибкой, его можно внести в графе ниже, заменив неправильный ответ на правильный. Однако, клетки для внесения результатов ограничены в количестве, а заданий в общей сложности 19!Несколько раз перепроверьте ответы, прежде чем внести их в бланк ответов.

Незнание степеней числа

В теореме Пифагора будут использованы не только маленькие числа (до 10). В профильной математике, могут быть крупные числа, которые тяжело посчитать в столбик.Также, степени числа могут понадобиться для других заданий. Выучите значение чисел в квадрате и кубе от 1 до 20. Помните, что на профильном экзамене, пользовать методической таблицей нельзя!

Полезные советы

Если в задаче указан объем – ищите высоту через него.
Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.
Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.

6.5 Total Score

Чтобы успешно решить задачу для нахождения высоты пирамиды, достаточно знать теорию и формулы. Добавив к своим знаниям немного практики и внимательности, вы легко и быстро будете решать подобные задачи!
Если вы не согласны с рейтингом статьи, то просто поставьте свои оценки и аргументируйте их в комментариях. Ваше мнение очень важно для наших читателей. Спасибо!

Достоверность информации

8.5

Актуальность информации

7.5

ПЛЮСЫ

Благодаря доступной информации можно легко научиться решать задачи по геометрии

МИНУСЫ

Необходимы знания математики

Добавить отзыв

Источник

Решение задач с использованием свойств различных видов пирамид

Как найти высоту в пирамиде: треугольной, четырехугольной, правильной

Теория

Правильная пирамида

Основные свойства

Четырехугольная пирамида

Треугольная пирамида

Необходимые знания для нахождения высоты

Формулы для нахождения высоты

ВИДЕО: Примеры решения задач

Нахождение высоты в правильной пирамиде

Треугольная пирамида

Четырехугольная пирамида

Часто задаваемые вопросы

Типичные ошибки на ЕГЭ

Полезные советы

Онлайн решение Пирамиды по координатам вершин

Как найти высоту пирамиды по векторам

Ответ

Проверено экспертом

Высота правильной треугольной пирамиды.

Как найти высоту в пирамиде: треугольной, четырехугольной, правильной

Теория

Правильная пирамида

Основные свойства

Четырехугольная пирамида

Треугольная пирамида

Необходимые знания для нахождения высоты

Формулы для нахождения высоты

ВИДЕО: Примеры решения задач

Нахождение высоты в правильной пирамиде

Треугольная пирамида

Четырехугольная пирамида

Часто задаваемые вопросы

Типичные ошибки на ЕГЭ

Полезные советы

Вам также может понравиться

Как найти запрос в базе данных

Как составить калькуляцию на сборку

Ошибка 611 как исправить

Добавить комментарий Отменить ответ