поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
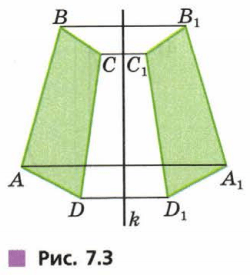
По рисунку 7.3 назовите: вершину, симметричную вершине A, вершине C; сторону, симметричную стороне BC, стороне DC; угол, симметричный углу ABC, углу CDA.

reshalka.com
ГДЗ учебник по математике 6 класс Дорофеев. 7.1 Вопросы к параграфу. Номер №2
Решение
![]() Получай решения и ответы с помощью нашего бота
Получай решения и ответы с помощью нашего бота
вершина
A
1
симметрична вершине A;
вершина
C
1
симметрична вершине C;
сторона
B
1
C
1
симметрична стороне BC;
сторона
D
1
C
1
симметрична стороне DC;
угол
A
1
B
1
C
1
симметричен углу ABC;
угол
C
1
D
1
A
1
симметричен углу CDA.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
-
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
-
прямая призма, все грани которой есть квадраты;
-
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
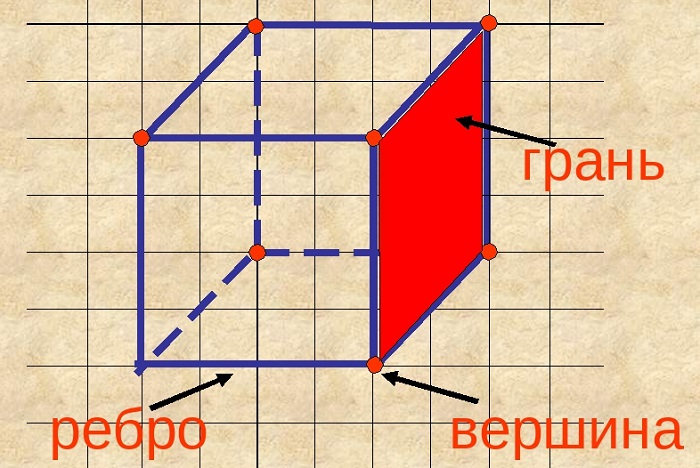
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
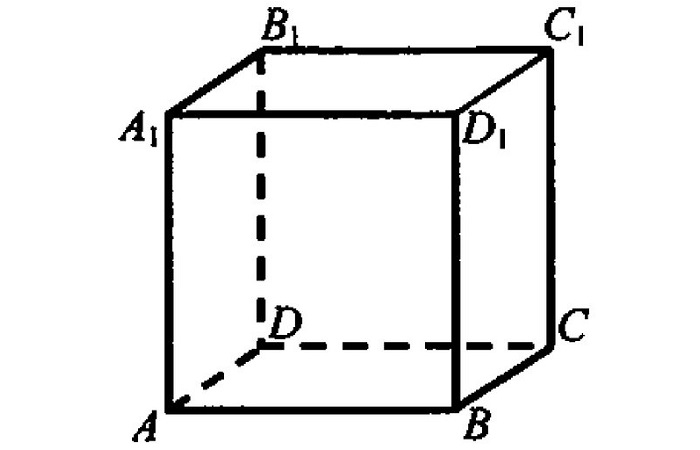
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
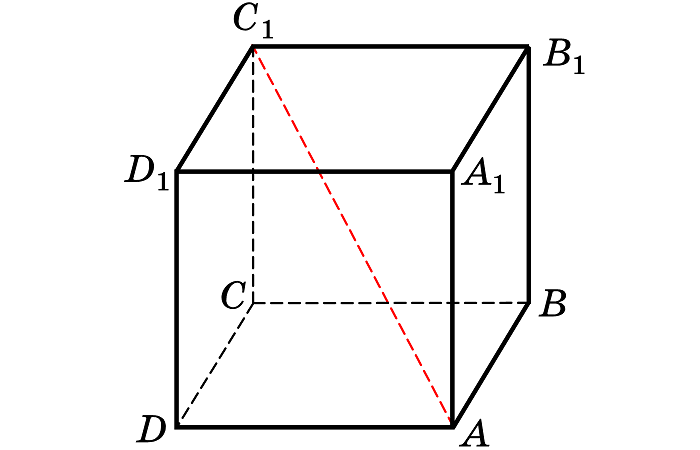
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
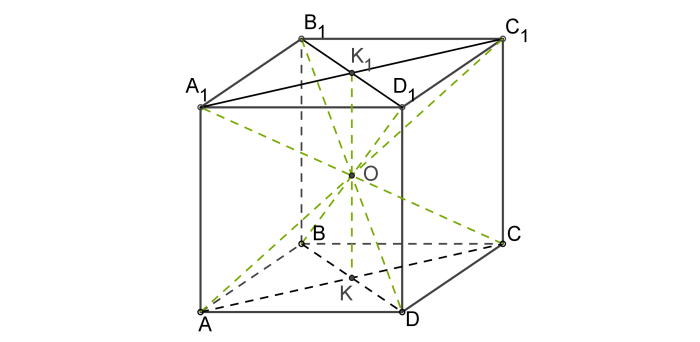
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
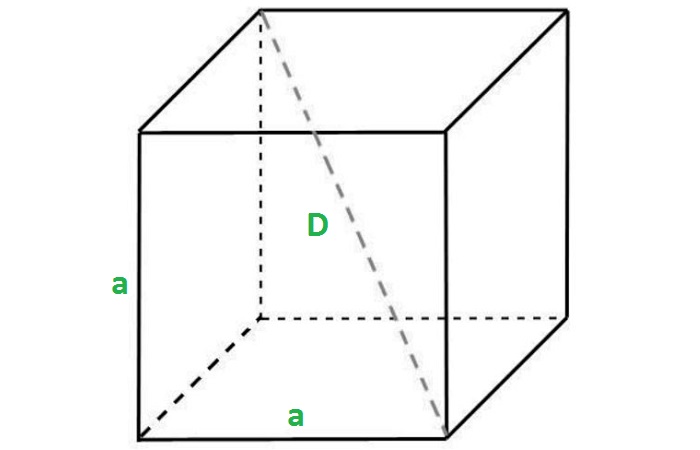
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
![]()
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба – одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
![]()
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
![]()
Периметр куба
Сумма длин всех рёбер равна:
![]()
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
![]()
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
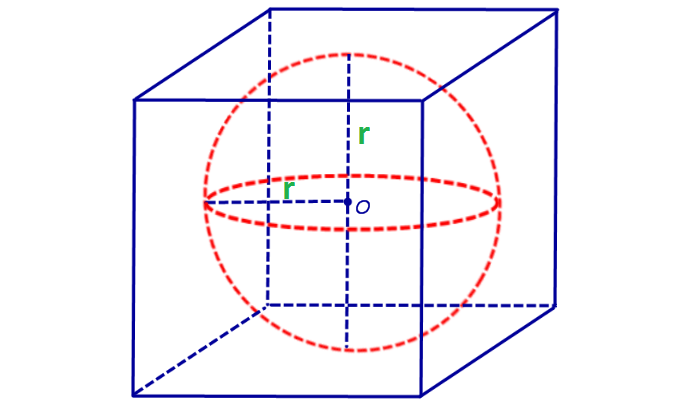
Радиус равен половине ребра:
![]()
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
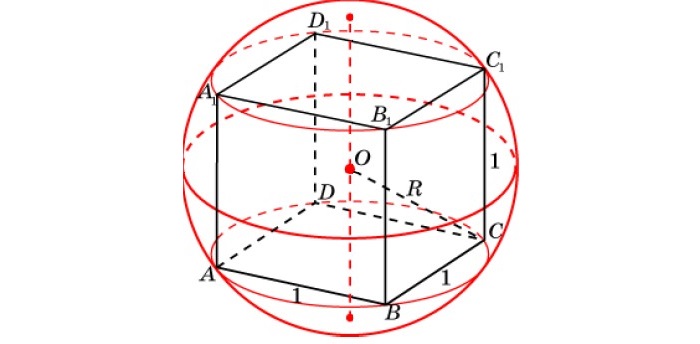
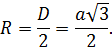
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
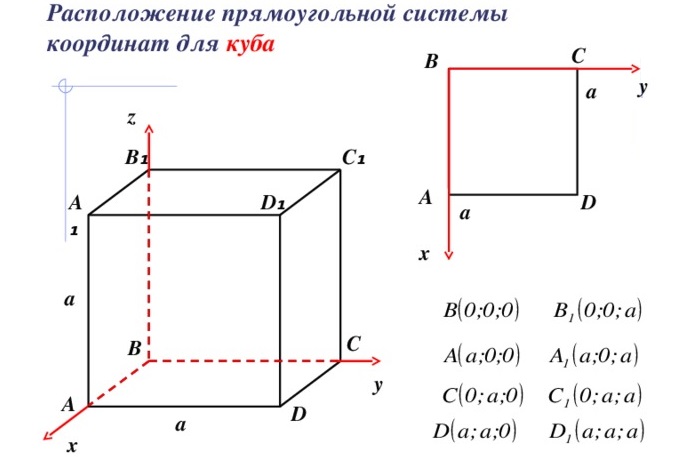
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
![]()
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
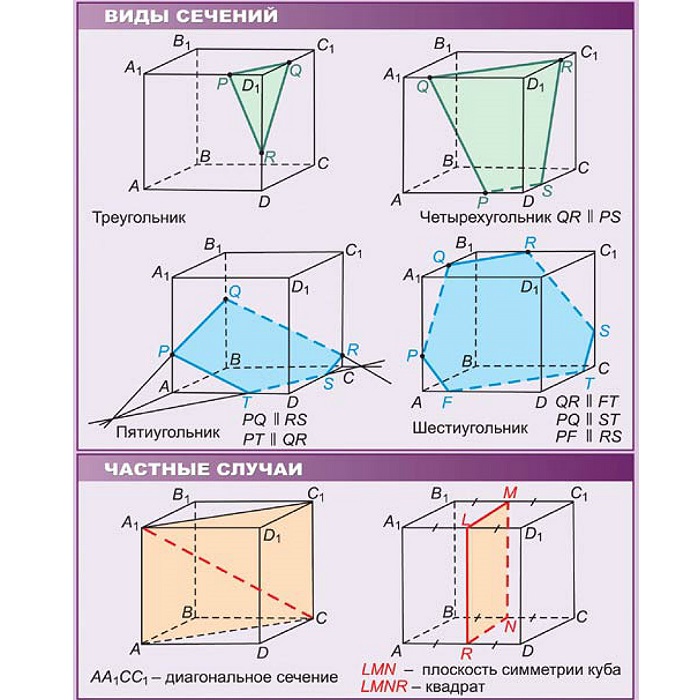
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
Прочие свойства:
-
у куба все грани равны, являются квадратами;
-
у куба все рёбра равны;
-
один центр и несколько осей симметрии.
![]()
LeraPtica
+10
Решено
7 лет назад
Математика
5 – 9 классы
Центр куба – это точка пересечения его диагоналей ( рис. 7.39 ). Назовите вершины куба, симметричные относительно его центра.

Смотреть ответ
Ответ проверен экспертом
5
(6 оценок)
6
![]()
Удачник66
3 года назад
Светило науки – 13615 ответов – 145139 раз оказано помощи
Ответ:
Пошаговое объяснение:
На рисунке все видно. Это пары вершин (A-C1); (B-D1); (C-A1), (D-B1).
(6 оценок)
Остались вопросы?
Задай вопрос
Найди нужный
Новые вопросы по предмету Математика
Обчисліть площу фігури, зображеної на рисунку.
9 Составь уравнение по задаче и реши Серик и Арман одновременно выехали на велосипедах из по- сёлка к реке. Через 10 минут Серик, ехавший со с …
У літній школі для юних математиків та програмістів вожаті вирішили провести логічну гру для всіх учнів, яких було рівно 1024. Діти домовились …
Відомо, що після множення на 20 натуральне число стане квадратом натурального числа. Якщо ж дане число домножити не на 20, а на 23, то воно ста …
Робота из 15 страниц содержит 10 процентов книги сколько страниц в книге
Куб – свойства, формы и узоры
Среди многогранников куб – один из самых знакомых объектов, известный с младенчества. Более подробно эта тема изучается на уроках геометрии в старших классах, когда мы переходим от фигур на плоскости к телам в пространстве.
- Элементы куба
- Объем куба
- Периметр куба
- Площадь поверхности
- Сфера, вписанная в куб
- Сфера, описанная вокруг куба
- Координаты вершины
- Свойства куба
Кубу можно дать определение различными способами, каждый из которых будет акцентировать внимание только на том или ином классе тел в пространстве, выделяя основные признаки и свойства:
многогранник, в котором все ребра равны, а грани попарно перпендикулярны;
простая призма, все стороны которой являются квадратами
прямоугольный параллелограмм с равными краями.
С помощью этих и многих других подобных формулировок геометрия позволяет нам описывать одну и ту же фигуру в пространстве.
Элементы куба
Стенки, ребра и вершины считаются основными элементами многогранника.
Край
Плоскости, образующие поверхность куба, называются гранями. Другое название для них – бока.
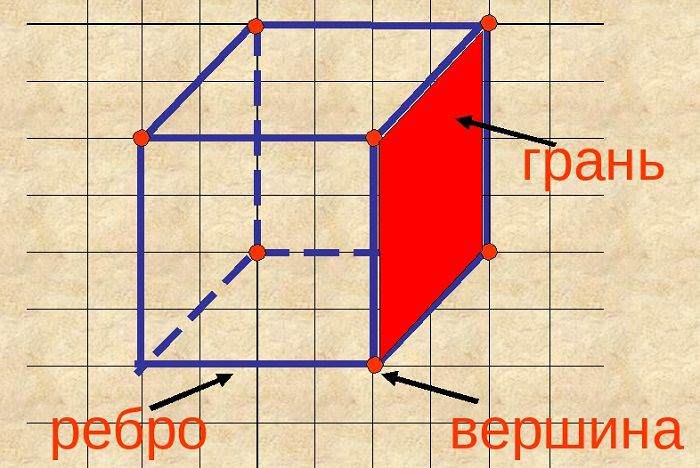
Нам интересно, сколько граней у куба и каковы их характеристики. Всего существует шесть лиц. Два из них, параллельные друг другу, считаются основаниями, остальные – сторонами.
Стенки куба попарно перпендикулярны, являются квадратами и равны друг другу.
Ребро
Линии, на которых сходятся стороны, называются краями.
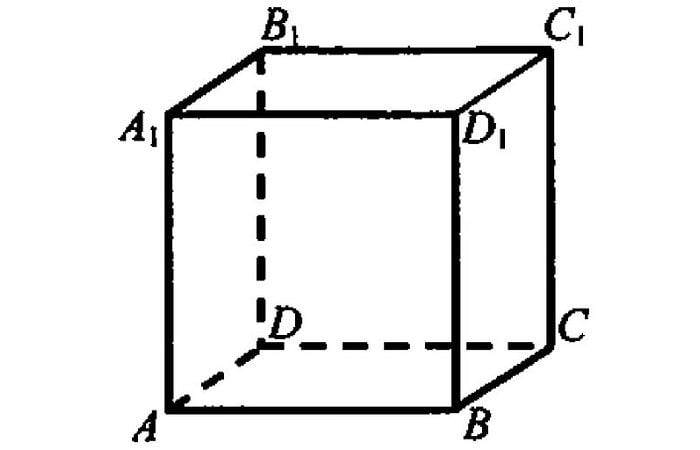
Не каждый студент может сказать, сколько граней у куба. Существует двенадцать граней. Их длина одинакова. Те, что имеют общий край, находятся под прямым углом к двум другим.
Грани могут пересекаться в вершине и быть параллельными. Ребра, не находящиеся в одной плоскости, пересекаются.
Пункт
Точки, в которых пересекаются ребра, называются вершинами. Их число – восемь.
Центр кромки
Отрезок, соединяющий две вершины и не являющийся ребром, называется диагональю.
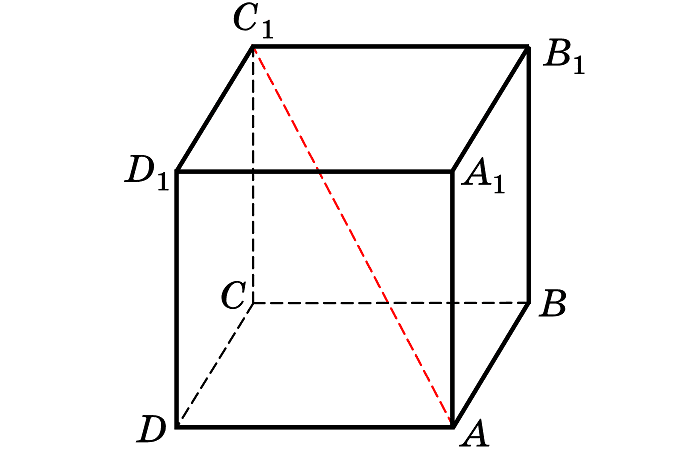
Точка пересечения диагоналей грани – это центр грани, точка, равноудаленная от всех вершин и сторон квадрата. Она является центром симметрии лица.
Средняя точка куба
Пересечение диагоналей куба является его центром – точкой, равноудаленной от всех вершин, ребер и граней многогранника.

Это центр симметрии куба.
Кубическая ось
Рассматриваемый многогранник имеет несколько осей ортогональной (прямоугольной) симметрии. Это диагонали куба и линии, проходящие через его центр параллельно граням.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю данного многогранника.

Учитывая, что ребра куба имеют равные размеры a, мы можем найти длину диагонали:
![]()
Формула доказывается путем двойного применения теоремы Пифагора.
Диагональ куба является одной из осей симметрии.
Все диагонали куба равны между собой, а точка пересечения является биссектрисой.
Диагональ стенки куба
Длина диагонали стены в √2 раз больше длины ребра, т.е:
![]()
Эту формулу также можно доказать с помощью теоремы Пифагора.
Объем куба
Как и для любого параллелограмма, объем куба равен произведению всех трех измерений, которые в данном случае равны:
![]()
Периметр куба
Сумма длин всех ребер равна:
![]()
Область
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
![]()
Сфера, вписанная в куб
Центр такой сферы совпадает с центром куба.

Радиус равен половине края:
![]()
Сфера, описанная вокруг куба
Что касается окружности, то ее центр совпадает с точкой пересечения диагоналей, а радиус равен половине диагонали:

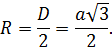
Координаты вершин куба
В зависимости от положения фигуры в системе координат, координаты вершин могут быть вычислены различными способами.

Наиболее распространенный метод заключается в следующем. Одна из вершин совпадает с началом координат, ребра параллельны или совпадают с координатными осями, а координаты единичного куба будут равны:
![]()
Такое расположение удобно для введения четырехмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, делящая куб на две части, является сегментом. Его форма напоминает выпуклый многоугольник.

Построение поперечных сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
Куб
Куб – это правильный многогранник, каждая грань которого представляет собой квадрат. Все грани куба равны.
Свойства куба:
1. У куба 6$ граней, и все они квадраты.
2. противоположные грани попарно параллельны.
3. все двугранные углы куба – прямые углы.
4. диагонали равны.
5. У куба $4$ диагонали пересекаются в одной точке и являются секущими в этой точке.
6.Диагональ куба в $√3$ раз больше его ребра.
7. диагональ стенки куба в $√2$ раза длиннее его ребра.
Пусть $a-длина ребра куба, $d-диагональ куба, тогда формула верна:
Общая площадь: $S_<п.п>=6a^2=2d^2$.
Радиус сферы, описанной вокруг куба: $R=<a√3>/<2>$
Радиус сферы, вписанной в куб: $r=/<2>$.
Если все линейные размеры куба увеличить в $k$ раз, то его объем увеличится в $k^3$ раз.
Если все линейные размеры куба увеличить в $k$ раз, то его площадь увеличится в $k^2$ раз.
Прямоугольный параллелограмм
Параллелограмм называется прямоугольным, если его боковые ребра перпендикулярны основанию, а основания являются прямоугольниками.
1 Квадрат диагонали прямоугольного параллелограмма равен сумме квадратов трех его размеров (длина, ширина, высота).
Формулы для вычисления объема и площади прямоугольного параллелепипеда.
Чтобы формулы были понятны, введем термины:
$c$- высота (она же боковая грань);
$S_<п.п>площадь общей поверхности;
$V=a-b-c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
Пирамида
Пирамида – это многогранник, одна грань которого (основание) – правильный многоугольник, а остальные грани (боковые) – треугольники с общей вершиной.
Высота ($h$) пирамиды – это перпендикуляр, опущенный из ее вершины на плоскость основания.
Формулы для вычисления объема и площади правильной пирамиды.
$h_a$ – высота боковой стенки (апофемы).
В основании лежат правильные многоугольники, рассмотрим их площади:
- Для равностороннего треугольника $S=<a^<2>√3>/<4>$, где $a$ – длина стороны.</a^<2>
- Квадрат $S=a^2$, где $a$ – сторона квадрата.
Задачи на нахождение объема сложного многогранника:
- Разделите составной многогранник на несколько параллелограммов.
- Найдите объем каждого из параллелограммов.
- Сложите объемы.
Задачи на нахождение площади сложного многогранника.
– Если составной многогранник можно представить в виде простой призмы, найдите площадь поверхности по формуле:
Чтобы найти площадь основания призмы, разделите ее на прямоугольники и найдите площадь каждого прямоугольника.
– Если составной многогранник нельзя представить в виде призмы, то общая площадь может быть найдена как сумма площадей всех граней, ограничивающих поверхность.
Что такое куб: определение, свойства, формулы
В этой публикации мы рассмотрим определение и основные свойства куба, а также формулы для этой геометрической фигуры (вычисление площади, периметра граней, объема, радиуса описанной/вложенной сферы и т.д.).
- Определение куба
- Свойства куба
- Собственность 1
- Собственность 2
- Собственность 3
- Диагональ
- Передняя диагональ
- Общая площадь поверхности
- Окружность ребер
- Объем
- Радиус окружности
- Радиус вписанной сферы
Определение куба
Куб – Куб – это правильный многогранник, все грани которого являются квадратами.

- Вершины куба – это точки, которые являются вершинами ребер.
Всего их восемь: A, B, C, D, A1, B1, C1 и D1. - Грани куба – это стороны его стен.
Всего их насчитывается 12: AB, BC, CD, AD, AA1, BB1, CC1, ДД1, A1B1, B1C1, C1D1 и A1D1.
Примечание: Куб – это частный случай параллелограмма или призмы.
Свойства куба
Собственность 1
Как следует из определения, все ребра и грани куба равны. Также противоположные стороны фигуры попарно параллельны, т.е:
- ABCD || A1B1C1D1
- AA1B1B | CC1D1D
- BB1C1C | AA1D1D
Собственность 2
Диагонали куба (всего их 4) равны и делятся пополам в точке пересечения.

Собственность 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, поэтому они прямые.

Например, на рисунке выше угол между гранями ABCD и AA1B1B это прямая линия.
Формулы для куба
Примите следующие обозначения, которые будут использоваться во всем остальном тексте:
- a – грань куба;
- d – диагональ куба или его ребро.
Диагональ
Длина диагонали куба равна длине его ребра, умноженной на квадратный корень из трех.

Диагональ лица
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Общая площадь поверхности
Общая площадь куба равна шести граням. В формуле можно использовать длину ребра или диагонали.

Периметр ребер
Периметр куба равен длине ребра, умноженной на 12. Его также можно вычислить по диагонали.
Куб и его свойства

В настоящее время видеоуроки нельзя просматривать или распространять среди студентов.
Чтобы получить доступ к этому и другим видеоурокам из комплекта, добавьте его в свой личный кабинет через покупку в каталоге.
Получите удивительные возможности



Конспект урока “Куб и его свойства”
На предыдущем уроке мы узнали о таких многогранниках, как Прямоугольный параллелограмм..
Решив задачу со спичками, мы получили геометрическую фигуру под названием пирамида.
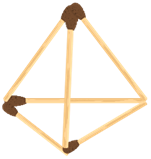
Перед этим вас познакомят и с другими многогранниками. Теперь вернемся к параллелепипеду.
Таким образом, поверхность параллелепипеда состоит из шести прямоугольников. Эти прямоугольники называются лица параллелограмм.
Обратите внимание, что два соседних прямоугольника имеют общую сторону, которую мы называем край прямоугольного параллелепипеда. Концы ребер называются вершины прямоугольного параллелепипеда.
Таким образом, прямоугольный параллелепипед имеет 6 граней, 12 ребер и 8 вершин.
Обратите внимание, что хотя многогранники различны, поверхность каждого многогранника состоит из правильных многоугольников, которые мы называем гранями многогранника. Два соседних правильных многоугольника имеют общую сторону – ребро многогранника. Концы ребер являются вершинами многогранника.
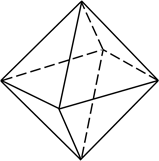
Этот многогранник называется октаэдр. Он имеет 8 ребер, которые являются треугольниками, 12 граней и 6 вершин.
Куб – это прямоугольный параллелограмм, у которого все ребра равны. Обратите внимание, что мы рисуем пунктирные линии для граней куба, которые не видны. Это дает полное представление о фигуре и ее положении относительно нас.
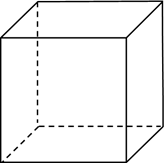
Все грани куба – равные квадраты. Поверхность куба состоит из 6 равных квадратов. Убедитесь, что грани напротив друг друга не имеют общих ребер. Эти называются напротив.
лицакоторые имеют общее ребро, называются прилегающая территория.
Теперь давайте проведем небольшой эксперимент. Возьмите коробку, имеющую форму куба. Мы раскрываем его, затем разрезаем вдоль четырех вертикальных ребер, а затем разворачиваем.

Форма, которую мы имеем, называется Разворачивание куба.. Он состоит из 6 равных квадратов.
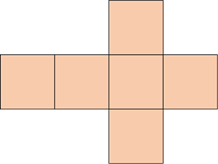
Фигуры ниже также являются взрывающимися кубами.
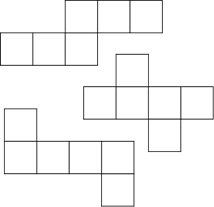
Используя каждую из разверток, вы можете сделать модель куба. Для этого выполните следующие действия. Нарисуйте чертеж куба на листе бумаги. Выключите его. Согните его вдоль секций, соответствующих граням куба, и склейте.
Теперь нарисуйте отрезок, который соединит самые удаленные вершины куба. Мы называем эти вершины противоположными вершинами.
Отрезок, соединяющий две противоположные вершины куба, называется диагональю куба.

Теперь давайте решим несколько задач.
Проблема первая. Определите, какой кубик мы получим из данной сборки.
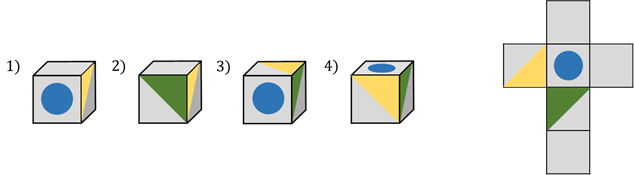
Давайте представим, какие грани куба являются смежными, то есть имеют общее ребро, и сравним с предложенными вариантами, чтобы найти правильный. Для этого нам удобнее всего сравнивать лица, которые отличаются в зависимости от рисунка на них. Обратите внимание на лицо с желтым треугольником и лицо с зеленым треугольником. Конечно, при сборке куба эти грани будут примыкать друг к другу. Следовательно, при различных поворотах куба возможны четыре варианта взаимного расположения этих граней.
Давайте теперь сравним четыре предложенных варианта. Сразу видно, что первый вариант неверен. Второй вариант неверен. Конечно, третий вариант также неверен. Однако вариант четыре является правильным, поскольку грани, на которых изображены треугольники, правильные. В этом случае на верхней поверхности должен быть синий круг. Это правильно.
Таким образом, мы выяснили, что из данного расширения получится куб с числом 4.
Вы можете решить эту проблему другим способом. Вы можете нарисовать этот контур на бумаге. Удобнее это делать на листе бумаги с квадратами, тогда вам не придется пользоваться линейкой, чтобы соблюсти размеры куба. Вы просто посчитаете количество квадратов, которое вам необходимо.
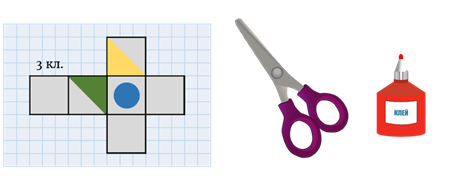
Затем вам нужно будет раскрасить и вырезать нарисованный контур. Затем скатайте его в кубик и склейте. После этого вы можете легко сравнить полученный куб с любым из предложенных вариантов и выбрать подходящий.
Вторая задача. Модель куба с длиной ребра 4 см была окрашена серой краской и разрезана вдоль ребра на кубики с длиной ребра 1 см. Сколько кубиков получилось: а) окрашенных по трем граням; б) окрашенных по двум граням?

Третья проблема. На рисунке показан скелет куба. Затем нарисуйте видимые грани так, чтобы на куб можно было смотреть: a) сверху слева; b) снизу справа.

Проблема четвертая .. Фигура, показанная на рисунке, состоит из пяти кубиков. Какой формы фигура, если смотреть на нее: a) спереди; b) слева; c) сверху?
Геометрические фигуры. Куб.
Куб или правильный шестигранник – это правильный многогранник, у которого все стороны – квадраты.
Куб – это частный случай параллелограмма и призмы. Четыре части куба имеют форму правильных шестиугольников.
Шестиугольники – это сечения через центр куба, перпендикулярные 4 главным диагоналям.
В кубе шесть квадратов. Все вершины куба являются вершинами 3 квадратов. Это,
сумма углов плоскости при каждой вершине = 270º.
Количество сторон стены равно 4;
Общее количество сторон равно 6;
Количество ребер, смежных с вершиной – 3;
Общее количество вершин – 8;
Общее количество граней – 12;
Предположим, что а – длина стороны куба, и d – является диагональю, тогда:



Диагональ куба – это отрезок, соединяющий две вершины, симметричные относительно центра.
Свойства куба.
- 4 сегмента куба являются правильными шестиугольниками – проходят через центр куба
перпендикулярно четырем главным диагоналям.
- Куб вписывается в правильный тетраэдр двумя способами. В каждом из них 4 вершины правильного тетраэдра всегда являются
совпадают с 4 вершинами куба, а каждое из 6 ребер тетраэдра принадлежит одной из граней куба. W 1.
каждая вершина правильного тетраэдра принадлежит грани треугольного угла, и эта вершина совпадает с одним
вершина куба. Во втором случае каждое ребро тетраэдра принадлежит паре
противоположные грани куба. Этот тетраэдр правильный, и его объем составляет одну треть от
- Октаэдр вписан в куб, поэтому все 6 вершин октаэдра совпадают с центрами 6 граней куба.
- Куб вписан в октаэдр, поэтому все 8 вершин куба совпадают с центрами 8 граней.
- Куб вписан в икосаэдр, поэтому 6 взаимно параллельных граней икосаэдра совпадают с гранями
6 граней куба, и еще 24 ребра находятся внутри куба. Каждая из 12 вершин икосаэдра
Удивительная форма: куб
Куб – это фигура, с которой мы сталкиваемся не только на уроках геометрии и искусства, но и в повседневной жизни. Другое название куба – обычный куб. Куб – это правильный многогранник, каждая грань которого представляет собой квадрат. Куб можно назвать объемным, трехмерным или даже трехмерным квадратом. Куб имеет 8 вершин, 6 граней и 12 ребер. Куб – это удивительная геометрическая фигура, в которой могут быть спрятаны или установлены другие фигуры, такие как октаэдр, тетраэдр, икосаэдр и другие.
Удивительная форма: куб
Куб или гексаэдр также называют кубом Неккера, по имени швейцарского кристаллографа Луи Альберта Неккера. В 1832 году Неккер предложил иллюзию: если смотреть в куб со стенками, то можно увидеть, что маленькая черная точка появляется то на переднем плане, то на заднем, то в углу, то в середине. Он перемещается с одного места на другое, как будто движется. Еще одна особенность куба Неккера заключается в том, что его параллельные боковые грани как бы расходятся. Вы можете покрасить один из краев в другой цвет и посмотреть, как этот цветной край причудливо движется.
Еще один необычный куб – куб художника Маурица Эшера. Этот куб невозможен.
Еще одно интересное открытие, связанное с кубом, было сделано в 1966 году фотографом Чарльзом Ф. Кокраном. Он сделал фотографию, которую назвали “сумасшедшей коробкой”. Что такое “сумасшедший язык”? Это внутренний и внешний каркас гексаэдра (куба). Сумасшедший ящик” основан на неправильных связях, которые были допущены при рисовании фигуры.
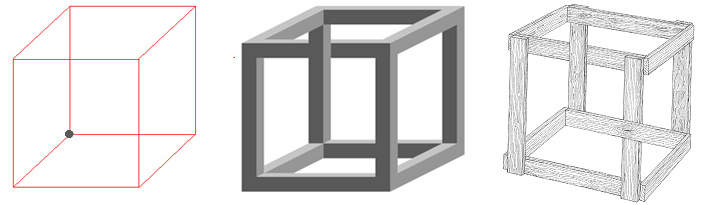
Куб Неккера Куб Эшера “Сумасшедший ящик В список самых удивительных и причудливых форм входят интегральный куб, расширяющийся куб (также называемый бесконечным кубом), повторяющиеся кубы, кубическая снежинка, плавающие кубы, двухэтажный куб и многие, многие другие. Все эти фигуры завораживают, от них невозможно оторвать взгляд. Каждый, кто их видит, хочет понять, как они создаются.
Куб всегда таил в себе множество загадок – это чрезвычайно сложная и в то же время чрезвычайно простая геометрическая фигура, которая помогает нам заглянуть в глубины сознания. В древности Платон называл его священной фигурой и ассоциировал со знаком Земли, потому что это самая стабильная фигура из всех. Куб – это фигура сакральной геометрии. Уже в 16 веке немецкий математик и астроном Иоганн Кеплер создал модель Солнечной системы, в которую вписал куб.
Где вы можете найти куб? Здания обычно имеют форму куба, поэтому достаточно выглянуть из окна, и вы сразу увидите куб. Самая известная игрушка-головоломка, которую каждый ребенок хотя бы раз в жизни держал в руках, а некоторые даже смогли собрать, – это кубик Рубика. Название говорит само за себя. В 1975 году венгерский архитектор Эрне Рубик создал головоломку “Кубик Рубика”, которая стала популярной во всем мире. Кубик Рубика – это кубик из пластика, который, в свою очередь, состоит из 26 кубиков. Когда кубик Рубика собран, каждая из его граней окрашивается в один определенный цвет.

Многие вещества кристаллизуются в виде кубиков, например, поваренная соль и минерал флюорит.
</п.п></a√3></п.п>
- Куб и его разложение – Начни учиться (Научный журнал для студентов).
- Как построить куб: объяснение перспективы с помощью пошагового метода.
- Как сделать квадрат из листа бумаги.
- Геометрические фигуры из бумаги.
- 3D куб и пирамида. Нарисуйте карандашом куб и объемную пирамиду.
- Как сделать бумажный куб – схема изготовления своими руками.
- Как расположены числа на кубиках?.
- Как сделать треугольник из бумаги – 100 фото и пошаговые видеоинструкции о том, как сложить треугольник.
- Кубик-трансформер.
- Мастер-класс по изготовлению кубиков из фетра. Для воспитателей дошкольных учреждений, школьных учителей и педагогов.
