Как найти вершину тетраэдра по координатам вершин

Как найти вершину тетраэдра по координатам вершин

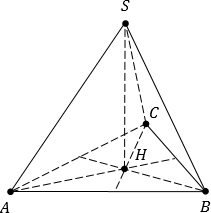
Координаты вершин правильного тетраэдра

20 июня 2013

Пирамиды традиционно считаются сложными фигурами в задаче C2. А уж если в основании пирамиды лежит треугольник (т.е. пирамида становится тетраэдром), то все становится совсем грустно. В общем, если в ЕГЭ по математике вам попадется правильный тетраэдр, примите мои поздравления: это самая мерзкая и сложная фигура, которая встречается на настоящем экзамене.

Тем не менее, после небольшой тренировки все становится вполне решаемо. И в этом уроке мы пошагово разберем каждую вершину тетраэдра и найдем каждую координату. Вы убедитесь: все, что нам действительно надо знать — это две теоремы:

  1. Теорема Пифагора — без нее не решается вообще ни одна задача C2, потому что на этой теореме построена сама идея декартовой системы координат;
  2. Теорема о медианах. А именно: медианы треугольника пересекаются в одно точке и делятся ею в отношении 2 : 1, считая от вершины.

Вот и весь список! Вы знаете эти теоремы? Тогда поехали!

Задача. В правильном тетраэдре SABC, все ребра которого равны 1, введите систему координат и найдите координаты вершин.

Правильный тетраэдр SABC и высота SH

[Подпись к рисунку]

Смотрите также:

  1. Четырехугольная пирамида: как найти координаты вершин
  2. Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
  3. Решение ЕГЭ-2011: вариант 1, часть B
  4. Не пишите единицы измерения в задаче B12
  5. Быстрое возведение чисел в квадрат без калькулятора
  6. Задача B4: тарифы на сотовую связь
Источник

Тетра́эдр (др.-греч. τετράεδρον «четырёхгранник»[1] ← τέσσαρες / τέσσερες / τέτταρες / τέττορες / τέτορες «четыре» + ἕδρα «седалище, основание») — простейший многогранник, гранями которого являются четыре треугольника[2].

Тетраэдр является треугольной пирамидой при принятии любой из граней за основание.
У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным. Правильный тетраэдр является одним из пяти правильных многогранников.

Свойства[править | править код]

  • Параллельные плоскости, проходящие через три пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед.
  • Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра, делит его на две равные по объёму части[3]:216-217.
  • Бимедианы тетраэдра пересекаются в той же самой точке, что и медианы тетраэдра.
    • Бимедианами тетраэдра называют отрезки, соединяющие середины его скрещивающихся рёбер (не имеющих общих вершин).
  • Центры сфер, которые проходят через три вершины и инцентр, лежат на сфере, центр которой совпадает с центром описанной сферы.
    • Также это утверждение верно и для внешних инцентров.
  • Плоскости, которые проходят через середину ребра и перпендикулярны противоположному ребру,пересекаются в одной точке (ортоцентр).
    • Ортоцентр в симплексе определяется как пересечение гиперплоскостей, которые перпендикулярны ребру и проходят через центр тяжести противоположного элемента.
  • Центр сферы(F),которая проходит через центры тяжести граней тетраэдра, центр тяжести тетраэдра(M), центр описанной сферы(R) и ортоцентр (H) лежат на одной прямой. При этом {displaystyle RM=MH=3cdot MF}.
  • Центр сферы (S) вписанный в дополнительный тетраэдр,центр сферы (N) вписанный в антидополнительный тетраэдр, центр тяжести тетраэдра (M) и центр вписанной сферы (I) лежат на одной прямой.
  • Пусть точка G1 делит отрезок соединяющий ортоцентр(H) и вершину 1 в отношении 1:2. Опустим перпендикуляр с точки G1 на грань противолежащей вершине 1. Перпендикуляр пересекает грань в точке W1. Точки G1 и W1 лежат на сфере (сфере Фейербаха), которая проходит через центры тяжести граней тетраэдра.
  • Сечение плоскостью, проходящей через середины четырёх рёбер тетраэдра, является параллелограммом.

Типы тетраэдров[править | править код]

Равногранный тетраэдр[править | править код]

Развёртка равногранного тетраэдра

Все грани его представляют собой равные между собой треугольники. Развёрткой равногранного тетраэдра является треугольник, разделённый тремя средними линиями на четыре равных треугольника. В равногранном тетраэдре основания высот, середины высот и точки пересечения высот граней лежат на поверхности одной сферы (сферы 12 точек) (Аналог окружности Эйлера для треугольника).

Свойства равногранного тетраэдра:

  • Все его грани равны (конгруэнтны).
  • Скрещивающиеся рёбра попарно равны.
  • Трёхгранные углы равны.
  • Противолежащие двугранные углы равны.
  • Два плоских угла, опирающихся на одно ребро, равны.
  • Сумма плоских углов при каждой вершине равна 180°.
  • Развёртка тетраэдра — треугольник или параллелограмм.
  • Описанный параллелепипед прямоугольный.
  • Тетраэдр имеет три оси симметрии.
  • Общие перпендикуляры скрещивающихся рёбер попарно перпендикулярны.
  • Средние линии попарно перпендикулярны.
  • Периметры граней равны.
  • Площади граней равны.
  • Высоты тетраэдра равны.
  • Отрезки, соединяющие вершины с центрами тяжести противоположных граней, равны.
  • Радиусы описанных около граней окружностей равны.
  • Центр тяжести тетраэдра совпадает с центром описанной сферы.
  • Центр тяжести совпадает с центром вписанной сферы.
  • Центр описанной сферы совпадает с центром вписанной.
  • Вписанная сфера касается граней в центрах описанных около этих граней окружностей.
  • Сумма внешних единичных нормалей (единичных векторов, перпендикулярных к граням) равна нулю.
  • Сумма всех двугранных углов равна нулю.
  • Центры вневписанных сфер лежат на описанной сфере.

Ортоцентрический тетраэдр[править | править код]

Все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.

  • Высоты тетраэдра пересекаются в одной точке.
  • Основания высот тетраэдра являются ортоцентрами граней.
  • Каждые два противоположных ребра тетраэдра перпендикулярны.
  • Суммы квадратов противоположных рёбер тетраэдра равны.
  • Отрезки, соединяющие середины противоположных рёбер тетраэдра, равны.
  • Произведения косинусов противоположных двугранных углов равны.
  • Сумма квадратов площадей граней вчетверо меньше суммы квадратов произведений противоположных рёбер.
  • У ортоцентрического тетраэдра окружности 9 точек (окружности Эйлера) каждой грани принадлежат одной сфере (сфере 24 точек).
  • У ортоцентрического тетраэдра центры тяжести и точки пересечения высот граней, а также точки, делящие отрезки каждой высоты тетраэдра от вершины до точки пересечения высот в отношении 2:1, лежат на одной сфере (сфере 12 точек).

Прямоугольный тетраэдр[править | править код]

Все рёбра, прилежащие к одной из вершин, перпендикулярны между собой.
Прямоугольный тетраэдр получается отсечением тетраэдра плоскостью от прямоугольного параллелепипеда.

Каркасный тетраэдр[править | править код]

Это тетраэдр, отвечающий любому из следующих условий[4]:

  • существует сфера, касающаяся всех рёбер,
  • суммы длин скрещивающихся рёбер равны,
  • суммы двугранных углов при противоположных рёбрах равны,
  • окружности, вписанные в грани, попарно касаются,
  • все четырёхугольники, получающиеся на развёртке тетраэдра, — описанные,
  • перпендикуляры, восставленные к граням из центров вписанных в них окружностей, пересекаются в одной точке.

Соразмерный тетраэдр[править | править код]

У этого типа бивысоты равны.

Свойства соразмерного тетраэдра:

Инцентрический тетраэдр[править | править код]

У этого типа отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Свойства инцентрического тетраэдра:

  • Отрезки, соединяющие центры тяжести граней тетраэдра с противоположными вершинами (медианы тетраэдра), всегда пересекаются в одной точке. Эта точка — центр тяжести тетраэдра.
  • Замечание. Если в последнем условии заменить центры тяжести граней на ортоцентры граней, то оно превратится в новое определение ортоцентрического тетраэдра. Если же заменить их на центры вписанных в грани окружностей, называемых иногда инцентрами, мы получим определение нового класса тетраэдров — инцентрических.
  • Отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
  • Биссектрисы углов двух граней, проведённому к общему ребру этих граней, имеют общее основание.
  • Произведения длин противоположных рёбер равны.
  • Треугольник, образованный вторыми точками пересечения трёх рёбер, выходящих из одной вершины, с любой сферой, проходящей через три конца этих рёбер, является равносторонним.

Правильный тетраэдр[править | править код]

Это равногранный тетраэдр, у которого все грани — правильные треугольники. Является одним из пяти платоновых тел.

Свойства правильного тетраэдра:

  • все рёбра тетраэдра равны между собой,
  • все грани тетраэдра равны между собой,
  • периметры и площади всех граней равны между собой.
  • Правильный тетраэдр является одновременно ортоцентрическим, каркасным, равногранным, инцентрическим и соразмерным.
  • Тетраэдр является правильным, если он принадлежит к двум любым видам тетраэдров из перечисленных: ортоцентрический, каркасный, инцентрический, соразмерный, равногранный.
  • Тетраэдр является правильным, если он является равногранным и принадлежит к одному из следующих видов тетраэдров: ортоцентрический, каркасный, инцентрический, соразмерный.
  • В правильный тетраэдр можно вписать октаэдр, притом четыре (из восьми) грани октаэдра будут совмещены с четырьмя гранями тетраэдра, все шесть вершин октаэдра будут совмещены с центрами шести рёбер тетраэдра.
  • Правильный тетраэдр состоит из одного вписанного октаэдра (в центре) и четырёх тетраэдров (по вершинам), причём рёбра этих тетраэдров и октаэдра вдвое меньше рёбер правильного тетраэдра.
  • Правильный тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба.
  • Правильный тетраэдр можно вписать в додекаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами додекаэдра.
  • Скрещивающиеся рёбра правильного тетраэдра взаимно перпендикулярны.

Объём тетраэдра[править | править код]

{displaystyle V={frac {1}{6}}{begin{vmatrix}1&x_{1}&y_{1}&z_{1}\1&x_{2}&y_{2}&z_{2}\1&x_{3}&y_{3}&z_{3}\1&x_{4}&y_{4}&z_{4}end{vmatrix}}={frac {1}{6}}{begin{vmatrix}x_{2}-x_{1}&y_{2}-y_{1}&z_{2}-z_{1}\x_{3}-x_{1}&y_{3}-y_{1}&z_{3}-z_{1}\x_{4}-x_{1}&y_{4}-y_{1}&z_{4}-z_{1}end{vmatrix}},}

или

{displaystyle V={frac {1}{3}} SH,}

где S — площадь любой грани, а H — высота, опущенная на эту грань.

  • Объём тетраэдра через длины рёбер выражается с помощью определителя Кэли-Менгера:
288cdot V^{2}={begin{vmatrix}0&1&1&1&1\1&0&d_{12}^{2}&d_{13}^{2}&d_{14}^{2}\1&d_{12}^{2}&0&d_{23}^{2}&d_{24}^{2}\1&d_{13}^{2}&d_{23}^{2}&0&d_{34}^{2}\1&d_{14}^{2}&d_{24}^{2}&d_{34}^{2}&0end{vmatrix}}.
  • Эта формула имеет плоский аналог для площади треугольника в виде варианта формулы Герона через аналогичный определитель.
  • Объём тетраэдра через длины двух противоположных рёбер a и b, как скрещивающихся линий, которые удалены на расстояние h друг от друга и образуют друг с другом угол phi , находится по формуле:

{displaystyle V={frac {1}{6}}abhsin phi .}

  • Объём тетраэдра через длины трёх его рёбер a, b и c, выходящих из одной вершины и образующих между собой попарно соответственно плоские углы alpha ,beta ,gamma , находится по формуле[5]
{displaystyle V={frac {1}{6}} abc{sqrt {D}},}

где

{displaystyle D={begin{vmatrix}1&cos gamma &cos beta \cos gamma &1&cos alpha \cos beta &cos alpha &1end{vmatrix}}.}

  • Аналогом для плоскости последней формулы является формула площади треугольника через длины двух его сторон a и b, выходящих из одной вершины и образующих между собой угол gamma :
S={frac {1}{2}} ab{sqrt {D}},

где
D={begin{vmatrix}1&cos gamma \cos gamma &1\end{vmatrix}}.

Замечание[править | править код]

Есть аналог формулы Герона для объёма тетраэдра [6]

Формулы тетраэдра в декартовых координатах в пространстве[править | править код]

Обозначения:

{displaystyle mathbf {r} _{1}(x_{1},y_{1},z_{1}),} {displaystyle mathbf {r} _{2}(x_{2},y_{2},z_{2}),}{displaystyle mathbf {r} _{3}(x_{3},y_{3},z_{3}),}{displaystyle mathbf {r} _{4}(x_{4},y_{4},z_{4})} — координаты вершин тетраэдра.

  • Объём тетраэдра (с учётом знака):

{displaystyle V={frac {1}{6}}{begin{vmatrix}1&x_{1}&y_{1}&z_{1}\1&x_{2}&y_{2}&z_{2}\1&x_{3}&y_{3}&z_{3}\1&x_{4}&y_{4}&z_{4}end{vmatrix}}}.

  • Координаты центра тяжести (пересечение медиан): {displaystyle mathbf {r} _{T}(x_{T},y_{T},z_{T})}

{displaystyle x_{T}={frac {x_{1}+x_{2}+x_{3}+x_{4}}{4}};}{displaystyle y_{T}={frac {y_{1}+y_{2}+y_{3}+y_{4}}{4}};}{displaystyle z_{T}={frac {z_{1}+z_{2}+z_{3}+z_{4}}{4}}.}

  • Координаты центра вписанной сферы: {displaystyle mathbf {r} _{r}(x_{r},y_{r},z_{r})}

{displaystyle x_{r}={frac {S_{1}x_{1}+S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}};}{displaystyle y_{r}={frac {S_{1}y_{1}+S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}};}{displaystyle z_{r}={frac {S_{1}z_{1}+S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}},}

где S_{1} — площадь грани, противолежащей первой вершине, {displaystyle S_{2}} — площадь грани, противолежащей второй вершине и так далее.

Соответственно уравнение вписанной сферы:

{displaystyle (x-{frac {S_{1}x_{1}+S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(y-{frac {S_{1}y_{1}+S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(z-{frac {S_{1}z_{1}+S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2}=({frac {3V}{S_{1}+S_{2}+S_{3}+S_{4}}})^{2},}

Уравнение вневписанной сферы, противолежащей первой вершине:

{displaystyle (x-{frac {-S_{1}x_{1}+S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(y-{frac {-S_{1}y_{1}+S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2}+(z-{frac {-S_{1}z_{1}+S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2}=({frac {3V}{-S_{1}+S_{2}+S_{3}+S_{4}}})^{2},}

Уравнение вневписанной сферы, противолежащей первой и второй вершинам (количество таких сфер может варьироваться от нуля до трёх):

{displaystyle (x-{frac {-S_{1}x_{1}-S_{2}x_{2}+S_{3}x_{3}+S_{4}x_{4}}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2}+(y-{frac {-S_{1}y_{1}-S_{2}y_{2}+S_{3}y_{3}+S_{4}y_{4}}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2}+(z-{frac {-S_{1}z_{1}-S_{2}z_{2}+S_{3}z_{3}+S_{4}z_{4}}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2}=({frac {3V}{-S_{1}-S_{2}+S_{3}+S_{4}}})^{2},}

  • Уравнение описанной сферы:

{displaystyle {begin{vmatrix}x^{2}+y^{2}+z^{2}&x&y&z&1\x_{1}^{2}+y_{1}^{2}+z_{1}^{2}&x_{1}&y_{1}&z_{1}&1\x_{2}^{2}+y_{2}^{2}+z_{2}^{2}&x_{2}&y_{2}&z_{2}&1\x_{3}^{2}+y_{3}^{2}+z_{3}^{2}&x_{3}&y_{3}&z_{3}&1\x_{4}^{2}+y_{4}^{2}+z_{4}^{2}&x_{4}&y_{4}&z_{4}&1end{vmatrix}}=0.}

Формулы тетраэдра в барицентрических координатах[править | править код]

Обозначения:

{displaystyle mathbf {J} (alpha _{1},alpha _{2},alpha _{3},alpha _{4})=alpha _{1}mathbf {J_{1}} +alpha _{2}mathbf {J_{2}} +alpha _{3}mathbf {J_{3}} +alpha _{4}mathbf {J_{4}} ,} — барицентрические координаты.

  • Объём тетраэдра (с учётом знака): Пусть {displaystyle mathbf {J} _{1}(x_{1},y_{1},z_{1},t_{1}),mathbf {J} _{2}(x_{2},y_{2},z_{2},t_{2}),mathbf {J} _{3}(x_{3},y_{3},z_{3},t_{3}),mathbf {J} _{4}(x_{4},y_{4},z_{4},t_{4}).} — координаты вершин тетраэдра.

Тогда

{displaystyle V={frac {begin{vmatrix}x_{1}&y_{1}&z_{1}&t_{1}\x_{2}&y_{2}&z_{2}&t_{2}\x_{3}&y_{3}&z_{3}&t_{3}\x_{4}&y_{4}&z_{4}&t_{4}\end{vmatrix}}{(x_{1}+y_{1}+z_{1}+t_{1})(x_{2}+y_{2}+z_{2}+t_{2})(x_{3}+y_{3}+z_{3}+t_{3})(x_{4}+y_{4}+z_{4}+t_{4})}}V',} где V' — объем базисного тетраэдра.

  • Координаты центра тяжести (пересечение медиан): {displaystyle mathbf {J} _{T}(1,1,1,1).}
  • Координаты центра вписанной сферы: {displaystyle mathbf {J} _{r}(S_{1},S_{2},S_{3},S_{4}).}
  • Координаты центра описанной сферы:

{displaystyle mathbf {J} _{R}={begin{vmatrix}0&mathbf {J_{1}} &mathbf {J_{2}} &mathbf {J_{3}} &mathbf {J_{4}} \1&0&alpha _{2,1}^{2}&alpha _{3,1}^{2}&alpha _{4,1}^{2}\1&alpha _{2,1}^{2}&0&alpha _{3,2}^{2}&alpha _{4,2}^{2}\1&alpha _{3,1}^{2}&alpha _{3,2}^{2}&0&alpha _{4,3}^{2}\1&alpha _{4,1}^{2}&alpha _{4,2}^{2}&alpha _{4,3}^{2}&0\end{vmatrix}}.}

  • Расстояние между точками {displaystyle mathbf {J} _{A}(A_{1},A_{2},A_{3},A_{4}),mathbf {J} _{B}(B_{1},B_{2},B_{3},B_{4})}:

Пусть {displaystyle C_{1}={frac {A_{1}}{A_{1}+A_{2}+A_{3}+A_{4}}}-{frac {B_{1}}{B_{1}+B_{2}+B_{3}+B_{4}}};C_{2}={frac {A_{2}}{A_{1}+A_{2}+A_{3}+A_{4}}}-{frac {B_{2}}{B_{1}+B_{2}+B_{3}+B_{4}}}} и так далее.

Тогда расстояние между двумя точками: {displaystyle d^{2}=-(C_{1}C_{2}alpha _{1,2}^{2}+C_{1}C_{3}alpha _{1,3}^{2}+C_{1}C_{4}alpha _{1,4}^{2}+C_{2}C_{3}alpha _{2,3}^{2}+C_{2}C_{4}alpha _{2,4}^{2}+C_{3}C_{4}alpha _{3,4}^{2}).}

Сравнение формул треугольника и тетраэдра[править | править код]

Площадь(Объём)
{displaystyle S={sqrt {-{frac {1}{16}}{begin{vmatrix}0&1&1&1\1&0&a^{2}&b^{2}\1&a^{2}&0&c^{2}\1&b^{2}&c^{2}&0\end{vmatrix}}}}} {displaystyle V={sqrt {{frac {1}{288}}{begin{vmatrix}0&1&1&1&1\1&0&alpha _{2,1}^{2}&alpha _{3,1}^{2}&alpha _{4,1}^{2}\1&alpha _{2,1}^{2}&0&alpha _{3,2}^{2}&alpha _{4,2}^{2}\1&alpha _{3,1}^{2}&alpha _{3,2}^{2}&0&alpha _{4,3}^{2}\1&alpha _{4,1}^{2}&alpha _{4,2}^{2}&alpha _{4,3}^{2}&0\end{vmatrix}}}}}, где {displaystyle alpha _{1,2}} — расстояние между вершинами 1 и 2
{displaystyle S={frac {1}{2}}ah_{a}} {displaystyle V={frac {1}{3}}S_{1}H_{1}}
{displaystyle S={frac {1}{2}}absin gamma } {displaystyle V={frac {2}{3}}{frac {S_{1}S_{2}}{alpha _{3,4}}}sin(phi _{1,2})},

где {displaystyle phi _{1,2}} — угол между гранями 1 и 2, {displaystyle S_{1}} и {displaystyle S_{2}} — площади граней, противолежащие вершинам 1 и 2

Длина(площадь) биссектрисы
l_{c}={frac {2abcos {frac {gamma }{2}}}{a+b}} {displaystyle L_{1,2}={frac {2S_{1}S_{2}cos({frac {phi _{1,2}}{2}})}{S_{1}+S_{2}}}}
Длина медианы
m_{c}={frac {{sqrt {2a^{2}+2b^{2}-c^{2}}}}{2}} {displaystyle m_{1}={frac {sqrt {3(alpha _{1,2}^{2}+alpha _{1,3}^{2}+alpha _{1,4}^{2})-(alpha _{2,3}^{2}+alpha _{2,4}^{2}+alpha _{3,4}^{2})}}{3}}}
Радиус вписанной окружности(сферы)
{displaystyle r={frac {2S}{a+b+c}}} {displaystyle r={frac {3V}{S_{1}+S_{2}+S_{3}+S_{4}}}}
Радиус описанной окружности(сферы)
R={frac {abc}{4S}} {displaystyle R={frac {S_{T}}{6V}}}, где {displaystyle S_{T}} — площадь треугольника со сторонами {displaystyle alpha _{1,2}alpha _{3,4},alpha _{1,3}alpha _{2,4},alpha _{1,4}alpha _{2,3}}
Теорема косинусов
cos {alpha }={frac {b^{2}+c^{2}-a^{2}}{2bc}} {displaystyle cos(phi _{1,2})={frac {A_{1,2}}{16S_{1}S_{2}}}},

где {displaystyle phi _{1,2}} — угол между гранями 1 и 2, {displaystyle S_{1}} и {displaystyle S_{2}} — площади граней, противолежащие вершинам 1 и 2, {displaystyle A_{1,2}} — алгебраическое дополнение элемента {displaystyle alpha _{2,1}^{2}} матрицы
{displaystyle {begin{pmatrix}0&1&1&1&1\1&0&alpha _{2,1}^{2}&alpha _{3,1}^{2}&alpha _{4,1}^{2}\1&alpha _{2,1}^{2}&0&alpha _{3,2}^{2}&alpha _{4,2}^{2}\1&alpha _{3,1}^{2}&alpha _{3,2}^{2}&0&alpha _{4,3}^{2}\1&alpha _{4,1}^{2}&alpha _{4,2}^{2}&alpha _{4,3}^{2}&0\end{pmatrix}}}

Теорема синусов
{frac {a}{sin alpha }}={frac {b}{sin beta }}={frac {c}{sin gamma }} {displaystyle {frac {S_{1}}{Psi _{1}}}={frac {S_{2}}{Psi _{2}}}={frac {S_{3}}{Psi _{3}}}={frac {S_{4}}{Psi _{4}}}},

где {displaystyle S_{1},S_{2},S_{3},S_{4}} — площади граней, противолежащие вершинам 1, 2, 3, 4, {displaystyle Psi ={sqrt {begin{vmatrix}1&-cos(A)&-cos(B)\-cos(A)&1&-cos(C)\-cos(B)&-cos(C)&1\end{vmatrix}}}}, где A,B,C — двугранные углы вершины.

Теорема о сумме углов треугольника(соотношение между двугранными углами тетраэдра)
alpha +beta +gamma =180^{circ } {displaystyle {begin{vmatrix}1&-cos left(phi _{2,1}right)&-cos left(phi _{3,1}right)&-cos left(phi _{4,1}right)\-cos left(phi _{2,1}right)&1&-cos left(phi _{3,2}right)&-cos left(phi _{4,2}right)\-cos left(phi _{3,1}right)&-cos left(phi _{3,2}right)&1&-cos left(phi _{4,3}right)\-cos left(phi _{4,1}right)&-cos left(phi _{4,2}right)&-cos left(phi _{4,3}right)&1\end{vmatrix}}=0},

где {displaystyle phi _{1,2}} — угол между гранями 1 и 2

Расстояние между центрами вписанной и описанной окружностей (сфер)
{displaystyle R^{2}-d^{2}=2Rr} {displaystyle R^{2}-d^{2}={frac {S_{1}S_{2}alpha _{1,2}^{2}+S_{1}S_{3}alpha _{1,3}^{2}+S_{1}S_{4}alpha _{1,4}^{2}+S_{2}S_{3}alpha _{2,3}^{2}+S_{2}S_{4}alpha _{2,4}^{2}+S_{3}S_{4}alpha _{3,4}^{2}}{(S_{1}+S_{2}+S_{3}+S_{4})^{2}}}},

где {displaystyle S_{1},S_{2},S_{3},S_{4}} — площади граней, противолежащие вершинам 1, 2, 3, 4.

Другая запись выражения: {displaystyle R^{2}-d^{2}=2rT,} где T — расстояние между центром описанной сферы и центром сферы, проходящая через три вершины и инцентр.

Тетраэдр в неевклидовых пространствах[править | править код]

Объём неевклидовых тетраэдров[править | править код]

Существует множество формул нахождения объёма неевклидовых тетраэдров. Например, формула Деревнина — Медных[7] для гиперболического тетраэдра и формула Дж. Мураками[8] для сферического тетраэдра. Объём тетраэдра в сферическом пространстве и в пространстве Лобачевского, как правило, не выражается через элементарные функции.

Соотношение между двугранными углами тетраэдра[править | править код]

{displaystyle operatorname {det} Psi >0} — для сферического тетраэдра.

{displaystyle operatorname {det} Psi <0} — для гиперболического тетраэдра.

Где {displaystyle Psi ={begin{pmatrix}1&-cos(A_{2,1})&-cos(A_{3,1})&-cos(A_{4,1})\-cos(A_{2,1})&1&-cos(A_{3,2})&-cos(A_{4,2})\-cos(A_{3,1})&-cos(A_{3,2})&1&-cos(A_{4,3})\-cos(A_{4,1})&-cos(A_{4,2})&-cos(A_{4,3})&1\end{pmatrix}}} — матрица Грама для двугранных углов сферического и гиперболического тетраэдра.

A_{{i,j}} — угол между гранями, противолежащими i и j вершине.

Теорема косинусов[править | править код]

{displaystyle cos(A_{i,j})=-{frac {Phi _{i,j}}{sqrt {Phi _{i,i}Phi _{j,j}}}}} — для сферического и гиперболического тетраэдра.

{displaystyle cos(alpha _{i,j})={frac {Psi _{i,j}}{sqrt {Psi _{i,i}Psi _{j,j}}}}} — для сферического тетраэдра.

{displaystyle operatorname {ch} (alpha _{i,j})={frac {Psi _{i,j}}{sqrt {Psi _{i,i}Psi _{j,j}}}}} — для гиперболического тетраэдра.

Где
{displaystyle Phi ={begin{pmatrix}1&cos(alpha _{2,1})&cos(alpha _{3,1})&cos(alpha _{4,1})\cos(alpha _{2,1})&1&cos(alpha _{3,2})&cos(alpha _{4,2})\cos(alpha _{3,1})&cos(alpha _{3,2})&1&cos(alpha _{4,3})\cos(alpha _{4,1})&cos(alpha _{4,2})&cos(alpha _{4,3})&1\end{pmatrix}}} — матрица Грама для приведённых рёбер сферического тетраэдра.

{displaystyle Phi ={begin{pmatrix}1&operatorname {ch} (alpha _{2,1})&operatorname {ch} (alpha _{3,1})&operatorname {ch} (alpha _{4,1})\operatorname {ch} (alpha _{2,1})&1&operatorname {ch} (alpha _{3,2})&operatorname {ch} (alpha _{4,2})\operatorname {ch} (alpha _{3,1})&operatorname {ch} (alpha _{3,2})&1&operatorname {ch} (alpha _{4,3})\operatorname {ch} (alpha _{4,1})&operatorname {ch} (alpha _{4,2})&operatorname {ch} (alpha _{4,3})&1\end{pmatrix}}} — матрица Грама для приведённых рёбер гиперболического тетраэдра.

{displaystyle alpha _{i,j}} — приведенное расстояние между i и j вершин.

{displaystyle Psi _{i,j}} — алгебраическое дополнение матрицы Psi .

Теорема синусов[править | править код]

{displaystyle {frac {Phi _{1,1}}{Psi _{1,1}}}={frac {Phi _{2,2}}{Psi _{2,2}}}={frac {Phi _{3,3}}{Psi _{3,3}}}={frac {Phi _{4,4}}{Psi _{4,4}}}} — для сферического и гиперболического тетраэдра.

Радиус описанной сферы[править | править код]

{displaystyle {begin{vmatrix}1&cos(alpha _{2,1})&cos(alpha _{3,1})&cos(alpha _{4,1})&1\cos(alpha _{2,1})&1&cos(alpha _{3,2})&cos(alpha _{4,2})&1\cos(alpha _{3,1})&cos(alpha _{3,2})&1&cos(alpha _{4,3})&1\cos(alpha _{4,1})&cos(alpha _{4,2})&cos(alpha _{4,3})&1&1\1&1&1&1&{frac {1}{cos ^{2}(R)}}\end{vmatrix}}=0} — для сферического тетраэдра.

Другая запись выражения: {displaystyle {frac {1}{cos(R)}}={frac {|{sqrt {Phi _{1,1}}}{overrightarrow {n_{1}}}+{sqrt {Phi _{2,2}}}{overrightarrow {n_{2}}}+{sqrt {Phi _{3,3}}}{overrightarrow {n_{3}}}+{sqrt {Phi _{4,4}}}{overrightarrow {n_{4}}}|}{sqrt {operatorname {det} Phi }}}}, где {displaystyle {overrightarrow {n_{1}}},{overrightarrow {n_{2}}},{overrightarrow {n_{3}}},{overrightarrow {n_{4}}}} нормали граней тетраэдра.

Или с координатами вершин тетраэдра: {displaystyle {frac {1}{cos(R)}}={frac {|{begin{vmatrix}0&{overrightarrow {i_{1}}}&{overrightarrow {i_{2}}}&{overrightarrow {i_{3}}}&{overrightarrow {i_{4}}}\1&X_{1}&Y_{1}&Z_{1}&T_{1}\1&X_{2}&Y_{2}&Z_{2}&T_{2}\1&X_{3}&Y_{3}&Z_{3}&T_{3}\1&X_{4}&Y_{4}&Z_{4}&T_{4}\end{vmatrix}}|}{sqrt {operatorname {det} Phi }}}}.

{displaystyle {begin{vmatrix}1&operatorname {ch} (alpha _{2,1})&operatorname {ch} (alpha _{3,1})&operatorname {ch} (alpha _{4,1})&1\operatorname {ch} (alpha _{2,1})&1&operatorname {ch} (alpha _{3,2})&operatorname {ch} (alpha _{4,2})&1\operatorname {ch} (alpha _{3,1})&operatorname {ch} (alpha _{3,2})&1&operatorname {ch} (alpha _{4,3})&1\operatorname {ch} (alpha _{4,1})&operatorname {ch} (alpha _{4,2})&operatorname {ch} (alpha _{4,3})&1&1\1&1&1&1&{frac {1}{operatorname {ch} ^{2}(R)}}\end{vmatrix}}=0} — для гиперболического тетраэдра.

Радиус вписанной сферы[править | править код]

{displaystyle {frac {1}{sin ^{2}(r)}}={frac {Phi _{1,1}+Phi _{2,2}+Phi _{3,3}+Phi _{4,4}+2{sqrt {Phi _{1,1}Phi _{2,2}}}cos(alpha _{1,2})+2{sqrt {Phi _{1,1}Phi _{3,3}}}cos(alpha _{1,3})+2{sqrt {Phi _{1,1}Phi _{4,4}}}cos(alpha _{1,4})+2{sqrt {Phi _{2,2}Phi _{3,3}}}cos(alpha _{2,3})+2{sqrt {Phi _{2,2}Phi _{4,4}}}cos(alpha _{2,4})+2{sqrt {Phi _{3,3}Phi _{4,4}}}cos(alpha _{3,4})}{operatorname {det} Phi }}} — для сферического тетраэдра.

Другая запись выражения: {displaystyle {frac {1}{sin(r)}}={frac {|{sqrt {Phi _{1,1}}}{overrightarrow {r_{1}}}+{sqrt {Phi _{2,2}}}{overrightarrow {r_{2}}}+{sqrt {Phi _{3,3}}}{overrightarrow {r_{3}}}+{sqrt {Phi _{4,4}}}{overrightarrow {r_{4}}}|}{sqrt {operatorname {det} Phi }}}}, где {displaystyle {overrightarrow {r_{1}}},{overrightarrow {r_{2}}},{overrightarrow {r_{3}}},{overrightarrow {r_{4}}}} единичные радиус векторы вершин тетраэдра.

{displaystyle {frac {1}{operatorname {sh} ^{2}(r)}}=-{frac {Phi _{1,1}+Phi _{2,2}+Phi _{3,3}+Phi _{4,4}+2{sqrt {Phi _{1,1}Phi _{2,2}}}operatorname {ch} (alpha _{1,2})+2{sqrt {Phi _{1,1}Phi _{3,3}}}operatorname {ch} (alpha _{1,3})+2{sqrt {Phi _{1,1}Phi _{4,4}}}operatorname {ch} (alpha _{1,4})+2{sqrt {Phi _{2,2}Phi _{3,3}}}operatorname {ch} (alpha _{2,3})+2{sqrt {Phi _{2,2}Phi _{4,4}}}operatorname {ch} (alpha _{2,4})+2{sqrt {Phi _{3,3}Phi _{4,4}}}operatorname {ch} (alpha _{3,4})}{operatorname {det} Phi }}} — для гиперболического тетраэдра.

Расстояние между центрами вписанной и описанной сфер[править | править код]

{displaystyle {frac {cos(d)}{sin(r)cos(R)}}={frac {{sqrt {Phi _{1,1}}}+{sqrt {Phi _{2,2}}}+{sqrt {Phi _{3,3}}}+{sqrt {Phi _{4,4}}}}{sqrt {operatorname {det} Phi }}}} — для сферического тетраэдра.

Формулы тетраэдра в барицентрических координатах[править | править код]

  • Координаты центра вписанной сферы:

{displaystyle mathbf {J} _{r}({sqrt {Phi _{1,1}}},{sqrt {Phi _{2,2}}},{sqrt {Phi _{3,3}}},{sqrt {Phi _{4,4}}}).} — для сферического тетраэдра.

  • Координаты центра описанной сферы:

{displaystyle mathbf {J} _{R}={begin{vmatrix}0&mathbf {J_{1}} &mathbf {J_{2}} &mathbf {J_{3}} &mathbf {J_{4}} \1&1&cos(alpha _{1,2})&cos(alpha _{1,3})&cos(alpha _{1,4})\1&cos(alpha _{2,1})&1&cos(alpha _{2,3})&cos(alpha _{2,4})\1&cos(alpha _{3,1})&cos(alpha _{3,2})&1&cos(alpha _{3,4})\1&cos(alpha _{4,1})&cos(alpha _{4,2})&cos(alpha _{4,3})&1\end{vmatrix}}.} — для сферического тетраэдра.

Тетраэдры в микромире[править | править код]

  • Правильный тетраэдр образуется при sp3-гибридизации атомных орбиталей (их оси направлены в вершины правильного тетраэдра, а ядро центрального атома расположено в центре описанной сферы правильного тетраэдра), поэтому немало молекул, в которых такая гибридизация центрального атома имеет место, имеют вид этого многогранника.
  • Молекула метана СН4.
  • Ион аммония NH4+.
  • Сульфат-ион SO42-, фосфат-ион PO43-, перхлорат-ион ClO4– и многие другие ионы.
  • Алмаз C — тетраэдр с ребром, равным 2,5220 ангстрем.
  • Флюорит CaF2, тетраэдр с ребром, равным 3,8626 ангстрем.
  • Сфалерит, ZnS, тетраэдр с ребром, равным 3,823 ангстрем.
  • Оксид цинка, ZnO.
  • Комплексные ионы [BF4] –, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+.
  • Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4-.

Тетраэдры в живой природе[править | править код]

Тетраэдр из грецких орехов

Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.

Тетраэдры в технике[править | править код]

  • Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм,Стержни испытывают только продольные нагрузки.
  • Прямоугольный тетраэдр используется в оптике. Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
  • Граф четверичного триггера представляет собой тетраэдр[9].

Тетраэдры в философии[править | править код]

«Платон говорил, что наименьшие частицы огня суть тетраэдры»[10].

См. также[править | править код]

  • Симплекс — n-мерный тетраэдр
  • Тетраэдр Мейсснера
  • Тетраэдр Рёло
  • Треугольник

Примечания[править | править код]

  1. ↑ Древнегреческо-русский словарь Дворецкого «τετρά-εδρον». Дата обращения: 20 февраля 2020. Архивировано из оригинала 28 декабря 2014 года.
  2. ↑ Селиванов Д. Ф.,. Тело геометрическое // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
  3. ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с. Архивная копия от 10 января 2014 на Wayback Machine
  4. ↑ В. Э. МАТИЗЕН Равногранные и каркасные тетраэдры «Квант» № 7, 1983 г.
  5. ↑ Моденов П.С. Задачи по геометрии. — М.: Наука, 1979. — С. 16.
  6. ↑ Маркелов С. Формула для объема тетраэдра// Математическое просвещение. Вып. 6. 2002. С. 132
  7. ↑ Источник. Дата обращения: 31 марта 2018. Архивировано 30 августа 2017 года.
  8. ↑ Источник. Дата обращения: 31 марта 2018. Архивировано 31 марта 2018 года.
  9. ↑ http://knol.google.com/k/триггер#view Архивная копия от 23 ноября 2010 на Wayback Machine Триггер
  10. ↑ Вернер Гейзенберг. У истоков квантовой теории. М. 2004 г. стр.107

Литература[править | править код]

  • Матизен В. Э., Дубровский. Из геометрии тетраэдра «Квант», № 9, 1988 г. С.66.
  • Заславский А. А. Сравнительная геометрия треугольника и тетраэдра // Математическое просвещение, сер. 3 (2004), № 8, стр. 78-92.
  • Понарин Я. П. Элементарная геометрия. Том 3. Треугольники и тетраэдры.2009 г.
Источник

Как найти вершину тетраэдра в трёхмерной плоскости, боковые рёбра которого равны, если даны координаты вершин основания?

Аркадий Иванович Свидригайлов



Мудрец

(11714),
закрыт



1 год назад

Дополнен 1 год назад

Ещё написано, что точка принадлежит плоскости yz…

Дополнен 1 год назад

…ТРХМЕРНОРНОЙ СИСТЕМЕ КООРДИНАТ, прошу прощения…

Лучший ответ

Рустам Искендеров

Искусственный Интеллект

(133392)


1 год назад

Решается система ур-й относительно уМ и zМ (хМ= 0 – это известно):
хА^2+(yM-yA)^2+(zM-zA)^2= хB^2+(yM-yB)^2+(zM-zB)^2 (1)
хА^2+(yM-yA)^2+(zM-zA)^2= хC^2+(yM-yC)^2+(zM-zC)^2 (2)
М – вершина тетраэдра.
Задача может и не иметь решения.

Аркадий Иванович СвидригайловМудрец (11714)

1 год назад

https://otvet.mail.ru/question/225457800

Остальные ответы

Александр Ильин

Просветленный

(26340)


1 год назад

Что такое трёхмерная плоскость?

Аркадий Иванович СвидригайловМудрец (11714)

1 год назад

А, да, дополнил…

Александр Ильин
Просветленный
(26340)
Аркадий Иванович Свидригайлов, Вершина тетраэдра находится в точке пересечения перпендикуляра к плоскости основания тетраэдра, проведённого из центра окружности описанной вокруг основания, с плоскостью yz/

Похожие вопросы

Источник

Онлайн решение Пирамиды по координатам вершин

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Как найти высоту тетраэдра формула

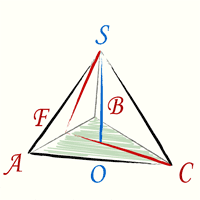
Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра

(h – высота тетраэдра, a – ребро тетраэдра)

Вывод формулы высоты тетраэдра

Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:

Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).

Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC .
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра

Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.

Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле

  • S – площадь любой грани,
  • H – высота, опущенная на эту грань

Правильный тетраэдр – частный вид тетраэдра

Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

  • Все грани равны.
  • Все плоские углы правильного тетраэдра равны 60°
  • Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
  • Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).

Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим

Вынесем 1/2a. Получим



Применим формулу разность квадратов

После небольших преобразований получим


Объем любого тетраэдра можно рассчитать по формуле
,
где ,

Подставив эти значения, получим

Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра

Вычисление объема тетраэдра, если известны координаты его вершин

Пусть нам даны координаты вершин тетраэдра

Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим


Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула

Свойства

Зная высоту тетраэдра, можно вычислить его ребро, перевернув формулу так, чтобы ребро было равно корню из трех вторых, умноженному на высоту. a=√(3/2) h

Выразив таким образом ребро тетраэдра через его высоту, можно найти периметр тетраэдра, то есть длину всех его ребер, площадь одной грани и площадь полной поверхности тетраэдра. Периметр тетраэдра будет равен шести длинам его ребер, площадь одной грани – ребру в квадрате, умноженному на корень из трех, деленный на четыре, а площадь полной поверхности – четырем площадям одной грани. P=6a=6√(3/2) h S_1=(√3 a^2)/4=(3√3 h^2)/8 S_(п.п.)=4S_1=(3√3 h^2)/2

Через высоту, подставленную вместо ребра в определенном соотношении можно найти соответственно и радиусы вписанной и описанной окружностей в основание тетраэдра. r=h/(2√2) R=h/√2

Апофема тетраэдра проходит из вершины к противоположной стороне грани под прямым углом и рассчитать ее можно как из прямоугольного треугольника с боковым ребром по той же грани, так и из прямоугольного треугольника во внутреннем пространстве тетраэдра с высотой. l=3h/(2√2)

Чтобы вычислить объем тетраэдра, необходимо возвести в куб ребро и разделить полученное значение на шесть корней из двух, либо подставить вместо ребра корень из трех вторых, умноженный на высоту и преобразовать формулу объема для высоты. V=(√3 h^3)/8

В тетраэдр можно вписать сферу или описать сферу около него, тогда, зная высоту, чтобы вычислить радиусы вписанной и описанной сфер, необходимо воспользоваться следующими, уже готовыми формулами. (рис.60.2, 60.3) r_1=h/4 R_1=3h/4

Примеры

Пример 1. Проверим, лежат ли точки A (1, −1, 1) , B (2, 2, 3) , C (3, 1, 3) и D (0, 0, 1) в одной плоскости.

Решение. Вычисляем смешанное произведение векторов A B = <1, 3, 2>, A C = <2, 2, 2>и A D = < −1, 1, 0>:

( A B , A C , A D ) = = 1 · ( −2) − 3 · 2 + 2 · 4 = 0 .

Так как смешанное произведение равно нулю, то векторы компланарны и, следовательно, точки лежат в одной плоскости.

Пример 2. Даны вершины тетраэдра A (2, 3, 1) , B (4, 1, −2) , C (6, 3, 7) и D ( −5, −4, 8) . Найдем длину высоты, опущенной из вершины D на плоскость основания A B C (рис. 1).

Решение. Из вершины A проводим векторы A B = <2, −2, −3>, A C = <4, 0, 6>и A D = < −7, −7, 7>.

В соответствии с геометрическим смыслом смешанногопроизведения имеем:

V тетр. =

· V параллелеп =

| ( A B , A C , A D ) | .

С другой стороны,

V тетр. =

S ΔABC · h ,   где   S ΔABC =

| [ A B , A C ] | .

Сравнивая эти равенства, получаем

1. Вычисляем смешанное произведение:

( A B , A C , A D ) = = 2 · 42 + 2 · 70 + ( −3) · ( −28) = 308 .

Следовательно, V тетр. = 308/6 .

2. Вычисляем координаты векторного произведения:

Онлайн решение Пирамиды по координатам вершин

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Источник

Добавить комментарий