Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.
1. Строим проекции треугольника АВС.

2. Строим проекции треугольника EDK.

3. Находим точку пересечения стороны АС с треугольником EDK

4. Находим точку пересечения стороны А B с треугольником EDK и строим линию пересечения MN

5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.

6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.

7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.
Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.

8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.
Определение видимости на чертеже.
В начертательной геометрии плоскости считаются непрозрачными, поэтому необходимо на проекциях определить видимость.
Для определения видимости на чертеже используем метод конкурирующих точек, сущность которого заключается в выборе двух скрещивающихся прямых.
Для определения видимости на фронтальной плоскости проекций V поступают так. Выбираем две скрещивающиеся прямые В²С² и М²N², фронтальные проекции которых пересекаются в точках 1 и 3. По горизонтальной проекции определяем, что проекция точки 3¢, лежащая на проекции прямой M¢N¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой В¢С¢, т. к она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на фронтальной плоскости проекций проекция М²N² будет закрывать проекцию В²С². Границей видимости является проекция точки пересечения К².
Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢С¢ и M¢N¢, горизонтальные проекции которых пересекаются в точках 4¢ и 5¢. По фронтальной проекции определяем, что проекция точки 5², лежащая на проекции прямой М²N², будет закрывать проекцию точки 4², лежащую на проекции прямой А²С², т. к. она будет ближе к наблюдателю. На чертеже направление взгляда наблюдателя показано стрелкой. Следовательно, на горизонтальной плоскости проекций проекция M¢N¢ будет закрывать проекцию А¢С¢. Границей видимости является проекция точки пересечения К¢.
Задача 3. Построение линии пересечения двух плоскостей, одна из которых занимает частное положение.
Даны две плоскости: плоскость ∆АВС – плоскость общего положения, плоскость ∆DЕК – плоскость частного положения, которая расположена перпендикулярно фронтальной плоскости проекций (рис. 3).
Рис. 3. Построение линии пересечения двух плоскостей, одна из которых занимает
частное положение
Фронтальная проекция ∆DЕК совпадает с фронтальным следом плоскости и фронтальной проекцией линии пересечения треугольников.
(KL) ‑ линия пересечения двух треугольников. Проекции этой линии пересечения – фронтальную и горизонтальную строят исходя из свойства принадлежности точек K и L сторонам (АВ) и (ВС), соответственно. Видимость треугольников на горизонтальной плоскости проекций определяем методом конкурирующих точек, рассмотренном в задаче 2.
Задача 4. Построение линии пересечения двух плоскостей общего положения.
Даны две плоскости общего положения, заданные треугольниками АВС и DЕК. Построить линию пересечения двух треугольников, определить видимость треугольников на проекциях.
Прямая линия, получаемая при взаимном пересечении двух плоскостей, определяется двумя точками, каждая из которых одновременно принадлежит обеим плоскостям. Общие точки определяются решением основной позиционной задачи начертательной геометрии – построение точки пересечения прямой с плоскостью (см. рис. 2).
Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (проецирующие плоскости). Решение задачи приведено на рис. 4.
Алгоритм решения задачи:
1. Определяют первую точку линии пересечения двух треугольников – точку М.
1.1. Фронтально-проецирующая плоскость a проведена через сторону DК и задана на чертеже фронтальным следом aV.
1.2. Плоскость a пересекает плоскость треугольника АВС по прямой (1,2), на чертеже строят две проекции этой прямой.
1.3. Прямая (1,2) пересекает сторону DК в точке М, строят две проекции точки М² и М¢.
2. Определяют вторую точку искомой линии пересечения двух треугольников – точку N.
2.1. Горизонтально-проецирующая плоскость b проведена через сторону АВ и задана на чертеже горизонтальным следом bН.
2.2. Плоскость b пересекает плоскость треугольника DЕК по прямой (3,4), на чертеже строят две проекции этой прямой.
2.3. Прямая (3,4) пересекает АВ в точке N, строят две проекции точки N² и N¢.
Плоскости треугольников АВС и DЕК пересекаются по прямой MN.
Рис. 4. Построение линии пересечения двух треугольников
3. Видимость плоских фигур на проекциях определяют методом конкурирующих точек.
Для определения видимости на фронтальной плоскости проекций V выбираем две скрещивающиеся прямые D²K² и A²B², фронтальные проекции которых пересекаются в точках 1² и 5². По горизонтальной проекции определяем, что проекция точки 5¢, лежащая на проекции прямой D¢K¢, будет закрывать проекцию точки 1¢, лежащую на проекции прямой А¢В¢, т. к. она будет ближе к наблюдателю. Следовательно, на фронтальной плоскости проекция D²K² будет закрывать проекцию A²B². Границей видимости является проекция линии пересечения M²N².
Для определения видимости на горизонтальной плоскости проекций Н выбираем две скрещивающиеся прямые А¢В¢ и D¢Е¢, горизонтальные проекции которых пересекаются в точках 3¢ и 6¢. По фронтальной проекции определяем, что проекция точки 3², лежащая на проекции прямой D²Е², будет закрывать проекцию точки 6², лежащую на проекции прямой A²B², т.к. она будет ближе к наблюдателю. Следовательно, на горизонтальной плоскости проекция D¢Е¢ будет закрывать проекцию А¢В¢. Границей видимости является проекция линии пересечения N¢M¢.
Задача 5. Построить две проекции линии пересечения плоскости a ‑ общего положения, заданной следами и плоскости b ‑ общего положения, заданной параллельными прямыми а и b.
Для решения данной задачи проводят вспомогательные плоскости-посредники частного положения (плоскости уровня), пересекающие заданные плоскости по прямым, недостающие проекции которых легко строятся и пересекаются в пределах чертежа.
Графическое решение задачи приведено на рис. 5.
Рис. 5. Построение линии пересечения двух плоскостей
Вспомогательная горизонтальная плоскость-посредник γ задана следом γV и пересекает плоскость a по горизонтали, проходящей через точку 3, а плоскость b по горизонтали (1, 2). Горизонтальные проекции этих горизонталей пересекаются в точке К. Строят фронтальную проекцию точки К, используя свойство принадлежности точки прямой линии. Точка К принадлежит обеим плоскостям a и b. Вторая точка N, общая для двух плоскостей a и b, определяется второй вспомогательной плоскостью-посредником частного положения δ (на чертеже задана следом δV). Искомая прямая (КN) является линией пересечения двух плоскостей a и b.
ПРИЛОЖЕНИЕ 1
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Гордон В.О., Семенцов-Огиевский М. А. Курс начертательной геометрии. Учеб. пособие. М.: Высшая школа. 2007.272 с.
2. Самохвалов Ю. И. Начертательная геометрия. Учебное пособие. Екатеринбург: Изд-во УГГУ. 2011. 121 с.
3. Самохвалов Ю. И., Шангина Е. И. Начертательная геометрия. Инженерная графика. Учебно-методическое пособие. Екатеринбург: Изд-во УГГУ. 2011. 96 с.
Определение видимости в начертательной геометрии с примерами
Определение видимости:
Точки, расположенные на одной проецирующей прямой, называются конкурирующими.
Точки, расположенные на одной горизонтально-проецирующей прямой, называются конкурирующими относительно горизонтальной плоскости проекций. Из двух точек A и B (рис. 7.1,а), конкурирующих на горизонтальной проекций, видима та, высота которой больше (B-видима, A-плоскости невидима).
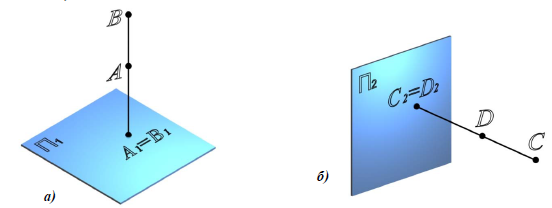
Рис. 7.1. Конкурирующие точки:
а – относительно горизонтальной плоскости проекций;
б – относительно фронтальной плоскости проекций
Точки, расположенные на одной фронтально-проецирующей прямой, называются конкурирующими относительно фронтальной плоскости проекций. Из двух точек C и D (рис. 7.1,б), конкурирующих относительно фронтальной плоскости проекций, видима та точка, у которой больше глубина (C- видима, D – невидима).
Рассмотрим определение видимости на комплексном чертеже на примере тетраэдра (рис. 7.2).
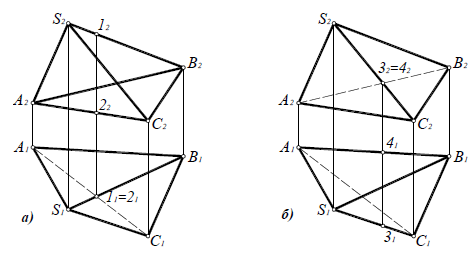
Рис. 6.17. Определение видимости ребер тетраэдра на комплексном чертеже:
а – относительно горизонтальной плоскости проекций;
б – относительно фронтальной плоскости проекций
Для определения видимости на горизонтальной плоскости проекций нужно найти точки, конкурирующие относительно П1 (рис. 7.2,а). Ребра SA, SC, AB и BC являются очерковыми, следовательно, видимыми. Остается выяснить видимость ребер AC и SB. Точки 1 ∈ SB и 2 ∈ACявляются конкурирующими на П1, поскольку находятся на горизонтально-проецирующем луче. Фронтальная проекция точки 1 лежит выше (высота точки 1 больше), поэтому она видима на П1, следовательно, видимо и реброSB, а ребро AC невидимо. Если хотя бы одно ребро грани невидимо, вся грань ABCневидима на П1.
Видимость на фронтальной проекции (рис. 7.2,б) определяется с помощью конкурирующих точек 3 ∈ SCи 4 ∈AB. Горизонтальная проекция точки 3 лежит ниже (глубина точки 3 больше), следовательно, точка 3 и ребро SCна фронтальной плоскости проекции видимы, а точка 4, ребро AB и грань ASB невидимы на П2.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Конструктивное отображение пространства
- Чертежи точки, отрезка прямой
- Чертежи плоскости
- Взаимное положение двух плоскостей, прямой линии и плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Геометрические тела
- Комплексный чертеж
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://poisk-ru.ru/s25018t12.html
http://www.evkova.org/-opredelenie-vidimosti
[/spoiler]
Как правильно обозначить вершины треугольника?
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.
Как найти вершину в геометрии?
Вершина — точка, в которой две кривые, две прямые либо два ребра сходятся. Из этого определения следует, что точка, в которой сходятся два луча, образуя угол, является вершиной, а также ею являются угловые точки многоугольников и многогранников.
Что называют вершинами треугольника?
Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.
Сколько у треугольника сторон и вершин?
И можно сделать вывод, что треугольник — это тоже многоугольник, у которого имеется ровно три угла, три стороны и три вершины.
Как обозначаются вершины в геометрии?
Стороны угла — это лучи, которые образуют угол. Вершина угла — точка «O». Стороны угла — «OA» и «OB».
Как обозначить стороны треугольника?
Треугольник – это многоугольник с тремя сторонами (или тремя углами). Стороны треугольника обозначаются часто малыми буквами, которые соответствуют заглавным буквам, обозначающим противоположные вершины. Если все три угла острые ( рис. 20 ), то это остроугольный треугольник.
Как обозначается вершина в геометрии?
Вершины принято обозначать заглавными буквами греческого алфавита, например, $A$, $B$, $C$. Задание.
Как определить вершину угла?
Стороны угла — это лучи, которые образуют угол. Вершина угла — точка «O».
Какие виды треугольников вы знаете?
Существует три вида треугольников по углам:
- остроугольные;
- прямоугольные;
- тупоугольные.
28 нояб. 2021 г.
Что такое вершины четырехугольника?
Четырехугольник обозначается его вершинами. Вершины четырехугольника называются соседними, если они являются концами одной из его сторон. Несоседние вершины называются противолежащими. Отрезки, которые соединяют противолежащие вершины четырехугольника, называются диагоналями.
Основное свойство Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Сколько вершин у пятиугольника?
Вспомним, сколько вершин имеет пятиугольник. У пятиугольника пять вершин. Определим, сколько диагоналей можно провести из одной вершины пятиугольника.
Что такое вершина и стороны?
Вершина угла — это точка, из которой выходят два луча, образующих угол и называемые сторонами угла (рис. 1).
Как можно обозначать углы?
Каждая сторона угла является лучом, а вершина — общим началом сторон. В математике существует специальный символ для обозначения угла, вот он: ∠. Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Как правильно обозначается треугольник?
Треугольник обычно называют по его вершинам. Вершины (точки, где сходятся две стороны треугольника) принято обозначать заглавными латинскими буквами (например, A, B, C). Тогда и треугольник будет называться теми же буквами — например, ABC.
Когда два треугольника называются равными?
Из определения непосредственно следует: в равных треугольниках против равных сторон лежат равные углы и обратно — против равных углов лежат равные стороны. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Как обозначить вершины многоугольника?
Обычно вершины многоугольника обозначают латинскими буквами и так его называют. Например, обозначив вершины четырехугольника буквами А, В, С и D, мы его будем обозначать — четырехугольник АВСD. Пятиугольник с вершинами E, F, G, H и К — пятиугольник EFGHK.
36. Мы уже рассматривали фигуру, состоящую из двух пересекающихся прямых (вертикальные углы, п. 18). Присоединим к ним еще третью прямую, пересекающую каждую из первых двух прямых в отдельно точке. Получим фигуру, данную на чер. 42: прямая a и прямая b пересекаются в точке C, прямые b и c – в точке A и прямые c и a – в точке B (мы называем для сокращения письма и речи каждую прямую одною малою буквою). Построенная фигура называется треугольником. Слово «треугольник» обозначается знаком Δ; обыкновенно треугольник обозначают тремя буквами, которыми названы три точки пересечения прямых. На чер. 42 имеем ΔABC.
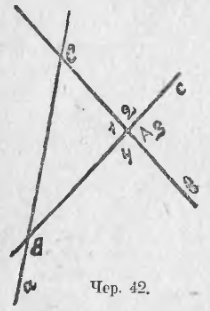
Прямые a, b и с называют сторонами треугольника, точки A, B и C – его вершинами. Треугольник разделяет плоскость на 7 областей, из которых 6 бесконечны, а одна конечная. Эта последняя ограниченна сторонами треугольника и называется площадью треугольника. При каждой вершине треугольника образуется по 4 угла меньших выпрямленного, например, ∠1, ∠2, ∠3 и ∠4 при точке A; внутренняя область одного из них, а именно ∠1, захватывает площадь треугольника (или: площадь треугольника лежит внутри ∠1) – этот угол называется внутренним углом треугольника, а остальные три (∠2, ∠3 и ∠4) – внешними. Среди внешних углов рассматривают обыкновенно лишь один при каждой вершине: при точке A ∠2 или ∠4, которые равны между собою как вертикальные, а ∠3 = внутреннему ∠1 на том же основании. Всего имеем в треугольнике 3 внутренних угла, которые часто называются просто углами треугольника.
Название «сторона треугольника» употребляется в двух смыслах: 1) этим именем называют, как указано выше, одну из трех прямых, напр., прямую a, неопределенно продолженную, 2) этим же именем называют отрезок этой прямой между двумя вершинами, напр., отрезок BC. Если вопрос таков, что приходится рассматривать только отрезки наших трех прямых, то треугольник изображают так, как на чер. 43.
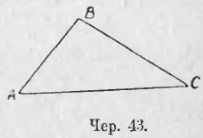
В треугольнике обыкновенно рассматривают 6 элементов: три стороны (отрезки) AB, BC и CA и 3 внутренних угла – ∠A, ∠B и ∠C.
37. Рассматривая ΔABC (чер. 42), мы видим, что здесь является возможным применить построение п. 29. Именно в конце п. 29 мы пришли к заключению, что если дана прямая и вне ее точка, то через эту точку можно построить прямую, параллельную данной. На чер. 42 мы можем, например, счесть прямую a за данную прямую и точку A за данную точку (либо: прямую b и точку B, либо прямую c и точку C). Построим же через точку A прямую, параллельную стороне BC (или прямой a). Получим фигуру, данную на чер. 44, где MN || BC. Назовем внутренние углы ΔABC нумерами 1, 2, 3 и занумеруем еще нумерами 4, 5 и 6 некоторые углы при точке A, полученные после построения прямой MN (см. чер. 44). Мы видим, что при точке A выполнено сложение нескольких углов. Например, мы видим, что
∠1 + ∠4 + ∠5,
причем сумма равна выпрям. углу BAD, т. е.
∠1 + ∠4 + ∠5 = выпрям. углу.
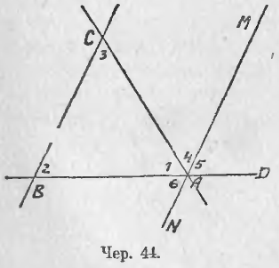
Но ∠4 = ∠3, так как это внутренние накрест-лежащие углы при параллельных BC и MN и секущей AC; также ∠5 = ∠2 как соответственные углы при параллельных BC и AM и секущей BD. Поэтому в предыдущем равенстве мы можем заменить ∠4 и ∠5 углами 3-м и 2-м; тогда получим
∠1 + ∠3 + ∠2 = выпр. углу,
т. е. оказывается, что во всяком треугольнике сумма внутренних углов (если их сложить) равна выпрямленному углу.
К тому же результату мы придем, если обратим внимание, что при точке A выполнено сложение ∠6, ∠1 и ∠4, причем сумма равна выпрям. углу NAM. Здесь, следовательно, мы видим:
∠6 + ∠1 + ∠4 = выпр. углу.
Но мы знаем, что ∠6 = ∠2, как внутр. накр.-леж. при параллельных BC и NM и секущей BD и ∠4 = ∠3, как внутр. накр.-леж. при тех же параллельных и секущей CA. Поэтому заключаем, что
∠2 + ∠1 + ∠3 = выпр. углу.
Обратим еще внимание на ∠CAD, являющийся внешним для ΔABC. Мы видим, что лучом AM он разбит на 2 слагаемых, на ∠4 и ∠5, т. е.
∠CAD = ∠4 + ∠5.
Но, как мы уже выяснили, ∠4 = ∠3 и ∠5 = ∠2; следовательно.,
∠CAD = ∠3 + ∠2.
Эти 2 угла (∠3 и ∠2) являются внутренними углами ΔABC, не смежными с ∠CAD (с ∠CAD смежен ∠1). Поэтому мы заключаем:
Внешний угол треугольника (образованный одною его стороною и продолжением другой) равен сумме двух внутренних углов с ним не смежных.
Мы можем из чертежа 44 выделить только те элементы, которые необходимы для выяснения полученных свойств, и удалить все остальное, не нужное, тогда получим упрощенный чертеж. На чертежах 45 и 46 даны 2 таких упрощенных чертежа. Для чер. 45 имеем:
1) ∠1 + ∠4 + ∠5 = выпр. углу, но ∠4 = ∠3 и ∠5 = ∠2; след., ∠1 + ∠3 + ∠2 = выпр. углу.
2) ∠CAD = ∠4 + ∠5, но ∠4 = ∠3 и ∠5 = ∠2. Следов, ∠CAD = ∠3 + ∠2.
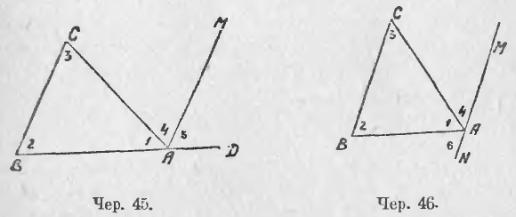
Для чер. 46 имеем: ∠6 + ∠1 + ∠4 = выпр. углу, но ∠6 = ∠2 и ∠4 = ∠3, следов., ∠2 + ∠6 + ∠3 = выпр. углу.
38. Задача. Построить Δ с такими же сторонами, как у данного треугольника. Пусть дан ΔABC (чер. 47). Строим где-либо прямую и на ней при помощи циркуля откладываем отрезок MN = AC. Таким образом мы получили две вершины искомого треугольника M и N. Чтобы найти третью вершину, воспользуемся задачею п. 27: надо найти такую точку, чтобы отрезок, соединяющий ее с точкой M, был равен AB и отрезок, соединяющий ее с точкою N, был = CB. Эти круги пересекутся в двух точках P и Q; соединив эти точки прямыми с M и N, получим два искомых треугольника: один ΔMPN и другой ΔMQN (MN = AC; MP = MQ = AB; NP = NQ = CB). Примем, что два круга не могут пресекаться более, чем в двух точках (впоследствии этот вопрос будет разъяснен в п. 128). Согласно п. 26 точки пересечения наших кругов P и Q расположены симметрично относительно линии центров MN. Поэтому при перегибании всей фигуры по оси симметрии MN точка P должна совместиться с точкою Q, а, следовательно, ΔMPN совместиться с ΔMQN. Согласно п. 2, мы можем назвать эти треугольники равными или конгруэнтными.
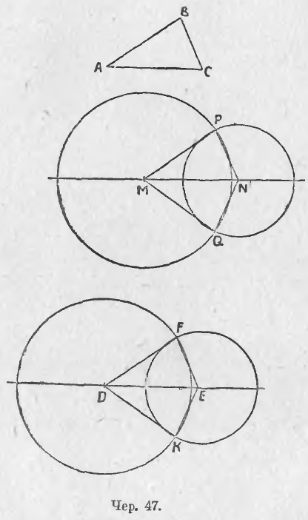
Если мы повторим где-либо на ином месте плоскости предыдущее построение, то получим еще 2 треугольника DEF и DEK с такими же сторонами, как у ΔABC (DE = AC; DF = DK = AB, EF = EK = CB). Также в силу того, что прямая DE есть ось симметрии всей фигуры, мы заключим, что эти два треугольника равны или конгруэнтны между собою. Возникает теперь вопрос: можно ли добиться того, чтобы какой-либо из треугольников второй пары (напр., ΔDEF) совпал с каким-либо треугольником первой пары (напр., с ΔMPN)?
Круги позволят решить этот вопрос. Передвинем нижнюю фигуру чертежа 47 так, чтобы точка D совпала с точкой M и точка E с точкой N (этого добиться можно потому, что MN = DE, – каждый из этих отрезков = AC). Тогда круги фигуры DFEK совпадут соотв. с кругами фигуры MPNQ (ибо радиусы этих кругов соотв. равны между собою и центры их совместились). Поэтому и точки пересечения этих двух пар кругов должны совместиться, т. е., напр., точка F совместится с точкою P и точка K с Q. Отсюда заключаем, что и ΔDEF должен совместиться с ΔMNP, что принято записывать в виде ΔDEF = ΔMNP. Мы также могли бы к ΔABC пристроить два круга, принимая точки A и C за центры и отрезки AB и CB за радиусы, и также при помощи этих кругов пришли бы к заключению, что
ΔABC = ΔMPN = ΔMQN = ΔDFE = ΔDKE.
Итак, если построить два треугольника с попарно равными сторонами, то эти треугольники конгруэнтны (или равны).
(Следует помнить, что для геометрических фигур слова «конгруэнтны» или «равны» означают, что эти фигуры совпадают при наложении).
39. В предыдущем п. мы научились строить равные треугольники. Пусть ΔA’B’C’ = ΔABC (чер. 48) и при наложении сторона A’B’ совпадает с AB, B’C’ – с BC и A’C’ – с AC. Тогда и углы этих треугольников совпадают, а именно ∠C’ с ∠C, ∠A’ с ∠A и ∠B с ∠B, т. е. ∠C’ = ∠C, ∠A’ = ∠A и ∠B = ∠B. Ясно, что в равных треугольниках равные углы лежат против равных сторон и обратно: равные стороны против равных углов.
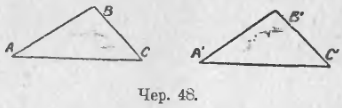
40. Задача. Построить треугольник по трем данным сторонам.
Пусть даны три отрезка a, b и c (чер. 49); требуется построить треугольник так, чтобы его стороны были соответственно равны данным отрезкам.
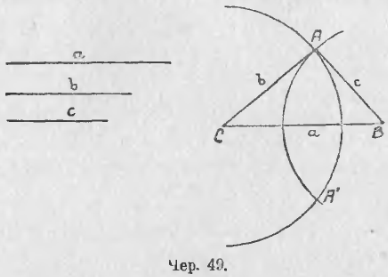
Строим где-либо один из данных отрезков a; тогда определяется две вершины треугольника B и C. Третья вершина должна расположиться так, чтобы отрезок, соединяющий ее с точкою B, был = с и отрезок, соединяющий ее с точкою C, был = b; поэтому нахождение ее сведется к задаче п. 27: надо, принимая B за центр, построить круг радиусом = c, и принимая C за центр, – круг радиусом = b и точку пересечения этих кругов, напр., точку A, соединить с точками B и C – тогда ΔABC и есть искомый. Соединив другую точку пересечения окружностей A’ с точками B и C, получим другой такой же Δ, расположенный симметрично с первым относительно оси BC.
Для того, чтобы задача была возможна, надо, чтобы: 1) a – b < c или c > a – b и 2) a + b > c или c < a + b, т. е. чтобы один из данных отрезков был больше разности двух других и меньше их суммы.
41. Пусть теперь даны 2 отрезка a и b (чер. 50). Требуется построить треугольник так, чтобы его стороны были a, b и b (задача возможна, если a < b + b или a < 2b).
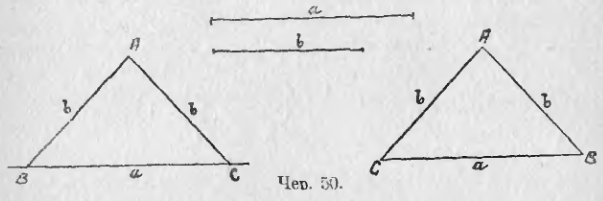
Согласно предыдущему п., построение легко выполняется и получим, напр., ∆ABC, у которого две стороны (AB и AC) равны между собой. Такой ∆ называется равнобедренным; та его сторона, которая не имеет себе равных (в ∆ABC сторона BC = a), называется основанием равнобедренного треугольника, а противоположная вершина A называется «вершиною равнобедренного треугольника», причем этим названием эта вершина A как бы выделяется из остальных вершин.
Вообразим, что ∆ABC повернут другою стороною, то новый ∆ABC (чер. 50 — справа) можно простым передвижением совместить с прежним: сторона BC левого треугольника равна стороне CB правого, сторона AB левого = стороне AC правого и сторона AC левого = стороне AB правого, а мы уже знаем, что если стороны двух треугольников попарно равны, то эти треугольники равны, т. е. при наложении совмещаются (п. 38) и ∠B левого треугольника равен, следовательно, углу C правого, или, что то же самое, углу C тоже левого треугольника. Итак, в равнобедренном ∆ABC, у которого AB = AC, ∠B также = ∠C. Это свойство выразим словами:
В равнобедренном треугольнике углы при основании равны
или
В треугольнике, у которого две стороны равны, против равных сторон лежат равные углы.
42. Построим, наконец, ∆, у которого все 3 стороны равнялись бы данному отрезку a. Построение легко выполнить (чер. 50 bis). Этот ∆ называется равносторонним. Легко видеть, что этот ∆ можно счесть за равнобедренный с основанием CB; тогда ∠C = ∠B. Но его можно принять и за равнобедренный с основанием AB и тогда ∠A = ∠B, откуда приходим к заключению, что в равностороннем треугольнике все 3 угла равны между собою.
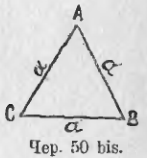
43. В п. 38 мы получили признак равенства треугольников: если стороны двух треугольников попарно равны, то и треугольники равны. Теперь мы можем, накладывая один треугольник на другой, получить еще другие признаки.
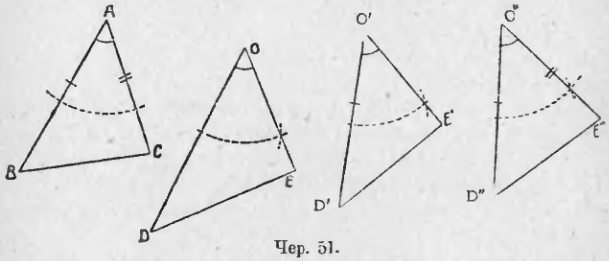
Построим какой угодно ∆ABC (чер. 51); затем построим ∠O = ∠A (п. 28) и на сторонах этого угла отложим отрезки OD > AB и OE < AC). На чер. 51 даны пунктиром те дуги, которые необходимы для построения ∠O = ∠A. Соединив точки D и E, получим ∆ODE. Наложим ∆ODE на ∆ABC так, чтобы ∠O совпал с ∠A (ведь ∠O = ∠A). В силу неравенств OD > AB и OE < AC, ∆ODE при этом наложении не совместится с ∆ABC (следует нарисовать, как именно расположится ∆ODE при этом наложении). Построим еще ∆O’D’E’ так, чтобы 1) ∠O’ = ∠A, 2) ∠O’D’ = ∠AB и 3) O’E’ < AC. Тогда при наложении треугольника O’D’E’ на ∆ABC так, чтобы ∠O’ совместился с ∠A, легко уясним, что и вершина D’ должна также совместиться с точкою B (в силу равенства O’D’ = AB), но точка E’ не совпадет с точкою C, – треугольники опять не совместятся (нарисовать их расположение при указанном наложении!). Теперь легко ответить на вопрос: как надо изменить сторону O’E’ треугольника O’D’E’, чтобы быть убежденным, что этот ∆ совместится с ∆ABC?
Надо, ответим мы, увеличить сторону O’E’ так, чтобы она сделалась равною стороне AC.
Итак, если мы построим ∆O”D”E” так, чтобы 1) ∠O” = ∠A, 2) O”D” = AB и 3) O”E” = AC, то мы можем быть убеждены, что ∆O”D”E” = ∆ABC. Замечая, что ∠O” и ∠A составлены попарно равными сторонами (на чертеже равные стороны и равные углы отмечены одинаковыми значками), мы можем сделать заключение:
Если построены два треугольника так, что у них по две равных стороны и углы, составляемые этими сторонами, также равны, то эти треугольники равны.
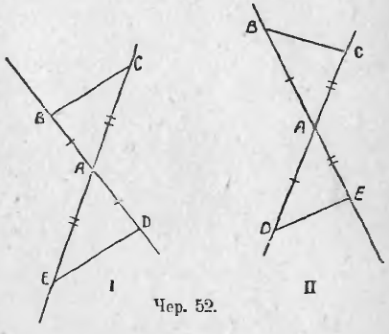
44. Построим два вертикальных угла при точке A – они, мы знаем, равны (чер. 52) и на сторонах этих углов отложим попарно равные отрезки AB = AD и AC = AE (это можно сделать двумя способами, почему на чер. 52 даны две фигуры I и II). Равны ли полученные треугольники? Как надо переместить ∆AED, чтобы он совпал с ∆ABC? Указать, какой угол одного из каждой пары треугольников равен какому-либо углу другого (можно воспользоваться п. 39 или выяснить, как именно расположится ∆AED при совмещении его с ∆ABC).
45. Построим какой-либо ∆ABC (чер. 53); затем построим ∆ODE так, чтобы сторона DE = стороне BC, чтобы ∠D был больше ∠B, но ∠E был меньше ∠C. Наложим ∆ODE на ∆ABC так, чтобы DE совпала с BC (точка D с B и точка E с C); этого добиться можно, так как эти стороны равны по построению.
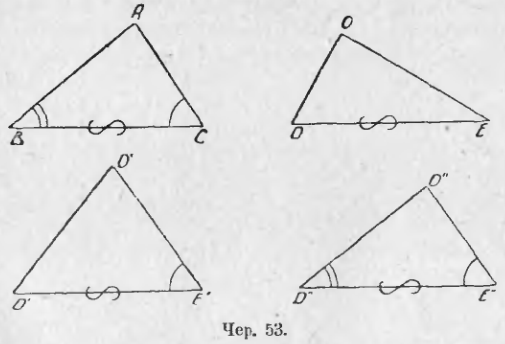
Тогда, в силу того, что ∠D > ∠B и ∠E < ∠C, ∆ODE не совместится ∆ABC (следует нарисовать, как именно при этом наложении расположится ∆ODE). Построим еще ∆O’D’E’ так, чтобы D’E’ = BC, а также ∠E = ∠C, но, по-прежнему, ∠D’ был больше ∠B. Тогда при наложении ∆O’D’E’ на ∆ABC так, чтобы точки D’ и E’ совпали соответственно с точками B и C, увидим, что сторона E’O’ пойдет вне угла B (∠D’ > ∠B) и точка O’ не совпадет с точкою A (следует нарисовать расположение этих треугольников при рассматриваемом наложении). ∆O’D’E’ опять не совместиться с ∆ABC.
Теперь не трудно ответить на вопрос: как надо изменить ∠D’, чтобы добиться совпадения ∠O’D’E’ с ∆ABC? Надо, ответим мы, уменьшить ∠D’ так, чтобы он сделался равен ∠B.
Итак, если мы построим ∆O”D”E” так, чтобы 1) D”E” = BC, 2) ∠E” = ∠C и 3) ∠D” = ∠B, то мы можем быть убеждены, что ∆O”D”E” = ∆ABC. Замечая, что равные стороны D”E” и BC этих треугольников расположены между соответственно равными углами (на чертеже равные стороны и равные углы отмечены одинаковым знаками), мы можем установить еще признак равенства треугольников:
Если построены 2 треугольника так, что они имеют по два равных угла и по равной стороне между этими углами, то такие треугольники равны.
46. Построим какой-либо ∆ABC (чер. 54) и при концах стороны AB построим ∠BAD = ∠CAB и ∠ABD = ∠ABC. Тогда получим ∆ABD.
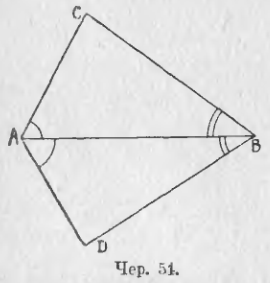
Равны ли треугольники ACB и ABD? Как можно добиться совмещения этих треугольников? Указать равные стороны в этих треугольниках (можно воспользоваться п. 39).
47. Имея в виду пп. 38, 43 и 45, мы можем теперь свести вместе признаки равенства треугольников:
1) Если три стороны одного треугольника равны соответственно трем сторонам другого, то эти треугольники равны.
2) Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого, то эти треугольники равны.
3) Если два угла и сторона между ними одного треугольника равны соответственно двум углам и стороне между ними другого, то эти треугольники равны.
Прибавим сюда еще заключение п. 39: в равных треугольниках равные углы расположены против равных сторон и равные стороны против равных углов.
Для совмещения равных треугольников иногда бывает необходимо один из них перевернуть другою стороною.
48. Задача. Построить треугольник по двум данным сторонам и углу между ними.
Пусть даны 2 отрезка a и b и угол m (чер. 55). Требуется построить ∆ так, чтобы данные отрезки были его сторонами и угол, ими составленный, был = ∠m.
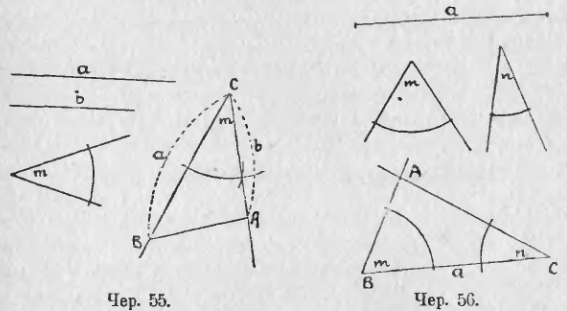
Строим: 1) при точке C угол, равный ∠m, 2) на сторонах построенного угла откладываем CB = a и CA = b, 3) соединяем точки A и B. Получим искомый ∆ABC.
49. Задача. Построить треугольник по данной стороне и двум прилегающим к ней углам.
Дан отрезок a и 2 угла m и n (чер. 56); требуется построить ∆ так, чтобы одна из его сторон = a и углы, к ней прилегающие, были равны ∠m и ∠n.
Строим: 1) отрезок BC = a, 2) при точке B угол = ∠m и при точке C угол = ∠n так, чтобы одна сторона каждого из этих углов шла по BC; точка пересечения A других сторон построенных углов даст вершину A искомого треугольника.
Может случиться, что стороны построенных углов или вовсе не пересекаются (параллельны между собою – это случится, если ∠m + ∠n = выпр. углу) или пересекутся по другой стороне от BC; в последнем случае получится треугольник, у которого к стороне a прилегают углы не m и не n, а дополняющие их до выпрямленного.
Мы знаем, что сумма всех трех внутренних углов треугольника равна выпрямленному углу, а сумма двух внутренних его углов должна быть, следовательно, меньше выпрямленного. Поэтому для возможности данной задачи необходимо, чтобы было: ∠m + ∠n < выпрямленного угла.
Упражнения
- Построить равнобедренный треугольник по углу при его вершине и по боковой стороне.
- Построить равнобедренный треугольник по основанию и по углу при основании.
Как найти вершину треугольника?

Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.
1 способ (графический)

- В системе координат отмечаем две заданные вершины.
- Ставим ножку циркуля в одну из построенных точек.
- Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
- Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
- Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
- Определяем координаты полученных точек, исходя из полученного чертежа.
Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.
2 способ (аналитический)
Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)
- Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
- Составляем соотношения
AC=√((x-x1)^2+(y-y1)^2)
BC=√((x-x2)^2+(y-y2)^2)
AB=√((x2-x1)^2+(y2-y1)^2) - Учитывая, что треугольник равносторонний, составляем систему уравнений:
AC=BC
AC=AB
Или система уравнений:
√((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
√((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2) - Методом подстановки решаем полученную систему.
Теперь вы знаете, как найти вершину треугольника.
Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
![]()
получим систему уравнений
![[ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)
Вычтем из первого уравнения системы второе:
![]()
![]()
![]()
![]()
Теперь из второго уравнения системы вычтем третье:
![]()
![]()
![]()
Приравняем правые части равенств b=-2a+10 и b=3a-20:
![]()
![]()
![]()
![]()
Подставим в первое уравнение системы a=6 и b=-2:
![]()
![]()
![]()
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
![]()
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Прямая на плоскости

Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X , Y координаты вектора; xi , yi — координаты точки Аi ; xj , yj — координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5 ; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой: 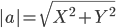
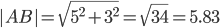
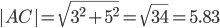
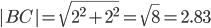
3) Угол между прямыми. Угол между векторами a1(X1;Y1) , a2(X2;Y2) можно найти по формуле: 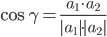
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC 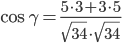
γ = arccos(0.88) = 28.07 0
8) Уравнение прямой. Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2) , представляется уравнениями: 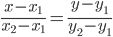
Уравнение прямой AB . Каноническое уравнение прямой: 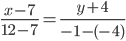 или
или 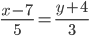
y= 3 /5x- 41 /5 или 5y-3x+41=0
Треугольник
- Высота
- Биссектриса
- Медиана
Треугольник — это замкнутая ломаная линия, состоящая из трёх звеньев:

Вершины ломаной называются вершинами треугольника, а её звенья — сторонами треугольника. Углы, образованные двумя сторона треугольника, называются углами треугольника:

В треугольнике ABC вершины A, B и C — это вершины треугольника, звенья AB, BC и CA — стороны треугольника. Три угла — ∠ABC, ∠BCA и ∠CAB — углы треугольника. Часто углы треугольника обозначаются только одной буквой: ∠A, ∠B, ∠C.
Треугольник обычно обозначается тремя буквами, стоящими при его вершинах. Например, треугольник ABC, или BCA, или CBA. Вместо слова треугольник часто используется знак  . Так, запись
. Так, запись  ABC будет читаться:
ABC будет читаться: треугольник ABC
.
У каждого треугольника 3 вершины, 3 стороны и 3 угла.
Высота
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на его основание. Высота треугольника может быть опущена и на продолжение основания.

Отрезок BN — это высота  ABC. Отрезок EL высота
ABC. Отрезок EL высота  DEF, опущенная на продолжение стороны DF.
DEF, опущенная на продолжение стороны DF.
Длина высоты — это длина отрезка от вершины угла до пересечения с основанием.
Каждый треугольник имеет три высоты.
Биссектриса
Биссектриса угла треугольника — прямая, делящая угол треугольника пополам. Длина отрезка этой прямой от вершины угла до точки пересечения с противоположной стороной называется длиной биссектрисы.

Отрезок BN — это биссектриса  ABC.
ABC.
Каждый треугольник имеет три биссектрисы.
Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Длина этого отрезка называется длиной медианы.

Отрезок BN — это медиана  ABC.
ABC.
Каждый треугольник имеет три медианы.
