Вершина треугольника – определение
В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.

Определение вершины треугольника
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.

Рис. 1. Вершина в треугольнике.
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.

Рис. 2. Обозначение вершин в треугольнике.
Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.

Рис. 3. Свойство внешнего угла треугольника.
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.
Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Примеры решений по аналитической геометрии на плоскостиВ этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п. Решения задач о треугольнике онлайнЗадача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти: Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$. Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти: Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$. Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон. Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$. Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$. Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$. [spoiler title=”источники:”] http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik http://www.matburo.ru/ex_ag.php?p1=agtr [/spoiler] |
Как найти вершину треугольника?

Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.
1 способ (графический)

- В системе координат отмечаем две заданные вершины.
- Ставим ножку циркуля в одну из построенных точек.
- Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
- Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
- Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
- Определяем координаты полученных точек, исходя из полученного чертежа.
Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.
2 способ (аналитический)
Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)
- Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
- Составляем соотношения
AC=√((x-x1)^2+(y-y1)^2)
BC=√((x-x2)^2+(y-y2)^2)
AB=√((x2-x1)^2+(y2-y1)^2) - Учитывая, что треугольник равносторонний, составляем систему уравнений:
AC=BC
AC=AB
Или система уравнений:
√((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
√((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2) - Методом подстановки решаем полученную систему.
Теперь вы знаете, как найти вершину треугольника.
Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
![]()
получим систему уравнений
![[ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)
Вычтем из первого уравнения системы второе:
![]()
![]()
![]()
![]()
Теперь из второго уравнения системы вычтем третье:
![]()
![]()
![]()
Приравняем правые части равенств b=-2a+10 и b=3a-20:
![]()
![]()
![]()
![]()
Подставим в первое уравнение системы a=6 и b=-2:
![]()
![]()
![]()
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
![]()
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Прямая на плоскости
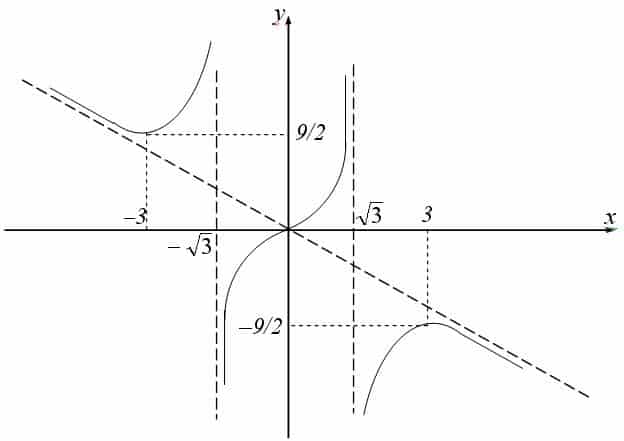
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X , Y координаты вектора; xi , yi — координаты точки Аi ; xj , yj — координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5 ; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой: 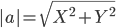
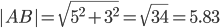
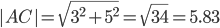
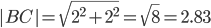
3) Угол между прямыми. Угол между векторами a1(X1;Y1) , a2(X2;Y2) можно найти по формуле: 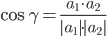
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC 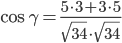
γ = arccos(0.88) = 28.07 0
8) Уравнение прямой. Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2) , представляется уравнениями: 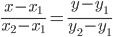
Уравнение прямой AB . Каноническое уравнение прямой: 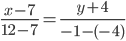 или
или 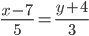
y= 3 /5x- 41 /5 или 5y-3x+41=0
Вершина треугольника


4.2
Средняя оценка: 4.2
Всего получено оценок: 215.
4.2
Средняя оценка: 4.2
Всего получено оценок: 215.
В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.
Определение вершины треугольника
В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.
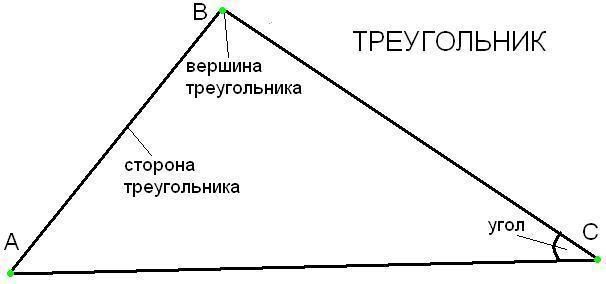
Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.
Характеристики понятия
Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).
Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.
Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.
Использование вершины треугольника
При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.
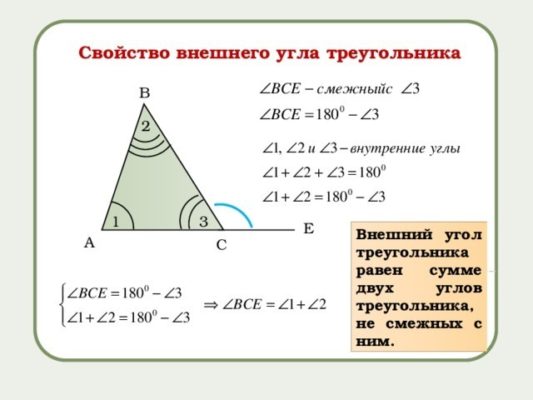
Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.

Что мы узнали?
Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Лёня Кондратьев
5/5
-

Али Юсупов
3/5
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 215.
А какая ваша оценка?
1.
координаты центра
xCenter = 0
yCenter = 0
радиус и хорда
radius = 5
horda = 3
координаты первой точки
xCircle для первой точки на окружности берем центр
yCircle и длинну радиуса т.е. координаты получаются (0;5)
Считаем угол при центре в радианах
alpha = arctan((radius^2 + horda^2 – radius^2) / (2 * radius * horda));
Вычисляем синусы/косинусы
cosAlpha = Math.cos(alpha);
sinAlpha = Math.sin(alpha);
Вычисляем координаты последней точки
xCircle1 = xCenter + (xCircle – xCenter) * cosAlpha – (yCircle – yCenter) * sinAlpha;
yCircle1 = yCenter + (xCircle – xCenter) * sinAlpha + (yCircle – yCenter) * cosAlpha;
Для следующей точки берем в качестве xCircle и yCircle полученные ранее xCircle1 и yCircle1 и т.д.
2. т.к. известны две координаты – получаем длинну одного катета, известная сторона/2 второй катет, по теореме пифагора – гипотенуза, аналогично первому пункту находим вершину, повторить 4 раза получаем координаты прямоугольника.
3. бъём прямоугольник на два треугольника и
считаются произведения (1, 2, 3 – вершины треугольника, 0 – точка):
(x1 – x0) * (y2 – y1) – (x2 – x1) * (y1 – y0)
(x2 – x0) * (y3 – y2) – (x3 – x2) * (y2 – y0)
(x3 – x0) * (y1 – y3) – (x1 – x3) * (y3 – y0)
Если они одинакового знака, то точка внутри треугольника, если что-то из этого – ноль, то точка лежит на стороне, иначе точка вне треугольника.
4. Находим расстояние между точкой и центром окружности. Если оно окажется меньше радиуса окружности R, то точка внутри, если больше R, то вне, а если равна R, то на окружности.
Всем откликнувшимся спасибо за помощь, а не откликнувшимся за то, что не мешали.
Прошу поправить, если есть ошибки.
| Треугольник | |
|---|---|
 |
|
| Рёбра | 3 |
| Символ Шлефли | {3} |
Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника. Часть плоскости, ограниченная сторонами, называется внутренностью треугольника: нередко треугольник рассматривается вместе со своей внутренностью (например, для определения понятия площади)[1].
Стороны треугольника образуют в вершинах треугольника три угла, поэтому треугольник можно также определить как многоугольник, у которого имеется ровно три угла[2], т.е. как часть плоскости, ограниченную тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Треугольник является одной из важнейших геометрических фигур, повсеместно используемых в науке и технике, поэтому исследование его свойств проводилось начиная с глубокой древности.
Понятие треугольника допускает различные обобщения. Можно определить это понятие в неевклидовой геометрии (например, на сфере): на таких поверхностях треугольник определяется как три точки, соединённые геодезическими линиями. В 

Иногда рассматривают вырожденный треугольник, три вершины которого лежат на одной прямой. Если не оговорено иное, треугольник в данной статье предполагается невырожденным.
Основные элементы треугольника[править | править код]
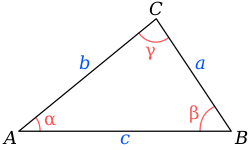
Вершины, стороны, углы[править | править код]
Традиционно вершины треугольника обозначаются заглавными буквами латинского алфавита: 







Треугольник 
Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (


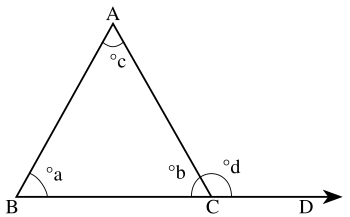
Внешним углом 



Внешним углом 





Периметром треугольника называют сумму длин трёх его сторон, а половину этой величины называют полупериметром.
Классификация треугольников[править | править код]
По виду наибольшего угла[править | править код]
Основной источник: [3]
Поскольку в евклидовой геометрии сумма углов треугольника равна 

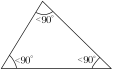
- Если все углы треугольника острые, то треугольник называется остроугольным.
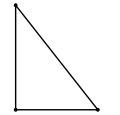
- Если один из углов треугольника прямой (равен
), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
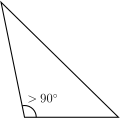
- Если один из углов треугольника тупой (больше
), то треугольник называется тупоугольным, Остальные два угла, очевидно, острые (треугольников с двумя тупыми или прямыми углами быть не может).
По числу равных сторон (или по степени симметричности)[править | править код]
- Разносторонним называется треугольник, у которого все три стороны не равны.
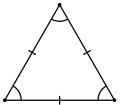
- Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием[4]. В равнобедренном треугольнике углы при основании равны.
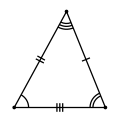
- Равносторонним или правильным называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают. Равносторонний треугольник является частным случаем равнобедренного треугольника.
| Треугольник | Количество осей симметрии | Количество пар равных сторон |
|---|---|---|
| Разносторонний | Нет | Нет |
| Равнобедренный | 1 | 1 |
| Равносторонний | 3 | 3 |
Медианы, высоты, биссектрисы[править | править код]

Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, центр тяжести находится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы. Треугольник с вершинами в серединах медиан называется срединным треугольником. Основания медиан данного треугольника образуют так называемый дополнительный треугольник.
Длину медианы 

для других медиан аналогично.
-

Высота в треугольниках различного типа
-

Высоты пересекаются в ортоцентре
Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника. Треугольник с вершинами в основаниях высот называется ортотреугольником.
Длину высоты 

; для других высот аналогично.
Длины высот, опущенных на стороны. можно также найти по формулам:[5]:p.64
.

Биссектриса 
Биссектрисой (биссéктором) треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности (инцентром).
Если треугольник разносторонний (не равнобедренный), то биссектриса, проведённая из любой его вершины, лежит между медианой и высотой, проведёнными из той же вершины. Ещё одно важное свойство биссектрисы: она делит противоположную сторону на части, пропорциональные прилегающим к ней сторонам[6].
Длину биссектрисы 

, где
— полупериметр.
.
; здесь
— высота.
Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный.
Описанная и вписанная окружности[править | править код]

Треугольник АВС и его окружности: вписанная (синяя), описанная (красная) и три вневписанные (зелёные)
Описанная окружность (см. рис. справа) — окружность, проходящая через все три вершины треугольника. Описанная окружность всегда единственна, её центр совпадает с точкой пересечения перпендикуляров к сторонам треугольника, проведённых через середины сторон. В тупоугольном треугольнике этот центр лежит вне треугольника[6].
Вписанная окружность (см. рис. справа) — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром, он совпадает с точкой пересечения биссектрис треугольника.
Следующие формулы позволяют вычислить радиусы описанной 

где
— площадь треугольника,
— его полупериметр.
,
где 
Ещё два полезных соотношения:
[7]
.
Существует также формула Карно[8]:
,
где 











Расстояние от центра описанной окружности например до стороны 
;
расстояние от ортоцентра например до вершины 
.
Признаки равенства треугольников[править | править код]

Равенство по двум сторонам и углу между ними

Равенство по стороне и двум прилежащим углам

Равенство по трем сторонам
Треугольник на евклидовой плоскости однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:[9]
,
,
(равенство по двум сторонам и углу между ними);
,
,
(равенство по стороне и двум прилежащим углам);
,
,
(равенство по трём сторонам).
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.
Дополнительный признак: треугольники равны, если у них совпадают две стороны и угол, лежащий против большей из этих сторон[10].
Дополнительный признак {по двум сторонам и углу не между ними, если этот угол прямой или тупой}.
Если в треугольниках 




В сферической геометрии и в геометрии Лобачевского существует признак равенства треугольников по трём углам.
Признаки подобия треугольников[править | править код]
Основные свойства элементов треугольника[править | править код]
Свойства углов[править | править код]
Во всяком треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы[10].
Каждый внешний угол треугольника равен разности между 180° и соответствующим внутренним углом. Для внешнего угла также имеет место теорема о внешнем угле треугольника: внешний угол равен сумме двух других внутренних углов, с ним не смежных[10].
Неравенство треугольника[править | править код]
В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном — равна. Иначе говоря, длины сторон невырожденного треугольника связаны следующими неравенствами:
.
Дополнительное свойство: каждая сторона треугольника больше разности двух других сторон[10].
Теорема о сумме углов треугольника[править | править код]
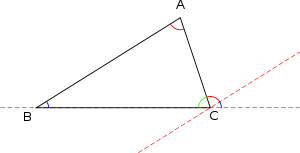
Сумма внутренних углов треугольника всегда равна 180°:
.
В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше.
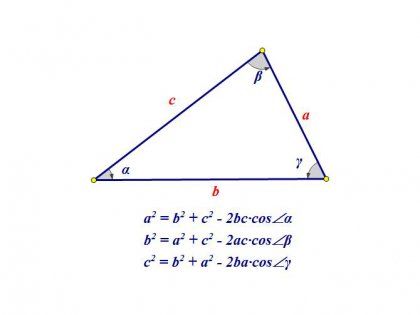
Теорема синусов[править | править код]
,
где 
Теорема косинусов[править | править код]
.
Является обобщением теоремы Пифагора.
- Замечание. теоремой косинусов также называют следующие две формулы, легко выводимые из основной теоремы косинусов (см. с. 51, ф. (1.11-2))[12].
.
Теорема о проекциях[править | править код]
Источник: [13].
.
Теорема тангенсов (формулы Региомонтана)[править | править код]
Теорема котангенсов[править | править код]
.
Формулы Мольвейде[править | править код]
.
Решение треугольников[править | править код]
Вычисление неизвестных сторон, углов и других характеристик треугольника, исходя из известных, исторически получило название «решения треугольников». При этом используются приведенные выше общие тригонометрические теоремы, а также признаки равенства и подобия треугольников.
Площадь треугольника[править | править код]
- Далее используются обозначения
- Площадь треугольника связана с его основными элементами следующими соотношениями.
— формула Герона
[14]
[15]
— ориентированная площадь треугольника.
— см. Аналоги формулы Герона
- Частные случаи
-
— для прямоугольного треугольника
— для равностороннего треугольника
Другие формулы[править | править код]
- Существуют другие формулы, такие, как например,[16]
для угла 
- В 1885 г. Бейкер (Baker)[17] предложил список более ста формул площади треугольника. Он, в частности, включает:
,
,
,
.
Неравенства для площади треугольника[править | править код]
Для площади справедливы неравенства:
и
,
где в обоих случаях равенство достигается тогда и только тогда, когда треугольник равносторонний (правильный).
История изучения[править | править код]
Свойства треугольника, изучаемые в школе, за редким исключением, известны с ранней античности. Зачатки тригонометрических знаний можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э.[21]
Общая и достаточно полная теория геометрии треугольников (как плоских, так и сферических) появилась в Древней Греции[22]. В частности, во второй книге „Начал“ Евклида теорема 12 представляет собой словесный аналог теоремы косинусов для тупоугольных треугольников[23]. Следующая за ней теорема 13 — вариант теоремы косинусов для остроугольных треугольников. Свойствами элементов треугольников (углов, сторон, биссектрис и др.) после Евклида занимались Архимед, Менелай, Клавдий Птолемей, Папп Александрийский[24].
В IV веке, после упадка античной науки, центр развития математики переместился в Индию. Сочинения индийских математиков (сиддханты) показывают, что их авторы были хорошо знакомы с трудами греческих астрономов и геометров[25]. Чистой геометрией индийцы интересовались мало, но их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен.
В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Их астрономические трактаты, аналогичные индийским сиддхантам, назывались „зиджи“; типичный зидж представлял собой сборник астрономических и тригонометрических таблиц, снабжённый руководством по их использованию и (не всегда) изложением общей теории[26]. Сравнение зиджей периода VIII—XIII веков показывает быструю эволюцию тригонометрических знаний. Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век).
Сабит ибн Курра (IX век) и ал-Баттани (X век) первыми открыли фундаментальную теорему синусов для частного случая прямоугольного сферического треугольника. Для произвольного сферического треугольника доказательство было найдено (разными способами и, вероятно, независимо друг от друга) Абу-л-Вафой, ал-Худжанди и ибн Ираком в конце X века[27]. В другом трактате ибн Ирака сформулирована и доказана теорема синусов для плоского треугольника[28].
Фундаментальное изложение тригонометрии (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году[29]. Его „Трактат о полном четырёхстороннике“ содержит практические способы решения типичных задач, в том числе труднейших, решённых самим ат-Туси[30]. Таким образом, к концу XIII века были открыты базовые теоремы, необходимые для практической работы с треугольниками.
В Европе развитие тригонометрической теории стало чрезвычайно важным в Новое время, в первую очередь для артиллерии, оптики и навигации при дальних морских путешествиях. В 1551 году появились 15-значные тригонометрические таблицы Ретика, ученика Коперника, с шагом 10»[31]. Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов, причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций.
Изучение треугольника продолжилось в XVII веке: была доказана теорема Дезарга (1636), открыта точка Торричелли (1640) и изучены её свойства. Джованни Чева доказал свою теорему о трансверсалях (1678). Лейбниц показал, как вычислять расстояние от центра тяжести треугольника до других его замечательных точек[24]. В XVIII веке были обнаружены прямая Эйлера и окружность шести точек (1765).
В начале XIX века была открыта точка Жергонна. В 1828 году была доказана теорема Фейербаха. К концу XIX века относится творчество Эмиля Лемуана, Анри Брокара, Жозефа Нойберга. Окружность девяти точек исследовали Понселе, Брианшон и Штейнер, Были обнаружены ранее неизвестные геометрические связи и образы — например, окружность Брокара, точки Штейнера и Тарри. В 1860 году Шлёмильх доказал теорему: три прямые, соединяющие середины сторон треугольника с серединами его соответствующих высот, пересекаются в одной точке. В 1937 году советский математик С. И. Зетель показал, что эта теорема верна не только для высот, но и для любых других чевиан. Исследования перечисленных выше геометров превратили геометрию треугольника в самостоятельный раздел математики[32].
Значительный вклад в геометрию треугольника внёс в конце XIX — начале XX века Фрэнк Морли. Он доказал, что геометрическое место центров кардиоид, вписанных в треугольник, состоит из девяти прямых, которые, взятые по три, параллельны трём сторонам равностороннего треугольника. Кроме того, 27 точек, в которых пересекаются эти девять прямых, являются точками пересечения двух трисектрис треугольника, принадлежащих к одной и той же его стороне. Наибольшую известность получил частный случай этой теоремы: внутренние трисектрисы углов треугольника, прилежащих к одной и той же стороне, пересекаются попарно в трёх вершинах равностороннего треугольника. Обобщение этих работ опубликовал Анри Лебег (1940), он
ввел 
С 1830-х годов в геометрии треугольника стали широко использоваться трилинейные координаты точек. Активно развивалась теория преобразований — проективное, изогональное, изотомическое и другие. Полезной оказалась идея рассмотрения задач теории треугольников на комплексной плоскости.
[32].
Дополнительные сведения[править | править код]
Все факты, изложенные в этом разделе, относятся к евклидовой геометрии.
- Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой. Обычно под чевианой понимают не один такой отрезок, а один из трёх таких отрезков, проведённых из трёх разных вершин треугольника и пересекающихся в одной точке. Они удовлетворяют условиям теоремы Чевы. Чевианы, соединяющие вершину треугольника с точками противоположной стороны, отстоящими на заданное отношение
от её концов, называют недианами.
- Средней линией треугольника называют отрезок, соединяющий середины двух сторон этого треугольника. Три средние линии треугольника разделяют его на четыре равных треугольника в 4 раза меньшей площади, чем площадь исходного треугольника.
- Серединные перпендикуляры (медиатрисы) к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.
- Чевианы, лежащие на прямых, симметричных медианам относительно биссектрис, называются симедианами. Они проходят через одну точку — точку Лемуана.
- Чевианы, лежащие на прямых, изотомически сопряжённых биссектрисам относительно оснований медиан, называются антибиссектрисами. Они проходят через одну точку — центр антибиссектрис.
- Кливер треугольника — это отрезок, одна вершина которого находится в середине одной из сторон треугольника, вторая вершина находится на одной из двух оставшихся сторон, при этом кливер разбивает периметр пополам.
- Некоторые точки в треугольнике — «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли. Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это — точки Аполлония. Точки
и
такие, что
и
называются точками Брокара.
Некоторые замечательные прямые треугольника[править | править код]
- В любом треугольнике центр тяжести, ортоцентр, центр описанной окружности и центр окружности Эйлера лежат на одной прямой, называемой прямой Эйлера.
- В любом треугольнике центр тяжести, центр круга, вписанного в него (инцентр), его точка Нагеля и центр круга, вписанного в дополнительный треугольник
(или Центр Шпикера), лежат на одной прямой, называемой второй прямой Эйлера (прямой Нагеля)
- Прямая, проходящая через центр описанной окружности и точку Лемуана, называется осью Брокара. На ней лежат точки Аполлония.
- Также на одной прямой лежат точки Торричелли и точка Лемуана.
- Если на описанной окружности треугольника взять точку, то её проекции на стороны треугольника будут лежать на одной прямой, называемой прямой Симсона данной точки. Прямые Симсона диаметрально противоположных точек описанной окружности перпендикулярны.
Трилинейные поляры треугольника[править | править код]
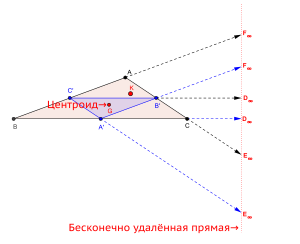
Бесконечно удалённая прямая — трилинейная поляра центроида
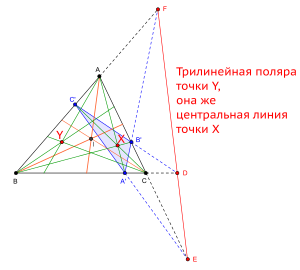
Построение трилинейной поляры точки

Ось Лемуана — трилинейная поляра точки Лемуана показана красным цветом
- Трилинейная полярой точки Лемуана служит ось Лемуана (см. рис.)

Ось внешних биссектрис или антиортовая ось (antiorthic axis) — трилинейная поляра центра вписанной окружности (инцентра) треугольника 

Ортоцентрическая ось (Orthic axis) — трилинейная поляра ортоцентра
- Ортоцентрическая ось
(Orthic axis) — трилинейная поляра ортоцентра (см. рис.)
- Трилинейные поляры точек, лежащих на описанной конике, пересекаются в одной точке (для описанной окружности это — точка Лемуана, для описанного эллипса Штейнера — центроид).
Вписанные и описанные фигуры для треугольника[править | править код]
Преобразования[править | править код]
Ниже описаны 3 вида преобразований: 1) Изогональное сопряжение, 2) Изотомическое сопряжение, 3) Изоциркулярное преобразование.
Изогональное сопряжение[править | править код]
- Если прямые, проходящие через вершины и некоторую точку, не лежащую на сторонах и их продолжениях, отразить относительно соответствующих биссектрис, то их образы также пересекутся в одной точке, которая называется изогонально сопряжённой исходной (если точка лежала на описанной окружности, то получившиеся прямые будут параллельны).
- Изогонально сопряжёнными являются многие пары замечательных точек:
- Центр описанной окружности и ортоцентр (точка пересечения высот),
- Центроид (точка пересечения медиан) и точка Лемуана (точка пересечения симедиан),
- Центр девяти точек и точка Косниты треугольника, связанная с теоремой Косниты[34];
- Две точки Брокара;
- Точки Аполлония и точки Торричелли.
- Точка Жергонна и центр отрицательной гомотетии вписанной и описанной окружности.
- Точка Нагеля и центр положительной гомотетии вписанной и описанной окружности (точка Веррьера).
- Описанные окружности подерных треугольников изогонально сопряжённых точек совпадают.
- Фокусы вписанных эллипсов изогонально сопряжены.
- Изогональное сопряжение имеет ровно четыре неподвижные точки (то есть точки, которые сопряжены самим себе): центр вписанной окружности и центры вневписанных окружностей треугольника[35].
- Если для любой внутренней точки треугольника построить три точки, симметричные ей относительно сторон, а затем через три последние провести окружность, то ее центр изогонально сопряжен исходной точке[36].
Изогональные сопряжения линий треугольника[править | править код]
- Под действием изогонального сопряжения прямые переходят в описанные коники, а описанные коники — в прямые.
- Так, изогонально сопряжены:
- гипербола Киперта и ось Брокара,
- гипербола Енжабека и прямая Эйлера,
- гипербола Фейербаха и линия центров вписанной и описанной окружностей.
- Некоторые известные кубики — например, кубика Томсона — изогонально самосопряжены в том смысле, что при изогональном сопряжении всех их точек в треугольнике снова получаются кубики.
Изотомическое сопряжение[править | править код]
Если вместо симметричной чевианы брать чевиану, основание которой удалено от середины стороны так же, как и основание исходной, то такие чевианы также пересекутся в одной точке. Получившееся преобразование называется изотомическим сопряжением. Оно также переводит прямые в описанные коники.
- Изотомически сопряжены следующие точки:
- точка Жергонна и Нагеля,
- точка пересечения биссектрис (инцентр) и точка пересечения антибиссектрис,
- Точке Лемуана (точке пересечения симедиан) треугольника изотомически сопряжена его точке Брокара,
- Центроид (точка пересечения медиан) изотомически сопряжён сам себе.
При аффинных преобразованиях изотомически сопряжённые точки переходят в изотомически сопряжённые. При изотомическом сопряжении в бесконечно удалённую прямую перейдёт описанный эллипс Штейнера.
Композиция изогонального (или изотомического) сопряжения и трилинейной поляры[править | править код]
Изоциркулярное преобразование[править | править код]
Если в сегменты, отсекаемые сторонами треугольника от описанного круга, вписать окружности, касающиеся сторон в основаниях чевиан, проведённых через некоторую точку, а затем соединить точки касания этих окружностей с описанной окружностью с противоположными вершинами, то такие прямые пересекутся в одной точке. Преобразование плоскости, сопоставляющее исходной точке получившуюся, называется изоциркулярным преобразованием [39]. Композиция изогонального и изотомического сопряжений является композицией изоциркулярного преобразования с самим собой. Эта композиция — проективное преобразование, которое стороны треугольника оставляет на месте, а ось внешних биссектрис переводит в бесконечно удалённую прямую.
Тригонометрические тождества только с углами[править | править код]
(первое тождество для тангенсов)
Замечание. Соотношение выше применимо только тогда, когда ни один из углов не равен 90° (в таком случае функция тангенса всегда определена).
,[40]
(второе тождество для тангенсов)
,
(первое тождество для синусов)
,[40]
(второе тождество для синусов)
,[7]
(тождество для косинусов)
(тождество для отношения радиусов)
Замечание. При делении обеих частей второго тождества для тангенсов на произведение 
,
по форме (но не по содержанию) очень похожее на первое тождество для тангенсов.
Разные соотношения[править | править код]
Метрические соотношения в треугольнике приведены для 
Где:
,
и
— стороны треугольника,
,
— отрезки, на которые биссектриса
делит сторону
,
,
,
— медианы, проведённые соответственно к сторонам
,
и
,
,
,
— высоты, опущенные соответственно на стороны
,
и
,
— радиус вписанной окружности,
— радиус описанной окружности,
— полупериметр,
— площадь,
— расстояние между центрами вписанной и описанной окружностей.
- Для любого треугольника, у которого стороны связаны неравенствами
, а площадь равна
, длины срединных перпендикуляров или медиатрис, заключённых внутри треугольника, опущенных на соответствующую сторону (отмеченную нижним индексом), равны[41]:Corollaries 5 and 6
,
и
.
Формулы площади треугольника в декартовых координатах на плоскости[править | править код]
- Обозначения
-
— координаты вершин треугольника.
Общая формула площади треугольника в декартовых координатах на плоскости[править | править код]
В частности, если вершина A находится в начале координат (0, 0), а координаты двух других вершин есть B = (xB, yB) и C = (xC, yC), то площадь может быть вычислена в виде 1⁄2 от абсолютного значения определителя
Последнюю формулу площади треугольника в английской литературе именуют формулой площади, заключенной внутри ломаной натянутого на гвозди шнурка (shoelace formula), или геодезической формулой (surveyor’s formula[42]), или формулой площади Гаусса.
Вычисление площади треугольника в пространстве с помощью векторов[править | править код]
Пусть вершины треугольника находятся в точках 


Введём вектор площади ![mathbf {S} ={frac {1}{2}}[mathbf {r} _{B}-mathbf {r} _{A},mathbf {r} _{C}-mathbf {r} _{A}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b21515fcc2caefebf9c4876eab2cfdb298b8b05)
Положим 



и аналогично
Площадь треугольника равна 
Альтернативой служит вычисление длин сторон (по теореме Пифагора) и далее по формуле Герона.
Вычисление площади треугольника через комплексные декартовы координаты его вершин[править | править код]
Если обозначить комплексные декартовы координаты (на комплексной плоскости) вершин треугольника соответственно через 





,
что эквивалентно формуле площади, заключенной внутри ломаной натянутого на гвозди шнурка (shoelace formula), или геодезической формуле (surveyor’s formula[42]), или формуле площади Гаусса.
Треугольник в неевклидовых геометриях[править | править код]
На сфере[править | править код]
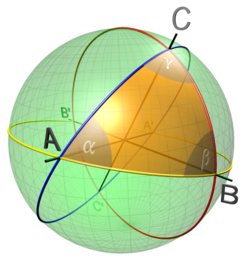
Свойства треугольника со сторонами 





Сумма углов (невырожденного) треугольника строго больше 
Любые подобные треугольники равны.
Теорема синусов (здесь и далее сторону сферического треугольника принято измерять не линейной мерой, а величиной опирающегося на неё центрального угла):
,
Теоремы косинусов:
,
.
На плоскости Лобачевского[править | править код]
Для треугольника со сторонами 





Сумма углов (невырожденного) треугольника строго меньше 
Как и на сфере, любые подобные треугольники равны.
Теорема синусов
,
Теоремы косинусов
,
.
Связь суммы углов с площадью треугольника[править | править код]
Значение для суммы углов треугольника во всех трёх случаях (евклидова плоскость, сфера, плоскость Лобачевского) является следствием формулы Гаусса — Бонне
.
В случае треугольника эйлерова характеристика 





|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 января 2017) |
Треугольник в римановой геометрии[править | править код]
|
|
Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 января 2017) |
Обозначение[править | править код]
| Символ | Юникод | Название |
|---|---|---|
| △ | U+25B3 | white up-pointing triangle |
См. также[править | править код]
- Глоссарий планиметрии
- Тригонометрические тождества
- Тригонометрия
- Энциклопедия центров треугольника
Дополнительные статьи о геометрии треугольника можно найти в категориях:
- Категория:Геометрия треугольника.
- Категория:Теоремы евклидовой геометрии
- Категория:Планиметрия
- Категория:Теоремы планиметрии
Примечания[править | править код]
- ↑ Треугольник // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5.
- ↑ 1 2 Справочник по элементарной математике, 1978, с. 218.
- ↑ Подходова Н. С. [и др.] Раздел II. Теория обучения математике. Глава 7. Математические понятия. Методика работы с ними (п. 7.5. Классификация понятий) // Методика обучения математике в 2 ч. Часть 1 : учебник для вузов / под ред. Н. С. Подходовой, В. И. Снегуровой. — М.: Издательство Юрайт, 2023. — С. 139. — 274 с. — ISBN 978-5-534-08766-6, ББК 74.202.5я73. — ISBN 978-5-534-14731-5.
- ↑ Основанием равнобедренного треугольника всегда называют сторону, не равную двум другим.
- ↑ 1 2 Altshiller-Court, Nathan, College Geometry, Dover, 2007.
- ↑ 1 2 Справочник по элементарной математике, 1978, с. 221.
- ↑ 1 2 Longuet-Higgins, Michael S., «On the ratio of the inradius to the circumradius of a triangle», Mathematical Gazette 87, March 2003, 119—120.
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.: Учпедгиз, 1962. задача на с. 120—125. параграф 57, с.73.
- ↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 41.
- ↑ 1 2 3 4 Справочник по элементарной математике, 1978, с. 219.
- ↑ Шарыгин И. Ф. Глава 3. (п. 3.2. Признаки равенства треугольников) // Геометрия. 7—9 кл.: учеб. для общеобразоват. учреждений / И. Ф. Шарыгин, ответств.ред. Т. С. Зельдман. — М.: Дрофа, 2012. — С. 79—80. — 462 с. — 3000 экз. — ISBN 978-5-358-09918-0, ББК 22.151я72, УДК 373.167.1:514.
- ↑ Корн Г., Корн Т. Справочник по математике, 1973.
- ↑ Корн Г., Корн Т. Справочник по математике, 1973, ф. 1.11-4.
- ↑ Sa ́ndor Nagydobai Kiss, «A Distance Property of the Feuerbach Point and Its Extension», Forum Geometricorum 16, 2016, 283—290. http://forumgeom.fau.edu/FG2016volume16/FG201634.pdf Архивная копия от 24 октября 2018 на Wayback Machine
- ↑ Pathan, Alex, and Tony Collyer, “Area properties of triangles revisited, ” Mathematical Gazette 89, November 2005, 495—497.
- ↑ Mitchell, Douglas W., “The area of a quadrilateral, ” Mathematical Gazette 93, July 2009, 306—309.
- ↑ Baker, Marcus, “A collection of formulae for the area of a plane triangle, « Annals of Mathematics, part 1 in vol. 1(6), January 1885, 134—138; part 2 in vol. 2(1), September 1885, 11-18. The formulas given here are #9, #39a, #39b, #42, and #49. The reader is advised that several of the formulas in this source are not correct.
- ↑ Chakerian, G. D. „A Distorted View of Geometry.“ Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
- ↑ Rosenberg, Steven; Spillane, Michael; and Wulf, Daniel B. „Heron triangles and moduli spaces“, Mathematics Teacher 101, May 2008, 656—663.
- ↑ Posamentier, Alfred S., and Lehmann, Ingmar, The Secrets of Triangles, Prometheus Books, 2012.
- ↑ van der Waerden, Bartel Leendert. Geometry and Algebra in Ancient Civilizations. — Springer, 1983. — ISBN 3-540-12159-5.
- ↑ Глейзер Г. И., 1982, с. 77.
- ↑ Глейзер Г. И., 1982, с. 94—95.
- ↑ 1 2 Из истории геометрии треугольника, 1963, с. 129.
- ↑ Матвиевская Г. П., 2012, с. 40—44.
- ↑ Матвиевская Г. П., 2012, с. 51—55.
- ↑ Матвиевская Г. П., 2012, с. 92—96.
- ↑ Матвиевская Г. П., 2012, с. 111.
- ↑ Туси Насирэддин. Трактат о полном четырёхстороннике. Баку, Изд. АН АзССР, 1952.
- ↑ Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I. — С. 105.
- ↑ История математики, том I, 1970, с. 320.
- ↑ 1 2 Из истории геометрии треугольника, 1963, с. 130—132.
- ↑ Из истории геометрии треугольника, 1963, с. 132—133.
- ↑ Rigby, John (1997), Brief notes on some forgotten geometrical theorems. Mathematics and Informatics Quarterly, volume 7, pages 156—158 (as cited by Kimberling).
- ↑ В. В. Прасолов. Точки Брокара и изогональное сопряжение. — М.: МЦНПО, 2000. — (Библиотека «Математическое просвещение»). — ISBN 5-900916-49-9.
- ↑ Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду. Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова. Москва: МЦНМО, 2009.
- ↑ Kimberling, Clark. Central Points and Central Lines in the Plane of a Triangle (англ.) // Mathematics Magazine : magazine. — 1994. — June (vol. 67, no. 3). — P. 163—187. — doi:10.2307/2690608.
- ↑ Kimberling, Clark. Triangle Centers and Central Triangles. — Winnipeg, Canada: Utilitas Mathematica Publishing, Inc., 1998. — С. 285. Архивная копия от 10 марта 2016 на Wayback Machine
- ↑ Мякишев А.Г. Элементы геометрии треугольника(Серия: «Библиотека „Математическое просвещение“») М.:МЦНМО,2002.с.14—17
- ↑ 1 2 Vardan Verdiyan & Daniel Campos Salas, «Simple trigonometric substitutions with broad results», Mathematical Reflections no 6, 2007.
- ↑ Mitchell, Douglas W. (2013), «Perpendicular Bisectors of Triangle Sides», Forum Geometricorum 13, 53-59.
- ↑ 1 2 Bart Braden. The Surveyor’s Area Formula (англ.) // The College Mathematics Journal (англ.) (рус. : magazine. — 1986. — Vol. 17, no. 4. — P. 326—337. — doi:10.2307/2686282. Архивировано 6 апреля 2015 года.
Литература[править | править код]
- Адамар Ж. Элементарная геометрия. Часть 1: Планиметрия. Изд. 4-е, М.: Учпедгиз, 1957. 608 с.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 с.
- Ефремов Дм. Новая геометрия треугольника. Одесса, 1902.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Мякишев А. Г. Элементы геометрии треугольника. — М.: МЦНМО, 2002.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 48-50. — ISBN 5-94057-170-0.
- История
- Гайдук Ю. М., Хованский А. М. Из истории геометрии треугольника // Вопросы истории физико-математических наук. — М.: Высшая школа, 1963. — С. 129—133. — 524 с.
- Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76—95. — 240 с.
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.
Ссылки[править | править код]
- Расчёт элементов треугольника.
- Расчёт параметров треугольника по координатам его вершин.




![{displaystyle {dfrac {a-b}{a+b}}={dfrac {operatorname {tg} {dfrac {alpha -beta }{2}}}{operatorname {tg} {dfrac {alpha +beta }{2}}}}={dfrac {operatorname {tg} {dfrac {alpha -beta }{2}}}{operatorname {ctg} {dfrac {gamma }{2}}}};quad {frac {b-c}{b+c}}={frac {operatorname {tg} [{frac {1}{2}}(beta -gamma )]}{operatorname {tg} [{frac {1}{2}}(beta +gamma )]}};{frac {a-c}{a+c}}={frac {operatorname {tg} [{frac {1}{2}}(alpha -gamma )]}{operatorname {tg} [{frac {1}{2}}(alpha +gamma )]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04c97f77f6f451b3556bf0038f041c4f87fa2095)






















