Собрание уникальных книг, учебных материалов и пособий, курсов лекций и отчетов по геодезии, литологии, картированию, строительству, бурению, вулканологии и т.д.
Библиотека собрана и рассчитана на инженеров, студентов высших учебных заведений по соответствующим специальностям. Все материалы собраны из открытых источников.
Разбивка трассы.
Закрепление и измерение углов. Выбранную трассу надёжно закрепляют на местности. Вершину угла, образуемого прямыми линиями трассы, закрепляют забиваемым вровень с поверхностью земли колом (рис. 15.1, а). На расстоянии 1 м от кола с внешней стороны угла на его биссектрисе устанавливают столб с затёсом. На затёсе, обращённом в сторону вершины угла, делают надпись, указывающую номер вершины угла, год, угол поворота трассы, радиус вписываемой в угол кривой, расстояние от начала трассы. Измеряют расстояния от вершины угла до расположенных вблизи приметных местных предметов (дерево, угол здания, валун и др.) и показывают их на абрисе – схеме, составляемой для облегчения отыскания вершины угла в последующем, особенно в случае разрушения опознавательного столба.
Над колом, закрепляющим вершину угла, устанавливают теодолит и измеряют лежащий справа по ходу трассы угол b между направлениями на соседние вершины углов. Измерение выполняют одним приёмом с точностью 0,5¢. Угол поворота трассы (рис. 15.2) вычисляют по формулам:
αпр = 180°– b2 (при повороте трассы вправо: b < 180°) или
αлев = b3 – 180° (при повороте трассы влево: b > 180°).
Для контроля буссолью измеряют магнитные азимуты линий.
б)
а)
![inj_geo_2-112.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-112.jpg)
Рис. 15.1 Закрепление точек на трассе:
а – закрепление вершины угла: 1 – кол; 2 – столб;
б – закрепление пикета и плюса: 1 – кол; 2 – сторожок
![inj_geo_2-113.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_2-113.jpg)
Рис. 15.2 Углы поворота трассы
Разбивка пикетажа и измерение длин линий. Расстояния между вершинами углов поворота трассы измеряют светодальномером или мерной лентой. Измерение выполняют дважды с предельной относительной погрешностью измерений не более 1:1000-1:2000. В ходе одного из измерений трассу разбивают на отрезки длиной 100 метров по горизонтальному проложению. Конец каждого отрезка – пикет; его закрепляют, забивая вровень с землёй кол. Впереди него по ходу трассы на расстоянии 20-25 см забивают второй, возвышающийся над поверхностью земли кол – сторожок (рис. 15.1, б). На сторожке надписывают порядковый номер пикета, например, ПК13, что означает: номер пикета – 13, расстояние от начала трассы – 1300 м.
Чтобы получить 100-метровые горизонтальные проложения, следует, учитывая наклон местности, увеличивать длину откладываемых наклонных отрезков. Поэтому в них вводят поправки за наклон со знаком плюс. Часто вместо введения поправок, натягивая мерную ленту, удерживают её в горизонтальном положении и проектируют отвесом её приподнятый конец на землю. Чтобы лента меньше провисала, поддерживают её в середине.
Кроме пикетов, колышком и сторожком закрепляют плюсовые точки (или просто “плюсы”), где на трассе изменяется наклон местности. На сторожке в этом случае пишут номер предыдущего пикета и расстояние от него в метрах, например ПК13+46, что означает 46 м после пикета № 13 или 1346 м от начала пикетажа.
Плюсовыми точками фиксируют также места пересечения трассой любых сооружений, дорог, линий связи, водотоков, границ угодий и т. д.
Поперечники. Там, где местность имеет заметный (более 1:5) поперечный уклон, на каждом пикете и плюсовой точке разбивают перпендикуляры к трассе, называемые поперечниками. Поперечники разбивают в обе стороны длиной 15-30 м с таким расчётом, чтобы обеспечить съёмкой всю ширину полосы местности под будущие сооружения дороги (земляное полотно, водоотводные устройства, здания и пр.). Конечные точки поперечника закрепляют точкой и сторожком, плюсовые точки, располагаемые в местах изменения наклона местности, – только сторожком. На сторожках пишут расстояние от оси трассы с буквой “П” (справа от оси трассы) или “Л” (слева от оси трассы).
Плановая привязка трассы. Начало и конец трассы привязывают к пунктам государственной геодезической сети, например, с помощью теодолитных ходов. В результате измеренные на трассе углы и расстояния совместно с ходами привязки образуют единый разомкнутый теодолитный ход. Это позволяет проконтролировать правильность выполненных линейных и угловых измерений и вычислить координаты вершин углов поворота трассы.
На длинной трассе привязку к государственной геодезической сети выполняют не реже чем через 25 км, а при удалении пунктов от трассы более чем на 3 км – не реже чем через 50 км.
Съёмка полосы местности. В ходе разбивки пикетажа выполняют съёмку ситуации в полосе местности шириной по 100 м в обе стороны от оси трассы. При этом полосу шириной 25 м вправо и влево снимают инструментально – главным образом, методом перпендикуляров, а дальше – глазомерно. Результаты съёмки в виде абриса масштаба 1:2000 заносят в пикетажный журнал, изготовляемый из листов миллиметровой бумаги размером 10´15 см.
По середине листа проводят вертикальную прямую, изображающую ось трассы. На ней штрихами отмечают положение пикетов и плюсов и рядом подписывают их значения. Каждая новая страница начинается с пикета, которым закончена предыдущая. В местах поворота трассы стрелкой показывают направление поворота и надписывают румб следующей прямой. На свободном месте пишут основные элементы кривой. Показывают расстояния от местных предметов до оси трассы и габариты строений. Делают записи о типе дорог, характеристике леса, карьерах – обо всём, что может иметь значение для предстоящего строительства.
Закрепленные
Понравившиеся

Рис. 82. Пикетажный журнал
По середине страницы пикетажного журнала проводят прямую, изо– бражающую ось трассы, на ней в масштабе 1:2000 штрихами отмечают положение пикетов и плюсовых точек, подписывая рядом с ними их зна– чения. Каждую новую страницу начинают с пикета, которым закончена предыдущая. В местах поворота трассы от оси стрелкой указывают на–
правление поворота и вблизи на свободном месте в столбик записывают величину угла поворота и элементы кривой. На оси трассы отмечают главные точки кривых (начало, середину и конец), подписывают их пике– таж. Напротив прямых участков трассы выписывают их румбы и длины. Ситуацию в журнале зарисовывают схематично, указывая расстояния от оси трассы до предметов и габариты строений.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
111
1.Какие работы включает в себя трассирование?
2.Что представляет собой план трассы?
3.Что представляет собой продольный профиль трассы?
4.Что является углом поворота трассы и как его определяют?
5.Как разбивают пикетаж, плюсовые точки и поперечники?
6.Как определяют дирекционные углы сторон трассы по углам пово–
рота?
7.Что представляет собой пикетажный журнал и каково его содержа–
ние?
Лекция 12 ДОРОЖНЫЕ ЗАКРУГЛЕНИЯ
План лекции
12.1.Круговые кривые.
12.2.Вычисление пикетажа главных точек круговой кривой.
12.3.Разбивка кривой в главных точках на местности.
12.4.Детальная разбивка круговой кривой.
12.5.Вынос пикетов на кривую.
12.1. Круговые кривые
На всех линейных сооружениях, предназначенных для движения транспорта, в местах изменения направления трассы для сопряжения прямых участков с целью плавного и постепенного поворота движущего– ся транспортного средства устраивают закругления или кривые. Закруг– ления могут быть любыми. Простейшим является дуга окружности опре– деленного радиуса, т. е. круговая кривая.
На железных дорогах применяют круговые кривые со следующими радиусами: 4000, 3000, 2000, 1800, 1500, 1200, 1000, 800, 700, 600, 400 и 300 м. Конкретное решение о применении радиусов железнодорожных кривых принимают в соответствии с конкретными условиями и строи– тельно–техническими нормами СТН Ц-01-95 [6].
Круговая кривая характеризуется четырьмя главными точками и ше– стью основными элементами (рис. 83).
112

Рис. 83. Схема круговой кривой
Главными точками кривой, которые определяют положение кривой на местности, являются: вершина угла ВУ; начало круговой кривой НКК; се– редина круговой кривой СКК; конец круговой кривой ККК.
Основными элементами кривой являются:
1.Угол поворота трассы У.
2.Радиус закругления R.
Во время изысканий угол У вычисляют, а радиус R назначают. Ос– тальные элементы находят по формулам, вытекающим из прямоугольно– го треугольника с вершинами ВУ, НКК, О (рис. 83).
3.Тангенс кривой (касательная) Т – расстояние по прямой от верши–
ны угла до начала или конца кривой
Т= R × tg У2 .
4.Длина кривой К от начала кривой до её конца
K= 3602πR° ×У = 180πR° ×У .
5.Биссектриса кривой Б – отрезок от вершины угла до середины кривой
|
Б = |
R |
– R = |
R |
(1- cos |
У |
) = R(sec |
У |
-1) . |
|||
|
cos |
У |
2 |
cos |
У |
2 |
2 |
2 |
||||
6.Домер Д – разность между длиной двух тангенсов и кривой
Д= 2Т − K .
113
Все элементы кривой можно вычислить по вышеприведенным фор– мулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла по– ворота и радиуса, то для их определения составлены специальные таб– лицы для разбивки кривых.
12.2.Вычисление пикетажа главных точек круговой кривой
Вычислить пикетажные значения главных точек кривой – значит узнать, на каких пикетах и плюсовых точках они находятся.
Сначала определяют пикетаж вершины угла поворота ВУ, а затем на– ходят пикетажное значение начала, конца и середины кривой
НКК = ВУ − Т ,
ККК = НКК + K, СКК = НКК + 12K.
Для контроля вторично вычисляют пикетажное значение конца кривой
ККК = ВУ + Т − Д .
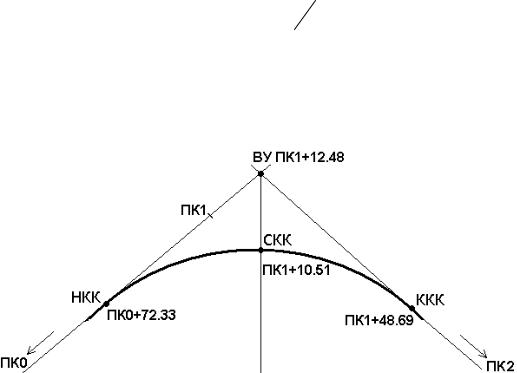
Пример (рис. 84)
Рис. 84. Разбивка пикетажа с учетом кривой
Определены: пикетаж ВУ ПК1+12.48 и основные элементы круговой кривой:
У = 43°45′ ;
R= 100 м;
Т= 40.15 м;
K= 76.36 м;
Б = 7.76 м;
114

Д = 3.94 м.
Найти пикетажные значения НКК, ККК, СКК.
Расчет пикетажа главных точек кривой выполняется в следующей форме:
|
_ВУ |
ПК1+12.48 |
Контроль |
||
|
+ |
ВУ |
ПК1+12.48 |
||
|
Т |
ПК0+40.15 |
Т |
ПК0+40.15 |
|
|
НКК |
ПК0+72.33 |
–Д |
ПК1+52.63 |
|
|
+K |
ПК0+76.36 |
ПК0+03,94 |
||
|
ККК ПК1+48.69 |
ККК ПК1+48.69 |
|||
|
+ |
НКК ПК0+72.33 |
|||
|
12 K ПК0+38.18 |
СКК ПК1+10,51
12.3. Разбивка кривой в главных точках на местности
Разбить кривую в главных точках на местности – значит найти поло– жение её главных точек на оси линейного сооружения и закрепить их. Положение начала кривой НКК определяют, отложив вычисленное рас– стояние от ближайшего пикета.
В нашем примере (см. рис. 84) ближайшим пикетом является ПК1. От него к ПК0 откладывают расстояние 27,67. В этой точке забивают колы– шек, а на расстоянии 15 – 20 см по направлению трассы забивают сто– рожок и на нем записывают НКК ПК0 + 72.33.
Середину кривой СКК закрепляют, отложив от ВУ по направлению биссектрисы угла, образованного направлениями трассы, отрезок, рав– ный Б.
На следующем, после вершины угла, направлении трассы отклады– вают величину домера (см. рис. 83), после чего продолжают разбивку пи– кетажа. При этом в месте отложения домера две точки – начало домера и его конец получают одно и тоже пикетажное наименование, благодаря чему в конце кривой пикетаж совпадает с пикетажем прямой. Положение
ККК получают, отложив от конца домера расстояние Т − Д , в примере оно равно 36.21 м. Найденное положение ККК закрепляют колышком и сторожком.
12.4. Детальная разбивка круговой кривой
По трем главным точкам точно построить кривую на местности не– возможно, поэтому при строительстве трассы её обозначают рядом до–
115

полнительных точек. Данные работы называются детальной разбивкой кривой.
Расстояние между соседними точками на кривой K при детальной разбивке зависит от её радиуса R и характера сооружения, однако чем меньше R кривой, тем меньше значение K. При R > 500 м разбивку про– изводят через промежутки k = 20 м, при 500 > R > 100 м k = 10 м, при
R < 100 м k = 5 м.
Из всех существующих способов детальной разбивки, различающихся между собой по виду измерений и условиям использования, рассмотрим два способа.
Способ прямоугольных координат от тангенсов
Пусть М – начало кривой радиуса R (рис. 85). Примем тангенс МА за ось абсцисс, а радиус МО за ось ординат. Положение точки кривой 1 в принятой системе координат определяется абсциссой X1 и ординатой Y1.
Рис. 85. Способ прямоугольных координат от тангенсов
116

Из прямоугольного треугольника ОN1 находим
X1 = R sin ϕ и Y1 = R − R cos ϕ = 2R sin2 ϕ2 .
Если условимся производить разбивку через промежутки с длиной ду– ги k , то получим
ϕ = 360°k = 180° k . 2πR πR
Тогда для точек 2, 3 и т. д. координаты вычисляют, подставляя в вы– шеприведенные формулы углы 2ϕ, 3ϕ и т. д.
X2 = R sin 2ϕ , Y2 = 2R sin2 ϕ,
X3 = R sin 3ϕ , Y3 = 2R sin2 3ϕ . 2
По указанным формулам составлены таблицы, из которых по аргу– ментам R и k можно выбрать значение Х и У.
В виду того, что значения k и Х близки между собой, в таблицах часто вместо графы Х дают значения (k – Х), называемые «кривая без абсцис– сы». Разбивку кривой производят с двух сторон – от начала и конца к се– редине кривой. По тангенсам отмеряют значение k и от полученной точки в обратном направлении откладывают значение (k – Х). Из данной точки восстанавливают перпендикуляр и откладывают на нём ординату Y.
Достоинство способа прямоугольных координат состоит в том, что каждая точка кривой выносится независимо от других с примерно одина– ковой точностью.
Детальную разбивку кривой способом прямоугольных координат удобно проводить в открытой и непересеченной местности.
Детальная разбивка кривой способом углов и хорд
Данный способ основывается на том, что углы с вершиной в какой– либо точке круговой кривой, образованные касательной и секущей и за– ключающие равные дуги, равны половине соответствующего централь– ного угла (рис. 86).
Для разбивки кривой при помощи углов и хорд вычисляют цен–
тральный угол ϕ, опирающийся на хорду s sin ϕ2 = 2sR .
Рассчитывают углы ϕi между касательной и направлением на опреде–
ляемые точки
117

ji = i × ϕ2 , (i = 1,2,3,….,n ) .
Рис. 86. Способ углов и хорд
Сначала выполняют разбивку кривой от её начала НКК до середины СКК. Для этого теодолит устанавливают в начале кривой НКК, совмеща– ют нуль алидады с нулем лимба и вращением лимба направляют визир– ную ось по тангенсу. Затем, освободив алидаду, в сторону кривой откла–
дывают от тангенса угол j1 = j2 и по направлению луча визирования
отмеряют лентой заданное расстояние s. Так находят точку 1. После это– го откладывают угол ϕ2 = ϕ , а ленту переносят и совмещают её нуль с
точкой 1. Взявшись пальцем у деления, равного s, вращают ленту вокруг точки 1 в сторону кривой до тех пор, пока деление не попадет на луч ви– зирования. В данном месте отмечают точку 2. Продолжают действовать в той же последовательности, откладывая точку 3 и т. д.
Аналогичным образом выполняют разбивку кривой от её конца ККК до середины СКК.
В рассмотренном способе линейные измерения выполняют вблизи кривой, что выгодно при разбивке точек в стесненных условиях, напри–
118

мер, на насыпи. Но так как положение последующей точки получают от– носительно предыдущей, то с возрастанием длины кривой точность её детальной разбивки быстро падает. В этом главный недостаток способа
углов и хорд.
12.5. Вынос пикетов на кривую
Так как при разбивке пикетажа на трассе мерщики перемещаются по тангенсам кривых, то возникает необходимость выноса пикетов, распо– ложенных на тангенсах, на кривые. Вынос пикетов на кривые выполняет– ся способом прямоугольных координат и в принципе не отличается от де– тальной разбивки кривой с помощью данного способа. Разница лишь в том, что при детальной разбивке кривой необходимые данные берут из таблиц, в которых они даются через определенные расстояния по кривой (20, 10, 5 или 1м). При выносе пикетов с касательной (тангенса) на кри– вую такие данные находят также из таблиц, но при этом используют ме– тод интерполирования.
Например, ПК1 лежит на тангенсе (рис. 87). Для того, чтобы его выне– сти на кривую, вычисляют расстояние K от ПК1 до НКК. Оно равно 27,67 м.
Рис. 87. Вынос пикетажной точки с тангенса на кривую.
Из таблиц при R = 100 м для K = 27,67 м путем интерполяции опреде– ляют X = 27,32 м и Y = 3,80 м. Затем рулеткой от НКК в сторону ПК1 по тангенсу отмеряют X = 27,32 м и из точки М по перпендикуляру отклады– вают ординату Y = 3,80 м.
Основание перпендикуляра М можно определить, отложив от ПК1 в направлении НКК отрезок (k – X) = 0.35 м.
119

В конце ординаты забивают кол и с тангенса в данное место на кри– вой переносят сторожок. Подобным образом выносят на кривую и другие пикеты до СКК.
Вынос пикета на кривую, когда она находится на втором тангенсе, производят аналогично, только за начало координат в данном случае принимают конец кривой.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.Что такое круговая кривая и для чего она устраивается на трассе?
2.Как называются основные элементы кривой и как они определяются?
3.Какие точки кривой называются главными и как находят их пике– тажное значение?
4.Как находят положение главных точек кривой на местности?
5.Для чего выполняется детальная разбивка кривой?
6.Как выполняют детальную разбивку кривой способом прямоуголь– ных координат от тангенсов?
7.Как выполняют детальную разбивку кривой способом углов и хорд?
8.Как производят вынос пикетов на кривую?
Лекция 13 ЖЕЛЕЗНОДОРОЖНЫЕ КРИВЫЕ
План лекции
13.1.Переходная кривая
13.2.Железнодорожная кривая, её элементы и главные точки
13.3.Вычисление пикетажа главных точек железнодорожной кривой и разбивка кривой в главных точках на местности
13.1. Переходная кривая
Непосредственное сопряжение прямого участка пути с круговой кри– вой приводит к тому, что во время движения поезда в местах сопряжения внезапно возникает центробежная сила F (рис. 88), прямо пропорцио– нальная квадрату скорости движения v и обратно пропорциональная радиусу кривой R
(F = mvR 2 ).
120
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Техникум мелиорации и механизации сельского.
хозяйства (филиал) ФГАОУ ВО « КФУ им. В.И. Вернадского» в пгт Советский
ПРАКТИЧЕСКАЯ РАБОТА № 2
По МДК 01.01. Технология производства полевых геодезических работ
Количество часов: 6
Тема занятия: «Определение элементов кривой и координат для детальной разбивки»
Наименование работы: расчетно-графическая работа.
Цель занятия:
-закрепление и развитие знаний, полученных при изучении теоретического материала по модулю;
– приобретение профессиональных навыков и умений по производству полевых геодезических работ;
– выполнить расчет элементов кривой и вычислить координаты для ее детальной разбивки, составить схему.
Приобретаемые умения и навыки:
– выполнения полевых геодезических работ на производственном участке;
– обрабатывать результаты полевых измерений;
– рассчитывать координаты опорных точек;
– осуществлять контроль производства геодезических работ;
Учебно-методическое оснащение рабочего места:
1. Инструкционно-технологическая карта.
2. Методические рекомендации.
3. Исходные данные (индивидуально).
Особые правила техники безопасности:
Инструкция по технике безопасности при выполнении камеральных работ.
Правила техники безопасности при выполнении чертежных работ.
Литература
Согласно пункта 4.2 рабочей программы ПМ 01
Исходные данные:
Вариант №__________
1. Пикетажное наименование вершины угла поворота ВУ ___________________
2. Измеренный угол поворота β = ______________
3. Радиус поворота R = _____________
Порядок выполнения практической работы
На всех линейных сооружениях, предназначенных для движения транспорта, в местах изменения направления трассы для сопряжения прямых участков с целью плавного и постепенного поворота движущего транспортного средства устраивают закругления или кривые. Закругления могут быть любыми. Простейшим является дуга окружности определенного радиуса, т.е. круговая кривая.
Конкретное решение о применении радиусов автомобильных, железнодорожных и других кривых принимают в соответствии с конкретными условиями и строительно-техническими нормами того или иного сооружения.
Разбивочные работы круговых кривых делятся на два этапа:
1. Разбивка главных точек круговой кривой выполняется одновременно с разбивкой пикетажа. Цель – определить пикетажное наименование конца кривой и затем продолжить разбивку пикетажа.
2. Детальная разбивка кривых – выполняется в период строительства.
Круговая кривая характеризуется четырьмя главными точками и шестью основными элементами.
Главными точками кривой, которые определяют положение кривой на местности, являются:
– вершина угла ВУ;
– начало кривой НК;
– середина кривой СК;
– конец кривой КК.

Рис.1 Главные точки кривой.
Основными элементами кривой, которые определяют положение главных точек, являются:
– угол поворота трассы – α;
– радиус закругления – R;
– длина кривой вставки – К;
– тангенсы – Т;
– биссектриса – Б;
– домер – Д.
Все линейные величины выражаются в метрах до сотых.
Во время изысканий угол α вычисляют, а радиус R назначают. Остальные элементы находят по формулам, вытекающим из прямоугольного треугольника с вершинами ВУ, НК, О (рис. 1).
Ход работы
1. Вычисляем угол поворота трассы – α:
α = 1800 – β
______________________________________________________________________________________
2. Вычисляем тангенс по формуле:
Т = R*tg*α/2
____________________________________________________________________________________
3. Вычисляем длину кривой по формуле:
K = α/1800*πR
_____________________________________________________________________________________
4. Вычисляем биссектрису по формуле:
Б = R(sek α/2 – 1) = (√R2 + T2 )– R
_____________________________________________________________________________________
5. Вычисляем домер по формуле:
D = 2T – K
__________________________________________________________________________________________
Все элементы кривой можно вычислить по вышеприведенным формулам. Но так как Т, K, Б и Д находятся в прямой зависимости от угла поворота и радиуса, то для их определения составлены специальные таблицы которыми пользуются для быстрой разбивки кривых.
6. Вычисляем пикетажные значения главных точек кривой, то есть определяем на каких пикетах и плюсовых точках они находятся. Для этого используем ниже следующие формулы:
НК = ВУ – Т =_______________________________________________________________________________
КК = НК + К=_______________________________________________________________________________
СК = НК + К/2=______________________________________________________________________________
Контроль:
КК = ВУ + Т – Д = ___________________________________________________________________________
КК = ВУ – Т + К =___________________________________________________________________________
СК = КК – К/2 =_____________________________________________________________________________
Расхождения в расчетах по двум формулам должны быть не более 0,01 м.
7. Вычерчиваем схему, на которую наносим все вычисленные величины и пикетажные наименования, необходимые для закрепления главных точек кривой и дальнейшей разбивки трассы.
Вывод:___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Выполнил:____________________________________________________________________________
Исходные данные к практической работе:
«Определение элементов кривой и координат для детальной разбивки»
2. Определение координат для детальной разбивки кривой.
По трем главным точкам НК, СК и КК точно построить кривую на местности невозможно, поэтому при строительстве трассы её обозначают рядом дополнительных точек. Данные работы называются детальной разбивкой кривой.
Расстояние между соседними точками на кривой К при детальной разбивке зависит от её радиуса R и характера сооружения, однако чем меньше R кривой, тем меньше значение К тем меньше промежутки k.
– если R > 500 м, то k = 20 м;
– если 500 > R > 100 м, то k = 10 м;
– если R ≤ 100 м, то k = 5 м.
Задание № 2 Определить координаты для детальной разбивки кривой применяя способ прямоугольных координат от тангенсов.
Ход работы:
1. За начало координат принимаем точку М – НК начало круговой кривой.
2. Тангенс МА принимаем за ось абсцисс (Х), а радиус МО за ось ординат (У).
3. Положение точки N, кривой в принятой системе координат определяется абсциссой X1 и ординатой Y1.
4. Из прямоугольника ON1 находим Х1 и У1 используя формулы:
![]()
![]()
5. Угол φ находим в зависимости от длины дуги k, через которую производится разбивка кривой, используя формулу:
![]()
________________ φ = ______________________________________________
6. Для точек 2, 3 и т.д. координаты вычисляем, подставляя в вышеприведенные формулы углы 2φ, 3φ и т.д. до середины кривой:
![]()
![]()
7. На основании вычислений строим чертеж детальной разбивки круговой кривой способом прямоугольных координат. Масштаб подобран индивидуально:__1:_________
Вдоль тангенсов (ось абсцисс) откладываем длины х, восстанавливаем прямой угол в полученной точке. Точка 1 круговой кривой фиксируется расстоянием у, отмеренным по перпендикуляру. Так же получем другие точки круговой кривой. Вторую половину круговой кривой разбиваем от ее конца, выполняя аналогичные действия и используя значения х и у, полученные для первой половины.
Таблица 1 – Вычисление координат для детальной разбивки кривой
точки
Формула для Хп
Координаты по Х
Формула для Уп
Координаты по У
№ точки
1
Х1=Rφ
У1=2R 2 φ/2
2
Х2=R2φ
У2=2R 2 φ
3
Х3=R3φ
У3=2R 2 3φ/2
4
Х4=R4φ
У4=2R 2 4φ/2
5
Х5=R5φ
У5=2R 2 5φ/2
6
Х6=R6φ
У6=2R 2 6φ/2
7
Х7=R7φ
У7=2R 2 7φ/2
8
Х8=R8φ
У8=2R 2 8φ/2
9
Х9=R9φ
У9=2R 2 9φ/2
10
Х10=R10φ
У10=2R 2 10φ/2
11
Х11=R11φ
У11=2R 2 11φ/2
12
Х12=R12φ
У12=2R 2 12φ/2
13
Х13=R13φ
У13=2R 2 13φ/2
14
Х14=R14φ
У14=2R 2 14φ/2
Вывод:___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Выполнил:____________________________________________________________________________
