Как найти вершины прямых углов 1 класс

Вид урока: урок изучения и первичного закрепления новых знаний.

Цель: формирование общего понятия об угле, прямой угол.

Задачи:

Образовательная:
– учить различать прямой;
– учить строить прямой угол;

Развивающая:
– развивать познавательный интерес, умение сопоставлять и сравнивать, обобщать;

– развивать творческое мышление, внимание, воображение учащихся, интерес к
математике.

Воспитывающая – воспитание аккуратности, сплоченности, добросовестного
отношения к труду.

Оборудование: таблички со словами: “геометрия, луч, вершина, сторона,
прямой угол”; рисунки домиков, выставка книг Житомирский, Шеврин “Путешествие по
стране Геометрии”, “Все обо всем”; для учеников: угольник, лист бумаги,
компьютер; презентация Power Point.

Ход урока

I. Организационный момент.

Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте, Все ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.

От кроем тетради и запишем число.

1) Минутка чистописания “Гусеница-растеряша”.

– Гусеница растеряла числа, посмотрите на оставшиеся, разгадайте по какому
правилу можно продолжить ряд чисел. (Дети называют правило: это четные числа;
каждое последующее число на 2 больше предыдущего). Допишите.

– Какие же числа растеряла гусеница? (2, 4, 6, 8, 10, 12, 14, 16 и т. д.)

II. Устный счет.

1) Индивидуальная работа по карточкам.

2) Игра “Математический баскетбол”.

– Любой из вас забьет гол, если правильно решит пример. (Дети по цепочке
решают примеры.)

30 + 7
25 + 5
32 – 12
66 + 4
80 – 7
28 – 10
45 – 45

53 + 7
59 – 9
90 + 9

3) Решение задач.

– В саду росли 2 березы, 4 яблони, 5 вишен. Сколько всего фруктовых
деревьев росло в саду?

– Сестре 9 лет, брату 3 года. На сколько сестра будет старше брата через 5
лет?

– Посмотрите на фигуры. Как назвать их одним словом? Почему? (Геометрические
фигуры.)

– Вы сказали “геометрические”? А от какого слово оно произошло? (Геометрия.)

– А что такое геометрия?

– Табличка с этим словом вывешивается на доске.

– Слово геометрия пришло из греческого языка. “Ге” – земля “метрио” – мерить.

Геометрия – это раздел математики, в котором изучают фигуры, их
формы, положение предметов в пространстве.

– На какие группы можно разделить все фигуры?

(В первую группу фигуры 1, 3, 5; во вторую – фигуры 2, 4.)

– Что общего между фигурами каждой группы? (I группа – есть углы; II
группа – нет углов.)

III. Работа над новым материалом

Как вы думаете, о чем мы сегодня будем говорить?

Сегодня на уроке мы поговорим об углах, познакомимся с прямым углом, их
свойствами, научимся их обозначать буквами. Все ли углы в фигурах первой группы
одинаковы? (Нет.)

1) Практическая работа. Построение модели
прямого угла.

Какие бывают углы? Углы бывают разные, но сначала мы познакомимся с самым
главным углом. Сейчас мы сложим модель угла, а вы скажите какой это угол.

Возьмет лист бумаги, который лежит на парте.

Согните лист, как на рисунке 1. Согните еще раз, как на рисунке 2. Получилась
модель прямого угла.

рис. 1

рис. 2

рис.3

рис.4

Обведите линии сгиба карандашом. На сколько частей прямые линии разделили
плоскость? (На четыре.)

– Сколько углов получилось? (Четыре.)

– Это особенные углы.

– На пересечении линий сгиба поставьте точку. Обозначьте один прямой угол
буквами. Заштрихуйте цветным карандашом его внутреннюю часть.

Может быть, кто-то знает название этих углов? (Эти углы прямые.)

Покажите стороны прямого угла и вершину.

Дети показывают.

Где в жизни мы встречаемся с прямыми углами?

Моделью прямого угла является также прямой угол чертежного треугольника.
Найдите на нем с помощью своей модели прямой угол.

Прямой угол на чертежном треугольнике – это модель прямого угла.

2) Знакомство с угольником.

Рассмотрите чертежный треугольник. Вы уже убедились, что у него один угол
прямой.

С помощью модели прямого угла узнайте, будут ли прямыми остальные углы этого
треугольника.

Какие у вас получились углы? (Меньше прямого.)

Работа в тетради.

С помощью угольника удобно не только определять прямые углы, но главное –
строить их. Построим прямой угол в тетради, каждый сам назовет его тремя
буквами.

(Учитель на доске, а дети в тетрадях строят прямой угол. Выполняется
взаимопроверка в парах.)

Что есть у угла? (Вершина, две стороны.)

– С помощью линейки-угольника проверьте работу друг друга в парах. Определить
угол сначала “на глаз”, потом проверить с помощью угольника. Чтобы определить
вид угла, надо совместить его вершину и сторону соответственно с вершиной и
стороной прямого угла на угольнике.

– Как вы думаете, как образовались углы? Как отличить два угла друг от друга?

Давайте сформулируем правило. Что такое угол?

Угол – это геометрическая фигура, образованная двумя разными лучами с
общим началом.

– Точка О – вершина угла. Угол можно назвать одной буквой, записанной около
его вершины. Угол О. Но может быть несколько углов, имеющих одну вершину. Как
быть тогда?

– В таких случаях если называть разные углы одной буквой, то будет непонятно,
о каком угле идет речь. Что этого не произошло, на каждой стороне угла можно
отметить по одной точке, поставить около нее букву и обозначить угол тремя
буквами, при этом всегда в середине записывают букву, обозначающую вершину угла.
Угол АОВ. Лучи АО и ОВ – стороны угла.

Обратите внимание угол выделяется дугой.

IV. Актуализация знаний. Повторение изученного.

1) Работа по учебнику. Стр.38 № 2. Запиши различное название углов.
Назови их вершины и стороны.

– Рассмотрите рисунки. Какое правило работы важно помнить, при определении
вида угла с помощью линейки-угольника? (Нужно совмещать вершину и одну сторону
угла с вершиной и стороной прямого угла на линейке-угольнике.)

V. динамическая пауза.

Физкультминутка “Буратино”.

Буратино потянулся, раз нагнулся, два нагнулся
Руки в стороны развел, ключик, видно не нашел.
Чтобы ключик нам достать, нужно на носочки встать.

2) Работа в учебнике.

Стр. 40 № 8.

1) Игра “Самый внимательный”.

– Посмотрите внимательно на рисунок, части всех предметов похожи на какие-то
геометрические фиуры.

– Самый внимательный из вас найдет на рисунке нужные предмет. Подсказку ищите
в верхнем правом углу. (Дети указкой показывают треугольник в квадрате.)

А кто подскажет, если здесь прямые углы?

VI. Итог урока. Рефлексия.

– Кто доволен своей работой на уроке? Прикрепите на нашей полянке красный
цветочек.

– Кто считает, что работал не во всю силу и хотел бы на следующий раз
работать лучше – желтый цветочек.

– Кто не доволен своей работой – синий цветочек.

– Посмотрите, какая полянка у нас получилась. Я вижу, что в основном дети
старались и работали хорошо.

Д/з. Стр. 40 № 11. Придумайте и нарисуйте различные
предметы, используя круги, овалы, точки, лучи и углы.

– Что вы узнали нового, интересного? С чем познакомились? Выставить оценки.

– Какое задание понравилось больше всего?

Спасибо за урок.

                                                             
МАТЕМАТИКА   (1
класс)

ТЕМА.  ЗНАКОМСТВО
С УГЛОМ. ВЕРШИНА И СТОРОНЫ  УГЛА.

(По мотивам сказки
«Колобок»)

ЦЕЛЬ: знакомство  с новыми
понятиями «угол», «вершина угла», «сторона угла».

ЗАДАЧИ:

–       
закрепить
умения выполнять мыслительные операции на основе полученных знаний;

–       
развивать
логическое мышление, математическую речь;

–       
мотивировать
учащихся к учебной деятельности через игру; 

–       
совершенствовать
вычислительные навыки; 

–       
развивать
мыслительные операции сравнения, анализа, классификации;

–       
развивать
познавательный интерес и творческие способности;

–       
прививать
любовь к предмету;

–       
воспитывать
умение работать в коллективе.

ОБОРУДОВАНИЕ. Учебник «Математика. 1
класс» (часть 3) (авт. И. Аргинская, Е. Бененсон, Л. Итина); магнитофон,
таблица с шифром, сигнальные карточки, магнитная доска, геометрические фигуры, 
плакаты со словами пословицы, модели точки, прямой линии, угла, костюмы к
сказке «Колобок» .

ХОД
УРОКА

Психологический
настрой

( Звучит медленная музыка)

Дети, представьте себе, что
каждый из вас маленькое семечко (дети присаживаются и закрывают головки
руками). Садовник очень бережно относится к каждому семечку, поливает его,
ухаживает за ним. (Учитель ходит и гладит по головкам детей). С первыми лучами
солнышка семечко медленно начинает расти, появляются зеленые листочки. (Дети
поднимают руки, тянутся вверх). Растет стебелек.  (Дети потягиваются,
расправляют плечики). И вот наступает радостный момент, появляется прекрасный
цветок.  (Дети поднимают руки вверх, показывая распустившиеся лепестки). Цветок
хорошеет.  (Дети улыбаются друг другу).  Он тянется к свету, к солнцу.
(Заканчивается музыка).

Ребята, как цветы тянутся к
весенним лучам солнца, так и человек тянется к знаниям. Он хочет узнать много
нового и интересного. Ведь мир освещается солнцем, а человек – знанием.

Как вы понимаете смысл этой
пословицы?  (Когда человек много знает, ему легче ориентироваться в жизни).

А где получают знания? (В
школе, колледже, в институте, читая книги).

Какие качества вам
понадобятся на уроке, чтобы овладеть новыми знаниями?

Мы все успеем сделать и
покажем хорошие знания. А урок у нас сегодня необычный.  Много гостей  пришло к
нам (давайте молча поприветствуем их).  Но это еще не все гости. Мы ожидаем
героев из всеми известной и любимой сказки. А из какой узнайте сами.

Арифметический
диктант.

(Все дети пишут диктант в
тетрадях, а двое детей работают у доски).

На доске шифр. Каждой цифре
соответствует определенная буква. Название сказки получится лишь в том случае, если
все ответы арифметического диктанта будут верными.

3         2        9        4        7        5        6        1        8

Л        М       К        А       И       О        С        Б        Т

Во время работы
помните, что  «Ум имей хоть маленький, но свой».

И не забывайте еще одну
пословицу « Семь раз отмерь, один раз отрежь»

·                      
Найди закономерность,
скрытую в данной последовательности

4       2                   
3        5                    7      2

     6                            
8                             ?

·                      
У
одного мужчины спросили, сколько у него детей? Он ответил: « У меня 4 сына, и у
каждого из них есть родная сестра.         ( 5 )

·                      
Мне
навстречу бежали поросята: один впереди двух, один между двух и один сзади
двух. Сколько всего бежало поросят?      ( 3 )

·                      
Определить количество
треугольников на данном чертеже.

·                      
Шел
человек в город, а навстречу ему  шли  четверо его знакомых. Сколько человек
шло в город?          ( 1 )

·                      
Когда
гусь стоит на одной ноге, он весит  5 кг. Сколько будет весить гусь, если он
встанет на две ноги?        ( 5 кг )

·                      
Три
гуся летят над нами, три других за облаками, три спустились за ручей. Сколько
было всех гусей?       ( 9)

На доске запись       9   5   3   5   1   5   9

Самопроверка.

Поднимите руку, кто
справился с этим заданием. Кто допустил ошибки?

Настало время расшифровать
название сказки.           «К  о  л  о  б  о  к «

– Герои сказки «Колобок»

Пришли сегодня на урок.

Каждый задание принес,

И вместо ответа поставил
вопрос.

?                ?    
         ?                ?              ?              ?              ?      

А вопросов мы вовсе и не
боимся, особенно тех, которые связаны с математикой, ведь

«Математику  уже за тем
учить следует, что она ум в порядок приводит.»  (М. В. Ломоносов)

«Наука математика – царица
всех наук»     (Гаусс)

«Математика  –  гимнастика
ума.   (А. В. Суворов)

Отвечая правильно на вопросы
каждого героя, мы узнаем замечательную пословицу.

Минутка
чистописания

– Я – Колобок, сбежал с
окошка,

Деда с бабой огорчил.

Покатился по дорожке,

В лапы к Зайцу угодил.

Заяц съесть меня хотел.

-Колобочек наш запел.

– Хорошо поешь, дружок!

Если ты решишь заданье,

Я тебя без наказанья

В путь – дорожку снаряжу

И на волю отпущу.

– Надо быстро Колобочка
спасать,

Помочь от Зайчишки ему
убежать!

« Один за всех и все  за
одного»

Какие цифры нам нужно
прописать?       (6    9    1)

  

Пропишите цифры так, чтобы
единицы располагались выше девяток, но ниже шестерок и чтобы всех цифр было
поровну. Подчеркните правильно написанные цифры.

Пользуясь только данными
цифрами, запишите:

           мальчики – 3
суммы,

           девочки – 3
разности

Как называются полученные
математические записи?   (выражения)

Запишите три
неравенства               девочки со знаком   <

                                   
                               мальчики со знаком   >

Взаимопроверка

Какое наибольшее двузначное
число можно записать при помощи  данных цифр? (цифры повторять нельзя)     (96)

Наименьшее двузначное?   (16)

Выполнив это задание,  мы
узнали первые  два слова из пословицы:

БЫТЬ                                       СИЛЬНЫМ

Решение
выражений

-Вот навстречу серый Волк,

В Колобках он знает толк.

Чтобы Волк его не съел,

Колобочек наш запел.

– С песней, Колобочек, не
спеши,

Лучше ты заданье мне реши.

Если ты примеры решишь,

Дальше смело побежишь.

« Усердие-мать удачи»

7+2           
2+2            4+2            6+2

5 -1            5 –
4          5 -3          5 -2

1 группа

Найдите значение выражений
при помощи натурального ряда  чисел.

2 группа

Запишите суммы в порядке
возрастания их значений.

Запишите разности в порядке
убывания их значений.

3 группа

Расшифруйте загадочные
записи и запишите по четыре равенства, подходящих к данным записям

А+О=М                                         
К-М=А

М=5                                              
А=1

В каждой группе работают
консультанты.

Как называются получившиеся
записи?    (равенства)

Вторые слагаемые
подчеркните синим карандашом, а уменьшаемые – красным.

Ещё одно слово из пословицы
становится известным нам. Это слово:

ХОРОШО

Знакомство
с углом. Вершина и стороны угла. Построение угла с заданной вершиной.

Не попал он Волку в лапы,

Вдруг навстречу Косолапый.

Колобочек испугался,

На пенек скорей забрался.

Только начал песню петь,

Как Медведь давай реветь.

– Ты не пой мне, Колобок,

Лучше разбери, дружок,

Геометрические задания

И получи скорее новые
знания.

– Мы поможем тебе, Колобок,

Ведь  Геометрия – это наш
конек.

« Не имей сто рублей, а
имей сто друзей»

А вот и наша старая
знакомая – Точка.               Она такие чудеса умеет творить.

Поставьте точку, проведите
через нее прямую линию.

Сколько прямых линий можно
провести через одну точку?

А теперь поставьте две точки
и соедините их. Какая геометрическая фигура у вас получилась?

Чем отличается отрезок от
прямой линии? А от луча?

Начертите прямую и кривую
линии так, чтобы у них было 4 точки пересечения. Синим карандашом поставьте
точку, которая не принадлежит ни одной из линий, а зеленым  – принадлежащую
одной из линий.

Без конца и края

Линия прямая.

Хоть сто лет по ней идти,

Не найти конца пути.

Начертите прямую линию.
Поставьте на ней точку. Какое превращение сделала точка с прямой?

Начертите угол с вершиной в
точке  О, выделите цветным  карандашом стороны.

( Возникновение проблемной
ситуации).

Вы смогли справиться с
заданием?

 ( Побуждение к осознанию
противоречия).

Почему? В чем причина?

( Осознание противоречия)

Какой возникает вопрос? (
Побуждение к формулированию проблемы).

Что такое угол, как
правильно обозначать вершину и стороны угла.

(Учебная проблема как
вопрос).

Надо вам сказать, что эта
маленькая Точка  большая проказница. И вот, что однажды произошло. Как-то Точка
подкралась к спящей  Прямой линии, взобралась на нее и начала подпрыгивать.
Сначала проказница подпрыгивала так, чтобы не разбудить и не сломать Прямую. И
это ей удавалось. Но затем забыла малышка – Точка об осторожности, да так
подпрыгнула, что Прямая не выдержала и сломалась. Прямая линия исчезла. Вместо
Прямой остались два ее обломка, две части. Эти две части не разлетелись в
разные стороны только потому, что Точка успела схватить их. И тогда появилась
на свет новая геометрическая фигура, которую назвали Углом. Место, где Точка
держит части развалившейся Прямой называется вершиной угла. А сами части Прямой
называются сторонами угла.

Постройте угол из двух
карандашей. Найдите и покажите углы вокруг себя.

Назовите геометрические
фигуры. Разделите их на две группы.

Начертите те из них, которые
имеют отношение к новому знанию.

Сколько у угла вершин?
Сторон?

Работа с учебником.

Начертите углы с вершинами
в точках М, О, К, Е.( №34)

Дорисуйте, чтобы получился
предмет.

                                                                      

Ещё два слова найдены. Эти
слова:

                   
                     БЫТЬ  УМНЫМ

Физминутка

Колобок наш утомился,

На пенечке развалился.

Вмиг поднимем дух ему,

Вам  зарядка по уму.

Можно открыть ещё одно
слово. Это слово:

ЛУЧШЕ

Работа
по пройденному материалу

Вот и Лисонька идет

И такую речь ведет.

-Съем тебя я, Колобок,

Но прежде дам тебе я срок:

Чтоб сумел за пять минут

Все решить, что есть вот
тут.

Получай ты мой билет

И готовь скорей ответ.

– Мы, Лиса, тебя проучим,

Колобочка не получишь,

Колобочка мы спасем,

Бабе с дедом унесем!

«Повторенье-мать ученья»

Давайте вновь  вернемся к 
числам шифра. Расположите числа:

Мальчики – в порядке
возрастания,

Девочки – в порядке
убывания.

У кого получился отрезок
натурального ряда чисел? Назовите признаки отрезка натурального ряда. Запишите 
другие отрезки натурального ряда, используя не все числа данного отрезка.

Как переместить кубики,
чтобы  желтый стал крайним, не перемещая его.

Выполнение заданий учебника
№ 36,40.

И заключительным словом
является слово:

ВДВОЕ

Итог
урока

Сегодня на уроке вы были
самыми активными, сплоченными, благодаря своему упорству смогли быстро все
сделать. Наш урок подошел к концу. У нас получилась замечательная пословица.
Она вам нравится? Почему? Кому вы пришли на помощь сегодня? Вы как палочки – выручалочки
приходили на помощь нашему гостю. Вы смогли помочь Колобку благодаря уму и
прочным знаниям. Ум  –  добро, ум  –  сила. Помните об этом.

– Колобок повеселел,

Напоследок песню спел.

– Заяц, Волк, Медведь, Лиса

Все хотели съесть меня.

Но не вышло ничего,

 Ведь быть сильным хорошо,

Но быть умным вдвое лучше.

Этому мы всех научим.

Математику учите,

Каждый день свой ум точите.

Ничего не забывайте и
почаще повторяйте:

Что «Быть
сильным хорошо, быть умным лучше вдвое».

Слайд 1

«Моя математика» 1 класс Урок 27 Тема урока: «Угол. Прямой угол» Советы учителю. Презентация к уроку составлена на основе заданий, расположенных в учебнике. Рекомендую открыть учебник на странице с данным уроком, прочитать задания и просмотреть их в данной презентации в режиме демонстрации. Внимание! Некоторые задания можно выполнять интерактивно. Например, продолжить ряд, сравнить или вставить пропущенные числа. Для этого презентацию надо перевести в режим редактирования. Автор презентации Татузова Анна Васильевна http://avtatuzova.ru учитель школы № 1702 г. Москвы

Слайд 2

Задание из «Методических рекомендаций» Угадайте фигуру. МАТЕМАТИКА Урок 27. Угол. Прямой угол

Слайд 3

1. Сколько лучей провел Петя из каждой точки? ? Как бы ты назвал фигуры на рисунке? ! Это – углы. Точки – вершины углов. Лучи – стороны углов. МАТЕМАТИКА Урок 27. Угол. Прямой угол

Слайд 4

? Можно ли сказать, что ваши углы равны? МАТЕМАТИКА Урок 27. Угол. Прямой угол 2. Катя сделала из листа бумаги модель угла. Сделайте похожую фигуру из листа бумаги. Разверни лист и обведи линии сгиба. ! Это – прямой угол. 3. Сравните свою модель с моделями других ребят.

Слайд 5

! Углы равны , если при наложении их стороны и вершины совпадают . МАТЕМАТИКА Урок 27. Угол. Прямой угол Все прямые углы равны. 4. Катя, Петя, Лена и Вова начертили углы. Кто из них начертил прямой угол? Внимание! Данное задание можно выполнять интерактивно. Во время демонстрации навести курсор на нужную карточку до появления ладошки. Кликнуть!

Слайд 6

! Углы равны , если при наложении их стороны и вершины совпадают . МАТЕМАТИКА Урок 27. Угол. Прямой угол Все прямые углы равны. 4. Катя, Петя, Лена и Вова начертили углы. Кто из них начертил прямой угол? ПРОВЕРЬ!

Слайд 7

1 3 2 4 – 1 Влево – минус МАТЕМАТИКА Урок 27. Угол. Прямой угол 5. Выполни вместе с Катей, Петей, Леной и Вовой сложение и вычитание. Какие равенства у них получились? 1 2 3 4 + – = Внимание! Данное задание можно выполнить интерактивно. Для этого презентацию надо перевести в режим редактирования.

Слайд 8

1 3 2 4 – 1 Влево – минус МАТЕМАТИКА Урок 27. Угол. Прямой угол 5. Выполни вместе с Катей, Петей, Леной и Вовой сложение и вычитание. Какие равенства у них получились? 1 2 3 4 + – = ПРОВЕРЬ!

Слайд 9

1 3 2 4 +1 МАТЕМАТИКА Урок 27. Угол. Прямой угол 1 2 3 4 + – = 5. Выполни вместе с Катей, Петей, Леной и Вовой сложение и вычитание. Какие равенства у них получились? Вправо – плюс Внимание! Данное задание можно выполнить интерактивно. Для этого презентацию надо перевести в режим редактирования

Слайд 10

1 3 2 4 +1 МАТЕМАТИКА Урок 27. Угол. Прямой угол 1 2 3 4 + – = 5. Выполни вместе с Катей, Петей, Леной и Вовой сложение и вычитание. Какие равенства у них получились? Вправо – плюс ПРОВЕРЬ!

Слайд 11

1 3 2 4 – 1 Влево – минус МАТЕМАТИКА Урок 27. Угол. Прямой угол 5. Выполни вместе с Катей, Петей, Леной и Вовой сложение и вычитание. Какие равенства у них получились? Внимание! Данное задание можно выполнить интерактивно. Для этого презентацию надо перевести в режим редактирования. 1 2 3 4 + – = 1

Слайд 12

1 3 2 4 – 1 Влево – минус МАТЕМАТИКА Урок 27. Угол. Прямой угол 5. Выполни вместе с Катей, Петей, Леной и Вовой сложение и вычитание. Какие равенства у них получились? 1 2 3 4 + – = 1 ПРОВЕРЬ!

Слайд 13

1 3 2 4 – 1 Влево – минус МАТЕМАТИКА Урок 27. Угол. Прямой угол 5. Выполни вместе с Катей, Петей, Леной и Вовой сложение и вычитание. Какие равенства у них получились? 1 2 3 4 + – = 1 Внимание! Данное задание можно выполнить интерактивно. Для этого презентацию надо перевести в режим редактирования.

Слайд 14

1 3 2 4 – 1 Влево – минус МАТЕМАТИКА Урок 27. Угол. Прямой угол 5. Выполни вместе с Катей, Петей, Леной и Вовой сложение и вычитание. Какие равенства у них получились? 1 2 3 4 + – = 1 ПРОВЕРЬ!

Слайд 15

4 – 1 3 + 1 4 – 2 4 – 3 2 + 2 6. Помоги Вове выбрать к рисунку нужные выражения: МАТЕМАТИКА Урок 27. Угол. Прямой угол Внимание! Данное задание можно выполнить интерактивно. Для этого презентацию надо перевести в режим редактирования.

Слайд 16

4 – 1 3 + 1 4 – 2 4 – 3 2 + 2 6. Помоги Вове выбрать к рисунку нужные выражения: МАТЕМАТИКА Урок 27. Угол. Прямой угол ПРОВЕРЬ!

Слайд 17

МАТЕМАТИКА 4 – 1 4 – 2 4 – 3 2 + 2 3 + 1 6. Помоги Вове выбрать к рисунку нужные выражения: Урок 27. Угол. Прямой угол ПРОВЕРЬ!

Слайд 18

МАТЕМАТИКА 4 – 1 3 + 1 4 – 2 4 – 3 2 + 2 6. Помоги Вове выбрать к рисунку нужные выражения: Урок 27. Угол. Прямой угол ПРОВЕРЬ!

Слайд 19

МАТЕМАТИКА 4 – 1 3 + 1 4 – 2 4 – 3 2 + 2 6. Помоги Вове выбрать к рисунку нужные выражения: Урок 27. Угол. Прямой угол ПРОВЕРЬ!

Слайд 20

МАТЕМАТИКА 4 – 1 3 + 1 4 – 2 4 – 3 2 + 2 6. Помоги Вове выбрать к рисунку нужные выражения: Урок 27. Угол. Прямой угол ПРОВЕРЬ!

Слайд 21

Спасибо! МАТЕМАТИКА

Введение термина «угол», «вершина угла», «стороны угла».

Построение угла. Обозначение.

1 класс ДС Занкова.

ФГОС. Урок изучения нового материала.

Ганьжина Ольга Владимировна

МБОУ «СОШ № 2 с УИОП»

г. Лысьва Пермский край

Цель: 1. Сформировать понятие «угол». Дать определение новой геометрической фигуре. Ввести понятие «вершина», «Стороны» угла.

2. Научить строить угол и обозначать.

3. Развивать пространственное мышление.

4. Развивать умения работать в паре и в группах.

5. Воспитывать аккуратность при выполнении чертежей, при организации раюбочего места.

Метапредмет: модель, построение моделей.

Приёмы и методы обучения: технология развивающего обучения, технология диалогового общения, анализ конкретных учебных ситуаций, частично-поисковый, игровые.

Используемые формы организации познавательной деятельности учащихся: фронтальная, групповая, индивидуальная, парная.

Методы контроля: устный опрос, рефлексия (тест-опрос)

Ход урока.

I. Мотивация.

– Что такое моделирование? ( Замена реального объекта моделью, построение похожего объекта на реальный) Слайд 1.

– Зачем люди делают модели? ( С целью изучения, исследования) Слайд 2.

Существует множество способов моделирования и одно из них – математическое. Слайд 3.

– А что такое математическое моделирование? (Исследование математических моделей, фигур) Слайд 4.

Моделирование – это ещё и способ исследования.

Сегодня мы будем заниматься математическим исследованием.

(Слайд 5 пустой для отдыха глаз)

II. Актуализация знаний и фиксация затруднений.

– Как вы считаете, вы умеете моделировать?

Давайте попробуем. (Работа в парах.)

Для работы у вас на партах – 5 белых квадратов из картона, шарики из пластилина и палочки. (Строят каждую фигуру на отдельном квадрате)

1) Постройте модель самой маленькой геометрической фигуры. ( Точка)

2) Постройте модель геометрической фигуры с помощью 1 палочки и 2 шариков пластилина. ( Отрезок)

3) Построй фигуру из 4 отрезков. ( Ломаная, квадрат и т.п.)

4) Построй модель фигуры с помощью 1 спички и 1 шарика. ( Луч)

5) Построй модель геометрической фигуры с помощью 2-ух спичек и 1 шарика пластилина. (У ребят возникают затруднения, так как с этой фигурой ещё не знакомы. Но пытаются сконструировать. В результате получается новая геометрическая фигура – угол

– Как называется эта фигура? Как бы вы назвали эту фигуру? ( Угол.)

– Что такое угол? (Возникают затруднения)

– Почему вы не можете дать определение? ( Ничего ещё о ней не знаем)

– Какой объект выберем для исследования? (Угол)

– Сформулируйте тему урока. (Угол) Слад 6.

III. Построение проекта.

– Давайте поставим цель нашего урока. (Слова УЗНАТЬ, НАУЧИТЬСЯ, ПОЗНАКОМИТЬСЯ, ПОНАБЛЮДАТЬ на доске на карточках)

УЗНАТЬ …. что такое угол, из чего он состоит.

НАУЧИТЬСЯ …. строить

ПОЗНАКОМИТЬСЯ …. со способом обозначения углов.

ПОНАБЛЮДАТЬ …. разные углы. Слайд 6.

IV. Реализация проекта. Работа в группах.

(Задания записаны на карточках. Приложение 1.)

1 группа. Составляет определение.

2 группа. Называет части угла. Записывает на приготовленных карточках.

3 группа . Как построить угол.

4 группа. Предложить способы обозначения.

• ЗАДАНИЕ 1 ГРУППЕ

ЧТО ТАКОЕ УГОЛ?

• СОСТАВЬ ИЗ КАРТОЧЕК ОПРЕДЕЛЕНИЕ И ПРИКЛЕЙ НА ЛИСТ

• ПРИГОТОВЬСЯ ПРОЧИТАТЬ БЕЗ ОШИБОК

• ЗАДАНИЕ 2 ГРУППЕ

КАК ПОСТРОИТЬ УГОЛ? НАЧЕРТИТЬ?

• СНАЧАЛА НАДО ПОСТАВИТЬ _____________

• ПОТОМ ОТ НЕЁ ПРОВЕСТИ __________________

• ЗАДАНИЕ 3 ГРУППЕ

УЗНАТЬ КАК НАЗЫВАЮТСЯ ЧАСТИ УГЛА

НАПИШИТЕ НА КАРТОЧКАХ

ВАМ ПОМОЖЕТ УЧЕБНИК

• № 52, УЧЕБНИК

• № 61, УЧЕБНИК

• ЗАДАНИЕ 4 ГРУППЕ

КАК ОБОЗНАЧИТЬ УГОЛ?

ВАМ ПОМОЖЕТ УЧЕБНИК № 72

ПОПРОБУЙТЕ ЗДЕСЬ

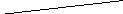
(Выступления групп)

V.Первичное закрепление.

Начертить в тетради угол и обозначить. (Задание выполняется на доске.)

Слайд 7.

VI. Самостоятельная работа. (Слайд 8 пустой для отдыха глаз)

№ 26 (печатная тетрадь)

№ 37 (печатная тетрадь)

(Начертить углы и обозначить)

VII. Включение в систему знаний.

– Все ли углы одинаковые? (Нет)

Давайте проведём эксперимент. Сейчас мы построим модель прямого угла.

(Работа по схеме на слайде) Слайд 9.

Углы, которые меньше прямого называются острыми. Углы, которые больше прямого угла называются тупыми.

– Найдите в классе различные углы и обозначьте

• 1 ряд красным кружком прямые углы

• 2 ряд синим кружком тупые углы

• 3 ряд зелёным кружком острые углы.

VIII. Итог Рефлексия. (Выполняют тест) Слайд 12 – 15.

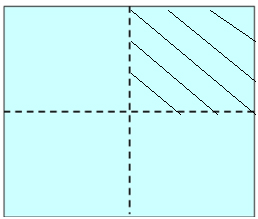
• Найди угол

П) Л) А)

• Найди угол К.

К

А) К Я) К С)

• Стрелки часов образуют

М) прямой угол

Т) острый угол

Ю) тупой угол

• Стороны угла – это

О) вершины

Ь) лучи

А) никак не называются

( В результате получается слово ПЯТЬ)

– Встаньте те, кто в результате теста получил ПЯТЬ.

IX. Давайте построим модель полученных знаний.

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.

Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

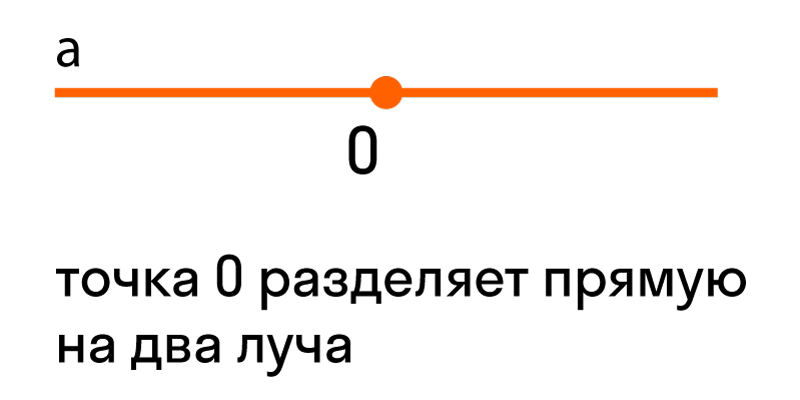
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

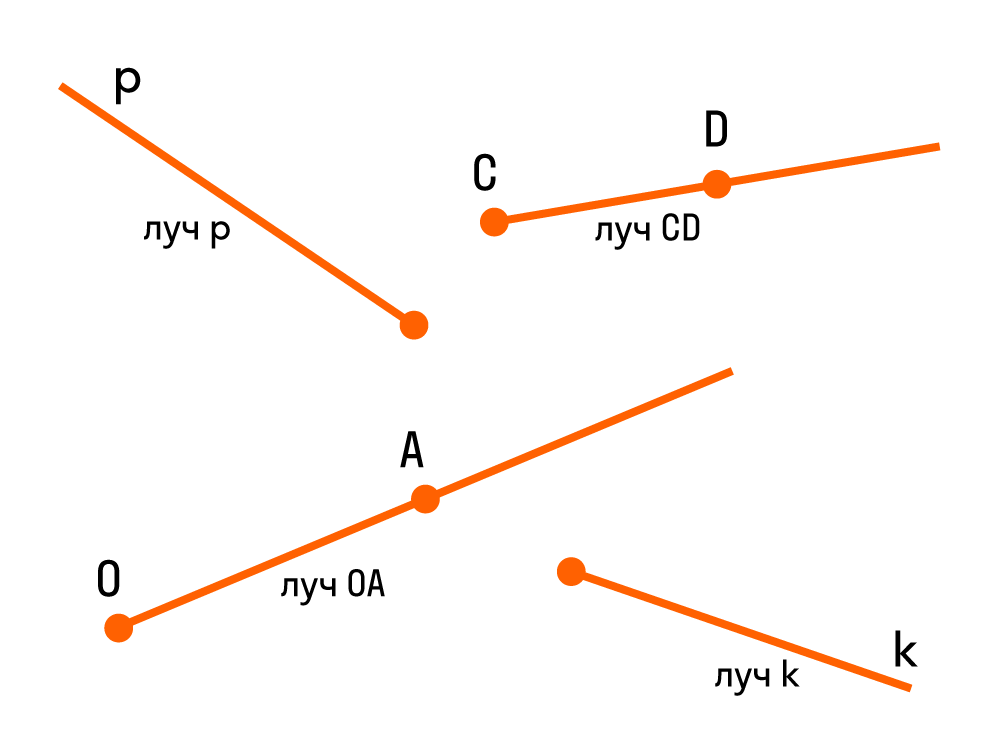
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

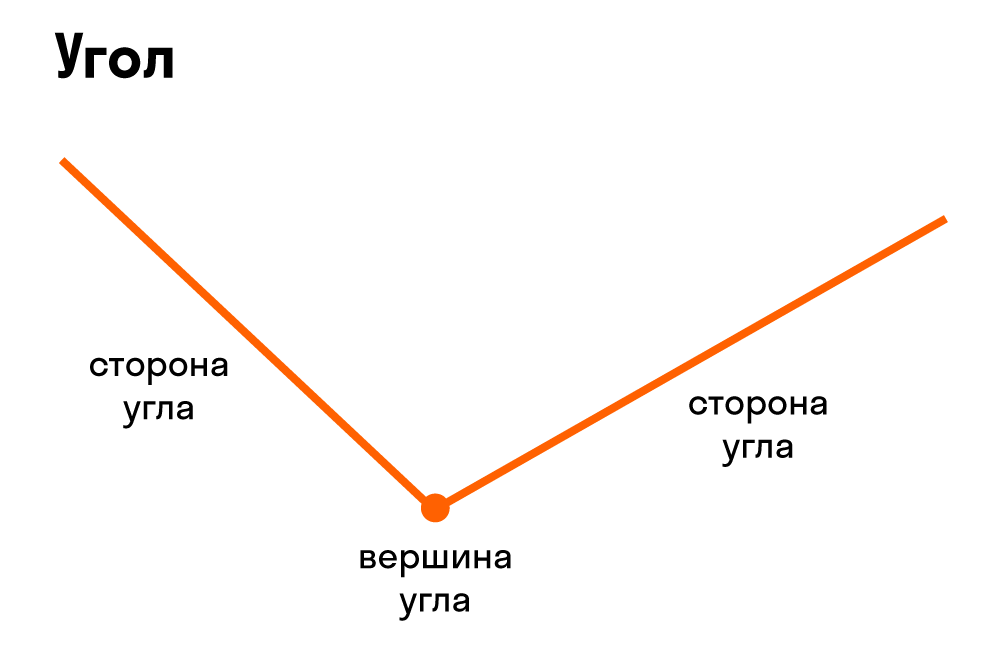
Что такое вершина и стороны угла

В математике существует специальный символ для обозначения угла, вот он: ∠.

Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.

Иногда встречается обозначение в виде цифр — так тоже можно.

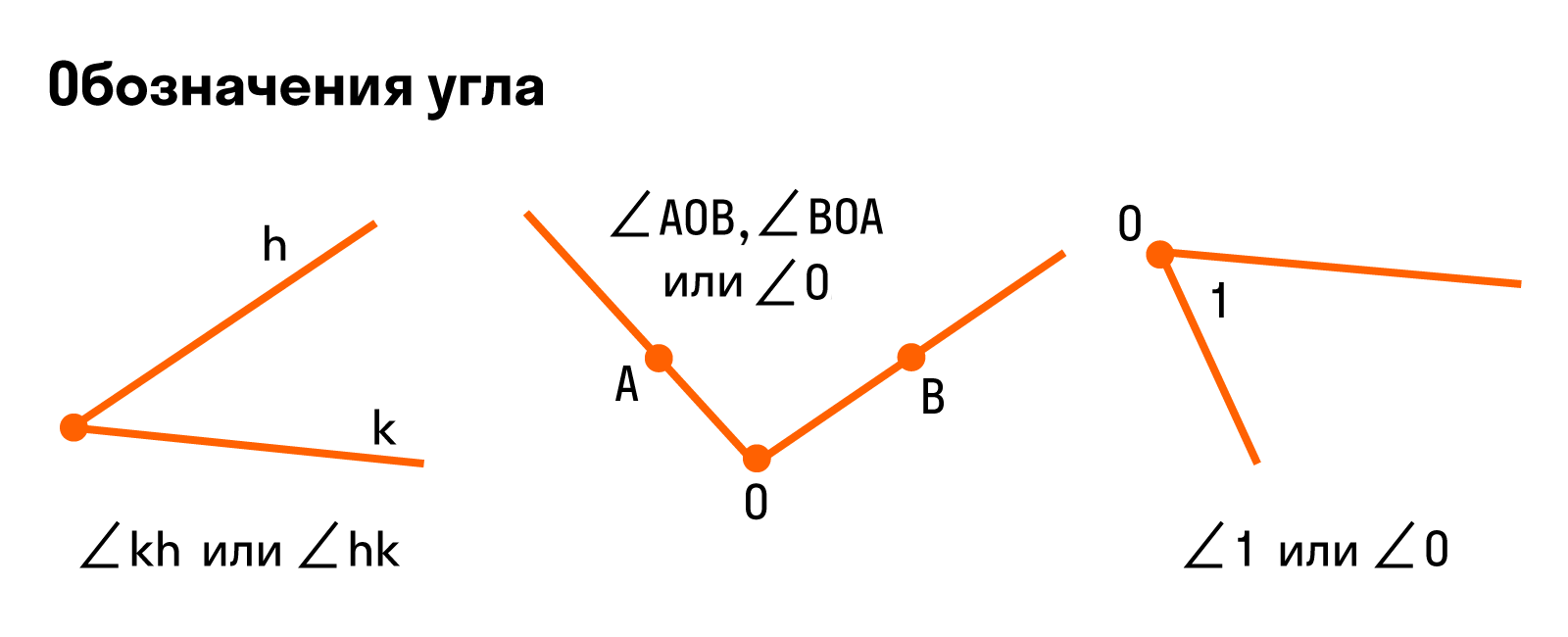
Для наглядности — все способы обозначения углов:

Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:

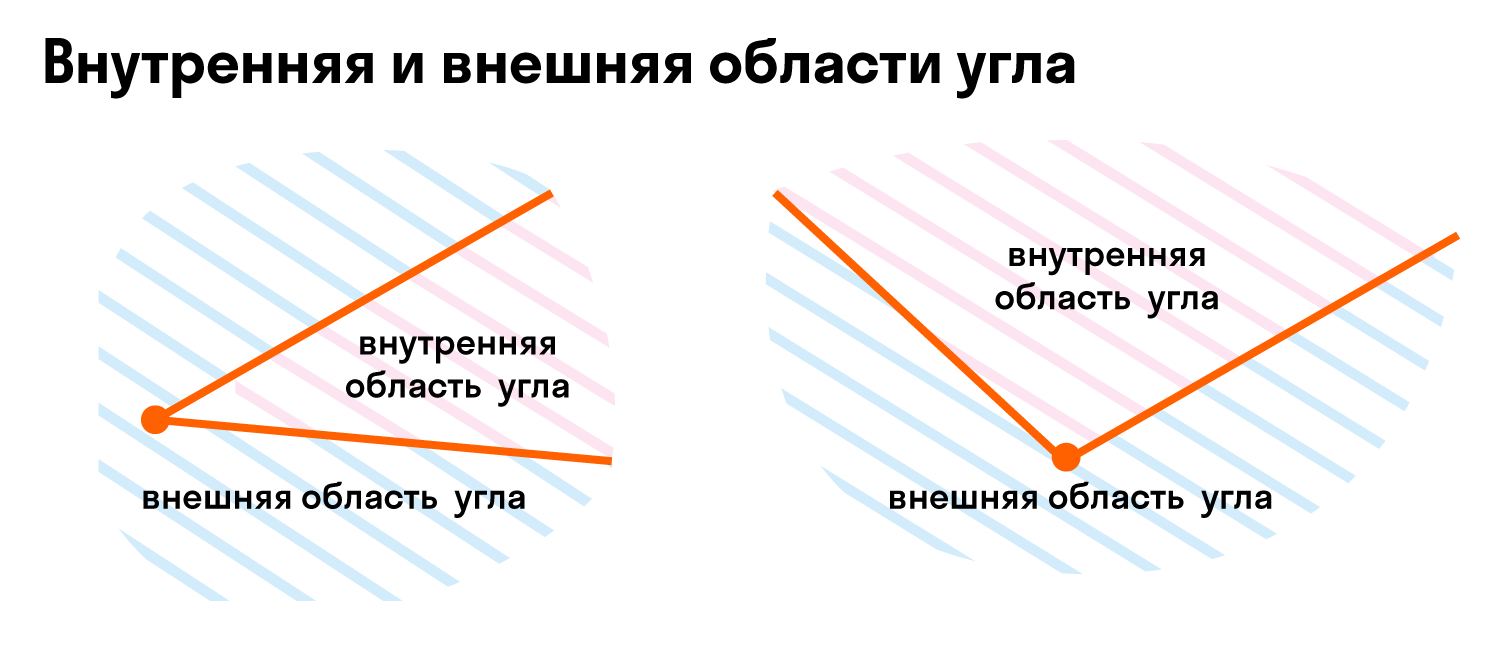
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.

Виды углов

Есть разные типы углов и у каждого своё название:

• острый
• прямой
• тупой
• развернутый
• выпуклый
• полный

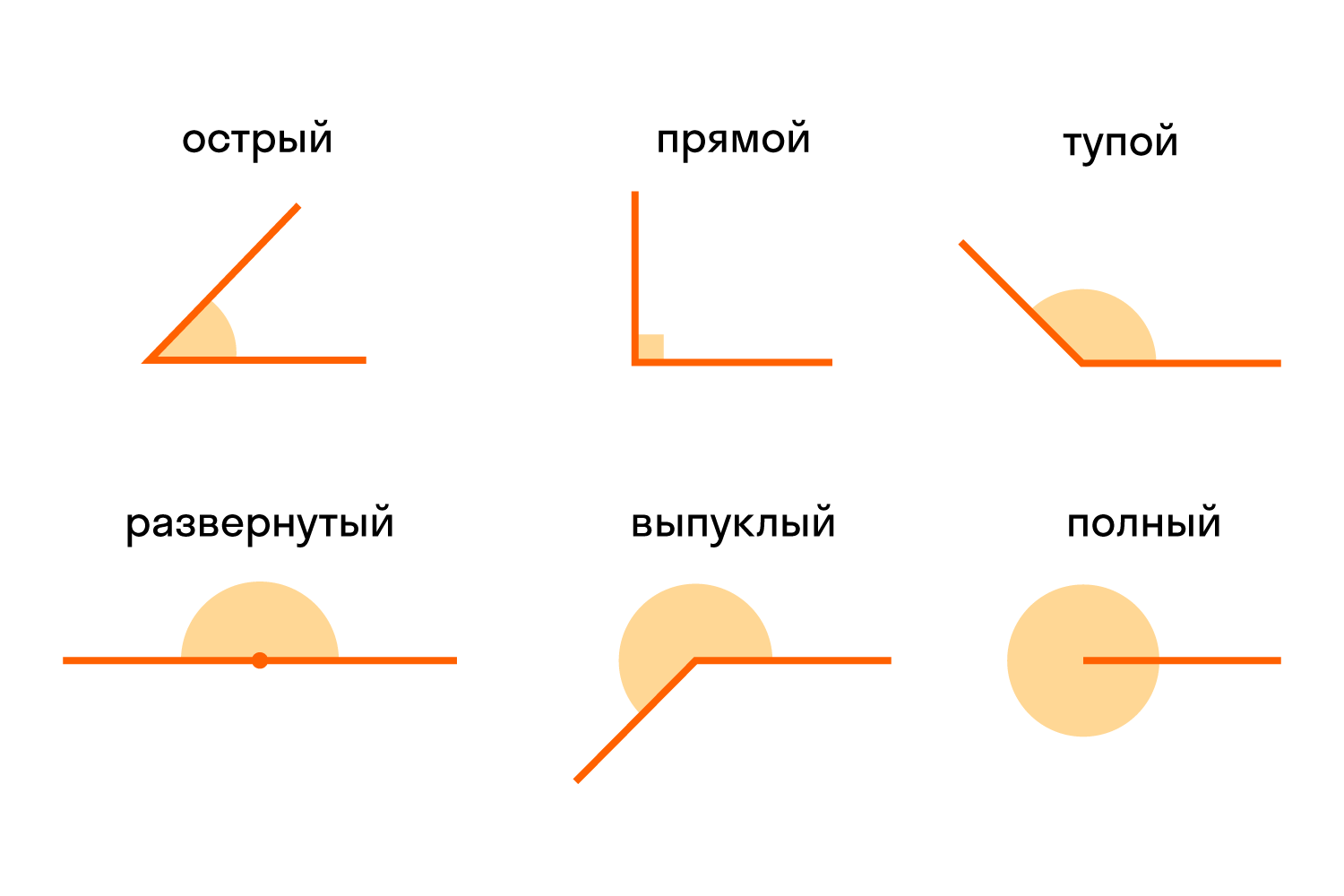
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.

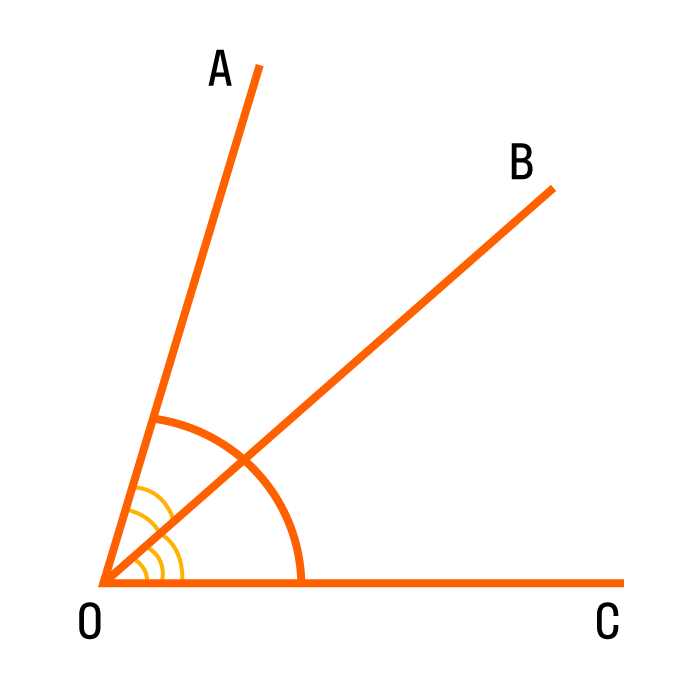
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

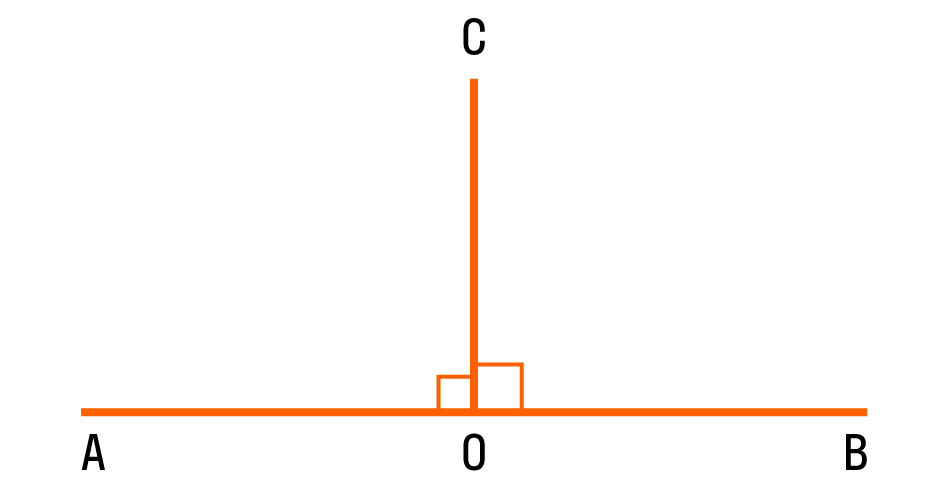
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Острый угол — это угол, который меньше прямого угла, то есть < 90°.

Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.

Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.

Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.

Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.

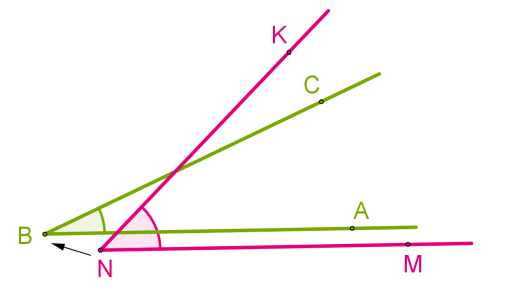
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.

На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.

Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.

Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:

• ∠AOC = ∠AOB − ∠COB,
• ∠COB = ∠AOB − ∠AOC.

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Сравнение углов

Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

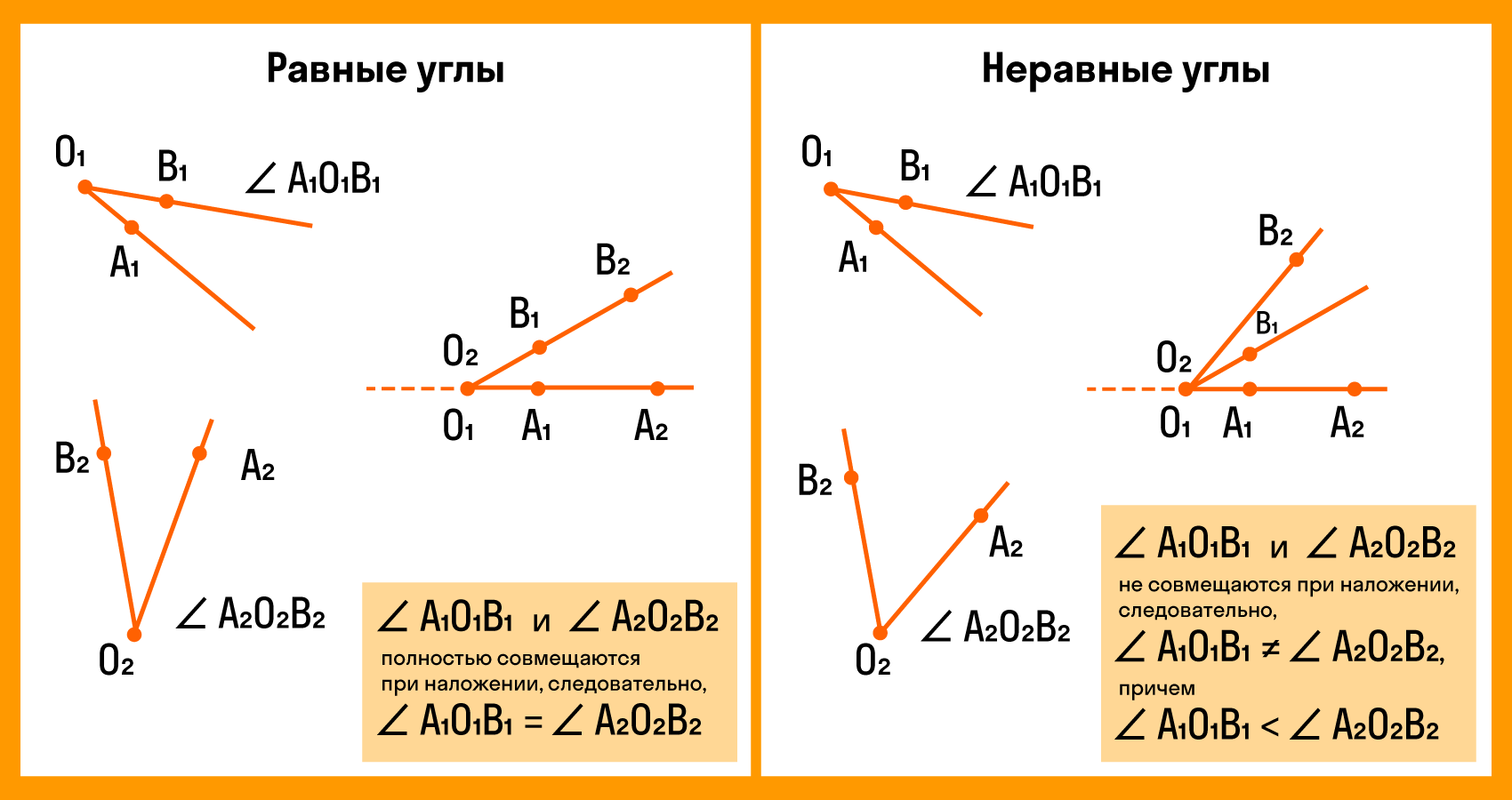
При этом развернутые углы всегда являются равными.

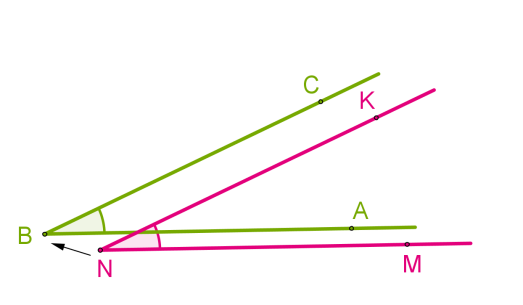
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:

 

1. Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
2. Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.

Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.

Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.

Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот как он выглядит:

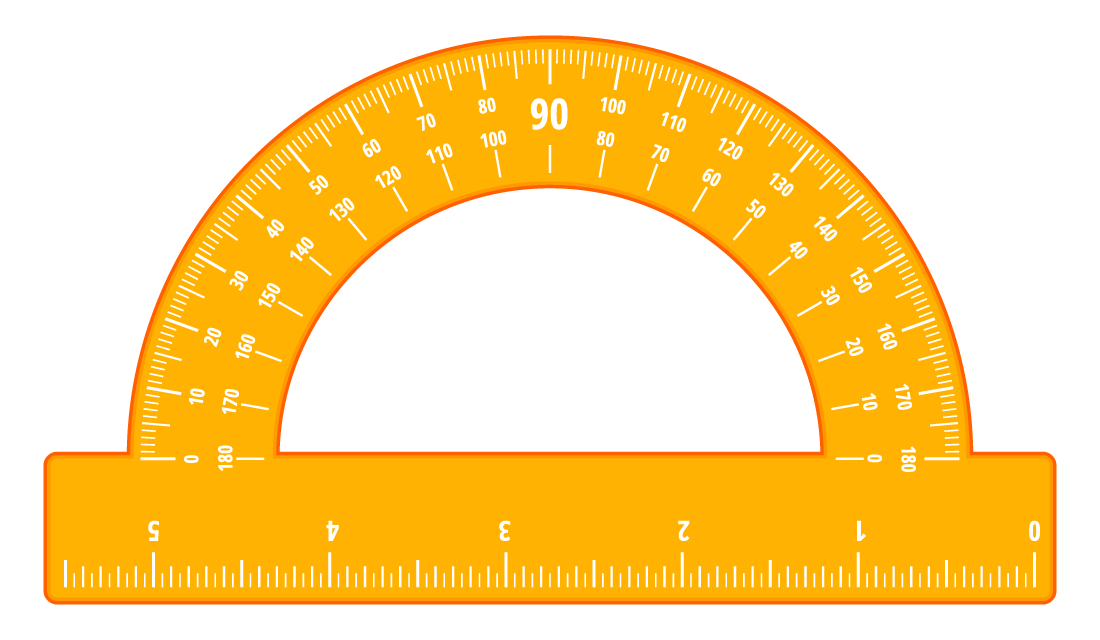
Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается ´.

Секунда — 1/60 часть минуты. Обозначается ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.

Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

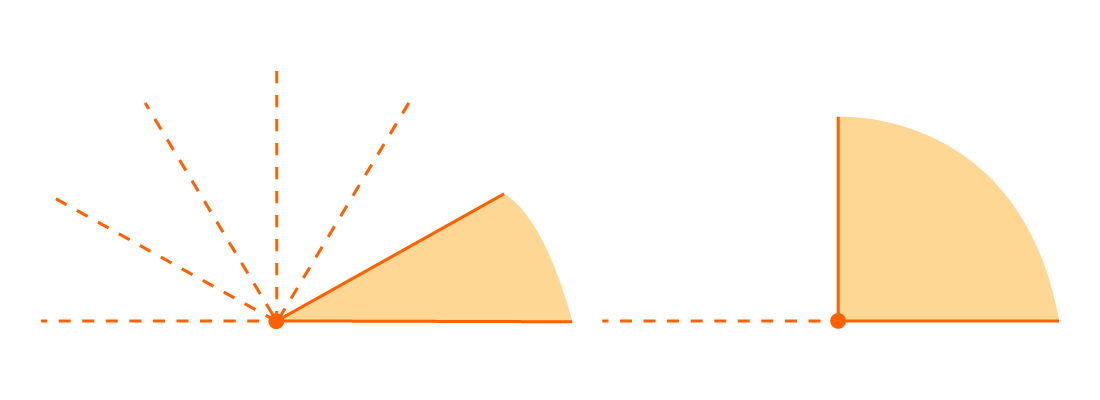
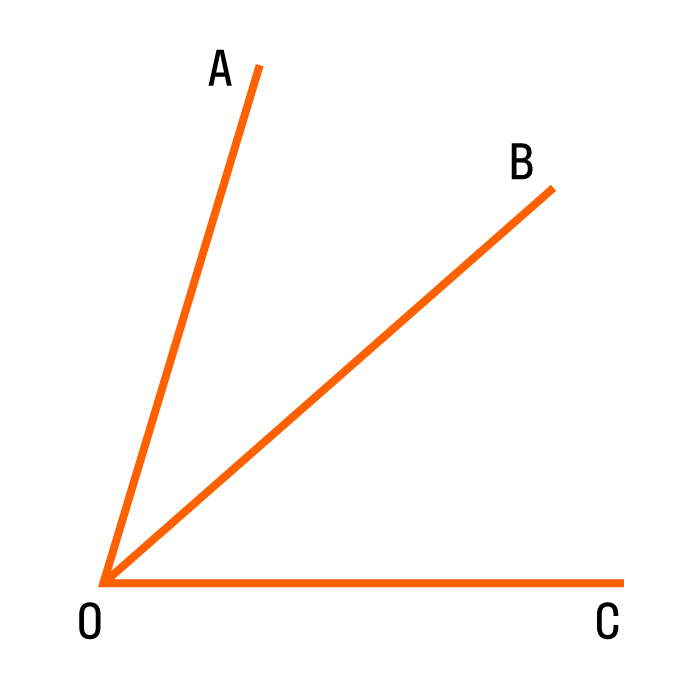
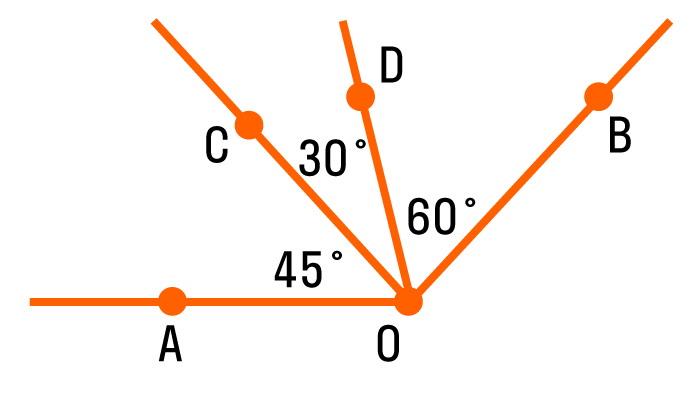
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.

Равные углы имеют равную градусную меру.

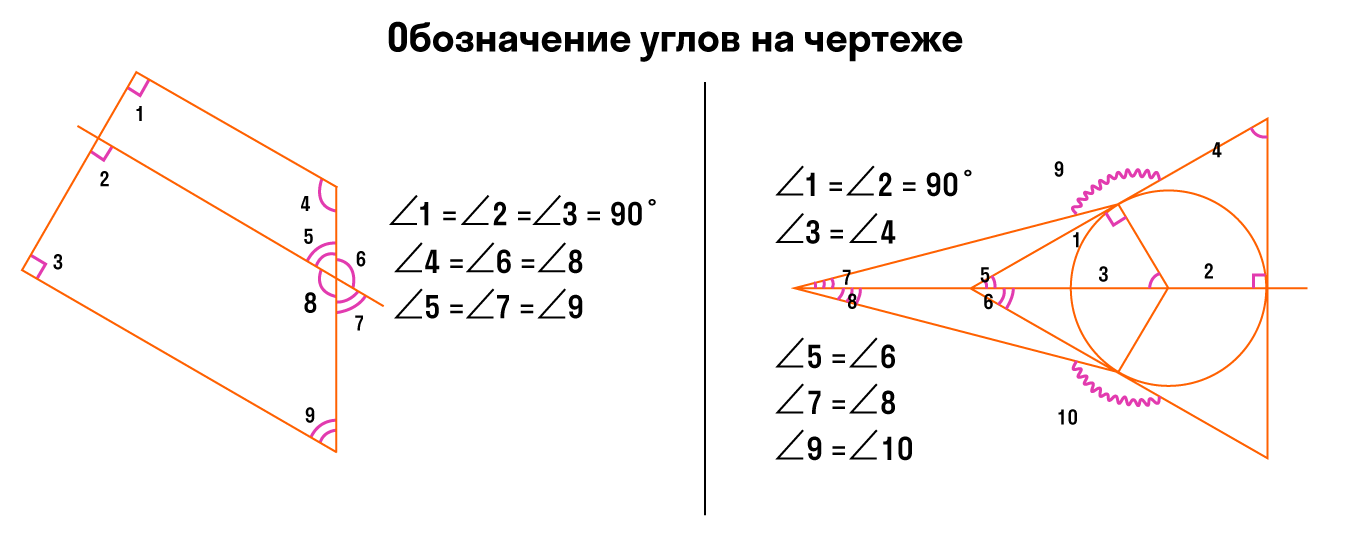
Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:

• Равные углы обозначают одинаковым количеством дуг.
• Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.

На чертеже отмечены три неравных угла:

Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.