Задания
Версия для печати и копирования в MS Word
Задания Д4 № 23205
i
Найдите площадь трапеции, вершины которой имеют координаты (2;2), (10;2), (5;8), (3;8).
Решение.
Это задание ещё не решено, приводим решение прототипа.
Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (8;6), (5;6).
Площадь трапеции равна произведению полусуммы оснований на высоту. Поэтому
Ответ: 30.
Аналоги к заданию № 27571: 22487 24221 22489 … Все
Кодификатор ФИПИ/Решу ЕГЭ:
5.1.3 Трапеция;
5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора;
5.6.1 Координаты на прямой, декартовы координаты на плоскости и в пространстве.
Прототип задания
·
Видеокурс
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Найти координаты вершины
|
|||
|
Даны вершины А(-2;-2) В(5;-1) и точка С(2;3) трапеции АВСD (AD ПАРАЛЕЛЬНО ВС). Известно что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции чертеж((((
|
||
| Вернуться к началу |
|
||
|
Andy |
Заголовок сообщения: Re: Найти координаты вершины
|
|
mad_math писал(а): Если это школьная задача, то её не через уравнения прямых решают. mad_math, если не ошибаюсь, уравнение прямой, проходящей через две точки, в школе проходят. Но, конечно же, можно воспользоваться и сложением векторов. Пусть, однако, автор вопроса отзовётся – тогда разберёмся.
|
|
| Вернуться к началу |
|
|
mad_math |
Заголовок сообщения: Re: Найти координаты вершины
|
|
Andy писал(а): mad_math, если не ошибаюсь, уравнение прямой, проходящей через две точки, в школе проходят. Да, но в курсе алгебры и мат.анализа, а не геометрии. В геометрии проходят координатный метод.
|
|
| Вернуться к началу |
|
|
mad_math |
Заголовок сообщения: Re: Найти координаты вершины
|
|
Andy писал(а): но векторы-то в курсе геометрии проходят Да. Это и есть координатный метод. Andy писал(а): Впрочем, автор вопроса, похоже не интересуется нашим обсуждением. Этточно. Я даже не уверена, что автор вопроса не ошиблась разделом.
|
|
| Вернуться к началу |
|
Главная
-
- 0
-
Даны три вершины А (-2; -3; 1), В (1;4;3), С (3; 1; -2) трапеции ABCD. Найдите координаты вершины D при условии что основание AD в пять раз больше основания BC
Игорь Силуанов
Вопрос задан 23 сентября 2019 в
10 – 11 классы,
Геометрия.
-
Комментариев (0)
Добавить
Отмена
1 Ответ (-а, -ов)
- По голосам
- По дате
-
- 0
-
ВекторВС {3-1; 1-4; -2-3} или векторВС {2; -3; -5}
векторAD {x+2; y+3; z-1} где D(x; y; z)
векторВС сонаправлен (т.е. и коллинеарен) векторуAD,
причем коэффициент коллинеарности указан: 5
x+2 = 5*2 —> x = 8
y+3 = 5*(-3) —> y = -18
z-1 = 5*(-5) —> z = -24
Отмена
Екатерина Кинжебулатова
Отвечено 23 сентября 2019
-
Комментариев (0)
Добавить
Отмена
Ваш ответ
Лучший ответ
|
|
 |
|
|
0 / 0 / 0 Регистрация: 08.10.2018 Сообщений: 4 |
|
|
1 |
|
|
08.10.2018, 02:08. Показов 14565. Ответов 4
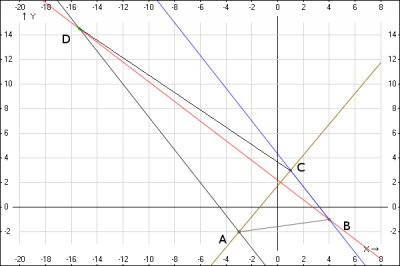
В равнобедренной трапеции ABCD известны координаты вершин A(0,5) B(-2,4) C(4,2) Найти координаты вершины D и площадь трапеции
0 |
|
8692 / 6303 / 3380 Регистрация: 14.01.2014 Сообщений: 14,464 |
|
|
08.10.2018, 09:49 |
2 |
|
Некорректные данные задачи – получается невыпуклый четырехугольник с параллельными сторонами ВС и AD. Возможно, имелось в виду, что параллельными сторонами являются стороны ВС и AD. Сейчас рассмотрю это случай. Миниатюры
0 |
|
8692 / 6303 / 3380 Регистрация: 14.01.2014 Сообщений: 14,464 |
|
|
08.10.2018, 10:37 |
3 |
|
Как ни странно, ничего не изменилось, потому что получается тот же ломанный четырехугольник, вершины которого являются вершинами параллелограмма.
0 |
|
6352 / 4061 / 1509 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
08.10.2018, 12:10 |
4 |
|
Проводим серединный перпендикуляр к отрезку ВС и ищем точку, симметричную точке А относительно этого перпендикуляра.
1 |
|
8692 / 6303 / 3380 Регистрация: 14.01.2014 Сообщений: 14,464 |
|
|
08.10.2018, 13:07 |
5 |
|
Решение Да, там было два решения в первом варианте! Первое было показано выше, а второе просто не заметил.
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
08.10.2018, 13:07 |
|
Помогаю со студенческими работами здесь
Найти площадь грани ABC, в пирамиде ABCD. Где заданы координаты вершины пирамиды
Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 5 |








 Сообщение было отмечено MaximFix как решение
Сообщение было отмечено MaximFix как решение
