Даны
координаты середин сторон треугольника:
E(7,
8); F(-4,
5); K(1,
-4). Определить координаты вершин
треугольника.
Решение.
пусть
точки A,
B
и C
– вершины треугольника, точка E
– середина стороны AB,
точка F
– середина стороны AC,
а K
– середина стороны BC.
Требуется найти координаты точек A,
B
и C.
Обозначим
через xA
и yA
– координаты вершины A,
xB
и yB
– координаты вершины B,
xC
и yC
– координаты вершины C.
По
формулам
![]()
![]()
![]()
![]()
![]()
![]()
![]()
имеем
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (1)
(1)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (2)
(2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (3)
(3)
Подставляя
в эти формулы координаты точек E,
F
и K,
мы для определения неизвестных получим
следующие уравнения:
а)
Уравнения, отмеченные (1), после подстановки
в них координат точки E
запишутся так:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
или
xA
+ xB
= 14; yA
+ yB
= 16.
б)
уравнения, отмеченные (2), если подставить
в них координаты точки F,
запишутся в виде
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
или
xA
+ xС
= -8; yA
+ yС
= 10.
в)
Если же в уравнения, отмеченные (3),
подставить координаты точки K,
то эти уравнения запишутся так:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
или
xB
+ xС
= 2; yB
+ yС
= -8.
Итак,
для определения шести неизвестных мы
получили такие две системы уравнений:
|
первая |
вторая |
|
|
|
Складывая
почленно уравнения первой системы,
будем иметь
xA
+ xB
+ xA
+ xC
+ xB
+ xC
= 8.
После
приведения подобных членов и деления
обеих частей уравнения на 2 получим
xA
+ xB
+ xC
= 4. (4)
Так
как на основании третьего уравнения
первой системы xB
+ xC
= 2, то из (4) получаем xA
+ 2 = 4, а xA
= 2; используя второе уравнение первой
системы xA
+ xC
= -8, получим xB
– 8 = 4; xB
= 12; на основании первого уравнения
первой системы xA
+ xB
= 14, и уравнение (4) примет вид: xC
+ 14 = 4, а xC
= -10. Итак, xA
= 2; xB
= 12; xC
= -10. Поступая так же, найдем из второй
системы уравнений yA
= 17; yB
= -1; yC
= -7. Вершины треугольника имеют такие
координаты: A(2,
17); B(12,
-1); C(-10,
-7)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти вершины треугольника, зная середины его сторон?
Помогите, пожулуйста.
На этой странице сайта, в категории Алгебра размещен ответ на вопрос
Как найти вершины треугольника, зная середины его сторон?. По уровню сложности вопрос рассчитан на учащихся
10 – 11 классов. Чтобы получить дополнительную информацию по
интересующей теме, воспользуйтесь автоматическим поиском в этой же категории,
чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы
расположена кнопка, с помощью которой можно сформулировать новый вопрос,
который наиболее полно отвечает критериям поиска. Удобный интерфейс
позволяет обсудить интересующую тему с посетителями в комментариях.
-
Алгебра
Предыдущий вопрос
Следующий вопрос
Как найти вершины треугольника, зная середины его сторон?
Помогите, пожулуйста
oksixd
7 лет назад
Ответ
Ответ дан
JaverGame
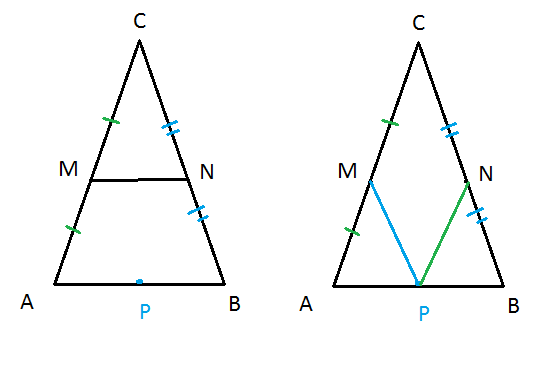
Соедините две середины, получите среднюю линию треугольника. Средняя линия параллельна третьей стороне, от которой у вас есть середина. Так что проводите через эту середину прямую параллельную средней линии и получите сторону. Так же можно получить остальные стороны треугольника, а затем вершины как пересечения сторон.
Ответы и объяснения
- oksixd
Не тот ответ, который тебе нужен?
Найди нужный
Задача 26413 4.1.25) Даны середины сторон…
Условие
![]()
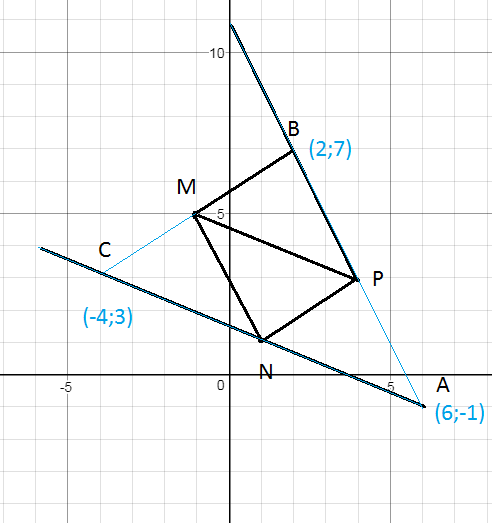
4.1.25) Даны середины сторон треугольника M (-1; 5), N( 1; 1), P(4; 3).
Найти координаты его вершин.
математика 10-11 класс
6206
Решение
![]()
★
Уравнение прямой MN:
(х–x_(M))/(x_(N)–x_(M))=(y–y_(M))/(y_(N)–y_(M))
(х–(-1))/(1–(-1))=(y–5))/(1–5);
-2(x+1)=y-5 ⇒ y=-2x+3
MN- средняя линия треугольника, параллельна стороне.
Пусть это сторона АВ. Тогда уравнение прямой АВ имеет вид
у=-2х+b
Для нахождения b подставляем координаты точки P(3;4)
3=-2*4+b
b=11
y= – 2x +11
Аналогично находим уравнение прямой
MP:
(x+1)/(4+1)=(y-5)/(3-5) ⇒ y=(-2/5)x+(23/5)
Уравнение прямой AС имеет вид у=(-2/5)х+p
Подставляем координаты точки N
1=(-2/5)+p
p=7/5
y=(-2/5)x+(7/5)
Находим точку пересечения прямых АВ и AС
Решаем систему
{y= – 2x +11
{у=(-2/5)x+(7/5)
-2х+11=(-2/5)х+(7/5)
-2х+(2/5)х=(7/5)-11
(-8/5)х=-48/5
х=6
y=-2*6+11=1
А(6;-1)
и прямой
NP:
(x-1)/(4-1)=(y-1)/(3-1) ⇒ y=(2/3)x+(2/3)
Уравнение прямой ВС имеет вид у=(2/3)х+q
Подставляем координаты точки M
5=(2/3)*(-1)+q
q=17/3
y=(2/3)x+(17/3)
Находим точку пересечения прямых АВ и ВС
Решаем систему
{y= – 2x +11
{у=(2/3)x+(17/3)
-2х+11=(2/3)х+(17/3)
-2х-(2/3)х=(17/3)-11
(-8/3)х=-16/3
х=2
y=-2*2+11=7
B(2;7)
Находим координаты точки С
{у=(-2/5)x+(7/5)
{у=(2/3)x+(17/3)
(-2/5)x+(7/5)=(2/3)x+(17/3)
(-2/5)x-(2/3)x=(17/3)-(7/5)
-16x/15=64/15
x=-4
y=(-2/5)*(-4)+(7/5)=15/5=3
C(-4;3)
Написать комментарий
![]()
TITANIA1 год назад
0
0
<span>Соедините две середины, получите среднюю линию треугольника. Средняя линия параллельна третьей стороне, от которой у вас есть середина. Так что проводите через эту середину прямую параллельную средней линии и получите сторону. Так же можно получить остальные стороны треугольника, а затем вершины как пересечения сторон.</span>
