Как найти вершины треугольника по уравнениям прямых

Как найти координату вершины треугольника

Стороны треугольника заданы уравнениями:

Найти координаты вершин треугольника.

Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:

Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем

Вершина A имеет координаты

Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:

получаем .

Координаты вершины C получим, решая систему из уравнений сторон BC и AC:

Вершина C имеет координаты .

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Вершина треугольника – определение

В геометрии нередко рассматривают такое понятие, как «вершина треугольника». Это точка пересечения двух сторон данной фигуры. Практически в каждой задаче встречается это понятие, поэтому имеет смысл рассмотреть его более подробно.

Определение вершины треугольника

В треугольнике есть три точки пересечения сторон, образующие три угла. Их называют вершинами, а стороны, на которые они опираются – сторонами треугольника.

Рис. 1. Вершина в треугольнике.

Вершины в треугольниках обозначают большими латинскими буквами. Поэтому чаще всего в математике стороны обозначают двумя заглавными латинскими буквами, по названию вершин, которые входят в стороны. Например стороной АВ называют сторону треугольника, соединяющую вершины А и В.

Рис. 2. Обозначение вершин в треугольнике.

Характеристики понятия

Если взять произвольно ориентированный в плоскости треугольник, то на практике очень удобно выразить его геометрические характеристики через координаты вершин этой фигуры. Так, вершину А треугольника можно выразить точкой с определенными числовыми параметрами А(х; y).

Зная координаты вершин треугольника можно найти точки пересечения медиан, длину высоты, опущенную на одну из сторон фигуры, и площадь треугольника.

Для этого используются свойства векторов, изображаемых в системе декартовой системе координат, ведь длина стороны треугольника определятся через длину вектора с точками, в которых находятся соответствующие вершины этой фигуры.

Использование вершины треугольника

При любой вершине треугольника можно найти угол, который будет смежным внутреннему углу рассматриваемой фигуры. Для этого придется продлить одну из сторон треугольника. Поскольку сторон при каждой вершин две, то и внешних углов при каждой вершине два. Внешний угол равен сумме двух внутренних углов треугольника, несмежных с ним.

Рис. 3. Свойство внешнего угла треугольника.

Если построить при одной вершине два внешних угла, то они будут равны, как вертикальные.

Что мы узнали?

Одним из важных понятий геометрии при рассмотрении различных типов треугольников является вершина. Это точка, где пересекаются две стороны угла данной геометрической фигуры. Ее обозначают одной из больших букв латинского алфавита. Вершину треугольника можно выразить через координаты x и y, это помогает определять длину стороны треугольника как длину вектора.

[spoiler title=”источники:”]

http://www.matburo.ru/ex_ag.php?p1=agtr

http://sprint-olympic.ru/uroki/matematika-uroki/15500-vershina-treygolnika-opredelenie.html

[/spoiler]

Найти координаты вершин треугольника,
если стороны заданы уравнениями:

x – 2y + 3 = 0;
2x – y – 3 = 0;
x + y – 3 = 0;

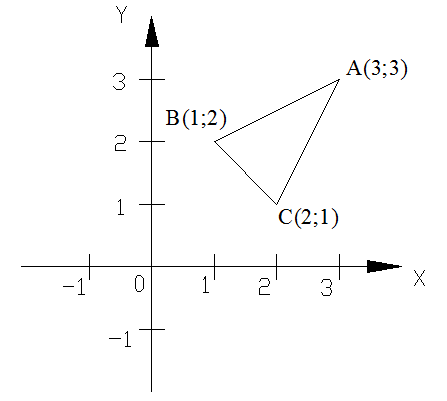
Дано: АВ: х-2у+3=0, АС: 2х-у-3=0, ВС: х+у-3=0

Найти: А,В и С.

Решение.

Найдем вершины треугольника АВС, как
точки пересечения сторон треугольника.

т.А:

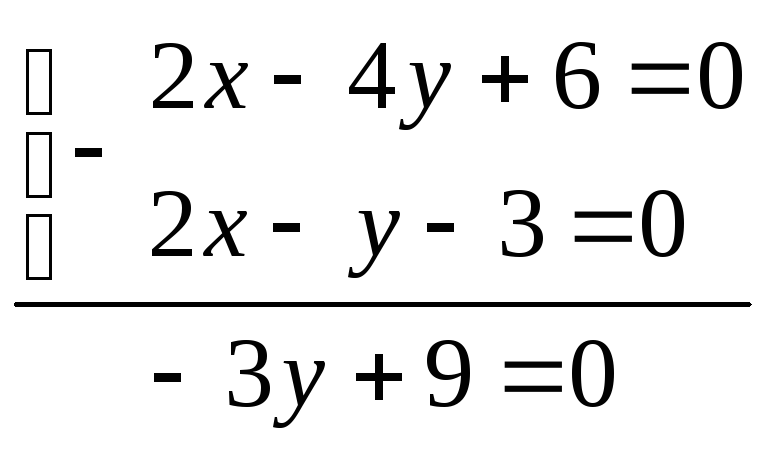
3у=-9 у=3,
x-2*3+3=0, у=3, х=3

имеем: A(3;3)

т. В:

.

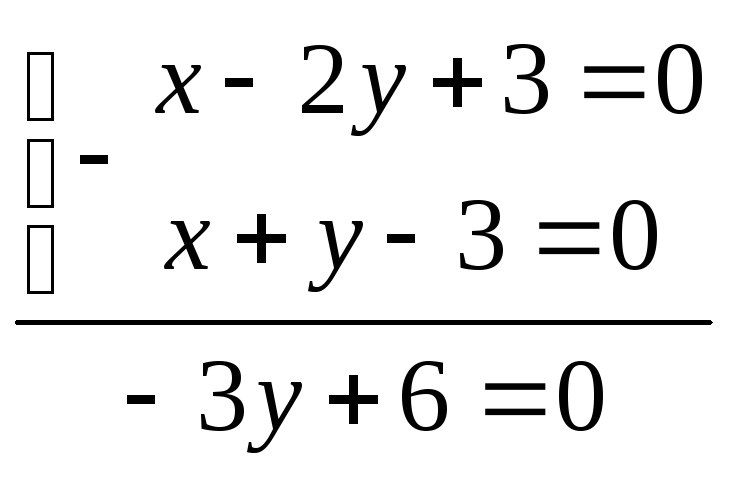х-2*2+3=0,
у=2, х=1

имеем: т. B(1;2)

т.С :

.

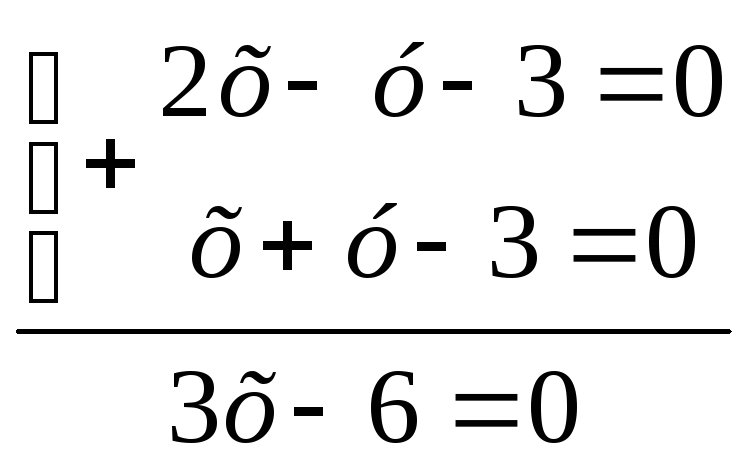3х=6 х=2, 2+y-3=0,
х=3, y=1

имеем: т. C(2;1)

Ответ: координаты вершин треугольника:
А (3;3); В(1;2); С(2;1).

Задача №2

Даны вершины треугольника:;2);

;3);

;1).

Написать уравнение высоты, опущенной
из точки

Решение

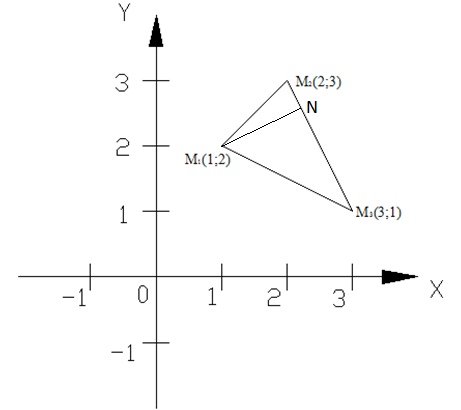
Дано:
(1;2);
(2;3);

(3;1)
– вершины треугольника

Решение: проведем из точки
высоту
к стороне

запишем уравнение стороны

_{откуда имеем}

-2х+4-у+2=0,

у+2х-6=0, у = -2х+6, т.е. угловой коэффициент
прямой k= -2. Тогда, угловой
коэффициент перпендикулярной прямой
(высоты
)
будет
.
Найдем уравнение высоты, как уравнение
прямой, проходящей через одну точку:
y-y₁
=k(x-x₁),
Где x₁ и y₁
– координаты точки .

y-2=
(x-1), откуда имеем 2y-x-3=0

.

откуда, преобразовав, получим

_2у-х-3=0

Ответ: уравнение высоты 2у-х-3=0

Задача №3.

Даны
вершины треугольника M₁M₂M₃:
М₁(-3;0), M₂(2;5),
M₃(3;2).

а)
Найти периметр треугольника, вершинами
которого служат середины сторон.

б)
Найти периметр треугольника, вершинами
которого служат основания высот,
проведенных из вершин M₁
M₂ M₃
к противоположным сторонам.

в)
Найти периметр треугольника, вершинами
которого служат основания биссектрис,
проведенных из вершин M₁
M₂ M₃
к противоположным сторонам.

Решение.

а)
Построение:

К, Е,
F – середины соответствующих
сторон М₁М₃, М₁М₂,
М₂М₃.

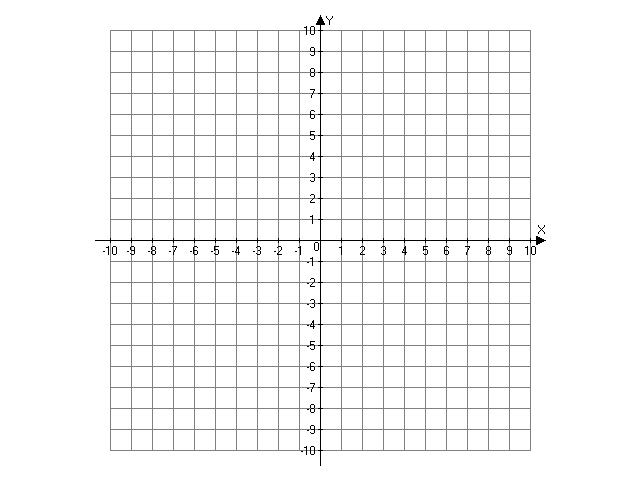
F

E

K

M₁

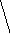
M₂

M₃

К –
середина М₁М₃, тогда координаты
середины стороны будут:

Тогда К(0;1).

Е –
середина М₁М₂, тогда координаты
середины стороны будут:

тогда Е(-0,5; 2,5).

F
– середина М₂М₃, тогда
координаты середины стороны будут:

.

тогда
F(2,5; 3,5).

KF=

Аналогично: EF=;
EK=.

Тогда периметр
треугольника будет:

б)

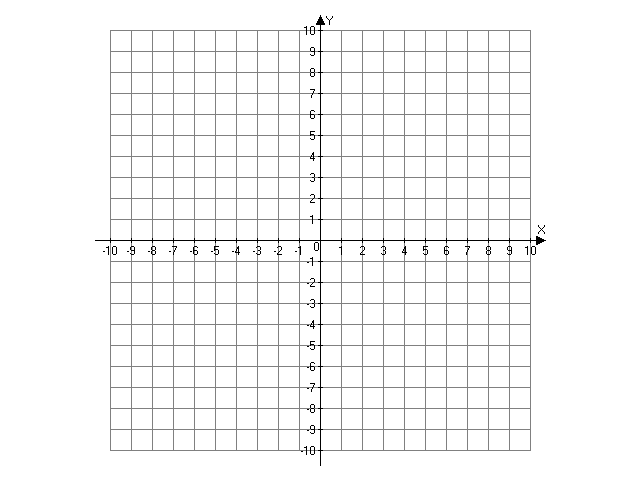
M₁

M₂

M₃=N=M

K

Где
М₁ ?

Покажем,
что треугольник прямоугольный и его
три высоты не могут составить замкнутую
фигуру.

Найдем
уравнение стороны М₁М₂:

откуда имеем

5x+15=5y;
y=x+3. Хорошо
видно, что угловой коэффициент этой
прямой k₁=1, а

т. к. высота М₃К перпендикулярна
стороне М₁М₂, то k₂

Используя уравнение прямой через точку:
у-y₁=k(x-x₁)
имеем

M₃K:

y-2=-1(x-3),
y-2=-x+3
откуда получаем y+x-5=0.

Уравнение
пучка прямых:

.

2y=8,

y=4,
то x=1, тогда М₃КМ₁М₂=К(1;4).

Найдем
уравнение стороны М₂М₃:

.

-3x+6=y-5,
y=-3x+11, откуда
видно что угловой коэффициент этой
прямой k₁=-3,

т. к. М₁N
перпендикуляреныМ₂М₃, k₂

тогда уравнение стороны М₂М₃
будет

,
3y-x-3=0

Уравнение
пучка прямых:

.

у=11-3x,
33-9x-x-3=0.
x=3 y=2, то
x=3,

тогда
М₁NМ₂М₃=N(3;2).

Найдем
уравнение стороны М₁М₃:

.

2x+6=6y,
3x-x-3=0,

y=x+1,
k₁=,
то k₂
т. к. М₂M перпендикулярна
М₁М₃, k₂=.
Найдем уравнение
стороны М₁N:

y-5=-3(x-2),
y-5=-3x+6,
y+3x-11=0.

Уравнение
пучка прямых:

.

y=2,
то x=3,

тогда М₂MМ₁М₃=N(3;2).

Имеем:

KN=;
КM=;
NM=0; т.е. мы доказали, что

ΔКNM не существует

_в)Построение:
М₁А, М₂В и М₃С –
биссектрисы углов при вершинах М₁М₂
М₃

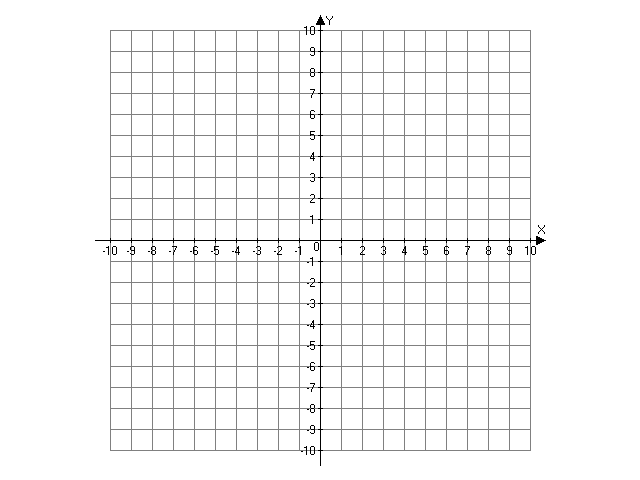
A

C

B

M₃

M₂

M₁

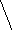
Найти
периметр треугольника АВС

1)

.

(у-х-3)=3у-х-3;

у-х-3=3у-х-3;

у(-3)+х(-+1)+(3-3)=0
– уравнение биссектрисы

2)

.

(у-х-3)=у+3х+11;

у-х-3=у+3х+11;

у(-1)+х(--3)+(-3+11)=0
– уравнение биссектрисы

3)

.

3у-х-3=у+3х-11;

2у-4х+8=0 – уравнение
биссектрисы

Найдем основания биссектрис, как точки
пересечения сторон треугольника и с
ответствующей биссектрисы :

1)
=-4_;

=-20+20;

₌

.

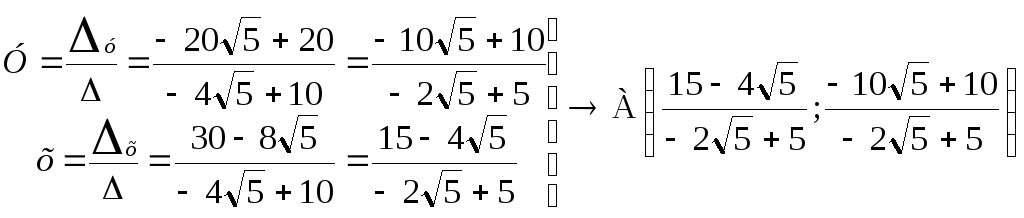2)

_;

;

.

.

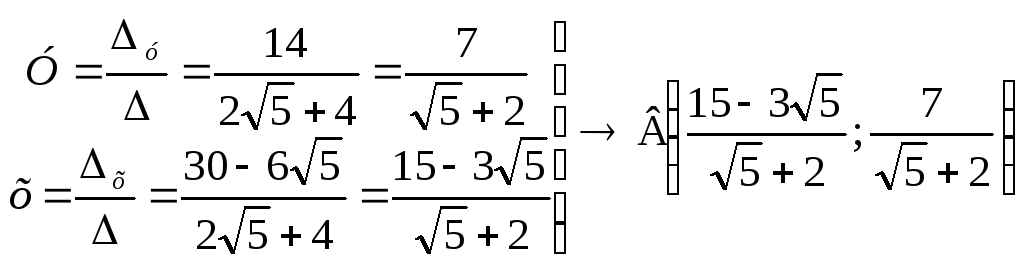3)

.

у =10,
х=7 Следовательно С(7,0)

Найдем

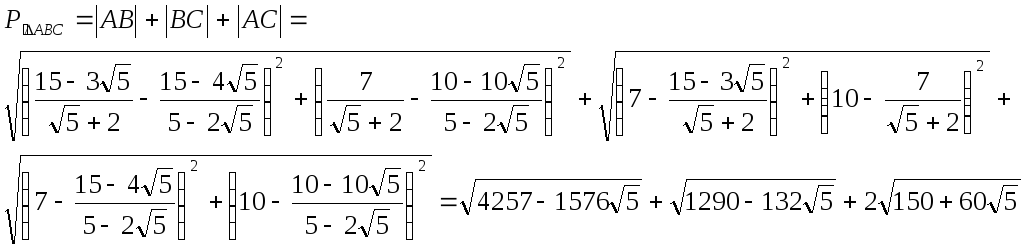
Задача №4

Даны вершины равнобедренного треугольника

а)Доказать, что середины сторон
равнобедренного треугольника являются
также вершинами равнобедренного
треугольника.

б) Доказать, что биссектриса, проведенная
из вершины при основании равны.

в) Медианы, проведенные из вершин при
основании равны.

а)Дано: ΔАВС

Доказать, что середины сторон
равнобедренного треугольника являются
также вершинами равнобедренного
треугольника.

Доказательство.

Найдем середины сторон треугольника

1) Найдём середину отрезка A

А(2;
2)

2) Найдём середину отрезка B

В(4;0)

3) Найдём середину отрезка C(

С(2;0)

4)
АС=CB

треугольник
АВС – равнобедренный, что и
требовалось доказать

б)Дано:

Доказать, что биссектриса, проведенная
из вершины при основании равны.

Доказательство.

1)

Найдём каноническое уравнение 2-ух точек
M₃, M₁

4-x=y+2,

x+y-2=0

x-4=0

Найдём каноническое уравнение 2-ух точек

y+x-3=

у+(1-

_у=2,

y-2=0

.

Составим систему уравнения из

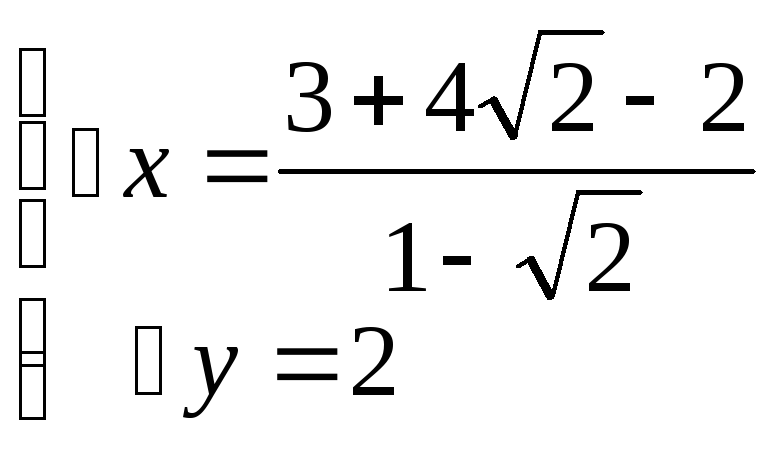
K

Найдем длину.

2) Найдём каноническое уравнение 2-ух
точек

у

Составим систему уравнения из

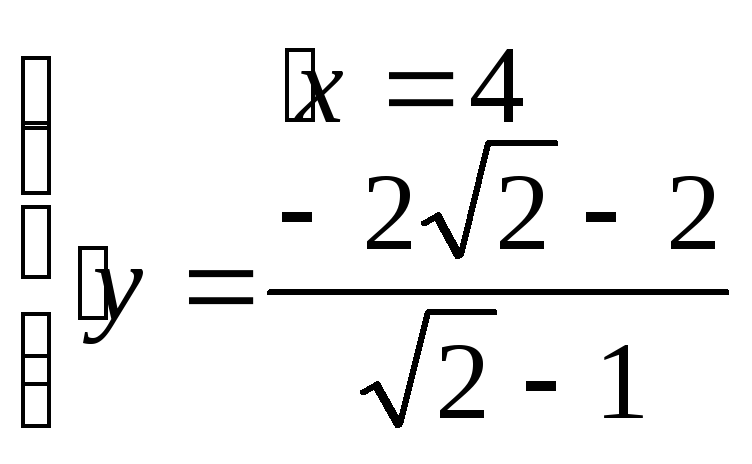
Найдем длину

что и требовалось доказать

в)Дано: ΔАВС и
оказать,
что медианы, проведенные из вершин при
основании равны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Как найти вершину треугольника?

Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.

1 способ (графический)

1. В системе координат отмечаем две заданные вершины.
2. Ставим ножку циркуля в одну из построенных точек.
3. Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
4. Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
5. Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
6. Определяем координаты полученных точек, исходя из полученного чертежа.

Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.

2 способ (аналитический)

Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)

1. Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
2. Составляем соотношения
   AC=√((x-x1)^2+(y-y1)^2)
   BC=√((x-x2)^2+(y-y2)^2)
   AB=√((x2-x1)^2+(y2-y1)^2)
3. Учитывая, что треугольник равносторонний, составляем систему уравнений:
   AC=BC
   AC=AB
   Или система уравнений:
   √((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
   √((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2)
4. Методом подстановки решаем полученную систему.

Теперь вы знаете, как найти вершину треугольника.

Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).

Уравнение описанной окружности

Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?

Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.

Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).

Подставив координаты вершин треугольника в уравнение окружности

получим систему уравнений

Вычтем из первого уравнения системы второе:

Теперь из второго уравнения системы вычтем третье:

Приравняем правые части равенств b=-2a+10 и b=3a-20:

Подставим в первое уравнение системы a=6 и b=-2:

a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности

Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.

Прямая на плоскости

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=x_j-x_i; Y=y_j-y_i
здесь X , Y координаты вектора; x_i , y_i — координаты точки А_i ; x_j , y_j — координаты точки А_j
Например, для вектора AB: X=x₂-x₁=12-7=5 ; Y=y₂-y₁=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой: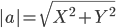




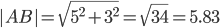
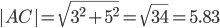
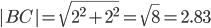
3) Угол между прямыми. Угол между векторами a₁(X₁;Y₁) , a₂(X₂;Y₂) можно найти по формуле: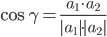

где a₁a₂=X₁X₂+Y₁Y₂
Найдем угол между сторонами AB и AC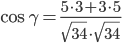

γ = arccos(0.88) = 28.07 0
8) Уравнение прямой. Прямая, проходящая через точки A₁(x₁; y₁) и A₂(x₂; y₂) , представляется уравнениями: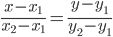

Уравнение прямой AB . Каноническое уравнение прямо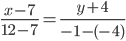й:
или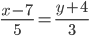
y= 3 /₅x- 41 /₅ или 5y-3x+41=0